Динамика системы управления гидротурбиной с пидрегулятором

Вид материала

Содержание

Укрупненная математическая модель гидротурбины
Рисунок 3 - Переходный процесс при ступенчатой нагрузке
Список литературы

Подобный материал:

УДК 621.224

Динамика системы управления гидротурбиной с пидрегулятором

З.Я. Лурье, д-р.техн.наук, проф.; В.Н. Дмитерко, асп.

НТУ «ХПИ»

Введение

Современные системы управления частотой вращения ротора гидротурбины (СУЧВР) представляют собою сложные динамические системы, включающие механические, гидравлические, электрические и электронные элементы, в том числе и ЭВМ 1,2.

Введение ЭВМ в СУЧВР гидротурбины, с одной стороны, повышает значимость разработки укрупненных и более полных математических моделей, а с другой – открывает возможность с помощью программных средств реализовать различные законы управления, повышающие показатели качества переходных процессов. CУЧВР в процессе эксплуатации подвержена различным возмущающим воздействиям: управляющим (изменение открытия направляющего аппарата (НА)), нагрузочным (поддержание частоты при изменении нагрузки на электрогенератор), случайным помехам (влияние пульсации давлений в проточном тракте). Существенное значение имеет характеристика нагрузочного воздействия, особенно при быстрых изменениях нагрузки, включая сброс, пуск и останов гидротурбины, когда линейная модель системы не отражает соответствующих переходных процессов.

Таким образом, одна и та же СУЧВР гидротурбины должна обладать высоким качеством регулирования с учетом широкого диапазона различных условий ее работы.

Современные электрогидравлические регуляторы предусматривают выполнение следующих основных функций: пуск и синхронизацию на холостом ходу, работу под нагрузкой при слабых возмущениях и переходных процессов при больших возмущениях.

Настоящая статья посвящена исследованию переходных процессов СУЧВР с использованием укрупненной математической модели гидротурбины, включающей в себя ПИД – регулятор для формирования закона управления.

Укрупненная математическая модель гидротурбины

На рис.1 изображена функциональная схема системы регулирования гидротурбины (укрупненная). В качестве управляющего воздействия на гидротурбину рассматривается открытие

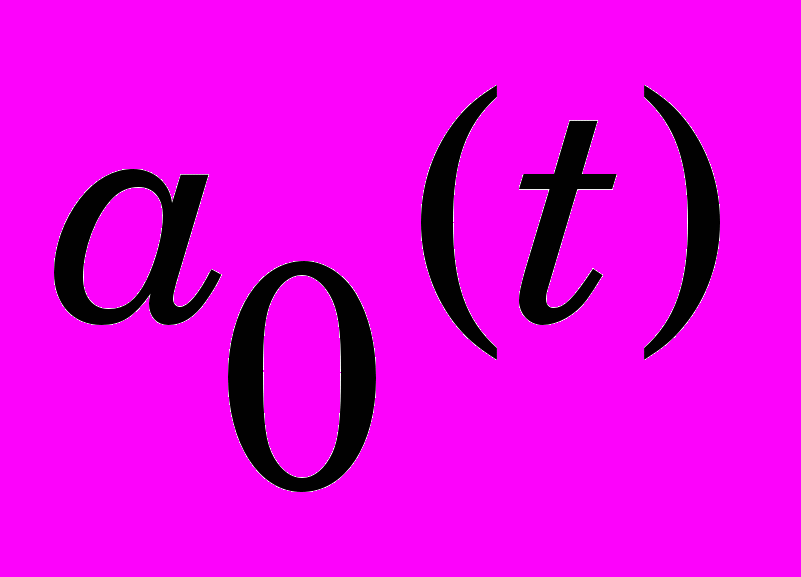лопаток НА, управляемым процессом служит угловая скорость вращения ротора

, главной обратной отрицательной связью является фактическая угловая скорость вращения вала в виде сигнала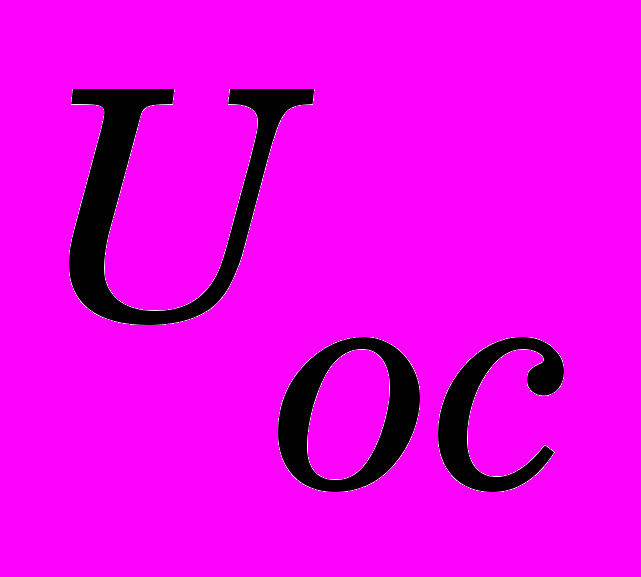

с входа измерительного преобразователя ИП. Наличие ЭВМ позволяет формировать законы управления на основе сигнала рассогласования между заданной и фактической скоростью . Гидромеханическая часть системы включает электрогидравлический преобразователь, главный гидрораспределитель, сервомоторы (изображены одним блоком на схеме) и маслонапорную установку (другим блоком). Схема рис.1 используется для математического описания системы.

Движение ротора гидрот урбины представляется уравнением

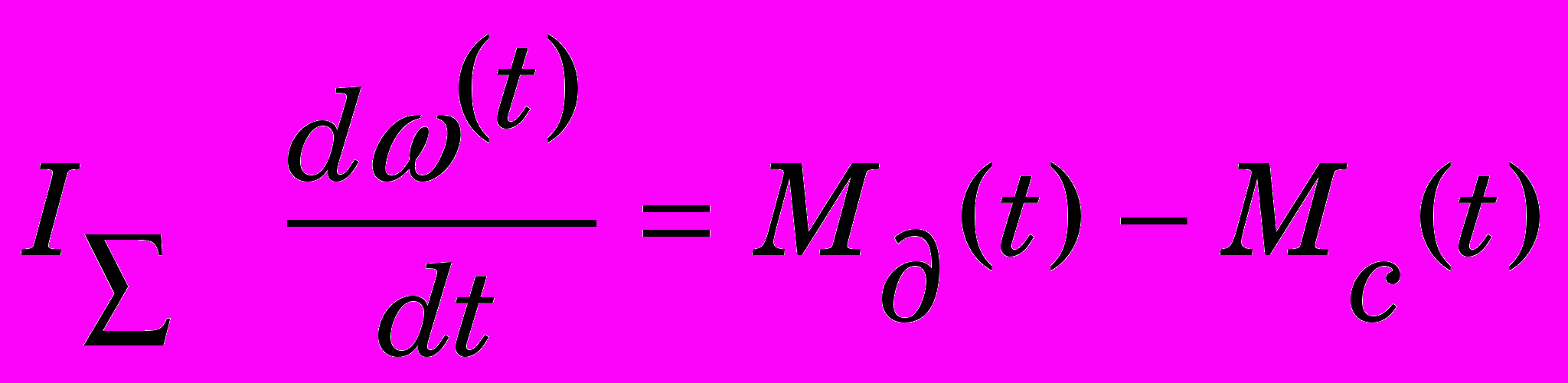, (1)

где

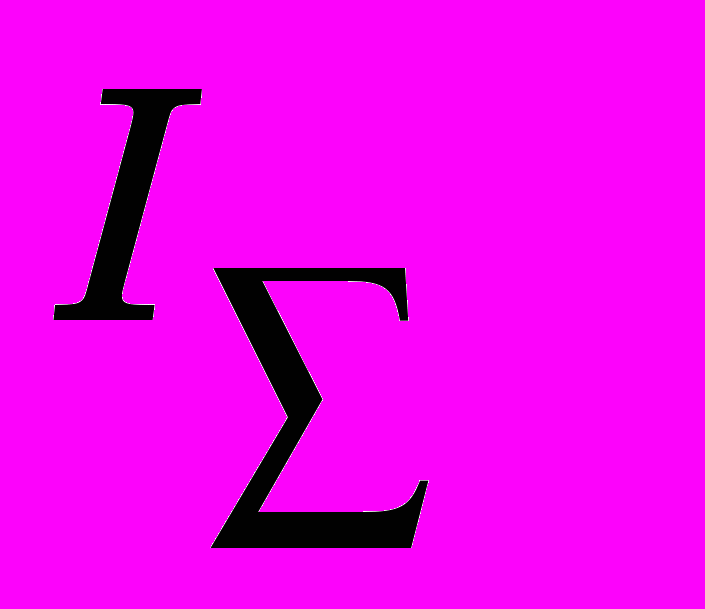- приведенный к валу турбины суммарный момент инерции вращающихся масс;

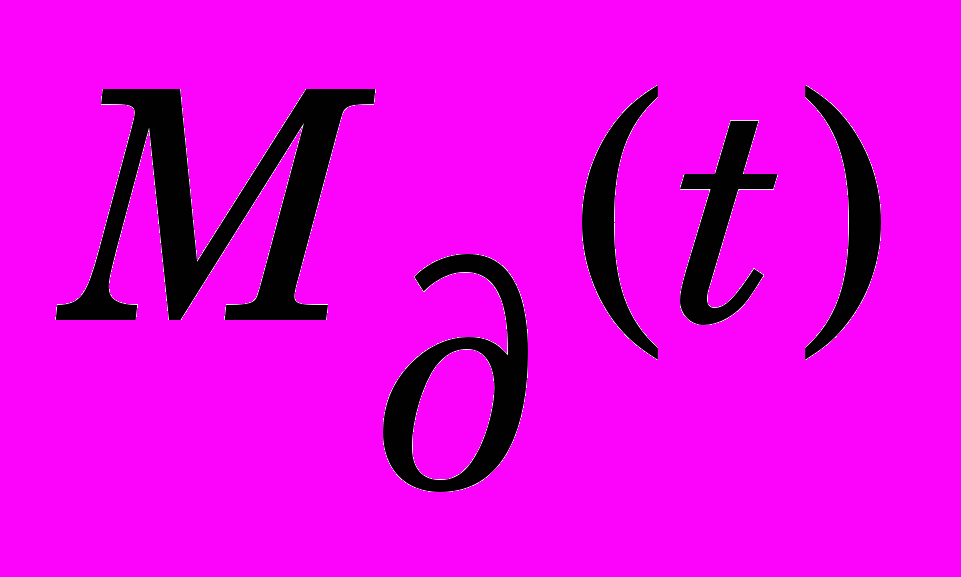- движущийся момент;

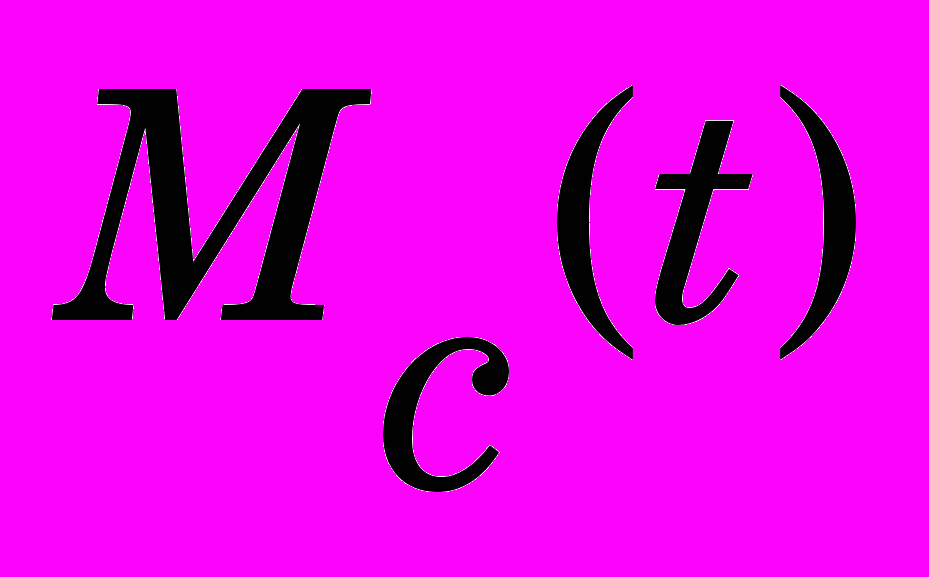- момент сопротивления движению вала.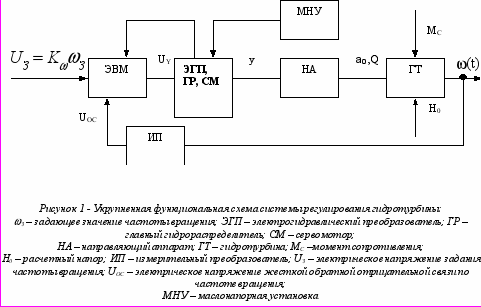

Движущий момент определяется выражением

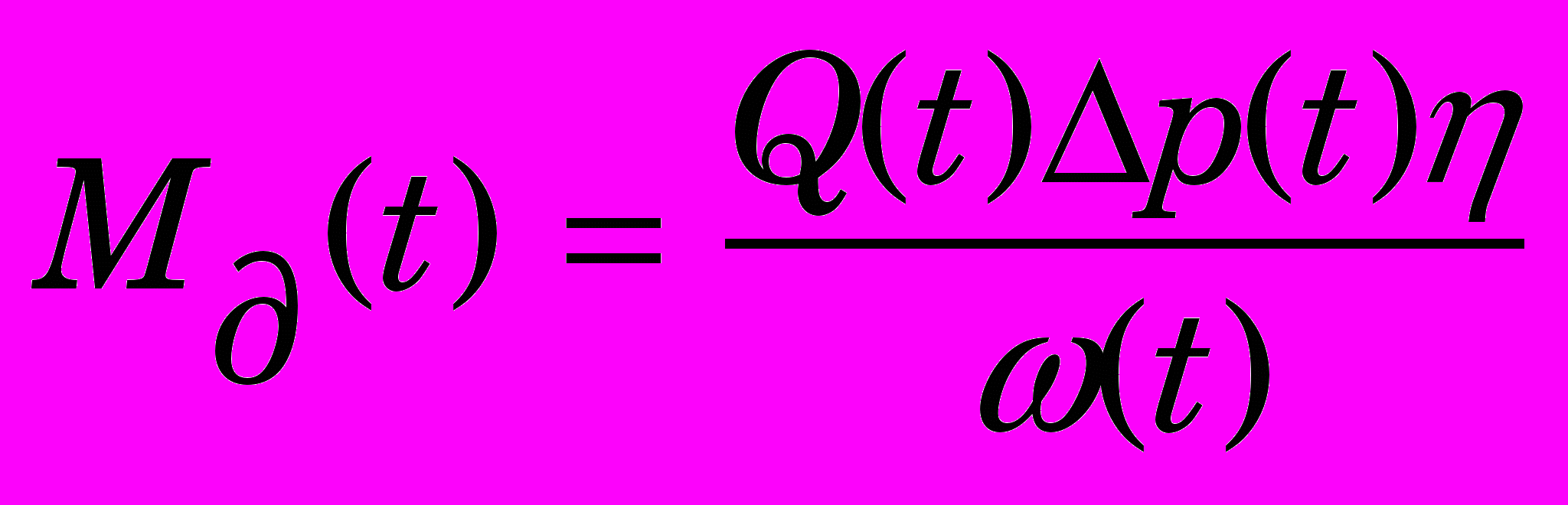, (2)

где

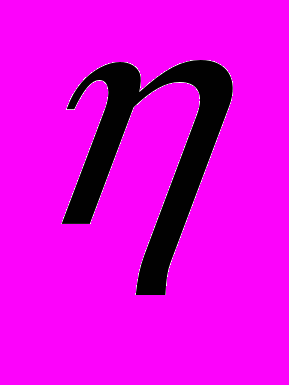- КПД4

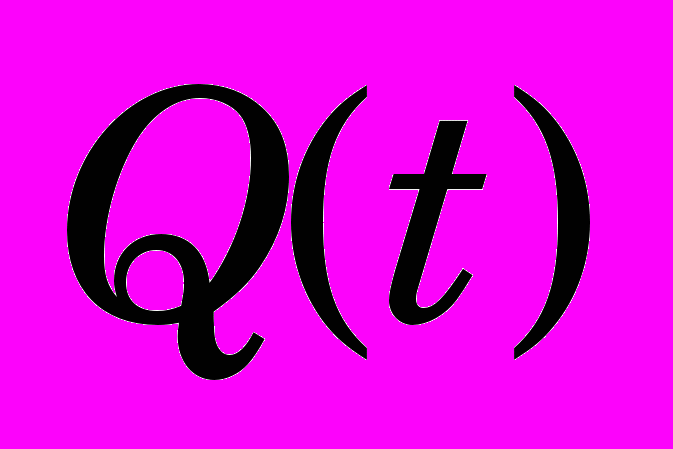– расход воды через турбину;

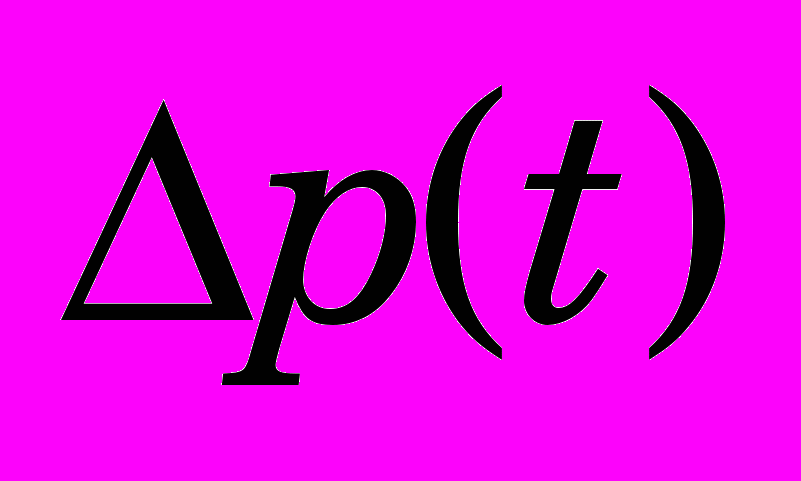– перепад давления на турбине.

Расход

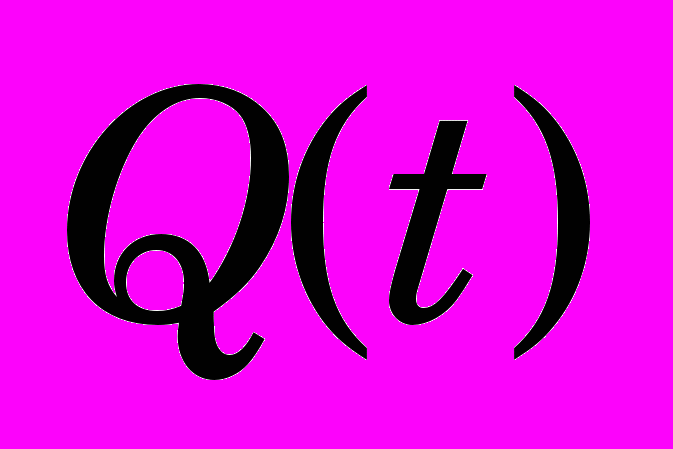связан с открытием НА

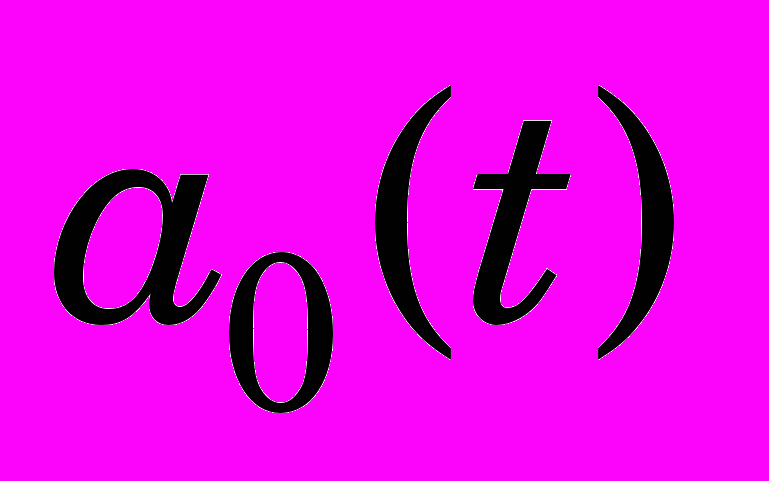и перепадом

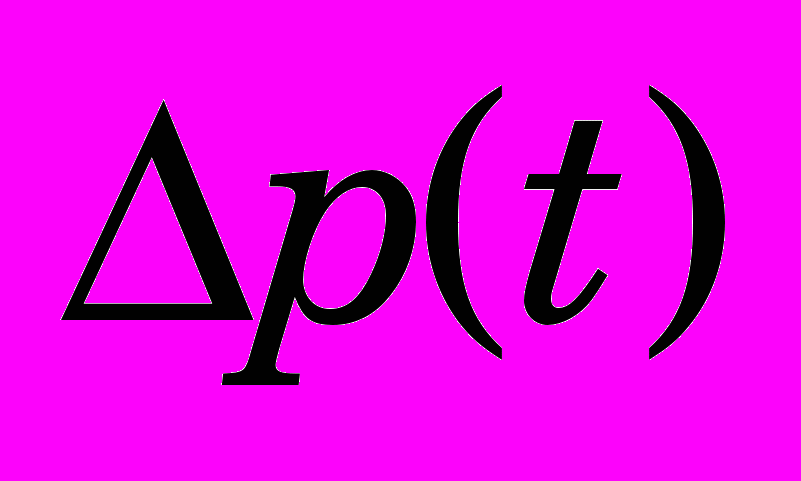и вычисляется по формуле 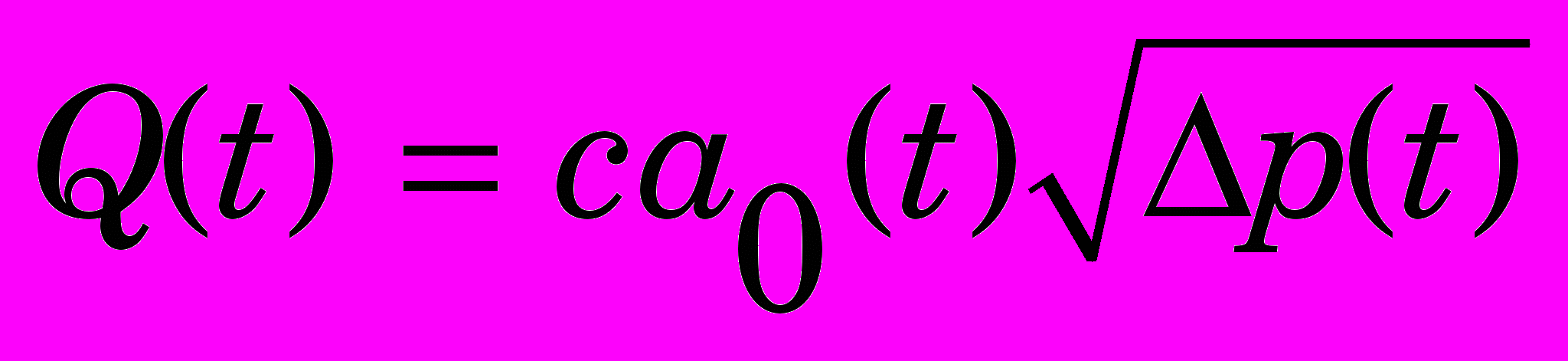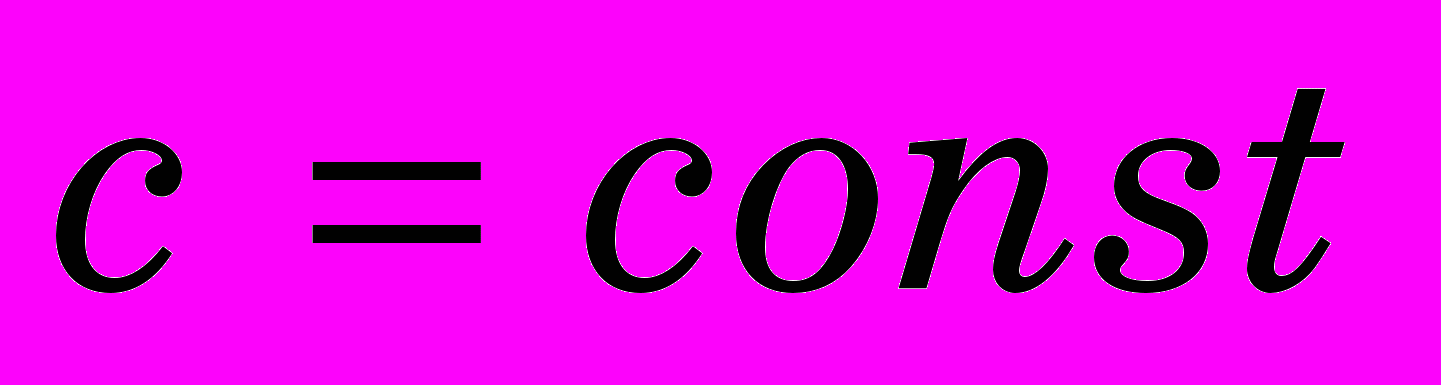3;

. (3)

Для определения

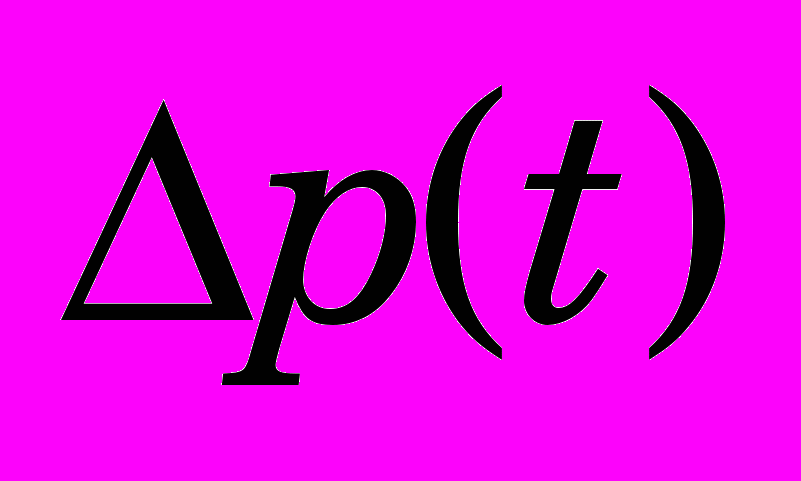воспользуемся законом сохранения количества движения столба воды, заключенного в водоводе, и, не принимая во внимание сил сопротивления, можно записать 3:

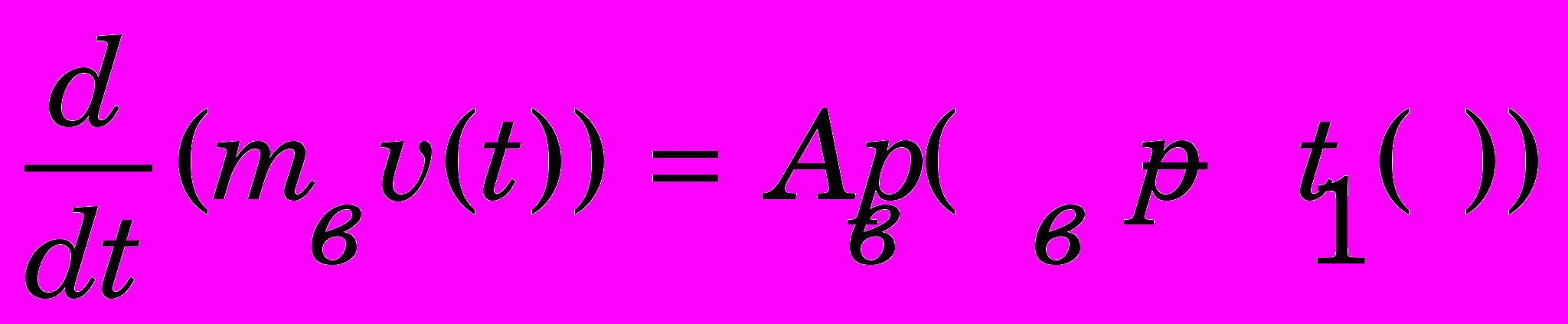, (4)

где

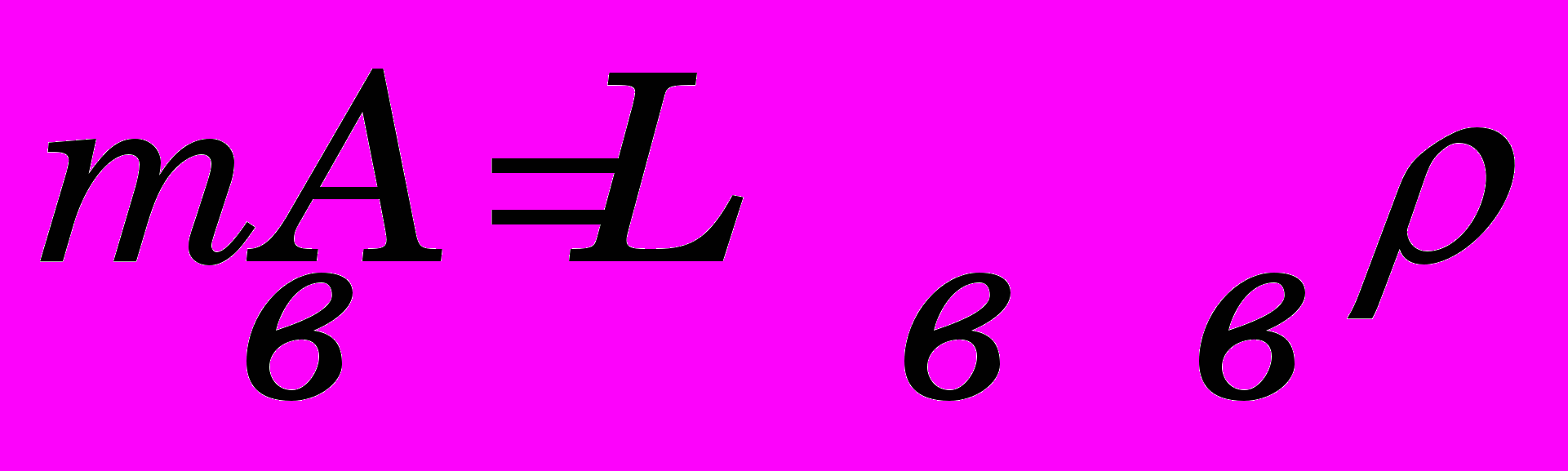- масса столба воды; А_В, L_В – соответственно площадь сечения и длина водовода;  - плотность воды; р_В – постоянное давление на верхнем конце водовода; р₁(t) – давление перед НА; v(t) – скорость воды перед НА.

Перепад давления на турбине и расход через турбину определяются по формулам:

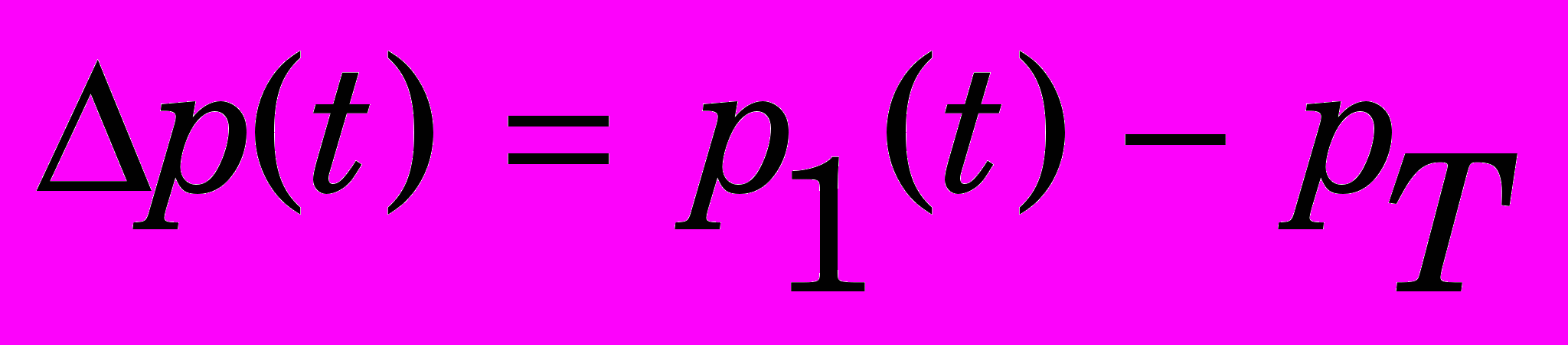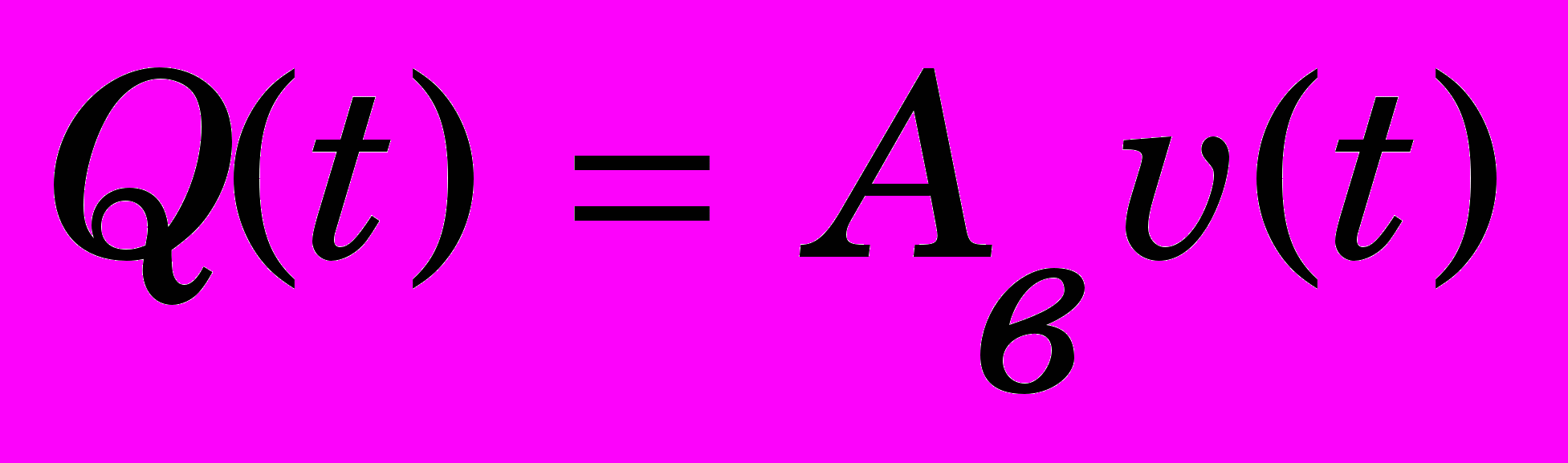. (5)

где р_Т – постоянное давление за турбиной.

Подставляя формулы (5) в выражение (4), получаем

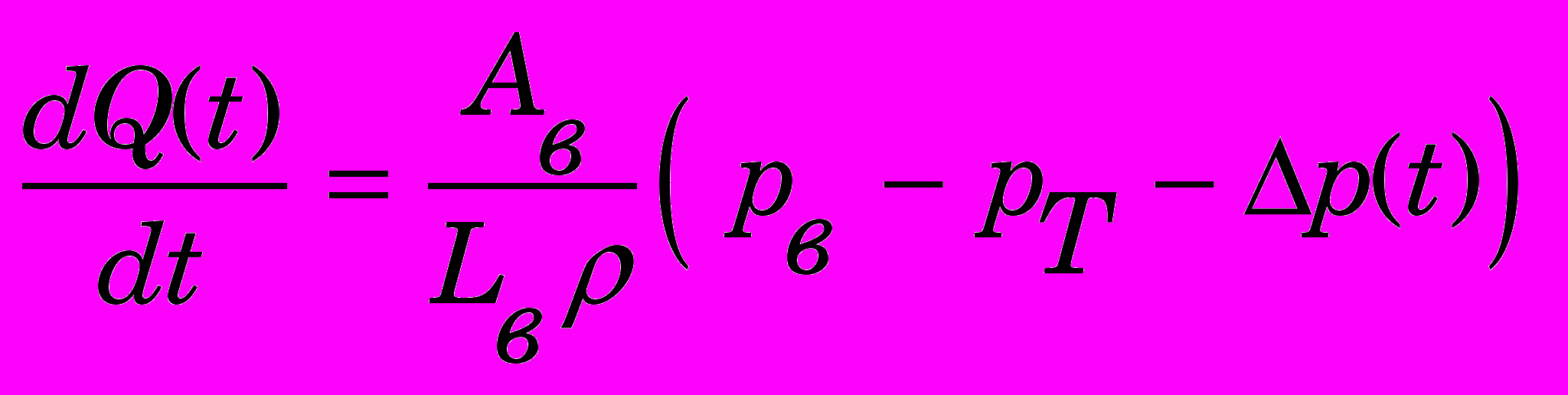. (6)

Если вместо давлений р перейти к напору, то выражения (3) и (6) запишутся следующим образом

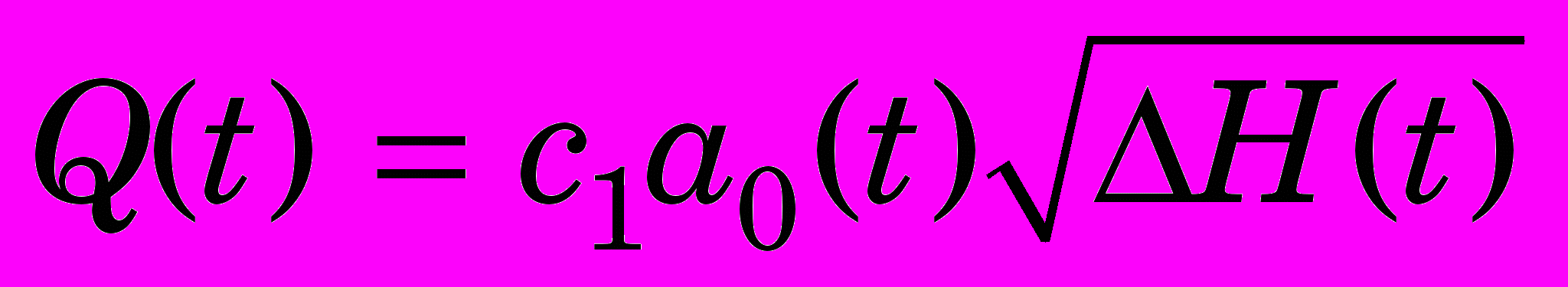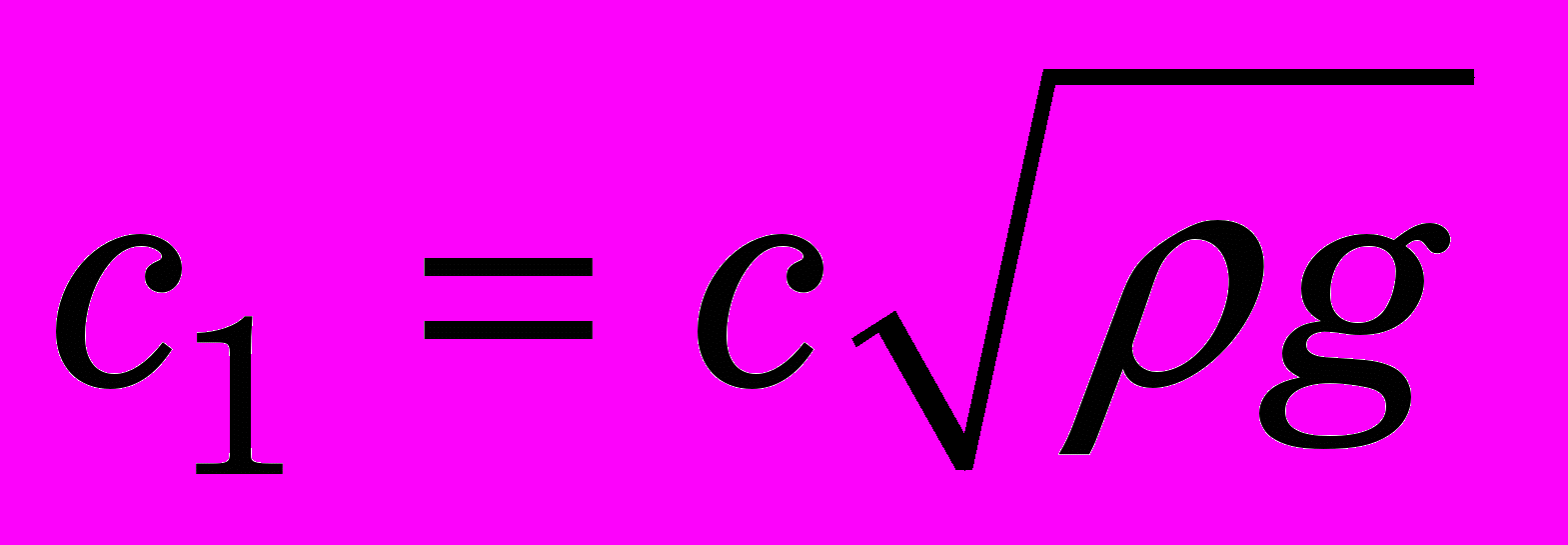, (7)

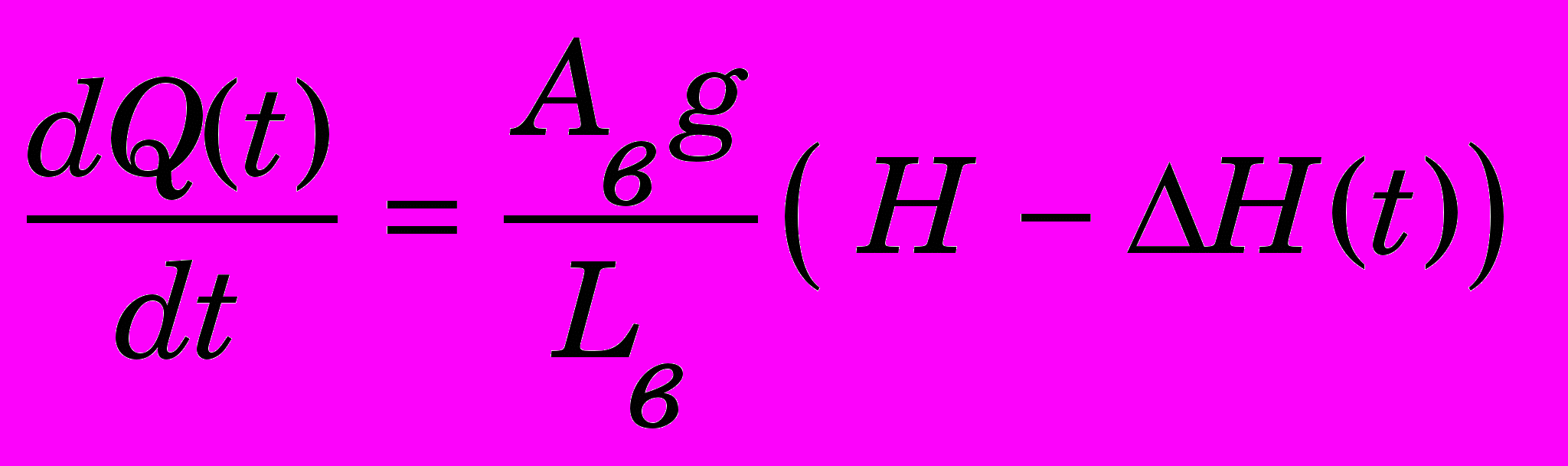, (8)

где

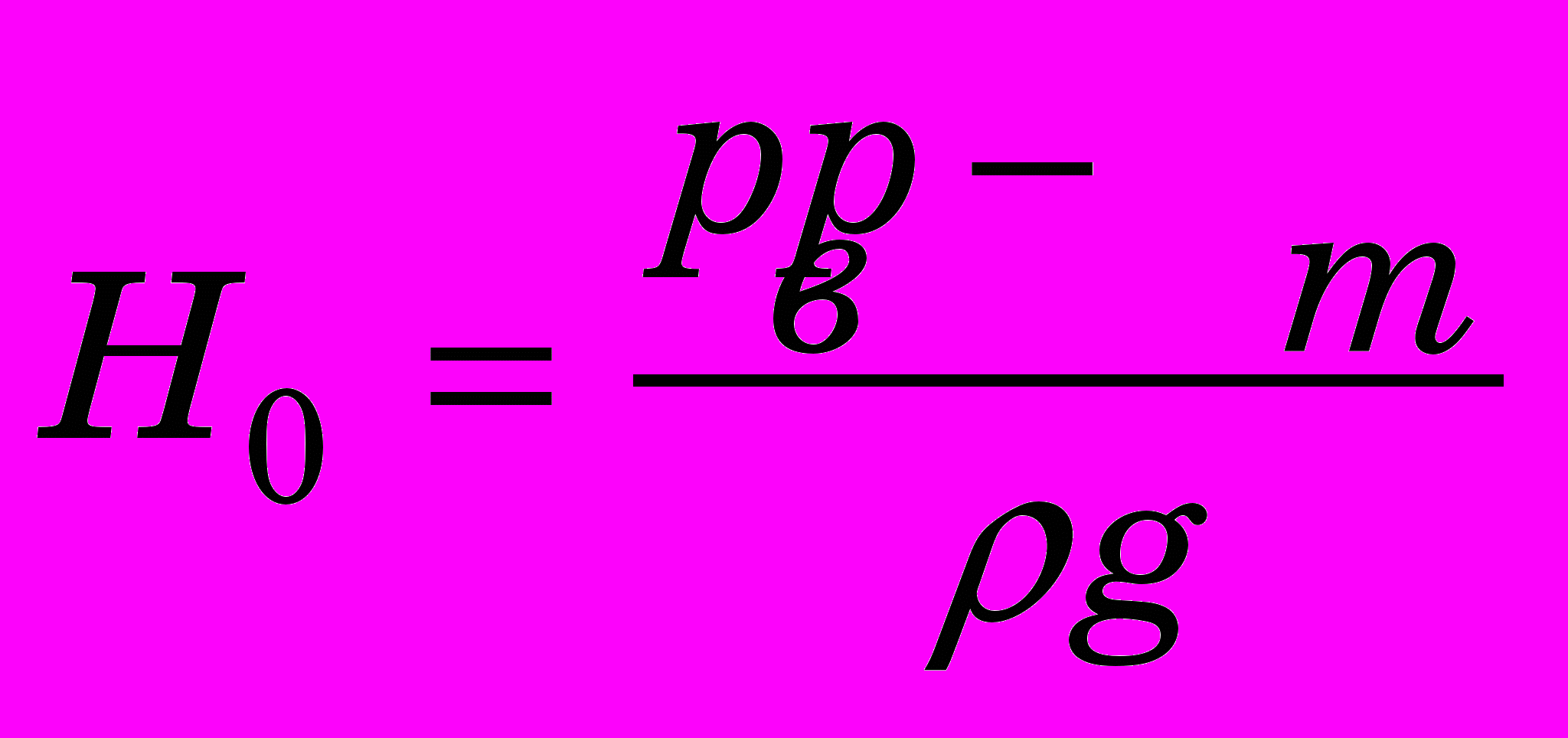- постоянный напор; Н(t) – изменение напора на гидротурбине; g – ускорение земного притяжения.

С целью последующего решения на ЭВМ, представим выражения (7) и (8) в виде дифференциального уравнения, содержащего производную Н(t) и саму функцию Н(t). Для этого дифференцируем выражение (7) и, приравнивая после дифференцирования левую часть с левой частью формулы (8), получаем

,

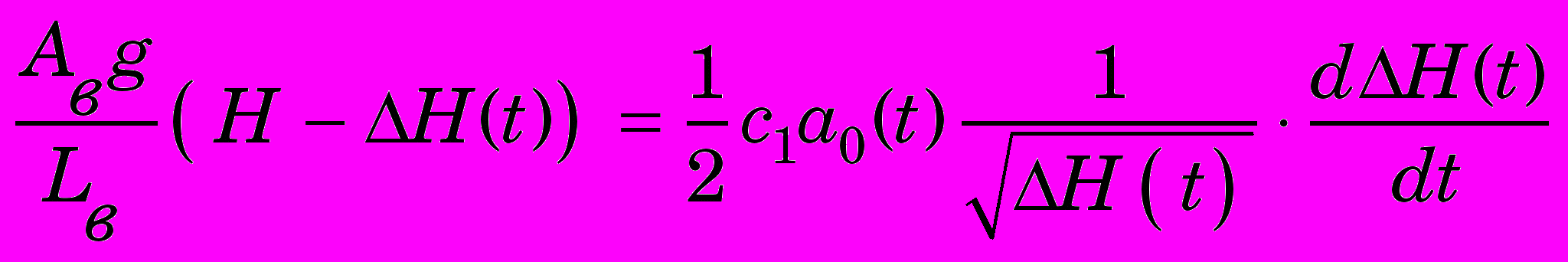или

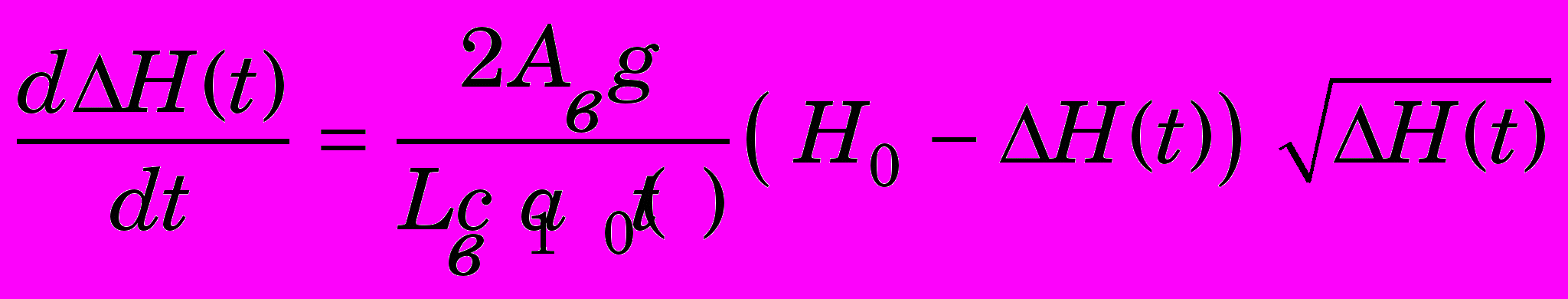. (9)

Таким образом, укрупненная модель гидротурбины с управляющим воздействием

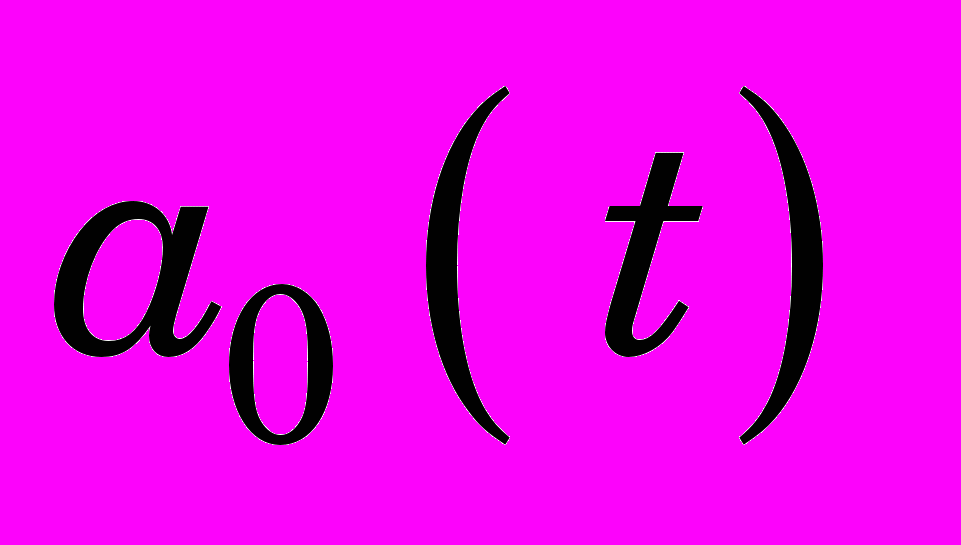представлена уравнениями (1), (7) и (9), выражением (2), в котором вместо р(t) подставляем gН(t), и уравнениями нагрузки.

Математическую модель электрогидромеханической части системы представим, исходя из следующих соображений. Поворот лопаток НА осуществляется в компьютерной системе с помощью последовательного срабатывания ЭГП и ГР, через который рабочая жидкость поступает от МНУ в соответствующую полость СМ (здесь рассматривается один обобщенный сервомотор). Перемещение штока СМ через поворотное устройство вызывает поворот лопаток НА. На вход ЭГП от ЭВМ поступает управляющий сигнал, содержащий информацию об отклонении частоты (t) от заданной в соответствии с принятым законом управления.

Опираясь на результаты ряда авторов, изложенных в работах 3,4, будем укрупненно считать, что процесс передачи во времени сигнала со входа ЭГП до формирования управляющего воздействия

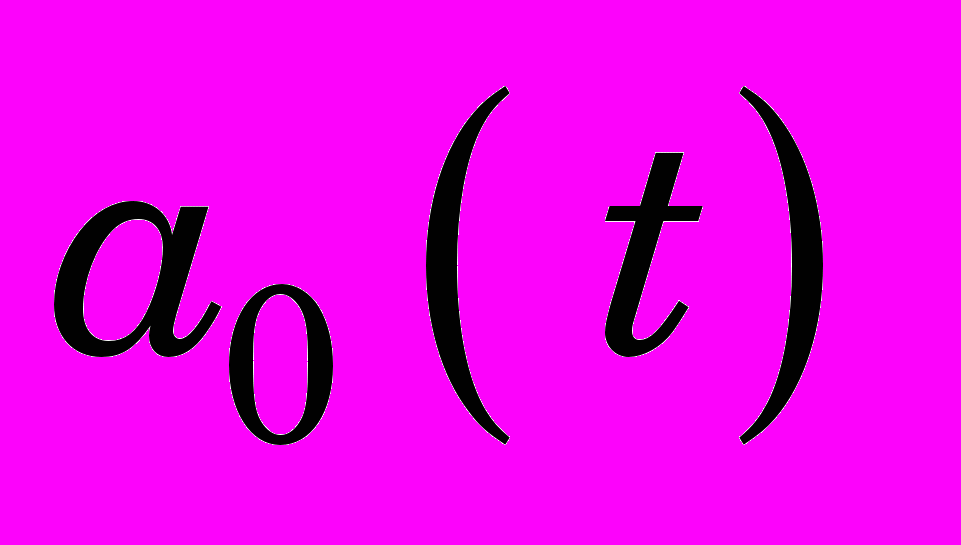описывается линейными дифференциальными уравнениями первого порядка, представляемые произведением двух передаточных функций

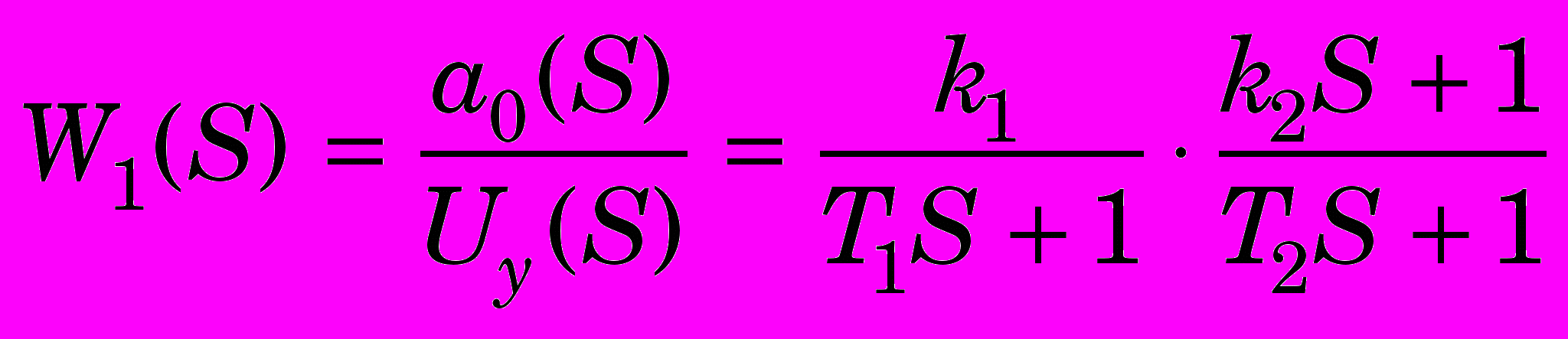(10)

и ограничивающим неравенством

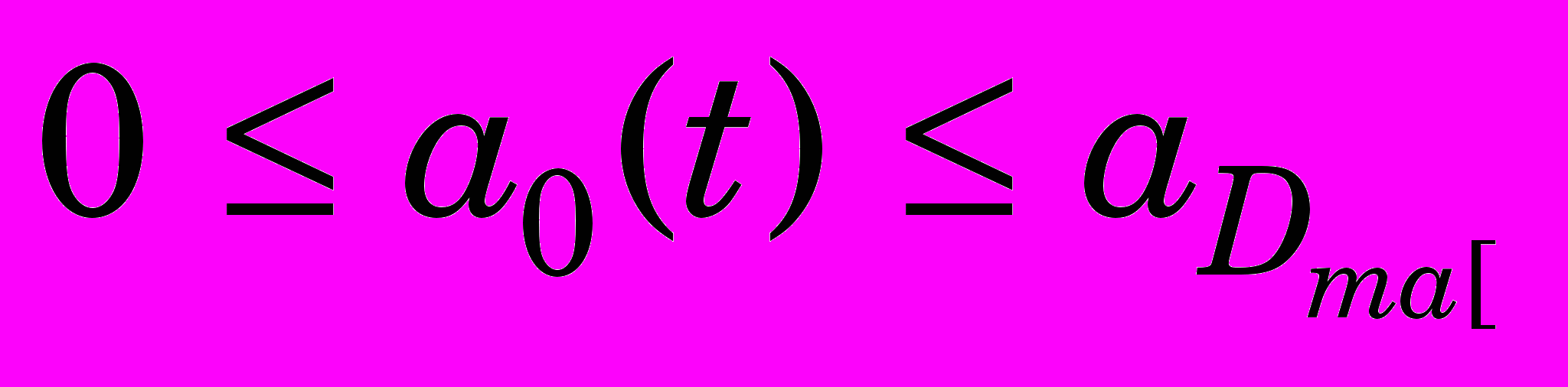, где S – оператор Лапласа; Т₁, Т₂ – постоянные времени; k₁, k₂ – коэффициенты усиления; U_Y(S) – сигнал, поступающий с ЭВМ на вход ЭГП.

Перейдем к математическому описанию устройства управления с использованием ПИД – регулятора для формирования закона управления. При наличии жесткой обратной связи по скорости  величина рассогласования составит

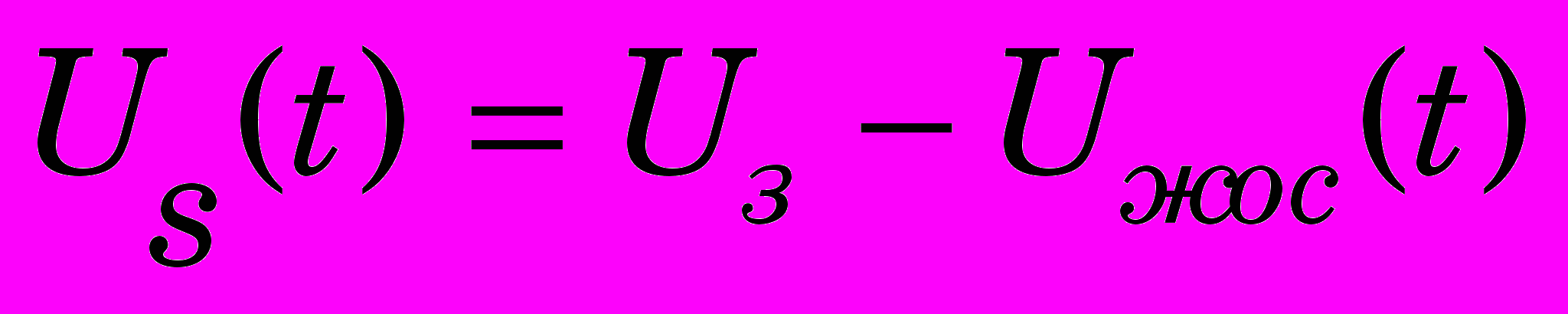, (11)

где

;

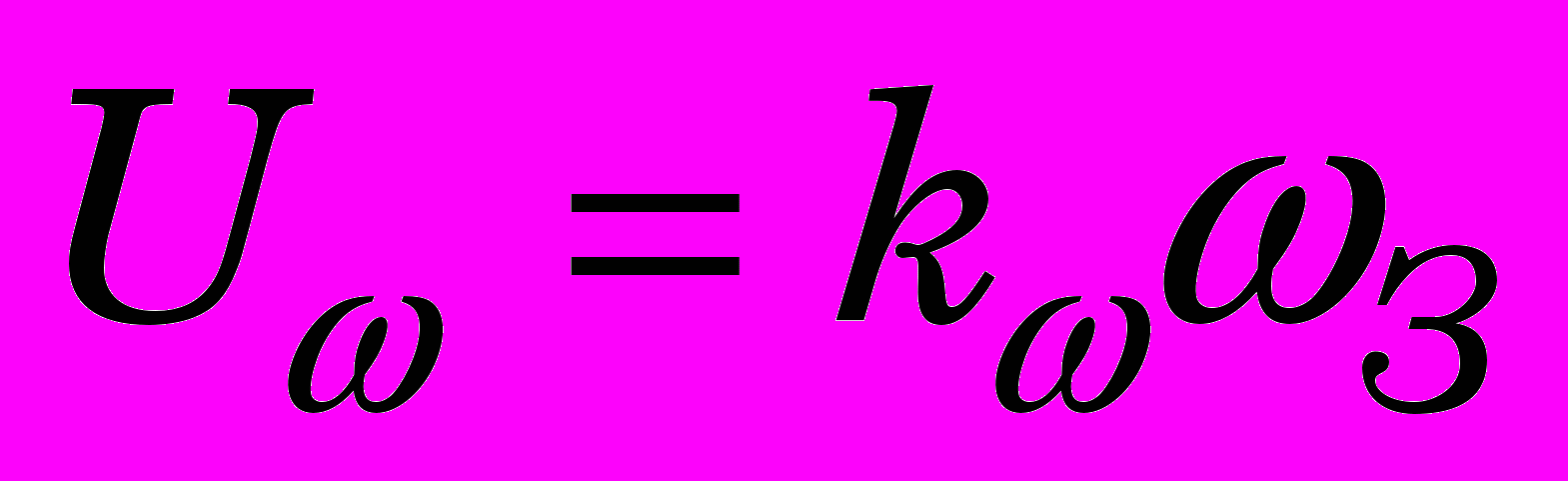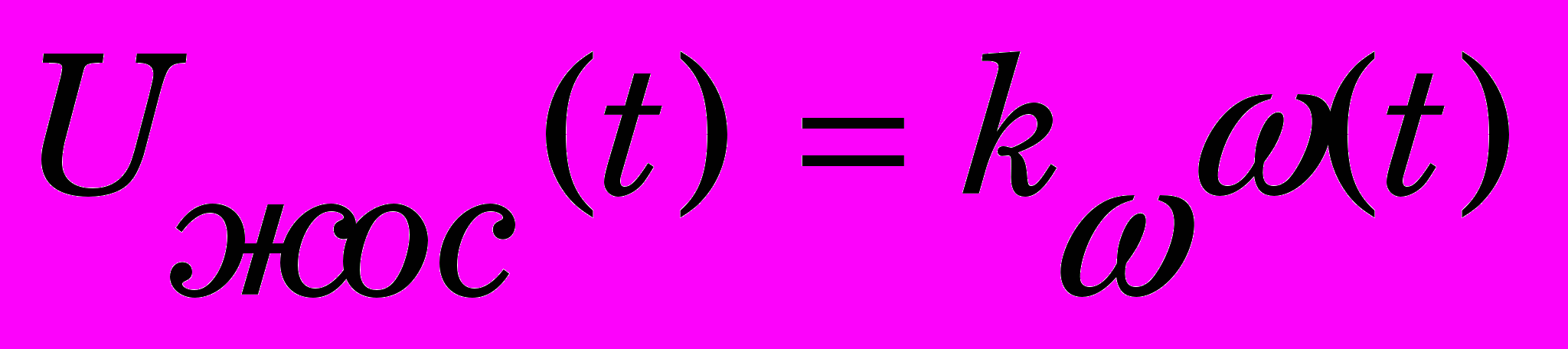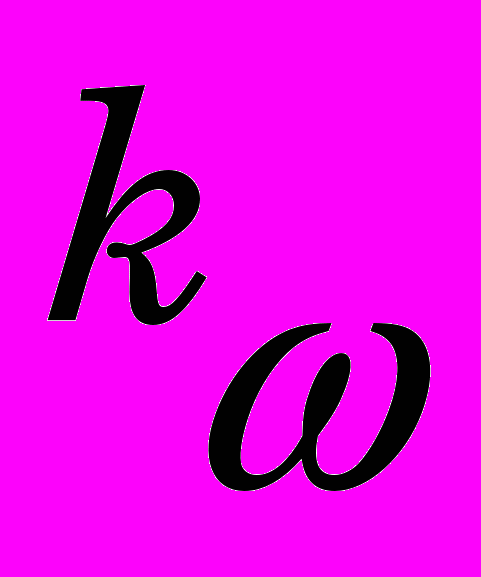- коэффициент усиления;

- задание по скорости.

Тогда ПИД – регулятор представляется уравнением 5:

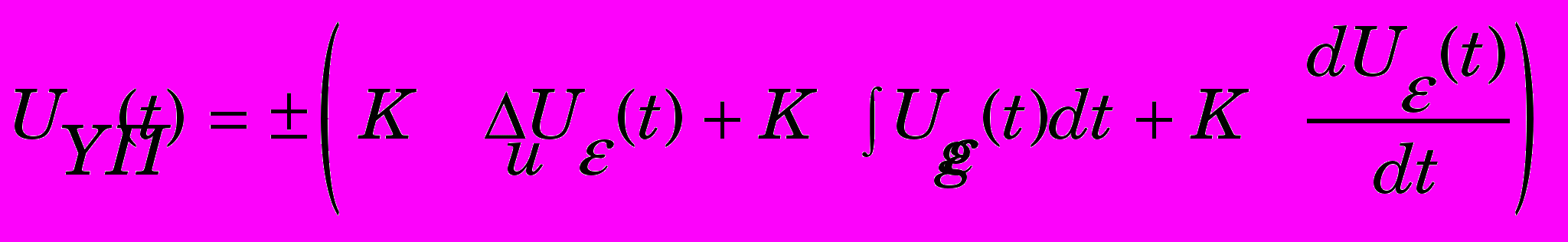. (12)

Здесь К_П, К_U и К_g – параметры настройки и каналов. Входным сигналом на каждый канал ПИД – регулятора (пропорциональный П, интегральный И, дифференциальный Д) является сигнал рассогласования.

В модели следует задать лишь время t_п (время переключения), времена t_p и t₀ определяются динамическими характеристиками системы, на которые влияют параметры ПИД – регулятора.

Процесс торможения формируется управляющим воздействием согласно неравенствам

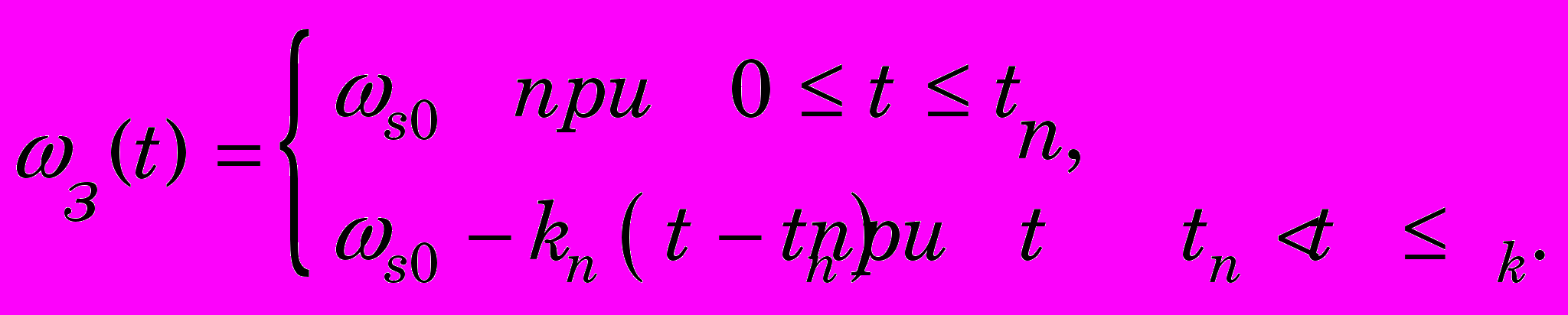(13)

Время t_к соответствует моменту, когда

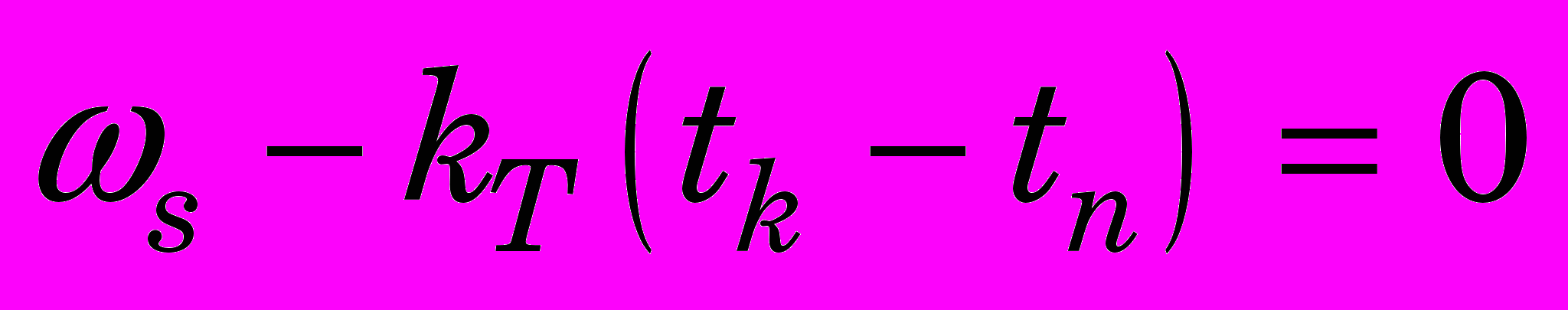и происходит торможение вала турбины.

Для формирования кривой задания скорости

при торможении вводится линейное дифференциальное уравнение 1-го порядка, представляемое передаточной функцией апериодического звена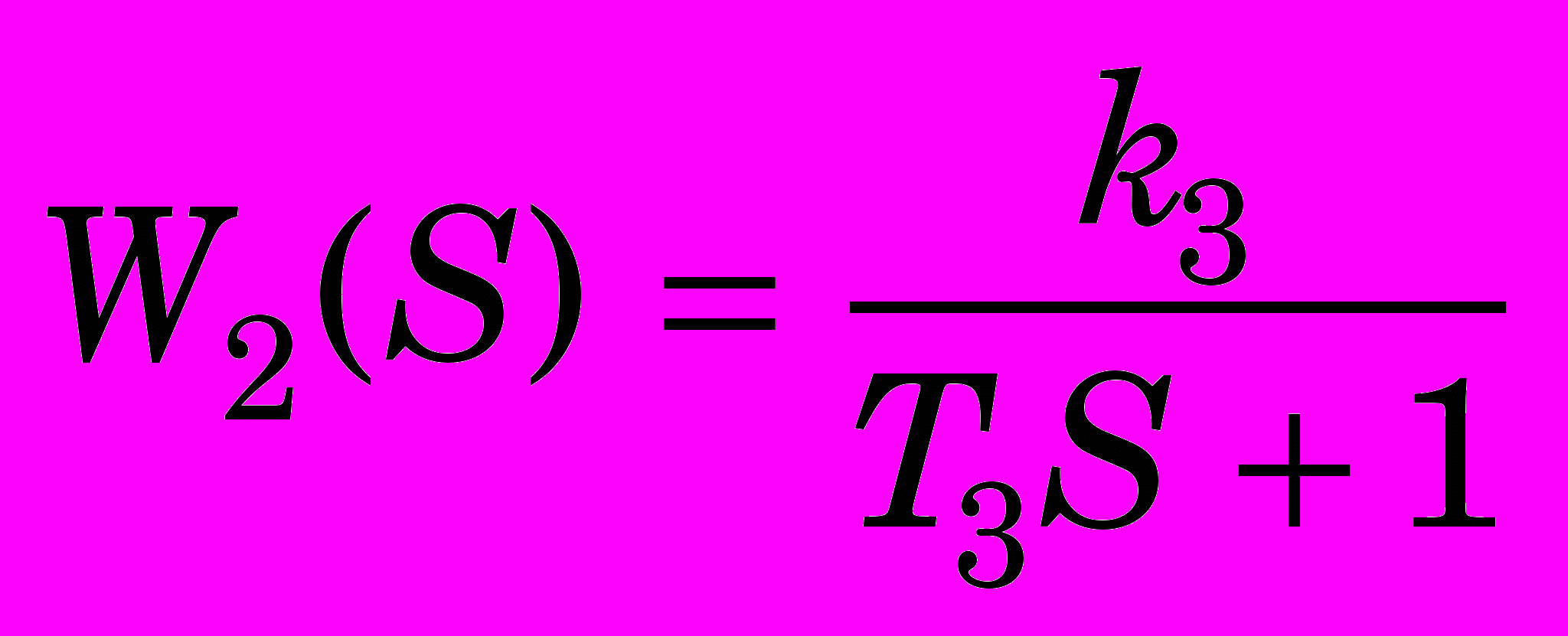

. (14)

Параметры К₃, Т₃ выбираются при исследовании модели для обеспечения требуемого качества перехода от установившегося движения к остановке гидротурбины.

Внешние нагрузки выполняются в модели с помощью логических уравнений в функции времени при необходимости для любого режима работы. Структурно-функциональная схема модели, построенная на основе уравнений и неравенств (1) – (14), изображена на рис. 2. В квадратах схемы изображены коэффициенты, передаточные функции, функции обработки информации. На выходе ряда блоков схемы указаны соответствующие переменные:

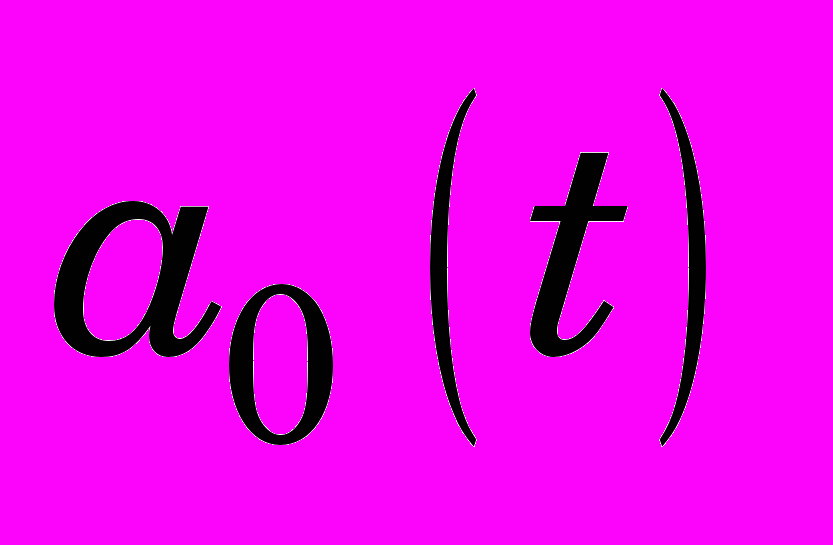, H, Q, ,

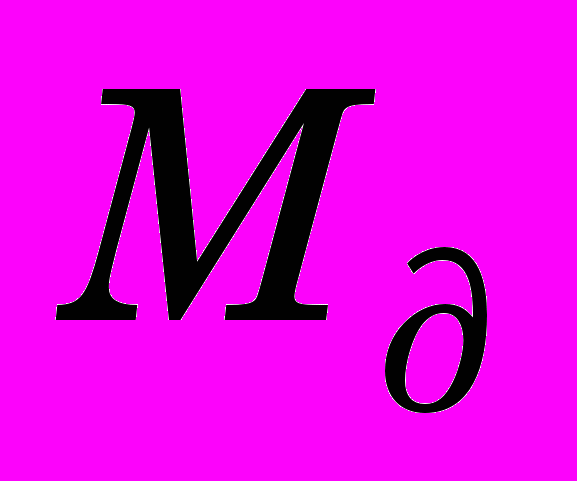и др. Как видно из схемы, вход системы – задание по угловой скорости ₃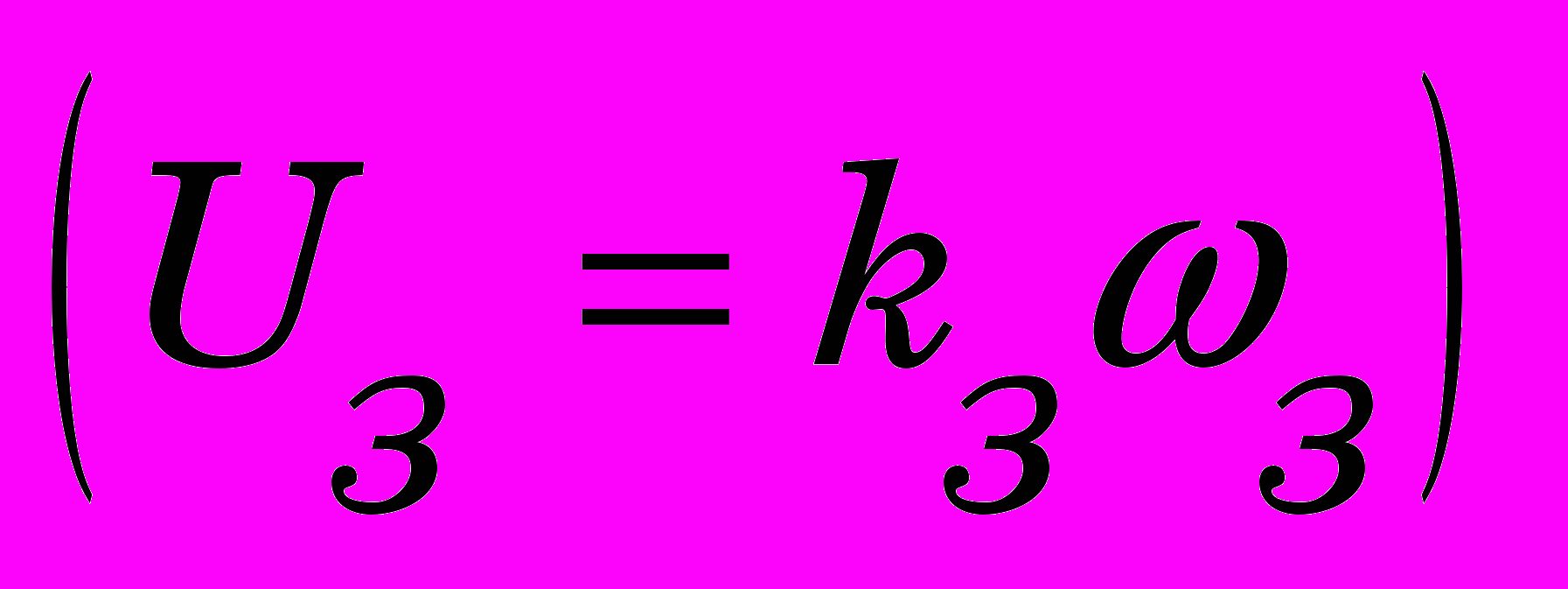, выход – фактическая скорость (t). При таком построении модели появляется возможность включения различных устройств,формирующих по величине рассогласования различные законы управления. В качестве такого в схеме предусмотрен ПИД- регулятор, который может быть реализован программными средствами компьютерной системы.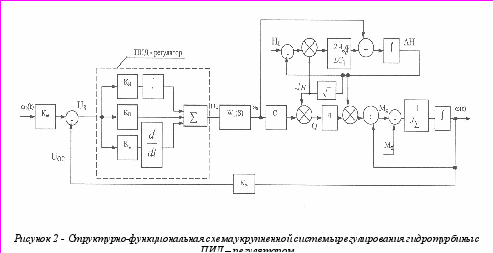

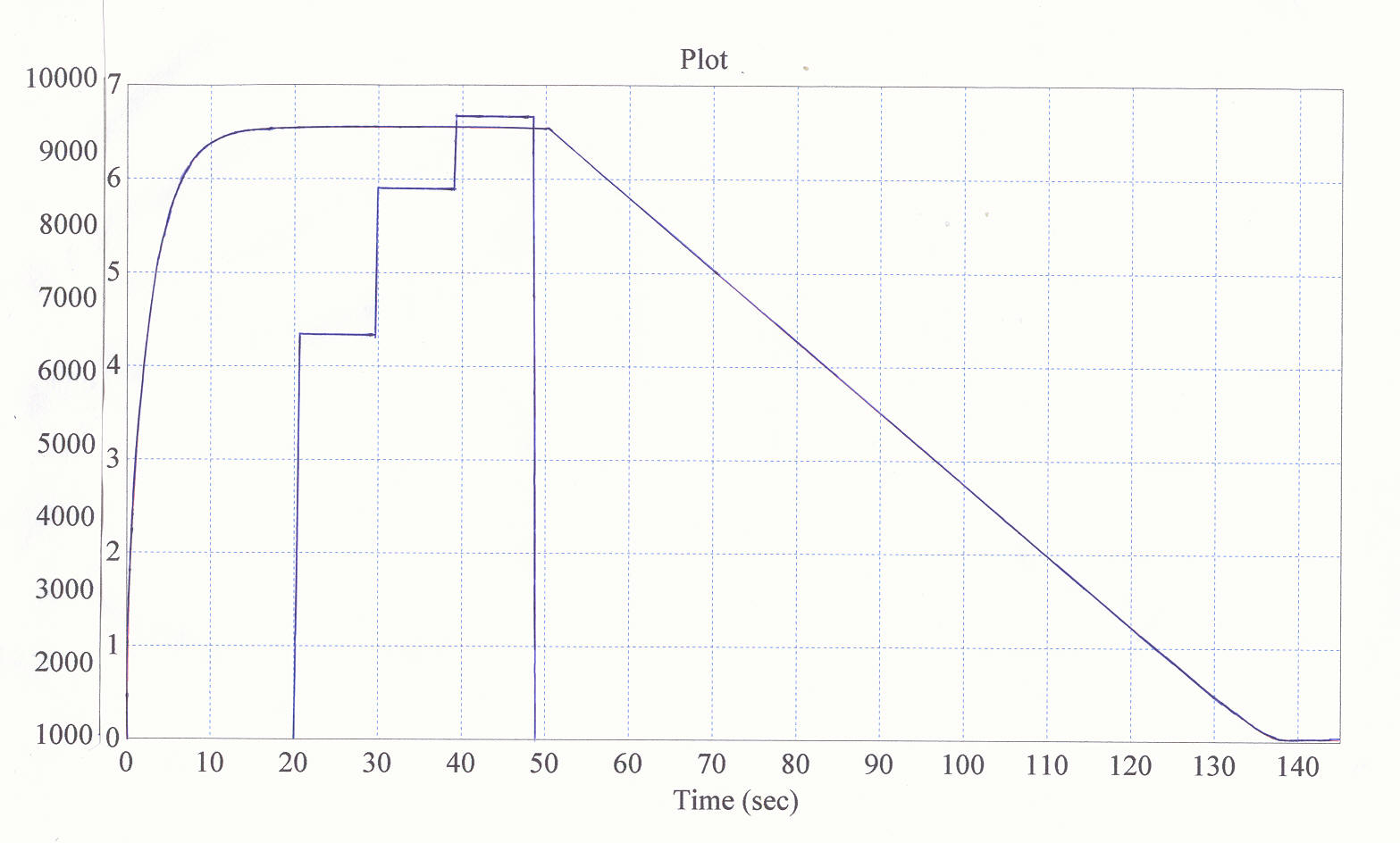
М_с, кНм (t),c^-1

t(c)

Рисунок 3 - Переходный процесс при ступенчатой нагрузке

Исследование динамических характеристик системы

Указанная схема была использована для набора модели системы в пакете математического имитационного моделирования, в котором имеются блоки различных математических операций и функций. При моделировании приняты следующие данные гидротурбины ПЛ 661–ВБ– 800 Кременчугской ГЭС:

А_В = 16 м², L_В = 40 м, _З = 6,54 с^-1, номинальный расход воды Q_Н = 490 м³/с, максимальное открытие а₀_max = 0,5 м, номинальный движущий момент М_g_Н = 9 592 кНм,  = 0,92, J = 1,310⁴ кНм²,

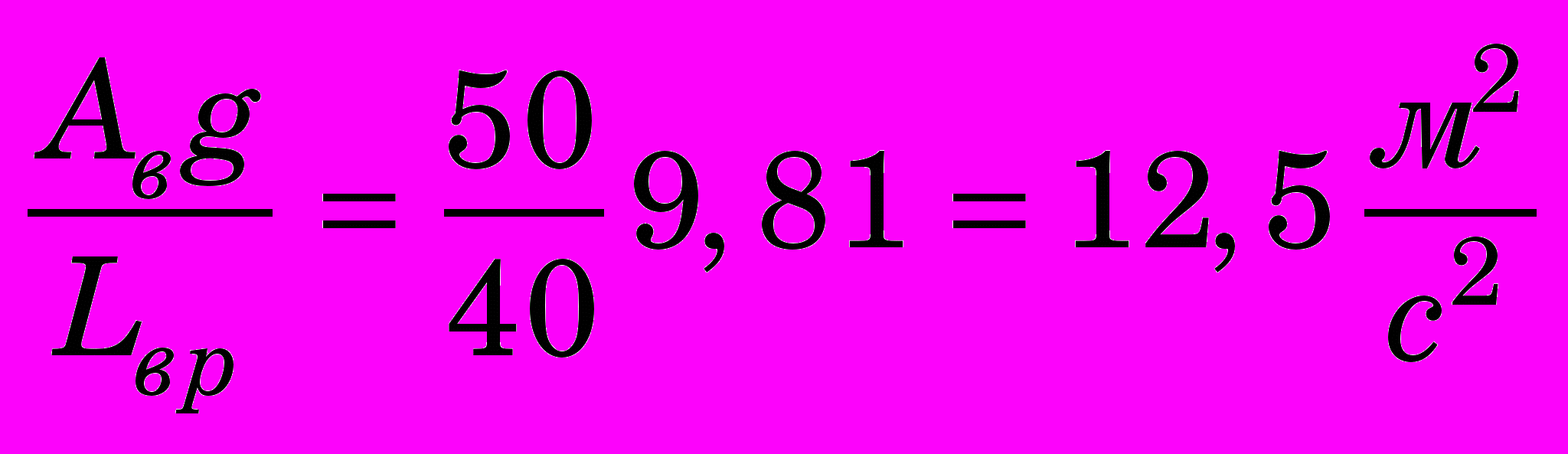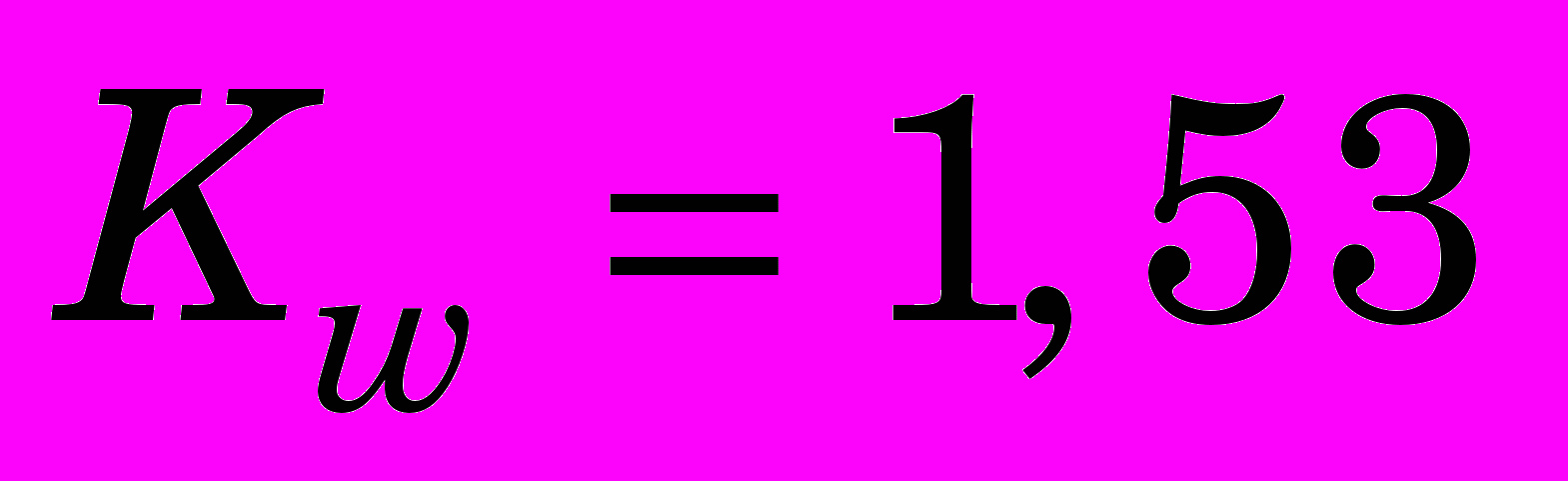Вс,

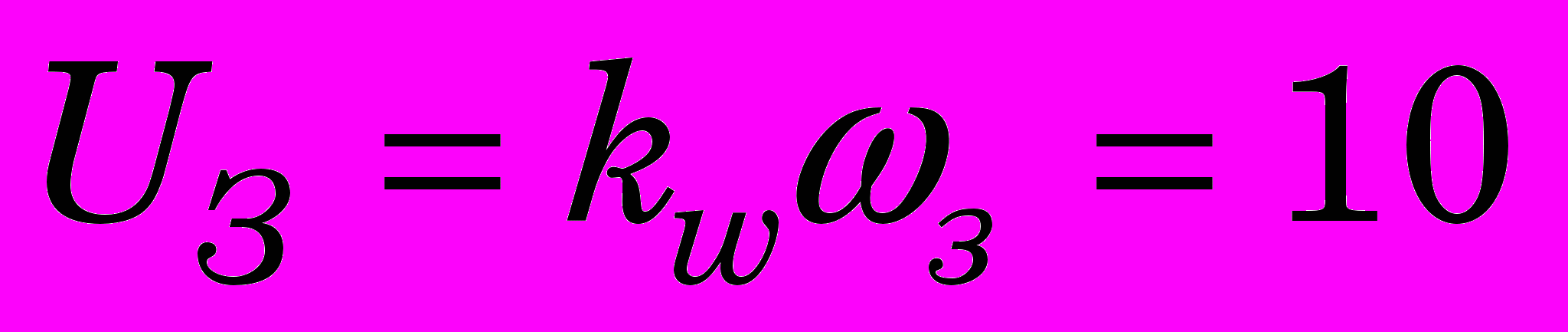В,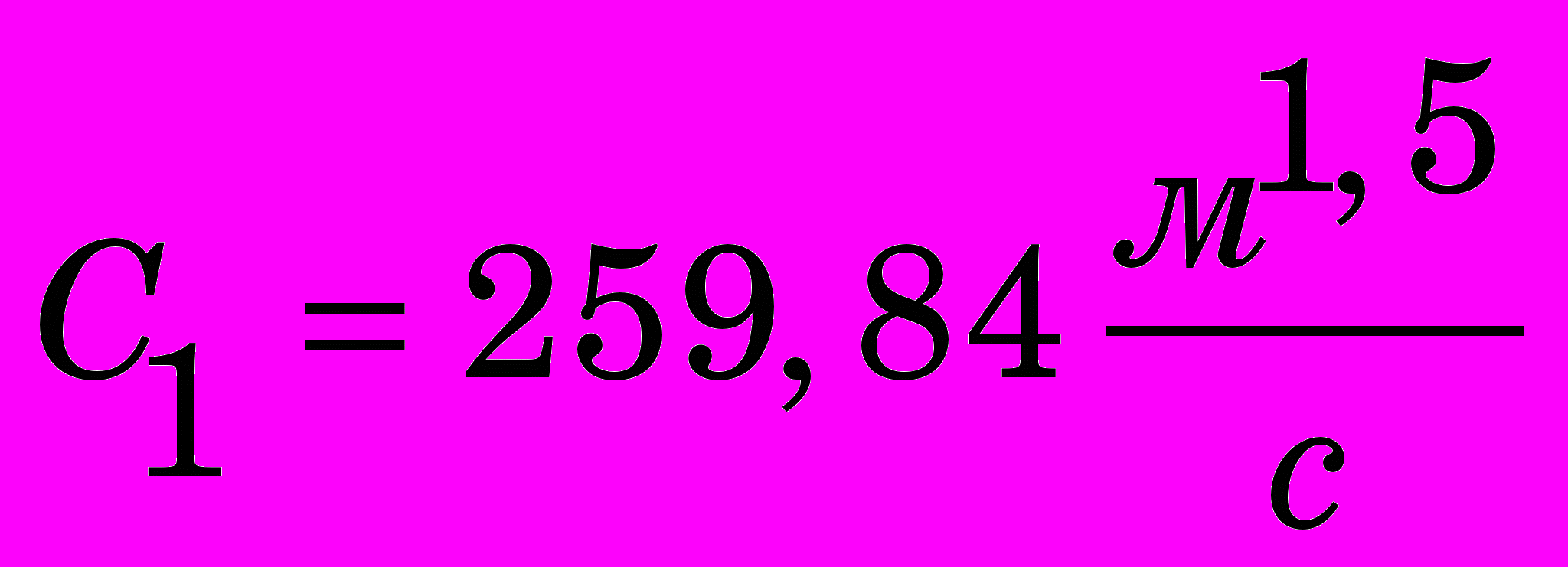

.

Переходный процесс (t) пуска гидротурбины на холостом ходу при дальнейшем движении с возрастающей нагрузкой и последующей остановкой изображен на рис.3.

Как следует из рисунка, время разгона составляет 20 с. После синхронизации электрогенератора гидротурбины с электрической сетью и включении под нагрузку частота вращения практически не изменилась.

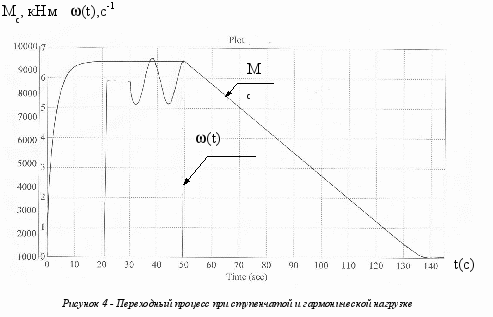
На рис. 4 изображен переходный процесс (t) пуска гидротурбины на холостом ходу и дальнейшем движении со ступенчатой и гармонической нагрузкой и последующей остановкой.

Как следует из представленного рис. 4, система практически сохраняет скорость при гармонической нагрузке с амплитудой 2000 кНм.

Вывод

Представленная нелинейная укрупненная математическая модель системы регулирования гидротурбины с законом управления в виде ПИД-регулятора имеет высокие показатели качества переходных процессов (быстродействие, отсутствие колебаний при гармонической нагрузке).

СПИСОК ЛИТЕРАТУРЫ

Лычак В. С., Клявин Д. А. Современные системы автоматического управления и регулирования гидротурбин и насосов – турбин // Энергомашиностроение.–1986.-№5.–С.23–26.
Жерняк А. И., Лурье З. Я. , Дмитерко В. Н. Компьютерная система регулирования скорости гидротурбины // Вестник НТУ «ХПИ». Технологии в машиностроении. – 2001.– С.90–92.
Первозванский А. А. Курс теории автоматического управления. – М.: Наука,1986.–616с.
Пивоваров В. А. Проектирование и расчет систем регулирования гидротурбин. – Л.: Машиностроение, 1973. – 288 с.
Гаркави Ю. Е., Смирнов М. И. Регулирование гидротурбин.–М.:Машгиз,1954.–374с.