Фельдман А. Б. Производные финансовые и товарные инструменты

Вид материала

Документы

Содержание 8.2.3. Формальные модели ценообразования и алгоритмы их реализации 8.2.4. Аналитические показатели (измерители)

Подобный материал:

• Программа дисциплины Производные финансовые инструменты для направления 080105., 107.25kb.
• Программа дисциплины Производные финансовые инструменты и реальные опционы для направления, 423.51kb.
• Лекции по курсу «Производные финансовые инструменты», 258.65kb.
• Лекции по курсу «Производные финансовые инструменты», 158.65kb.
• Лекции по курсу «Производные финансовые инструменты», 358.4kb.
• Лекции по курсу «Производные финансовые инструменты», 239.66kb.
• Производные финансовые инструменты посещаемость: сентябрь – октябрь 201 1 года, 394.53kb.
• Лекции Селищева А. С. «Производные финансовые инструменты», 171.47kb.
• Лекционый курс: «Производные финансовые инструменты» Содержание: Часть I. Деривативы, 1515.17kb.
• Вопрос 6 раздел 2 Инвестирование в финансовые инструменты, 95.53kb.

8.2.3. Формальные модели ценообразования и алгоритмы их реализации


Перейдем, основываясь на изложенном ранее, непосредственно к формальным моделям и алгоритмам ценообразования на опционы.

Цена опциона имеет ту же единицу измерения, что и цена (стоимость) базисной ценности. Затраты на приобретение опционов (цена их приобретения) включают премию и трансакционные издержки. На биржевом рынке опционы выторговывают по ценам приобретения. Соответственно при создании моделей требуется ответить на вопрос об учете в теоретических построениях дополнительных расходов по сделке.

В числе центральных факторов, определяющих цену опциона, значатся:

цена базисной ценности (текущая и исполнения);

процентные (краткосрочные) ставки;

колебания (изменчивость) цены базисной ценности;

время (остаток времени) до исполнения;

соотношение спроса-предложения;

тенденции (ситуации), формирующиеся в ходе биржевых торгов.

Признано, что трудно выяснить стоимость опциона, используя стандартные методы дисконтирования. Лучше, если будет найден эквивалент цены опциона при сопоставлении денежных затрат на текущее приобретение базисной ценности с суммарными затратами собственно на опционы и получение денежного займа на недостающие средства. Чистые затраты (текущая цена опциона за вычетом расходов на займ) в общем виде определят цену опциона. Как было показано ранее [равенство (8.1)], внутренняя стоимость опциона (при эквивалентном обмене) не может превышать стоимость базиса. Если в финансировании покупки базиса участвует при опционе займ (правильно – скрытый займ), то, следовательно, стоимость (внутренняя) опциона соответствует разнице между текущей ценой базиса и приведенной стоимостью цены исполнения по опциону. Это еще одно общее соображение относительно моделей цен на опционы.

Изменчивость цен определяется как среднеквадратическое отклонение ежедневных колебаний цен базиса в расчете на год. Как показывает опыт, при незначительном изменении цен базиса (ориентировочно на 1–2%) контракт имеет меньшую ценность, по сравнению с опционами, связанными с переменой цен базиса на многие проценты. Если текущая цена базиса падает ниже цены исполнения, покупатель

не должен исполнять опцион, он потеряет инвестированные деньги вне зависимости от того, как низко упала текущая цена относительно цены исполнения. Если текущая цена базиса оказывается выше цены исполнения, то успех для покупателя опциона будет тем больше, чем выше эта пропорция (текущей цены и цены исполнения). Следовательно, держатель (покупатель) опциона при увеличении изменчивости цены при неудаче дополнительно ничего не теряет, а при удаче, очевидно, выигрывает.

Отсюда вытекает, что польза и стоимость опциона растут с повышением произведения показателя дисперсии цены базиса и длительности периода до истечения срока опциона (или произведения дисперсии на время).

Кроме того, считается, чем выше рыночная ставка процента и продолжительнее оставшийся срок до исполнения, тем дороже скрытый займ. Отсюда следует, что стоимость опциона должна возрастать с ростом произведения процентной ставки на время, оставшееся до исполнения опциона.

Если допустить, что инвесторы безразличны к риску, то в виде такой ставки будет выступать безрисковая процентная ставка. Сообразно с этим покупатель и продавец теоретически находятся в равном положении по вероятности получения дохода, свободного от риска.

При принятии для расчета стоимости опционов безрисковой процентной ставки биржа должна использовать различные варианты платежей (маржи) для возмещения рисков.

О том, как влияют факторы отдельно на стоимость колла и пута, известно следующее: чем выше цена исполнения, тем ниже биржевая цена (курс) самого контракта колл и тем выше курс контракта пут; чем длиннее остаточный период опциона (время до исполнения), тем выше курс опциона; чем выше колебания кассового курса базиса, тем выше курс опциона; при этом с ростом ссудного процента курс колла повышается, а курс пута снижается.

Нижняя граница премии (цены) по опциону равна внутренней стоимости (Intrinsic Value), или доходу покупателя (держателя) опциона, который может быть получен при немедленной реализации контракта, т.е. разнице между текущей и исполнительной ценами базисного актива.

Внутренняя стоимость позволяет распределить контракты на группы: в деньгах (in-the-money – ITM), при деньгах, по номиналу – без внутренней стоимости (at the money – ATM), без денег, сверх денег (out-of the money – OTM). Представим следующие ситуации для покупателя:

Опцион	Цена исполнения
	ниже текущей цены базиса	равна текущей цене базиса	выше текущей цены базиса
Колл (Call)	в деньгах	при деньгах	без денег
Пут (Put)	без денег	при деньгах	в деньгах

Значительное место в теории и практике занимает модель Блэк– Шолза (Black–Scholes)¹, удовлетворяющая общим и частным принципам опционного ценообразования, приведенным ранее. Подробно исходные положения, структура и формулы этой модели представлены в приложении 5.

Распространенным подходом для выявления алгебраических зависимостей стал расчет цен на опционы с основанием акция (особенно для разновидности Call-опционов), в том числе и в данной модели.

Модель Блэк–Шолза (Black–Scholes) понимается сегодня как аналитическая модель, раскрывающая связи и зависимости факторов стоимости опционов, и сохраняет также значение вычислительной модели для цен опционов с основанием в виде акции (индексов курсов акций).

Эта модель неоднократно подвергалась верификации, расширилось пространство ее применения за счет опционов с иными основаниями, появились модификации для разных оснований. Привлекательность модели усиливается специально разработанными на ее базе таблицами стоимости опционов и коэффициентов хеджирования при их применении (представлены соответственно в приложениях 6 и 7).

Зависимости, выявленные моделью Блэк–Шолза (Black–Scholes) в связи с учтенными факторами, показаны (отдельно для каждого фактора) на рис. 8.1–8.8. На них демонстрируются тенденции в переменах стоимости опционов колл (Call) и пут (Put) при последовательных переменах величины каждого из факторов.



Рис. 8.1. Зависимость цены опциона колл (Call) от цены базиса




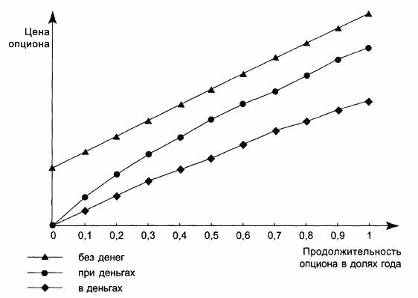
Рис. 8.2. Зависимость цены опциона колл (Call) от времени до его исполнения



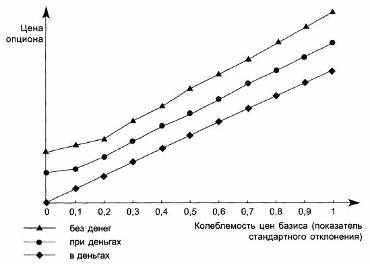
Рис. 8.3. Зависимость цены опциона (Call) от колебания (изменчивости) цен базиса



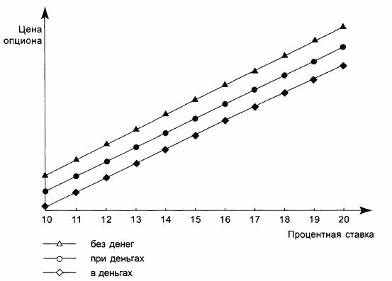
Рис. 8.4. Зависимость цены опциона колл (Call) от размера процентной ставки



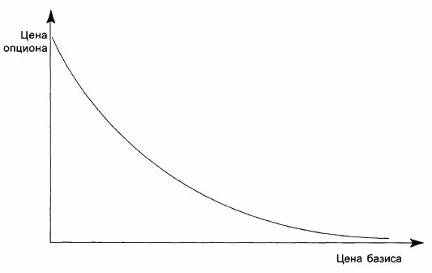
Рис. 8.5. Зависимость цены опциона пут (Put) от цены базиса



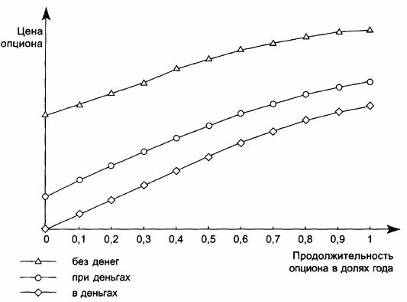
Рис. 8.6. Зависимость цены опциона пут (Put) от времени до его исполнения



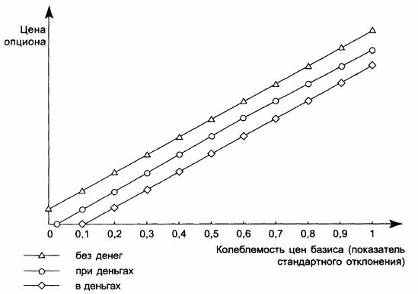
Рис. 8.7. Зависимость цены опциона пут (Put) от колебания (изменчивости) цен базиса



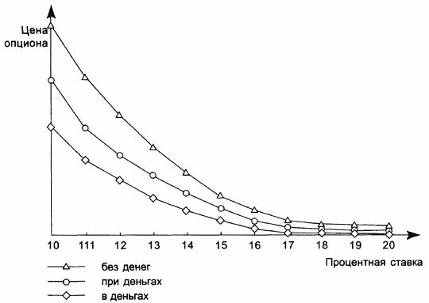
Рис. 8.8. Зависимость цены опциона пут (Put) от размера процентной ставки


В 1983 г. появилась модель цены европейского валютного опциона, разработанная Гарманом M. (Garman M.) и Колхагеном С. (Kohlhagen S.), основанная на классической модели Блэк–Шолза (Black–Scholes) (приложение 8). В алгебраической формуле и алгоритме расчета теоретической цены валютного опциона найдено удачное решение учета в стоимости опциона различий в доходности денежных вкладов на внутренних рынках сопоставляемых валют, что позволило модели Гармана–Колхагена (Garman–Kohlhagen) стать распространенным биржевым способом определения цен.

Модель Гармана–Колхагена (Garman–Kohlhagen) решает задачу для европейского опциона, для оценки американского опциона используется данная модель вместе с дополнительными расчетами (в электронном режиме), фиксирующими отклонения от нее, связанные с особенностями этого варианта опционов.

Модель Блэк–Шолза (Black–Scholes) также явилась исходной для разработки особенных формулы и алгоритма определения стоимости опциона с базисом в виде фьючерса, исключая фьючерсы, базирующиеся на экспертном суждении (приложение 9). В этом варианте расчета дисконтированию подвергается не только стоимость фьючерса при исполнении опциона, но и текущий курс фьючерса для принятого момента времени. Этот подход оказался полезным, поскольку (об этом упоминалось ранее и будет показано в дальнейшем) цена фьючерса определяется наращением доходов.

Перемены в биржевой торговле, в частности расширение режима отметки по рынку и применения правил предстоящей премии (Futures Style Premium), создали предпосылки для появления и освоения в опционной торговле новой модели и нового алгоритма расчета теоретической цены – биномиальной модели определения цены опционов (приложение 10), предъявленной в 1979 г. в соавторстве Д. Кокса, С. Росса, M. Рубинштейна (J. Сох, S. Ross, M. Rubinstein)¹. B приложении также показано развитие этого подхода в образе триномиальной модели.

Если модель Блэк–Шолза (Black–Scholes) основывается на математическом постулате стохастической аппроксимации, то модель Кокса–Росса–Рубинштейна (Сох–Ross–Rubinstein) исходит из постулата биномиального распределения – распределения суммы случайных величин, каждая из которых принимает одно из двух значений с противоположными вероятностями. Биномиальная модель, так же как и классическая модель, выявляет зависимости цен опционов от одних и тех же факторов – цены базиса, процентной ставки, колебаний цен базиса; однако алгоритмы учета влияния этих факторов, содержание расчетов и вычислительные приемы качественно различаются (см. приложения 5 и 10). В биномиальной модели больше объем вычислений, что в современных условиях не является ограничением. Ее применение широко распространено для сложных опционов (в частности, с базисом фьючерс), по которым также используется режим отметки по рынку. В то же время известно, что результаты расчетов по обеим моделям приблизительно совпадают. Последнее замечание не может служить основанием для отказа от биномиальной (триномиальной) модели (или для ограничений в ее применении), поскольку высокодинамичный рынок производных нуждается в возможно точных вычислениях цен (что облегчается современными электронными программами).

Биномиальная модель и ее продолжение в триномиальной модели вместе с моделью Блэк–Шолза (Black–Scholes), включая ее модификации, создали теоретико-вычислительный фундамент для выяснения возможных "справедливых" цен опционов, воздействия на них через осмысленное влияние на факторы цен (как порознь, так и в различных сочетаниях), предвидения тенденций и уровня опционных цен.



¹ Предложена для цен биржевых опционов: Black, Fischer / Scholes, Myron. The Pricing of Options and Corporate Liabilities // Journal of Political Economy. – 1973. – Vol. 81. – P. 637–654; Merton, Robert C. Theory of Ration Option Pricing // Bell Journal of Economices and Management Science. – 1973. – Vol. 4. – P. 141–183.

¹ В литературе и на практике для обозначения этой модели в ряде случаев используется словосочетание "модель опционного ценообразования" (Option Pricing Model – OPM).


8.2.4. Аналитические показатели (измерители)


Вместе с моделями для расширения инструментария участников рынков введен и освоен ряд аналитических показателей (измерителей), предназначенных для оценки рисков в сделках с опционами, оценки позиции и оказания помощи в принятии решений участниками торговли. Эти измерители группируются под различными названиями: "буквы греческого алфавита", "значимые показатели". Нужда в этих критериях вызвана асимметричным распределением рисков, профилем рисков, обусловленных характером самих опционов. В их ряд включены показатели дельта, ламбда, гамма, тета, вега, ро. Ими измеряется чувствительность (нем. Sensitivitat, Sensitivity), эластичность цен опционов от цены базиса, цены исполнения по базису, изменчивости цен базиса, длительности (срока) опциона, процентных ставок. Среди перечисленных и учитываемых этими измерителями факторов единственным постоянным для данного контракта (в пределах только неэкзотических опционов) является цена исполнения.

Совокупность критериев может служить для корректировки теоретических цен опционов, рассчитанных по тем или иным моделям, не замещая их. Проверка проводится по показателям, рассчитанным по историческим данным, тем самым вносятся поправки, выявленные по информации прошлого реального рынка. В этом просматриваются и ограничения на применение букв греческого алфавита: требуется предположение о приемлемости прошлых зависимостей для настоящего и будущего и соответственно появляется дополнительный (методический) риск.

Однако теоретики и практики рынков производных нашли основное применение этих показателей, отражающих риски, в оценке позиций и принятии в связи с этой оценкой решений. Такова сложившаяся традиция.

Включение букв греческого алфавита в раздел стоимостей опционов также сложилось исторически, хотя главным образом найденные зависимости используются для формирования позиций участников и стратегий их поведения. При использовании показателей дельта и гамма возможно формирование дельта-нейтрального и гамма-нейтрального портфелей.

Данные показатели неоднородны: те же дельта-фактор и гамма-фактор могут быть теоретически обоснованно определены для настоящего и будущего по моделям Black–Scholes, Cox–Ross– Rubinstein; для других критериев подобные решения не разработаны и не предложены.

Напомним, что в модели Black–Scholes элемент N(d₁) рассматривается и как дельта-фактор, а в биномиальной модели производится расчет коэффициента хеджирования, по величине обратного значению N(d₁).

Дельта (дельта-фактор, дельта опциона, Δ) – показывает зависимость изменений цены опциона от изменений курса (цен) основания (базиса) и тем самым выявляет чувствительность (эластичность) цены опциона от курса (цен) базиса¹:

Δ =	Абсолютная величина изменений (прироста, снижения) цены опциона (Call или Put)
	Абсолютная величина изменений (прироста, снижения) курса (цены) основания

Расчет производится по данным одного и того же прошлого периода (периодов), что справедливо и для других показателей.

Связь между ценой опциона (Call, Put) и ценой базиса является криволинейной (см. главу 5). Для одного и того же базиса у опциона колл (Call) – положительная Δ и у опциона пут (Put) – отрицательная Δ. Дельта опциона Call принимает значения от 0 до 1 (Δ > O); дельта опциона Put находится в границах от –1 до 0 (Δ < О), или соответственно

Δс =	dC
	dS

  = N(d₁)>0;

ΔP =	dP
	dS

  = N(d₁) – 1 = –N(–d₁)<0,


где Δ_C, Δ_P – значения дельта-фактора соответственно для колла (Call) и пута (Put); dC, dS, dP – приращение значений С, S, P.

Величина показателя тем больше (при прочих равных условиях), чем значительнее ситуация в деньгах. Величина дельта-фактора для многих опционов с одним и тем же базисом аддитивна. Агрегированный показатель Δ многих позиций вычисляется как средневзвешенная (арифметическая) величина отдельных значений.

Ламбда (Λ), встречается обозначение этого показателя греческой буквой "омега" – Ω¹ – показатель процентного изменения цены опциона при изменении цены (курса) базиса на 1%. Соответствует классическому представлению о показателе эластичности по цене товарного рынка и толкуется одинаково.

Показатель для колла (Call) – положительный и для пута (Put) – отрицательный. В случае, если Λ ≤ 1 (опцион эластичен), то этот показатель свидетельствует при изменении цены базиса о повышенном риске для участника опционной торговли по сравнению с риском для участника реального рынка.

Значение Λ для опциона Call плавно (по гиперболе) возрастает для ситуаций без денег и снижается в ситуации в деньгах; для Put – плавно (по параболе) возрастает (стремится к нулю) в ситуации в деньгах и снижается в ситуации без денег.

Согласно модели Сох – Rubinstein²:

Λ(ΩC) =	SΔC
	C

  =

SN(d1)

C

 

и

ΛP = (ΩP) =	SΔP
	P

  =

S[N(d1) – 1]

P

 

Гамма (Г) – показывает зависимость изменения Δ от изменений курса (цен) основания (базиса) и тем самым выявляет чувствительность (эластичность) величины Δ от курса (цен) базиса¹:

Г =	Абсолютная величина изменений (прироста, снижения) дельта-фактора
	Абсолютная величина изменений (прироста, снижения) курса (цены) основания

 

Сообразно с этим (по формуле Dubofsky²)




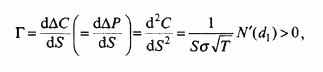
где N'(d₁) – распределение по N(d₁).

Значение показателя положительное. При нарастании абсолютной разницы между текущей ценой базиса и ценой исполнения стремится к нулю. Наивысшая величина Г соответствует равенству



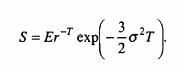
Критерий Г – единственный среди критериев, обозначенных буквами греческого алфавита, непосредственно не связанный с ценой опциона.

Тета (Θ) – показывает, сколько (как много) временной стоимости теряет опцион в каждый день, оставшийся до окончания опциона.

Соответственно модели Сох – Rubinstein³:



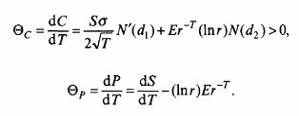
Показатель Θ данного опциона сохраняет близкое к постоянной величине значение приблизительно на протяжении 2/3 всего срока

опциона и повышается к концу этого срока. Значение показателя у опционов с краткими сроками исполнения в ситуации "при деньгах" близко к максимуму.

Вега (V – латинский алфавит)¹ – показывает изменение цены опциона в зависимости от изменения колебаний цен основания на 1%:



В знаменателе указывается абсолютное значение изменений цен при перемене колебаний на 1%. По модели Сох – Rubinstein²:



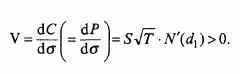
"Вега" всегда положительная, для Put и Call одинакова. Этот показатель особенно значим для длительных опционов (в отличие от критерия Θ).