5 Ионные реакции осаждения, нейтрализации, гидролиза

Вид материала

Документы

Содержание Практическая работа Определение некоторых катионов и анионов в растворе Первый закон термодинамики и его применение Теплота (Q), сообщаемая системе, расходуется на увеличение внутренней энергии системы (U) и на совершение этой системой работы ( Р. Поэтому уравнение первого закона термодинамики:Q Н следовало бы называть изменением энтальпии, но для краткости называют энтальпией.Пример. Нr положительны. Такие реакции называют эндотермическими. Стандартное состояние и стандартная Стандартные энтальпии образования некоторых веществ при 298 К Нf = 393,5 кДж/мольН2(г) + 1/2О2(г) = Н2О(ж) Н Нf =  74,9 кДж/моль2С(графит) + Н2(г) = С2Н2(г); Н Вопросы для проверки знаний

Подобный материал:

• Рекомендации к зачёту, 133.1kb.
• Написать краткие ионные и молекулярные уравнения реакций гидролиза карбоната натрия,, 4.27kb.
• Методический пакет учебного курса, 331.54kb.
• Молекулярно-динамическое моделирование осаждения металлического нанокластера на подложку, 66.11kb.
• Наносимые электрохимическими методами на поверхность детали в результате осаждения, 96.3kb.
• Для подготовки к экзамену по общей химии (2 семестр) Кинетика, 73.49kb.
• Программа коллоквиумов по курсу физической химии, 99.84kb.
• Оглавление, 334.79kb.
• Календарный план занятий по физической химии в весеннем семестре 2008/2009 уч года, 32.67kb.
• Отчет 86 с., 34 рис., 15 табл., 53 источника, 2 приложения. Ключевые слова : структура, 56.56kb.

Решение

Воспользуемся уравнением:

с₁×V₁ = с₂×V₂

с(NaOH)×24 мл× = 0,12 моль/л(НСl)× 20 мл

с(NaOH) = 0,1 моль/л.

Практическая работа

Определение концентрации водных растворов щелочи

При помощи метода нейтрализации или кислотно-основного титрования определяют концентрации кислот и щелочей. Простейшим случаем является титрование сильной кислоты щелочью или сильной щелочи сильной кислотой. Образующаяся в результате реакции соль не гидролизуется, значение рН в конце титрования 7.

Задание. Определить концентрации двух растворов NaOH.

1. 
   Из мерной колбы, в которой находится анализируемый раствор щелочи, пипеткой отбирают пробу – 20,0 мл раствора и осторожно помещают в коническую колбу для титрования на 100 или 200 мл.
   
2. К щелочи добавляют индикатор (фенолфталеин), раствор приобретает малиновую окраску. Осуществляют титрование раствора. Из бюретки медленно приливают стандартный раствор кислоты до тех пор, пока не установится точка нейтральности: раствор станет бесцветным (рис. 61).
   
3. Рассчитывают концентрацию щелочи по уравнению:
   

с(NaOH) = с(HCl) ^. V(HCl) / V(NaOH);

Повторяют измерения со следующим неизвестным раствором (рис. 61).


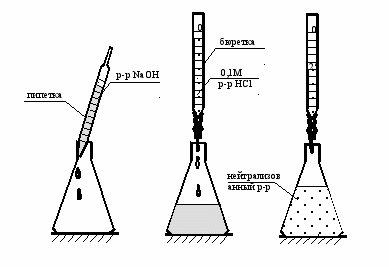
в)


Рис. 61. Титрование раствора гидроксида натрия неизвестной концентрации стандартным раствором соляной кислоты

Определение некоторых катионов и анионов в растворе

Для проведения качественного анализа используют от 0,5 до 5 мл раствора.

Для определения катионов Ag⁺ и Pb²⁺ используют в качестве реагента 2М раствор НСl. К 2-3 каплям раствора нитрата серебра прилейте 1-2 капли 2М раствора НСl – выпадает белый творожистый осадок AgCl.

AgNO₃ + HCl ® АgCl¯ + HNO₃

На прямом солнечном свету осадок довольно быстро разлагается. Его окраска становится сероватой, затем темно-серой и, наконец, черной:

АgCl¯ ® Ag¯ + Cl×

При определении иона Pb²⁺ к 3-4 каплям раствора соли свинца добавьте 2-3 капли 2М раствора НСl – выпадает белый творожистый осадок PbCl₂. Для более полного осаждения PbCl₂ добавляют этанол. Чтобы различить осадки АgCl и PbCl₂, используют хорошую растворимость последнего в горячей воде.

Для определения ионов Са²⁺ и Ва²⁺ используют 1М раствор H₂SO₄. К раствору, содержащему катионы Са²⁺ и Ва²⁺, добавляют 1М раствор H₂SO₄ и этанол для более полного осаждения ионов в виде сульфатов:

СaCl₂ + H₂SO₄ ® СaSO₄ ¯ + 2HCl

BaCl₂ + H₂SO₄ ® BaSO₄ ¯ + 2HCl


Чтобы различить соли кальция и бария, следует помнить, что соли кальция окрашивают пламя горелки в кирпично-красный цвет, а соли бария – в зеленый с оттенком желтого.

Катионы Al³⁺, Zn²⁺ осаждаются в виде амфотерных гидроксидов 2М раствором NaOH:


AlCl₃ + 3NaOH ®Al(OH)₃¯ + 3NaCl

ZnCl₂ + 2NaOH ®Zn(OH)₂¯ + 2NaCl


Образующиеся гидроксиды легко растворяются в разбавленных кислотах и в избытке щелочи c образованием бесцветных гидроксоалюминатов [Al(OH)₄]^– и гидроксоцинкатов [Zn(OH)₄]^2–

При обнаружении галогенид-анионов в качестве реагента используют раствор AgNO₃. При добавлении его к хлоридам, бромидам и иодидам образуются осадки солей серебра, нерастворимые в азотной кислоте: AgCl – белого, AgBr – желтоватого, AgI – ярко-желтого цвета.

При обнаружении сульфат анионов используют в качестве реагента раствор BaCl₂ в нейтральной или слабощелочной среде. Образуется нерастворимый осадок BaSO₄:

Na₂SO₄ + BaCl₂ ® BaSO₄¯ + 2NaCl

Тема 6. Законы термодинамики и кинетики


6.1. Законы термодинамики

Твердые, жидкие и газообразные тела, занимающие некоторый объем, могут находиться в относительном покое, но атомы и молекулы тел непрерывно совершают невидимые человеческому глазу движения. Неподвижное тело обладает внутренней энергией U, слагающейся из кинетической (энергии движения микрочастиц) и потенциальной энергии (энергии притяжения и отталкивания микрочастиц).


Первый закон термодинамики и его применение

к химическим реакциям

В соответствии с законом сохранения энергии между теплотой Q, сообщаемой нагревателем, и изменением энергетического состояния газообразного тела существует равенство:

Q = U + А,

где U  изменение внутренней энергии газа в результате нагревания, А работа расширения, совершаемая газом при постоянном давлении Р.

Работа расширения вычисляется по уравнению:

А = Р V,

где V  изменение объема газа при его расширении.

Уравнение

Q = U + РV


есть математическая форма выражения первого закона термодинамики.



Теплота (Q), сообщаемая системе, расходуется на увеличение внутренней энергии системы (U) и на совершение этой системой работы (A=PV).



Формулировка первого закона термодинамики эквивалентна формулировке закона сохранения энергии: энергия не возникает из ничего и не исчезает бесследно: она лишь превращается из одних видов в другие, причем в строго эквивалентных количествах. В термодинамике рассматривают только две формы передачи энергии  теплоту Q и работу А.

Обычно химические реакции проводят при постоянном внешнем давлении Р. Поэтому уравнение первого закона термодинамики:


Q = U + РV

преобразуют следующим образом:

Q_p = U₂ – U₁+ P(V₂ – V₁) или


Q_p = (U₂ – РV₂) – (U₁ – PV₁)


Функцию U+PV, которая не зависит от пути процесса, а лишь от начального (оно обозначено цифрой 1) и конечного (оно обозначено цифрой 2) состояний, называют энтальпией и обозначают символом Н. Тогда


Q_р = (U + РV) = Н

или

Q_р = (H_кон –Н_нач) = Н


Уравнение Q_р = Н представляет математическую форму основного закона термохимии, который установлен русским академиком Г. И. Гессом в 1836 г.:


энтальпия реакции Н_r, протекающей при постоянном давлении Р и температуре Т, не зависит от промежуточных стадий, а определяется лишь начальным и конечным состояниями системы.



Обозначение  Н следовало бы называть изменением энтальпии, но для краткости называют энтальпией.


Пример. Вычислить энтальпию реакции (Н_r, символ «r» означает reaction  реакция) графита с кислородом:

С(гр.) + ½ О₂(г) = СО (г),

если известны энтальпии реакций:

1) С(гр.) + О₂(г) = СО₂ (г); Н_r = 393,5 кДж и

2) СО(г) + ½О₂(г) = СО₂ (г); Н_r = 283 кДж

С химическими уравнениями и их энтальпиями можно оперировать так же, как с алгебраическими уравнениями. Интересующую нас реакцию можно получить, если вычесть из уравнения (1) уравнение (2):

С(графит) + О₂(г)  СО(г)  ½О₂(г) = СО₂ (г)  СО₂ (г); и Н_r(1)  Н_r(2) = [(393,5)  ( 283)]

или

С(графит) + ½ О₂(г) = СО (г); Н_r =  110,5 кДж


Следовательно, энтальпию этой реакции можно получить вычитая из энтальпии Н_r первой реакции энтальпию Н_r второй реакции.

Приведенные в примере химические уравнения называются термохимическими. В них указаны физические состояния реагирующих веществ и энтальпии реакций.

Если превращения веществ сопровождаются поглощением энергии, то  Н_r положительны. Такие реакции называют эндотермическими. Если превращения веществ сопровождаются выделением энергии, то Н_r отрицательны. Такие реакции называют экзотермическими.


Стандартное состояние и стандартная

энтальпия образования вещества

Стандартное состояние индивидуального вещества  это физическое состояние 1 моль индивидуального химического соединения при внешнем давлении 1 атм (1, 01310⁵ Па) и температуре Т К в том агрегатном состоянии, которое устойчиво в данных условиях. Стандартное состояние индивидуального вещества характеризуется стандартной энтальпией образования Н_f ⁰. Нижний символ «f» означает formation  образование, верхний индекс нуль служит указанием стандартного состояния, т.е. значение энтальпии образования определено при внешнем давлении, равном 1 атм. Стандартное состояние и стандартная энтальпия могут относиться к любой температуре. В табл. 10 приведены стандартные энтальпии образования некоторых веществ при 298 К. Энтальпии образования простых веществ равны нулю при любых температуре и давлении.

Вещество, состоящее из атомов одного химического элемента, может быть представлено различными молекулярными структурами, но простому веществу в термодинамике соответствует только одно из них. Например, из двух молекулярных образований кислорода О₃(г) и О₂(г) только О₂(г) отвечает простому веществу, для которого Н_f⁰ принято равным нулю. Из двух химических веществ С(графит) и С(алмаз) только графит рассматривается как простое вещество, для которого Н_f⁰ принято равным нулю.


Т а б л и ц а 10

Стандартные энтальпии образования некоторых веществ при 298 К

Вещество	Нf0, кДж/моль	Реальные или гипотетические реакции образования, для которых приведены значения Нf0
Al(т) Al2О3(т)	0  1676,0	 2Al(т) + 3/2О2(г) = Al2О3(т)
О2(г) O3(г)	0 +142,3	 3/2О2(г) = О3(г)
С(графит) С(алмаз)	0 1,828	 С(графит) = С(алмаз)
Н2(г) СН4(г)	0  74,9	 С(графит) + 2Н2(г) = СН4(г)
С2Н2(г) С2Н5ОН (ж)	+ 226,8  277,6	2С(графит) + Н2(г) = С2Н2(г) (ацетилен) 2С(графит) + 3Н2(г) + 1/2О2(г) = С2Н5ОН (ж)
СО(г) СО2(г)	110,5 393,5	С(графит) + 1/2О2(г) = СО(г) С(графит) + О2(г) = СО2(г)
Са(т) СаСО3(т)	0 1207,0	 Са(т) + С(графит) + 3/2О2(г) = СаСО3(т)
СаО(т) Са(ОН)2(т)	635,5 986,6	Са(т) + 1/2О2(г) = СаО(т) Са(т) + О2(г) + Н2(г) = Са(ОН)2(т)
Н2О(г) Н2О(ж)	241,8 285,8	Н2(г) + 1/2О2(г) = Н2О(г) Н2(г) + 1/2О2(г) = Н2О(ж)
N2(г) NO(г)	0 +90,25	 1/2N2(г) + 1/2О2(г) = NO(г)
NO2(г) NH3(г)	+33 46,2	1/2N2(г) + О2(г) = NO2(г) 1/2N2(г) + 3/2Н2(г) = NH3(г)
Au(т) Au2O3(т)	0 3	 2Au(т) + 3/2O2(г) = Au2O3(т)
Fe(т) Fe2O3(т)	0 822,2	 2Fe(т) + 3/2O2(г) = Fe2O3(т)

Стандартная энтальпия образования сложного вещества  это энтальпия реакции синтеза его из простых веществ, при 1 атм. Например, при сжигании углерода (графита) или при сжигании водорода определяют энтальпии образования СО₂ и Н₂О по реакциям:

С(графит) + О₂(г) = СО₂(г);  Н_f⁰ = 393,5 кДж/моль


Н₂(г) + 1/2О₂(г) = Н₂О(ж) Н_f⁰ =  285,8 кДж/моль


Не всегда значения Н_f⁰ сложных веществ определяют в реакции синтеза этого вещества из простых. Трудно представить, что из одних и тех же простых веществ (водорода и графита) в одном случае можно получить метан, а в другом  ацетилен:


С(графит) + 2Н₂(г) = СН₄(г);  Н_f⁰ =  74,9 кДж/моль


2С(графит) + Н₂(г) = С₂Н₂(г); Н_f⁰ = + 226,8 кДж/моль


Метод расчета Н_f⁰ большинства органических соединений основан на измерении количества тепла, выделяющегося при сжигании их в атмосфере кислорода. Например, чтобы определить Н_f⁰ метана, его сжигают в кислороде и определяют количество выделившейся энергии, т. е. энтальпию химической реакции, Н_r⁰:


СН₄(г) + 2О₂(г) = СО₂(г) + 2Н₂О(ж); Н_r⁰ =  890,2 кДж


Подобным образом поступают с водородом и углеродом, сжигая их в кислороде:

1. С(гр) + О₂(г) = СО₂(г); Н_f⁰(1) = 393,5 кДж
   

2. Н₂(г) + ½О₂(г) = Н₂О(ж) Н_f⁰(2) =  285,8 кДж

Результаты сжигания трех веществ позволяют рассчитать энтальпию образования метана. Нетрудно убедиться, что если из суммы уравнений (1) и (2) вычесть уравнение реакции горения метана, то получим, соответственно, энтальпию образования метана из простых веществ.




С(гр) + О₂(г) = СО₂(г); Н_f⁰(1) = 393,5 кДж

+

2Н₂(г) + О₂(г) = 2Н₂О(ж); Н_f⁰(2) =  2285,8 кДж



СН₄(г) + 2О₂(г) = СО₂(г) + 2Н₂О(ж); Н_r⁰ =  890,2 кДж




С(гр) + 2Н₂(г) = СН₄(г)

Н_f⁰(СН₄)=[393,5]+[2285,8][890,2]=74,9 кДж/моль


В соответствии с законом Гесса для расчета энтальпии химической реакции (Н_r⁰) следует из алгебраической суммы энтальпий образования продуктов реакции вычесть сумму энтальпий образования исходных веществ:

Н_r⁰ =[сумма энтальпий образования продуктов реакции]  [сумма энтальпий образования исходных веществ]


Вопросы для проверки знаний

1. Какая формулировка первого закона термодинамики устанавливает связь между теплотой, работой и внутренней энергией?
   
2. Теплота процесса при постоянном давлении связана с изменением энтальпии процесса равенством: Q_p = . Можно ли утверждать на основании этого равенства, что энергия в форме теплоты расходуется на изменение внутренней энергии системы и на совершение этой системой работы?
   
3. Какое состояние вещества в термодинамике называется стандартным?
   
4. *Можно ли утверждать, что закон Гесса  это закон сохранения энергии, примененный к химическим реакциям?
   

*Упражнения

1. Объясните, почему энтальпия образования жидкой воды (285,8 кДж/моль) больше энтальпии образования газообразной воды ( 241,8 кДж/моль).
   
2. Докажите, что при сгорании 1 кг этанола теплоты выделиться больше, чем при сгорании 1 кг ацетилена.
   

**Второй закон термодинамики

Первый закон термодинамики можно выразить всего двумя словами: энергия сохраняется. Добавим, не вдаваясь в детали, что энергия  это способность совершать работу. Приведенная характеристика энергии необходима нам, чтобы понять сущность второго закона термодинамики.

Полное количество энергии должно сохраняется в любом процессе. Об этом говорит закон сохранения энергии. Как показывает многовековая практическая деятельность людей, перераспределение энергии между телами происходит необратимым образом. Эта асимметрия в природе позволяет разделить все процессы на два типа:

1. самопроизвольные процессы, идущие сами по себе, без какого-либо воздействия извне. Для осуществления этих процессов не требуется совершения работы;
   
2. несамопроизвольные процессы, не идущие сами по себе, требующие для своей реализации определенного воздействия извне, совершения работы.
   

Расширение газа в пустоту является самопроизвольным процессом, но для того, чтобы газ вернуть в исходное положение, требуется затратить работу на его сжатие. Самопроизвольно сжатие газа не происходит.

Энергия от горячего к холодному телу переходит в форме теплоты самопроизвольно, но обратный процесс требует затраты работы и является несамопроизвольным. Чтобы морозильная камера холодильника работала, отдавая теплоту в окружающую среду, должен совершать работу электромотор.

На гидроэлектростанции вода, самопроизвольно падающая с высоты и вращающая ротор турбины, производит электрическую энергию. Но вода не возвращается самопроизвольно с нижнего на верхний бьеф. Чтобы поднять воду требуется совершить работу. Можно убедиться на ряде примеров в том, что самопроизвольный процесс приводит к рассеянию энергии и увеличению беспорядка в системе.

Взаимодействие металлического натрия с водой представляет собой пример самопроизвольного процесса, результатом которого является образование раствора NaOH и выделение газообразного водорода. Процесс получения металлического натрия из гидроксида натрия – несамороизвольный процесс, чтобы реализовать его надо затратить энергию.

Вывод: единственным результатом любого самопроизвольного процесса в природе является движение к устойчивому состоянию или, как говорят в термодинамике, к состоянию равновесия.

От качественного описания самопроизвольных процессов в системе необходимо перейти к их количественной характеристике. Параметр пригодный для оценки направления самопроизвольного процесса был найден и назван энтропией S. Изменение энтропии системы позволяет определить направление самопроизвольного процесса. В термодинамике доказано, а мы примем в качестве постулатов следующие положения:

1. изменение энтропии системы S_сис = S_кон  S_нач определяется уравнением:
   

S_сист = Q/Т,

где S_кон и S_нач – энтропии конечного и начального состояния системы, т.е. изменение энтропии системы определяется количеством теплоты Q, сообщенной системе в равновесном процессе, отнесенное к абсолютной температуре Т;

2. в самопроизвольном процессе:


S_сист  Q/Т


3. если система изолирована от окружающей среды, то Q = 0 и

S_сист  0


Из неравенства S_сист  0 следует важный вывод: изменение энтропии системы служит тем параметром, который определяет направление самопроизвольного процесса. Теперь мы можем дать следующую формулировку второго закона термодинамики: в системе самопроизвольный процесс происходит в направлении увеличения энтропии системы.

Таким образом, чем больше беспорядок в системе, чем в большей степени рассеяна энергия между телами её составляющими, тем больше энтропия системы.

Энтропия S оправдывает свое название. Название состоит из греч. еn  предлог «в» и trope  «превращение». Буквально «превращение в». Имеется в виду направленность превращения энергии во все менее ценные формы, т.е. рассеяние энергии и увеличение беспорядка.