Прикладная графическая программа. Прикладная программа передает данные и сформированные графические команды в графическую систему (рис. 1) [14]. Рис. Схема взаимодействия прикладной программы и графической системы

Вид материала

Программа

Содержание 7.4. Параметрические бикубические поверхности 7.5. Преобразования параметрических кривых и кусков поверхностей 7.6. Визуализация трехмерных объектов 7.7. Методы удаления скрытых линий и поверхностей 7.8. Закрашивание поверхностей Зеркальное отражение Не идеальное зеркальное отражение Метод Гуро Метод анализа излучательности 7.9. Детализация поверхностей 7.10. Построение трехмерных сцен

Подобный материал:

• Рабочая программа дисциплины для студентов магистратуры, обучающихся по направлению, 120.54kb.
• Магистерская программа «Информационные технологии и информационные системы» по направлению, 34.28kb.
• Программа вступительного испытания по предмету прикладная этика для поступающих, 307.5kb.
• Рис Физический и логический обмен данными по сети 21 Рис Ахитектура процессов в распределенных, 932.01kb.
• Рис. Сферы взаимодействия психики и личности (Управляющей психики) Рис., 2.3kb.
• Методика ми5 проверки цепи фаза нуль в электроустановках до 1 кВ с глухим заземлением, 53.81kb.
• Программа дисциплины Современная прикладная алгебра для направления 010500 Прикладная, 214.78kb.
• Основная образовательная программа высшего профессионального образования 230700., 513.26kb.
• Программа вступительного экзамена по математике подготовки магистров по направлению, 86.94kb.
• Прикладная программа для создания, редактирования (обработки) и просмотра графических, 47.05kb.

При аппроксимации управляющих точек Р₁, Р₂, …, Р_n последовательностью В-сплайнов между каждой парой соседних точек Р_i и Р_i+1 последовательно используются геометрические матрицы:

Gⁱ_sх = 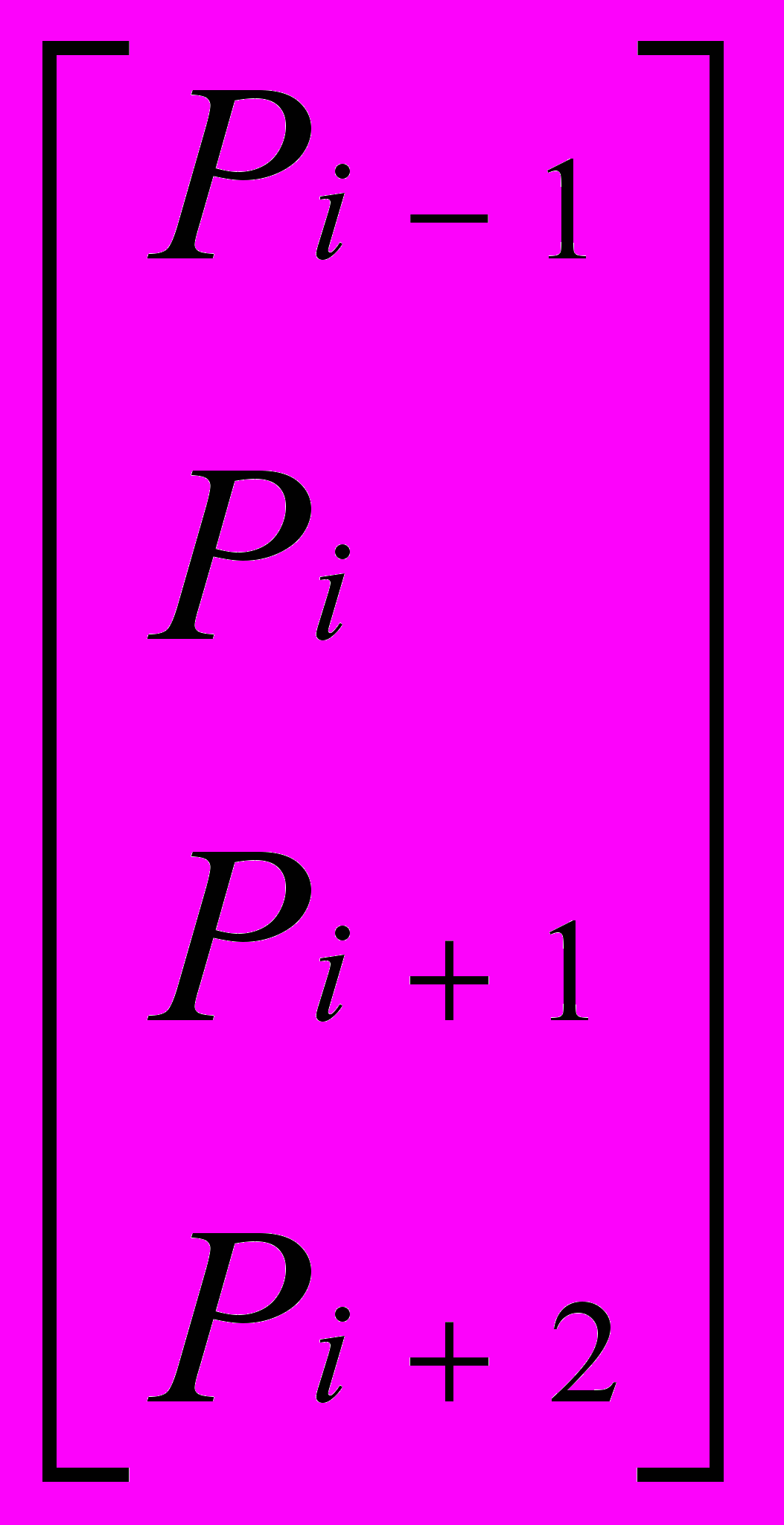, 2  i  n – 2.

В общем случае управляющие точки В-сплайна не лежат на кривой, однако, при определенных условиях В-сплайн может проходить через любые управляющие точки. В-сплайн, описываемый приведенной выше формулой, пройдет через управляющую точку Р_i в случае, если точки Р_i, Р_i+1 и Р_i+2 совпадают. Обычно форму В-сплайнов применяют для аппроксимации продолжительных отрезков кривых, задаваемых значительным (более пяти) числом управляющих точек.

Наиболее широко в компьютерной графике используются так называемые неравномерные рациональные В-сплайны (NURBS – Non-Uniform Rational B-Splines). NURBS широко применяются в системах геометрического моделирования и трехмерной графике.


7.4. Параметрические бикубические поверхности


Параметрические бикубические поверхности задаются многочленами третьей степени от двух параметров s и t. Как и прежде, будем рассматривать только уравнение для координаты х:

x(s, t) = a_11xs³t³ + a_12xs³t² + a_13xs³t + a_14xs³ +

+ a_21xs²t³ + a_22xs²t² + a_23xs²t + a_24xs² +

+ a_31xst³ + a_32xst² + a_33xst + a_34xs +

+ a_41xt³ + a_42xt² + a_43xt + a_44x.

Или:

x(s, t) = [s³ s² s 1] 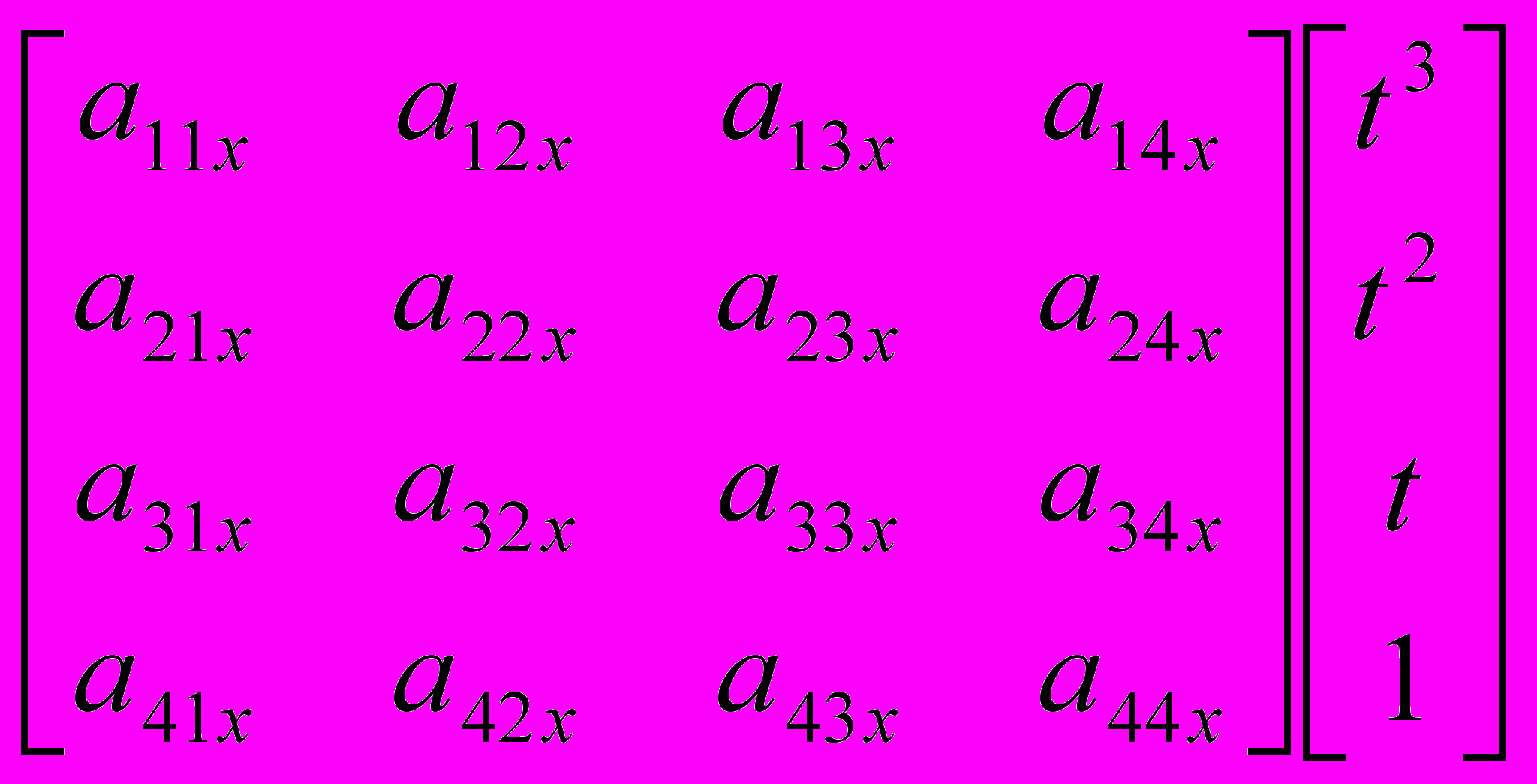= S C_x T^T,

где: S = [s³ s² s 1],

T = [t³ t² t 1],

T^T – транспонированная матрица Т.

Матрица С_x задает коэффициенты бикубического многочлена. Существуют еще матрицы С_y и С_z, которые определяют коэффициенты бикубических уравнений y(s, t) и z(s, t).

Изменяя оба параметра s и t от 0 до 1, можно определить все точки на куске поверхности. Если одному из параметров присвоить постоянное значение, а второй параметр изменять в пределах 0…1, то в результате получается кубическая кривая.

Форма Эрмита для задания бикубической поверхности: перепишем уравнение кубической кривой Эрмита от параметра s так, чтобы геометрический вектор Эрмита был не константой, а функцией от параметра t:

x(s, t) = S M_h G_hx(t) = S M_h .

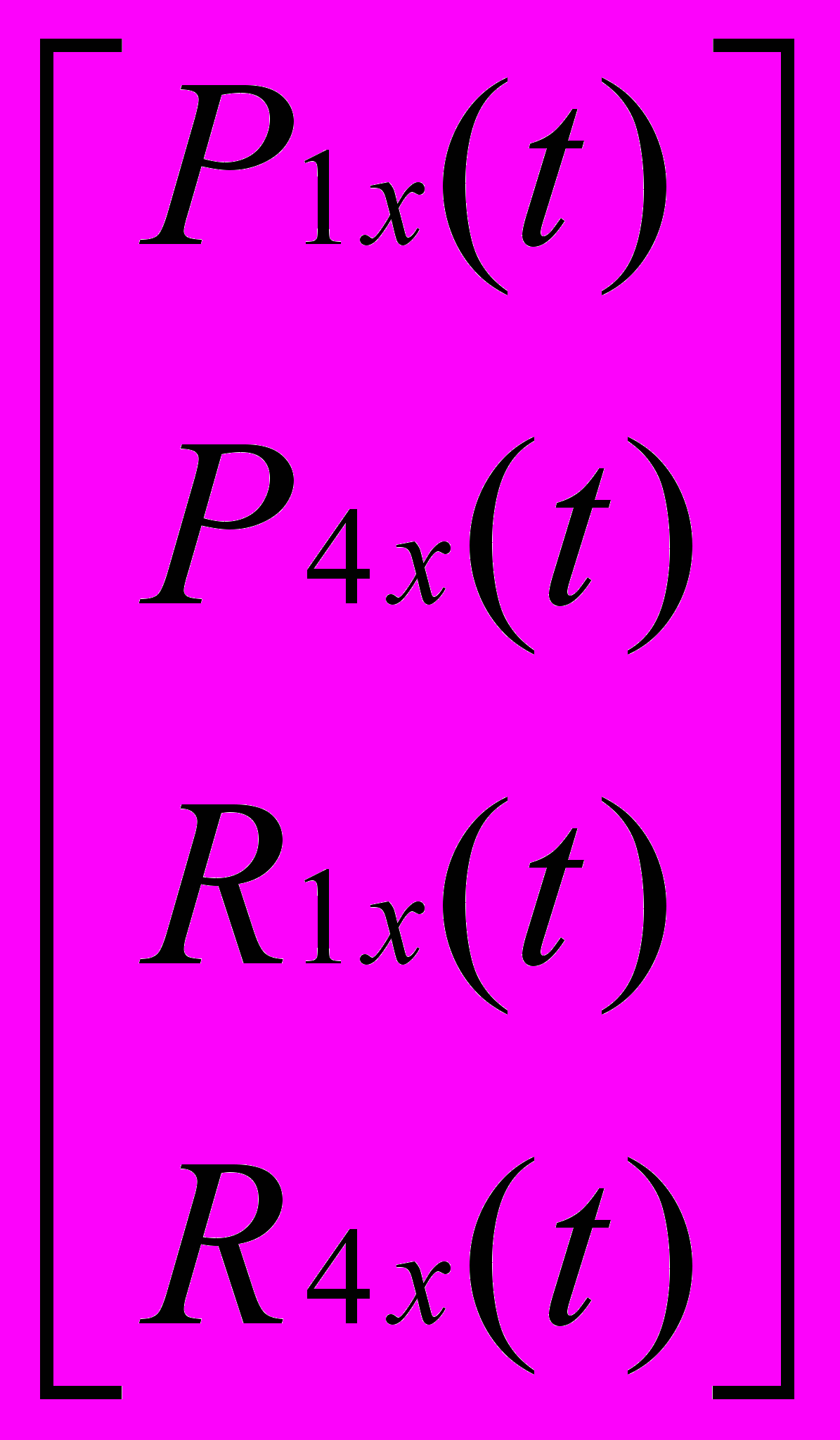При фиксированном значении параметра t функции P_1x(t) и P_4x(t) описывают х-компоненты начальной и конечной точек кривой, задаваемой параметром s. Аналогично, R_1x(t) и R_4x(t) описывают касательные векторы в конечных точках кубической кривой. Каждая из кривых P_1x(t), P_4x(t), R_1x(t), R_4x(t) представлена кубическим многочленом в форме Эрмита:

P_1x(t) = T M_h , P_4x(t) = T M_h ,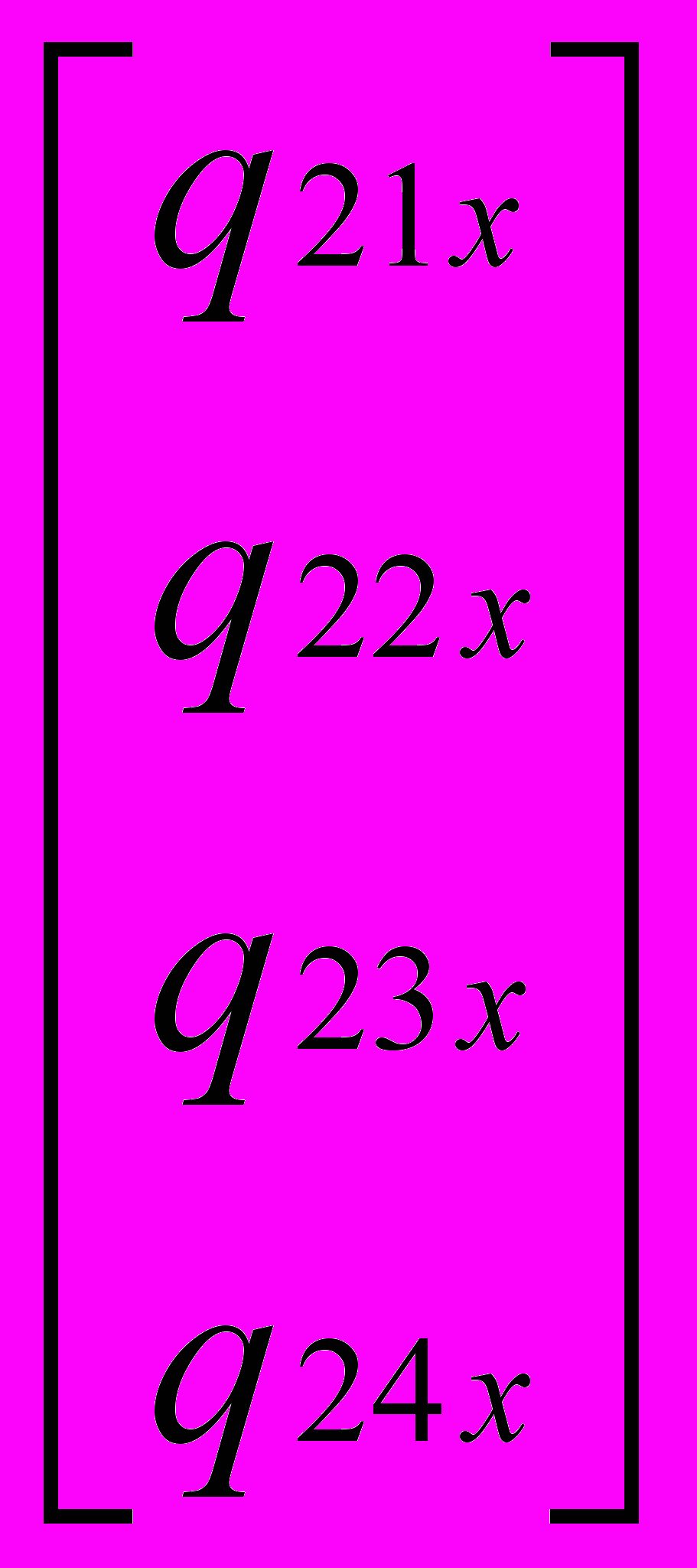

R_1x(t) = T M_h 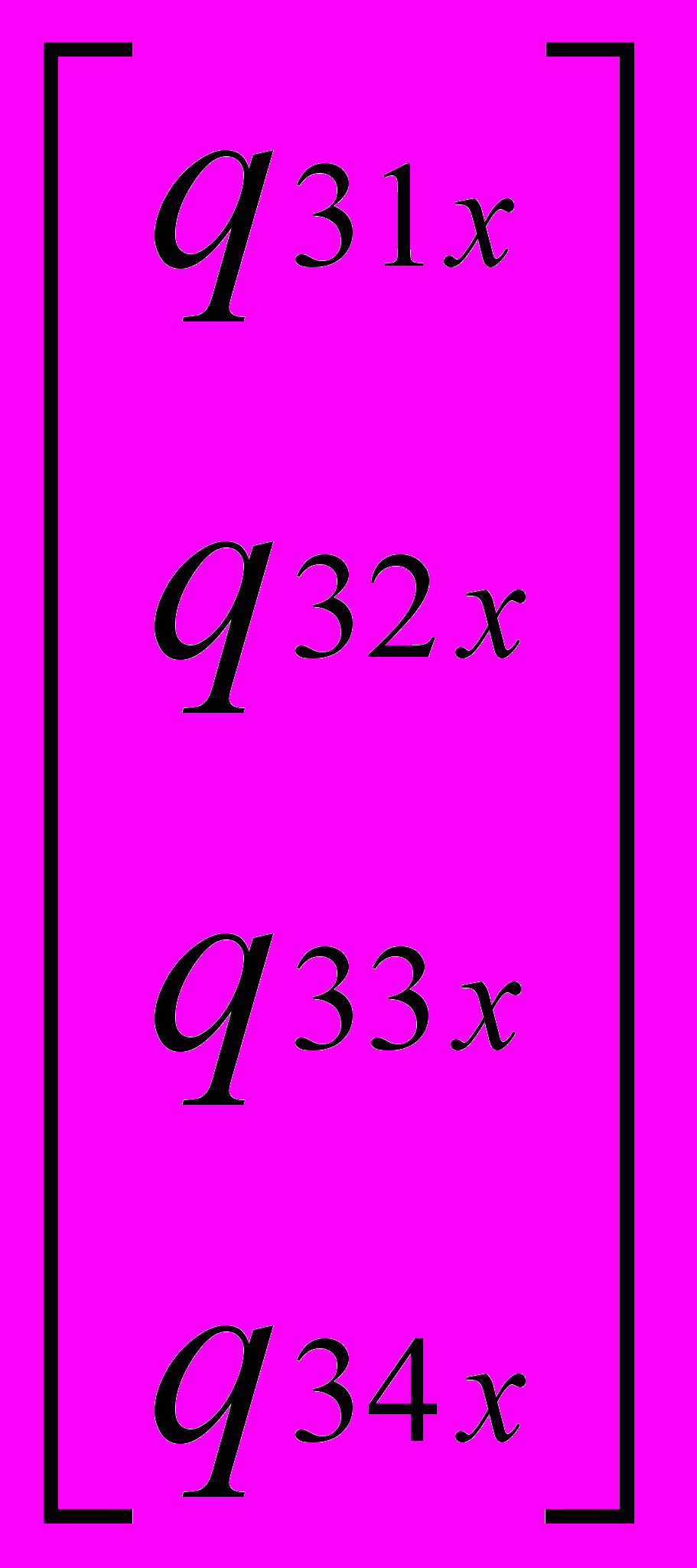, R_4x(t) = T M_h .

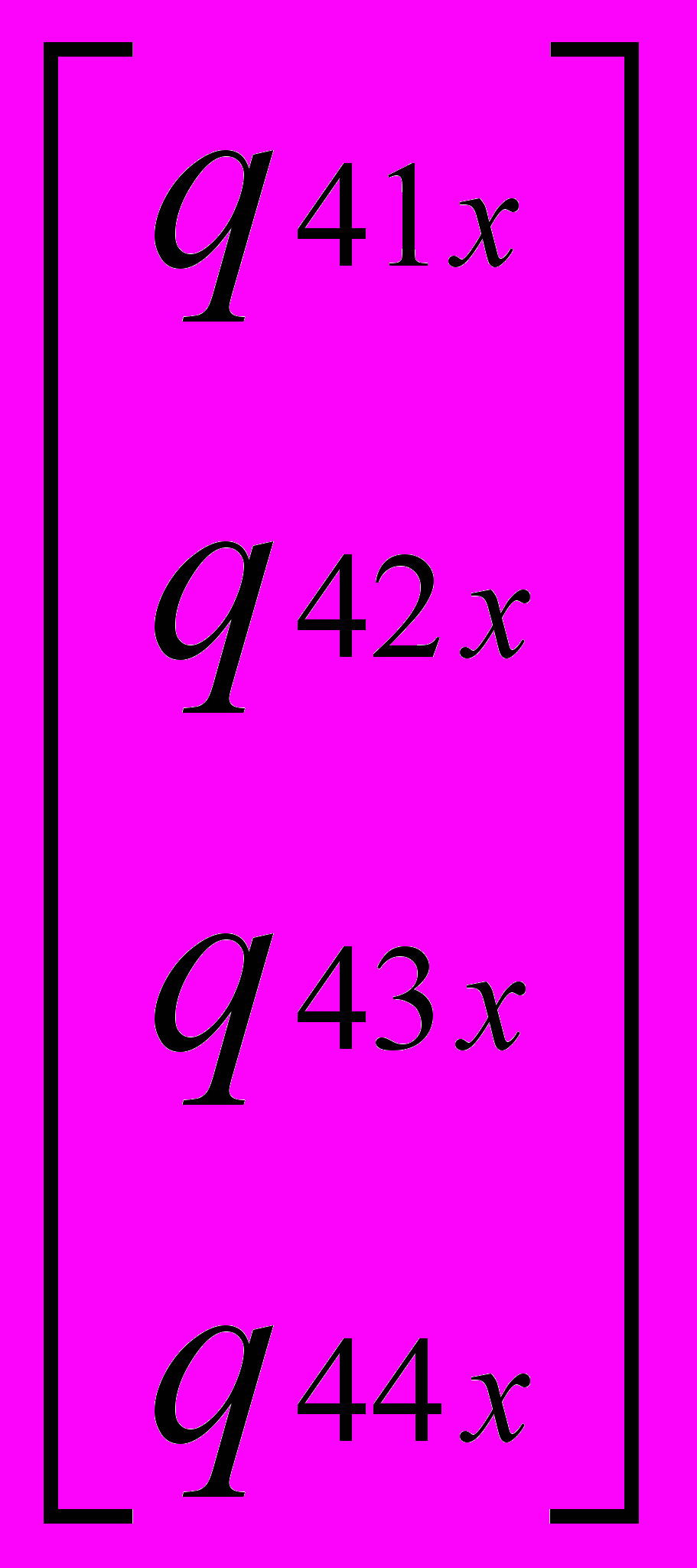Объединяя эти выражения, получим:

x(s, t) = S M_h Q_hx M_h^T T^T = S M_h 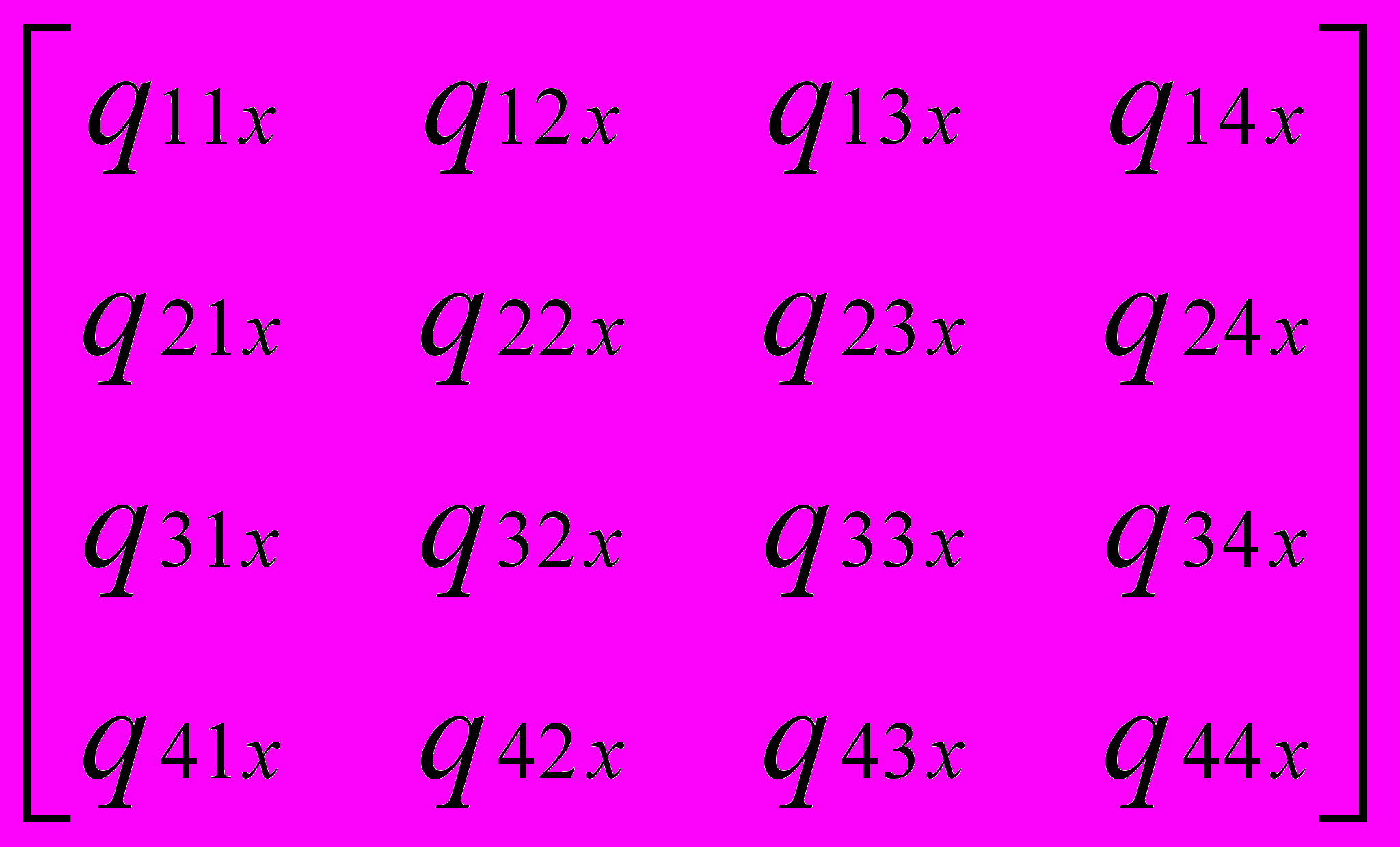M_h^T T^T.

Таким образом, бикубическая поверхность Эрмита задается 16 параметрами, из которых:

q_11x = x(0, 0), q_12x = x(0, 1), q_21x = x(1, 0), q_22x = x(1, 1) – координаты углов куска поверхности;

q_13x = dx/dt (0, 0), q_14x = dx/dt (0, 1), q_23x = dx/dt (1, 0), q_24x = dx/dt (1, 1), q_31x = dx/ds (0, 0), q_32x = dx/ds (0, 1), q_41x = dx/ds (1, 0), q_42x = dx/ds (1, 1) – х-компоненты касательных векторов в угловых точках для каждой из ограничивающих кусок поверхности параметрических кривых;

q_33x = d²x/dsdt (0, 0), q_34x = d²x/dsdt (0, 1), q_43x = d²x/dsdt (1, 0), q_44x = d²x/dsdt (1, 1) – частные производные по обоим параметрам s и t в угловых точках куска поверхности (кривизна).

При соединении кусков бикубических поверхностей должны выполняться условия непрерывности: кривые, заданные на общем ребре, должны быть одинаковыми (должны совпадать начальные и конечные точки кривых и значения касательных векторов к кривым в этих точках); касательные вектора, пересекающие ребро, должны иметь одно и тоже направление для обоих сочленяющихся кусков.

Уравнения для кусков Безье выводятся также, как и для формы Эрмита. В результате получается:

x(s, t) = S M_b P_bx M_b^T T^T = S M_b 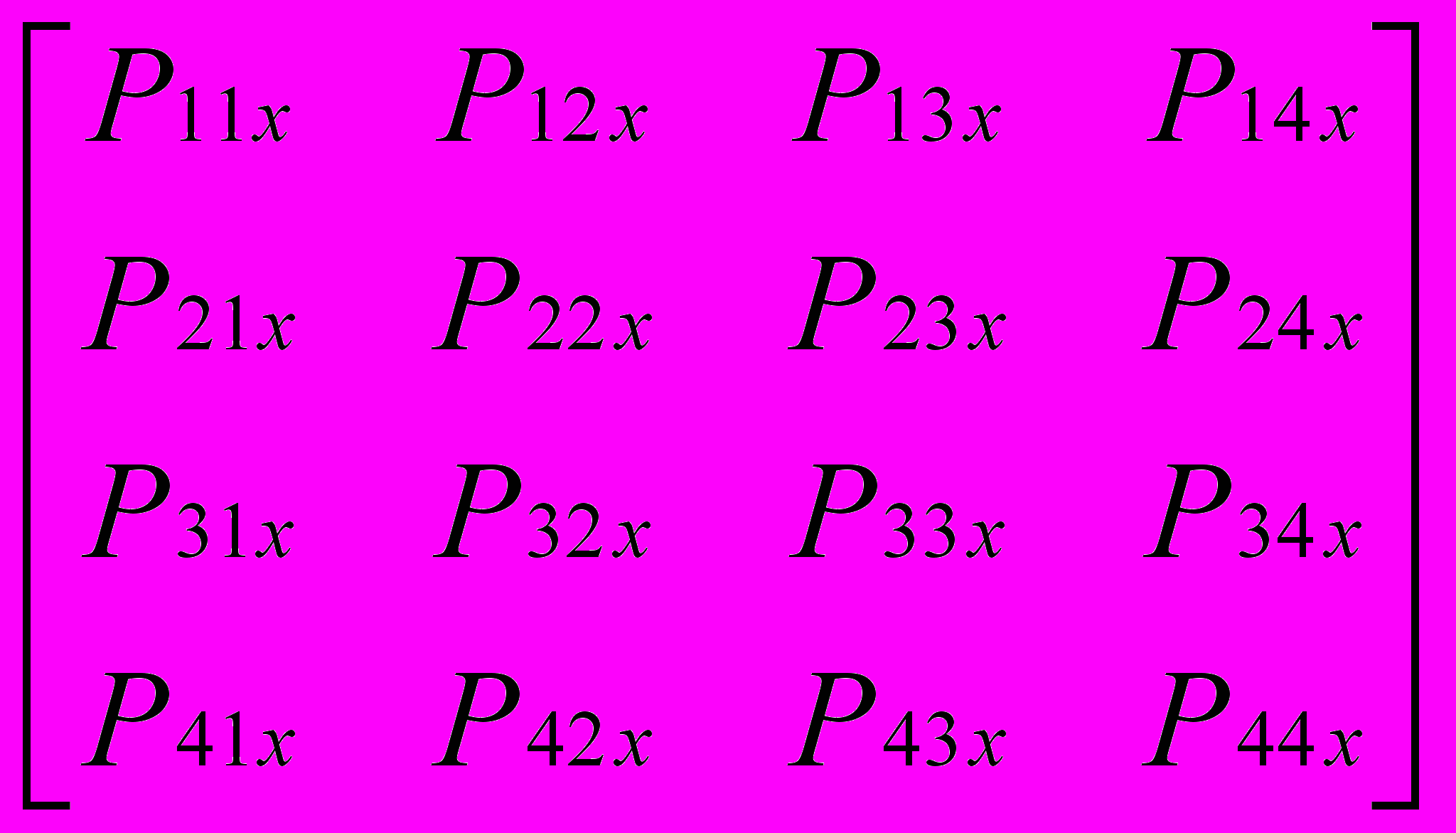M_b^T T^T.

Геометрическая матрица Р_bx состоит из 16 управляющих точек, причем точки Р_11х, Р_14х, Р_41х и Р_44х являются угловыми точками куска поверхности.

Поверхности Безье, также как и кривые, обладают свойством выпуклых оболочек.

При соединении двух кусков поверхностей для выполнения условия непрерывности необходимо равенство четырех управляющих точек, принадлежащих общим ребрам кусков. Кроме того, для достижения непрерывности касательного вектора требуется, чтобы две четверки управляющих точек, лежащих по обеим сторонам общего ребра были коллинеарны (лежали на одной прямой) четверке управляющих точек общего ребра и друг другу. Отношения длин коллинеарных отрезков должны быть постоянными.

Куски в форме В-сплайнов представляются в виде:

x(s, t) = S M_s P_sx M_s^T T^T.= S M_s 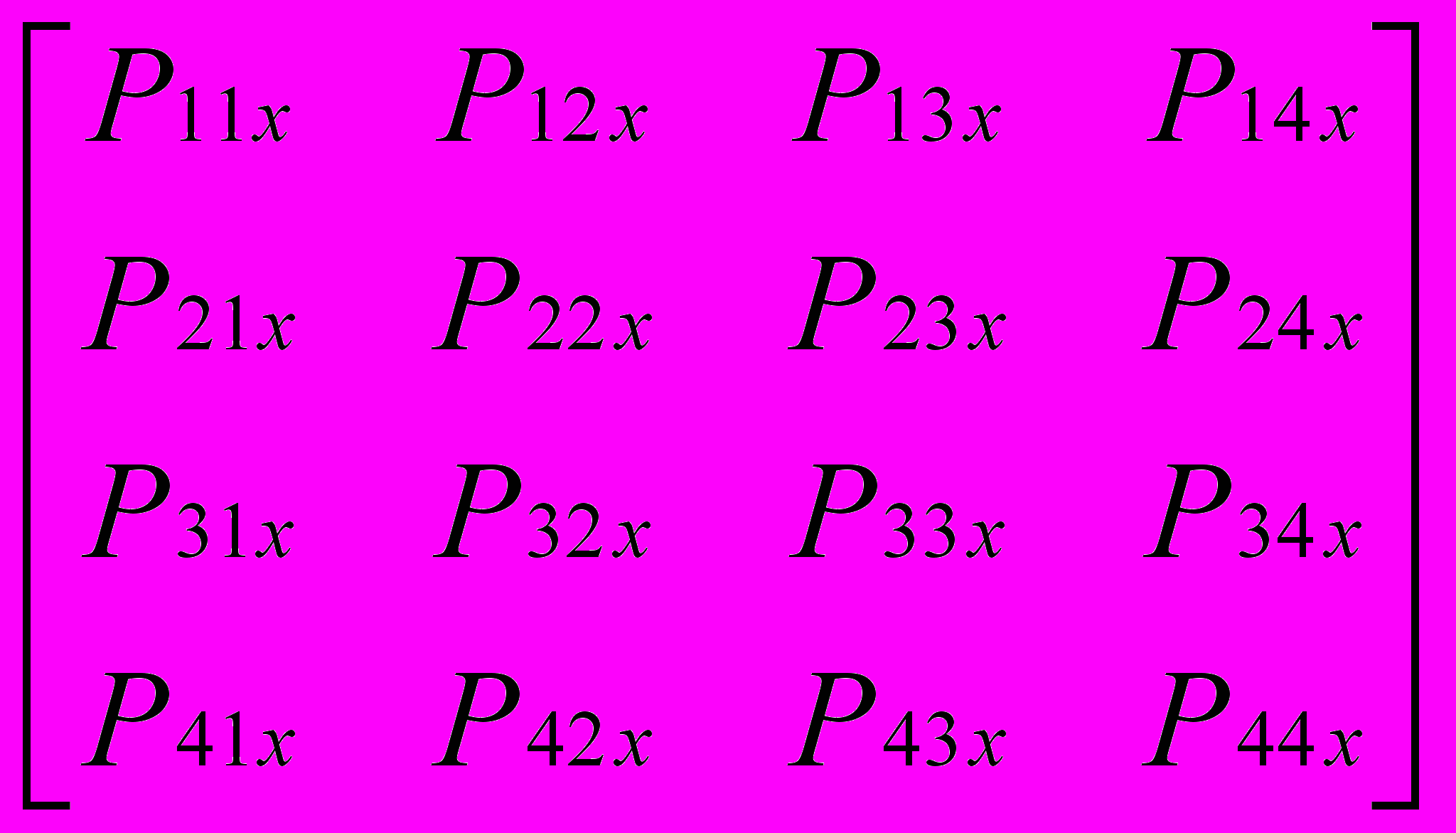M_s^T T^T.

Шестнадцать управляющих точек задают кусок поверхности, находящийся около четырех центральных точек Р₂₂, Р₂₃, Р₃₂ и Р₃₃.


7.5. Преобразования параметрических кривых и кусков поверхностей


Для выполнения аффинных преобразований с параметрическими кривыми или поверхностями не обязательно применять матрицу преобразования к каждой точке кривой (поверхности). Достаточно перемножить матрицу аффинного преобразования и геометрическую матрицу управляющих точек и касательных векторов (G_h, G_b, G_s, Q_h, P_b, P_s). Для выполнения перемножения матриц каждая управляющая точка и касательный вектор записываются в однородных координатах (к координатам точки добавляется четвертая координата, равная единице, а к координатам вектора – равная нулю) [11, 14].


7.6. Визуализация трехмерных объектов


Трехмерный объект может быть изображен разными способами.

Способы визуализации можно достаточно условно разделить на несколько уровней по нарастанию сложности [10]:

• каркасный – рисуются все вершины и ребра объекта – хорошо показывает внутреннюю структуру объекта, но дает самое нереалистичное изображение;
  
• с удалением невидимых вершин и ребер;
  
• удаление невидимых граней объекта + различные виды закраски видимых граней (однотонная, с учетом освещения, с имитацией плавных переходов между гранями).
  

7.7. Методы удаления скрытых линий и поверхностей


Существуют различные алгоритмы, позволяющие удалять и не выводить как отдельные ребра объектов, скрытые видимыми поверхностями, так и невидимые грани [10, 14, 17].

Все методы удаления невидимых ребер и граней можно разделить на два класса:

• методы, работающие непосредственно в пространстве самих объектов;
  
• методы, работающие в пространстве картинной плоскости.
  

Получаемый результат в первом случае представляет собой набор видимых отрезков или поверхностей, т.е. имеет непрерывный вид, а во втором случае – информацию о ближайшем объекте для каждого пикселя экрана, т.е. имеет дискретный вид.

Непрерывные методы, как правило, достаточно сложные. Дискретные методы более просты, но они определяют видимость только в некотором наборе точек растровой решетки. Изменение разрешения растра приводит к необходимости пересчета всего изображения.

Для уменьшения времени расчетов используют когерентность различных видов:

• когерентность в картинной плоскости – если данный пиксель соответствует точке некоторой грани, то, скорее всего, соседние пиксели также соответствуют точкам этой грани;
  
• когерентность в пространстве объектов – если данная грань видима, то, скорее всего, и соседние с ней грани видимы;
  
• временная когерентность (для анимации) – грани, видимые в данном кадре, скорее всего будут видны и в следующем кадре.
  

7.7.1. Методы оптимизации

Методы оптимизации широко используются для уменьшения затрат времени на удаление невидимых линий и поверхностей.

Процедура отсечения нелицевых граней позволяет заранее исключить из рассмотрения грани, повернутые от наблюдателя и заведомо невидимые. Вычисляется угол между внешней нормалью к грани и направлением на наблюдателя. Если этот угол тупой, то грань – нелицевая.

При выполнении различных операций по выявлению перекрывающих друг друга граней широко используют ограничивающие грань тела (оболочки). В качестве оболочек чаще всего используют параллелепипеды с гранями, параллельными координатным плоскостям. Если такой ограничивающий грань параллелепипед задан координатами своих диагональных углов (x_min, y_min, z_min) и (x_max, y_max, z_max), то проверка пересечения оболочек двух граней сводится к простой процедуре проверки пересечения трех промежутков: от x_min до x_max, от y_min до y_max и от z_min до z_max. Если хотя бы один из этих промежутков не пересекается с аналогичным промежутком для оболочки другой грани, то оболочки граней не пересекаются и, следовательно, грани тоже не пересекаются. Грани, оболочки которых пересекаются, могут как пересекаться, так и не пересекаться, и в этом случае проводят более сложные вычисления.

В компьютерной графике часто встречается задача визуализации внутренних помещений архитектурных сооружений (комнат, коридоров, лабиринтов). Данная задача имеет свою специфику – при очень большом общем числе граней количество граней, видимых из данной точки, сравнительно невелико. При решении данной задачи применяются специальные методы оптимизации, позволяющие как можно раньше отбросить заведомо невидимые грани. Обычно сцену заранее разбивают на набор областей и для каждой области составляют список потенциально видимых граней (PVS – Potentially Visible Set).

Один из методов, позволяющих построить PVS – метод порталов. В начале сцена разбивается на набор выпуклых областей. Все грани внутри области могут быть видны, следовательно, они автоматически заносятся в PVS для этой области. Рассматриваются соседние области, соединенные с текущей порталами. Порталами называются те соединения, через которые можно видеть (окна, двери и т.п.). В соседних областях определяются грани, которые могут быть видны из текущей области через порталы. Эти грани заносятся в PVS для текущей области. На следующем этапе рассматриваются области, соединенные с соседними с текущей областями через порталы, в этих областях определяются грани, которые могут быть видны из текущей области (но уже через два портала), и т.д.


7.7.2. Метод сортировки граней по глубине

Визуализация граней проводится в порядке от самых дальних от наблюдателя к самым близким. Ближайшие многоугольники преобразуются в растр последними и закрывают более отдаленные многоугольники, т.к. записываются в буфер регенерации поверх старых.

При выполнении метода могут возникать неопределенности при перекрытии z-оболочек некоторых граней. Существуют различные модификации метода, позволяющие решать эту проблему.


7.7.3. Метод плавающего горизонта

Используется при построении графика функции двух переменных z=f(x,y) в виде сетки координатных линий x=const, y=const.

Грани выводятся в порядке от самых ближайших к самым дальним от наблюдателя. Все линии z=f(x, y_i), где y_i=const лежат в параллельных плоскостях и, следовательно, не пересекаются. Допустим, что координатные оси сориентированы так, что при y_i>y_i-1 плоскость y=y_i расположена ближе к наблюдателю, и значения у меняются от у₀ до у_n. На первом шаге рисуются ближайшие к наблюдателю грани (у_i= у_n).

Выведенные на первом шаге грани видимы (они самые ближние и их ничего не заслоняет) и образуют так называемый горизонт. На следующих шагах рисуются только те части линий z=f(x, y_i), которые не закрываются ранее нарисованными, т.е. лежат выше верхнего или ниже нижнего горизонтов.

Нижняя линия горизонта в любой из точек равна минимуму из уже выведенных линий, а верхняя линия горизонта – максимуму. Каждая новая грань поднимает верхний и опускает нижний горизонты.


7.7.4. Метод z-буфера

Этот метод работает в пространстве картинной плоскости.

Используется дополнительный массив (буфер) в памяти, в котором сохраняются координаты z (глубины) для каждого пикселя растра. Значение z отвечает за расстояние от объекта до наблюдателя (но не обязательно равно ему).

Предположим, что ближе к наблюдателю располагаются объекты с наибольшими значениями z. Тогда метод z-буфера будет действовать так.

На первом этапе z-буфер будет заполнен минимальными значениями z, а буфер регенерации будет заполнен соответствующими значениями пикселей фона.

На следующих этапах производится вывод объектов (в любом порядке). Для каждого пикселя каждого выводимого объекта рассматривается значение z. Если рассматриваемое значение z больше, чем значение, хранимое для данного пикселя в z-буфере, то данный пиксель заносится в буфер регенерации (рисуется), а его значение z заносится в z-буфер поверх старого.

После рассмотрения всех объектов буфер регенерации изображения будет состоять из пикселей, соответствующих точкам объектов с наибольшими значениями z (т.е. ближайших к наблюдателю).

Данный метод прост и эффективен, не требует предварительной сортировки граней.


7.8. Закрашивание поверхностей


После удаления скрытых поверхностей для повышения реалистичности изображения все видимые грани объектов необходимо закрасить. Существуют различные модели закрашивания поверхностей, которые учитывают расположение источников света, характеристики материала поверхности, взаимное расположение граней.


7.8.1. Модели отражения и преломления света

В компьютерной графике рассматриваются объекты, которые по отношению к свету обладают следующими свойствами:

• излучают свет;
  
• отражают и поглощают свет;
  
• пропускают свет сквозь себя.
  

Каждое из этих свойств можно описать некоторым набором характеристик.

Излучение можно охарактеризовать интенсивностью, спектральным составом (цветом), геометрическими размерами источника (точечный, протяженный и т.п.), направленностью излучения (во все стороны, вдоль узкого луча, конусом).

Отражение света может быть нескольких видов – зеркальное, диффузное, обратное [10].

Зеркальное отражение (рис. 7.2, а) – падающий на поверхность луч (l) и отраженный луч (s) лежат в одной плоскости, причем угол падения светового луча равен углу отражения. Цвет отраженного луча совпадает с цветом падающего луча, т.е. собственного цвета у зеркальной поверхности нет. Наблюдатель будет видеть отраженный луч только если угол  между направлением отраженного луча (s) и направлением на наблюдателя (v) равен нулю (рис. 7., а).

Не идеальное зеркальное отражение происходит при падении света на слегка шероховатую поверхность (рис. 7.2, б). В этом случае возникает несколько отраженных лучей, рассеиваемых по различным направлениям. Зона рассеивания зависит от качества полировки и, как правило, симметрична относительно направления идеально отраженного луча, а ее форма может быть описана некоторым законом распределения. Одной из простейших моделей распределения, наиболее часто используемой в компьютерной графике, является модель Фонга:

I_s = I k_s cos^Р,

где I_s – интенсивность отраженного луча, I – интенсивность падающего луча, k_s – коэффициент пропорциональности, р=1…200 – показатель качества полировки поверхности,  – угол отклонения от направления идеально отраженного луча.

Сильно шероховатым (матовым) поверхностям присуще диффузное отражение, при котором падающий луч равномерно рассеивается во все стороны (рис 7.2, в). Матовая поверхность имеет свой цвет – наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета падающего луча. Интенсивность диффузно отраженного света не зависит от положения наблюдателя.

Диффузное отражение описывается законом Ламбера:

I_d = I k_d cos ,

где I_d – интенсивность диффузно отраженного луча, I – интенсивность падающего луча, k_d – коэффициент, учитывающий свойства материала поверхности,  – угол между нормалью (n) к поверхности и направлением падающего луча (l).




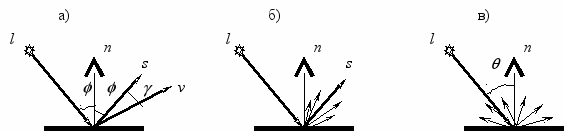
Рис. 7.2. Отражение света: а) идеальное зеркальное, б) не идеальное зеркальное, в) диффузное.

Существует еще и обратное отражение, при котором максимум интенсивности отраженного света соответствует направлению на источник света.

При изображении объектов в компьютерной графике обычно моделируют сумму зеркального и диффузного отражений:

I_отр = I (k_d cos  + k_s cos^Р),

где I_отр – интенсивность отраженного луча.

При некоторых значениях углов  и  интенсивность отраженного света будет равна нулю. Однако, в реальных сценах полностью затемненные объекты используют редко, т.к. учитывают освещение отраженным от других объектов светом (фоновую подсветку) с интенсивностью I_а:

I_отр = I_а k_а + I (k_d cos  + k_s cos^Р).

Можно учесть и то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. На практике обычно используют следующую (не совсем точную) формулу:

I_отр = I_а k_а + I (k_d cos  + k_s cos^Р) / (R + k),

где R – расстояние до источника света, k – константа.

При прохождении световых лучей через полупрозрачную среду происходит их преломление. Падающий и преломленные лучи лежат в одной плоскости, причем:

₁ sin₁ = ₂ sin₂,

где ₁ и ₂ – показатели преломления двух сред, ₁ и ₂ – углы падения и преломления светового луча (рис. 7.3.).




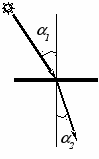
Рис. 7.3. Преломление светового луча на границе двух сред.

Показатель преломления зависит не только от материала среды, но и от длины световой волны: чем меньше длина волны (фиолетовые цвета), тем сильнее отклоняется луч. Существует и диффузное преломление, когда преломленный луч рассеивается равномерно во все стороны, но в компьютерной графике оно используется редко из-за трудности расчета.

Таким образом, при рассмотрении полупрозрачных материалов необходимо учитывать и отраженный и преломленный свет.


7.8.2. Определение цвета закрашивания

Наиболее просто выполняется расчет при закрашивании в градациях серого цвета (для источника белого света и серых объектов). В этом случае вычисленная интенсивность отраженного света будет просто соответствовать яркости.

Для цветных объектов, освещаемых цветным источником света, составляются три формулы расчета интенсивности отраженного света – по одной на каждую цветовую компоненту в модели RGB. Цвет источника будет выражаться значениями интенсивности I для каждой цветовой компоненты. Коэффициенты k_а и k_d выражают собственный цвет поверхности и, следовательно, для одной и той же поверхности будут различны для каждой из компонент. Коэффициент k_s будет одинаков для всех цветовых компонент, т.к. цвет зеркально отраженного луча равен цвету источника.


7.8.3. Модели закрашивания

Существует несколько моделей закрашивания плоских граней.

На закрашивание грани в общем случае влияют направления четырех векторов: нормали к плоскости грани (n), направления на источник света (l), направления идеального зеркального отражения (s) и направления на наблюдателя (v). При переходе от одной точки плоской грани к другой направление вектора n остается постоянным, изменяются только вектора l, s и v. Однако, в случае удаленного источника света и далеко расположенного наблюдателя этими изменениями можно пренебречь.

Это свойство используется в самой простой модели плоского закрашивания, когда освещенность одной, произвольной точки грани, принимают за освещенность всей грани, т.е. грань закрашивается равномерно. Недостаток этого метода – резкие переходы цвета между соседними гранями.

Резкость цветовых переходов дополнительно увеличивается из-за возникновения т.н. полос Маха, когда светлая грань вблизи ее границы с более темной гранью субъективно воспринимается глазом человека еще светлее, чем она есть на самом деле. На темной грани вблизи ее границы с более светлой гранью, наоборот, создается иллюзия более темной полосы.

Для сглаживания полос Маха применяются интерполяционное закрашивание и закрашивание методом Гуро.

При интерполяционном закрашивании интенсивность освещенности определяется отдельно для каждой вершины грани. Освещенность вдоль ребер грани интерполируется от значения освещенности в начальной вершине ребра до значения освещенности в конечной вершине. Поверхность грани закрашивается горизонтальными отрезками с изменяющейся интенсивностью освещенности (интенсивность освещенности в начальной и конечной точках каждого отрезка была определена при закраске ребер грани).

Метод Гуро похож на метод интерполяционного закрашивания, но значения освещенности в вершинах грани определяются для осредненного значения нормали. Нормаль в вершине получается при усреднении значений нормалей всех сходящихся в этой вершине граней. При k сходящихся в вершине граней и единичной длине векторов нормалей усредненное значение нормали в вершине:

n = .

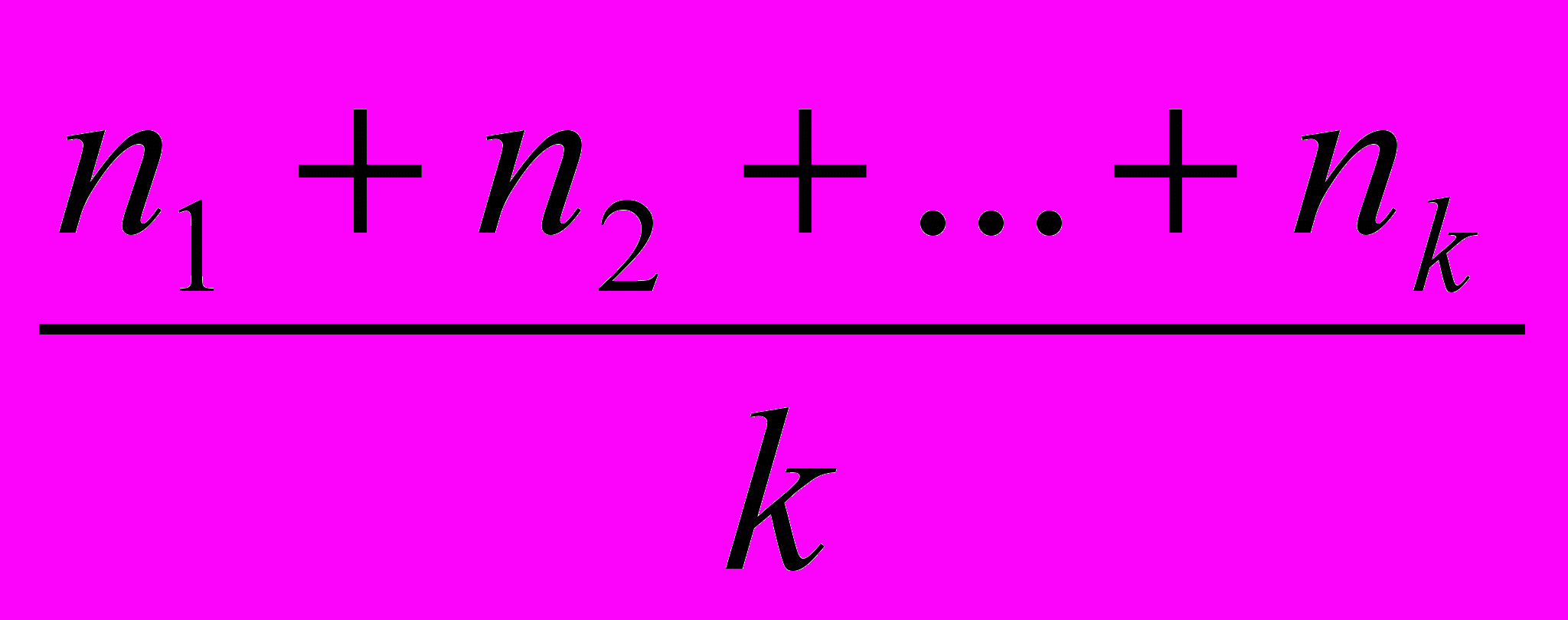Закраска методом Гуро позволяет визуально сгладить переходы между гранями, однако в некоторых случаях не удается избежать появления полос Маха.

При закрашивании граней методом Фонга также вычисляются усредненные значения нормалей в вершинах, однако при закраске поверхности грани интерполируются не значения освещенности, а значения нормалей в каждой точке, и лишь потом вычисляется освещенность.

Расчет затененности объектов в случае точечных источников света аналогичен расчетам при удалении скрытых линий и поверхностей: поверхности, видимые и из точки зрения, и из источника света, освещены; поверхности, видимые из точки зрения, но не видимые от источника света, находятся в тени и на их закраску влияет только рассеянный свет.

Расчет закраски объектов в сложно построенных сценах с несколькими источниками освещения выполняется более сложно. Обычно в этом случае используют трассировку лучей или метод анализа излучательности.

При выполнении трассировки лучей предполагается, что световой луч в свободном пространстве распространяется вдоль прямой линии. От источников излучения в разных направлениях исходит бесчисленное множество лучей. Некоторые лучи уходят в свободное пространство, а некоторые лучи попадают на объекты. При попадании на прозрачный объект световой луч преломляется, при этом некоторая часть световой энергии поглощается. При попадании на зеркальную поверхность луч изменяет направление (отражается), часть световой энергии при этом также поглощается. Если объект и отражает и поглощает, то световой луч расщепляется. Таким образом, в результате действия на объекты первичных лучей возникают вторичные лучи, которые также могут попадать на объекты. После многократных отражений и преломлений световой некоторая часть световых лучей попадает в точку зрения, т.е. изображение сцены формируется множеством световых лучей [10, 14, 20].

Трассировку лучей обычно выполняют в обратном порядке (обратная трассировка) – от наблюдателя. Трассируется не бесконечное, а конечное множество лучей, исходящих из точки зрения и проходящих через каждый пиксель изображения. Каждый луч проверяется на пересечение с объектами сцены. Когда выясняется, что текущий луч обратной трассировки не пересекает никакого объекта, а уходит в пространство, трассировка для этого луча заканчивается.

Для повышения быстродействия метода используются некоторые ограничения, например:

• источники света могут только излучать свет, но не могут его отражать и преломлять;
  
• рассматриваются только точечные источники света;
  
• для учета освещенности светом, рассеиваемым другими объектами сцены, вводится фоновая составляющая;
  
• для прозрачных объектов не учитывается зависимость коэффициента преломления от длины волны или вообще прозрачность моделируют без преломления луча света;
  
• отражение описывается диффузной и зеркальной составляющими;
  
• зеркальное отражение, в свою очередь, описывается двумя составляющими: световые блики от источников света и отражение от других объектов;
  
• при диффузном отражении игнорируются лучи от зеркально отражающих поверхностей;
  
• для завершения трассировки вводят некоторое пороговое значение освещенности или ограничивают число итераций.
  

Метод анализа излучательности используется для тонирования сцен, в которых подавляющее число объектов имеет поверхности с диффузным рассеиванием [20]. Формируется глобальное уравнение энергетического баланса, решение которого позволяет получить цвет каждой матовой поверхности.

Закрашиванием объектов можно передать иллюзию глубины пространства или эффект тумана.

В природе контуры отдаленных объектов кажутся наблюдателю размытыми, затуманенными. Этот эффект можно смоделировать в процессе закраски объектов [20]. Для этого среда, в которой находятся объекты формируется полупрозрачной. Итоговый цвет объекта С расчитывается по формуле:

C = f C_o + (1 – f) C_f,

где C_o – исходный цвет объекта, рассчитанный с учетом его освещенности, C_f – цвет полупрозрачной среды (тумана), f – функция туманности, которая зависит от расстояния между объектом и наблюдателем.

Для передачи глубины пространства используют линейную функцию туманности, для создания эффекта тумана – нелинейную (экспоненциальную и т.п.).


7.9. Детализация поверхностей


Существуют два типа детализации поверхностей – цветом (наложение проективных текстур) и фактурой (микрорельефом поверхности) [14].

Текстура представляет собой массив растрового узора, который налагается на поверхность трехмерного объекта на этапе тонирования. Узор текстуры задается функцией интенсивности, которая используется либо для модификации цвета основной поверхности, определяемого с учетом освещенности, либо для назначения для основной поверхности цвета только текстуры.

Основные трудности возникают при наложении плоской текстуры на трехмерные кривые поверхности объектов (например, на шар).

Текстуры обладают теми же недостатками, что и все растровые изображения – для их хранения может потребоваться большой объем памяти. Для экономии памяти обычно применяют блочное текстурирование: текстура представляет собой не всю грань целиком, а лишь отдельный фрагмент, который циклически повторяется в грани. По возможности текстуры хранят в градациях, а для получения цветного узора их накладывают на тонированную поверхность объекта.

В качестве текстур могут использоваться не только простые узоры, но и сложные рисунки. Например, для имитации зеркально отражающей поверхности на объект налагают текстуру, представляющую собой рисунок с изображением отражающихся предметов. Результат будет не такой реалистичный, как при расчете зеркального отражения (особенно, если отражающиеся объекты или наблюдатель перемещаются в пространстве), но вычислений потребуется значительно меньше.

Текстуры могут быть и анимированными (движущимися) [1].

Текстуры можно использовать и для имитации фактуры (микрорельефа) поверхности. Однако, если положение объекта относительно источников света будет изменяться, ненатуральность такого «микрорельефа» будет сразу заметна.

Для имитации микрорельефа поверхности зачастую используется технология внесения возмущений в нормаль к поверхности объекта (непосредственно перед тонированием поверхности). Результат применения этого метода будет достаточно реалистичным, хотя непосредственное геометрическое моделирование рельефа поверхности не проводится.

Существуют и более сложные способы непосредственного моделирования рельефа поверхности, например использование фрактальных поверхностей [14]. Фрактал – это объект довольно сложной формы, получающийся в результате выполнения простого итерационного цикла. Фракталы хорошо описывают природные объекты и большинство искусственных [4, 10, 15].


7.10. Построение трехмерных сцен


Сложные трехмерные модели, включающих множество геометрических примитивов, а также объектов другого типа (источников света, камер), влияющих на то, как будут выглядеть геометрические объекты, называют сценами (реже – мирами).

Для описания трехмерных моделей используются разные подходы.

Неиерархический подход – все примитивы рассматриваются как символы, из которых строится модель. Обычно символы в библиотеке представлены как объекты стандартного размера и ориентации. Например, примитив цилиндр может иметь единичные высоту и радиус основания, ось цилиндра может совпадать с одной из координатных осей, а центр цилиндра – находиться в точке начала координат. Размещение таких примитивов внутри модели будет задаваться комплексом аффинных преобразований. Для изменения геометрических размеров примитивов используется масштабирование, вращением задается ориентация примитивов в пространстве, перемещение центра примитива позволяет установить примитив в нужное место сцены. Описание сцены при таком подходе представляет собой список примитивов с указанием для каждого из них выполняющихся геометрических преобразований.

При иерархическом подходе указываются соотношения между компонентами модели. Наглядно эти соотношения можно представить в виде графа, состоящего из узлов и ребер. В узлах графа могут содержаться графические примитивы, свойства материалов объектов, камеры, источники света и т.п. [1, 20].

В качестве графа сцены обычно используются ориентированные ациклические и древовидные графы. Ребра ориентированного графа исходит из одного узла и заходит в другой, но узел не может содержать сам себя. Ациклический граф не может содержать циклов (замкнутых путей), но каждый узел может иметь несколько заходящих и исходящих ребер. Древовидный граф – это ориентированный ациклический граф, в котором в каждый узел, кроме корневого, может заходить только одно ребро.