Прикладная графическая программа. Прикладная программа передает данные и сформированные графические команды в графическую систему (рис. 1) [14]. Рис. Схема взаимодействия прикладной программы и графической системы

Вид материала

Программа

Содержание 6.3. Системы координат в компьютерной графике Координаты проекции 7. Методы и алгоритмы трехмерной графики 7.2 Полигональные сетки 7.3. Параметрические кубические кривые

Подобный материал:

• Рабочая программа дисциплины для студентов магистратуры, обучающихся по направлению, 120.54kb.
• Магистерская программа «Информационные технологии и информационные системы» по направлению, 34.28kb.
• Программа вступительного испытания по предмету прикладная этика для поступающих, 307.5kb.
• Рис Физический и логический обмен данными по сети 21 Рис Ахитектура процессов в распределенных, 932.01kb.
• Рис. Сферы взаимодействия психики и личности (Управляющей психики) Рис., 2.3kb.
• Методика ми5 проверки цепи фаза нуль в электроустановках до 1 кВ с глухим заземлением, 53.81kb.
• Программа дисциплины Современная прикладная алгебра для направления 010500 Прикладная, 214.78kb.
• Основная образовательная программа высшего профессионального образования 230700., 513.26kb.
• Программа вступительного экзамена по математике подготовки магистров по направлению, 86.94kb.
• Прикладная программа для создания, редактирования (обработки) и просмотра графических, 47.05kb.

Диметрия – это частный случай триметрической проекции с двумя одинаковыми коэффициентами искажения (третий коэффициент может иметь любое значение). Диметрическая проекция может быть получена путем поворота на угол  вокруг оси ординат, затем поворота на угол  вокруг оси абсцисс и проецирования вдоль оси аппликат:

[P_дим] = =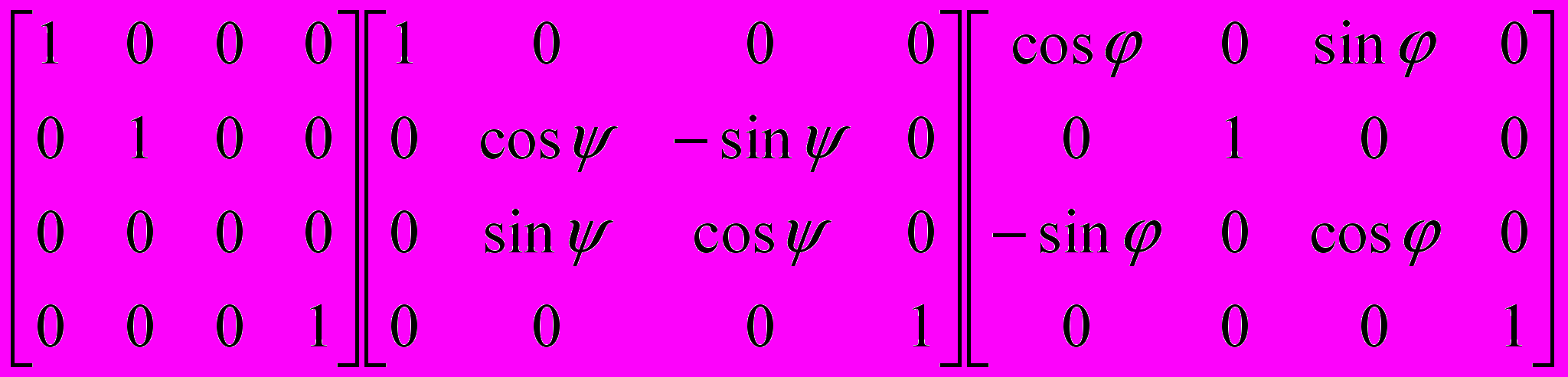

= .

Найдем величины этих углов поворота.

Квадраты длин проекций единичных векторов координатных осей, совпадающие с коэффициентами искажения по этим осям, равны:

f_x² = cos² + sin² sin²,

f_y² = cos²,

f_z² = sin² + cos² sin².

Приравнивая любые два коэффициента искажения получают ограничения, налагаемые в случае диметрии на значения углов  и .

Если f_х² = f_y², то:

 = arcsin(f_z),

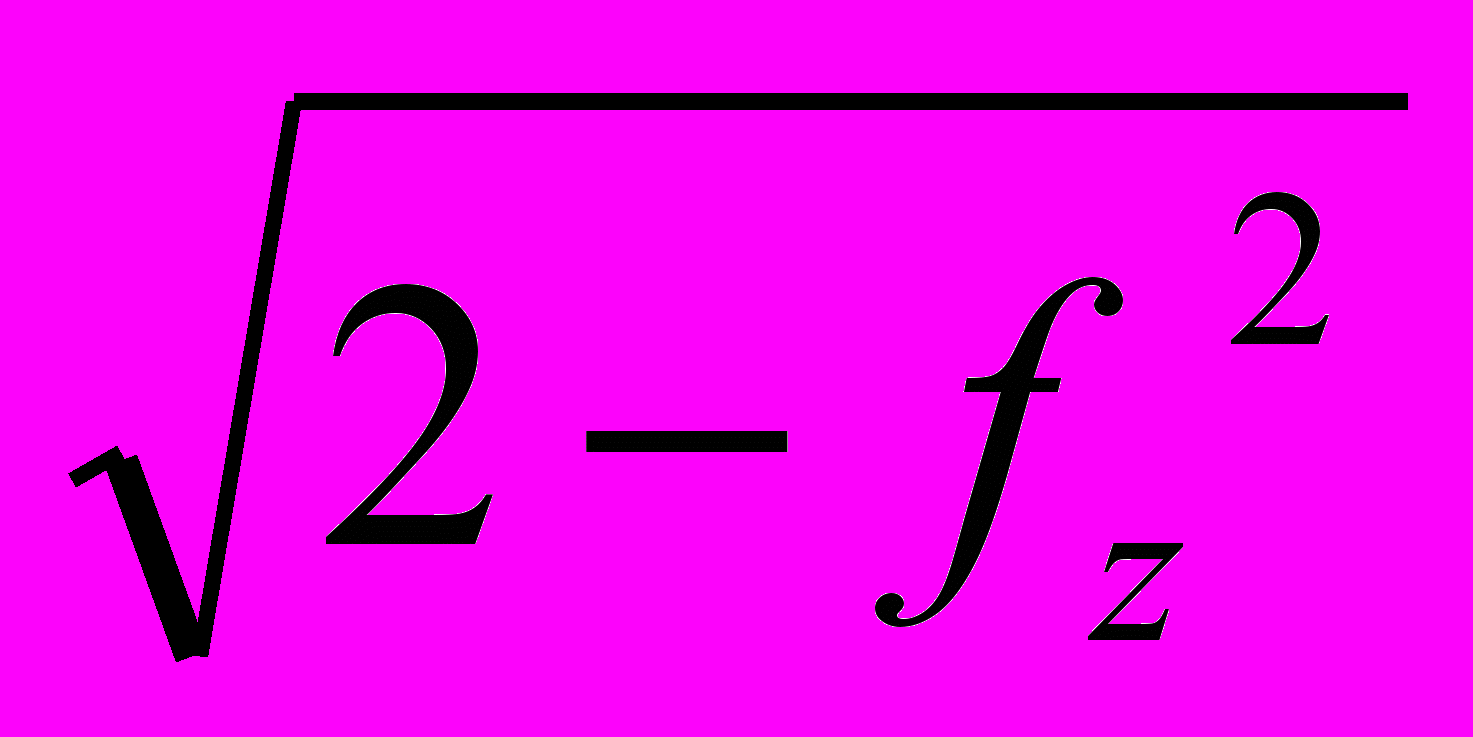 = arcsin(f_z /).

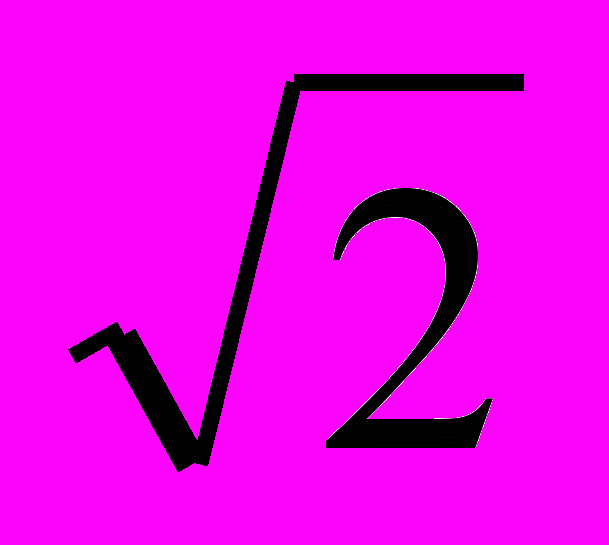В изометрической проекции все три коэффициента искажения равны: f_х² = f_y² = f_z².

Для изометрии получаем:

sin² = ½,  = 45⁰, sin² = 1/3,  =  35,26⁰.

При косоугольных проекциях проецирующие прямые не перпендикулярны картинной плоскости, картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей. Таким образом, косоугольные проекции сочетают в себе свойства ортографических и аксонометрических проекций.

Косоугольная проекция на плоскость z = 0 задается значениями двух углов:  и , где  – это угол между осью абсцисс и проекцией оси аппликат на картинную плоскость, а  – это угол наклона проецирующих прямых к картинной плоскости (рис. 6.4).




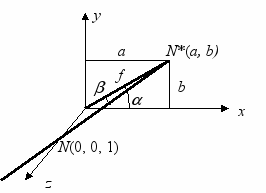
Рис. 6.4. Косоугольная проекция точки N(0, 0, 1) на плоскость z =0.

Рассмотрим косоугольную проекцию точки N(0, 0, 1) на плоскость z=0. В результате проецирования точка N преобразуется в точку N*(a, b). Коэффициент искажения f по оси аппликат равен длине проекции единичного вектора (0 0 1):

f = ctg.

Косоугольная проекция любой точки получается путем сдвига на величину za вдоль оси x, на величину zb вдоль оси y и последующего проецирования на плоскость z=0. Матрица косоугольной проекции:

[P_кос] = 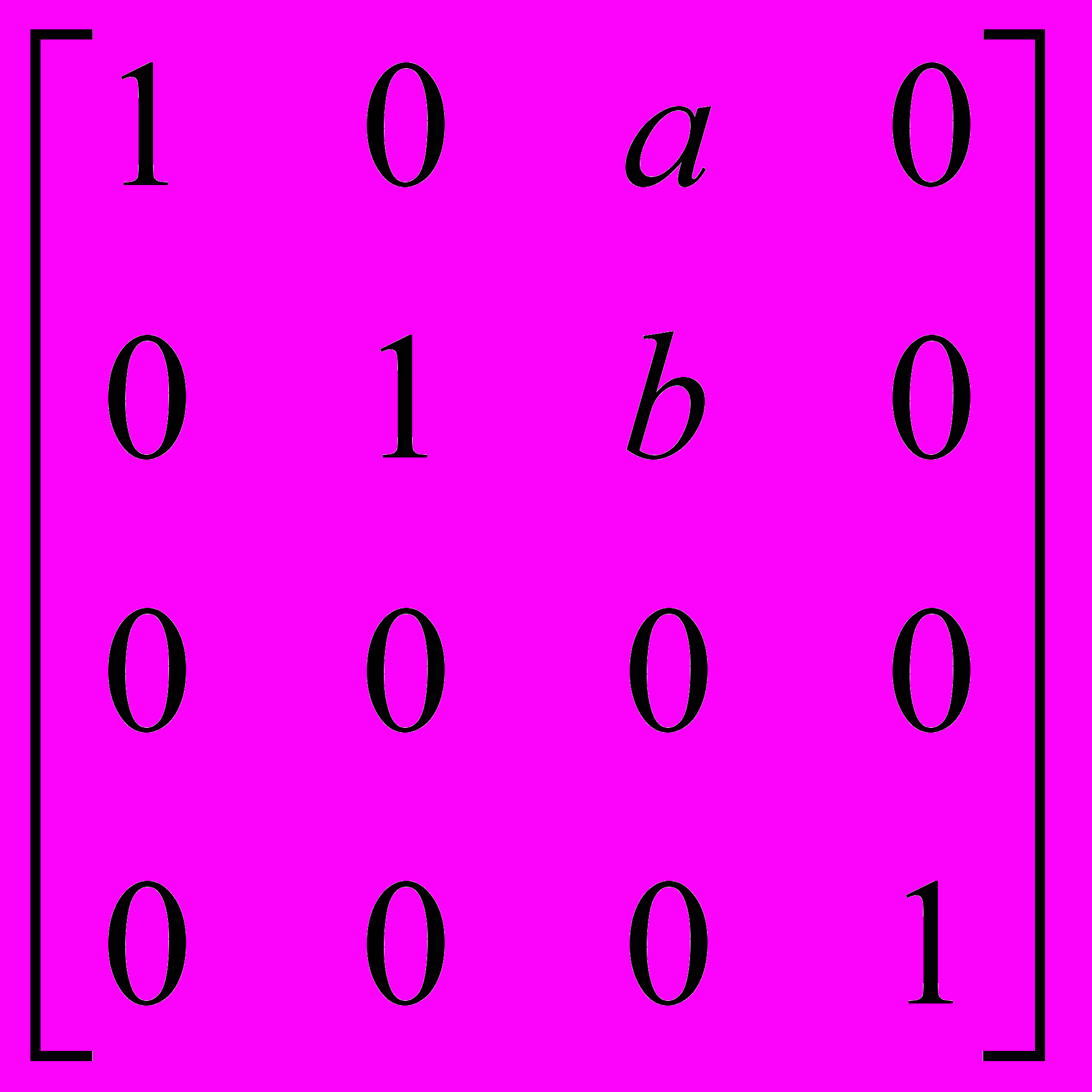, a = f cos, b = f sin.

Наиболее часто используют две косоугольных проекции – кавалье и кабине.

Проекция кавалье получается, когда угол между картинной плоскостью и проецирующими прямыми =45⁰. В этой проекции коэффициенты искажения для каждой из проецируемых координатных осей одинаковы и равны единице (т.е. без искажения):

f=1, a=cos, b=sin.

Результат проекции кавалье выглядит неестественно утолщенным.

У проекции кабине коэффициент искажения для ребер, перпендикулярных картинной плоскости, составляет ½:

f=1/2, a=0,5cos, b=0,5sin.

Для получения проекции кабине угол  между картинной плоскостью и проецирующими прямыми должен составлять 63.43⁰.

Угол  может быть любым, однако, наиболее часто используются проекции со значениями угла =30⁰ или =45⁰.


6. 2. Центральные (перспективные) проекции


В центральных проекциях грани отображаемого объекта, параллельные картинной плоскости, изображаются без искажения формы, но с искажением размера.

Центральные проекции любой совокупности параллельных прямых, которые не параллельны картинной плоскости, будут сходиться в точке схода. Точка схода прямых, параллельных одной из координатных осей, называется главной точкой схода. Т.к. координатных осей три, то и главных точек схода не может быть больше трех.

В зависимости от расположения осей координат и картинной плоскости различают одно-, двух- и трехточечные центральные проекции.

Одноточечная проекция получается, когда картинная плоскость совпадает с одной из координатных плоскостей (или параллельна ей). Т.е., только одна ось координат не параллельна картинной плоскости и имеет главную точку схода.

Двухточечная проекция получается, когда только одна из координатных осей параллельна картинной плоскости. Две другие оси координат не параллельны картинной плоскости и имеют две главные точки схода. При изображении объектов, расположенных на поверхности земли, наиболее часто используется двухточечная проекция, при которой картинной плоскости параллельна вертикальная ось координат. Обе главные точки схода расположены на одной горизонтальной линии – линии горизонта (рис. 6.5).

При трехточечной проекции все три координатные оси не параллельны картинной плоскости и, следовательно, имеются три главные точки схода.





Рис. 6.5. Двухточечная центральная проекция.

Рассмотрим более подробно случай одноточечного проецирования точки Р на плоскость z=0 с центром проецирования С, лежащим на оси z (рис. 6.6).




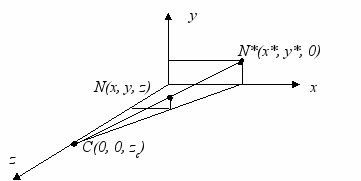
Рис. 6.6. Одноточечное проецирование.

Одноточечное проецирование будет задаваться формулами:

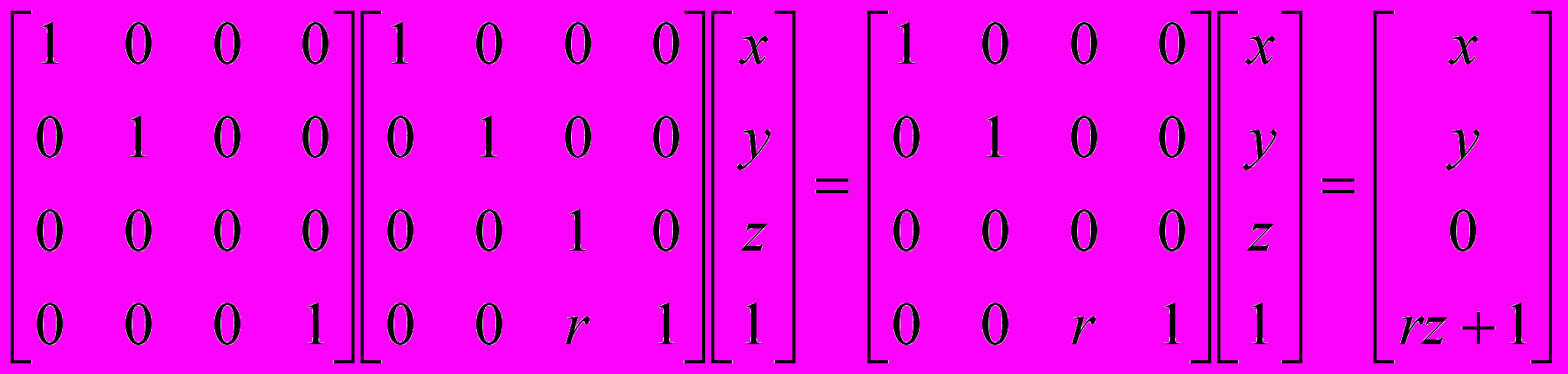, где r = -1/z_c.

Однородные координаты точки N* получаются после деления на величину rz+1:

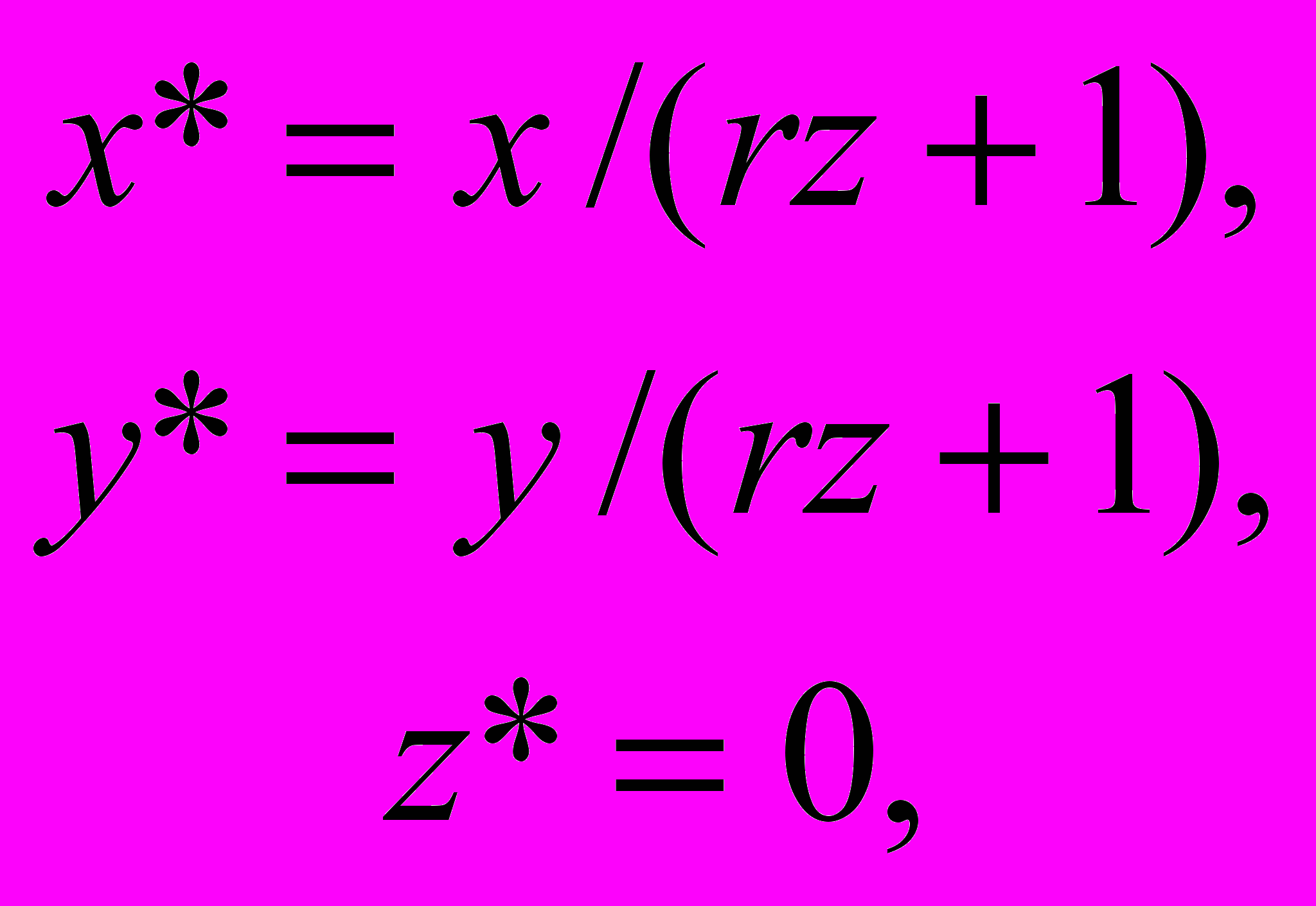или .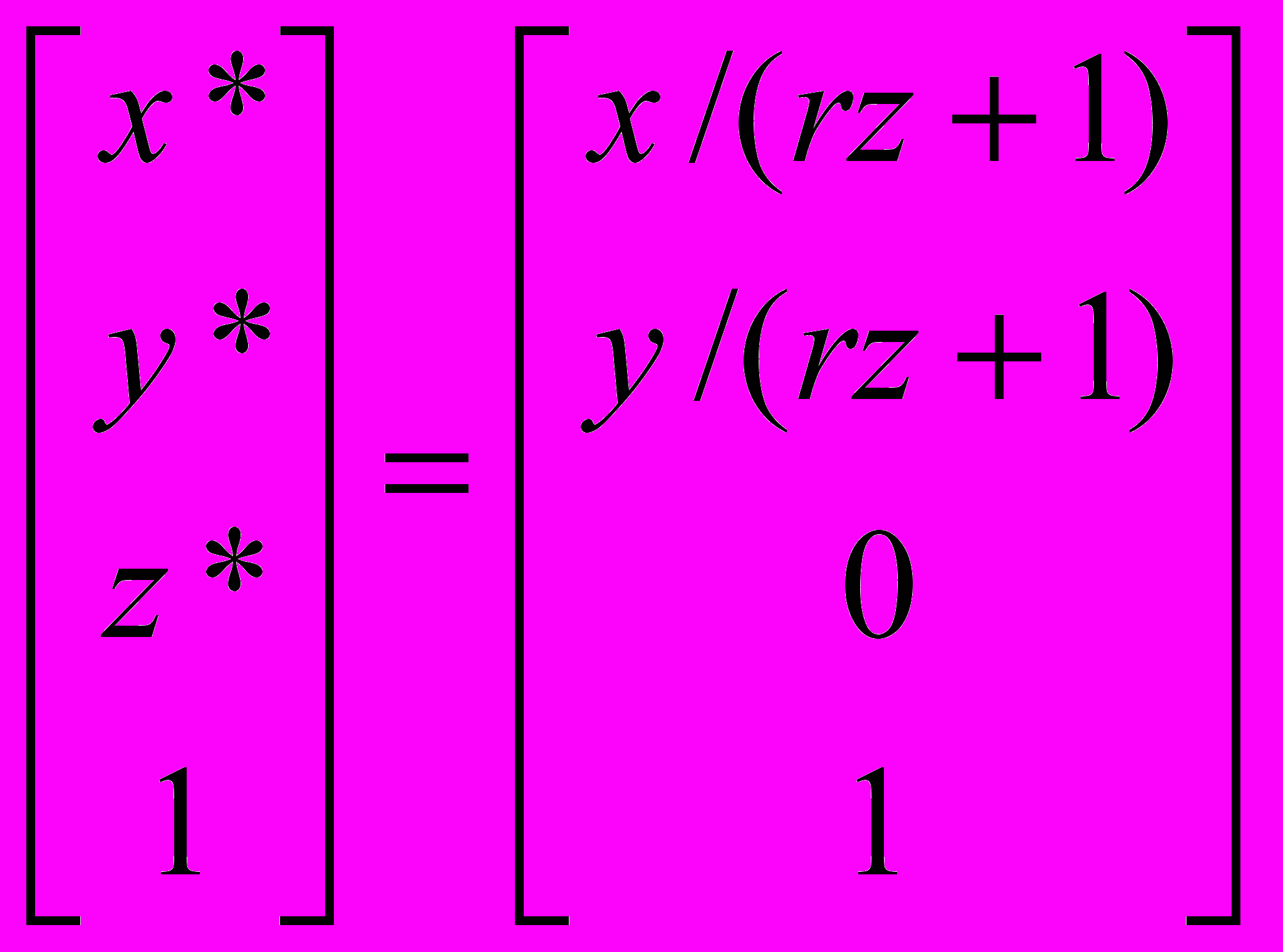

При удалении центра проекции в бесконечность (z_c, r0) центральная проекция переходит в ортографическую.

Из-за особенностей человеческого зрения к удаленным от наблюдателя объектам лучше применять перспективную проекцию, к достаточно близким (на расстоянии вытянутой руки) – ортографическую или аксонометрическую, а к еще более близким объектам – обратную перспективную проекцию.

Для создания стереоизображений используются две центральные проекции, центры которых совпадают с расположением глаз гипотетического наблюдателя, т.е. они расположены на некотором расстоянии друг от друга на прямой, параллельной картинной плоскости. После выполнения проецирования получают два изображения объекта – для левого и правого глаза. Устройство вывода должно обеспечивать подачу этих изображений к каждому глазу пользователя отдельно. Для этого может использоваться система цветных или поляризационных фильтров. Более сложные устройства вывода (например, шлемы) подают каждое из изображений на отдельные экраны для каждого глаза.

Все рассмотренные выше проекции относятся к классу плоских геометрических проекций, т.к. проецирование производится на плоскость (а не искривленную поверхность) и с помощью пучка прямых линий (а не кривых). Этот класс проекций наиболее часто используются в компьютерной графике. В отличие от нее, в картографии часто используются неплоские или негеометрические проекции.


6.3. Системы координат в компьютерной графике


При визуализации объектов на экране монитора или печатающем устройстве необходимо знать его координаты. В компьютерной графике основными являются две системы координат – мировые координаты, описывающие истинное положение объектов в пространстве с заданной точностью, и координаты устройства вывода (например, экрана), на котором осуществляется визуализация.

Цепочку преобразований от мировых к экранным координатам можно представить в следующем виде (рис. 6.7) [10, 14]:




Рис. 6.7. Переход от мировых координат объекта к экранным.

Видовые координаты применяются в случае необходимости и определяются видом последующего проецирования. При переходе от мировых координат к видовым могут выполняться: смена системы координат (например, правосторонней декартовой на левостороннюю), разворот системы координат в пространстве в соответствии с выбранным направлением проецирования, отсечение координат объекта по выбранному видимому объему.

Координаты проекции получаются после применения операции проецирования к видовым координатам объекта. В случае визуализации двумерных объектов мировые координаты и координаты проекции совпадают (проецирования не требуется).

Для каждого конкретного случая визуализации цепочка преобразований систем координат может сильно отличаться от приведенной. Самый крайний случай – когда мировые координаты объекта сразу заданы в экранных пикселях и никаких преобразований не требуется.


7. МЕТОДЫ И АЛГОРИТМЫ ТРЕХМЕРНОЙ ГРАФИКИ


7.1. Геометрические модели трехмерных объектов


Геометрические модели описывают предметы и явления, обладающие геометрическими свойствами. Необходимость в описании пространственных объектов возникает при решении многих задач компьютерной графики.

В общем случае реально существующий объект не может, конечно, в точности соответствовать своему описанию. Для этого бы потребовалось бесконечное число троек координат (x, y, z) – по одной для каждой точки поверхности объекта.

В настоящее время при моделировании объектов используют несколько основных типов геометрических моделей [10, 14, 20].

Для описания каркасной модели используются геометрические объекты первого порядка – линии или ребра. Каркасные модели применяют, как правило, для задания объектов, представляющих собой полиэдры, т.е. замкнутые многогранники произвольной формы, ограниченные плоскими гранями. Каркасная модель содержит в этом случае список координат вершин полиэдра с указанием связей между ними (т.е. указанием ребер, ограниченных соответствующими вершинами).

При использовании каркасной модели для описания объектов, ограниченных поверхностями более чем первого порядка, такие поверхности интерполируют плоскими гранями.

Каркасное представление объекта часто используется не при моделировании, а при отображении моделей как метод визуализации.

Преимуществами каркасной модели являются низкие требования к вычислительным ресурсам, недостатком – невозможность построения высоко реалистичных изображений, так как совокупность отрезков не является адекватным описанием объекта – отрезки сами по себе не определяют поверхностей (рис. 7.1).





Рис. 7.1. Одна и та же каркасная модель (а) может описывать и куб (б), и открытую сверху коробку (в).

Развитием каркасной модели является кусочно-аналитическая граневая модель, которая задается перечислением всех отдельных граней. Объект задается множеством ограничивающих его граней и нормалью, направленной из объекта; каждая грань задается циклом ограничивающих ее ребер; каждое ребро – двойкой ограничивающих его точек (вершин); каждая точка – тройкой координат в трехмерном пространстве. Т.е. граневая модель представляет трехмерный объект в виде замкнутой поверхности.

Совокупность граней, представленных плоскими многоугольниками и ограниченных прямолинейными ребрами, образует полигональную сетку. Грани могут иметь любую форму, но в подавляющем большинстве случаев используются выпуклые многоугольники с минимальным количеством вершин (треугольники и четырехугольники), т.к. их обсчет выполняется проще.

Основным недостатком полигональной сетки является приблизительность представления формы объекта при описании искривленных поверхностей. Для улучшения кусочно-линейной аппроксимации таких объектов увеличивают число граней, что приводит к дополнительным затратам памяти и увеличению объема вычислений.

В рамках граневой модели грани могут представлять собой и искривленные поверхности, ограниченные криволинейными ребрами. Наиболее часто в качестве граней используются параметрические бикубические куски, ограниченные параметрическими кубическими кривыми.

При использовании бикубических кусков для представления объекта с заданной точностью требуется значительно меньшее число граней, чем при аппроксимации полигональной сеткой. Однако, вычисления при работе с бикубическими поверхностями значительно сложнее, чем при работе с плоскими гранями.

В отличие от граневой модели, объемно-параметрическая модель рассматривает объект как сплошное тело. Объект описывается как совокупность некоторых базовых объемных элементов формы (объемных примитивов). Каждый примитив в модели задается двумя группами параметров:

• размерные параметры – определяют геометрические размеры примитива;
  
• параметры положения – устанавливают положение и ориентацию примитива относительно мировой системы координат.
  

В качестве примитивов используются простые геометрические тела: цилиндр, конус, усеченный конус, параллелепипед, шар, тор.

В качестве параметров положения обычно используют координаты центральной точки примитива и координаты единичного вектора, направленного вдоль высоты примитива.

Кроме этих параметров задаются операции над примитивами, в качестве которых используются три основные операции теории множеств – объединение, пересечение и вычитание. Объединением двух примитивов является объект, включающий все точки исходных примитивов. Пересечением двух примитивов является объект, все точки которого принадлежат одновременно и первому, и второму примитиву. Результатом вычитания двух примитивов является объект, состоящий из тех точек первого примитива, которые не принадлежат второму примитиву [20].

Недостатком объемно-параметрической модели является отсутствие явных границ отсеков граней в случае взаимопроникновения примитивов.

В рамках кинематической модели объект может быть задан совокупностью объемных элементов, каждый из которых представляет собой объем, «вырезаемый» в пространстве при движении по определенной траектории замкнутого плоского контура. Траектория движения контура может быть как прямой, так и искривленной.

Вид элемента определяется формой контура и траекторией его движения. Например, цилиндр в рамках кинематической модели может быть описан как движение круга вдоль отрезка, представляющего собой высоту цилиндра.

Для моделирования элементов сложной формы можно использовать изменение размеров контура или его положения относительно траектории во время движения.

Достоинством модели является практическое отсутствие ограничений на сложность формируемого объекта. К недостаткам относится сложность задания элементов.


7.2 Полигональные сетки


Полигональные сетки представляют собой совокупность вершин, ребер и многоугольников.

Сетку можно представить несколькими различными способами [14].

При явном задании многоугольников каждый многоугольник представляется в виде списка координат его вершин:

P = ((x₁, y₁, z₁), (x₂, y₂, z₂), …(x_n, y_n, z_n)).

Вершины многоугольника запоминаются в том порядке, в котором они встречаются при обходе вокруг многоугольника. Все последовательные вершины многоугольника, а также первая и последняя вершины, соединяются ребрами.

Этот способ записи является эффективным для каждого отдельного многоугольника. Для полигональной сетки этот метод приводит к большим потерям памяти из-за дублирования информации о координатах общих вершин многоугольников, а также не дает явного описания общих ребер и вершин. Для поиска всех многоугольников, имеющих общую вершину, требуется сравнение троек координат одного многоугольника с тройками координат всех остальных многоугольников. Если же из-за ошибок округления одна и та же вершина в разных многоугольниках имеет разные координаты, то результат поиска может быть нулевой.

При визуализации полигональной сетки общие ребра рисуются дважды – по одному разу для каждого многоугольника.

При задании многоугольников с помощью указателей в список вершин каждый узел полигональной сетки запоминается лишь один раз в списке вершин. Каждый многоугольник определяется списком указателей в список вершин.

Этот метод требует меньшего объема памяти, но общие ребра многоугольников по-прежнему рисуются дважды.

При явном задании ребер многоугольников полигональная сетка задается в виде иерархической модели. Координаты каждого узла полигональной сетки запоминаются в списке вершин.

Создается список ребер, где каждое ребро указывает на две вершины в списке вершин. Каждый многоугольник задается как совокупность указателей на элементы списка ребер.

Полигональная сетка изображается вычерчиванием всех ребер (а не всех многоугольников).

Заданную таким способом полигональную сетку наиболее просто проверять на непротиворечивость представления, т.е. на выполнение некоторых условий: что все многоугольники замкнуты, что все ребра используются по крайней мере один раз, но не более некоторого максимального числа раз, что на каждую вершину есть ссылка по крайней мере от двух ребер и т.п. Проверка непротиворечивости представления наиболее важна для полигональных сеток, созданных в интерактивном режиме (например, при оцифровке объектов), когда ошибки практически неизбежны.


7.3. Параметрические кубические кривые


Для визуализации кривых линий с помощью компьютера надо знать их математическое описание [7, 10, 11, 14, 16, 18 20].

Существуют два основных способа представления кривых.

Первый способ заключается в задании кривой с помощью функций переменных x, y, z:

z = f(x, y), или F(x, y, z) = 0.

Этот способ представления влечет за собой многие ограничения, особенно, если некоторым значениям координат x и y будут соответствовать несколько значений z, т.е. если кривая образует петлю. Кроме того, в некоторых точках кривой значение тангенса угла наклона может оказаться равным бесконечности.

Эти проблемы снимаются в случае параметрического способа представления кривых, когда координаты x, y и z описываются как функции от некоторого параметра t:

x = f(t),

y = f(t),

z = f(t).

При таком способе представления легко описываются замкнутые и многозначные функции, а вместо тангенсов углов наклона используются касательные вектора, которые никогда не бывают бесконечными.

В качестве функций от параметра t наиболее часто используются многочлены третьей степени (кубические):

x(t) = a_xt³ + b_xt² + c_xt + d_x,

y(t) = a_yt³ + b_yt² + c_yt + d_y,

z(t) = a_zt³ + b_zt² + c_zt + d_z.

Формулы для x(t), y(t) и z(t) аналогичны друг другу, поэтому далее будут рассматриваться только уравнения для координаты x.

Диапазон изменения параметра t может быть любым, но наиболее часто его ограничивают 0  t  1. Все последующие выводы будут рассмотрены для этого диапазона.

Значение касательного вектора к кривой определяется как первая производная функции x(t) по параметру t:

dx/dt = 3a_xt² + 2b_xt + c_x.

Кривая линия описывается как последовательность отдельных сегментов параметрических кубических кривых. В точках соединения сегментов должна соблюдаться непрерывность самой кривой (без разрывов) и непрерывность касательных векторов (без изменения наклона). Многочлены более низкой степени, чем третья, не могут обеспечить выполнения этих условий. При использовании многочленов более высоких степеней увеличивается сложность расчетов, возникают нежелательные осцилляции кривых.

Существует несколько способов описания параметрических кубических кривых. Рассмотрим основные: формы Эрмита, Безье и В-сплайны. Каждая из этих форм имеет свои достоинства и недостатки.

В рамках формы Эрмита кривая задается через координаты конечной и начальной точек (P₁ и Р₄) и значений касательных в этих точках (R₁ и R₄). Точкам присваиваются индексы 1 и 4, а не 1 и 2 для совместимости с выражениями, которые используются при построении кривых методами Безье и В-сплайнов. При этом полагают, что для начальной точки t=0, а для конечной t=1.

Перепишем формулы для функции x(t) и касательной x’(t) в матричном виде:

x(t) = [t³, t², t, 1] = T C_x, x’(t) = [3t², 2t, 1, 0] C_x.

Задача построения кривой сводится к нахождению значений элементов матрицы C_x (т.е. коэффициентов a_x, b_x, c_x, d_x), удовлетворяющих условиям:

х(0) = Р_1х = [0, 0, 0, 1] С_х,

х’(0) = R_1х = [0, 0, 1, 0] С_х,

х(1) = Р_4х = [1, 1, 1, 1] С_х,

х’(1) = R_4х = [3, 2, 1, 0] С_х.

Объединяя полученные выражения в одно матричное уравнение, получим:

G_hx = = С_х.

Искомое выражение для С_х:

С_х = = M_h G_hx,

где M_h – эрмитова матрица, G_hx – геометрический вектор Эрмита.

Итоговое уравнение для координаты х:

x(t) = T M_h G_hx = P_1x(2t³ – 3t² + 1) + P_4x(– 2t³ + 3t²) +

+ R_1x(t³ – 2t² + t) + + R_4x(t³ – t²).

Недостатком формы Эрмита является необходимость явного задания значения касательных векторов в концевых точках кривой, что не всегда удобно при реализации интерактивных режимов аппроксимации, кроме того, само понятие вектора незнакомо некоторым пользователям. Форма Эрмита удобна при аппроксимации уже имеющихся кривых, когда приблизительно известны длина или направление касательных векторов.

Для обеспечения условий непрерывности при стыковке сегментов кривой необходимо, чтобы конечная точка первого сегмента совпадала с начальной точкой второго сегмента, а касательные вектора к сегментам в этих точках имели одинаковое направление (длина векторов может быть разной):

P₄^I = P₁^II, R₄^I = kR₁^II.

В форме Безье для задания кубической кривой используются четыре управляющих точки: Р₁, Р₂, Р₃ и Р₄. Данная форма задания кубической кривой очень близка к эрмитовой форме, но касательные вектора в конечных точках R₁ и R₄ задаются отрезками Р₁Р₂ и Р₃Р₄:

R_1x = 3(Р_2x – Р_1x) = x’(0), R_4x = 3(Р_4x – Р_3x) = x’(1).

Переход от геометрического вектора Безье G_b к геометрическому вектору Эрмита G_h определяется как:

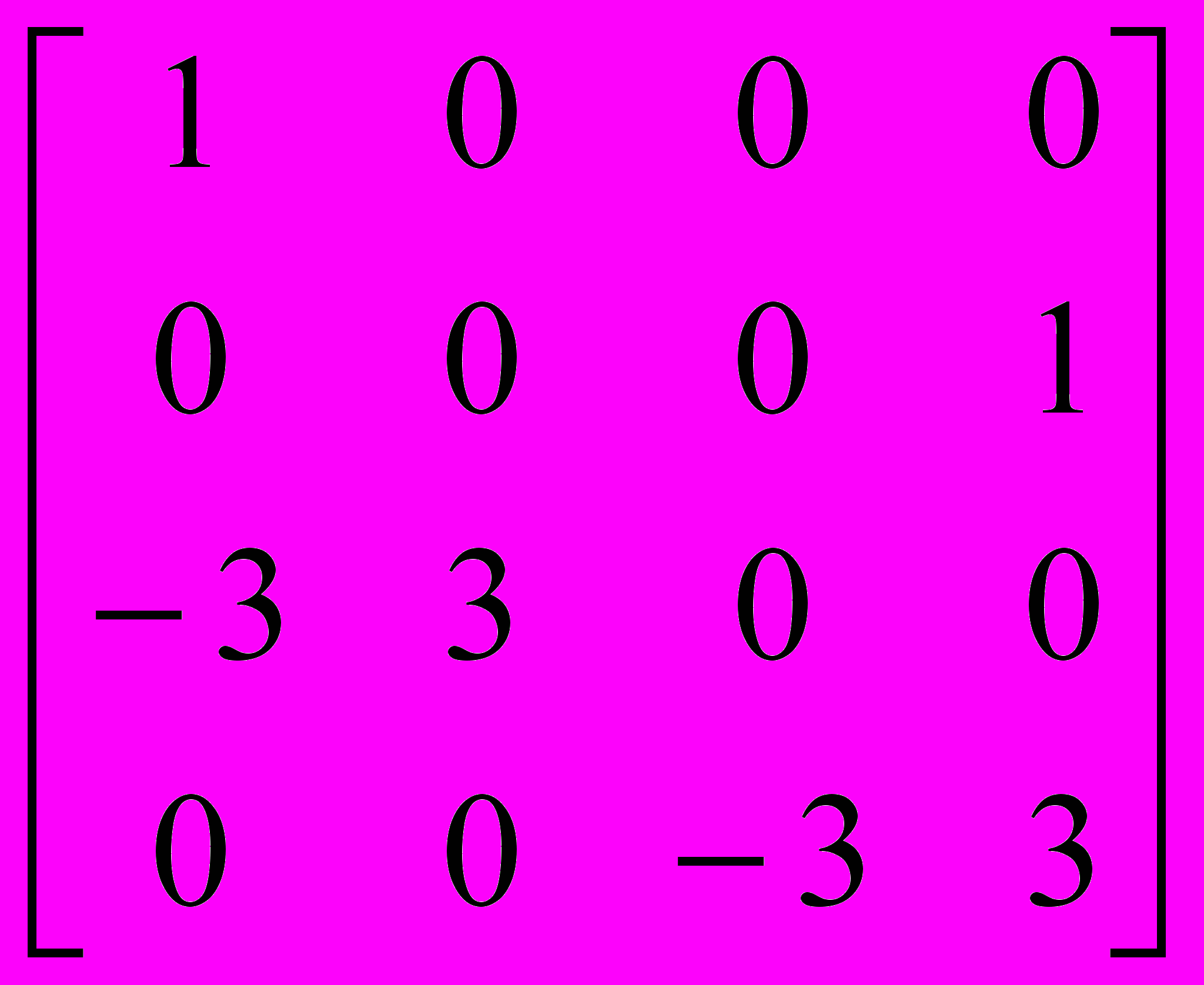
G_hх = = = 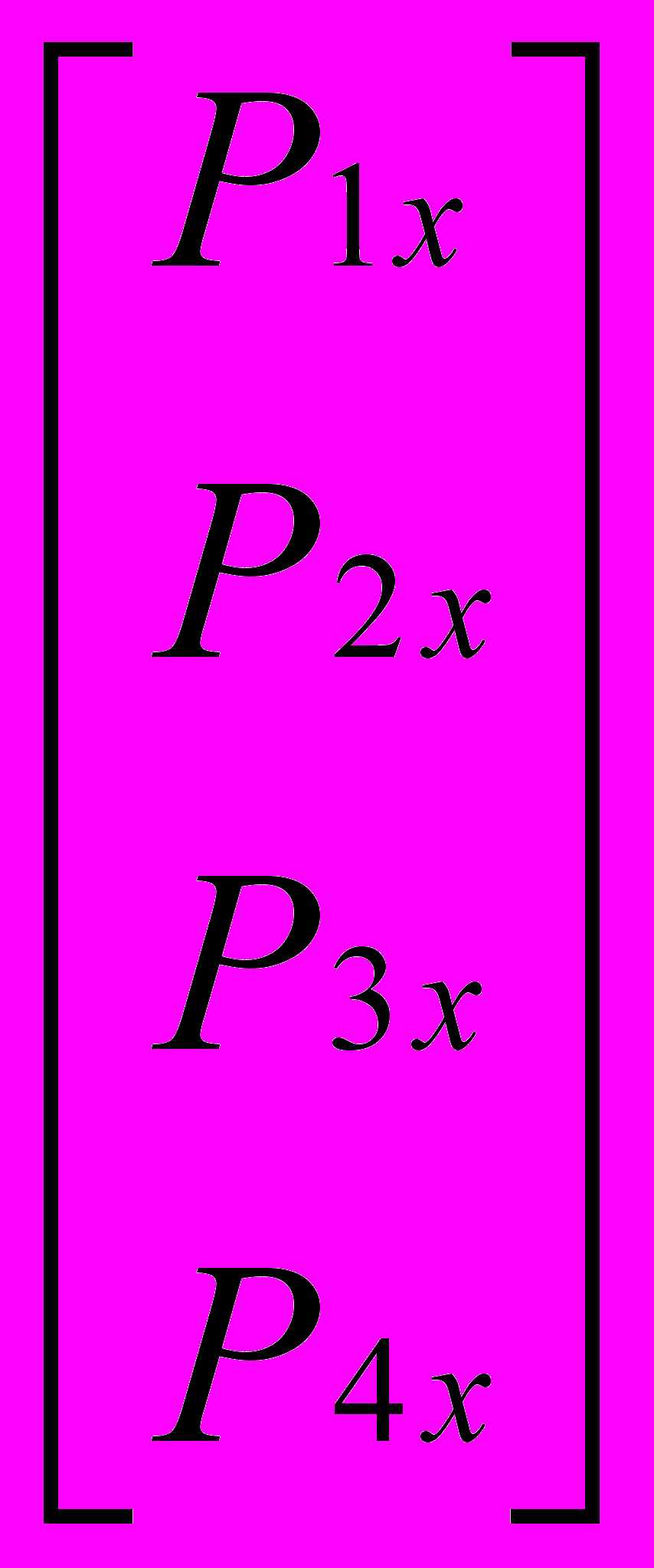M_hb G_bх,

где M_hb – матрица перехода от геометрического вектора Безье к геометрическому вектору Эрмита.

Выражение для функции выглядит x(t) так:

x(t) = T M_h G_hx = T M_h M_hb G_bx = T M_b G_bx,

M_b = M_h M_hb = .

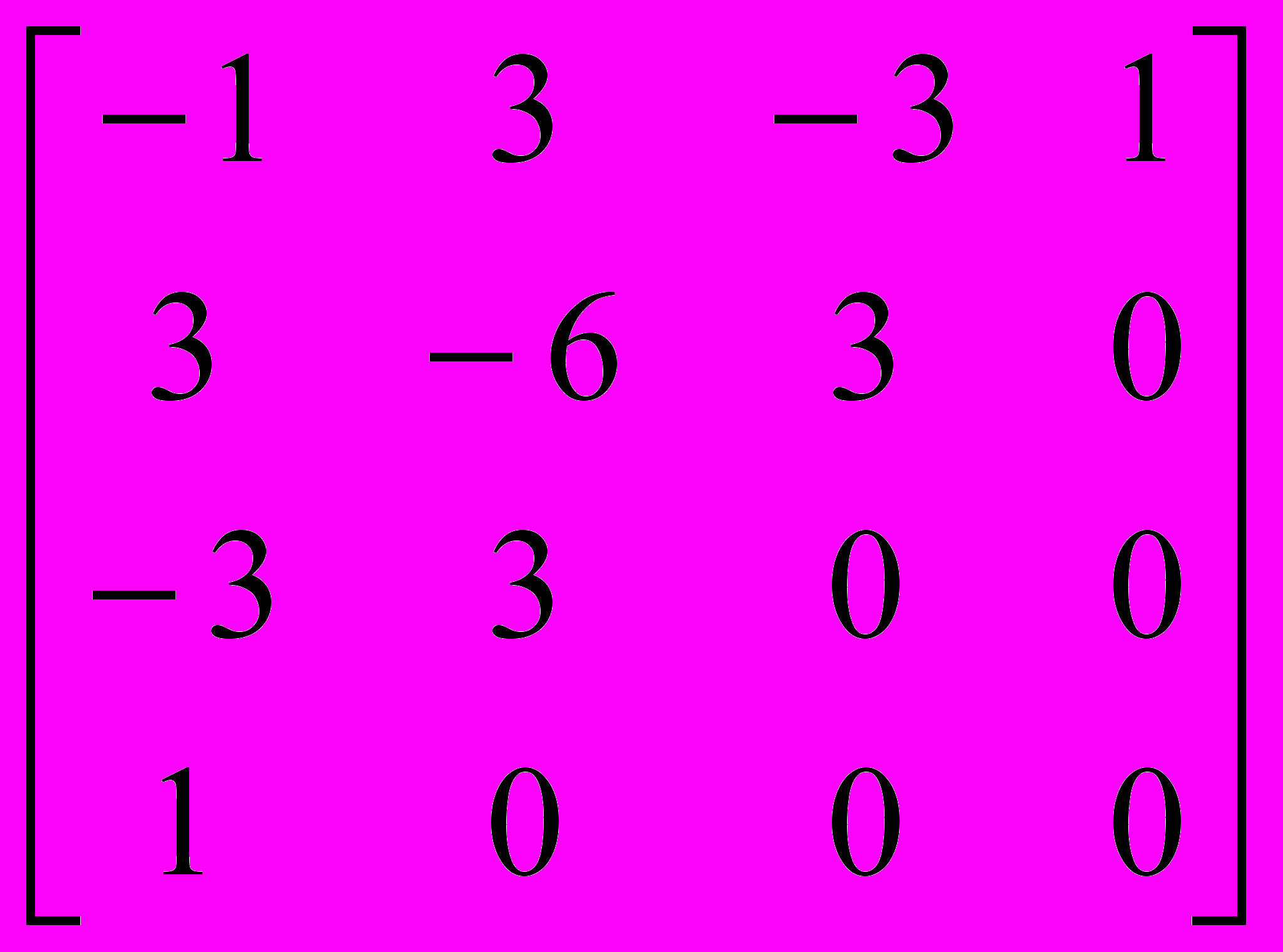Отсюда:

x(t) = (1 – t)³P_1x + 3t(t – 1)²P_2x + 3t²(1 – t)P_3x + t³P_4x.

Форма Безье наиболее удобна при аппроксимации кривых, заданных набором точек. В компьютерной графике чаще используется форма Безье, чем форма Эрмита.

Четыре управляющих точки в форме Безье определяют выпуклый четырехугольник, внутри которого находится сама кривая. Выпуклый многоугольник оказывается полезным при выполнении многих операций, например, при отсечении кривой по видимому объему. При выполнении этой операции вместо того, чтобы сразу проводить проверку отсечения кривой, сначала проверяется ее выпуклая оболочка и только в случае пересечения выпуклой оболочкой видимого объема возникает необходимость в проверке самой кривой.

Для обеспечения условий непрерывности при соединении сегментов кривой необходимо, чтобы конечная точка первого сегмента совпадала с начальной точкой второго сегмента, а точки P₃^I и P₂^II лежали на одной прямой, проходящей через точку соединения сегментов:

P₄^I = P₁^II, (P₄^I – P₃^I) = k(P₂^II – P₁^II).

Форма В-сплайнов является более гладкой, чем другие формы представления, т.к. непрерывностью изменения обладают ее касательный вектор и кривизна (т.е. первая и вторая производные кривой непрерывны в конечных точках) в отличие от форм Эрмита и Безье (у которых в конечных точках непрерывны лишь первые производные) [11, 14, 20].

Термин «сплайн» происходит от названия длинных гибких реек, которыми пользовались чертежники при разметке поверхности самолетов, кораблей.

В-сплайн описывается следующей формулой:

x(t) = T M_s G_sx,

где M_s = 1/6 .
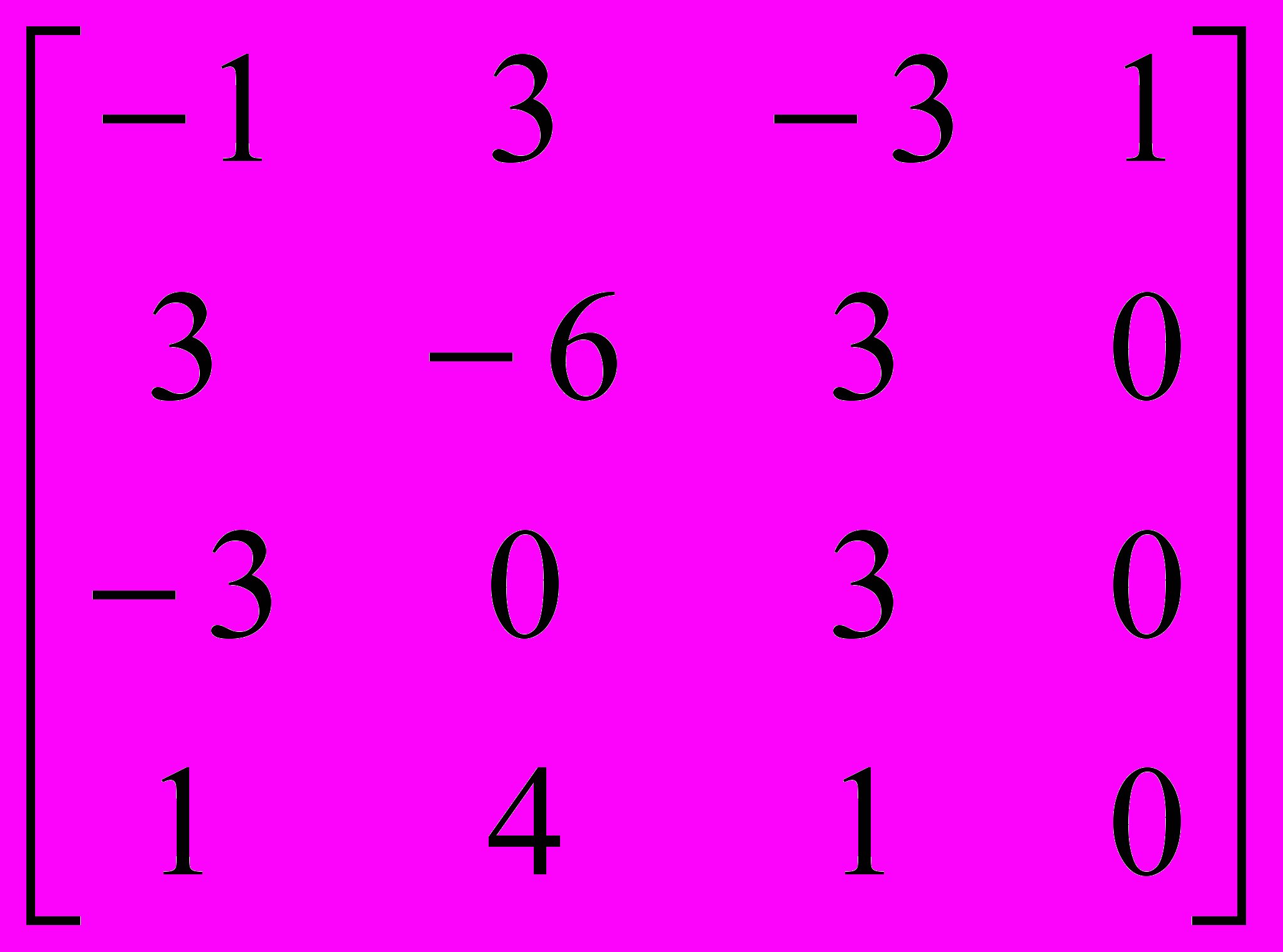