Прикладная графическая программа. Прикладная программа передает данные и сформированные графические команды в графическую систему (рис. 1) [14]. Рис. Схема взаимодействия прикладной программы и графической системы

Вид материала

Программа

Подобный материал:

• Рабочая программа дисциплины для студентов магистратуры, обучающихся по направлению, 120.54kb.
• Магистерская программа «Информационные технологии и информационные системы» по направлению, 34.28kb.
• Программа вступительного испытания по предмету прикладная этика для поступающих, 307.5kb.
• Рис Физический и логический обмен данными по сети 21 Рис Ахитектура процессов в распределенных, 932.01kb.
• Рис. Сферы взаимодействия психики и личности (Управляющей психики) Рис., 2.3kb.
• Методика ми5 проверки цепи фаза нуль в электроустановках до 1 кВ с глухим заземлением, 53.81kb.
• Программа дисциплины Современная прикладная алгебра для направления 010500 Прикладная, 214.78kb.
• Основная образовательная программа высшего профессионального образования 230700., 513.26kb.
• Программа вступительного экзамена по математике подготовки магистров по направлению, 86.94kb.
• Прикладная программа для создания, редактирования (обработки) и просмотра графических, 47.05kb.

6. ПРОЕЦИРОВАНИЕ

В настоящее время абсолютное большинство устройств вывода графической информации создают изображения на плоскости – экране монитора, бумаге и т.п. Несоответствие между объемными объектами и плоскими изображениями устраняется путем введения проекций, которые отображают трехмерные объекты на двумерной картинной плоскости.

Проекция объекта на картинную плоскость строится при помощи проецирующих лучей, которые выходят из одной точки (центра проекции) и проходят через каждую точку объекта. Пересечение этих лучей с картинной плоскостью и образует проекцию.

В зависимости от удаленности центра проекции и взаимного расположения картинной плоскости, проецирующих лучей и осей координат выделяется несколько видов проекций (рис. 6.1) [10, 14, 16, 17].





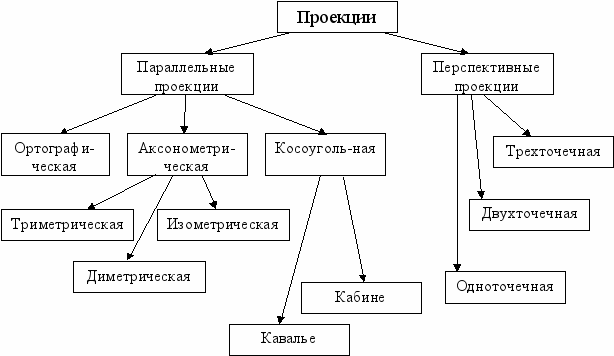
Рис. 6.1. Виды проекций.

При параллельном проецировании центр проекции считается лежащим в бесконечности (проецирующие лучи параллельны друг другу), а при перспективном (центральном) проецировании расстояние между центром проекции и картинной плоскостью конечно.

6.1. Виды параллельных проекций

В ортографических и аксонометрических проекциях проецирующие лучи перпендикулярны картинной плоскости (направление проецирования совпадает с нормалью к проекционной плоскости).

Во всех параллельных проекциях грани отображаемого объекта, параллельные картинной плоскости, изображаются без искажения формы и размеров; параллельные в пространстве прямые сохраняют параллельность и после проецирования, а также остаются постоянными относительные длины параллельных в исходном пространстве линий.

Самой простой из параллельных проекций является ортографическая проекция, при которой картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей (рис. 6.2), а проецирующие лучи параллельны одной из координатных осей.




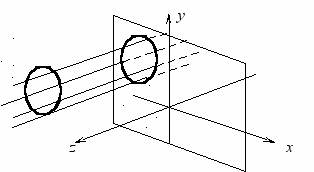
Рис. 6.2. Ортографическая проекция на плоскость z = 0.

Матрица проецирования на координатную плоскость z = 0 имеет вид:

[P_{орт z}] = ,

а при проецировании на параллельную ей плоскость z = r:

[P_{орт z}] = .

Аналогично, матрицы проецирования на плоскости x = p и y = q равны:

[P_{орт x}] = , [P_{орт y}] = .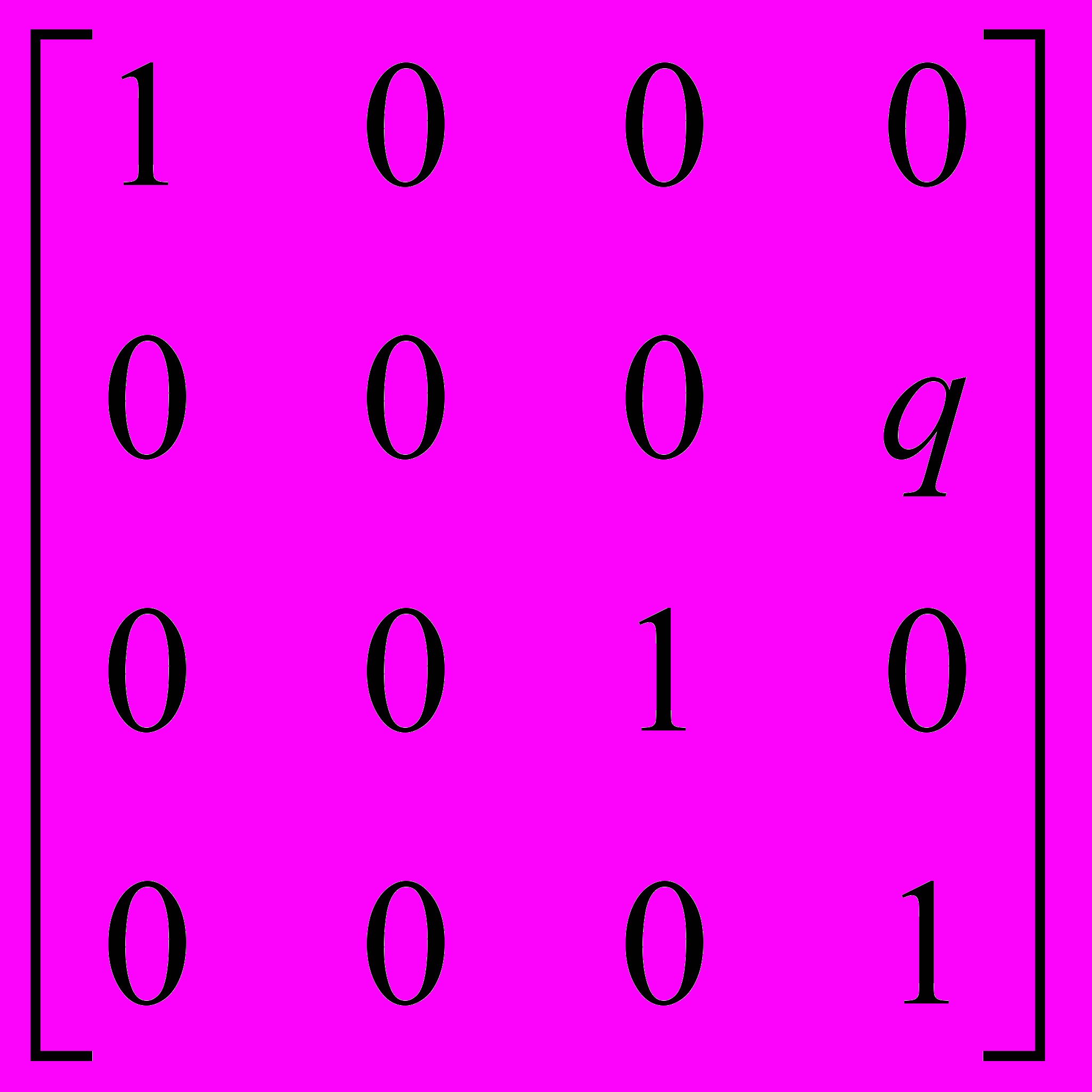

Наиболее часто используются наборы ортографических проекций отдельных сторон объекта (вид спереди, вид сверху, вид сбоку).

В аксонометрических проекциях нормаль к картинной плоскости (а, следовательно, и направление проецирования) не совпадает ни с одной из координатных осей (рис. 6.3).

Рис. 6.3. Аксонометрическая проекция.

В зависимости от взаимного расположения картинной плоскости и осей координат выделяют следующие виды аксонометрических проекций:

а) триметрия – нормаль к картинной плоскости образует с координатными осями попарно различные углы (  ,   ,   );

б) диметрия – два угла между нормалью к картинной плоскости и координатными осями равны;

в) изометрия – все три угла между нормалью к картинной плоскости и координатными осями равны ( =  = ).

Каждая из этих проекций получается комбинацией поворотов с последующим параллельным проецированием.

Триметрическая проекция строится последовательными поворотами вокруг координатных осей, совершаемыми в произвольном порядке, с последующим проецированием на плоскость z = 0. Коэффициенты искажения (отношение длины проекции отрезка к его истинной длине) по каждой из проецируемых координатных осей не равны друг другу.