Прикладная графическая программа. Прикладная программа передает данные и сформированные графические команды в графическую систему (рис. 1) [14]. Рис. Схема взаимодействия прикладной программы и графической системы

Вид материала

Программа

Содержание 2.1. Система аддитивных цветов XYZ. В этой системе в качестве базовых были приняты три цвета X 2.2. Система субтрактивных цветов 2.3. Система «Тон – Насыщенность – Яркость» 3. Базовые растровые алгоритмы Простейший пошаговый алгоритм 3.2. Устранение ступенчатого эффекта 3.3. Заполнение области (закрашивание) 3.4. Алгоритмы закрашивания, использующие математическое описание контура 4. Алгоритмы отсечения 5. Аффиные преобразования 5.1. Аффинные преобразования на плоскости N – произвольная точка плоскости с координатами x 5.2. Аффинные преобразования в пространстве 5.3. Композиция преобразований М с координатами (х, у, z

Подобный материал:

• Рабочая программа дисциплины для студентов магистратуры, обучающихся по направлению, 120.54kb.
• Магистерская программа «Информационные технологии и информационные системы» по направлению, 34.28kb.
• Программа вступительного испытания по предмету прикладная этика для поступающих, 307.5kb.
• Рис Физический и логический обмен данными по сети 21 Рис Ахитектура процессов в распределенных, 932.01kb.
• Рис. Сферы взаимодействия психики и личности (Управляющей психики) Рис., 2.3kb.
• Методика ми5 проверки цепи фаза нуль в электроустановках до 1 кВ с глухим заземлением, 53.81kb.
• Программа дисциплины Современная прикладная алгебра для направления 010500 Прикладная, 214.78kb.
• Основная образовательная программа высшего профессионального образования 230700., 513.26kb.
• Программа вступительного экзамена по математике подготовки магистров по направлению, 86.94kb.
• Прикладная программа для создания, редактирования (обработки) и просмотра графических, 47.05kb.

2.1. Система аддитивных цветов

Эта система цветов используется для излучаемого цвета (для мониторов, светящихся материалов). Аддитивный (add – присоединять) цвет в модели RGB получается при сложении лучей трех основных (базовых) цветов – красного (Red), зеленого (Green) и синего (Blue) разной интенсивности. Если интенсивность каждого из основных цветов достигает 100%, то получается белый цвет. Отсутствие всех трех цветов дает черный цвет. Схема смешивания базовых цветов для модели RGB представлена на рис. 2.1.




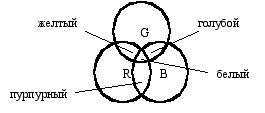
Рис. 2.1. Схема смешивания базовых цветов в модели RGB.

Цветовая модель RGB используется в мониторах и жидкокристаллических дисплеях.

Для некоторых цветов коэффициенты в модели RGB должны иметь отрицательные веса. То есть система RGB имеет неполный цветовой охват: некоторые насыщенные цвета (все насыщенные спектральные цвета, кроме базовых цветов самой модели) не могут быть представлены смесью трех компонент.

Для решения проблемы отрицательных коэффициентов в модели RGB в 1931 г. Международная комиссия по освещению приняла систему XYZ. В этой системе в качестве базовых были приняты три цвета X, Y и Z, которые носят условный характер (не соответствуют никаким реальным цветам), величина Y совпадает с чувствительностью глаза к свету.

Цветовой график для модели XYZ в хроматических координатах

x = X / (X + Y + Z) и y = Y / (X + Y + Z) представлен на рис. 2.2.




Рис. 2.2. Цветовой график в хроматических координатах

На цветовом графике все видимые цвета попадают внутрь замкнутой области, ограниченной с одной стороны кривой линией (соответствующей насыщенным спектральным цветам), а с другой стороны – прямой, соответствующей неспектральным сиреневым цветам.

2.2. Система субтрактивных цветов

Для печати графических изображений используется субтрактивная (subtract – вычитать) система цветов, работающая с отраженным светом. Белая бумага при освещении отражает все цвета, окрашенная же бумага поглощает часть цветов, а остальные – отражает.

В системе субтрактивных цветов CMY основными являются голубой или, скорее, бирюзовый (Cyan), пурпурный (Magenta) и желтый (Yellow). Каждый из них вычитает (т.е. поглощает) определенные цвета из белого света, падающего на печатную страницу: голубой краситель вычитает красный цвет, оставляя зеленую и синюю компоненту, малиновый краситель поглощает зеленый, а желтый краситель – синий цвет. Голубой, желтый и малиновый красители поглощают красный, зеленый и синий цвета, оставляя в результате черный (см. рис. 2.3). Белый цвет получается при отсутствии всех трех основных цветов.





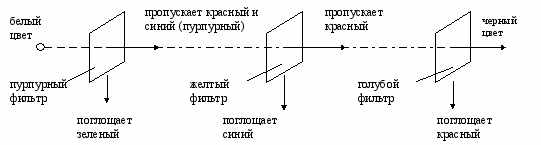
Рис. 2.3. Взаимосвязь цветов в моделях RGB и CMY.

Значения цветов в системе CMY – это просто инвертированные значения системы RGB.

Преобразование из модели RGB в модель CMY выполняется следующим образом:

= -

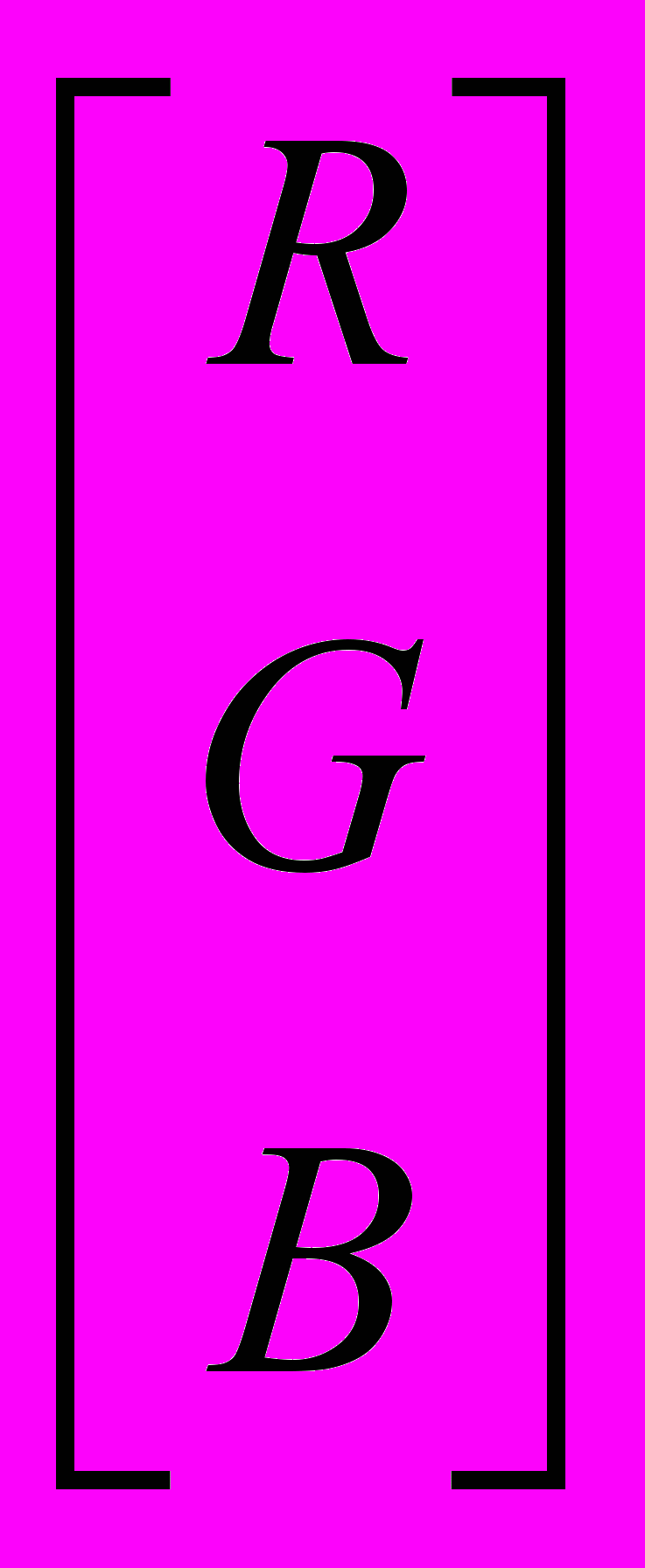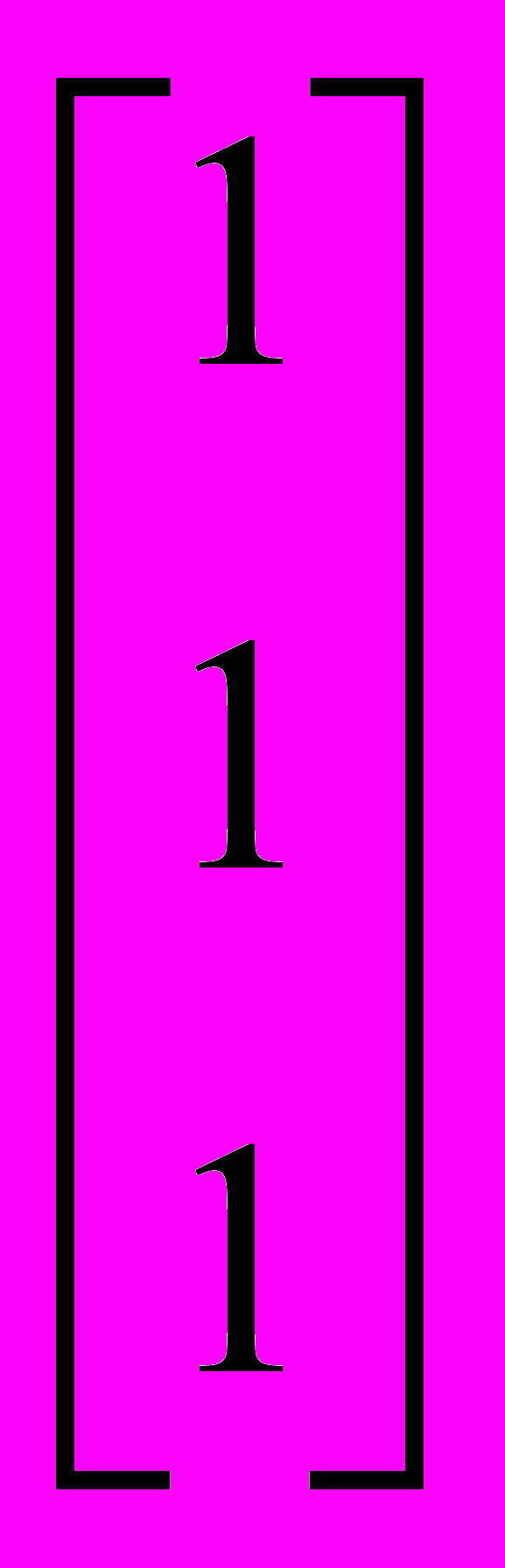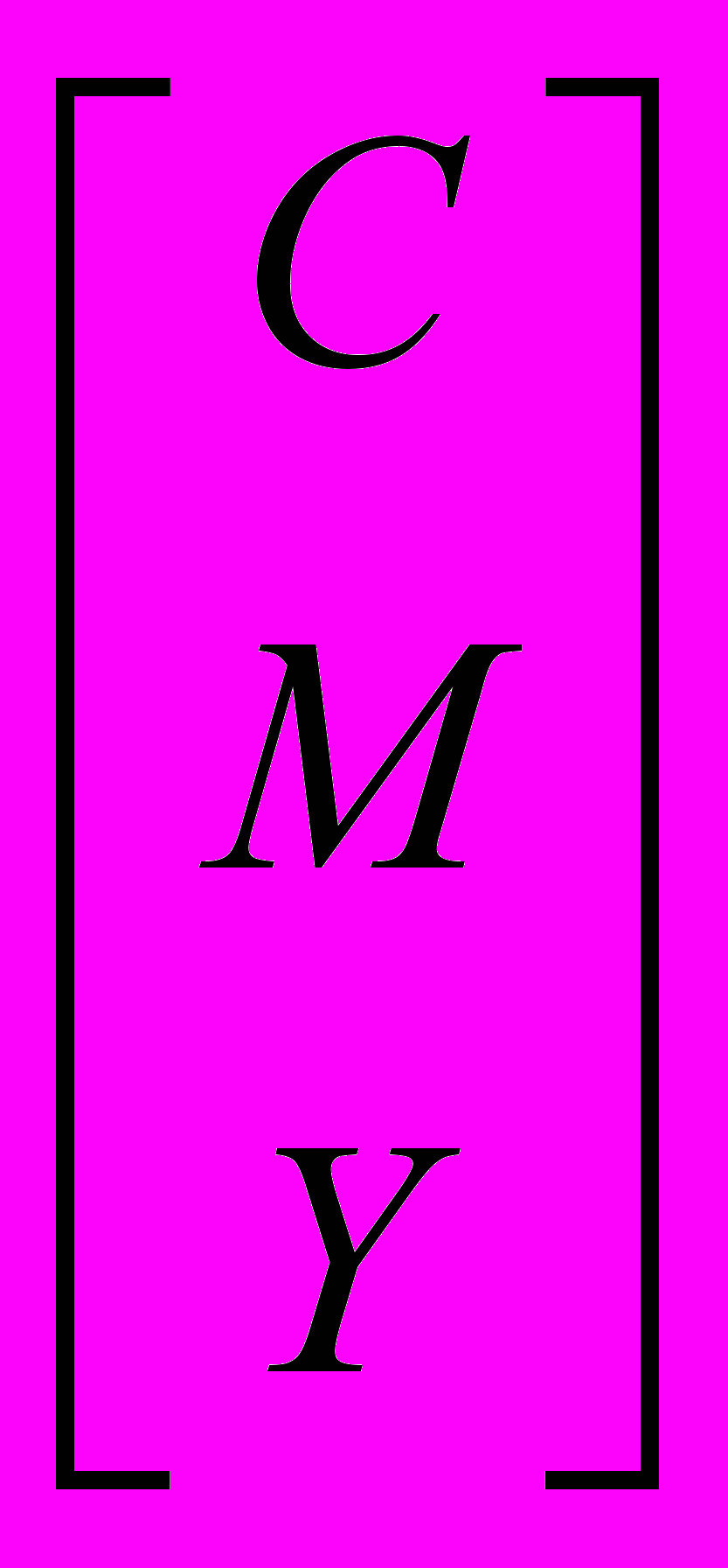
Однако при печати использование трех красителей для получения черного цвета оказывается дорогостоящим и неудобным, поэтому используется модель CMYK (Cyan, Magenta, Yellow, blacK) – т.е. дополнительно используется черная краска.

Из-за различия природы получения цветов в моделях RGB и CMYK достаточно трудно точно воспроизвести при печати цвет, который мы видим на мониторе. Обычно на экране цвет выглядит несколько ярче.

2.3. Система «Тон – Насыщенность – Яркость»

Более интуитивным способом описания цвета является система HSB – тон (Hue), насыщенность (Saturation), яркость (Brightness).

Тон – это конкретный оттенок цвета: красный, желтый, зеленый, пурпурный и т.п.

Насыщенность характеризует чистоту, т.е. степень ослабления данного цвета белым цветом. Уменьшая насыщенность, мы «разбавляем» его белым цветом.

Яркость зависит от количества черной краски, добавленной к данному цвету – чем меньше черного, тем больше яркость.

Для отображения на мониторе компьютера система HSB преобразуется в систему RGB, а для печати – в систему CMYK.


3. БАЗОВЫЕ РАСТРОВЫЕ АЛГОРИТМЫ


Базовые растровые алгоритмы переводят простейшие векторные примитивы (отрезки, окружности и т.п.) в их растровые образы (при растрировании векторных изображений) или служат для обработки растровых изображений [10, 14, 17].

В общем случае, растровое представление векторного примитива не является единственным и возможны различные способы его построения.

Важным понятием для растровой сетки является связность, определяющая когда два пикселя можно считать соседними. Вводится два понятия связности (рис. 3.1) [17]:

• четырехсвязность – пиксели считаются соседними, если либо их х-координаты, либо их у-координаты отличаются на единицу; т.е. у каждого пикселя может быть четыре соседа;
  
• восьмисвязность - пиксели считаются соседними, если их х-координаты и у-координаты отличаются не более, чем на единицу; т.е. у каждого пикселя может быть восемь соседей.
  

Рис. 3.1. Соседние пиксели: а – четырехсвязные, б – восьмисвязные.

Любые два 4-связных пикселя являются и 8-связными, но не наоборот.


3.1. Растровое представление отрезка


В качестве отрезка на растровой сетке выступает набор пикселей Р₁, Р₂, …, Р_n, где любые два пикселя Р_i и Р_i+1 являются соседними в смысле заданной связности. Таким образом, возникает понятие 4- и 8-связных отрезков.

Пусть заданы координаты (х₁, у₁) и (х₂, у₂) начального и конечного пикселей отрезка. Для вывода отрезка необходимо знать координаты каждого из составляющих его пикселей.

Наиболее просто нарисовать отрезок горизонтальной или вертикальной линии. Например, для горизонтальной линии при х₁ < x₂ и у₁= у₂ выполняется цикл по х:

for (x=x1; x<=x2; x=x+1) putpixel (x, y1, COLOR);

Вычисление координат пикселей, составляющих наклонную линию, происходит более сложно. Известно несколько методов таких вычислений, рассмотрим некоторые из них.

Простейший пошаговый алгоритм выполняется следующим образом – на каждом шаге координаты х, у пикселей отрезка вычисляются исходя из их значений на предыдущем шаге:

х_i+1 = x_i + x,

y_i+1 = y_i + y,

где x и у – приращения координат.

у / х = (у₂ - у₁ )/( x₂ - x₁)= tg,

где tg – тангенс угла наклона отрезка к оси х.

Принимая х = 1, получим:

у = tg, х_i+1 = x_i + 1, у_i+1 = у_i + tg.

При значении tg >1 при вычислениях координат пикселей х и у меняют местами, принимая у= 1, а х = 1 / tg.

Так как тангенс угла наклона отрезка в общем случае не является целой величиной, в данном алгоритме используется процедура округления значений второй координаты до целого, что замедляет вычисления.

Из-за погрешности представления в компьютере дробных чисел с каждым шагом может накапливаться ошибка вычисления второй координаты и возможен случай, когда вычисленная на последнем шаге координата у не совпадет с координатой конца отрезка у₂.

Алгоритм Брезенхэма – это инкрементный алгоритм, использующий только целочисленные операции сложения, вычитания и сравнения, не использующий умножение и деление. Вещественные переменные в алгоритме не используются совсем и, следовательно, операции округления не требуется.

Алгоритм выполняется как пошаговое вычисление координат соседних пикселей. На каждом шаге на основе анализа функции погрешности е координаты х и у предыдущего пикселя либо изменяются на единицу, либо остаются прежними. Значение функции погрешности, вычисляемой на i–ом шаге, зависит от значения погрешности на i+1–ом шаге и от того, выполнялось ли на этом шаге изменение координат пикселя.

Восьмисвязный алгоритм Брезенхэма [10]:

lx=x2–x1; //Длина отрезка по оси х.

ly=y2–y1; //Длина отрезка по оси у.

ex=0; //Функции

ey=0; // погрешности.

if (lx>0) dx=1; //Выбор значений приращений

else if (lx==0) dx=0; //координаты х за один

else dx=-1; //шаг.

if (ly>0) dy=1; //Тоже, для координаты у.

else if (ly==0) dy=0;

else dy=-1;

lx=abs(lx);

ly=abs(ly); //Абсолютные длины отрезка по осям х и у.

if (lx>ly) l=lx; else l=ly; //Количество шагов алгоритма l.

x=x1;

y=y1;

putpixel (x, y, COLOR); //Рисуется начальный пиксель

for (i=1; i<=l; i=i+1)

{

ex=ex+lx;

ey=ey+ly;

if (ex>=l)

{ ex=ex-l;

x=x+dx; }

if (ey>=l)

{ ey=ey-l;

y=y+dx;}

putpixel (x, y, COLOR);

}

Четырехсвязные алгоритмы выполняются за большее число циклов, т.к. на каждом шаге может изменяться либо координата х, либо координата у, но не обе сразу.

Существуют алгоритмы Брезенхэма, служащие для построения других векторных примитивов: окружности, эллипса и др [10, 17, 19].


3.2. Устранение ступенчатого эффекта


Для устранения ступенчатого эффекта в растровых изображениях используют методы выравнивания и сглаживания. Основная идея этого метода состоит в том, что видимые линии и отрезки имеют ненулевую толщину. И для их отображения на экране или бумаге используются пиксели, которые также имеют ненулевую площадь.

Чтобы растровое изображение выглядело более гладким, цвет угловых пикселей «ступенек» заменяется на некоторый оттенок, промежуточный между цветом объекта и цветом фона:

C_x = (CS_x + C_ф(S – S_x)) / S,

где C_x – искомый оттенок цвета углового пикселя; S – площадь пикселя; S_x – часть площади пикселя, перекрываемая идеальным контуром векторного объекта; C_ф – цвет фона; C – цвет объекта.

Таким образом, устранение ступенчатого эффекта достигается за счет размывания контура объекта (рис. 3.2).




Рис. 3.2. Устранение ступенчатого эффекта.


3.3. Заполнение области (закрашивание)


Область представляет собой группу примыкающих друг к другу связанных пикселей.

Области пикселей могут задаваться различными способами [17].

Внутренне-определенные области задаются своими внутренними значениями: все пиксели в области имеют одно значение цвета и ни один из пикселей, принадлежащих границе области, не принимает этого значения.

Гранично-определенные области – все пиксели, принадлежащие границе, имеют одинаковое значение цвета и ни один из пикселей области не принимает этого значения.

Заполнение области – это присваивание всем пикселям, лежащим внутри области, некоторого общего значения цвета.

Рассмотрим простейший алгоритм закрашивания гранично-определенной области. На первом этапе находится пиксель, лежащий внутри области. Ему присваивается значение цвета заполнения. Затем проводится анализ цветов всех соседних пикселей. Если цвет соседнего пикселя не равен цвету границе или цвету заполнения, то цвет этого пикселя изменяется на цвет заполнения. Потом анализируется цвет пикселей, соседних с уже рассмотренными, и для них повторяется процедура закраски.

Восьмисвязные алгоритмы закраски могут давать выход за пределы области (рис. 3.3).




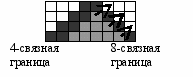
Рис. 3.3. Выход за границу области при 8-связном алгоритме закрашивания.

Как видно из рисунка, для правильного выполнения алгоритма закрашивания граница 8-связной области должна быть 4-связна.

Большую скорость закрашивания обеспечивают алгоритмы, которые обрабатывают не отдельные пиксели, а сразу блоки пикселей (отрезки, прямоугольники).

Закрашивание области линиями заключается в том, что на каждом шаге закрашивания рисуется горизонтальный отрезок максимальной длины, который размещается между пикселями границы. Затем проверяются пиксели, лежащие непосредственно над и под отрезком. Если находятся незаполненные пиксели, то отрисовывается новый отрезок.


3.4. Алгоритмы закрашивания, использующие математическое описание контура


Данные алгоритмы закрашивания не требуют обязательного предварительного создания пикселей границы области. Математическим описанием контура фигуры может служить уравнение кривой (окружности, эллипса). Для многоугольников контур задается множеством координат вершин (х_i, у_i) и соединяющих их отрезков.

Наиболее просто заполнить прямоугольник со сторонами, параллельными осям координат, заданный координатами диагональных углов (х₁, у₁) и (х₂, у₂), причем x₁₂, y₁₂:

for (y=y1; y<=y2; y=y+1)

{ // Рисуется горизонтальная линия

line (x1, y, x2, y); // от точки с координатами (x₁, y)

} // до точки (x₂, y).

Рассмотрим более подробно алгоритм заполнения многоугольника произвольной формы [10].

П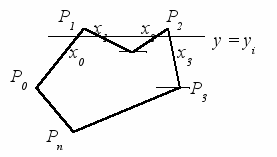усть задан многоугольник с вершинами Р₀, Р₁, …, Р_n (рис. 3.4). Наиболее популярный алгоритм закрашивает многоугольник отрезками прямых горизонтальных линий. Для каждой из горизонталей у = у_i. находятся ординаты точек пересечения со всеми отрезками контура многоугольника. Затем проводится сортировка по возрастанию значений массива х_j. Многоугольник закрашивается путем рисования отрезков (х₀, у_i; х₁, у_i), (х₂, у_i; х₃, у_i), (х₄, у_i; х₅, у_i) и так далее.


Для правильного заполнения многоугольника рассмотренным способом количество точек пересечения отрезков контура с каждой из горизонталей у = у_i должно всегда быть четным. Если горизонталь проходит через вершину многоугольника, то должен проводиться дополнительный анализ:

• если горизонталь при прохождении через вершину пересекает контур многоугольника (на рис. 3.4 это вершины Р₀ и Р₄), то в массив х_j записывается только одна координата точки пересечения;
  
• если горизонталь касается вершины (вершины Р₁, Р₂, Р₃ и Р_n), не пересекая в этой точке контур, то координаты точки касания в массив х_j или не записываются, или записываются дважды.
  

4. АЛГОРИТМЫ ОТСЕЧЕНИЯ


Очень часто координаты некоторых точек рисуемых объектов, хранимые в прикладной базе данных, могут выходить за границы видимости (окна устройства вывода). То есть, объекты сначала должны пройти процесс отсечения и перевода координат составляющих их точек в координаты устройства вывода, лишь затем они могут быть визуализированы. Область отсечения, как правило, представляет из себя прямоугольник.

В простейшем случае – при отсечении двумерного отрезка относительно прямоугольного окна необходимо произвести вычисление координат точек пересечения отрезка с границами окна. Для сокращения объема вычислений и уменьшения числа операций умножения и деления используются различные алгоритмы, одним их которых является алгоритм Коэна-Сазерленда [20]. В этом алгоритме картинная плоскость разбивается на девять областей прямыми, проходящими через стороны отсекающего прямоугольника. Каждой из областей присваивается 4-битовый код, где установленный нулевой бит означает, что область лежит выше прямоугольника, первый бит – что область лежит ниже прямоугольника, второй бит – что область лежит правее прямоугольника, а третий бит – что область лежит левее прямоугольника (рис. 4.1).




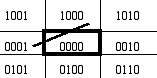
Рис. 4.1. Коды областей картинной плоскости.

Путем анализа кодов областей, в которые попадают начальная и конечная точки каждого отрезка, выявляются отрезки, для которых необходимо проводить отсечение, и отбрасываются отрезки, которые лежат за границами отсекающей области. Вычисление точек пересечения выполняется только там, где это действительно необходимо. Для анализа кодов достаточно только булевых побитовых операций над двоичными числами.

Р
1001
ассмотрим алгоритм Сазерленда и Ходгмана, используемый для отсечения многоугольников относительно видимого окна [14]. Этот алгоритм позволяет свести задачу отсечения относительно прямоугольной области (рис. 4.2-а) к серии более простых задач отсечения многоугольника вдоль прямой, проходящей через одну из границ окна (рис. 4.2-б, в, г, д).




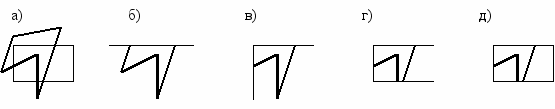
Рис. 4.2. Последовательное применение алгоритма Сазерленда-Ходгмана для отсечения многоугольника относительно видимого окна.

На вход алгоритма поступает последовательность вершин исходного многоугольника. Алгоритм последовательно «обходит» по периметру весь многоугольник, проверяя на каждом шаге соотношение между последовательными вершинами и отсекающей границей. В выходной список вершин последовательно заносятся координаты вершин многоугольника, лежащие внутри отсекающей границы, и координаты точек пересечения ребер многоугольника с границей. То есть, если ребро полностью лежит внутри границы, то в выходной список заносятся обе вершины; если ребро сечется границей, то в выходной список заносятся вершина, лежащая внутри отсекаемой области, и точка пересечения ребра с отсекающей границей.

5. АФФИНЫЕ ПРЕОБРАЗОВАНИЯ


Геометрические преобразования широко применяются в компьютерной графике при выводе изображения на экран и проведении с ним разнообразных действий [2, 10, 14, 16, 17].

Перед тем, как приступить к рассмотрению различных случаев аффинных преобразований, определим используемые системы координат.

Аффинные преобразования рассматриваются в прямоугольных декартовых системах координат. На плоскости используется правосторонняя система координат – ось х (ось абсцисс) направлена направо, ось у – вверх, за положительное направление поворота принято направление против часовой стрелки. Трехмерная система координат правосторонняя – ось z (ось аппликат) направлена на наблюдателя; положительное направление поворота – против часовой стрелки, если смотреть из конца положительной полуоси в начало координат.

5.1. Аффинные преобразования на плоскости


Пусть на плоскости в прямоугольной системе координат задана точка N (х, у), которая в результате последовательных преобразований переводится в точку N* с координатами (х*, у*). В случае аффинных преобразований координаты конечной точки можно описать уравнениями вида:

x* = a_xx + b_xy + c_x,

y* = a_yx + b_yy + c_y,

где a_x, b_x, c_x, a_у, b_у и c_у – некоторые коэффициенты.

В аффинных преобразованиях на плоскости особую роль играют несколько важных частных случаев (поворот, масштабирование, отражение и перенос), имеющих хорошо прослеживаемые геометрические характеристики [7].

П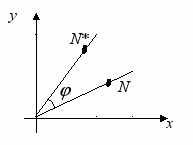оворот вокруг начала координат на угол  описывается следующими уравнениями (рис. 5.1):

x* = x cos - y sin,

y* = x sin + y cos.


Рис. 5.1. Поворот вокруг начала координат

Растяжение-сжатие (масштабирование) вдоль координатных осей и относительно начала координат:

x* = M_x x,

y* = M_y y.

M_x > 0, M_y > 0.

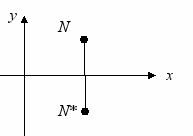
Растяжение вдоль оси абсцисс (ординат) имеет место при M_x > 1 (M_y> 1), сжатие – при M_x < 1 (M_y < 1).

Отражение относительно координатных осей (рис. 5.2) описывается следующими уравнениями:

• относительно оси абсцисс
  

x* = x, y* = -y;

• относительно оси ординат
  

x* = -x, y* = y.


Рис. 5.2. Отражение относительно оси абсцисс

Перенос точки вдоль оси абсцисс на величину x, и на величину y вдоль оси ординат:

x* = x + x,

y* = y + y.

В компьютерной графике чаще используется матричная запись этих формул. Матрицы, соответствующие случаям поворота, масштабирования и отражения, строятся легко, но для записи уравнений переноса в матричной форме приходится использовать однородные координаты.

Пусть N – произвольная точка плоскости с координатами x и y. Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел x₁, x₂, x₃, связанных с заданными числами x и y следующими соотношениями:

x = x₁ / x₃, y = x₂ / x₃, x₃  0.

В проективной геометрии для однородных координат принято следующее обозначение:

x : y : 1 (третья координата равна единице, поэтому операции деления не требуется; более общая форма записи x₁ : x₂ : x₃ ).

При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование на плоскости уравнениями вида:

= [P],

где и – векторы-столбцы координат конечной и начальной точек соответственно, [P] – матрица соответствующего преобразования, имеющая для двумерного случая размер 3X3.

Поворот:

= ,

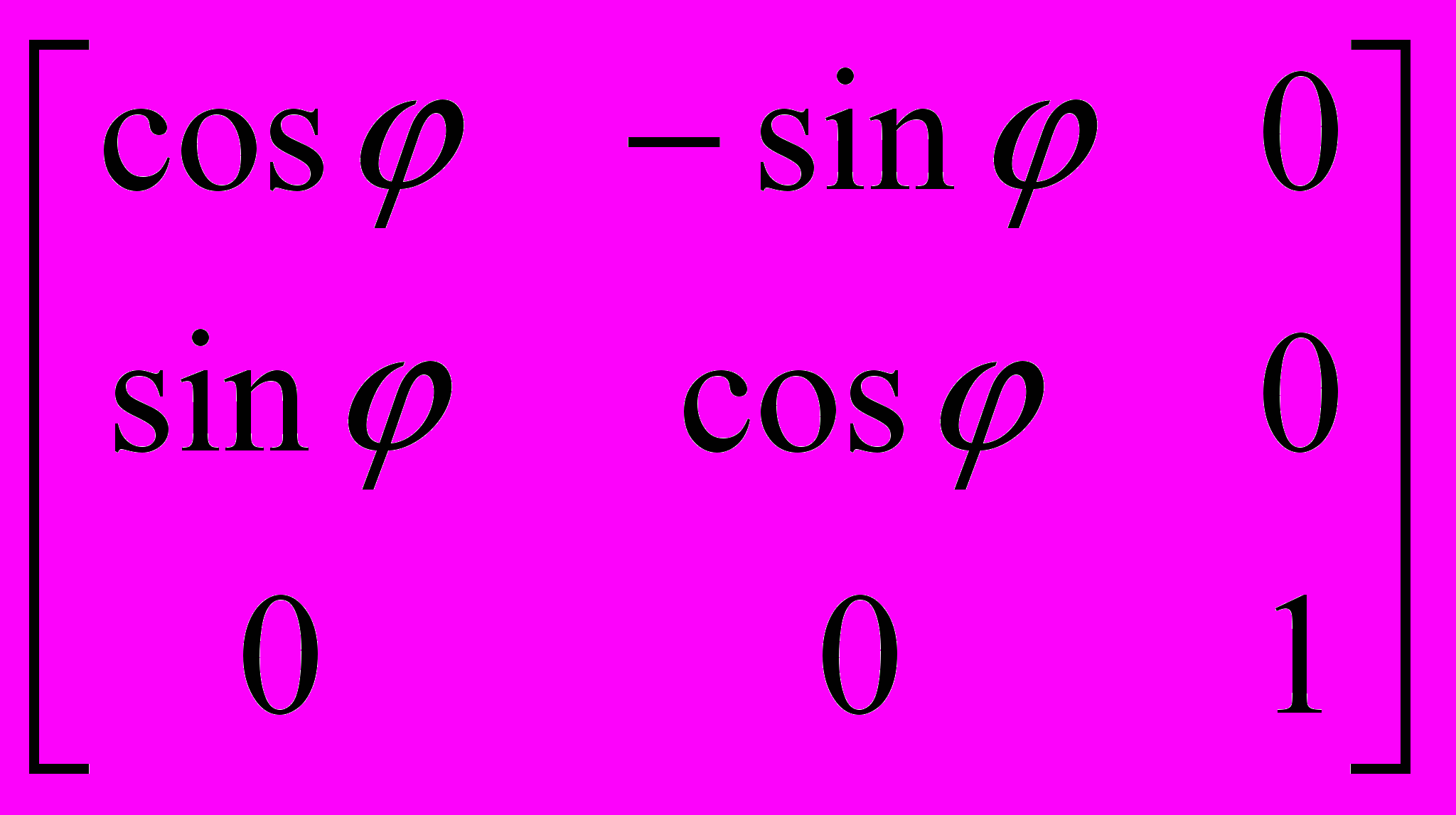
Масштабирование:

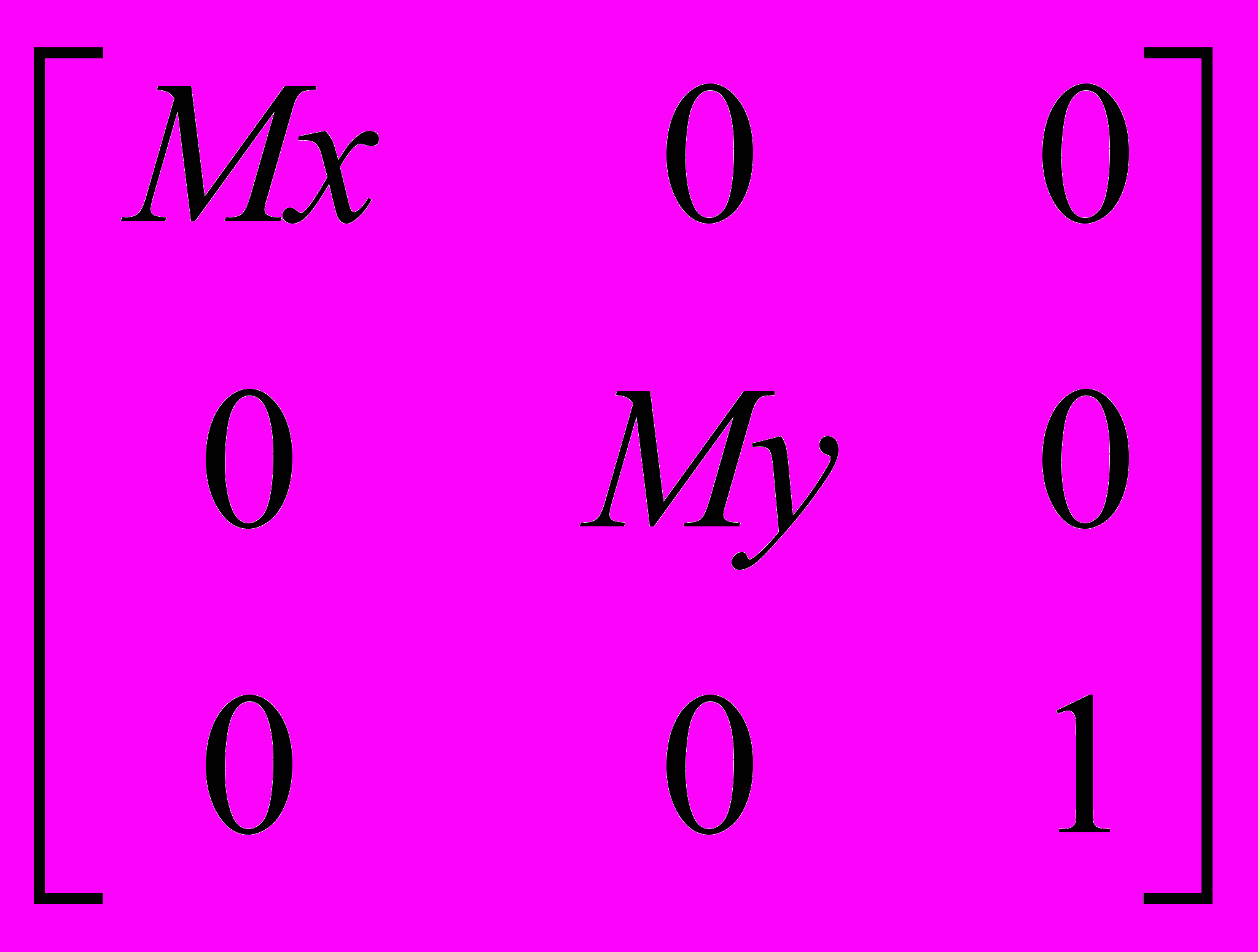
= , M_x > 0, M_y > 0.

Отражение:

относительно оси абсцисс относительно оси ординат

= . = .

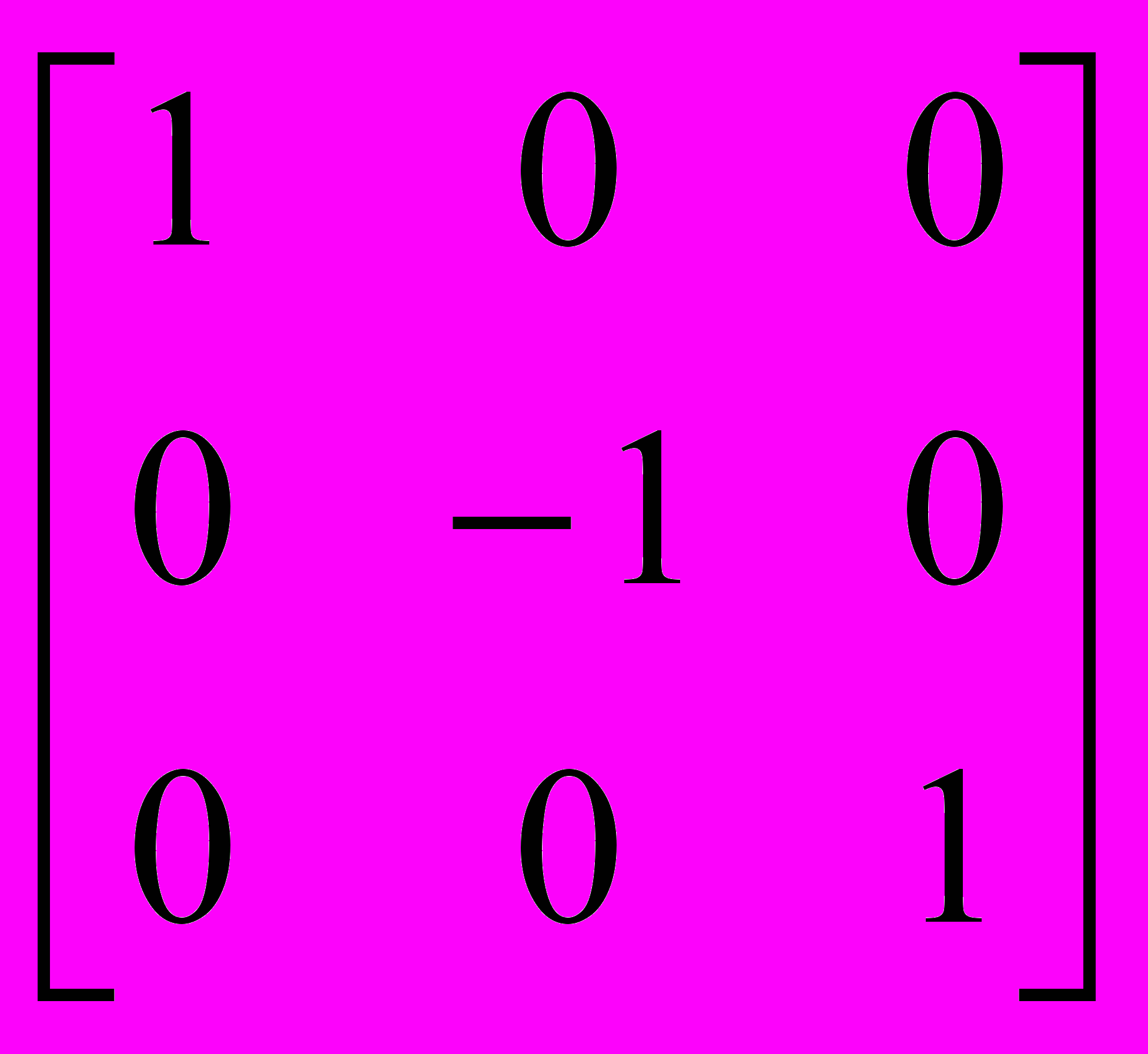
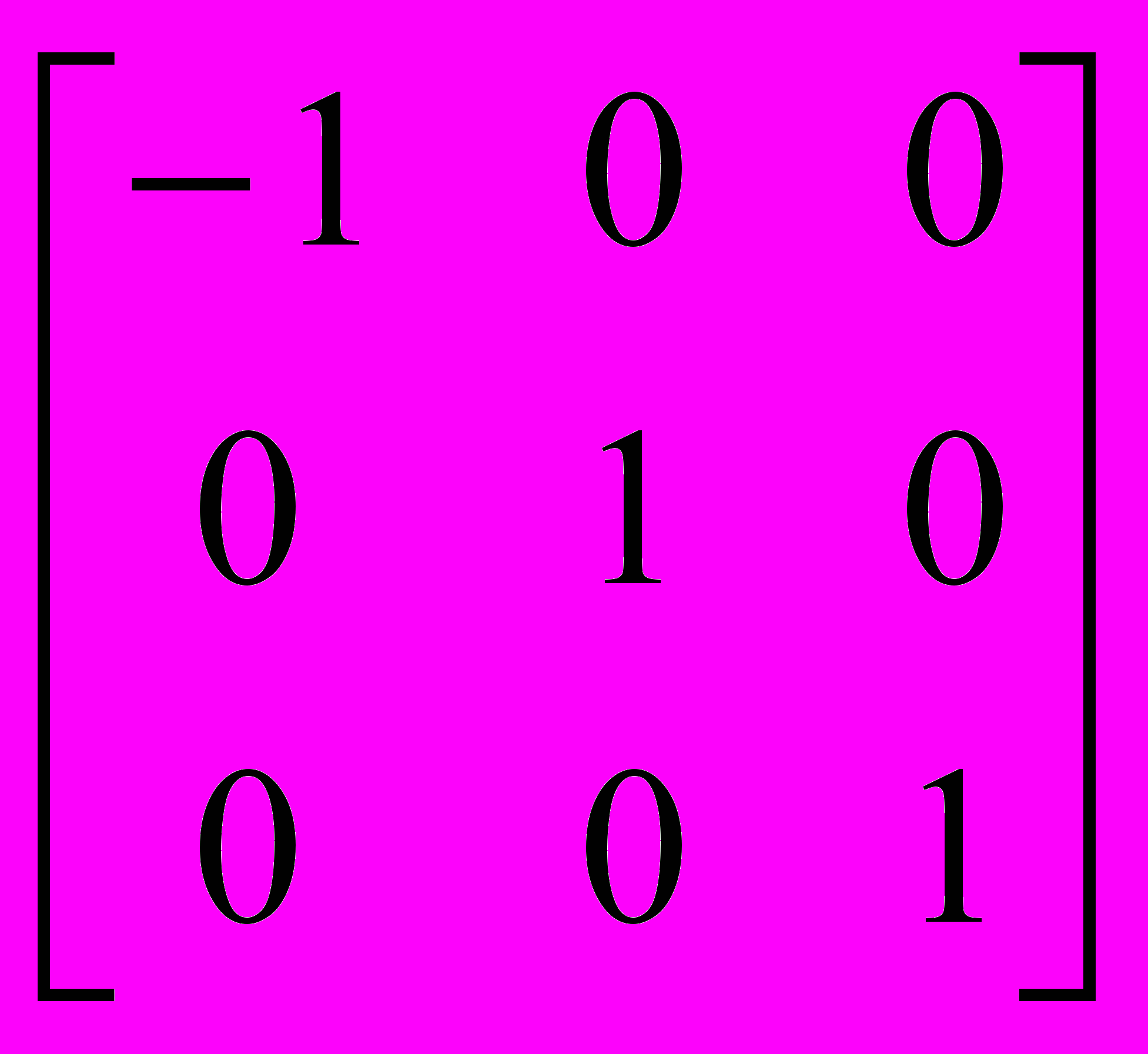
Перенос:

= .


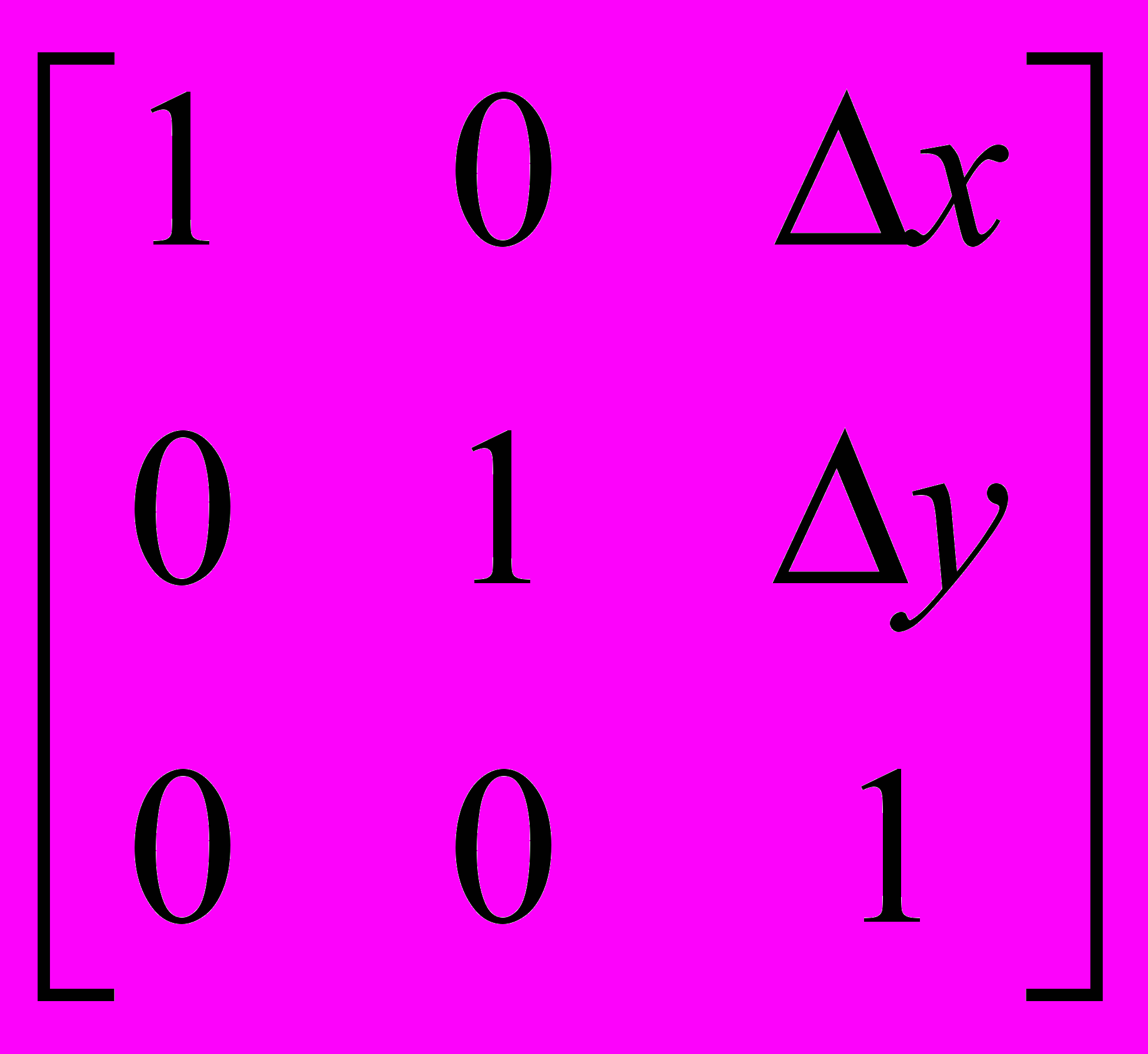
5.2. Аффинные преобразования в пространстве


Общее уравнение трехмерного аффинного преобразования:

x* = a_xx + b_xy + c_xz + d_x,

y* = a_yx + b_yy + c_yz + d_y,

z* = a_zx + b_zy + c_zz + d_z,

где a_x, b_x, c_x, d_x, a_у, b_у, c_у, d_y, a_z, b_z, c_z и d_z – некоторые коэффициенты.

В пространственных преобразованиях выделяются те же основные частные случаи, что и в двумерных преобразованиях.

Повороты.

• Поворот вокруг оси абсцисс (оси х) на угол :
  

x* = x,

y* = y cos - z sin,

z* = z cos + y sin.

В матричной форме с использованием однородных координат:

.

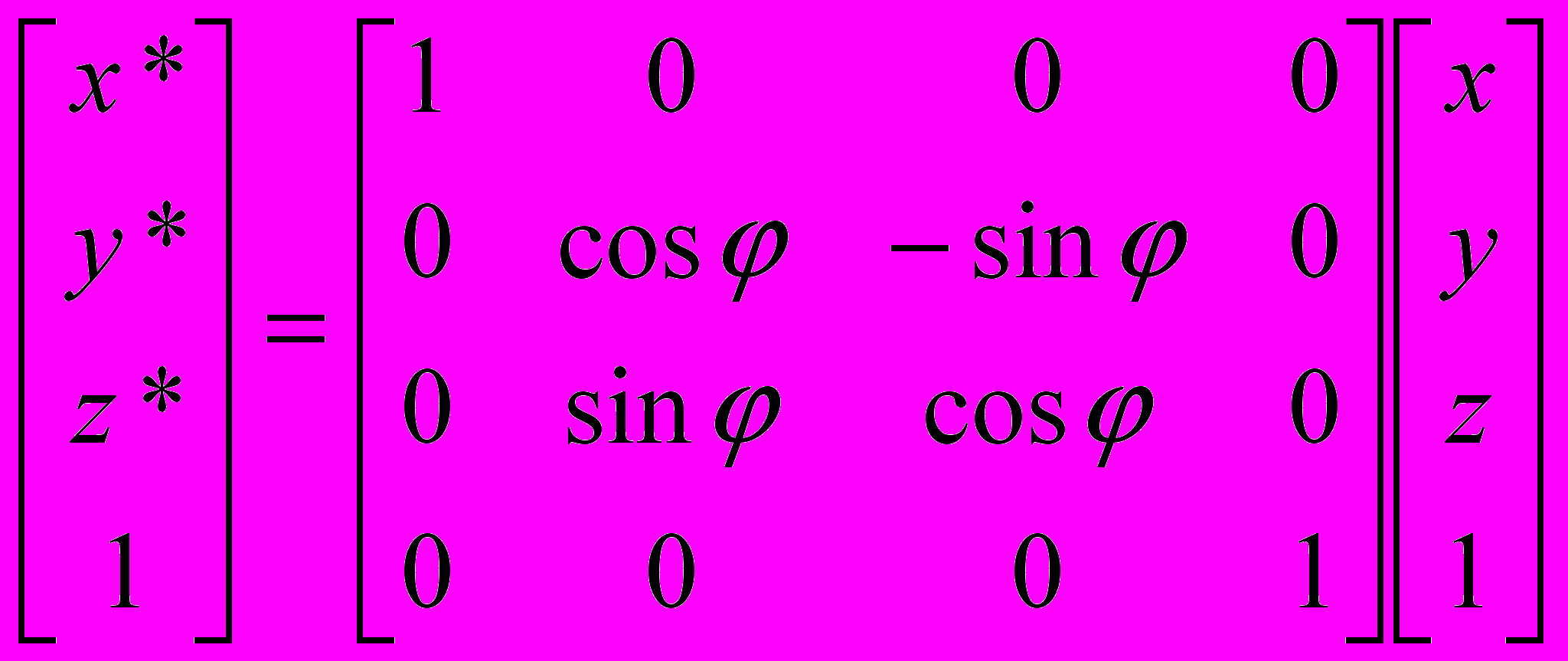• Поворот вокруг оси ординат (оси у) на угол :
  

x* = x cos + z sin,

y* = y,

z* = z cos - x sin.

В матричной форме: .

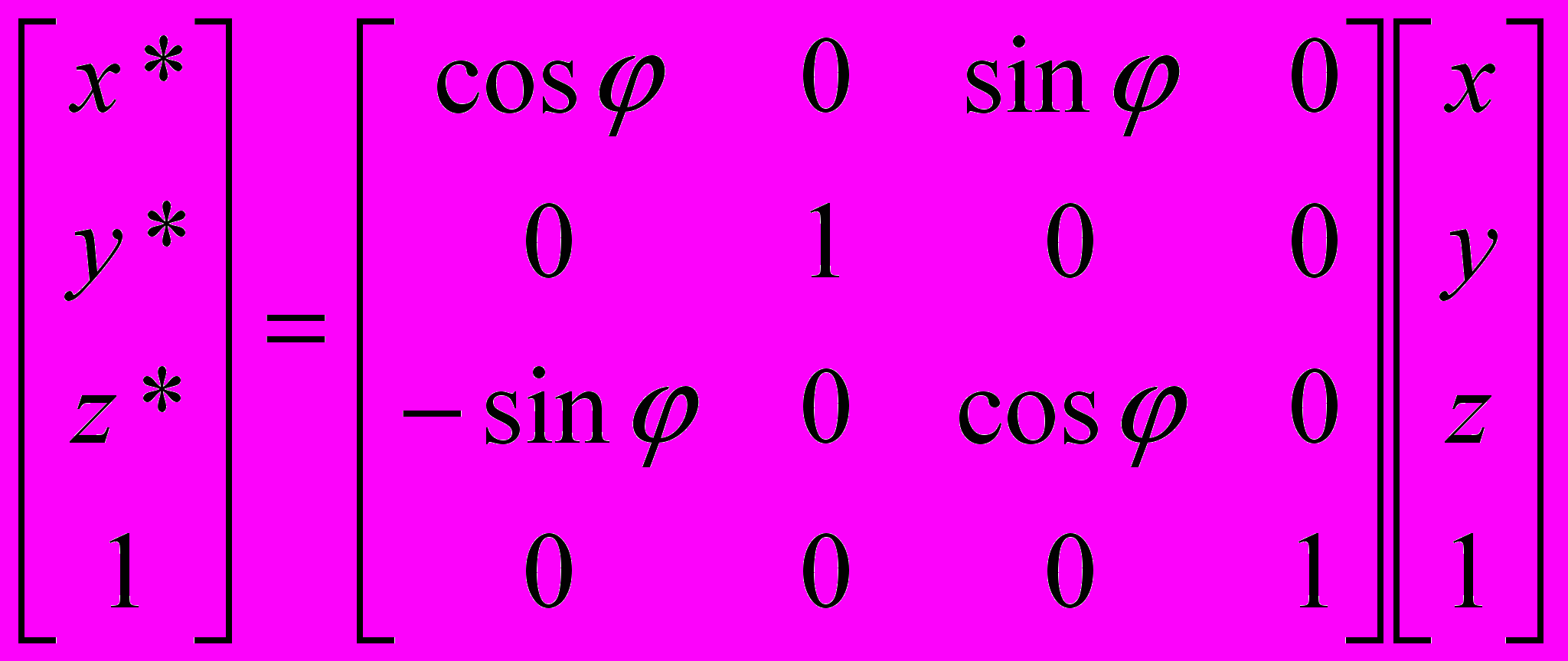• Поворот вокруг оси аппликат (оси z) на угол :
  

x* = x cos - y sinx,

y* = y cos + x sin,

z* = z.

Или, в матричной форме: .

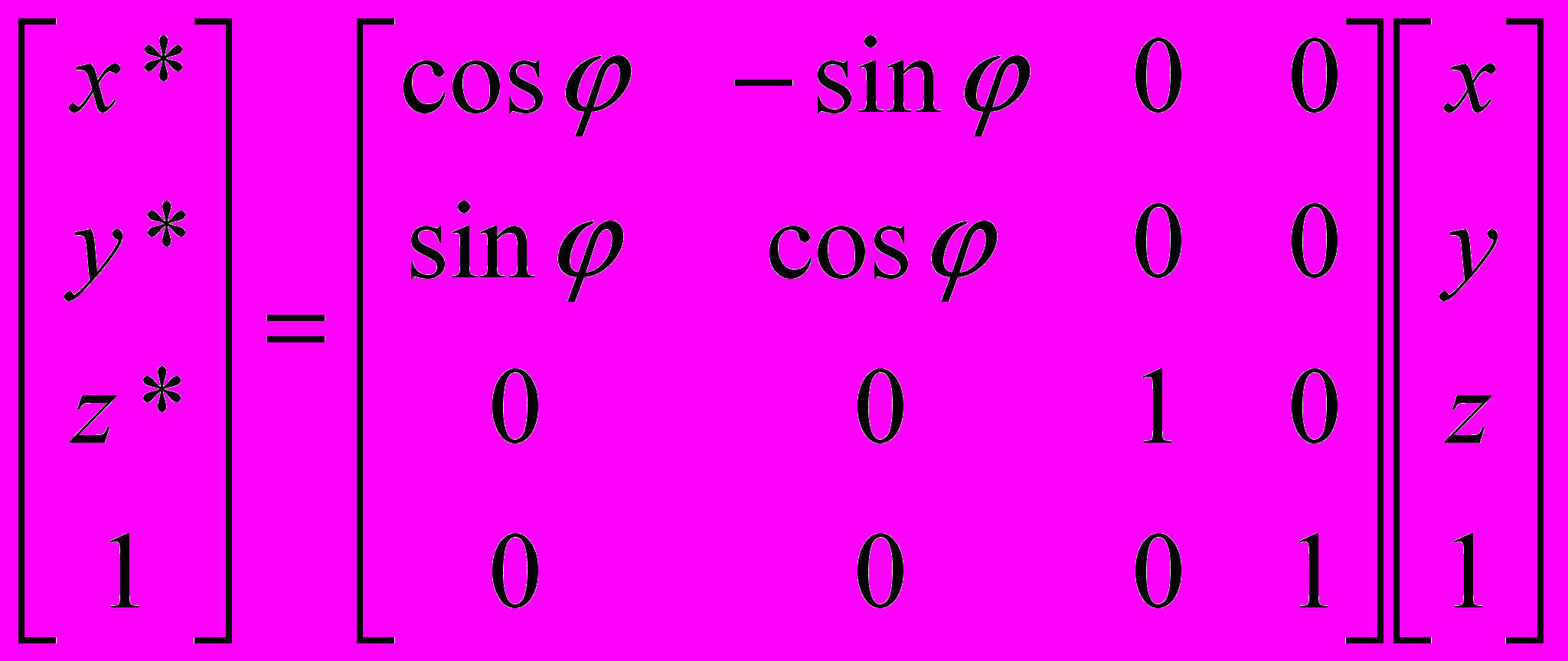В случае поворотов в отрицательных направлениях значения углов берутся со знаком минус и используются тождества:

cos(-) = cos, sin(-) = -sin.

Трехмерный перенос является простым расширением двумерного случая:

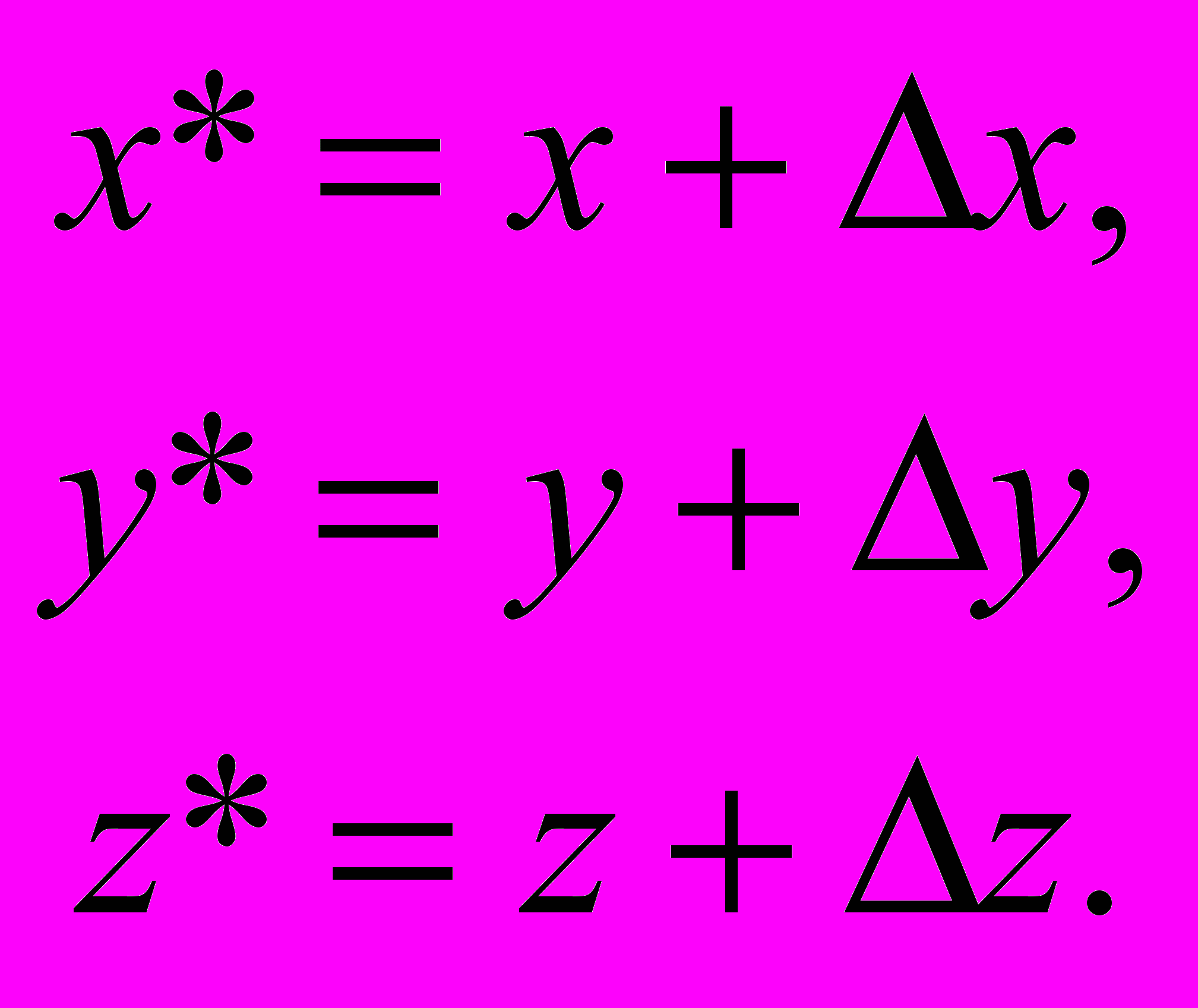или .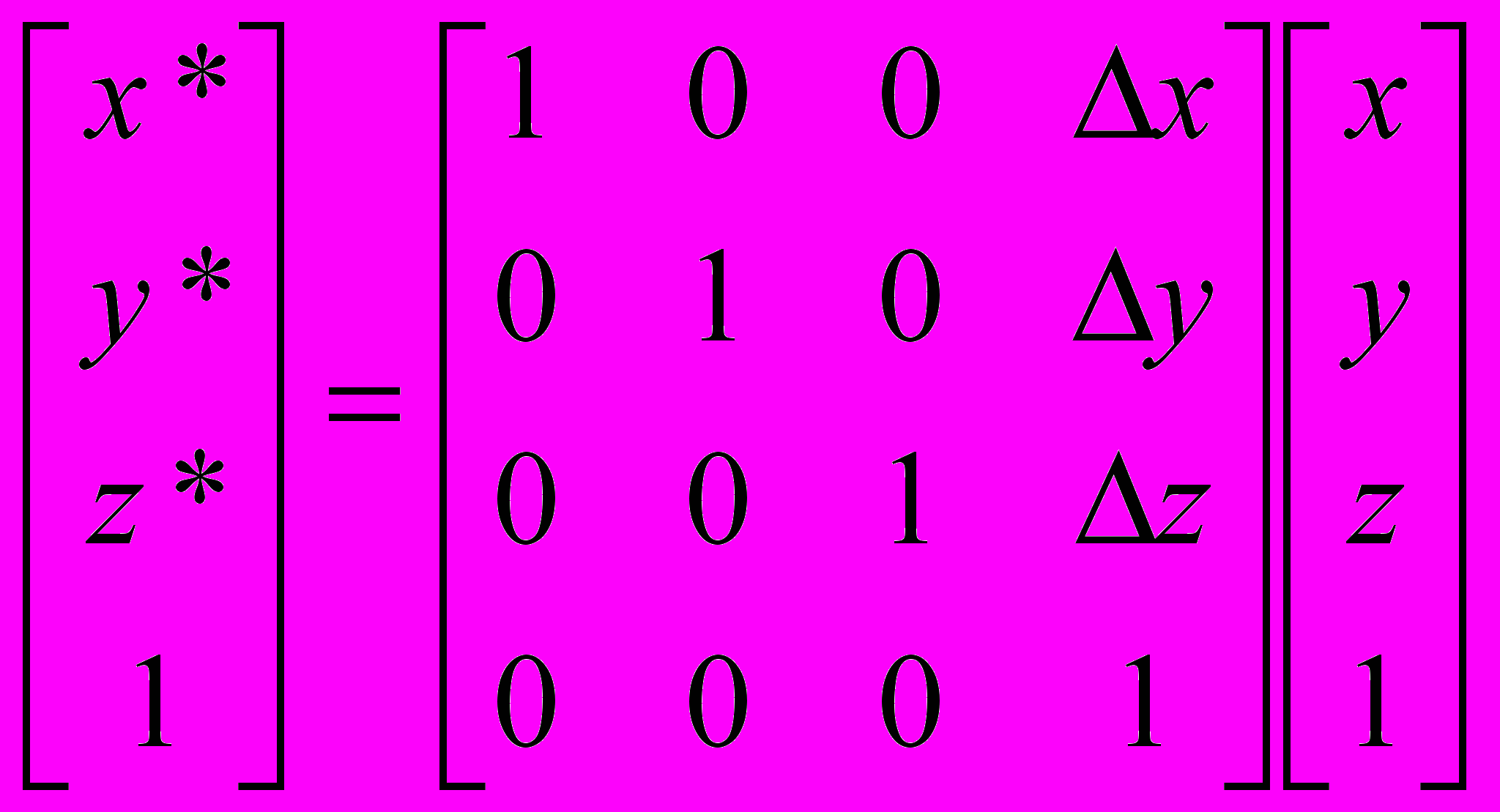

Иногда необходимо выполнить перенос на величину, не являющуюся константой, а зависящую от начальных координат точки [11]. Это преобразование описывается следующими формулами:

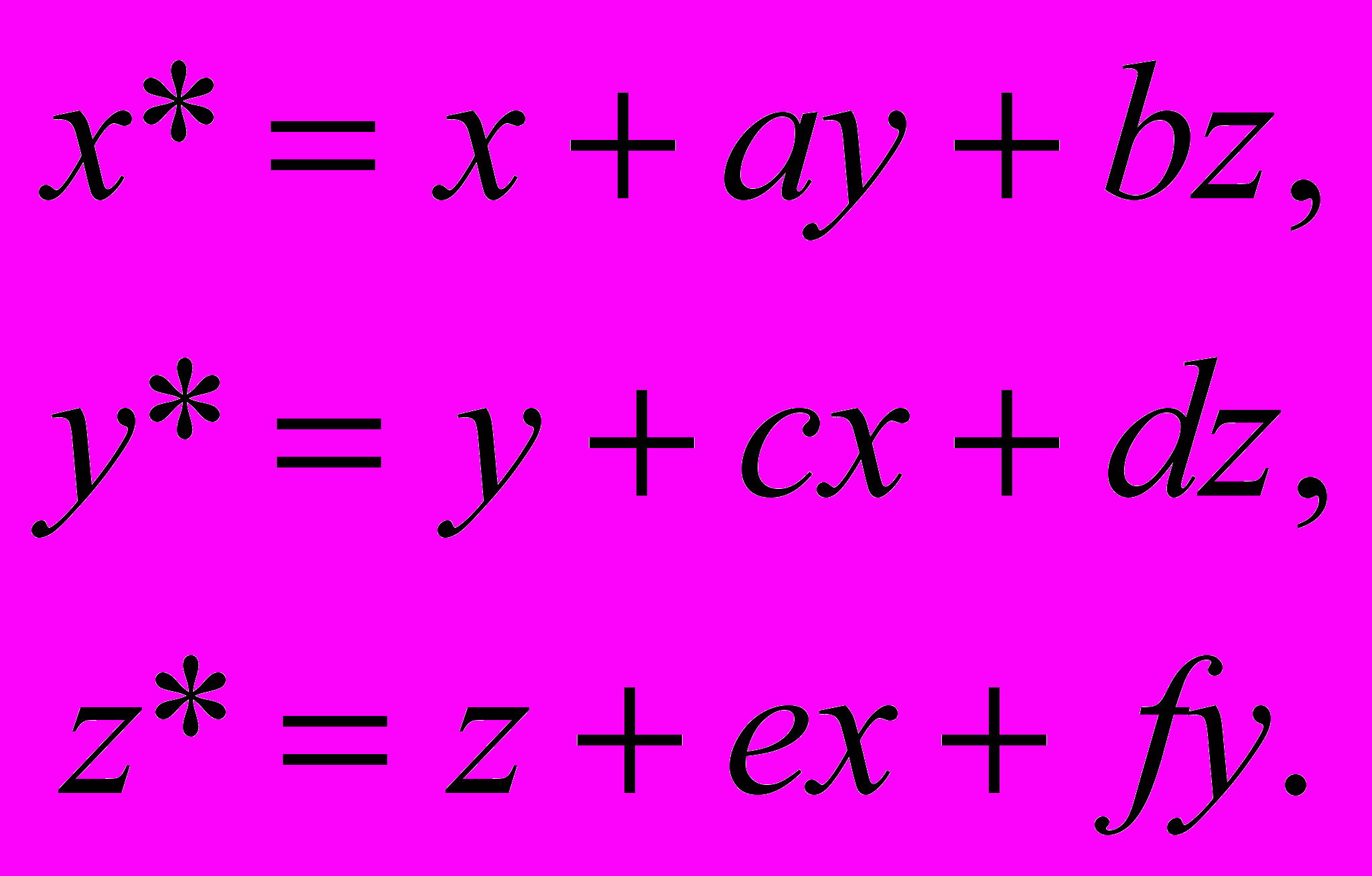или .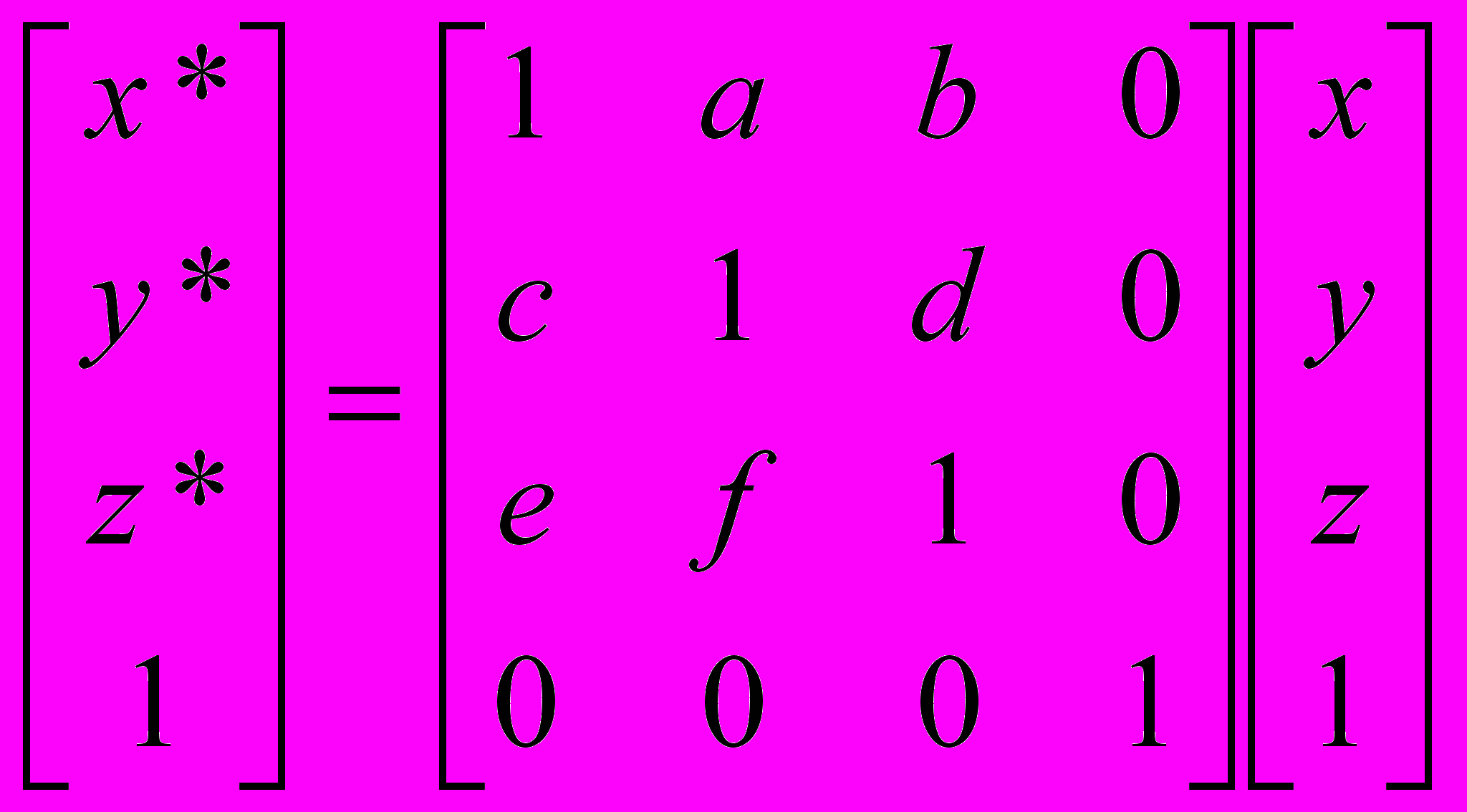

Масштабирование описывается следующими уравнениями:

x* = M_xx,

y* = M_yy, M_x>0, M_y>0, M_z>0.

z* = M_zz.

Или: .

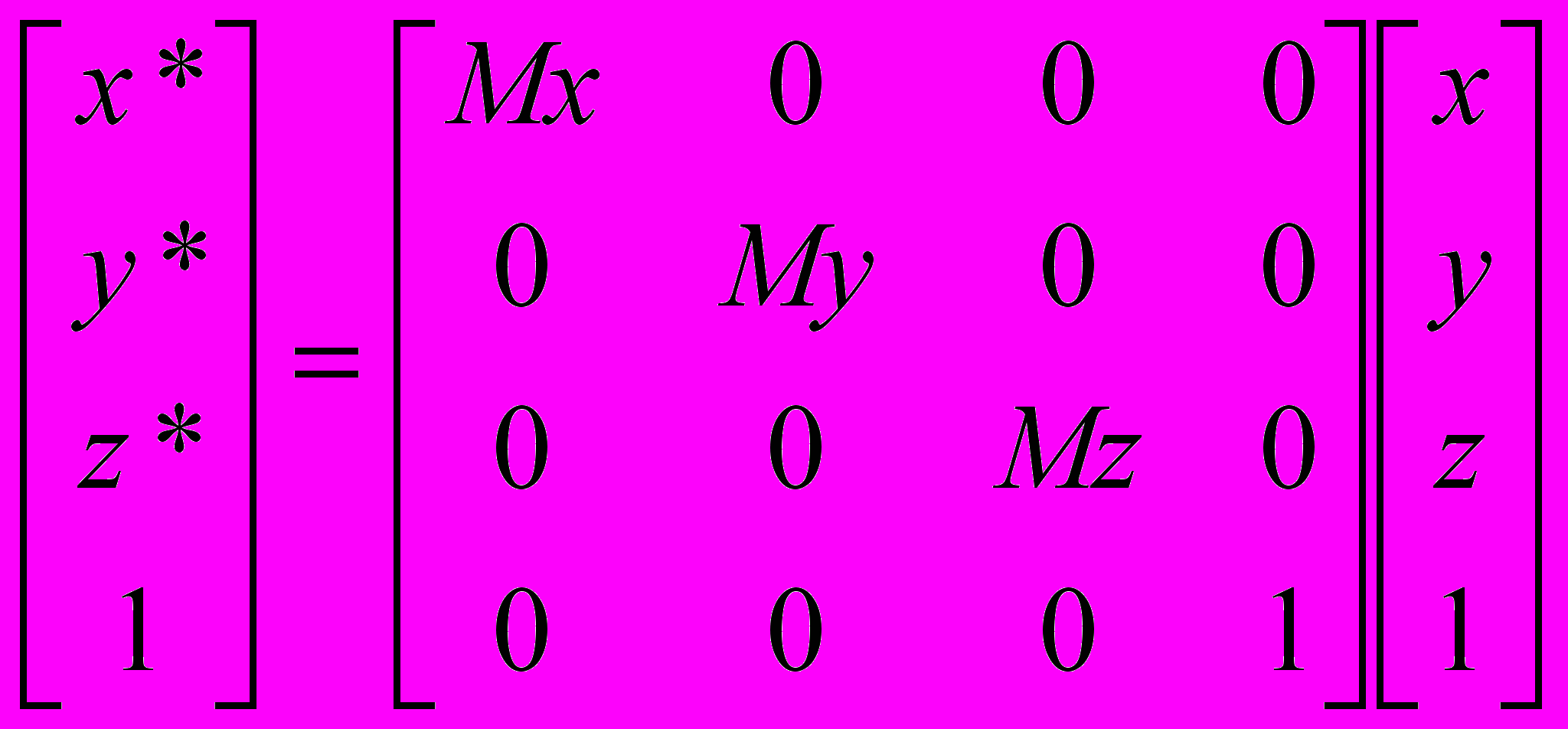В отличие от двумерного случая, в пространстве рассматриваются случаи отражения относительно координатных плоскостей.

• Отражение относительно плоскости z = 0:
  

или .

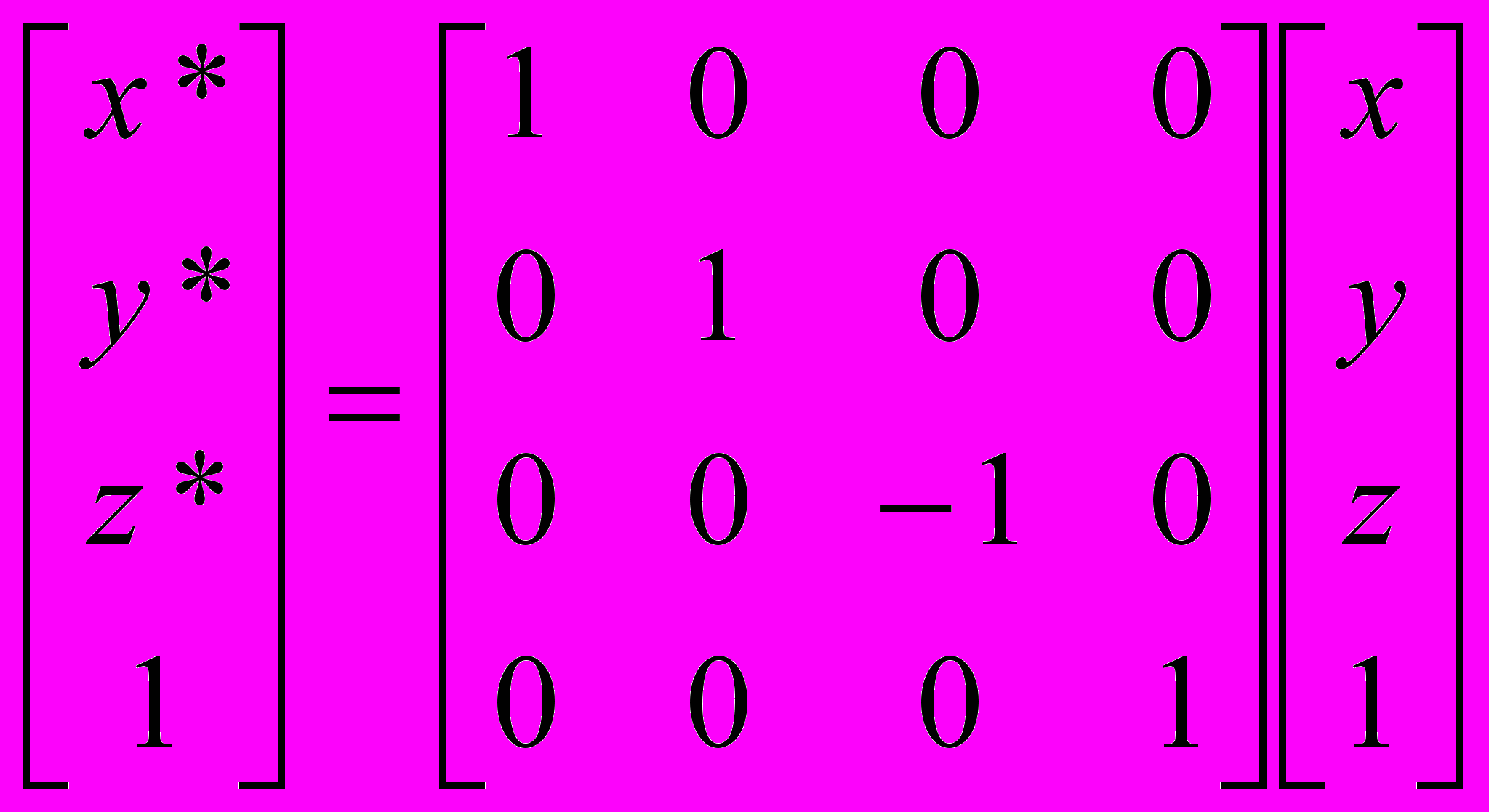• Отражение относительно плоскости у = 0:
  

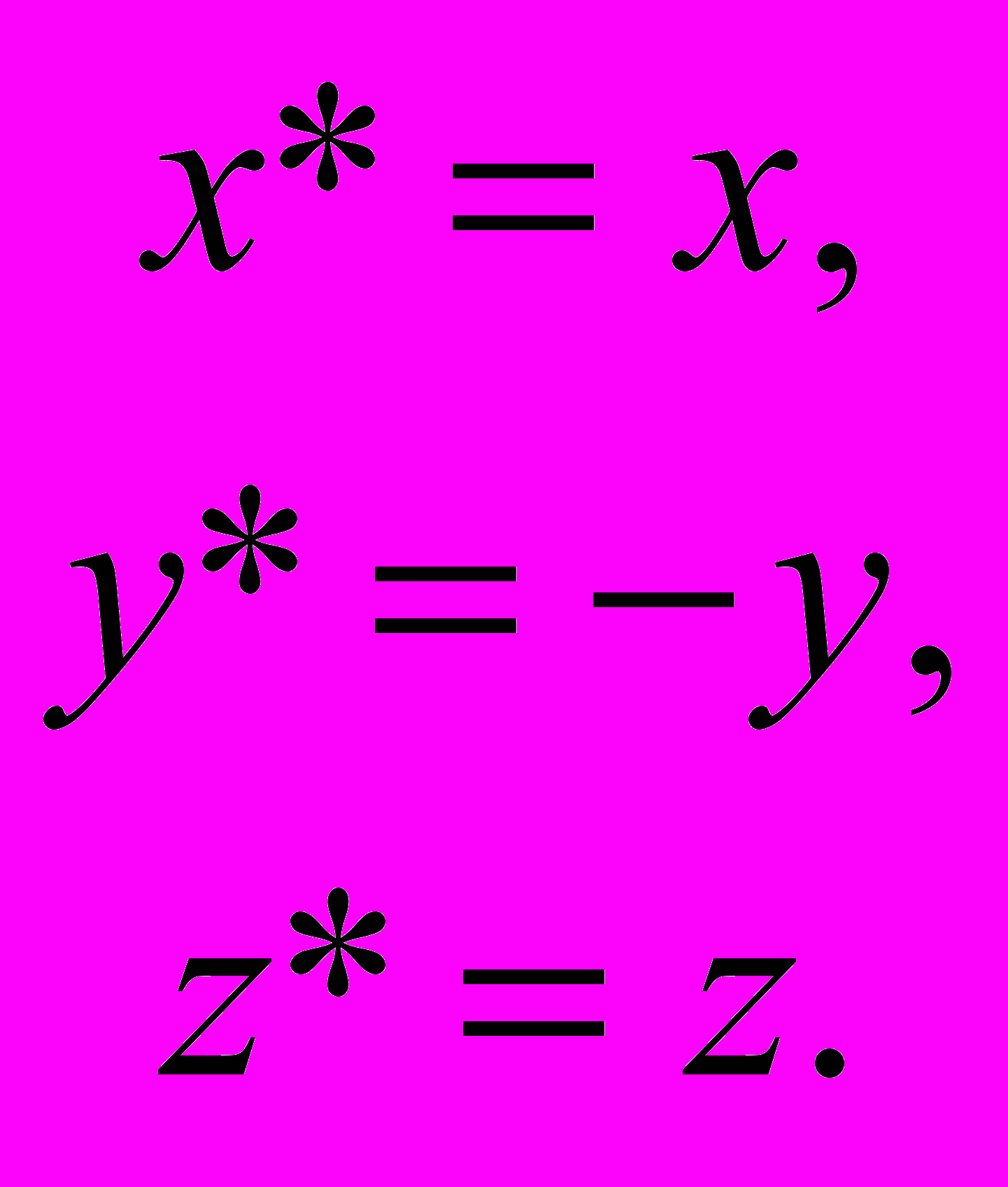или .

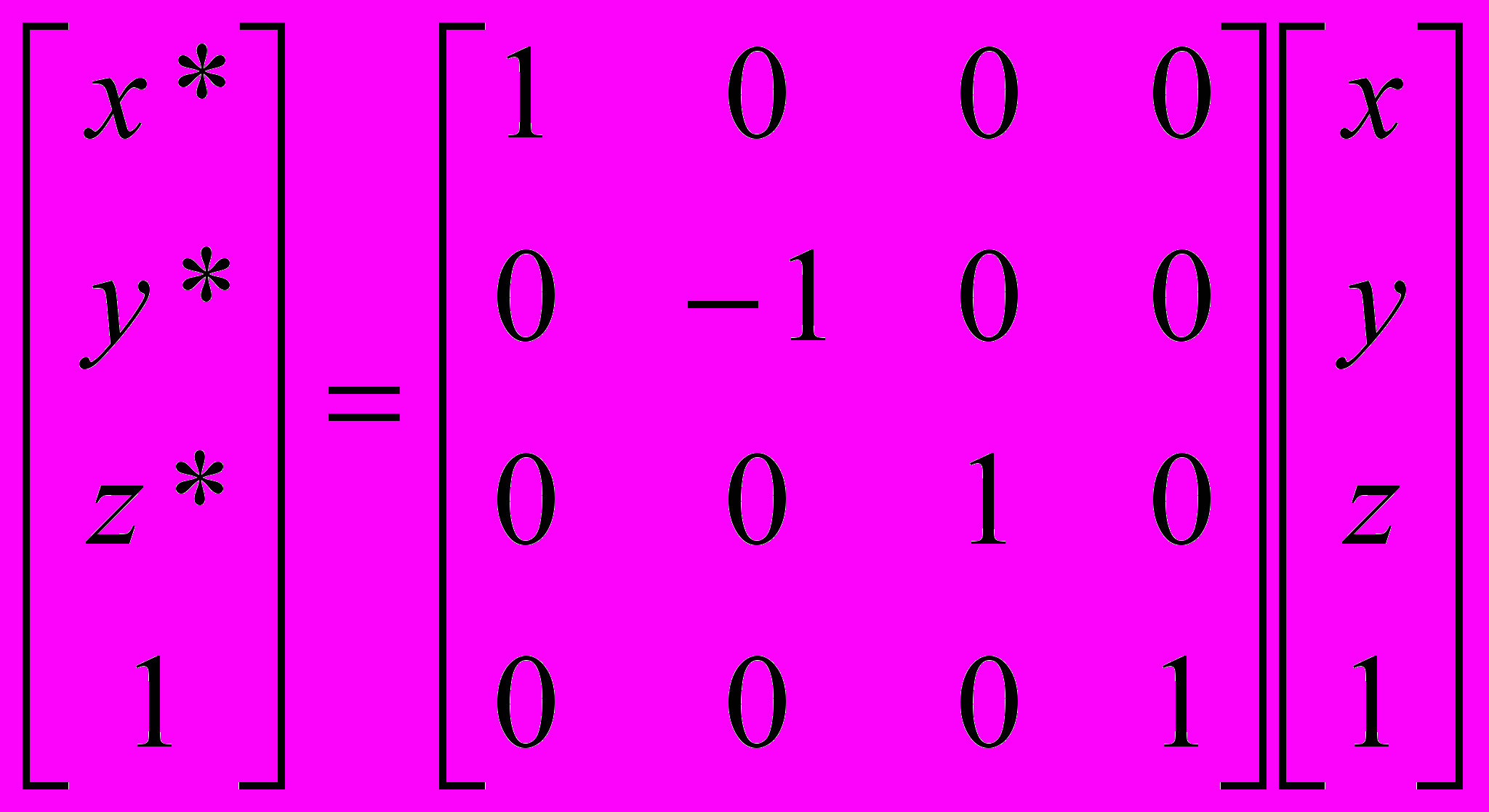• Отражение относительно плоскости х = 0:
  

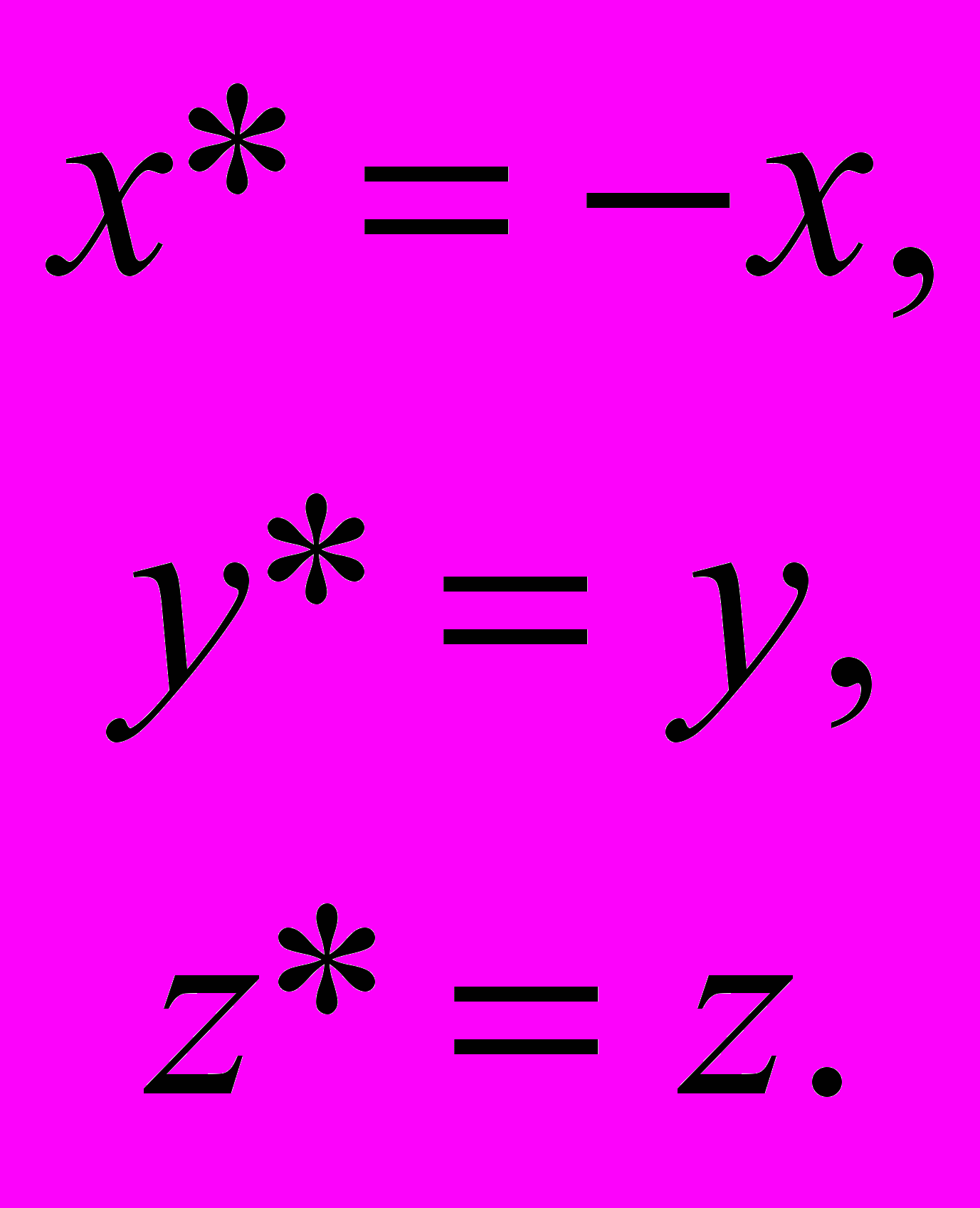или .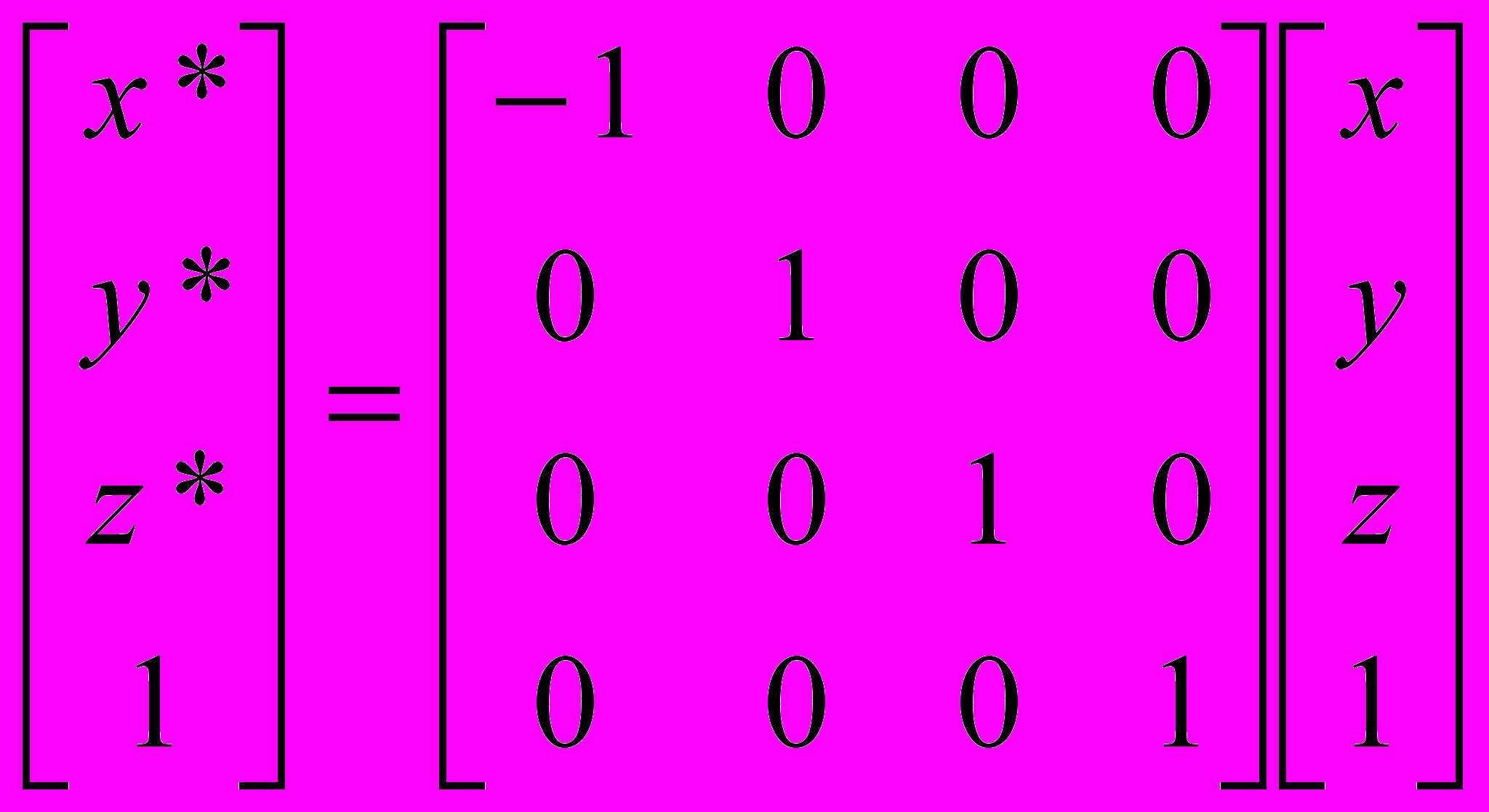


5.3. Композиция преобразований


Любое аффинное преобразование на плоскости или в пространстве можно представить как последовательное исполнение рассмотренных выше частных случаев. При таком подходе итоговую матрицу преобразования вычисляют как произведение матриц частных случаев, из которых складывается итоговое преобразование.

Следует помнить, что перемножение матриц является некоммутативной операцией, т.е. важен порядок ее выполнения.

Правильный порядок перемножения определяется положением матрицы частного преобразования относительно матрицы координатного вектора. Матрица, ближайшая к матрице координатного вектора, задает первое частное преобразование; а наиболее удаленная от него матрица задает последнее частное преобразование.

Пусть точка М с координатами (х, у, z) последовательно подвергается преобразованиям вида P₁, P₂, …, P_n. Причем, [P₁] – матрица первого преобразования (размером 4х4), а [P_n] – последнего. Итоговые координаты точки (х*, у*, z*) могут быть вычислены по уравнению:

= [P_n] …[P₂] [P₁],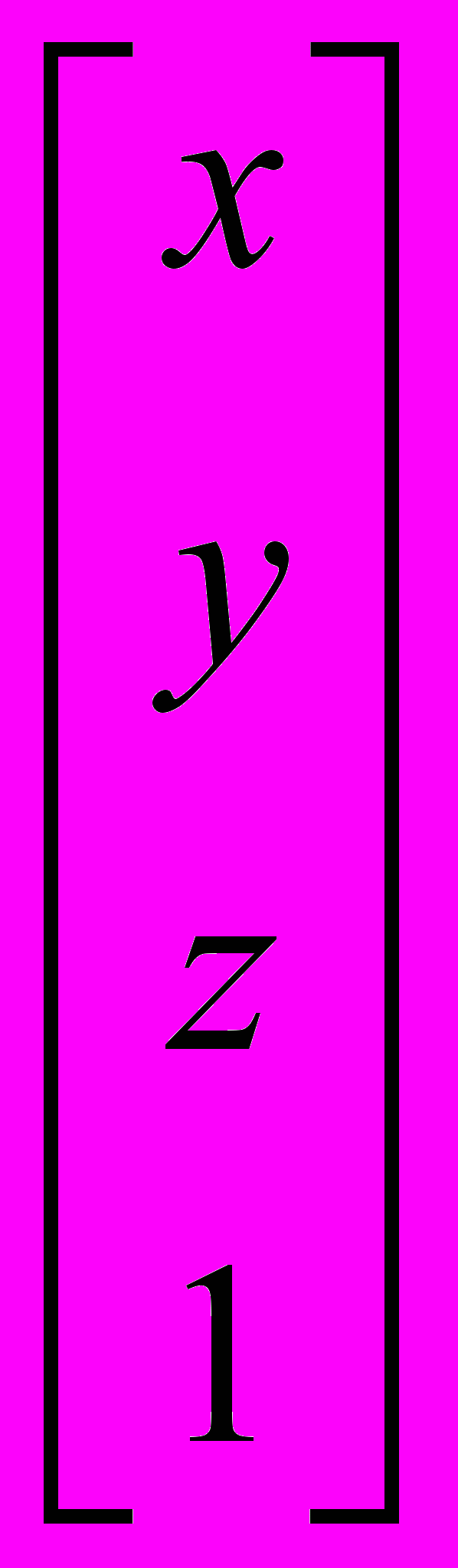

или, в другой форме записи:

(x* y* z* 1) = (x y z 1) [P₁]^Т [P₂]^Т … [P_n]^Т,

где [P_i]^Т – транспонированная матрица [P_i].

Во второй форме записи координаты точек записываются как векторы-строки, а не вектора-столбцы.