Физ величина, характеризующая интенсивность нормальных (перпендикулярных к поверхности) сил, с к-рыми одно тело действует на поверхность другого (напр
| Вид материала | Документы |
- Реферат По Физике, 58.66kb.
- Тема: определение реакций связей при действии на конструкцию произвольной плоской системы, 15.41kb.
- Головной мозг, 139.71kb.
- Работы режущего инструмента, основная нагрузка приходится на его рабочую поверхность,, 335.67kb.
- Головной мозг, с окружающими его оболочками находится в полости мозгового черепа, 437.52kb.
- Представьте себе некоторую поверхность и сидящего на ней муравья. Представили, 409.6kb.
- Лекция №8 Тема: «Продолжение», 81.36kb.
- Твует равновесию, установившемуся под действием силы тяжести, при условии, если, 669.51kb.
- Лабораторная работа метод естественного электрического поля (ЕП), 82.61kb.
- 1. Резьба Резьба поверхность, образованная при винтовом движении плоского контура, 223.58kb.
ДОЗИМЕТРИЧЕСКИЕ ПРИБОРЫ (дозиметры), устройства для измерения доз ионизирующих излучений и их мощностей. Существуют Д. п. для измерения одного вида излучения (напр., нейтронные Д. п., -дозиметры и др.), либо для измерения в полях смешанного излучения. Д. п. для измерения экспозиц. доз рентгеновского и -излучений (градуированные в рентгенах) наз. р е н т г е н о м е т р а м и, а приборы для определения эквивалентной дозы (градуированные в бэрах) — б э р м е т р а м и. Осн. части Д. п.: детектор и измерит. устройство. Обе части Д. п. либо постоянно связаны между собой, либо соединяются на время измерения отклика на облучение, накопленного в автономном детекторе.
В зависимости от типа детектора большинство Д. п. делится на ионизационные (с ионизационной камерой, пропорциональными счётчиками или Гейгера счётчиками), радиолюминесцентные (сцинтилляционные, термо- и фотолюминесцентные), полупроводниковые, фотографич., хим. и калориметрические. Д. п. с ионизац. камерами могут использоваться для всех
видов излучении, как рентгенометры и измерители поглощённой дозы, или кермы. При измерениях рентгеновских и -лучей и нейтронов, кроме состава газа, существен материал стенок камеры, а при измерениях экспозиц. дозы и кермы — толщина стенок (она должна быть близка к макс. пробегу любых образующихся ионизирующих ч-ц). Обычно в камерах обеспечивают условия насыщения (полного сбора образованных зарядов), однако камеры, работающие в условиях т. н. колонной рекомбинации, когда ионизац. ток зависит от линейной передачи энергии (ЛПЭ), могут быть использованы для оценок эквивалентной дозы. Д. п. с пропорциональным счётчиком (из ткане-эквивалентных материалов) позволяют, кроме измерений собранного заряда, измерять спектр ЛПЭ и микродозиметрич. величин z и у (см. Дозиметрия), Показания Д. п. с гейгеровскими счётчиками нельзя непосредственно связать со значениями поглощённых или экспозиц. доз. Однако выбором геометрии счётчика, подбором материала стенок и введением спец. фильтров можно сделать их приблизительно пропорциональными керме или экспозиц. дозе в ограниченном диапазоне энергии ч-ц. С помощью низкоэффективных счётчиков Гейгера оценивают спектры ЛПЭ смешанного нейтронного и -излучений. Сцинтилляц. Д. п., отградуированные по скорости счёта, пригодны для измерений плотности потока ч-ц (а не дозы), хотя, ввиду приблизительного постоянства энергетич. выхода радиолюминесценции, они могут измерять дозы. Сочетание органич. сцинтиллятора (с зависимостью светового выхода от ЛПЭ) и ионизац. камеры позволяет реализовать бэрметр для смешанного -нейтронного излучения. Термолюминесцентные и в меньшей степени фотолюминесцентные Д. п. распространены как индивидуальные дозиметры для лиц, находящихся в зоне облучения. В качестве индивидуальных Д. п. часто применяются дозиметры с фотоплёнкой, они пригодны для измерений эл.-магн. излучений с энергией квантов от 30 кэВ до 5 МэВ, причём для частичной компенсации зависимости их показаний от энергии фотонов применяются фильтры. Калориметрич. Д. п. из-за их низкой чувствительности применяют для абс. измерения поглощённых доз (и интегральных поглощённых доз) в интенсивных полях излучения.
• Матвеев В. В., Хазанов Б. И., Приборы для измерения ионизирующих излучений, 2 изд., М., 1972; ГОСТ 14105 — 76. Детекторы ионизирующих излучений, М., 1977. См. также лит. при ст. Детекторы.
Г. Б. Радзиевский.
ДОЗИМЕТРИЯ (от греч. dosis — доля, порция, приём и metreo — измеряю), измерение, исследование и теор. расчёты тех характеристик ионизирующих излучений (и их вз-ствия со средой), от к-рых зависят радиац. эффекты в облучаемых объектах живой и неживой
природы. Первоначально развитие Д. определялось гл. обр. необходимостью защиты от воздействия рентгеновского и -излучений естеств. радиоактивных в-в. Радиац. эффекты, в частности ионизация ч-ц среды, зависят от поглощённой энергии излучения. Т. к. воздух для - и рентг. излучений может служить моделью воды или мышечной ткани (у них близкие эффективные атомные номера) и ионизацию, пропорциональную поглощённой, легко измерить с помощью ионизационных камер, то измерение экспозиц. дозы было в течение длит. периода основой практич. Д., обслуживавшей гл. обр. медицину.
В дальнейшем, с развитием реакторостроения (см. Ядерный реактор), ускорительной техники и производства радиоактивных нуклидов, появились новые мощные источники излучения, в т. ч. и отличного от рентгеновских и -лучей. Это потоки нейтронов, ускоренных эл-нов, позитронов и тяжёлых заряж. ч-ц. Применения Д. распространились на службу радиац. безопасности, радиобиологию, радиац. химию, яд. физику и радиац. технологию. Знание поглощённой энергии стало необходимо не только для воды и биол. ткани; воздух уже не мог рассматриваться как модель облучаемой среды. В этой связи в Д. утвердилось понятие поглощённой дозы как универсальной величины, применимой ко всем видам ионизирующего излучения и ко всем средам. Однако при равных поглощённых дозах воздействие излучения зависит также от его вида и др. хар-к— «качества» излучения. Количеств. хар-кой «качества» вначале служила ср. плотность ионизации, впоследствии уточнённая, как линейная передача энергии (ЛПЭ). Влияние ЛПЭ на радиац. эффекты наиболее подробно было исследовано в радиобиологии, где изучалась зависимость относительной биологической эффективности от ЛПЭ. Применительно к хронич. облучению людей (для обеспечения радиац. безопасности и нормирования условий труда) регламеитиров. зависимость такого рода — зависимость коэфф. качества излучения от ЛПЭ.
Микродозиметрия. Передача энергии на микроуровне происходит малыми порциями и носит дискретный, стохастич. характер. Структуры, чувствительные к начальным стадиям радиац. эффектов, обычно имеют микроскопич. размеры и расположены также случайным образом. В этих условиях отклик на облучение должен определяться не столько поглощённой дозой, сколько распределением энерговыделений по чувствит. структурам объекта. Исследование микроскопич. распределений передаваемой энергии для разных видов радиации, разных доз и объектов составляет предмет м и к-
181
р о д о з и м е т р и и. Последняя, в отличие от обычной Д., оперирующей с макроскопич. величинами, имеет дело с дискретно изменяющимися стохастич. величинами: с переданной в микрообъёме энергией ξ, удельной энергией Z=ξ/m (m — масса микрообъёма) и линейной энергией у. Акты передачи энергии внутри микрообъёма при попадании в него заряж. ч-цы рассматриваются как случайные события. Переданная в микрообъёме энергия равна разности между суммарной кинетич. энергией всех ионирующих ч-ц, попавших в данный микрообъём, и энергией ч-ц, покинувших его, в сумме с увеличением энергии внутри объёма за счёт яд. реакций. Ср. энергия по микрообъёмам рассматривается как «интегральная доза» в объёме. Стохастич. аналог ЛПЭ — линейная энергия y=ξ/lср, где l — ср. длина хорды рассматриваемого микрообъёма (линейная энергия измеряется в КэВXмкм--1). Распределение f(Z), соответствующее определённой величине поглощённой дозы D, может быть записано в виде /(Z, D). Пусть, напр., гибель клеток при облучении наступает тогда, когда уд. энергия Z в чувствит. объёме клетки превосходит нек-рое критич. значение Z0. При этом доля S клеток, выживших после облучения:
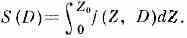
В более реалистич. случае, когда вероятность выживания клетки при поглощённой в её чувствительном объёме уд. энергии Z описывается, как (Z):
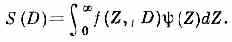
Ф-ция f(Z, D) может быть измерена или вычислена для разных микрообъёмов, а левые части соотношений найдены экспериментально.
• Исаев Б. М., Брегвадзе Ю. И., Нейтроны в радиобиологическом эксперименте, М., 1967; И в а н о в В. И., Л ы с ц о в В. Н., Основы микродозиметрии, М., 1979. Г. В. Радзиевский.
ДОЛЬНЫЕ ЕДИНИЦЫ, составляют определённую часть (долю) от установленной единицы физ. величины. В Международной системе единиц (СИ) приняты след. приставки для образования наименований Д. е.:
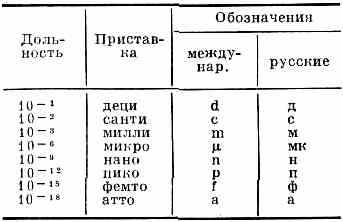
Пример: 1пФ (пикофарада)=10-12 Ф (фарад).
ДОМЕНЫ (от франц. domaine — владение; область, сфера), области химически однородной среды, отличающиеся электрич., магн. или упругими свойствами, либо упорядоченностью в расположении частиц. Соответственно различают антиферромагн. и ферромагн. Д. (см. также Цилиндрические магнитные домены), сегнетоэлоктрич. Д., Д. Ганна, упругие Д., Д. в жидких кристаллах и др.
Домены ферромагнитные, области самопроизвольной намагниченности, намагниченные до насыщения части объёма ферромагнетика, на к-рые он разбивается ниже критич. темп-ры (см. Кюри точка). Векторы намагниченности Д. в отсутствии внеш. магн. поля ориентированы т. о., что результирующая намагниченность ферромагн. образца в целом, как правило, равна нулю.

Рис. 1. Порошковые фигуры на поверхности кристалла кремнистого железа; видны границы доменов в объёме образца и замыкающих доменов у его поверхности. Стрелками показано направление намагниченности доменов.
Обычно Д. имеют размеры ~10-3— 10-2 см, они доступны непосредств. наблюдению (при помощи микроскопа): если покрыть поверхность ферромагнетика слоем суспензии, содержащей ферромагн. порошок, то ч-цы порошка осядут в основном на границах Д. и обрисуют их контуры (рис. 1). Широко применяют и др. методы исследования доменной структуры, в частности магнитооптический, обладающий большей разрешающей способностью (используют Керра эффект, Фарадея эффект и т. д.). Разбиение ферромагнетика на Д. объясняется след. причинами. Если бы весь ферромагнетик был намагничен до насыщения в одном направлении, то на его поверхности возникли бы магн. полюсы и в окружающем пр-ве было бы создано магн. поле. На это потребуется больше энергии, чем на разбиение ферромагнетика на Д., при к-ром магн. поле вне образца отсутствует (магн. поток замыкается внутри образца). При неизменном объёме и пост. темп-ре в ферромагнетике реализуются лишь такие доменные структуры, для к-рых свободная энергия минимальна.
Общим термодинамич. критерием равновесного распределения самопроизвольной намагниченности в ферромагнетике (его доменной структуры) явл. миним. значение полного термодинамич. потенциала ферромагн. образца. Этот потенциал сложно зависит от внеш. условий — темп-ры, упругих напряжений, внеш. эл.-магн. полей, структурного состояния образца, его формы и размеров. Из-за сложности определения термодинамич. потенциала в общем случае задача о доменной структуре решается последовательным расчётом отд. элементов доменной структуры (граничных слоев между Д., внутр. дефектов и т. д.). Направление векторов намагниченности Д. обычно совпадает с направлением осей лёгкого намагничивании. В этом случае для ферромагнетика выполняется условие минимума энергии магнитной анизотропии. При уменьшении размеров ферромагнетика до нек-рой критич. величины разбиение на Д. может стать энергетически невыгодным, образуется т. н. однодоменная структура: каждая ферромагн. ч-ца представляет собой один Д. На практике это реализуется в ферромагн. порошковых материалах в ряде гетерогенных сплавов (см. Магнитные материалы, Однодоменные Ферромагнитные частицы).
А. В. Ведяев, В. Е. Роде.
Домены сегнетоэлектрические, области однородной спонтанной поляризациии в сегнетоэлектриках. Размеры Д. обычно ~10-5—10-3 см. Д. разделены переходной областью (доменная граница или стенка) толщиной 10-5— 10-7 см.
На поверхности кристалла Д. можно наблюдать методами травления и порошков (скорости травления и осаждения мелких ч-ц в местах выхода на поверхность различно поляризованных Д. различны). Оптич. методы наблюдения основаны на том, что в разных Д. нек-рые оптич. постоянные кристалла могут иметь противоположные знаки (напр., угол, к-рый составляет гл. ось эллипсоида показателей преломления света с плоскостью до-

Рис. 2. Микрофотография доменов сегнетовой соли в поляризованном свете. Тёмные и светлые области соответствуют доменам с противоположным направлением спонтанной поляризации, перпендикулярной к плоскости рисунка.
182
менной границы; см. Кристаллоптика). В поляризов. свете одни Д. выглядят светлее, другие — темнее (рис. 2). Различие оптич. свойств Д. можно вызвать искусственно, прикладывая к кристаллу внеш. электрич. поле или упругие напряжения. Домены Ганна, области с разным уд. электрич. сопротивлением и разной напряжённостью электрич. поля, на к-рые расслаивается однородный полупроводник с N-образной вольт-амперной хар-кой в достаточно сильном внеш. электрич. поле (см. Ганна эффект).
• См. лит. при ст. Ферромагнетизм, Сегнетоэлектрики, Ганна эффект.
ДОННОЕ СОПРОТИВЛЕНИЕ, часть аэродинамического сопротивления, обусловленная понижением ср. давления рд на донной торцевой поверхности летящего тела по сравнению с давлением в атмосфере р на высоте полёта. Обтекающий летящее тело наружный поток интенсивно перемешивается с воздухом, находящимся в застойной зоне за дном тела, увлекая и отсасывая часть воздуха из застойной зоны. Т. к. новые порции воздуха в застойную зону не поступают, в ней возникает разрежение (pд<p), что приводит к появлению силы Д. с. Хд=(р-pд)Sд, (где Sд — площадь проекции донной поверхности на направление, нормальное оси тела), действующей против направления скорости тела. Возникновение Д. с. объясняется необратимым превращением части кинетич. энергии тела в теплоту при образовании за дном тела вихрей, а в сверхзвук. потоке — и хвостовых ударных волн. Отсасывающее действие наружного потока зависит от толщины пограничного слоя на боковой поверхности тела перед донным срезом, от формы головной и гл. обр. кормовой части тела, от скорости полёта и (в меньшей мере) от угла атаки.
Д. с. артиллерийских снарядов, корпусов ракет, фюзеляжей самолётов, спускаемых в атмосфере космич. летат. аппаратов и боевых частей ракет может составлять значит. часть полного аэродинамич. сопротивления. Струи, вытекающие из сопел двигат. установок ракет, усиливают отсасывание воздуха за дном ракеты и увеличивают Д. с. Теор. предельная величина Д. с. (максимальная) отвечает возникновению полного вакуума на дне тела (рд=0).
Безразмерный коэфф. Д. с. Сxд=xд/qS, где q=pov2/2, po — плотность атмосферы на высоте полёта, v — скорость тела, S — площадь его миделееого сечения, зависит от подобия критериев — Маха числа и Рейнольдса числа.
• Краснов Н. Ф., Аэродинамика тел вращения, 2 изд., М., 1964.
С. Л. Вишневецкий.
ДОНОР (от лат. dono — дарю), примесный атом в полупроводнике, ионизация к-рого (в результате теплового движения или внеш. воздействия) при-
водит к появлению эл-на в зоне проводимости. Напр., для Ge и Si типичные Д.— атомы элементов V группы периодич. системы P, As, Sb. Д. может быть точечный дефект кристаллич. решётки. Э. М. Эпштейн.
ДОНОРНО-АКЦЕПТОРНАЯ СВЯЗЬ (координационная связь), химическая связь между атомами, молекулами, радикалами, обычно не имеющими неспаренных эл-нов. Одна из ч-ц при образовании такой связи явл. донором пары эл-нов, другая — акцептором. Акцептор способен принимать эл-ны, к ним чаще всего относятся положительно заряж. ат. системы. Донор же имеет свободную неподелённую пару эл-нов, к-рая при образовании Д.-а. с. становится общей. Когда Д.-а. с. уже образована, она практически не отличается от ковалентной связи. Донорами часто явл. мол. системы, содержащие атомы N (напр., NH3), О, F, Cl и атомы переходных металлов.
В. Г. Дашевский.
ДОПЛЕРА ЭФФЕКТ, изменение частоты колебаний или длины волны , воспринимаемой наблюдателем, при движении источника колебаний и наблюдателя относительно друг друга. Возникновение Д. э. проще всего объяснить на след. примере. Пусть неподвижный источник испускает последовательность импульсов с расстоянием между соседними импульсами, равным 0, к-рые распространяются в однородной среде с пост. скоростью v, не испытывая никаких искажений (т. е. в линейной среде без дисперсии). Тогда неподвижный наблюдатель будет принимать последовательные импульсы через временной промежуток Т0=0/v. Если же источник движется в сторону наблюдателя со скоростью V<
=0/(1-V/v).(1)
При удалении источника от наблюдателя принимаемая частота уменьшается, что описывается той же ф-лой (1), но с изменённым в ней знаком скорости V.
Для движений с произвольными скоростями (в т. ч. со скоростями, равными или близкими к скорости света) в однородных средах необходимо учитывать угол между скоростью V и волновым вектором k излучаемой волны, а также принимать во внимание эффект релятив. замедления времени (см. Относительности теория), описываемый фактором =(1-2)-1/2, где =V/c. В этом случае
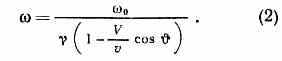
Здесь, как и в ф-ле (1), v — фазовая скорость волнового возмущения с частотой , распространяющегося в среде в направлении .
Таким образом, Д. э. имеет чисто кинематич. происхождение и возникает как для волновых, так и неволновых движений любой природы при наблюдении их в двух движущихся относительно друг друга системах отсчёта. С точки зрения теории относительности Д. э. для плоских однородных волн вида AехрiФ=Aехрi(t-kr) есть следствие инвариантности 4-скаляра (фазы) Ф при релятив. преобразованиях координат и времени (т. е. компонентов 4-вектора {r, ct}). Другими словами, волновой вектор k и частота ведут себя как компоненты единого 4-вектора {k, /с}, что позволяет рассматривать Д. э. (преобразование частоты) и изменение направления k (релятив. аберрации) как две стороны одного и того же явления.
Из соотношения (2) можно выяснить все осн. физ. проявления Д. э. При =0 или наблюдается продольный Д. э., когда источник движется прямо на наблюдателя или от него, и изменение частоты максимально. При =/2 имеет место поперечный Д. э., к-рый связан с чисто релятив. эффектом замедления времени и не имеет никакой волновой специфики (в частности, не зависит от фазовой скорости волн v).
В средах с дисперсией волн может возникнуть сложный Д.э. При этом фазовая скорость зависит от частоты v=v() и соотношение (2) становится ур-нием относительно , к-рое может допускать неск. действит. решений для заданных 0 и , т. е. под одним и тем же углом от монохроматич. источника в точку наблюдения могут приходить неск. волн с разл. частотами. Появление сложного Д. э. означает, что вследствие релятив. аберраций две плоские волны, испущенные движущимся источником под разными углами, воспринимаются наблюдателем под одним и тем же углом.
Дополнит. особенности Д. э. возникают при движении источника со скоростью V>v, когда на поверхности конуса углов, удовлетворяющих условию cos 0=v/V, знаменатель в ф-ле (2) обращается в нуль, а доплеровская частота неограниченно возрастает — т. н. а н о м а л ь н ы й Д.э. Внутри указанного конуса (соответствующего конусу Маха в аэродинамике или черенковскому конусу в электродинамике; см. Черенкова—Вавилова излучение), где имеет место аномальный Д. э., излучение доплеровских частот сопровождается не затуханием, как при норм. Д. э., а, наоборот, раскачкой колебаний излучателя (осциллятора) за счёт энергии его поступат. движения. С квант. точки зрения это соответствует излучению фотона с одно-
183
врем. переходом осциллятора на более высокий энергетич. уровень. При аномальном Д. э. частота растёт с увеличением угла , тогда как при норм. Д. э. (в т. ч. в случае V>v вне конуса cos0=v/V) под большими углами излучаются меньшие частоты.
Асимметрия Д. э. относительно движения источника и наблюдателя следует из того, что фазовая скорость г, входящая в ур-ние (2), различна в движущейся и неподвижной среде: распространение звука по ветру идёт скорее, чем против ветра, свет частично увлекается движущейся диэлектрич. средой и т. п. Другими словами, величина Д. э. определяется величиной и направлением скорости как источника, так и приёмника относительно среды, в к-рой распространяются волны. Исключение составляет случай эл.-магн. волн в вакууме, когда v=c во всех системах отсчёта, и Д. а. полностью определяется относит. скоростью источника и приёмника.
Разновидностью Д. э. явл. т. н. двойной Д. э.— смещение частоты волн при отражении их от движущихся тел, поскольку отражающий объект можно рассматривать сначала как приёмник, а затем как переизлучатель волн. Если 0 и vо — частота и скорость падающей волны, то частоты i вторичных (отражённых и прошедших) волн оказываются равными:
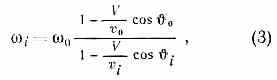
где 0 и i — углы между волновым вектором соответствующей волны и нормальной составляющей скорости движения отражающей поверхности V. Ф-ла (3) справедлива и в том случае, когда отражение происходит от движущейся неоднородности, создаваемой за счёт изменения состояния макроскопически неподвижной среды (напр., волны ионизации в газе). Из неё следует, в частности, что при отражении от движущейся навстречу границы частота повышается, причём эффект тем больше, чем ближе скорость границы и скорость распространения отражённой волны.
В случае нестационарных сред (когда параметры среды меняются во времени) изменение частоты может происходить даже для неподвижного излучателя и приёмника — т. н. параметрический Д. э.
Д. э. назван в честь австр. физика К. Доплера (Ch. Doppler), к-рый впервые теоретически обосновал этот эффект в акустике и оптике (1842). Первое эксперим. подтверждение Д. э. в акустике относится к 1845. Франц. физик А. Физо ввёл (1848) понятие доплеровского смещения спектральных линий, к-рое вскоре было обнаружено (1867) в спектрах нек-рых звёзд
и туманностей. Поперечный Д. э. был обнаружен амер. физиками Г. Айвсом и Д. Стилуэллом (1938). Обобщение Д. э. на случай нестационарных сред принадлежит В. А. Михельсону (1899), на возможность сложного Д. э. в средах с дисперсией и аномального Д. э. при V>v впервые указали В. Л. Гинзбург и И. М. Франк (1942).
Д. э. позволяет измерять скорость движения источников излучения или рассеивающих волны объектов и находит широкое практич. применение. Так, в астрофизике Д. э. используется для определения скорости движения звёзд, а также скорости вращения небесных тел. Измерения доплеровского смещения линий в спектрах излучения удалённых галактик привели к выводу о расширяющейся Вселенной (см. Красное смещение). В спектроскопии доплеровское уширение линий излучения атомов и ионов даёт способ измерения их темп-ры. В радио- и гидролокации Д. э. используется для измерения скорости движущихся целей, а также при синтезе апертуры (см. Антенна).
• Угаров В. А., Специальная теория относительности, 2 изд., М., 1977; Ф р а н к ф у р т У. И., Ф р е н к А. М., Оптика движущихся тел, М., 1972; Гинзбург В. Л., Теоретическая физика и астрофизика. (Дополнительные главы), М., 1975; Франк И. М., Эйнштейн и оптика, «УФН», 1979, т. 129, в. 4.
М. А. Миллер, Ю. И. Сорокин, Н. С. Степанов.
