Физ величина, характеризующая интенсивность нормальных (перпендикулярных к поверхности) сил, с к-рыми одно тело действует на поверхность другого (напр
| Вид материала | Документы |
- Реферат По Физике, 58.66kb.
- Тема: определение реакций связей при действии на конструкцию произвольной плоской системы, 15.41kb.
- Головной мозг, 139.71kb.
- Работы режущего инструмента, основная нагрузка приходится на его рабочую поверхность,, 335.67kb.
- Головной мозг, с окружающими его оболочками находится в полости мозгового черепа, 437.52kb.
- Представьте себе некоторую поверхность и сидящего на ней муравья. Представили, 409.6kb.
- Лекция №8 Тема: «Продолжение», 81.36kb.
- Твует равновесию, установившемуся под действием силы тяжести, при условии, если, 669.51kb.
- Лабораторная работа метод естественного электрического поля (ЕП), 82.61kb.
- 1. Резьба Резьба поверхность, образованная при винтовом движении плоского контура, 223.58kb.
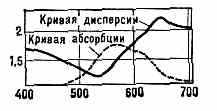
Рис. 1. Зависимость показателя преломления (сплошная линия) и поглощения (пунктирная линия) от длины волны в нм для тонкой призмы из красителя цианина.
Вблизи полос поглощения в-ва изменение n с изменением значительно сложнее. Так, для тонкой призмы из р-ра цианина в области поглощения (рис. 1) красные лучи преломляются сильнее фиолетовых, а наименее преломляемым будет зелёный, затем синий (т. н. аномальная Д. с.— уменьшение и с уменьшением ). У всякого в-ва имеются свои полосы поглощения, и общий ход показателя

Рис. 2. Аномальная дисперсия в парах натрия (фотография Д. С. Рождественского).
преломления обусловлен распределением этих полос по спектру. Для наблюдения Д. с. в узких спектр. линиях разработаны спец. методы, основанные на интерференции. На рис. 2 показан вид интерференц. полос в области аномальной дисперсии паров натрия.
167
Преломление света в в-ве возникает вследствие изменения фазовой скорости света; показатель преломления n=c/cф, где cф—фазовая скорость его в данной среде. По эл.-магн. теории света cф=с/, где — диэлектрич. проницаемость, — магн. проницаемость. В оптич. области спектра для всех в-в очень близка к единице. Поэтому n= и Д. с. объясняется зависимостью от частоты. Эта зависимость определяется вз-ствием эл.-магн. поля световой волны с атомами и молекулами, приводящими к поглощению; показатель преломления при этом становится комплексной величиной n=n+i, где — характеризует поглощение. В видимой и УФ областях спектра осн. значение имеют колебания эл-нов, а в ИК — колебания ионов.
Согласно классич. представлениям, под действием электрич. поля световой волны эл-ны атомов или молекул совершают вынужденные колебания с частотой, равной частоте приходящей волны. При приближении частоты световой волны к частоте собств. колебаний эл-нов возникает явление резонанса, обусловливающее поглощение света. Наличие собств. частоты колебаний приводит к зависимости n от , хорошо передающей весь ход Д. с. как вблизи полос поглощения, так и вдали от них. Для того чтобы получить количеств. совпадение с опытом, в классич. теории приходилось вводить для каждой линии поглощения нек-рые эмпирич. константы («силы осцилляторов»). Согласно электронной теории, справедливы приближённые ф-лы:
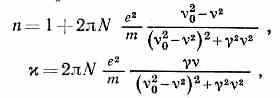
где N — число ч-ц в ед. объёма, m — масса эл-на, — коэфф. затухания. На рис. 3 приведены графики зависимости n и от /0.
Квант. теория подтвердила качеств. результаты классич. теории и, кроме того, дала возможность связать эти константы с др. хар-ками электронных оболочек атомов (с их волновыми функциями в разных энергетич. состояниях).
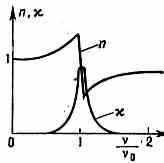
Рис. 3. Графики зависимости n и от /0.
Квант. теория объяснила также особенности Д. с., наблюдающиеся в тех случаях, когда имеется значит.
число атомов в возбуждённых состояниях (т. н. отрицательная Д. с.).
Д. с. в прозрачных материалах, применяемых в оптич. приборах, имеет большое значение при расчёте спектральных приборов, при расчёте ахроматич. линз или призм, для уничтожения Д. с., вызывающей хроматическую аберрацию, и др.
Вращательная дисперсия — изменение угла вращения плоскости поляризации в зависимости от длины волны К. В прозрачных в-вах угол обычно возрастает с уменьшением К, причём для нек-рых сред приближённо выполняется закон Био: =К/2 (К — постоянная для данного в-ва). Вращательная Д. с. такого типа наз. нормальной. В области поглощения света ход вращательной Д. с. значительно сложнее, причём угол может достигать огромных величин (аномальная вращат. дисперсия). См. Вращение плоскости поляризации.
•Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); Горелик Г. С., Колебания и волны, 2 изд., М., 1959.
М. Д. Галанин.
ДИССИПАТИВНЫЕ СИСТЕМЫ, механич. системы, полная механич. энергия к-рых (т. е. сумма кинетич. и потенц. энергии) при движении убывает, переходя в др. формы энергии, напр. в теплоту. Этот процесс наз. процессом диссипации (рассеяния) механич. энергии; он происходит вследствие наличия разл. сил сопротивления (трения), к-рые наз. также диссипативными силами. Примеры Д. с.: тв. тело, движущееся по поверхности другого при наличии трения; жидкость или газ, между ч-цами к-рых
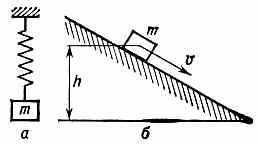
при движении действуют силы вязкости (вязкое трение).
Движение Д. с. может быть как замедленным, или затухающим, так и ускоренным. Напр., колебания груза т, подвешенного к пружине (рис., а), будут затухать вследствие сопротивления среды и внутреннего (вязкого) сопротивления, возникающего в материале самой пружины при её деформациях. Движение же груза т вдоль шероховатой наклонной плоскости, происходящее, когда скатывающая сила больше силы трения (рис., б), будет ускоренным. При этом его скорость v, а следовательно, и кинетич. энергия T=mv2/2 (где т — масса груза) всё время возрастают, но это возрастание происходит медленнее, чем убывание потенц. энергии П=mgh (g — ускорение свободного падения, h — высота положения груза). В результате полная механич.
энергия груза T+П всё время убывает.
Понятие «Д. с.» применяют в физике также по отношению и к немеханич. системам во всех случаях, когда энергия упорядоченного процесса переходит в энергию неупорядоченного процесса, в конечном счёте — в энергию теплового (хаотического) движения молекул. Так, система контуров, в к-рой происходят колебания электрич. тока, затухающие из-за наличия омич. сопротивления, будет также Д. с.; в этом случае электрич. энергия переходит в джоулеву теплоту.
Практически в земных условиях из-за неизбежного наличия сил сопротивления все системы, в к-рых не происходит притока энергии извне, являются Д. с. Рассматривать их как консервативные, т. е. такие, в к-рых имеет место сохранение механич. энергии, можно лишь приближённо, отвлекаясь от учёта сил сопротивления. Однако и неконсервативная система может не быть Д. с., если в ней диссипация энергии компенсируется притоком энергии извне. Напр., отдельно взятый маятник часов из-за наличия сопротивлений трения будет Д. с., и его колебания (как и груза на рис., а) будут затухать. Но при периодич. притоке энергии извне за счёт заводной пружины или опускающихся гирь диссипация энергии компенсируется, и маятник будет совершать автоколебания. С. М. Таре.
ДИССИПАЦИЯ ЭНЕРГИИ (от лат. dissipatio — рассеяние), у физ. систем — переход части энергии упорядоченного процесса (напр., электрич. тока) в энергию неупорядоченного процесса, в конечном счёте — в тепловую (напр., в джоулеву теплоту); у механич. систем — переход части их механич. энергии в др. формы (напр., в теплоту) за счёт наличия сил сопротивления. См. Диссипативные системы.
ДИССОЦИАЦИЯ (от лат. dissociatio — разъединение), распад молекулы, радикала, иона или комплексного соединения на две или неск. частей. В зависимости от фактора, индуцирующего Д.,— повышения темп-ры или действия света — Д. наз. термической или фотохимической. Количественной характеристикой Д. является степень Д.— отношение кол-ва диссоциировавших молекул к общему кол-ву молекул данного в-ва. Энергия Д. (энергия хим. связи) может быть определена с помощью электронного удара, спектроскопич. и кинетич. методами. Распад молекулы в р-ре наз. электролитич. Д.
В. Г. Дашееский.
ДИСТИЛЛЯЦИЯ (от лат. distillatio — отекание каплями) (перегонка), разделение жидких смесей, основанное на различии темп-р кипения компонентов смеси или на различии их скоростей испарения. Для Д. создаются условия, при к-рых один из компонентов переходит в пар, к-рый затем конденсируется.
168
ДИСТОРСИЯ (от лат. distorsio — искривление), одна из аберраций оптических систем, для к-рой характерно нарушение геом. подобия между объектом и его изображением. Д. обусловлена неодинаковостью линейного увеличения оптического на разных участках изображения. Пример искажений, даваемых системой, обладающей Д., приведённые на рисунке изображения квадрата. Слева показано изображение, искажённое за счёт
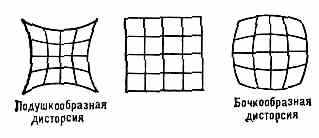
т. н. подушкообразной, или положительной, Д., справа — искажённое за счёт т. н. бочкообразной, или отрицательной, Д. Количественно Д. оптич. системы характеризуют относительной Д. v=bet/0-1, где 0 — линейное увеличение идеальной системы без Д., а — увеличение, имеющее место в действительности. Относит. Д. выражается в %.
Д. особенно стараются избежать в фотогр. объективах, применяемых в геодезии, фотограмметрии и аэрофотосъёмке. Для хороших фотообъективов v близка к 0,5%. В отд. случаях Д. можно устранить полностью.
ДИФРАКЦИОННАЯ РЕШЁТКА, оптич. прибор, представляющий собой периодич. структуру из большого числа регулярно расположенных элементов, на к-рых происходит дифракция света (напр., параллельных и равноотстоящих штрихов, нанесённых на плоскую или вогнутую оптич. поверхность). Штрихи с определённым и постоянным для данной Д. р. профилем повторяются через одинаковый промежуток d, наз. её периодом (рис. 1). Осн. св-во Д. р.— способность раскладывать падающий на неё пучок света по длинам волн, поэтому она используется в кач-ве диспергирующего элемента в спектральных приборах. Если штрихи нанесены на плоскую поверхность, то Д. р. наз. п л о с к о й, если на вогнутую (обычно сферическую) поверхность — в о г н у т о й. Различают отражательные и прозрачные Д. р. У отражательных Д. р. штрихи наносятся на зеркальную (обычно металлическую) поверхность, и наблюдение ведётся в отражённом свете. У прозрачных Д. р. штрихи наносятся на поверхность прозрачной (обычно стеклянной) пластинки (или вырезаются в виде узких щелей в непрозрачном экране), и наблюдение ведётся в проходящем свете. В совр. спектр. приборах применяются гл. обр. отражат. Д. р.
Наиболее наглядно описание действия Д. р. для прозрачной Д. р. При падении монохроматического параллельного пучка света с длиной волны под углом на Д. р. (рис. 1), состоящую из щелей ширины 6, разделённых непрозрачными промежутками, происходит интерференция волн, исходящих из разных щелей. В результате после фокусировки на экране образуются максимумы, положение к-рых определяется ур-нием: d(sin+sin)=m, где — угол между нормалью к решётке и направлением распространения дифракц. пучка
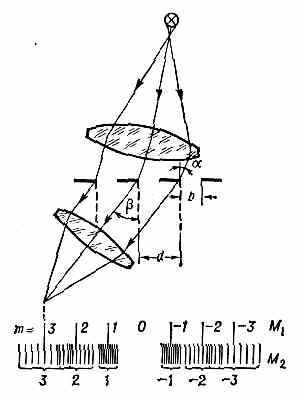
Рис. 1. Схема образования спектров с помощью прозрачной дифракц. решётки, состоящей из щелей.
(угол дифракции); целое число m=0, ±1, :±2, ±3, . . . равно кол-ву длин волн, на к-рое волна от нек-рого элемента данной щели Д. р. отстаёт от волны, исходящей от такого же элемента соседней щели (или опережает её). Монохроматич. пучки, относящиеся к разл. значениям m, наз. порядками спектра, а создаваемые ими изображения входной щели — спектральными линиями М1. Все порядки, соответствующие положит. и отрицат. значениям то, симметричны относительно нулевого. По мере возрастания числа щелей Д. р. спектр. линии становятся более узкими и резкими.
Если на Д. р. падает излучение сложного спектр. состава, то для каждой длины волны получится свой набор спектр. линий M2, и, следовательно, излучение будет разложено в спектры по числу возможных значений т. Относит. интенсивность линий определяется ф-цией распределения энергии от отдельной щели.
Осн. хар-ками Д. р. явл. угловая дисперсия и разрешающая способность. Угловая дисперсия /, характеризующая угл. ширину спектра, для данной не зависит от параметров решётки, а зависит только от углов и и возрастает с увеличением :
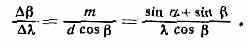
Т. о., угл. ширина спектров изменяется приблизительно пропорц. номеру порядка спектра. Разрешающая способность R измеряется отношением к наименьшему интервалу длин волн , к-рый ещё может разделить решётка:
R=/=mN =(W/)(sin+sin),
где N — число штрихов Д. р., а W — ширина всей Д. р. При заданных углах R может быть повышена только за счёт W. Д. р. даёт неск. налагающихся друг на друга спектров разл. порядков. Макс. интервал длин волн, к-рый можно наблюдать без переналожения, наз. свободной спектральной областью F=/m, где — мин. длина волны спектр. интервала.
Д. р., применяемые для работы в разл. областях спектра, отличаются размерами, формой, материалом поверхности, профилем штрихов и их частотой (от 6000 штрих/мм в рентгеновской до 0,25 штрих/мм в ИК).
Большинство совр. Д. р. имеют штрихи ступенчатого профиля, позволяющие сконцентрировать осн. часть падающей энергии в направлении к.-л. одного ненулевого порядка (см. Эшелетт).
Для УФ и видимой областей наиб. типичны Д. р., имеющие от 300 до 1200 штрих/мм. Штрихи этих Д. р. выполняют в тонком слое алюминия, предварительно нанесённом на стеклянную поверхность испарением в вакууме. Д. р. в вакуумной УФ области изготавливаются на стеклянных поверхностях. В этой области незаменимы вогнутые отражательные Д. р.,
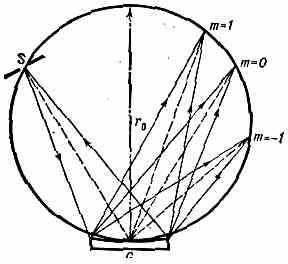
Рис. 2. Схема образования спектров с помощью вогнутой дифракц. решётки.
выполняющие одновременно роль Д. р. и собирающей линзы. Если поместить вогнутую Д. p. G (радиуса r0) и источник света S (рис. 2) на окружности радиуса r0/2, то спектр фокусируется на той же окружности (окружность Р о у л а н д а). Для уменьшения астигматизма вогнутые Д. р. иногда выполняют с перем. шагом и непрямолинейными штрихами или наносят их на асферич. поверхности.
169
В 70-х гг. разработана новая технология изготовления Д. р., основанная на создании периодич. распределения интенсивности на спец. фоточувствит. материалах (фоторезистах) в результате интерференции лазерного излучения. Такие Д. р., наз. топографическими, имеют высокое кач-во и применяются в видимой и УФ областях спектра; число штрихов в этих решётках доходит до 6000 на 1 мм, а размеры до 600X400 мм2. Д. Р. применяются не только в спектр. приборах, но также в кач-ве оптич. датчиков линейных и угл. перемещений (измерительные Д. р.), поляризаторов и фильтров ИК излучения, делителей пучков в интерферометрах и для др. целей.
•Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); Тарасов К. И., Спектральные приборы, Л., 1968. См. также лит. при ст. Дифракция света. Э. А. Яковлев.
ДИФРАКЦИЯ ВОЛН (от лат. diffractus — разломанный, преломлённый), в первоначальном узком смысле — огибание волнами препятствий, в современном более широком — любое отклонение при распространении волн от законов геометрической оптики. При таком общем толковании Д. в. переплетается с явлениями распространения и рассеяния волн в неоднородных средах. Благодаря дифракции волны могут попадать в область геом. тени: огибать препятствия, стелиться вдоль поверхностей, проникать через небольшие отверстия в экранах и т. п. Напр., звук может быть услышан за углом дома или радиоволна может проникнуть за горизонт даже без отражения от ионосферы.
Дифракц. явления практически не зависят от природы дифрагирующих полей и в большинстве случаев объясняются в рамках линейного волнового уравнения или вытекающих из него интегр. соотношений. Важнейшим из них явл. Гюйгенса — Френеля принцип, согласно к-рому волн. поле в произвольной точке пр-ва складывается из вторичных волн, испускаемых нек-рыми фиктивными источниками на поверхности (строго говоря, замкнутой), отделяющей эту точку от первичной падающей волны. Поэтому, поставив на пути волн экран с малым отверстием (размеры к-рого D, напр., порядка или меньше длины волны ), получим в отверстии экрана источник, излучающий вторичную сферич. волну, распространяющуюся также и в область тени. Два разнесённых отверстия (или щели) излучают две сферич. волны, к-рые, интерферируя, образуют дифракц. картину с чередующимися максимумами и минимумами излучения. Периодич. набор щелей (или, соответственно, рисок, нанесённых на прозрачную подложку) даёт дифракционную решётку. Когда такие системы применяются в кач-ве излучателей, они наз. дифракц. антеннами.
Структура дифракц. поля существенно зависит от расстояния L между излучателем и точкой наблюдения. Различают Френеля дифракцию при L ~D2/ и Фраунгофера дифракцию при L>>D2/,. Здесь D — характерный размер всего излучателя (диаметр отверстия, радиус кривизны края препятствия, длина решётки и т. п.). В первом случае вторичные волны от наиболее разнесённых участков излучателя могут приходить в нек-рые точки наблюдения с противоположными фазами, что приводит к образованию т. н. зон Френеля; во втором случае они приходят в одинаковых фазах, и результирующее поле представляет собой сферически сходящуюся волну с локально плоской структурой.
Эффективность излучения вторичных волн заметно падает с уменьшением отношения D/ [в дипольном приближении ~(D/)4], поэтому наиб. отчётливо дифракция начинает проявляться лишь при D ~ . Напр., Д. в. на воде ( ~ 1 м) или звука в воздухе (~1 см) может наблюдаться практически всегда, дифракция света (=10-4—10-5 см) требует выполнения особых условий (игольчатое отверстие, острый край бритвы и т. п.), а для дифракции рентгеновских лучей (10-7 —10-9 см) приходится использовать крист. решётки.
Явления дифракции имеют место и в микромире (см. Дифракция микрочастиц), поскольку объектам квант. механики свойственно волн. поведение.
М. А. Миллер.
ДИФРАКЦИЯ МИКРОЧАСТИЦ, рассеяние эл-нов, нейтронов, атомов и др. микрочастиц кристаллами или молекулами жидкостей и газов, при к-ром из нач. пучка ч-ц возникают дополнительные отклонённые пучки этих ч-ц. Направление и интенсивность таких отклонённых пучков зависят от строения рассеивающего объекта.
Д. м. может быть понята лишь на основе квантовомеханич. представлений о микрочастице как о волне (см. Корпускулярно-волновой дуализм). Согласно квант. механике, свободное движение ч-цы с массой m и со скоростью v (энергией ξ) можно представить как плоскую монохроматич. волну (волну де Бройля) с длиной волны =h/mv или, если v не слишком высока,
=h/2mξ, (1)
распространяющуюся в направлении движения ч-цы.
При вз-ствии ч-цы с кристаллом, молекулой и т. п. её энергия меняется: к ней добавляется потенц. энергия этого вз-ствия, что приводит к изменению движения ч-цы и соотв. меняется хар-р распространения связанной с ней волны, причём это про-
исходит согласно принципам, общим для всех волн. явлений. Поэтому осн. геом. закономерности Д. м. ничем не отличаются от закономерностей дифракции рентгеновских лучей и дифракции волн др. диапазонов. Общим условием дифракции волн любой природы явл. соизмеримость длины падающей волны с расстоянием d между рассеивающими центрами: d. Наиболее чёткая картина получается при Д. м. на кристаллах. Кристаллы обладают высокой степенью упорядоченности, атомы в них располагаются в трёхмерно-периодической крист. решётке, т. е. образуют пространств. дифракц. решётку для соответствующих . Дифракция волн на такой решётке происходит в результате рассеяния на системах параллельных кристаллографич. плоскостей, на к-рых в строгом порядке расположены рассеивающие центры. Дифракц. картина от кристалла представляет собой расположенные определ. образом максимумы интенсивности рассеянных кристаллом ч-ц (рис. 1). Условием наблюдения дифракц. максимума при отражении от
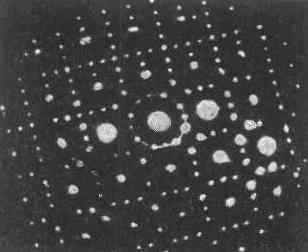
Рис. 1. Дифракц. картина, образованная пучком эл-нов (V=60 кВ, =0,05Å) при прохождении их через монокристальную плёнку моногидрата хлористого бария. Центр. пятно — след нач. пучка, остальные пятна — дифракц. максимумы от разл. систем кристаллографич. плоскостей.
кристалла явл. Брзгга — Вульфа условие:
2dsin=n; (2)
здесь — угол, под к-рым падает пучок ч-ц на данную кристаллографич. плоскость (угол скольжения), d — расстояние между соответствующими кристаллографич. плоскостями, n — целое число (порядок отражения).
Тепловое движение атомов в кристалле не меняет направлений днфрагиров. пучков, но интенсивность их с увеличением уменьшается. При Д. м. на жидкостях, аморфных телах или молекулах газа — объектах, не обладающих упорядоченным строением, обычно наблюдается несколько размытых дифракц. максимумов.
