Физ величина, характе­ризующая интенсивность нормальных (перпендикулярных к поверхности) сил, с к-рыми одно тело действует на поверхность другого (напр

Вид материала

Документы

Содержание Дальномер оптический Дарси — вейсбаха формула Двойное лучепреломление Двойной электрический слой Двойной электронно-ядер­ный резонанс H: M и m — проекции электронного и яд, спинов на направление H Двойственности принцип Двумерные проводники Двуосные кристаллы Двух тел задача Дебаевский радиус экрани­рования Дебая закон теплоемкости Дебая температура Температура дебая для некоторых кристаллов Дебая формулы Дебая — шеррера метод Де-бройлевская длина волны Девиатор напряжений Действительное изображе­ние Ядро атомное. ... Полное содержание

Подобный материал:

• Реферат По Физике, 58.66kb.
• Тема: определение реакций связей при действии на конструкцию произвольной плоской системы, 15.41kb.
• Головной мозг, 139.71kb.
• Работы режущего инструмента, основная нагрузка приходится на его рабочую поверхность,, 335.67kb.
• Головной мозг, с окружающими его оболочками находится в полости мозгового черепа, 437.52kb.
• Представьте себе некоторую поверхность и сидящего на ней муравья. Представили, 409.6kb.
• Лекция №8 Тема: «Продолжение», 81.36kb.
• Твует равновесию, установившемуся под действием силы тяжести, при условии, если, 669.51kb.
• Лабораторная работа метод естественного электрического поля (ЕП), 82.61kb.
• 1. Резьба Резьба поверхность, образованная при винтовом движении плоского контура, 223.58kb.

ДАЛЬНОДЕЙСТВИЕ, см. Взаимодей­ствие в физике.

ДАЛЬНОМЕР ОПТИЧЕСКИЙ, см. Сеетодальномер.

ДАЛЬТОНА ЗАКОНЫ, 1) давление смеси химически невзаимодействую­щих идеальных газов равно сумме пар­циальных давлений. Приближённо применим к реальным газам при зна­чениях темп-р и давлений, далёких от критических. 2) При пост. темп-ре рас­творимость в данной жидкости каж­дого из компонентов газовой смеси, находящейся над жидкостью, пропорц. его парц. давлению. Каждый газ сме­си растворяется так, как будто осталь­ных компонентов нет, т. е. в соответ­ствии с Генри законом. Строго выпол­няется для смеси идеальных газов; применим и к реальным газам, если их растворимость невелика, а поведе­ние близко к поведению идеального газа. Д. з. открыты англ. учёным Дж. Дальтоном (J. Dalton) в 1801 и 1803.

ДАРСИ — ВЕЙСБАХА ФОРМУЛА (в гидравлике), определяет величину потерь напора на трение при движении жидкости в трубах: h_v=(l/d)(v²/2g), где

 — коэфф. гидравлич. трения, l и d— длина и диаметр трубы, ч — ср. ско­рость течения жидкости, g — ускоре­ние свободного падения. Коэфф.  за­висит от хар-ра течения: при лами­нарном течении =⁶⁴/Rе, где Rе —

Рейнольдса число: при турбулентном

течении (приближённо) =0,11(K_э/d +⁶⁸/Re)^1/4, где K_э — эквивалентная ше­роховатость стенок трубы. Выведена нем. учёным Ю. Вейсбахом (J. Weisbach, 1845) и франц. инженером А. Дарси (Н. Darcy, 1857).

ДВОЙНИКОВАНИЕ, образование в монокристалле областей с разл. ори­ентацией крист. структуры, связан­ных друг с другом операцией точечной симметрии, напр. зеркальным отраже­нием в определ. плоскости (плоскости Д.), поворотом вокруг кристаллографич. оси (оси Д.), либо др. преобра­зованиями (см. Симметрия кристал­лов). Осн. структура вместе с двойни­ковым образованием наз. двойником.

Д. может происходить в процессе кристаллизации, при механич. де­формации, а также при срастании со­седних зародышей (двойники роста, рис. 1). Д. происходит также при быстром тепловом расширении или сжатии, при нагревании деформиров. кристаллов (двойники рекристалли­зации), при переходе из одной крист. модификации в другую (см. Поли­морфизм).

Переброс в двойниковое положение часто осуществляется послойным сдви-



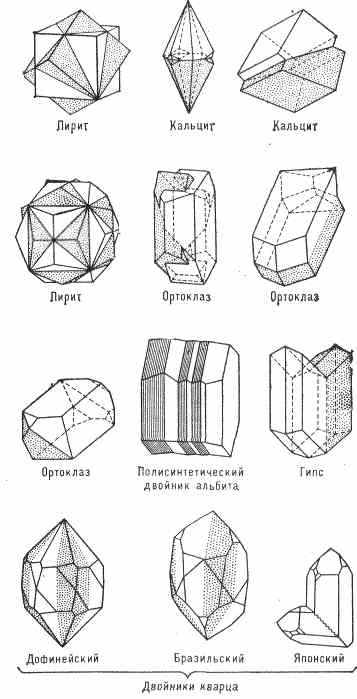
Рис. 1. Двойники роста.


Рис. 1. Двойники роста.

гом ат. плоскостей. Каждый ат. слой последовательно смещается на долю межат. расстояния, при этом все атомы в двойниковой области пере­мещаются на длину, пропорц. их расстоянию от плоскости Д. (плоско­сти зеркального отражения). Меха­нич. двойники образуются в тех слу­чаях, когда деформация сдвига за­труднена (см. Пластичность). Д. может сопровождаться изменением размеров и формы кристалла, что характерно, напр., для кристалла СаСO₃.




Рис. 2. а — двойникование кальцита при нажатии лезвием ножа (метод Баумгауэра); б — сдвойникованный кристалл кальцита.



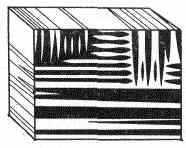
Рис. 3. Полисинтетич. двойник сегне­товой соли, выяв­ленный травлением (фотография в отра­жённом свете).

Д. СаСО₃ можно осуществить нажатием лезвия ножа (рис. 2, а), при этом в двойни­ковое положение переходит участок в правой части кристалла (рис. 2, б). Д. с изменением формы имеют место у всех металлов, нек-рых ПП (Ge, Si) и диэлектриков. Другой вид Д., не вызывающий изменений формы кри­сталла, наблюдается, напр., у кварца и триглицинсульфата.

Если однородность структуры моно­кристалла нарушена многочисл. двой­никовыми образованиями, то его наз. полисинтетическим двой­ником. В кристаллах сегнетовой соли двойники, являющиеся одновре­менно сегнетоэлектрич. доменами, возникают в результате перехода кри­сталла из ромбич. сингонии в моно­клинную (при темп-ре Кюри). Двой­ники сегнетовой соли имеют различ­ные оптич. св-ва. Это позволяет об­наруживать доменное строение кри­сталлов сегнетовой соли оптически­ми методами (рис. 3).

М. В. Классен-Неклюдова.

143


ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ,

раздвоение световых лучей при про­хождении через анизотропную среду {напр., кристалл), обусловленное за­висимостью преломления показателя этой среды от направления электрич. вектора световой волны (см. Кристал­лооптика, Оптическая анизотропия). При падении световой волны на ани­зотропную среду в ней возникают две волны с взаимно перпендикулярными плоскостями поляризации (см. Поля­ризация света). В одноосных кристал­лах одна из волн имеет плоскость поляривации, перпендикулярную гл. се­чению, т. е. плоскости, проходящей через направление луча света и оп­тическую ось кристалла (обыкновен­ный луч), а другая — плоскость, па­раллельную главному сечению (не­обыкновенный луч). Скорость распро­странения обыкновенной волны и, следовательно, показатель преломле­ния для неё n₀ не зависят от направ­ления её распространения, а скорость распространения и показатель пре­ломления n_е необыкновенной волны — зависят. Для необыкновенного луча обычные законы преломления изме­няются; в частности, он может не ле­жать в плоскости падения. При рас­пространении вдоль оптич. оси n₀=n_е и Д. л. отсутствует. Одноосные кристаллы наз. положительными или отрицательными в зависимости от зна­ка разности n_е - n₀. Макс. абс. ве­личина этой разности служит число­вой хар-кой Д. л. В двуосных кри­сталлах показатели преломления обо­их лучей, возникающих при Д. л., зависят от направления распростране­ния. Д. л. двуосных кристаллов мож­но характеризовать тремя главными показателями преломления.

Д. л. может наблюдаться не только в естественно-анизотропной среде, но и в среде с искусственно вызванной анизотропией, напр. при наложении внеш. поля — электрического (см. Керра эффект), магнитного (см. Коттона — Мутона эффект), поля упру­гих сил (см. Поляризационно-оптический метод исследования напряжений, Фотоупругость).

Явление, аналогичное Д. л., наб­людается и в др. диапазонах эл.-магн. волн, напр. в диапазоне СВЧ в плазме, находящейся в магн. поле (а следова­тельно, анизотропной); см. Распрост­ранение радиоволн в ионосфере.

• См. лит. при ст. Кристаллооптика.

М. Д. Галанин.

ДВОЙНОЙ ЭЛЕКТРИЧЕСКИЙ СЛОЙ, совокупность электрич. зарядов противоположных знаков, распределён­ных вдоль границы соприкосновения двух фаз. В образовании Д. э. с. могут принимать участие эл-ны, ионы и ориентированные полярные (обла­дающие собств. дипольным моментом) молекулы. Так, Д. а. с. образуется при погружении металла в электролит, напр. цинка в серную к-ту. Цинк при этом отдаёт в электролит положи­тельно заряж. ионы, сам заряжаясь отрицательно. Положительно заряж. ионы электролита притягиваются по­верхностью металла, и вдоль поверх­ности соприкосновения фаз образуется Д. э. с. Электрич. поле, возникающее между заряж. слоями, препятствует растворению цинка, а при определ. значении прекращает его совсем. На границе электрод — электролит воз­никает скачок потенциала.

В целом Д. э. с. электрически нейт­рален, внутри же слоя напряжён­ность электрич. поля может достигать больших значений. Благодаря значит. размерам заряж. поверхностей и ма­лым расстояниям между ними Д. э. с. обладает большой электроёмкостью. Образование Д. э. с. обусловливает электрокинетические явления, строе­ние Д. э. с. существенно для электрохим. реакций (напр., в хим. источни­ках тока), для электролиза и т. д.

ДВОЙНОЙ ЭЛЕКТРОННО-ЯДЕР­НЫЙ РЕЗОНАНС, один из методов радиоспектроскопии, состоящий в ре­гистрации квант. переходов между яд. магн. подуровнями (ядерный магнит­ный резонанс) по их влиянию на сиг­нал электронного парамагнитного резонанса. Предложен амер. физиком Дж. Феером (G. Feher) в 1956. Пусть исследуемое в-во содержит парамагн. ч-цы с электронным спином s=1/2 и спином ядра I=1; расщепление уров­ней ч-цы в пост. магн. поле Н опреде­ляется вз-ствием электронного и яд. спинов с полем Н (см. Зеемана эффект), т. н. сверхтонким вз-ствием эл-на и ядра и вз-ствием электрич. кеадрупольного момента ядра с внутрикристаллическим полем (рис. а). Под действием эл.-магн. поля СВЧ на частоте _э, соответствующей одному из электронных переходов (рис. б), населённости соответствующих уров­ней выравниваются, поглощение эл.-магн. энергии прекращается, сигнал ЭПР исчезает.



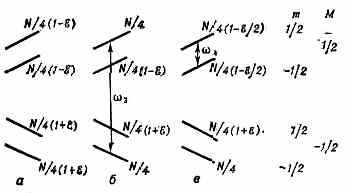
Рис. а — Расщепление уровней энергии па­рамагн. ч-цы с электронным спином s=1/2 и спином ядра I=1 в пост. магн. поле H: M и m — проекции электронного и яд, спинов на направление H; N — общее число па­рамагн. атомов; ξ=h_э/kT. б — Выравнива­ние населённостей уровней под действием эл.-магн. поля частоты _э. в — Изменение населённостей после подключения радиоча­стотного поля частоты _я.


Если далее приложить радиочастотное поле частоты _э, соот­ветствующей яд. переходу, то населён­ности всех уровней изменяются, что

приводит к появлению сигнала ЭПР на частоте _я (рис., в). Приведённое описание справедливо при адиабати­чески быстром прохождении через резонанс, когда можно пренебречь релаксац. процессами (см. Релаксация).

Сочетая высокую чувствительность ЭПР с высокой разрешающей способ­ностью ЯМР, Д. э.-я. р. позволяет получить информацию о природе па­рамагн. центров в диэлектриках и ПП и распределении в них эл-нов, о кон­стантах сверхтонкого и квадрупольного вз-ствий, а также о зонной струк­туре, внутрикристаллических полях и деформац. потенциалах в кристалле.

Исследования Д. э.-я. р. послужили толчком к развитию др. комбиниров. резонансов, напр. двойных резонансов, где одно или оба эл.-магн. поля заменены акустическими (двойной акустомагн. электронно-ядерный ре­зонанс и др.). Идея регистрации квант. переходов на другой, более высокой частоте лежит в основе оптич. методов детектирования в радиоспект­роскопии.

• Грачев В. Г., Д е й г е н М. Ф., Двой­ной электронноядерный резонанс..., «УФН», 1978, т. 125, в. 4, с. 631; Голенищев-Кутузов В. А., Сабурова Р. В., Шамуков Н. А., Двойные магнитоакустические резонансы в кристаллах, там же, 1976, т. 119, в. 2, с. 201.

В. А. Голенищев-Кутузов.

ДВОЙСТВЕННОСТИ ПРИНЦИП, уста­навливает перекрёстную связь между эл.-магн. полями, образующимися в результате дифракции на отверстии S, прорезанном в бесконечно тонком иде­ально проводящем плоском экране, и на плоской пластине, совпадающей по форме с отверстием S. Д. п. и его оптич. аналог — теорема Бабине, свя­зывающая в оптике дифракц. явления во «взаимно дополняющих экранах»,— результат инвариантности Максвел­ла уравнений относительно одновре­менных перестановок Е Н-Е, , , где ,  — диэлектрич. и магн. проницаемости среды.

В теории антенн Д. п. приводит к соотношению между полями, созда­ваемыми электрич. вибратором (E₁,h₁), и щелевым излучателем точно таких же размеров (Е₂, Н₂):

E₁= H₂, h₁=-(1/)Е₂,

где =/ — волновое сопротивле­ние среды.

• См. лит. при ст. Антенна.

ДВУМЕРНЫЕ ПРОВОДНИКИ, ис­кусственно созданные электропрово­дящие системы на границе разде­ла двух плохо проводящих сред, напр. вакуум — диэлектрик, полу­проводник — диэлектрик. Простейший Д. п.— слой эл-нов, удерживаемых над поверхностью диэлектрика (напр., жидкого Не, рис.) силами электростатич. изображения (эл-ны поляризуют диэлектрик и притягиваются к нему), а также внешним пост. электрич. по­лем, приложенным перпендикулярно поверхности диэлектрика. Аналогич­но в гетероструктурах (напр., на ос-

144


нове GaAs) и у поверхности ПП (Si, Ge, InSb и др.) образуется двухмер­ный слой с избыточной концентра­цией носителей заряда или с инверс­ной проводимостью (см. Инверсион­ный слой) из-за изгиба зон или при



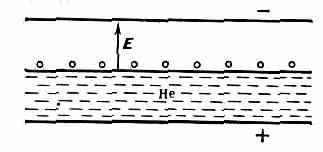
приложении разности потенциалов к структуре металл — диэлектрик — по­лупроводник (см. М—Д—П-структура). В Д. п., помещённых в пере­менное эл.-магн. поле достаточно ма­лой частоты, ток может течь только параллельно границе раздела.

• Electronic properties of two-dimensional systems (3-d international conference), Amst., 1980 (Surface sci., v. 98); Э д е л ь м а н В. С., Левитирующие электроны, «УФН», 1980, т. 130, в. 4, с. 675.

В. С. Эдельман.

ДВУОСНЫЕ КРИСТАЛЛЫ, кристал­лы, в к-рых происходит двойное луче­преломление при всех направлениях падающего на них луча света, кроме двух, каждое из к-рых наз. опти­ческой осью кристалла. См. Кристаллооптика.

ДВУХ ТЕЛ ЗАДАЧА, одна из част­ных задач небесной механики, состоя­щая в определении движения двух тел, взаимно притягивающихся со­гласно закону тяготения Ньютона. В общем случае, когда приходится учитывать неоднородность строения взаимодействующих тел и разл. виды возмущений движения, Д. т. з. точ­ного решения не имеет. Если притяги­вающиеся тела можно рассматривать как материальные точки (что прибли­жённо выполняется, напр., для Солн­ца и каждой из планет Солн. системы в отдельности или для двойной звёзд­ной системы), то Д. т. з. допускает ре­шение в конечном виде. Движение, соответствующее такому решению Д. т. з., наз. невозмущённым или кеплеровым. При кеплеровом движении в зависимости от нач. условий (скорости, её направления и др.) траектория тела в поле тяготения др. тела может быть окружностью или эллипсом (как у планет и их спутни­ков, см. Кеплера законы), параболой или гиперболой (у тел с пролётной траекторией), наконец прямой, со­единяющей центры масс тел. Учёт воз­мущений (отклонений от движения по эллипсу, параболе и т. д.), осо­бенно в столь сложной системе, как Солнечная, очень труден. В результа­те возмущающего действия на планету др. планет Солн. системы истинная траектория планеты — сложная про­странств. кривая, к-рую нельзя опи­сать простой аналитич. ф-лой. Поэтому при решении Д. т. з. с учётом возму­щений широко пользуются прибли­жёнными численными методами.

ДЕБАЕВСКИЙ РАДИУС ЭКРАНИ­РОВАНИЯ [по имени голл. физика П. Дебая (P. Debye)], характерное расстояние, на к-рое в плазме, элект­ролите или ПП распространяется дей­ствие электрич. поля отд. заряда. В вакууме электростатич. потенциал  уединённой n-цы с зарядом q на расстоянии r определяется по ф-ле: =q/r. В среде, содержащей положит. и отрицат. заряды, напр. в плазме, эл-ны в нек-рой окрестности иона притягиваются к нему и экранируют его электростатич. поле. Точно так же «неподвижный» эл-н отталкивает др. эл-ны и притягивает ионы. В резуль­тате поле вокруг заряж. ч-цы стано­вится очень слабым на расстояниях, превышающих Д. р. э. Выражение для потенциала заряда, покоящегося в плазме, принимает вид:

=(q/r)ехр(-r/D),

где D — Д. р. э., зависящий от кон­центрации заряж. ч-ц, энергии их теплового движения (темп-ры) и ве­личины заряда. Для изотермич. элек­трон-протонной плазмы

D=(kT/8ne²)^1/2 ,

здесь n — концентрация эл-нов (или ионов). Подстановка численных зна­чений констант даёт

D5(T/n)^1/2

(все величины в системе СГС). В ПП D² пропорц. ср. энергии тепловых коле­баний ионов и обратно пропорц. плот­ности носителей тока, к-рая увеличи­вается при возрастании темп-ры.

ДЕБАЕГРАММА, рентгенограмма, снятая по Дебая — Шеррера методу. Представляет собой дифракц. изобра­жение поликрист. образца в монохроматнч. рентг. излучении (см. Ди­фракция рентгеновских лучей).

Д., зафиксированная на плоской фотоплёнке в дебаевской рентгенов­ской камере, имеет вид системы концентрич. окружностей. Если образец состоит из очень мелких кристалли­ков, хаотически ориентированных в пр-ве, то дифракц. линии имеют рав­номерное почернение. Когда кристал­лики преим. ориентированы (т. н. текстура), почернение дифракц. линии неравномерно. Д., регистрируемая фотоэлектрич. или ионизац. приём­ником в рентгеновском дифрактометре, наз. дифрактограммой.

Углы раствора конусов (радиусы дифракц. линий на Д.) и интенсивности дифракц. линий характерны для каж­дой крист. структуры, что позволяет составить стандартные картотеки Д. и с их помощью определять фазовый состав образца (см. Рентгеновский структурный анализ, Рентгеногра­фия материалов). А. В. Колпаков.

ДЕБАЙ (Д, D), внесистемная ед. элект­рич. дипольного момента; применяет­ся в ат. физике. Названа в честь голл. физика П. Дебая (P. Debye). 1Д=1•10^-18 ед. СГС=3,33564•10^-30 Кл•м.

ДЕБАЯ ЗАКОН ТЕПЛОЕМКОСТИ,

кубич. зависимость теплоёмкости С кристалла от темп-ры Т в области низких темп-р:



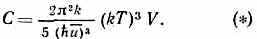
Здесь V — объём, и — усреднённая скорость звука. Ф-ла (*) теоретически выведена голл. физиком П. Дебаем в 1912. Д. з. т. относится и к теплоём­кости при пост. объёме С_V, и к тепло­ёмкости при пост. давлении С_р, т. к. при низких темп-pax разность С_р-С_V пропорц. Т⁷.

Д. з. т. имеет место в условиях, когда в кристалле возбуждены лишь НЧ колебания кристаллической решёт­ки, длина волны к-рых велика по срав­нению с постоянной решётки. Для кристаллов с простой решёткой (эле­менты и простые соединения) Д. з. т. начинает выполняться при Т порядка десятков К; для сложных решёток (в частности, для сильно анизотроп­ных крист. структур — слоистых и квазиодномерных) Д. з. т. наблюда­ется при значительно более низких темп-pax (см. Дебая температура).

• Л а н д а у Л. Д., Л и ф ш и ц Е. М., Статистическая физика, 3 изд., ч. 1, М., 1976.

Э. М. Эпштейн.

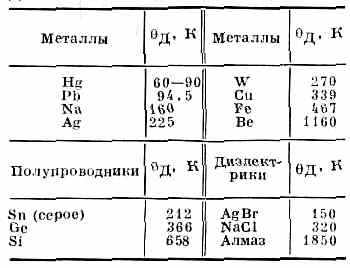
ДЕБАЯ ТЕМПЕРАТУРА, характеристич. темп-pa _Д тв. тела, опреде­ляемая соотношением k_Д=h_Д, где _Д=u(6²n)^1/3 — предельная частота упругих колебаний кристаллической решётки (n — число атомов в ед. объёма, и — усреднённая скорость зву­ка в тв. теле), наз. также дебаевской частотой. При темп-pax Т >>_Д (классич. область) теплоёмкость тв. тела описывается Дюлонга и Пти законом; при Т <<_Д (квант. область) — вы­полняется Дебая закон теплоёмкости. Д. т. зависит от упругих постоянных кристалла (см. табл.).


ТЕМПЕРАТУРА ДЕБАЯ ДЛЯ НЕКОТОРЫХ КРИСТАЛЛОВ



Д. т. табулируется как физ. пара­метр в-ва. Она даёт наиб. удобный в динамич. теории решётки масштаб темп-ры: величина k_Д представляет собой макс. квант энергии, способный возбудить колебания решётки. Выше 0д возбуждены все моды, ниже _Д

145


моды начинают «вымерзать». Д. т. от­деляет низкотемпературную область, где проявляются квант. эффекты и где необходимо пользоваться квант. ста­тистикой, от высокотемпературной, где справедлива классич. статистич. механика (см. Статистическая физи­ка).

• Ландау Л. Д., Л и ф ш и ц Е. М.,

Статистическая физика, 3 изд., ч. 1, М., 1976.

Э. М. Эпштейн.

ДЕБАЯ ФОРМУЛЫ, описывают зави­симость действительной ' и мнимой '' частей комплексной диэлектриче­ской проницаемости ='-i" среды с ориентац. поляризацией (разбавлен­ные р-ры диполей в жидкостях и тв. телах) от частоты со приложенного перем. электрич. поля и времени релаксации :



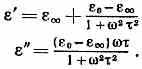
Здесь ₀ — значения ' для НЧ (<<1/), _ — для высоких (_>>1/). Величина " определяет потери энер­гий, рассеиваемой в диэлектрике в результате изменения поляризации. Д. ф. описывают св-ва диэлектрика в перем. электрич. поле в предполо­жении экспоненц. установления рав­новесия. Д. ф. установлены голл. фи­зиком П. Дебаем в 1929.

• См. лит. при ст. Диэлектрики.

И. Н. Грозное.

ДЕБАЯ — ШЕРРЕРА МЕТОД, метод исследования поликрист. материалов с помощью дифракции рентгеновских лучей. Предложен голл. физиком П. Дебаем и швейц. физиком П. Шеррером (P. Scherrer) в 1916. В Д.— Ш. м. тонкий пучок монохроматич. рентг. излучения падает на образец,



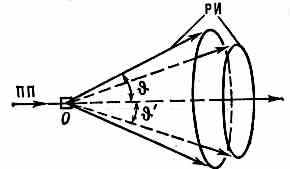
Рис. 1. Рассеяние первичного рентг. излуче­ния ПП на поликрист. образце 0. Рассеян­ное излучение РИ направлено к ПП под уг­лами  и '.


к-рый рассеивает излучение вдоль об­разующих соосных конусов с углом раствора  (рис. 1). При этом излуче­ние рассеивается только теми кристал­ликами, к-рые ориентированы в пр-ве так, что для них при данной длине волны излучения выполняется Брэг­га — Вульфа условие. Поскольку это условие может одновременно выпол­няться для неск. семейств кристаллографич. плоскостей, то возникает со­вокупность дифракц. конусов с раз­личными углами раствора 2. Для того чтобы все кристаллики последовательно вывести в отражающее поло­жение, образец равномерно вращают вокруг оси, перпендикулярной на­правлению первичного пучка. Рас­сеянное излучение можно регистриро­вать на фотоплёнке (дебаеграмма) в цилиндрич. (дебаевской) рентгенов­ской камере (рис. 2). В рентгеновском дифрактометре дифракц. максимумы регистрируются фотоэлектрич. или ионизац. приёмником



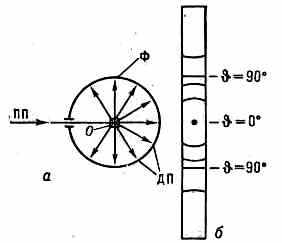
Рис. 2. Схема получения дебаеграммы б в цилиндрич. дебаевской камере а (0 — обра­зец, ПП — первичный рентг. пучок). На дебаеграмме б видны полосы, оставляемые на фотоплёнке Ф дифракц. пучками ДП.

.

Д.— Ш. м. применяется для уста­новления размеров и формы элем. крист. ячейки, размеров и пространств. ориентации кристалликов, определе­ния деформаций и напряжений, а так­же для фазового анализа поликрист. объектов (см. Рентгеновский струк­турный анализ, Рентгенография ма­териалов).

А. В. Колпаков.

ДЕ-БРОЙЛЕВСКАЯ ДЛИНА ВОЛНЫ, длина волны де Бройля.

ДЕ БРОЙЛЯ ВОЛНЫ, см. Волны де Бройля.

ДЕВИАТОР ДЕФОРМАЦИИ, тензор, определяющий в окрестности точки малую деформацию, не связанную с изменением объёма. Через компонен­ты тензора деформации _ij (см. Де­формация механическая) Д. д. вы­ражается ф-лами:

э₁₁=₁₁-, э₂₂=₂₂-, э₃₃=₃₃-,

э₁₂=₁₂, э₂₃=₂₃, э₃₁=₃₁,

где =(₁₁+₂₂+₃₃)/3 — ср. дефор­мация. При этом э₁₁+э₂₂+э₃₃=0. Д. д. пользуются в механике сплош­ной среды.

ДЕВИАТОР НАПРЯЖЕНИЙ, тензор, определяющий напряжения в точке, не связанные с гидростатич. напряже­нием (всесторонним давлением). Через компоненты тензора напряжений _ij выражается ф-лами

s₁₁=₁₁-, s₂₂ = ₂₂-, s₃₃=₃₃-,

s₁₂=₁₂, s₂₃=₂₃, s₃₁=₃₁,

где =(₁₁+₂₂+₃₃)/3 — гидроста­тич. (среднее) напряжение. При этом

s₁₁+s₂₂+s₃₃=0. Д. н. применяется в механике сплошной среды.

ДЕИОНИЗАЦИЯ газа, исчезновение носителей свободного электрич. заря­да (положит. и отрицат. ионов и эл-нов) из занимаемого газом объёма. К Д. приводят рекомбинация ионов и

эл-нов, их диффузия к границам за­нимаемого газом объёма, а также вы­ход заряж. ч-ц из занимаемого объёма под действием внеш. электрич. поля. Время, необходимое для уменьшения концентрации носителей заряда в определ. число раз (напр., в 10³ или 10⁶ раз от нач. концентрации), наз. временем Д. Оно явл. важной хар-кой газоразрядных и др. прибо­ров, для работы к-рых существенно поддержание определ. степени иони­зации. Время Д. зависит от природы газа, геометрии занимаемого им объё­ма, наличия и изменения во времени внеш. электрич. поля, а также от распределения полей пространств. за­рядов.

• См. лит. при ст. Ионизация.

ДЕЙСТВИЕ, физ. величина, имеющая размерность произведения энергии на время и являющаяся одной из су­ществ. хар-к движения системы. Для механич. системы Д. обладает след. важным св-вом: если рассмотреть нек-рую совокупность возможных движе­ний этой системы между двумя её положениями, то истинное (факти­чески происходящее) движение си­стемы будет отличаться от этих воз­можных движений тем, что для него значение Д. явл. наименьшим (см. Наименьшего действия принцип). Это позволяет найти ур-ния движения механич. системы и изучить это дви­жение.

В зависимости от св-в механич. си­стемы и применяемого метода изуче­ния её движения рассматривают разные выражения для величины Д. Если ввести т. н. функцию Лагранжа L=Т-П, где Т и П — кинетич. и потенц. энергии системы, то величина



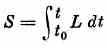
наз. действием по Гамиль­тону за промежуток времени t -t₀. Она входит в выражение принципа наименьшего действия в форме Гамиль­тона — Остроградского. Другая ве­личина



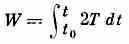
наз. действием по Л а г р а н ж у за промежуток времени t- t₀ и входит в выражение принципа наи­меньшего действия в форме Мопертюи — Лагранжа.

Для системы, в к-рой выполняется закон сохранения механич. энергии, величины S и W связаны соотноше­нием

S=W- h(t-t₀),

где h = Т +П — полная механич. энергия системы.

Помимо классич. механики, поня­тием Д. пользуются в теории упруго­сти, электродинамике, термодинами­ке обратимых процессов.

Если характерные для физ. задачи величины размерности действия срав-

146


нимы с квантом действия h, то рас­смотрение следует вести на основе квантовой механики.

С. М. Тарг

ДЕЙСТВИТЕЛЬНОЕ ИЗОБРАЖЕ­НИЕ, см. Изображение оптическое.

ДЕЙСТВИЯ И ПРОТИВОДЕЙСТ­ВИЯ ЗАКОН, один из осн. законов механики (третий закон Ньютона), со­гласно к-рому действия двух матер. тел друг на друга равны по величине и противоположны по направлению. Напр., сила, с к-рой груз, лежащий на плоскости, давит на эту плоскость, рав­на силе (реакции), с к-рой плоскость давит на груз; сила, с к-рой Земля притягивает Луну, равна силе, с к-рой Луна притягивает Землю, и т. д. Д. и п. з. играет важную роль при изучении движения механич. си­стем.

ДЕЙТРОН, ядро тяжёлого изотопа водорода — дейтерия, содержит один протон и один нейтрон. Обозначается ²Н, d, реже D. Масса равна 2,01423 атомной единицы массы, энергия свя­зи нейтрона — 2,23 (4) МэВ, спин — 1, магн. момент — 0,857348(9) яд. маг­нетона, квадрупольный электриче­ский момент — 2,738(4)•10^-27 см².

• См. лит. при ст. Ядро атомное.

ДЕКА... (от греч. deka — десять), приставка к наименованию ед. физ. величины для образования наимено­вания кратной единицы, равной 10 ис­ходным ед. Обозначения: да, da. Напр., 1 дал (декалитр) = 10 л.

ДЕКАДА (от греч. dekas, род. п. dekados — десяток), единица частотного интервала; равна интервалу между двумя частотами (f₁ и f₂), десятичный логарифм отношения к-рых lg(f₂/f₁)=1, что соответствует f₂/f₁=10.

ДЕКОРИРОВАНИЕ (от лат. decoro— украшаю), метод обнаружения в кри­сталлах точечных дефектов, дисло­каций, ступеней роста и др. дефек­тов, заключающийся в осаждении на поверхность кристалла из газовой или жидкой фазы либо во введении в его объём хим. путём в-в, осаждающихся в виде ч-ц на дефектах и тем самым их выявляющих. Декориров. кристал­лы изучаются методами оптич. или электронной микроскопии. Д. исполь­зуется при исследовании процессов кристаллизации, реальной структуры кристалла, эпитаксии, а также при изучении хим. реакций на поверхно­стях тв. тел.

• Декорирование поверхности твердых тел, М., 1976.

ДЕКРЕМЕНТ ЗАТУХАНИЯ (от лат. decrementum — уменьшение, убыль), количественная хар-ка быстроты зату­хания колебаний. Д. з.  равен нату­ральному логарифму отношения двух последующих макс. отклонений х ко­леблющейся величины в одну и ту же сторону: =ln(x₁/x₂). Д. з.— величи­на, обратная числу колебаний, по истечении к-рых амплитуда убывает в е раз. Напр., если =0,01, то амплиту­да уменьшится в е раз после 100 коле­баний. Д. з. характеризует число пе­риодов Т, в течение к-рых происходит затухание колебаний. Полное время затухания определяется отно­шением Т/. Напр., величина ср. зна­чений Д. з. колебательного контура =0,02—0,05, камертона 0,001, кварцевой пластинки 10^-4—10^-5, оптического резонатора 10^-6—10^-7.

Обычно вместо Д. з. пользуются понятием добротности колебательной системы Q, с к-рой Д. з. связан соот­ношением:

=/(Q²-¹/₄),

а при больших добротностях /Q.

• Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 1964.

ДЕЛЕНИЕ АТОМНОГО ЯДРА, де­ление ат. ядра на неск. более лёгких ядер (осколков), чаще всего на два ядра, близких по массе. В 1939 нем. учёные О. Ган и Ф. Штрасман уста­новили, что при бомбардировке урана нейтронами образуются ядра щёлоч­ноземельных элементов, в частности Ва. Вскоре австр. физики Л. Майтнер и О. Фриш показали, что ядро ²³⁵U делится под действием нейтрона на два осколка (рис. 1), и дали первое качеств. объяснение деления.



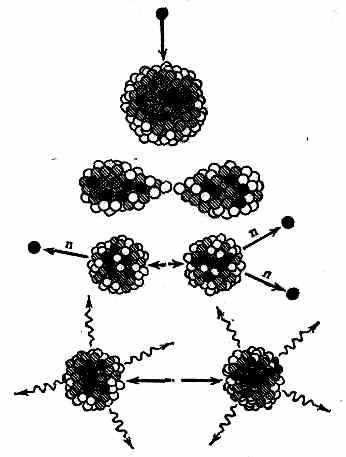
Рис. 1. Деление тяжёлого ядра ^23SU (n — нейтроны, испускаемые осколками).


В 1940 Г. Н. Флёров и К. А. Петржак обна­ружили спонтанное деление ядер. Для того чтобы ядро достигло формы, пред­шествующей его разрыву, необходима затрата определ. энергии для преодо­ления потенциального барьера, наз. барьером деления (рис. 2). Эту энергию ядро может получить извне, напр. при захвате нейтрона. В случае спонтанного деления ядер происходит туннельное просачивание через барьер (см. Туннельный эффект). Масса тяжёлого ядра больше суммы масс образующихся осколков. Раз­ница в массах соответствует энергии, выделяемой при делении. Значит.

часть этой энергии выделяется в виде кинетич. энергии осколков, равной энергии их электростатич. отталкива­ния в момент деления. Суммарная кинетич. энергия осколков несколько увеличивается по мере возрастания А (ат. массы) делящегося ядра и со­ставляет для урана и трансурановых элементов ок. 200 МэВ. Осколки быстро тормозятся в среде, вызывая ио­низацию, нагревание и нарушая её структуру.



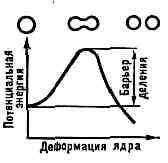
Рис. 2. Барьер деле­ния и последователь­ность форм, прини­маемых делящимся ядром.


Утилизация кинетич. энер­гии осколков деления за счёт нагрева­ния ими среды — основа использова­ния яд. энергии.

Осколки деления образуются в воз­буждённых состояниях. В дальней­шем энергия возбуждения осколков уменьшается в результате испускания ими нейтронов (нейтроны деле­ния). Энергетич. спектр нейтронов де­ления можно считать максвелловским со среднеквадратичной энергией 1,3 МэВ. Когда энергия возбуждения становится меньше энергии, необходи­мой для отделения нейтрона от ядра, эмиссия нейтронов прекращается, начинается испускание -квантов. В ср. на один акт деления испускается 8—10 -квантов.

Масса, заряд и энергия возбужде­ния осколков, образующихся в отд. актах деления, различны. Число нейтронов v, испущенных в одном акте деления, также флуктуирует. При бомбардировке ²³⁵U медленными нейт­ронами ср. число испускаемых нейт­ронов v=2,5. Для более тяжёлых элементов v увеличивается. Именно

•превышение v над 1 позволяет осуще­ствить ядерную цепную реакцию. Осколки перегружены нейтронами и радиоактивны. Соотношение между числами протонов Z и нейтронов N=А-Z в осколках зависит от энергии возбуждения делящегося ядра. При достаточно высоком возбуждении оно в осколках остаётся тем же, что у делящегося ядра. При малой энергии возбуждения нейтроны и протоны рас­пределяются между осколками так, что в дальнейшем происходит пример­но одинаковое число -распадов, прежде чем они превратятся в стабильные ядра. В отд. случаях (прибл. 0,7% по отношению к общему числу деле­ний) образующееся при -распаде воз­буждённое ядро также испускает нейт­рон. Эмиссия этого нейтрона из воз­буждённого ядра — процесс быстрый (~ 10^-16 с), однако он запаздывает по отношению к моменту деления ядра


147


на время, к-рое может достигать де­сятков с (запаздывающие нейтроны).

Деление наз. асимметричным, когда отношение масс наиболее часто воз­никающих осколков порядка 1,5. По мере увеличения энергии возбуждения ядра всё большую роль начинает играть симметричное деление на два осколка с близкими массами. Для нек-рых спонтанно делящихся ядер (U, Pu) характерно асимметричное деление (рис. 3), но по мере увеличе­ния А деление приближается к сим­метричному. Наиболее отчётливо это



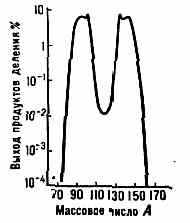
Рис. 3. Спектр масс осколков деления ядра ²³⁵U при за­хвате медленных нейтронов.


проявляется у ²⁵⁶Fm. Значительно реже наблюдается деление на три ос­колка, обычно сопровождающееся ис­пусканием -частицы, ядер ⁶Не, ⁸Не, Li, Be и др. Предельный слу­чай — деление на три почти равных осколка — наблюдался при бомбарди­ровке ядер ускоренными тяжёлыми ионами (⁴⁰Аг и др.).

Теория Д. а. я. впервые была дана дат. физиком Н. Бором и амер. физи­ком Дж. А. Уилером и независимо от них Я. И. Френкелем. Они развили капельную модель ядра, в к-рой ядро рассматривается как капля электри­чески заряженной несжимаемой жид­кости. На нуклоны действуют уравно­вешивающие друг друга яд. силы притяжения и электростатич. силы отталкивания, стремящиеся разорвать ядро. Деформация ядра нарушает рав­новесие; при этом возникают силы, аналогичные поверхностному натяже­нию жидкой капли, стремящиеся вер­нуть ядро к нач. форме. Деформация ядра при делении сопровождается уве­личением его поверхности, и, как в жидкой капле, силы поверхностного натяжения возрастают, препятствуя его дальнейшей деформации. Чем ниже барьер деления (чем больше ве­личина Z²/A), тем меньше период спонтанного деления.

Капельная модель описывает лишь усреднённые св-ва ядер. В действи­тельности же хар-р процесса деления может существенно зависеть от внутр. структуры ядра и состояния отд. нуклонов. Из-за этого, в частности, барьер деления больше для ядер с нечётным числом нуклонов, чем для соседних четно-чётных ядер (чётные Z и N). Напр., деление ядер ²³⁸U под действием нейтронов становится до-

статочно вероятным лишь в том случае, когда кинетич. энергия нейтронов превышает нек-рый порог, а в случае ²³⁵U даже при захвате теплового нейтрона энергия возбуждения состав­ного ядра ²³⁶U превышает барьер деле­ния (рис. 4). Влияние структуры ядра на Д. а. я. видно при сравнении пе­риодов спонтанного деления четно-нечётных ядер. Вместо регулярного увеличения периода спонтанного деле­ния ядра с ростом А иногда наблю­дается его резкое уменьшение. Этот эффект чётко проявляется при N=152, что необъяснимо в рамках капельной модели и свидетельствует о влиянии на барьер деления и вообще на процесс Д. а. я. оболочечной струк­туры ядра (см. Ядро атомное).



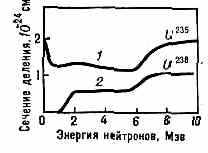
Рис. 4. Зависи­мость сечения де­ления ²³⁵U и ²³⁸U и от энергии нейт­ронов.


• Петржак К. А., Флеров Г. Н., Спонтанное деление ядер, «УФН», 1961, т. 73, в. 4, с. 655; X а л л е р н И., Деление ядер, пер. с англ., М., 1962; О б у х о в А. И., П е р ф и л о в Н. А., Деление ядер, «УФН», 1967, т. 92, в. 4; Струтинский В. М., Деление ядер, «Природа», 1976, №9; Л и х м а н Р. Б., Деление ядра, в кн.: Физика атомного ядра и плазмы, пер. с англ., М., 1974; Фриш О., У и л е р Дж., Открытие деления ядер, «УФН», 1968, т. 96, в. 4.

ДЕЛЯЩИЕСЯ ИЗОМЕРЫ, изомерные состояния ядер (см. Изомерия атом­ных ядер) с высокой вероятностью спонтанного деления ядер. Известно ок. 30 ядер (изотопы U, Pu, Am, Cm, Bk), для к-рых вероятность спон­танного деления в изомерном состоя­нии больше, чем в основном, примерно в 10²⁶ раз. Очевидно, форма ядра в таком состоянии более вытянута, чем в основном. Совр. рабочая модель Д. и. основывается на идее двугорбого барьера деления (рис.).




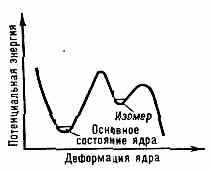
Рис. Двугорбый потенц. барьер деления в случае спонтанного деления из изомерного состояния. По оси абсцисс отложена степень отклонения ядра от сферич. формы (степень вытянутости).


Нижнее состо­яние во второй потенц. яме на барье­ре деления должно быть изомерным. Эл.-магн. переходы из этого состояния в основное, лежащее в первой яме, сильно подавлены из-за барьера, разделяющего обе ямы. В то же время барьер деления для изомерных состояний мал, и это объясняет высо­кую вероятность деления изомеров.

ДЕМБЕРА ЭФФЕКТ, возникновение электрич. поля и эдс в однородном полупроводнике при его неравномер­ном освещении. В частности, эдс возникает между освещаемой и не­освещаемой поверхностями ПП при сильном поглощении света в нём (диффузионная фотоэдс). Открыт нем. физиком X. Дембером (Н. Dember; 1931); теория разработана Я. И. Френкелем (1933), нем. физи­ком X. Фрёлихом (1935), Л. Д. Лан­дау и Е. М. Лифшицем (1936). При неравномерном освещении в ПП воз­никают градиент концентрации и, сле­довательно, диффузия неравновесных эл-нов и дырок от освещаемого уча­стка в сторону неосвещаемого. Т. к. коэфф. диффузии эл-нов и дырок раз­личны, то в образце появляется элект­рич. поле. Эдс Дембера (U), напр. в ПП n-типа при сильном освещении, равна:



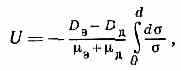
где D_э и D_д — коэфф. диффузии эл-нов и дырок, _э и _д — их подвижности, d — толщина образца, о — уд. элек­тропроводность.

Фотоэдс Д. э. мала и практич. при­менения не имеет.

• См. лит. при ст. Фотоэдс.

ДЕМОДУЛЯЦИЯ СВЕТА, то же, что детектирование света.

ДЕПОЛЯРИЗАЦИЯ СВЕТА, умень­шение степени поляризации света. Д. с. наблюдается при многих оптич. явлениях, напр. при рассеянии света в мутной среде или на матовой поверхности. При мол. рас­сеянии поляризов. света Д. с. зависит от анизотропии молекул в-ва. Д. с. поляризов. люминесценции р-ров про­исходит в результате вращения моле­кул за время жизни возбужденного состояния (вращательная Д. с.) или вследствие передачи энер­гии возбуждения от возбуждённых молекул к невозбуждённым (к о н ц е н т р а ц и о н н а я Д. с.). Д. с.— одно из проявлений магнитооптич. Ханле эффекта.

Искусств. уменьшение (подавление) степени поляризации как мешающего фактора при оптич. исследованиях также наз. Д. с. При этом световой пучок, как правило, не перестаёт быть поляризованным (получить естествен­ный свет из поляризованного практи­чески невозможно), но меняет состоя­ние поляризации во времени, по сече­нию пучка или по спектру т. о., что степень поляризации пучка значитель­но уменьшается.

• См. лит. при ст. Поляризация света.

ДЕСОРБЦИЯ (от лат. de — при­ставка, означающая удаление, и sorbeo — поглощаю), удаление адсорби­рованного в-ва с поверхности адсор­бента; процесс, обратный адсорбции. Происходит при уменьшении концентрации адсорбирующегося в-ва в среде, окружающей адсорбент, а также при повышении темп-ры. Скорость Д.

148


(кол-во молекул, покидающих поверх­ность адсорбента в секунду, отнесённое к её площади) зависит от темп-ры, дав­ления, а также природы и особенностей структуры адсорбирующей поверхно­сти. Д. применяется для извлечения из адсорбентов поглощённых ими га­зов или растворённых в-в, а также для исследования поверхностей.

ДЕТАЛЬНОГО РАВНОВЕСИЯ ПРИН­ЦИП, общее положение статисти­ческой физики, согласно к-рому лю­бой микропроцесс в равновесной си­стеме протекает с той же скоростью, что и обратный ему.

Когда система, состоящая из боль­шого числа ч-ц, находится в равно­весии, постоянными во времени ос­таются лишь физ. величины, относя­щиеся к системе в целом (т. н. термодинамич. величины). В то же время составляющие систему отд. микроча­стицы меняют своё состояние: в рав­новесной системе происходят столк­новения ч-ц, могут протекать хим. реакции и т. п. Чтобы равновесие системы сохранялось, наряду с лю­бым микропроцессом должен осуще­ствляться и обратный ему. Д. р. п. утверждает, что скорость любого мик­ропроцесса в состоянии равновесия совпадает со скоростью обратного ему процесса. Скорость при этом тракту­ется статистически: как среднее по большому числу одинаковых микро­процессов. В квант. теории Д. р. п. состоит в равенстве вероятностей пря­мого и обратного процессов. Этими процессами могут быть квантовые переходы, реакции между элем. ч-цами и т. п.

Д. р. п., связывая хар-ки прямого и обратного процессов, имеет важное прикладное значение. В нек-рых слу­чаях наблюдать один из этих процес­сов значительно легче, чем другой. Напр., легко измерить вероятность фотоионизации атома. Скорости этого процесса и обратного ему процесса рекомбинации легко выразить через соответствующие вероятности процес­сов. Таким образом, Д. р. п. позво­ляет вычислить вероятность рекомби­нации. Д. р. п. находит применение в физ. и хим. кинетике.

ДЕТЕКТИРОВАНИЕ (демодуляция) (от лат. detectio — открытие, обна­ружение), преобразование электрич. колебаний, в результате к-рого полу­чаются колебания более низкой ча­стоты (или пост. ток). В радиотехнике Д.— выделение НЧ модулирующего сигнала из модулиров. ВЧ колебаний (см. Модуляция колебаний). Д. приме­няется в радиоприёмном устройстве для получения колебаний звук. ча­стоты, сигналов изображений в теле­видении и т. д. В большинстве слу­чаев Д. осуществляют с помощью устройств с нелинейной проводимо­стью (диодов, электронных ламп, тран­зисторов и т. д.).

ДЕТЕКТИРОВАНИЕ СВЕТА (демо­дуляция света), преобразование моду­лиров. колебаний поля оптич. частоты

(10¹³—10¹⁵ Гц) с целью выявления за­кона модуляции интенсивности поля, его частоты или фазы (см. Модуляция света). Д. с. основано на нелинейной (чаще всего квадратичной) зависи­мости фототока приёмника (фотоэле­мента) от напряжённости Е электрич. поля световой волны. Вопрос о воз­можности Д. с. впервые возник в связи с исследованием дублетов в тонкой структуре ат. спектров. Любая модуляция (амплитудная, частот­ная, фазовая) световой волны ведёт к изменению спектр. состава первона­чально монохроматич. излучения. И



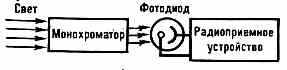
Рис. 1. Принципиальная схема устройства для детектирования света.


наоборот, наличие дублетов в спектре можно рассматривать как результат модуляции. Поэтому демодуляц. ана­лиз был применён для обнаружения дублетного расщепления. Схема соот­ветствующего устройства приведена на рис. 1 и является оптич. аналогом радиоприёмника. Монохроматор, вы­деляющий исследуемый дублет, играет роль резонансного контура, а фото­элемент — роль демодулятора.

Электрич. поле каждой линии дуб­лета может быть представлено в виде

E(t)=A(t)cos[t-(t)], (1)

где А (t) и (t) — ф-ции, изменяющие­ся со временем t медленно по сравне­нию с оптич. частотой  спектр. ли­нии. Результирующее поле дублета с частотами ₁ и ₂ на фотоэлементе имеет вид:



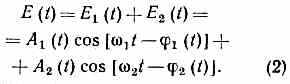
Ток фотоэлемента, усреднённый за время, малое по сравнению с периодом биений =1/(₁-₂), но большее по сравнению с периодом T=1/, изменяется по закону:



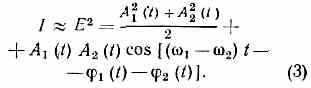
Если А, , ₁, и ₂ не зависят от времени, то спектры Е(t) и Е²(t) име­ют вид, изображённый на рис. 2. Спектр Е²(t) состоит из пост. состав­ляющей (0=0 и разностной частоты =|₁-₂|. Т. к. каждая линия дуб­лета имеет спектр, ширину , то реальные спектры Е(t) и E²(t) имеют вид, изображённый на рис. 3. Макси­мум в спектре E²(t) лежит вблизи раз­ностной частоты  и имеет ширину порядка ширины компонентов дуб­лета.

Для обнаружения дублетного рас­щепления посредством анализа спект­ра демодулиров. колебания необходим колебат. контур с добротностью Q=|₁-₂|/. При ~10⁹с^-1 даже

весьма плохой контур (с Q10) поз­воляет обнаружить дублетное расщеп­ление |₁-₂|=10¹⁰c^-1. В то же время для обнаружения такого дублетного расщепления обычными оптич. спектр. приборами необходимо, чтобы они

имели разрешение R=₁/10⁶ (₁10¹⁵ с^-1), что практически не дости­гается даже в лучших спектр. прибо­рах. Демодуляц. анализ имеет осо­бенно важное значение при анализе спектра излучения газовых лазеров, у к-рых значения  и |₁-₂| лежат в диапазоне 10⁴ с^-1 и |₁-₂|10⁶ с^-1.



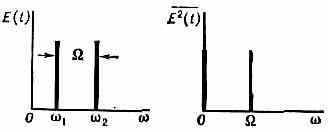
Рис. 2. Спектры Е(t) и Е²(t) в случае не за­висящих от времени A, , ₁ и ₂.



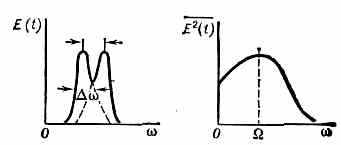
Рис. 3. Реальные спектры. Е (t) и E²(t) для дублета.


Высокая степень когерентности, на­правленности и монохроматичности лазерного излучения позволяет ис­пользовать также для демодуляц. ана­лиза т. н. супергетеродинный метод, где в кач-ве гетеродина применяется лазер. По гетеродинной схеме можно определить закон изменения частоты или фазы исследуемого излучения, что используется при т. н. доплеровском лоцировании объектов, позволяющем определять их скорости. В этом слу­чае принимаемым сигналом явл. из­лучение лазера, отражённое от дви­жущегося объекта. Частота этого из­лучения сдвинута относительно ча­стоты лазера-гетеродина на величину, пропорц. скорости объекта (Доплера эффект). Существ. развитие этот ме­тод получает при определении ско­рости сверхмедленно движущихся объ­ектов, напр. ледников или континен­тальных плит земной коры.

• Горелик Г. С. Колебания и волны, 2 изд., М., 1959; Белоусова И. М. [и др.], Исследование динамики движения ледников с помощью лазера, «Доклады АН СССР», 1971, т. 199, № 5.

О. Б. Данилов.

ДЕТЕКТОРЫ частиц, приборы и устройства для регистрации элем. ч-ц (протонов, нейтронов, эл-нов, мезо­нов и т. д.), ат. ядер (дейтронов, -частиц и др.), а также рентгеновских

149


л -квантов. Различают электрон­ные Д., вырабатывающие электрич. импульс, когда в объем Д. попадает ч-ца или квант. и трековые Д., позволяющие не только зарегистри­ровать факт и момент прохождения ч-цы, но и воспроизвести её траекто­рию (трек).

Важнейшие характеристики детек­торов: 1) эффективность — вероят­ность регистрации ч-цы при попадании её в рабочий объём Д.; 2) пространств. разрешение — точность, с к-рой Д. способен локализовать положение ч-цы в пр-ве; 3) временное разреше­ние (разрешающее время) — мин. интервал времени между прохожде­нием двух ч-ц через Д., когда они регистрируются порознь, т. е. сигналы Д. не накладываются друг на друга; 4) мёртвое время (время вос­становления) — время, за к-рое Д., зарегистрировавший одну ч-цу, успе­вает вернуться в исходное состояние и быть готовым для регистрации след. ч-цы.

характеристики различных детекторов



Частицы, прошедшие через Д. за это время, не регистрируются. Время нечувствительности явл. ме­рой инерционности Д. Оно ограничи­вает макс. интенсивность излучения, к-рое может регистрировать Д. (см. табл.).

Ионизационные детекторы состав­ляют наиб. обширную группу элект­ронных Д. Их действие основано на ионизации атомов и молекул, вызывае­мой регистрируемой ч-цей. Если ч-ца не имеет электрич. заряда (нейтроны, -кванты), то ионизацию могут вызы­вать вторичные заряж. ч-цы (протоны отдачи, эл-ны и позитроны). Один из первых Д., применявшихся англ. фи­зиком Э. Резерфордом,— ионизационная камера. Это — камера, заполненная газом с электродами, на к-рые подаётся напряжение. Заряж. ч-ца, проходя через камеру, ионизует газ; образующиеся ионы и эл-ны собира­ются на электродах, создавая в цепи

камеры ток. Ионизац. камеры приме­няются для регистрации как отд. ч-ц (импульс тока), так и для измерения их интегр. потоков. Т. к. время собира­ния на электрод эл-нов в 10³—10⁴ раз меньше, чем время собирания ионов, то при регистрации отд. ч-ц для получе­ния высокого временного разрешения используется, как правило, только электронный компонент сигнала. Вре­менное разрешение определяется по­движностью эл-нов и составляет 10^-6 с. Пространств. разрешение определя­ется геом. размерами камеры. Иони­зац. камеры применяются до сих пор, в частности в дозиметрии. Они про­сты, имеют высокую эффективность регистрации, позволяют оценивать энергию ч-цы (выходной сигнал пропорц. энергии, затраченной ч-цей на ионизацию) и т. п.; однако их вре­менное разрешение невелико и амп­литуда электрич. сигнала мала, что приводит к необходимости усиления сигнала и делает аппаратуру чувстви­тельной к помехам и шумам.




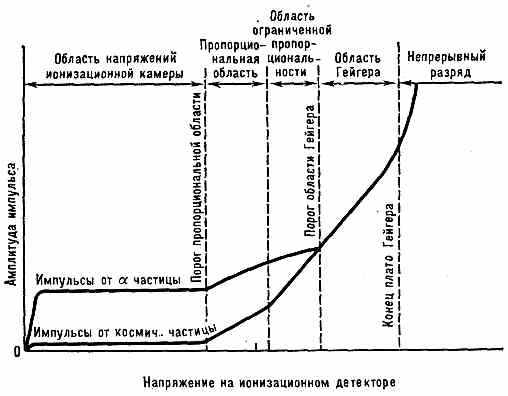
Рис. 1. Зависимость амплитуды импульсов, вырабатываемых иони­зац. детектором, от напряжения V на элект­родах в случае про­хождения через детек­тор быстрой косм. ч-цы, образующей 10—20 пар ионов, и -частицы, создающей 10⁵ пар ионов.


Недостатки ионизац. камеры в зна­чит. степени устранены в пропорцио­нальном счётчике, где эл-ны, образо­ванные заряж. ч-цей, двигаясь к ано­ду, приобретают энергию, достаточ­ную для вторичной ионизации. В ре­зультате на анод приходит электрон­ная лавина, амплитуда сигнала ве­лика и в ряде случаев (напр., при ре­гистрации ex-частиц) не требуется уси­ления. В пропорц. счётчике сигнал, так же как и в ионизац. камере, про­порц. энергии ч-цы, затраченной на ионизацию (рис. 1). Гл. недостатки: сильная зависимость амплитуды им­пульса от состава газовой смеси и приложенного напряжения и недо­статочно высокое временное разреше­ние (~10^-7 с). В связи с появлением ЭВМ пропорц. счётчики получили вто­рое рождение в виде пропорцио­нальных камер, к-рые пред­ставляют собой совокупность большего числа (~10³—10⁴) пропорц. счётчиков в одном объёме.

Если увеличивать напряжение на электродах пропорц. счётчика, то, начиная с нек-рого напряжения, все импульсы, какими бы ч-цами они ни были вызваны, становятся одинако­выми по величине и продолжают рас­ти с увеличением напряжения. Это т. н. область Гейгера, а Д. наз. счёт­чиками Гейгера (см. Гейгера счётчик). Счётчики Гейгера имеют высокую эф­фективность и большую амплитуду сигнала. Недостатки: невысокое вре­менное разрешение (10^-6 с), большое время восстановления (10^-4—10^-3 с), а также невозможность измерять энер­гию ч-цы.

Ионизац. Д. сыграли фундам. роль на раннем этапе развития яд. физики. Они применялись для регистрации

радиоакт. излучений от слабых естеств. радиоакт. источников (-, -частицы, -лучи, см. Радиоактивность) и космических лучей. С появлением уско­рителей, создающих интенсивные пуч­ки заряж. ч-ц (10⁶ —10⁷ частиц/с) высоких энергий, ионизац. Д. оказа­лись слишком медленными и были вытеснены сцинтилляционными счёт­чиками и черенковскими счётчиками. Появившись в экспериментах на уско­рителях, эти Д. оказались удобными и при исследовании космических лу­чей и др.

Сцинтилляционные детекторы состо­ят из сцинтиллятора, в к-ром заряж. ч-ца создаёт световую вспышку, и одно­го или нескольких ФЭУ, регистри­рующих эту вспышку. Высокое вре­менное разрешение сцинтилляц. счёт­чика ~10^-9 с; большая амплитуда сигнала на выходе ФЭУ и малое время восстановления ~10^-8 с обеспечили ему широкое применение. Пространств. разрешение определяется размерами сцинтиллятора. Существуют огром­ные сцинтилляц. Д., размер к-рых порядка неск. м³. Дальнейшее разви­тие этих Д. связано с разработкой более быстрых ФЭУ и сцинтилляторов (пластмасс) с более короткими вре­менами высвечивания.

150