Физ величина, характе­ризующая интенсивность нормальных (перпендикулярных к поверхности) сил, с к-рыми одно тело действует на поверхность другого (напр

Вид материала

Документы

Содержание Ландау диа­магнетизм). Диамагнетизм плазмы Диаскопическая проекция А. П. Гагарин. Рис. 1.растёт освещённость изображения. В фотогр. объективах для плавного изменения освещённости применяют т. н. ирисовую диафра Рис. 2.Д. поля зрения сильнее всего ограничивает лучи, идущие от уда­лённых от оси точек объекта АВ. Дигидрофосфат калия Н. В. Переломова. СГС системе единиц. Динамика разреженных га­зов Kn определяют как отношение длины свободного пробега l R1 м со скоростью v Рис. 2. Фотография обтекания сферы диам. 15 мм: а — в разреженном газе при числах Маха М=3,7 и Kn=2,5•10 Рис. 3. Изменение коэфф. лобового сопро­тивления сферы С Kn величины теплового потока q Аэродинамические из­мерения А. В. Иванов. Динамическая вязкость Динамический масс-спектро­метр Рис. 1.ДМ определяет электрич. поле Д. на большом расстоянии R ... Полное содержание

Подобный материал:

• Реферат По Физике, 58.66kb.
• Тема: определение реакций связей при действии на конструкцию произвольной плоской системы, 15.41kb.
• Головной мозг, 139.71kb.
• Работы режущего инструмента, основная нагрузка приходится на его рабочую поверхность,, 335.67kb.
• Головной мозг, с окружающими его оболочками находится в полости мозгового черепа, 437.52kb.
• Представьте себе некоторую поверхность и сидящего на ней муравья. Представили, 409.6kb.
• Лекция №8 Тема: «Продолжение», 81.36kb.
• Твует равновесию, установившемуся под действием силы тяжести, при условии, если, 669.51kb.
• Лабораторная работа метод естественного электрического поля (ЕП), 82.61kb.
• 1. Резьба Резьба поверхность, образованная при винтовом движении плоского контура, 223.58kb.

ДИАМАГНЕТИЗМ [от греч. dia -приставка, означающая здесь расхож­дение (силовых линий), и магнетизм], свойство в-ва намагничиваться на­встречу направлению действующего на него внеш. магн. поля. Д. свойствен всем в-вам. При внесении тела в магн. поле в электронной оболочке каждого его атома, в силу закона эл.-магн. индукции, возникают индуцирован­ные круговые токи, т. е. добавочное круговое движение эл-нов. Эти токи создают в каждом атоме индуцирован­ный магнитный момент, направлен­ный, согласно Ленца правилу, проти­воположно внеш. магн. полю (неза­висимо от того, имелся ли у атома собств. магн. момент или нет и как он был ориентирован).

Намагниченность, связанная с Д., обычно невелика; она значительно меньше, чем обусловленная ферро­магнетизмом, антиферромагнетизмом или электронным парамагнетизмом. У чисто диамагнитных в-в (диамагнетиков) электронные оболочки атомов (молекул) не обладают пост. магн. моментом. Магн. моменты эл-нов в таких атомах в отсутствии внеш. магн. поля взаимно скомпенсированы. В частности, это имеет место в атомах, ионах и молекулах с целиком запол­ненными электронными оболочками, напр. в атомах инертных газов, в мо­лекулах водорода, азота. Удлинён­ный образец диамагнетика в строго однородном магнитном поле ориенти­руется перпендикулярно к силовым линиям поля. Из неоднородного маг­нитного поля он выталкивается в на­правлении уменьшения напряжённости поля.

Индуцированный магн. момент М, приобретаемый единицей объёма диамагн. тела, пропорционален напря­жённости внеш. поля Н, т.е. М=Н. Коэфф.  наз. магнитной восприим­чивостью и имеет отрицат. знак (т. к. М и Н направлены навстречу друг другу). Обычно для диамагнетиков рассматривают восприимчивость 1 моля в-ва (молярную восприимчивость) , она мала (~10^-6).

В изолиров. атомах токи, создаю­щие Д., имеют простой хар-р. Вся со­вокупность эл-нов изолиров. атома приобретает под действием внеш. магн. поля Н синхронное вращат. движение вокруг оси, проходящей через центр атома параллельно направлению H. Это вращение эл-нов атома наз. Лармора прецессией. Вклад каждого эл-на

156


в диамагн. восприимчивость _e изоли­ров. атома равен:



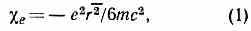
тде е — заряд эл-на, m — его масса покоя, с — скорость света в вакууме, r² — ср. квадрат расстояния эл-на от ядра атома. Из (1) видно, что наиболь­ший вклад в диамагн. восприимчи­вость  дают наиб. удалённые от ядра эл-ны. Если пренебречь влиянием близ­ких к ядру эл-нов, то r² можно рас­сматривать как значение ср. квадрата радиуса внеш. оболочки атома ². Т. о., зная, напр., диамагн. воспри­имчивость 1 моля в-ва и число n_e эл-нов в его внеш. оболочке, можно при помощи ур-ния (1) прибл. опре­делить размеры атомов и ионов:

=r²=0,598•10^-5 /n_e. (2) Так, для гелия ││=1,9•10^-6, n_е=2 и =0,58•10^-6, что близко к значе­ниям, найденным др. методами. Вы­ражение (1) позволяет теоретически рассчитать диамагн. восприимчивость совокупности изолиров. атомов (напр., одного моля в-ва), если известно число зл-нов в атомах и пространственное их распределение.

При темп-pax, недостаточных для возбуждения более высоких энергетич. уровней атомов, Д. практиче­ски постоянен (не зависит от темп-ры).

Если атомы не изолированы друг от друга и сильно взаимодействуют между собой, напр. в молекулах или кристаллах, то электронные оболочки в таких атомах деформируются и наблюдаемый Д. оказывается меньше, чем у изолиров. атомов.

Однако межат. связь не всегда проявляется только в уменьшении Д. В нек-рых случаях валентные эл-ны при образовании молекулы или кри­сталла приобретают возможность пе­ремещаться от одного атома к другому. Этой особенностью обладают, напр., молекулы ароматич. в-в, в к-рых име­ются замкнутые кольца из атомов (напр., бензольное кольцо). В этих молекулах под действием внеш. магн. поля возникают замкнутые электрич. токи по периферии колец. Поскольку магн. момент индуцированного коль­цевого тока направлен перпендикуляр­но плоскости кольца, то диамагн. восприимчивость ароматич. молекулы оказывается наибольшей, если внеш. поле направлено перпендикулярно к плоскости кольца, и наименьшей, если оно параллельно этой плоскости:



В металлах и ПП под воздействием внеш. магн. поля эл-ны проводимости начинают двигаться по спиральным

квантованным орбитам, что также вы­зывает небольшой Д. (см. Ландау диа­магнетизм). В нек-рых в-вах, где эти орбиты охватывают много атомов, диа­магнетизм Ландау особенно велик, напр, в висмуте и графите  достигает— (200—300) •10^-6. В графите, кристал­лизующемся в виде гексагональных призм, свободное движение эл-нов происходит гл. обр. в плоскостях, параллельных плоскости основания призмы. Поэтому диамагн. восприим­чивость графита оказывается очень большой (-260•10^-6) в направлении оси призмы и крайне малой (-6•10^-6) в направлениях, параллельных основанию призмы.

Во всех рассмотренных случаях диа­магн. восприимчивость не зависит от напряжённости поля. Однако при очень низких темп-pax в металлах и ПП наблюдается периодическое (осцилляционное) изменение восприимчиво­сти при плавном увеличении напря­жённости поля (см. Де Хааза — ван Альфена эффект).

Наибольшее по абс. величине зна­чение диамагн. восприимчивости име­ют сверхпроводники. Для них =- 1/(4), а магнитная индукция рав­на нулю, т. е. магн. поле не проникает в сверхпроводник. Д. сверхпроводни­ков обусловлен не внутриатомными, а макроскопическими поверхностными токами.

• Вонсовский С. В., Магнетизм, М., 1971; Дорфман Я. Г., Магнитные свой­ства и строение вещества, М., 1955, гл. 2; Киттель Ч., Введение в физику твер­дого тела, пер. с англ., М., 1978.

Я. Г. Дорфман.

ДИАМАГНЕТИЗМ ПЛАЗМЫ, свой­ство, характеризующее её магнитную восприимчивость, способность плазмы при помещении её в магн. поле намаг­ничиваться навстречу направлению внеш. поля (см. Диамагнетизм). Этот эффект обусловлен движением эл-нов и ионов плазмы по винтовым (ларморовским) траекториям, что эквива­лентно круговому току, создающему поле, противоположное внешнему, но меньшее по величине, так что в итоге поле внутри плазмы уменьшается. Если равновесная плазма удержива­ется стенками камеры, то появляются токи и Д. п. отсутствует; Д. п. прояв­ляется лишь при отсутствии стенок (в космосе) либо при магн. удержании плазмы. Следствием Д. п. явл. тен­денция к выталкиванию сгустков плазмы из области сильного магн. поля в области с более слабым магн. полем. Примерами этого можно счи­тать плазменный «солнечный ветер» (см. Космическая плазма) и т. н. гидромагн. плазменные неустойчивости в термояд. магнитных ловушках.

• См. лит. при ст. Плазма.

Б. А. Трубников.

ДИАМАГНЕТИК, вещество, намагни­чивающееся во внеш. магн. поле напря­жённостью Н в направлении, противо­положном направлению Н. В отсут­ствии внеш. магн. поля Д. немагни­тен. Под действием внеш. магн. поля каждый атом Д. приобретает магнитный момент (а каждый моль в-ва — суммарный момент М), пропорциональ­ный напряжённости поля Н и направ­ленный навстречу полю (см. Диамаг­нетизм). Поэтому магнитная вос­приимчивость Д. =M/H всегда отрицательна. По абс. величине к мала и слабо зависит как от напря­жённости магн. поля, так и от темп-ры.



К Д. относятся инертные газы, N₂, Н₂, Si, Р, Bi, Zn, Cu, Au, Ag, ряд др. элементов, а также многие органич. и неорганич. соединения (см. табл., где  — восприимчивость од­ного моля).

ДИАСКОПИЧЕСКАЯ ПРОЕКЦИЯ (от греч. dia — через, сквозь и skopeo — смотрю), разновидность оптич. проекции, при к-рой оптич. оси осве­тит. системы и объектива совпадают. В Д. п. изображение формируется светом, проходящим сквозь объект (если объект непрозрачен, получается теневое изображение), в отличие от э п и с к о п и ч е с к о й п р о е к ц и и, где изображение формируется светом, отражённым от объекта. Д. п. применяется в фотоувеличителях, диа- и кинопроекторах, микроскопах и пр. Яркость изображения при Д. п. может быть существенно выше, чем при эпископич. проекции при равных свето­силе оптич. системы и яркости источ­ника, т. к. потери света при Д. п. значительно меньше.

• М а р т и н Л., Техническая оптика, пер. с англ., М., 1960.

А. П. Гагарин.

ДИАФРАГМА (от греч. diaphragma — перегородка) в оптике, непрозрачная преграда, ограничивающая попереч­ное сечение световых пучков в оп­тич. системах (в телескопах, микро­скопах, фотоаппаратах и т. п.). Роль Д. часто играют оправы линз, призм, зеркал и др. оптич. деталей, зрачок глаза, границы освещённого предмета, в спектроскопах — щели. Размеры и положение Д. определяют освещён­ность и кач-во изображения, глубину резкости (глубину изображаемого про­странства) и разрешающую способ­ность оптической системы, поле зрения.

Д., наиболее сильно ограничиваю­щая световой пучок, падающий на оптич. систему, наз. апертурной, или действующей. Изобра­жением апертурной Д. Q₁Q₂ (рис. 1) в предшествующей ей части оптич. си­стемы L₁ (в пр-ве предметов) явл. входной зрачок Р₁Р₂ системы; изображение Д. в последующей части

157


системы L₂ — выходной зра­чок Р'₁P'₂. Входной зрачок Р₁Р₂ ограничивает угол раствора пучков лучей, идущих от точки О объекта АВ; выходной зрачок Р'₁Р'₂ играет ту же роль для лучей, идущих от точки О' изображения объекта А'В'. С уве­личением апертурной Д. (апертуры)



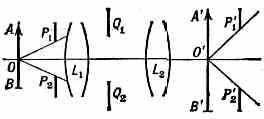
Рис. 1.


растёт освещённость изображения. В фотогр. объективах для плавного изменения освещённости применяют т. н. ирисовую диафрагму.

Уменьшение действующего отвер­стия оптич. системы (диафрагмирование) улучшает кач-во изображения, т. к. при этом из пучка лучей устра­няются краевые лучи, на ходе к-рых в наибольшей степени сказываются аберрации. Диафрагмирование уве­личивает также глубину резкости. С другой стороны, уменьшение дей­ствующего отверстия снижает из-за дифракции света на краях Д. разре­шающую способ­ность оптич. систе­мы. В связи с этим апертура оптич. си­стемы должна иметь оптимальное значение. Другие Д., имеющиеся в оптич. системе, гл. обр. препятствуют прохождению через систему лучей от точек объекта, расположенных в сто­роне от главной оси оптич. системы. Наиболее эфф. в этом отношении Д. наз. Д. п о л я з р е н и я. Она опре­деляет, какая часть пр-ва может быть изображена оптич. системой. Из цент­ра входного зрачка Р₁Р₂ Д. поля зре­ния L₁L₂ видна под наименьшим углом (рис. 2).



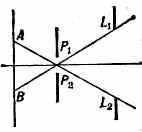
Рис. 2.


Д. поля зрения сильнее всего ограничивает лучи, идущие от уда­лённых от оси точек объекта АВ.

• см. лит. при ст. Окуляр.

ДИАФРАГМА в электронной и ион­ной оптике, отверстие в проводящей пластинке; применяется для ограни­чения поперечного сечения и измене­ния угла раствора (апертуры) пучка заряж. ч-ц. Круглая Д., имеющая электрич. потенциал и помещённая во внеш. электрич. поле, представляет собой простейшую осесимметричную электростатич. линзу (см. Электрон­ные линзы). Если напряжённости поля по разные стороны пластинки вдали от отверстия равны соотв. Е₁ и Е₂, то фокусное расстояние f такой линзы приближённо равно: f=4/(E₁-Е₂), где  — потенциал в центре Д. В за­висимости от знака f Д. играет роль собирающей или рассеивающей линзы.

Комбинации Д., имеющие разл. потенциалы, также явл. электроста­тич. линзами. См. также Электронная и ионная оптика.

ДИГИДРОФОСФАТ КАЛИЯ (KDP), синтетич. кристалл, КН₂РO₄, плотн. 2,38 г/см³ при 20°С, T_пл=252°С, мол. м. 136,09. Оптически прозрачен в об­ласти  от 0,25 до 1,7 мкм. Водораст­ворим и гигроскопичен. Сегнетоэлект­рик с точкой Кюри Т_C=-151°С; точечная группа симметрии выше точ­ки Кюри 4 2 m, ниже точки Кюри — mm2. Выражены пьезоэлектрич., электрооптич. и нелинейные оптич. св-ва, особенно вблизи Т_C. Кристаллы с за­мещением К на Rb или Cs и (или) Р на As химически изоморфны с KDP и имеют аналогичные симметричные и физ. св-ва. Исключение — CsH₂PO₄ (CDP). Это сегнетоэлектрик с точеч­ной симметрией 2/m и 2 (выше и ниже T_С=119°С). Кристаллы дигидрофосфата и дигидроарсената аммония (ADP и ADA) выше Т_C изоморфны с KDP, а ниже Т_C явл. антисегнетоэлектри­ками (точечная симметрия 222). У всех кристаллов группы KDP при за­мене Н на D наблюдается сильный сдвиг T_С в сторону высоких темп-р (T_С100°С). В микроскопич. теории фазовых переходов типа порядок — беспорядок кристаллы KDP и ADP рассматриваются как модельные. Кри­сталлы группы KDP (кроме CsPO₄) используются в электрооптике (для модуляции добротности лазеров, уп­равления световыми пучками и т. д.) и в нелинейной оптике (для параметрич. генерации света, умножения ча­стоты света и т. д.).

Н. В. Переломова.

ДИЛАТОМЕТР (от лат. dilato — рас­ширяю и греч. metreo — измеряю), прибор, измеряющий изменение раз­меров тела, вызванное воздействием темп-ры, давления, электрич. и магн. полей, ионизирующих излучений и



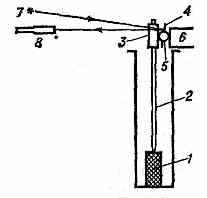
Схема оптико-механич. дилато­метра: 1 — исследуемый обра­зец; 2 — шток; 3 — зажим; 4 — зеркало, прикреплённое к валику 5; 6 — магнит, притя­гивающий зажим; 7 — источник света; 8 — зрит. труба. При изменении размеров образца зажим опуска­ется (или поднимается) и поворачивает ва­лик с зеркалом. По величине угла, на к-рый нужно переместить зрит. трубу, чтобы уви­деть световой луч, можно определить изме­нение размеров тела.


др. факторов. В оптико-механических Д. (чувствительность ~10^-6—10^-7 см) изменение размеров образца вызывает соответствующее смещение светового указателя (рис.). В ёмкостных Д. (чувствитель­ность ~10^-9 см) изменение размеров образца изменяет ёмкость конденса­тора, к-рый служит датчиком. В и н д у к ц и о н н ы х Д. (чувствитель­ность ~10^-9 см) при изменении размеров образца изменяется взаимное положение двух катушек индуктив­ности, а следовательно, их индук­тивность взаимная. В интерфе­ренционных Д. (чувствитель­ность ~10^-8 см) исследуемый обра­зец помещают между двумя оптич. пластинами и получают интерференц. картину при освещении их монохроматич. светом; об изменении размеров образца судят по смещению интерфе­ренц. полос. В радиорезонан­сных Д. (чувствительность до 10^-12 см) датчиком служит объёмный резонатор, стенки к-рого могут быть изготовлены из исследуемого материа­ла; об изменении размеров стенки ре­зонатора судят по изменению резонан­сной частоты. Изменение размеров образца может быть установлено с помощью методов рентгеновского стру­ктурного анализа по изменению пара­метров крист. решётки образца.

Конструкции Д. обычно предусмат­ривают возможность изменения внеш. воздействий на образец. Особое вни­мание уделяют учёту расширения (сжа­тия) окружающих образец тел (пере­дающих звеньев Д. и др.).

Для жидких и газообразных в-в рассматривается только объёмное расширение, к-рое устанавливается с помощью калиброванного капилляра, сообщающихся сосудов, определения объёма жидкости, вытекающей из цели­ком заполненного резервуара при наг­ревании.

ДИЛАТОМЕТРИЯ, раздел физики и измерит. техники, изучающий зави­симость изменения размеров тела от воздействий внеш. условий: темп-ры, давления, электрич. и магн. полей, ионизирующих излучений и т. д. В ос­новном Д. изучает тепловое расшире­ние тел и его разл. аномалии (при фазовых переходах и др.). Приборы, применяемые в Д., наз. дилатомет­рами.

ДИНА (от греч. dynamis — сила) (дин, dyn), единица силы в СГС системе единиц.

1 дин=1 г•см/с²=10^-5 Н=1,02•10^-6 кгс.

ДИНАМИКА (от греч. dynamis — сила), раздел механики, посвящённый изучению движения матер. тел под действием приложенных к ним сил. В основе Д. лежат Ньютона законы механики, из к-рых получаются все ур-ния и теоремы, необходимые для решения задач Д.

Согласно первому закону (закону инерции), матер. точка, на к-рую не действуют силы, находится в состоя­нии покоя или равномерного прямоли­нейного движения по отношению к инерциальной системе отсчёта; из­менить это состояние может только действие силы. Второй закон, являю­щийся осн. законом Д., устанавли­вает, что при действии силы матер. точка (или поступательно движущееся тело) с массой т получает ускорение w, определяемое равенством

mw=F. (1)

158


Третьим законом явл. закон о равен­стве действия и противодействия. Ког­да к телу приложено неск. сил, F в ур-нии (1) означает их равнодействую­щую. Этот результат следует из за­кона независимости действия сил, сог­ласно к-рому при действии на тело неск. сил каждая из них сообщает телу такое же ускорение, какое она сообщила бы, если бы действовала одна.

В Д. рассматриваются два типа за­дач, решения к-рых для матер. точки (или поступательно движущегося тела) находятся с помощью ур-ния (1). Задачи первого типа состоят в том, чтобы, зная движение тела, опреде­лить действующие на него силы. Классич. примером решения такой задачи явл. открытие Ньютоном закона все­мирного тяготения: зная установлен­ные И. Кеплером на основании обра­ботки результатов наблюдений законы движения планет (см. Кеплера зако­ны), Ньютон показал, что это движе­ние происходит под действием силы, обратно пропорц. квадрату расстоя­ния между планетой и Солнцем. В тех­нике такие задачи возникают при опре­делении сил, с к-рыми движущиеся тела действуют на связи, т. е. другие тела, ограничивающие их движение (см. Связи механические), напр. при определении сил давления колёс на рельсы, а также при нахождении внутр. усилий в разл. деталях машин и ме­ханизмов, когда законы движения этих машин (механизмов) известны.

Задачи второго типа явл. в Д. основ­ными и состоят в том, чтобы по дей­ствующим на тело силам определить закон его движения. Для решения этих задач необходимо знать т. н. нач. условия, т. е. положение и ско­рость тела в момент начала его дви­жения под действием заданных сил. Примеры таких задач: по величине и направлению скорости снаряда в мо­мент его вылета из канала ствола (нач. скорость) и действующим на снаряд при его движении силе тяжести и силе сопротивления воздуха найти закон движения снаряда, в частности его траекторию, горизонтальную даль­ность полёта, время движения до цели; по известным скорости автомо­биля в момент начала торможения и силе торможения найти время движе­ния и путь до остановки; по силе упругости рессор и весу кузова вагона определить закон его колебаний.

Задачи Д. для тв. тела (при его непоступат. движении) и разл. механич. систем решаются с помощью ур-ний, к-рые получаются как след­ствия второго закона Д., применяе­мого к отд. ч-цам системы или тела; при этом ещё учитывается равенство сил вз-ствия между этими ч-цами (третий закон Д.). В частности, таким путём для тв. тела, вращающегося во­круг неподвижной оси г, получается ур-ние:

I_z=M_z, (2)

где I_z — момент инерции тела относи­тельно оси вращения,  — угл. уско­рение тела, M_z — вращающий мо­мент, равный сумме моментов дейст­вующих сил относительно оси враще­ния. Если известен закон вращения, то ур-ние (2) позволяет найти вращаю­щий момент (задача первого типа); если же известны вращающий момент и нач. условия, т. е. нач. положение тела и нач. угл. скорость, то из ур-ния (2) можно найти закон вращения (за­дача второго типа).

При изучении движения механич. систем часто применяют т. н. общие теоремы Д., к-рые также могут быть получены как следствия второго и третьего законов Д. К ним относятся теоремы о движении центра масс (или центра инерции) и об изменении коли­чества движения, момента количеств движения и кинетич. энергии системы. Иной путь решения задач Д. связан с использованием вместо второго за­кона Д. принципов механики (см. Д'Аламбера принцип, Д'Аламбера — Лагранжа принцип, Вариационные принципы механики) и получаемых с их помощью ур-ний движения, в ча­стности Лагранжа уравнений механи­ки.

Ур-ние (1) и все следствия из него справедливы только при изучении движения по отношению к т. н. инерц. системе отсчёта, к-рой для движения внутри Солн. системы с высокой сте­пенью точности явл. звёздная система (система отсчёта с началом в центре Солнца и осями, направленными на удалённые звёзды), а при решении большинства инженерных задач — система отсчёта, связанная с Землёй. При изучении движения по отношению к неинерц. системам отсчёта, т. е. системам, связанным с ускоренно дви­жущимися или вращающимися тела­ми, ур-ние движения можно также составлять в виде (1), если к силе F прибавить т. н. переносную и Кориолиса силы инерции (см. Относитель­ное движение). Такие задачи возни­кают при изучении влияния вращения Земли на движение тел по отношению к земной поверхности, а также при изучении движения разл. приборов и устройств, установленных на дви­жущихся объектах (судах, самолётах, ракетах и др.).

Помимо общих методов изучения движения тел под действием сил, в Д. рассматриваются спец. задачи: тео­рия гироскопа, теория механич. коле­баний, теория устойчивости движе­ния, теория удара, механика тел переменной массы и др. С помощью законов Д. изучается также движение сплошной среды, в частности упруго и пластически деформируемых тв. тел, жидкостей и газов (см. Упругости тео­рия, Пластичности теория, Гидро­аэромеханика, Газовая динамика). На­конец, в результате применения методов Д. к изучению движения кон­кретных объектов возник ряд спец. дисциплин: небесная механика, внеш.

баллистика, Д. автомобиля, самолёта, динамика ракет и т. п.

• См. лит. при ст. Механика.

С. М. Тарг.

ДИНАМИКА РАЗРЕЖЕННЫХ ГА­ЗОВ, раздел газовой динамики, в к-ром при изучении течения газа низкой плотности учитывается его дискретная мол. структура. Методы Д. р. г., основанные на молекулярно-кинетич. теории газов, применяются для определения теплового и силового воздействия газа на поверхности летат. аппаратов, движущихся на боль­ших высотах, а также при расчёте движения газов в вакуумных систе­мах, истечения струй в пр-во с низким давлением и в задачах мол. физики.

Критерием, характеризующим сте­пень разреженности движущегося га­за, явл. число Кнудсена K_nl/L, где l — ср. длина свободного пробега молекул в газе, L — характерный раз­мер течения. Предположение о сплош­ности среды, лежащее в основе теор. методов гидроаэромеханики и газовой динамики, строго выполняется лишь в предельном случае K_n0, а прак­тически оно оказывается справедли­вым уже при K_n<10^-3.

В другом предельном случае K_n существенную роль играют толь­ко столкновения молекул газа с обте­каемыми телами, а роль межмол. столкновений незначительна. Поэтому набегающий на поверхность тела по­ток молекул и поток молекул, отра­жённый от поверхности, рассматри­ваются как невзаимодействующие. При этом из ур-ний движения молекул можно определить баланс между при­носимыми к поверхности и уносимыми от неё потоками массы, импульса и энергии, если известен механизм вз-ствия молекул газа с поверхностью. Такая схема позволяет с достаточной для практики точностью рассчитать аэродинамич. хар-ки разл. тел уже при K_n>1. Режим течения, для к-рого справедливы указанные пред­положения, наз. с в о б о д н о м о л е к у л я р н ы м. Одной из при­ближённых схем описания вз-ствия молекул газа с тв. поверхностью при свободномол. течении является т. н. зеркально-диффузная схема, согласно к-рой часть молекул отражается диффузно в соответствии с законом коси­нуса (Ламберта законом), а осталь­ные молекулы — зеркально, т. е. по закону — угол падения равен углу отражения. Отношение кол-ва диффузно рассеянных молекул к общему их числу определяет степень диффузности f рассеяния (при f=0 происходит только зеркальное отражение, при f=1 — только диффузное). Обмен энер­гией при вз-ствии молекул с тв. поверхностью характеризуют коэфф. аккомодации а, определяющим изме­нение энергии молекулы после её отражения от поверхности. Значения а меняются от 0 до 1. Если после

159


отражения энергия молекулы не из­менилась, то =0, если же ср. энер­гия отражённых молекул, характе­ризующая темп-ру газа, соответствует темп-ре стенки, то =1. В общем случае коэффициенты f и  зависят от скорости столкновения молекул с поверхностью, от материала и темп-ры этой поверхности, от степени её глад­кости, наличия на ней адсорбиров. молекул газа и т. д. Переход от течения сплошной среды (K_n0) к свободномол. течению (K_n), напр. при увеличении высоты полёта, осуществляется через ряд промежу­точных режимов течения разреженного газа. Каждому из них соответствует определ. диапазон конечных значений числа K_n. В переходном режиме ока­зывается важным как учёт межмол. столкновений, так и столкновений молекул газа с поверхностью обтека­емого тела. Для этого режима течения характерно проявление ряда сложных неравновесных мол. процессов, стро­гое теор. описание к-рых в промежу­точной области чисел K_n представляет огромные матем. трудности, свя­занные с решением интегродифф. ур-ния Больцмана для изменения во времени и в пр-ве ф-ции распреде­ления молекул по скоростям (см. Кинетическая теория газов). Поэтому широко применяются приближённые теор. методы, позволяющие распро­странить теор. модели свободномол. течения и течения сплошной среды на режимы, соответствующие проме­жуточной области значения чисел K_n, близких к предельным. Так, разра­ботаны приближённые методы рас­чёта аэродинамич. хар-к тел в случае, когда учитываются лишь однократ­ные столкновения падающих на по­верхность и отражённых от неё мо­лекул (режим, примыкающий к сво­бодномол. течению). Ур-ния газовой динамики сплошной среды применяют и при K_n>10^-3, но с новыми гра­ничными условиями, учитывающими характерные для течения разреженного газа условия «скольжения» и «скачка темп-ры». Первое условие состоит в том, что параллельная стенке состав­ляющая скорости газа на самой стенке отличается от нуля, а второе учиты­вает отличие темп-ры газа вблизи стенки от темп-ры стенки. Различные, постепенно сменяющие друг друга режимы течения — от свободномол. до континуального — наблюдаются в классич. задаче Д. р. г. об обтекании газом плоской полубесконечной пла­стинки (рис. 1).

При рассмотрении сверхзвук. об­текания затупленных тел в режимах, примыкающих к течению сплошной среды, число Kn определяют как отношение длины свободного пробега l_s молекул в сжатом слое газа за ото­шедшей от тела ударной волной к характерному размеру тела. В случае

полёта сферич. тела радиусом R1 м со скоростью v10 км/с и посте­пенном увеличении высоты полёта (уменьшении числа Kn=l_s/R) можно выделить след. режимы, а) При Kn<0,5•10^-3 (что соответствует выcoтaм~70 км) течение явл. конти­нуальным. Ударная волна толщиной порядка неск. l_s и вязкий пограничный слой на поверхности сферы разделены областью, где вязкость газа несущест­венна.




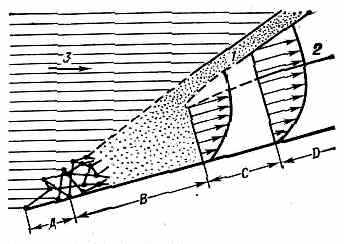
Рис. 1. Схема развития течения газа около плоской полубесконечной тонкой пласти­ны, обтекаемой сверхзвук. потоком под углом атаки: А — область свободномол. течения с однократными столкновениями; В — область с многократными столкнове­ниями; С — область течения со скольжением; D — континуум; 1 — ударная волна; 2 — граница пограничного слоя; 3 — макроскопич. движение потока молекул (масштабы зон и областей не соблюдены).


б) При Kn0,5•10^-2 (уве­личение высот до 85 км) отошедшая ударная волна и пограничный слой на теле утолщаются, а затем смыка­ются. Перед сферой образуется сплош­ная область (рис. 2, а). Уменьшение числа столкновений между молеку­лами в сжатом слое приводит к запаз­дыванию в установлении равновесия



Рис. 2. Фотография обтекания сферы диам. 15 мм: а — в разреженном газе при числах Маха М=3,7 и Kn=2,5•10^-2; б — в сплош­ной среде.


по колебат. степеням свободы молекул. Граничные условия на поверхности сферы соответствуют скольжению мо­лекул и скачку темп-ры. Течение разреженного газа, соответствующее диапазону 0,5•10^-3<Kn< 0,5•10^-2, иногда наз. течением со сколь­жением, в) При Kn ~ 0,1 (вы­сота 105 км), когда l_s становится сравнимой с поперечным размером сжатого слоя, в окрестности передней критич. точки сферы не успевает уста­новиться равновесие по вращат. и поступат. степеням свободы молекул.

Отошедшая ударная волна не форми­руется. г) При дальнейшем увели­чении числа Kn механизм обтекания целиком определяется дискр. струк­турой среды. Время пребывания каж­дой молекулы вблизи тела характе­ризуется всего неск. столкновениями. Дальнейшее уменьшение плотности газа приводит к свободномол. течению, граница к-рого в данном слу­чае соответствует высоте 200 км.



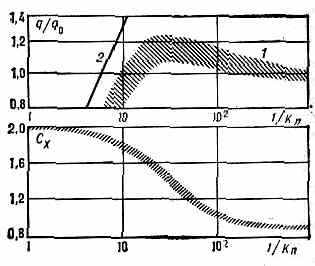
Рис. 3. Изменение коэфф. лобового сопро­тивления сферы С_х и относительного теплово­го потока q/q₀ в передней критич. точке сфе­ры в промежуточной области чисел Kn: q₀ — тепловой поток, рассчитанный по тео­рии пограничного слоя (Kn0); 1 — экспе­римент для сильного охлаждения сферы при М>5; 2 — расчёт для сильно охлаждённой сферы при Kn, =1.


В рассмотренном диапазоне чисел Kn величины теплового потока q и коэфф. сопротивления С_х изменя­ются от значений, соответствующих течению сплошной среды, до значе­ний, соответствующих свободномол. режиму, как это показано на рис. 3. С помощью методов Д. р. г. рассмат­риваются также задачи исследования хар-к течения в отверстиях, вакуум­ных трубопроводах и каналах. Важ­ным для техн. приложений явл. изу­чение законов уменьшения пропуск­ной способности каналов разл. форм и размеров при увеличении числа Kn. Исследуются эффекты разреженности при течении газов в соплах и струях двигателей, работающих на больших высотах.

Ввиду чрезвычайных матем. трудностей теор. методов исследования Д. р. г., важное значение имеет экс­перимент (см. Аэродинамические из­мерения). Эксперим. исследования те­чений разреженного газа проводятся на спец. вакуумных аэродинамических трубах, оборудованных мощными си­стемами откачки, включающими форвакуумные, пароструйные и криоген­ные насосы. Применяемые на этих установках методы обладают рядом специфич. особенностей по сравнению с методами, используемыми в обычных аэродинамич. установках. Малые плот­ности газа, низкие по абс. величинам, тепловые потоки и аэродинамич. силы требуют применения высокочувствит. датчиков и приборов, а также прин­ципиально новых физ. методов диаг­ностики. Так, широко используется

160


электронно-пучковая диагностика, ос­нованная на регистрации интенсив­ности видимого, УФ и рентг. излу­чения молекул газа, возбуждаемых пучком быстрых (10—30 кэВ) эл-нов. Этот метод позволяет проводить ви­зуализацию течения, а также изме­рять локальные величины плотности, темп-ры, скорости потока, а также концентрации компонентов разрежен­ной смеси газов.

• К о г а н М. Н., Динамика разреженного газа, М., 1967; Паттерсон Г. Н., Мо­лекулярное течение газов, пер. с англ., М., 1960; Кошмаров Ю. А., Ры­жов Ю. А., Прикладная динамика разре­женного газа, М., 1977; Экспериментальные методы в динамике разреженных газов, под ред. С. С. Кутателадзе, Новосиб., 1974; Кошмаров ,Ю. А., Рыжов Ю. А., Свирщевский С. Б., Эксперимен­тальные методы в механике разреженного газа, М., 1981; Б е р д Г., Молекулярная газовая динамика, пер. с англ., М., 1981.

А. В. Иванов.

ДИНАМИКА РАКЕТ (ракетодинамика), наука о движении летат. аппа­ратов, снабжённых реактивными дви­гателями. Наиболее важная особен­ность полёта ракеты с работающим (развивающим тягу) двигателем — су­щественное изменение её массы во время движения вследствие сгорания топлива. Так, одноступенчатые ра­кеты в процессе набора скорости теряют до 90% первоначальной (стар­товой) массы. Законы движения ра­кеты при работающем двигателе изу­чаются в механике тел переменной массы.

Труды И. В. Мещерского и К. Э. Ци­олковского в кон. 19 — нач. 20 вв. заложили теор. основу Д. р. Быстрое развитие Д. р. началось после окон­чания 2-й мировой войны в связи с ростом ракетостроения в ряде промышленно развитых стран (СССР, США, Великобритания и др.).

Важнейшие разделы Д. р.: 1) изу­чение движения центра масс (центра тяжести) ракет, т. е. создание тео­рии, посвящённой решению траекторных задач,— определение скорости на разл. высотах, перегрузок, обус­ловленных реактивной силой, даль­ности и продолжительности полёта, условий мягкой посадки на планеты и др.; 2) изучение движения ракет относительно центра масс — иссле­дование стабилизации ракет, возмож­ности маневрирования и управления ими, наведения их на заданную цель, стыковки летат. аппаратов с ракет­ными двигателями при движении в косм. пр-ве; 3) эксперим. Д. р., где изучаются методы исследования дви­жения ракет с использованием оптич. и радиотехн. приборов для определе­ния геом., кинематич. и динамич. хар-к полёта. Особенно важны ис­следования натурных объектов в реальном полёте, осуществляемые с помощью телеметрии, позволяющей записывать до 500 параметров, харак­теризующих поведение объекта.

К задачам Д. р. относится также программирование величины и на­правления реактивной силы для

получения при имеющемся кол-ве топ­лива (горючего и окислителя) наилуч­ших лётных хар-к, обеспечивающих достижение цели полёта (напр., макс. дальности полёта, мин. времени по­лёта до цели, макс. кинетич. энергии в конце работы двигателя). Такие задачи решаются методами вариацион­ного исчисления и способствуют раз­витию самих этих методов. В связи с созданием очень больших ракет на жидком топливе успешно разви­ваются новые разделы Д. р., в к-рых изучается движение корпуса ракеты с учётом колебаний жидкого топлива в её баках, а также исследуется движение ракеты как упругого тела. При решении таких (многопарамет­рических) задач применяют ЭВМ.

Для динамики управляемых ракет (напр., зенитных управляемых ракет, ракет противоракетной обороны) нек-рые из внеш. воздействий имеют вероятностный хар-р и количественно определяются «случайными» функция­ми времени. Решение таких задач требует использования теории веро­ятностных процессов. В связи с про­блемой обеспечения надёжности по­лёта возникли задачи оптимизации программ управления объектом, обес­печивающих заданную вероятность безотказной работы системы.

• Гродзовский Г. Л., Ива­нов Ю. Н., Токарев В. В., Механика космического полета. Проблемы оптимизации, М., 1975; Ильин В. А., К у з м а к Г. Е., Оптимальные перелеты космических аппа­ратов с двигателями большой тяги, М., 1976; Кротов В. Ф., Букреев В. 3., Гурман В. И., Новые методы вариаци­онного исчисления в динамике полета, М., 1969; М и е л е А., Механика полета, пер. с англ., т. 1, М., 1965; Справочное руковод­ство по небесной механике и астродинамике, под ред. Г. Н. Дубошина, 2 изд., М., 1976; Циолковский К. Э., Реактивные ле­тательные аппараты, М., 1964. См. также лит. при ст. Механика тел переменной массы.

ДИНАМИТРОН, разновидность кас­кадного генератора.

ДИНАМИЧЕСКАЯ ВЯЗКОСТЬ, см. Вязкость.

ДИНАМИЧЕСКАЯ ПОЛЯРИЗАЦИЯ ЯДЕР, совокупность методов ориента­ции яд. спинов в-ва в заданном на­правлении под действием ВЧ эл.-магн. полей (см. Ориентированные ядра).

• Ацаркин В. А., Динамическая поля­ризация ядер в твердых диэлектриках, «УФН», 1978, т. 126, в. 1. См. также лит. при ст. Ориентированные ядра.

ДИНАМИЧЕСКИЙ МАСС-СПЕКТРО­МЕТР, см. в ст. Масс-спектрометр.

ДИНАМО-ЭФФЕКТ (гидромагнитное динамо), самовозбуждение магн. по­лей вследствие движения проводящей жидкости или газовой плазмы. Д.-э. привлекают для объяснения проис­хождения и поддержания магн. полей Земли и др. планет с жидким ядром, Солнца и звёзд. Если магн. поле косм. тела содержит в кач-ве составляющих п о л о и д а л ь н о е поле (с силовыми линиями, направ­ленными по меридианам, как у ди­поля) и т о р о и д а л ь н о е поле (с линиями поля, направленными по параллелям), то при дифф. вращении

тела (когда его слои на разных глу­бинах имеют различные угл. скорости вращения) силовая линия полоидального поля, проходящая через разные слои, закручивается — одни её части уходят вперёд по сравнению с дру­гими. В результате тороидальное поле усиливается. Рост его энергии происходит за счёт энергии враще­ния слоев тела, поэтому с возрастанием тороидального поля относи­тельное вращение слоев должно тор­мозиться, если оно не поддерживается чем-либо другим. Усиление тороидального поля может привести к усилению полоидального или пре­пятствовать его затуханию, если меж­ду ними имеется обратная связь. Такую связь может обусловить, напр., тепловая конвекция, причём конвективные движения не должны быть осесимметричными (в осесимметрич. системе Д.-э. невозможен). Для Земли последнее условие выполняется (ось. вращения Земли и её магн. ось не совпадают). Д.-э. для Земли связы­вают с конвективным движением про­водящего в-ва её жидкого ядра и с всплытием в этой среде более лёгких примесей под действием архимедовой силы. Конвективные движения при­поднимают силовые линии тороидаль­ного поля и при определ. условиях они могут образовывать петли, к-рые потом сливаются с полоидальным по­лем и усиливают его. Теория Д.-э. приводит также к возможности са­мообращения магн. оси (переполюсовке магн. поля Земли) и долгопериодич. колебаниям геомагн. поля (вековым вариациям), что отражает реальные св-ва земного магн. поля. Магн. поля Солнца и звёзд в целом, а также их локальные поля, напр. поля пятен и активных областей, также могут быть в принципе объяс­нены Д.-э.

• П и к е л ь н е р С. Б., Основы косми­ческой электродинамики, М., 1961; О р а е в с к и й В. Н., Плазма на Земле и в космосе, К., 1980; Гудзенко Л. И., В поисках природы солнечных пятен, М., 1972 (Новое в жизни, науке, технике. Сер. «Физика»).

ДИОПТРИКА (греч. dioptrika, от dia — через, сквозь и opteuo — вижу), традиционное (постепенно выходящее из употребления) назв. раздела геометрической оптики, в к-ром рас­сматривается преломление света при прохождении его через отд. прелом­ляющие поверхности и системы таких поверхностей. Термин «Д.» часто при­меняется по отношению к глазу: Д. глаза — описание св-в глаза как оп­тич. прибора.

ДИОПТРИЯ (дп, D), единица оптич, силы линз и др. осесимметричных оптич. систем; 1 дп равна оптич. силе линзы или сферич. зеркала с, фокусным расстоянием 1 м.

ДИПОЛЬ (от греч. di — приставка, означающая дважды, двойной, и po­los — полюс) электрический, совокуп-

161


ность двух равных по абс. величине разноимённых точечных зарядов (+е, -е), находящихся на нек-ром рас­стоянии l друг от друга. Осн. хар-кой электрич. Д. явл. его дипольный момент (ДМ) — вектор р, численно равный произведению l на е:p=el; принято считать, что вектор р на­правлен от отрицат. заряда (-е) к положительному (+е; рис. 1).



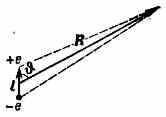
Рис. 1.


ДМ определяет электрич. поле Д. на большом расстоянии R от Д. (R>>l), а также воздействие на Д. внеш. электрич. поля.

Вдали от Д. напряжённость его электрич. поля Е убывает с расстоя­нием как 1/R³, т. е. быстрее, чем поле точечного заряда (~-1/R²). Компо­ненты напряжённости поля Е вдоль оси Д. (E_р) и в перпендикулярном направлении (Е_┴) пропорциональны р и в Гаусса системе единиц равны:



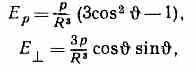
где О — угол между р и радиусом-вектором R точки пр-ва, в к-рой из-



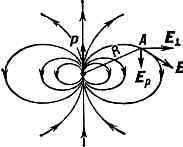
Рис. 2. Электрич. поле диполя: E — напряжённость по­ля в точке А, на­ходящейся на рас­стоянии R от цент­ра диполя; E_p и E_┴ — параллельная и перпендикуляр­ная оси диполя компоненты поля Е.


меряется поле Д.; полная напряжённость Е=(Е²_р+E²_┴). Т. о., на оси Д., т. е. при =0, Е_р вдвое больше, чем при =90° (Е_┴=0 в обоих случаях); направление Е_р в первом случае параллельно р, во втором — антипа­раллельно (рис. 2).

Действие внеш. электрич. поля на Д. также пропорц. р. Однородное внеш. электрич. поле Е создаёт вра­щающий момент M=pEsin ( — угол между Е и р; рис. 3), стремя­щийся повернуть Д. так, чтобы его ДМ был направлен по полю. В не­однородном электрич. поле на Д., кроме вращающего момента, дейст­вует также сила, стремящаяся втянуть Д. в область более сильного поля (рис. 4).

Электрич. поле любой в целом нейтр. системы на расстояниях, значительно больших её размеров, приближённо совпадает с полем эквивалентного Д.—

электрич. полем Д. с таким же ДМ, как и у системы зарядов. Поэтому во мн. случаях электрич. Д. явл. хо­рошим приближением для описания таких систем на расстояниях, зна­чительно превышающих размеры си­стемы (см. Излучение). Напр., по­лярные молекулы можно приближён­но рассматривать как электрич. Д.



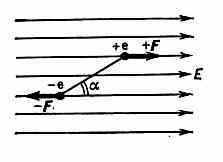
Рис. 3. Электрич. диполь в однородном внеш. электрич. поле Е. Пара сил -F и +F стремится повернуть диполь в направлении поля.




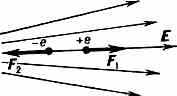
Рис. 4. Электрич. диполь в неодно­родном электрич. поле в случае, ког­да ДМ р направ­лен по полю. Сила F₂ больше силы F₁ ре­зультирующая сила F=f₂-F₁ стремится переместить диполь в область большей на­пряжённости внеш. поля.




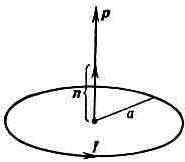
Рис. 5. Магн. мо­мент р кругового тока I радиуса а.


Атомы, неполярные молекулы и ионы в электрич. поле приобретают ДМ, т. к. составляющие их заряж. ч-цы несколько смещаются под действием внеш. поля (см. Поляризу­емость).

Электрич. Д. с изменяющимся во времени ДМ (вследствие изменения его длины или зарядов) явл. источником эл.-магн. излучения.

Д. магнитный. Исследование вз-ствий полюсов пост. магнитов (франц. физик Ш. Кулон, 1785) при­вело к представлению о существо­вании магн. зарядов. Пара таких зарядов, равных по величине и про­тивоположных по знаку, рассматри­валась как магн. Д., обладающий магн. ДМ. Позднее было установлено, что магн. зарядов не существует, а магн. поля создаются движущимися электрич. зарядами. Однако понятие «магн. ДМ» оказалось целесообразным сохранить, поскольку на больших расстояниях от замкнутых провод­ников с током магн. поля оказались такими же, как если бы их порождали магн. Д. Поле магн. Д. на больших расстояниях от Д. рассчитывается по тем же ф-лам, что и поле электрич. Д., причём с заменой электрич. ДМ на магн. момент тока. Магн. момент системы токов определяется силой и распределением токов. В простейшем случае тока I, текущего по круговому контуру (витку) радиуса а, магн. момент в системе Гаусса равен: р= ISn/c, где S=na² — площадь витка, а n — единичный вектор, перпендику­лярный плоскости витка и направлен­ный так, что с его конца ток виден

текущим против часовой стрелки (рис. 5).

Аналогию между магн. Д. и витком с током можно проследить при рас­смотрении действия магн. поля на ток. В однородном магн. поле на виток с током действует момент сил, стремящийся ориентировать виток так, чтобы его магн. момент был направлен

по полю; в неоднородном магн. поле такие замкнутые токи («магн. Д.») втягиваются в область с большей на­пряжённостью поля. На вз-ствии не­однородного магн. поля с магн. Д. основано, напр., разделение ч-ц с разл. магн. моментами — ат. ядер, атомов, молекул. Пучок ч-ц, проходя через неоднородное магн. поле, раз­деляется, т. к. поле сильнее изменяет траектории ч-ц с большим магн. мо­ментом.

Вблизи от витка с током аналогия его с магн. Д. (теорема эквивалент­ности) несправедлива. Так, напр., в центре кругового витка напряжён­ность магн. поля не только не равна



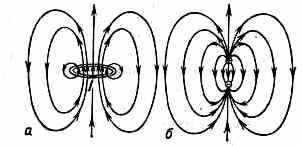
Рис. 6. Магн. поле вблизи кругового тока I (а) и магн. поля (б); на больших расстоя­ниях поля одинаковы.


напряжённости поля эквивалентного Д., но даже противоположна ей по направлению (рис. 6).

• Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, пер. с англ., в. 5 — Электричество и магнетизм, М., 1966; Калашников С. Г., Элект­ричество, М., 1958 (Общий курс физики, т. 2); Тамм И. Е., Основы теории электричест­ва, 9 изд., М., 1976.

ДИПОЛЬНОЕ ИЗЛУЧЕНИЕ, излу­чение эл.-магн. волн, обусловленное изменением во времени электрич. дипольного момента излучающей си­стемы. См. Излучение.

ДИПОЛЬНЫЙ МОМЕНТ электриче­ский, величина, характеризующая электрич. св-ва системы заряж. ч-ц. Д. м. р электронейтральной системы, состоящей из n заряж. ч-ц, равен:

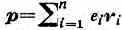,где e_i—заряд i-той ч-цы, r_i; — её радиус-вектор. Д. м. не за­висит от выбора начала координат и определяется взаимным расположе­нием и величинами зарядов в системе. Система из двух одинаковых по ве-

162


личине зарядов (-е, +е) образует электрич. диполь с Д. м. p=el, где l — расстояние между зарядами, к-рому приписывается направление от отрицат. заряда к положительному. Электрич. Д. м. определяет (в первом приближении) электрич. поле нейтр. системы на больших по сравнению с её размерами расстояниях и действие на неё внеш. полей. При изменении Д. м. такая система излучает эл.-магн. волны (дипольное излучение). В случае произвольной системы за­рядов её электрич. поле может опреде­ляться мультиполями разл. порядков. О магнитном Д. м. см. Диполь, Маг­нитный момент.

ДИРАКА МОНОПОЛЬ, то же, что магнитный монополь.

ДИРАКА УРАВНЕНИЕ, релятиви­стское дифф. ур-ние для волн. ф-ции свободной (невзаимодействующей) ч-цы со спином ¹/₂ (эл-н, мюон, кварки и др.), описывающее изменение её со­стояния со временем. Получено англ. физиком П. Дираком (P. Dirac). в 1928 на основе требований реляти­вистской инвариантности, линейно­сти (выражающей справедливость су­перпозиции принципа), первого по­рядка по времени (чтобы состояние в данный момент определяло состояния во все последующие моменты времени). Для ч-цы со спином ¹/₂ этим требо­ваниям удовлетворяет только система четырёх ур-ний, т. е. волн. ф-ция  должна состоять из четырёх компо­нент: ₁, ₂, ₃, ₄. При поворотах системы координат и преобразованиях Лоренца они преобразуются как пара

спинорных полей 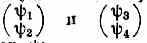, образующих биспинор :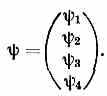



Д. у. имеет вид системы четырёх ур-ний:



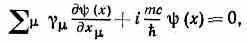
где =0, 1, 2, 3; х₁=х, х₂=у, x₃=z — пространств. координаты, x₀=ct — временная (t — время); m — масса ч-цы; _ — матрицы Дирака, к-рые выражаются через двухрядные мат­рицы Паули ₁, ₂, ₃ и единичную матрицу I:



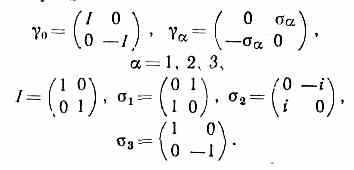
Для свободной ч-цы Д. у. приводит к релятив. соотношению между им­пульсом (р), энергией (ξ) и массой ч-цы:

ξ² = m²c⁴+p²c², или ξ=±(m²c⁴+p²c²);

для покоящейся ч-цы это соответст­вует ξ=±mc² (энергия покоя ч-цы). Интервал энергий - mc²<ξ2 явл. «запрещённым». В квант. теории поля (КТП) состояние ч-цы с отрицат. энергией интерпретируется как со­стояние античастицы, обладающей положит. энергией, но противополож­ным электрич. зарядом. Т. о., четыре независимых решения Д. у. описывают как состояние ч-цы со спином ¹/₂, так и состояние её античастицы, каж­дое с двумя возможными проекциями спина на направление импульса (+¹/₂ и -¹/₂). Эксперим. обнаружение по­зитрона (антиэлектрона), предска­занного Дираком, явилось триумфом

Д. у.

Д. у. взаимодействующих ч-ц со­держит дополнит. слагаемое, учиты­вающее это вз-ствие. В квантовой электродинамике, объединённой тео­рии слабого и эл.-магн. вз-ствий (см. Слабое взаимодействие), а также в квантовой хромодинамике вид этого слагаемого определяется требованием калибровочной симметрии. В элект­родинамике, напр., оно получается заменой производной d/dx_ в Д. у. на d/dx_+ieA_ /hc, где е — заряд ч-цы, а А_ — четырёхмерный потенциал эл.-магн. поля; слагаемое ieA_/hc описы­вает вз-ствие заряж. ч-цы с эл.-магн. полем. Аналогичные члены вз-ствия спинорной ч-цы с векторными кали­бровочными полями возникают и в др. названных теориях.

Заряж. ч-ца, описываемая Д. у., обладает магн. моментом eh/2mc (рав­ным для эл-на магнетону Бора). Од­нако вз-ствие с вакуумом в КТП при­водит к появлению дополнительного, т. н. аномального, магн. мо­мента, к-рый для адронов оказывается особенно большим. Так, эксперим. значение магн. момента протона в 2,8 раза больше его нормальной («дираковской») величины.

В нерелятив. пределе Д. у. для эл-на переходит в Паули уравнение, объ­ясняющее, в частности, тонкую структуру уровней энергии атома.

• См. лит. при ст. Квантовая механика.

А. В. Ефремов.

ДИСК РЭЛЕЯ [по имени англ. физика Дж. У. Рэлея (J. W. Rayleigh)], прибор для измерения колебательной




Обтекание диска по­током (диск постав­лен под углом 45° к потоку; стрелками по­мечены силы давле­ния).


скорости частиц в звук. волне. Пред­ставляет собой тонкую круглую пла­стинку из слюды или металла, под­вешенную на тонкой (обычно кварце­вой) нити, ориентированную под углом 45° (рис.) к направлению колебаний ч-ц среды (положение наиболь­шей чувствительности). В потоке, со­гласно Бернулли закону, диск стре­мится стать перпендикулярно к направлению скорости ч-ц; возникаю­щий при этом вращающий момент уравновешивается за счёт упругости нити. В пост. потоке угол поворота Д. Р. пропорционален квадрату ско­рости ч-ц, при звук. колебаниях — квадрату амплитуды колебат. скоро­сти, причём этот угол не зависит от частоты. По углу поворота диска определяют колебат. скорость и ин­тенсивность звука.

Д. Р. применяется для калибровки приёмников звука в воздухе, а также в воде.

• Б л и н о в а Л. П., Колесников А. Е., Л а н г а н с Л. Б., Акустические измерения, М., 1971.

ДИСЛОКАЦИИ (от позднелат. dislocatio — смещение), дефекты кристал­ла, представляющие собой линии, вдоль и вблизи к-рых нарушено ха­рактерное для кристалла правильное расположение ат. плоскостей. Ме­ханические свойства кристаллов — прочность и пластичность в значи­тельной мере обусловлены существо­ванием Д. и их движением. Простей­шими видами Д. явл. краевая и винтовая Д. Краевая Д. представ­ляет собой линию, вдоль к-рой обры­вается внутри кристалла край «лиш­ней» полуплоскости (рис. 1, слева). Её образование можно описать при помощи след. операции: надрезать



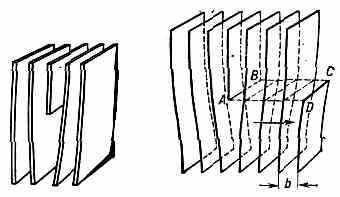
Рис. 1. Краевая дислокация: слева — обрыв ат. плоскости внутри кристалла; справа — схема образования краевой дислокации.


кристалл по плоскости АВCD (рис. 1, справа), сдвинуть нижнюю часть относительно верхней на один пери­од решётки 6 в направлении, пер­пендикулярном к АВ, а затем вновь сблизить атомы на противо­положных краях разреза внизу. Век­тор b, длина к-рого равна величине сдвига, наз. вектором Б ю р г е р с а. Электронные микроскопы с большой разрешающей способностью позволяют наблюдать специфичное для краевой Д. расположение ат. плоско­стей, представленное на рис. 1. Плоскость, проходящая через вектор b и линию Д., наз. плоскостью скольжения.

Если вектор сдвига b не перпен­дикулярен, а параллелен границе над­реза АВ, то получается винтовая

163




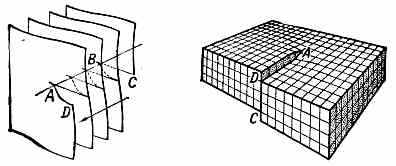
Рис. 2. Винтовая дислокация: слева — схе­ма образования винтовой дислокации; по­средине — расположение атомов в кристалле с винтовой дислокацией (атомы располага­ются в вершинах кубиков); справа — рас­положение атомов в плоскости ABCD.


Д. (рис. 2, слева). Винтовая Д. име­ет неск. плоскостей скольжения. Кри­сталл с винтовой Д. фактически со­стоит из одной ат. плоскости, прибли­зительно перпендикулярной оси вин­товой Д. и закрученной в виде поло­гого геликоида (рис. 2, посредине). В точке выхода винтовой Д. на внешнюю поверхность кристалла (рис. 2, справа) возникает ступенька AD, равная по высоте проекции вектора b на нормаль к поверхности. В про­цессе кристаллизации атомы в-ва, вы­падающие из пара или р-ра, легко присоединяются к ступеньке, что приводит к спиральному механизму роста кристалла (рис. 3).



Рис. 3. Спираль рос­та на поверхности кристалла парафина; ступень роста обры­вается в точке выхо­да винтовой дислока­ции на поверхность.