Физ величина, характе­ризующая интенсивность нормальных (перпендикулярных к поверхности) сил, с к-рыми одно тело действует на поверхность другого (напр

Вид материала

Документы

Содержание М, находящимся в газообразном состоянии в сосуде при абс. темп-ре Т Рис. 4. Дифракция нейтронов на кристалле NaCl. Интерпретация дифракционной кар­тины. Атомные амплитуды рассеяния для различных микрочастиц. Дифракция нейтронов Рент­геновская спектроскопия Дифракция света Рис. 1. Дифракц. кольца при прохождении света: слева — через круглое отверстие, в к-ром укладывается чётное число зон; спра­ва — С. Г. Пржибельский Рис. 1. Схема дифракции Рамана — Ната. Рис. 2. Схема дифракции Брэгга. К сущест­вует предельная звук. частота fмакс= 2с/ (с Дифракция электронов Диффузионная камера Диффузия нейтронов D и ср. квадратом расстояния L Диффузия носителей Диффузное отражение Рис. 2. Сверхзвук. диффузор прямоугольного сечения. 7 — сходящаяся часть; 2 — гор­ловина (цилиндрич. участок); 3 — расходя­щаяся Рис. Поляризация диэлектриков: а — ион­ная; б — электронная; в — ориентационная. ... Полное содержание

Подобный материал:

• Реферат По Физике, 58.66kb.
• Тема: определение реакций связей при действии на конструкцию произвольной плоской системы, 15.41kb.
• Головной мозг, 139.71kb.
• Работы режущего инструмента, основная нагрузка приходится на его рабочую поверхность,, 335.67kb.
• Головной мозг, с окружающими его оболочками находится в полости мозгового черепа, 437.52kb.
• Представьте себе некоторую поверхность и сидящего на ней муравья. Представили, 409.6kb.
• Лекция №8 Тема: «Продолжение», 81.36kb.
• Твует равновесию, установившемуся под действием силы тяжести, при условии, если, 669.51kb.
• Лабораторная работа метод естественного электрического поля (ЕП), 82.61kb.
• 1. Резьба Резьба поверхность, образованная при винтовом движении плоского контура, 223.58kb.

Историческая справка. Д. м. впер­вые была обнаружена эксперимен­тально в опыте амер. физиков К. Дэ-

170




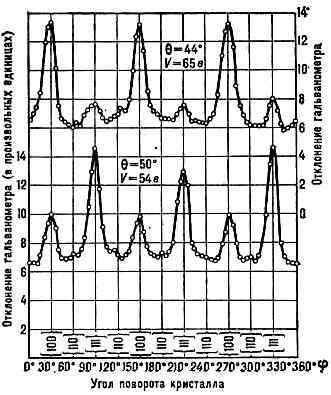
Рис. 2. Запись дифракц. максимумов в опыте Дэвиссона — Джермера, полученная при разл. углах  поворота кристалла для двух значений угла отклонений эл-нов  и двух ускоряющих напряжений V. Максимумы от­вечают отражению от разл. кристаллографич. плоскостей, индексы к-рых указаны в скобках.


виссона и Л. Джермера (1927). В этом опыте эл-ны, ускоренные электрич. полем (напряжением V~100 В, т. н. медленные эл-ны с  ~ 1 Å и менее), «отражались» от кристаллографич. по­верхностей вращающегося кристалла никеля (d ~ неск. Å). При определ. углах поворота возникали максимумы (рис. 2), к-рые регистрировались с помощью гальванометра под разными углами отклонения 0 к первичному пучку и при различных ускоряющих напряжениях (и, следовательно, раз­личных ). Расположение максимумов распределения отражённых эл-нов со­ответствовало ф-ле (2), и их появление могло быть объяснено только на ос­нове представлений о волнах и их дифракции; т. о., волн. св-ва эл-нов были доказаны экспериментально. Вскоре была обнаружена и дифракция быстрых эл-нов на прохождение (при ускоряющих электрич. напряжениях порядка десятков кВ эл-ны. могут проникать через плёнки в-ва толщи­ной 10^-5 см., рис. 1).

На рубеже 30-х гг. удалось наблю­дать и дифракцию атомов и молекул. Атомам с массой М, находящимся в газообразном состоянии в сосуде при абс. темп-ре Т, соответствует длина волны

=h/(3MkT) , (3)

т. к. ср. кинетич. энергия атома ξ=³l₂kT. Для лёгких атомов и молекул (Н, Н₂, Не) при, Т ~100К  также составляет ок. 1Å . Дифрагирующие атомы или молекулы практически не проникают в глубь кристалла; по­этому можно считать, что их дифрак­ция происходит при рассеянии от поверхности кристалла, т. е. как на плоской дифракционной решётке (рис. 3).

Позже наблюдалась дифракция про­тонов и дифракция нейтронов (рис. 4). Так было доказано экспериментально, что волн. св-ва присущи всем микро­частицам.

В широком смысле слова дифракц. рассеяние всегда имеет место при упругом рассеянии разл. элем. ч-ц атомами и ат. ядрами, а также друг другом. С другой стороны, представ­ление о корпускулярно-волновом дуа­лизме материи укрепилось при анализе явлений, всегда считавшихся типично волновыми, напр. дифракции рентг. лучей — коротких эл.-магн. волн с длиной волны 0,5—5 Å, к-рые



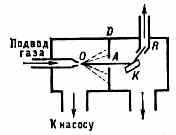
Рис. 3. Схема прибора для наблюдения диф­ракции ат. или мол. пучков: А — пучок ч-ц; К — кристалл; О — капилляр, подводя­щий газ; D — диафрагма; R — приёмник, соединённый с манометром. Манометр измеряет давление, созданное дифрагиров. пуч­ком.



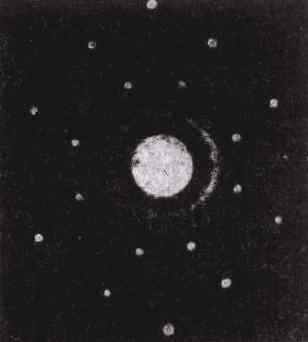
Рис. 4. Дифракция нейтронов на кристалле NaCl.


можно рассматривать и регистриро­вать как поток ч-ц — фотонов, оп­ределяя с помощью счётчиков число фотонов рентг. излучения.

Интерпретация дифракционной кар­тины. Волн. св-ва присущи каждой ч-це в отдельности, что было под­тверждено в опыте по дифракции эл-нов, поочерёдно летящих через образец. При этом постепенно, по истечении нек-рого времени, возни­кала обычная картина дифракции.

Это означало, что каждый отдель­ный эл-н подчиняется всем законам волн. оптики, а дифракц. эффект обя­зан вз-ствию волны де Бройля каж­дого эл-на со всеми атомами кристалла.

Образование дифракц. картины при рассеянии ч-ц интерпретируется в квант. механике след. образом. Про-

шедший через кристалл эл-н в ре­зультате вз-ствия с крист. решёткой образца отклоняется от первонач. на­правления движения и попадает в нек-рую точку фотопластинки, уста­новленной за кристаллом. При длит. экспозиции постепенно возникает упо­рядоченная картина дифракц. мак­симумов и минимумов в распределении эл-нов, прошедших через кристалл. Точно предсказать, в какое место фотопластинки попадёт данный эл-н, нельзя, но можно указать вероятность его попадания после рассеяния в ту или иную точку пластинки. Эта веро­ятность определяется квадратом мо­дуля волновой функции эл-на ||². Однако, поскольку вероятность при больших числах испытаний реализу­ется как достоверность, при прохож­дении огромного числа эл-нов через кристалл, как это имеет место в ре­альных экспериментах, величина ||² определяет наблюдаемое распределе­ние интенсивности в дифрагиров. пуч­ках.

Атомные амплитуды рассеяния для различных микрочастиц. Вследствие общности геом. принципов дифракции теория Д. м. многое заимствовала из развитой ранее теории дифракции рентг. лучей. Однако вз-ствие разного рода ч-ц с в-вом имеет разл. физ. природу, что и определяет специфику рассеяния разл. ч-ц атомами. Напр., рассеяние эл-нов определяется вз-ствием электрич. заряда эл-на с электростатич. потенциалом атома (r) (r — расстояние от ядра), к-рый склады­вается из потенциала положительно заряж. ядра и потенциала электрон­ной оболочки атома; потенц. энергия этого вз-ствия U=e(r). Рассеяние нейтронов определяется потенциалом их сильного вз-ствия с ат. ядром, а также вз-ствием магн. момента нейт­рона с магн. моментом атома (магн. рассеяние нейтронов).

Рассеивающую способность атома характеризуют атомной ампли­тудой рассеяния f() ( — угол рассеяния), к-рая определяется потенц. энергией вз-ствия ч-ц данного сорта с атомами рассеивающего в-ва (см. А томный фактор). Интенсивность рассеяния пропорц. f²(). Если из­вестны ат. амплитуда и взаимное расположение рассеивающих центров (ат. структура в-ва), то можно рас­считать общую картину дифракции, к-рая образуется в результате интер­ференции вторичных волн, исходящих из рассеивающих центров.

Ат. амплитуда рассеяния эл-нов f_э максимальна при =0 и спадает с увеличением . Величина f_э зависит также от ат. номера Z и от строения электронных оболочек атома, в ср. возрастая с увеличением Z приблизи­тельно как Z^1//3 для малых  и как Z при больших значениях О, но обна­руживает колебания, связанные с

171


периодичностью заполнения электрон­ных оболочек.

Ат. амплитуда рассеяния нейтронов f_н для тепловых нейтронов не зависит от угла рассеяния (рассеяние сфери­чески симметрично), т. к. ат. ядро с радиусом ~10^-13 см явл. для них «точкой» (длина волны тепловых ней­тронов ~10^-8 см). Для нейтронов нет явной зависимости f_н от Z. Вслед­ствие наличия у нек-рых ядер т. н. резонансных уровней энергии, близ­ких к энергии тепловых нейтронов, f_н для таких ядер отрицательны.

Атом рассеивает эл-ны значительно сильнее, чем рентг. лучи и нейтроны: абс. значения амплитуды рассеяния эл-нов ~10^-8 см, рентг. лучей ~10^-11см, нейтронов ~10^-12см. Т. к. интенсивность рассеяния ~f², эл-ны взаимодействуют с в-вом примерно в 10⁶ раз сильнее, чем рентг. лучи, и тем более нейтроны. Поэтому образ­цами для наблюдения дифракции быст­рых эл-нов обычно служат тонкие плёнки толщиной 10^-6—10^-5 см, а для дифракции рентг. лучей и нейт­ронов — толщиной в неск. мм.

Д. м., сыгравшая большую роль в установлении двойственной природы материи, в дальнейшем стала одним из осн. методов изучения структуры в-ва (см. Электронография, Нейтро­нография).

• Блохинцев Д. И., Основы квантовой механики, 4 изд., М., 1963, гл. 1, § 7—8; Пинскер 3. Г., Дифракция электронов, М.—Л., 1949; В Эйнштейн Б. К., Структурная электронография, М., 1956; Бэкон Дж., Дифракция нейтронов, пер. с англ., М., 1957; Рамзей Н., Молеку­лярные пучки, пер. с англ., М., 1960.

Б. К. Вайнштейн.

ДИФРАКЦИЯ НЕЙТРОНОВ, см. Дифракция микрочастиц.

ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ, явление, возникающее при упругом рассеянии рентгеновского из­лучения в кристаллах, аморфных те­лах, жидкостях или газах и состоящее в появлении отклонённых (дифраги­рованных) лучей, распространяющих­ся под определёнными углами к пер­вичному пучку. Д. р. л. обусловлена пространств. когерентностью между вторичными волнами, возникшими при рассеянии первичного излучения на эл-нах разл. атомов. В нек-рых на­правлениях, определяемых соотноше­нием между длиной волны излучения  и межатомными расстояниями в в-ве, вторичные волны складываются, находясь в одинаковой фазе, в ре­зультате чего создаётся интенсивный дифракц. луч. Дифракц. картина мо­жет быть зафиксирована на фотоплён­ке; её вид зависит от структуры объ­екта и эксперим. метода. Напр., рент­генограммы от монокристаллов (лауэграммы) образованы закономерно рас­положенными пятнами (рефлексами), от поликристаллов (дебаеграммы) — системой концентрич. окружностей, от аморфных тел, жидкостей и га-

зов — совокупностью диффузионных ореолов вокруг центр. пятна. Д. р. л. впервые была экспериментально об­наружена на кристаллах нем. физика­ми М. Лауэ, В. Фридрихом и П. Книппингом в 1912 и явилась доказатель­ством волновой природы рентгенов­ских лучей.

Наиболее чётко выражена Д. р. л. на кристаллах. Кристалл явл. естеств. трёхмерной дифракц. решёткой для рентгеновского излучения, т. к. расстояние между рассеивающими цен­трами (атомами) в нём одного порядка с  рентгеновского излучения (~1 Å =10^-8 см). Д. р. л. на кристаллах можно рассматривать как избиратель­ное (по ) отражение рентгеновских лучей от систем ат. плоскостей кри­сталлической решётки (см. Брэгга — Вульфа условие). Направление диф­ракц. максимума удовлетворяет усло­виям Лауэ:



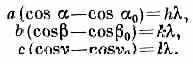
Здесь а, b, с — периоды крист. ре­шётки по трём её осям; ₀, ₀, ₀ — углы, образуемые падающим, а , ,  — рассеянным лучом с осями кри­сталла; h, k, l — целые числа (Мил­лера индексы).

Интенсивность дифрагиров. луча оп­ределяется атомными факторами, к-рые зависят от электронной плот­ности атомов, расположением атомов в элем. ячейке (структурным фак­тором), а также интенсивностью теп­ловых колебаний атомов крист. ре­шётки. На неё влияют также размеры и форма объекта, степень совершен­ства кристалла и др. хар-ки. Зависи­мость величины и пространств. рас­пределения интенсивности рассеян­ного рентгеновского излучения от структуры и др. хар-к объекта легла в основу рентгеновского структурного анализа и рентгенографии материалов.

Д. р. л. на кристаллах даёт воз­можность определять длину волны рентгеновского излучения (см. Рент­геновская спектроскопия).

Д. р. л, на аморфных твёрдых те­лах, жидкостях и газах позволяет оценивать средние расстояния между молекулами или расстояния между атомами в молекуле и определять распределение плотности в-ва.

Дифрагиров. пучки составляют часть всего рассеянного излучения. Из-за нарушений периодичности стро­ения кристаллов часть излучения рас­сеивается некогерентно и образует изотропный фон. Кроме того, на­блюдается комптоновское рассеяние с изменением  (см. Комптона эффект). ДИФРАКЦИЯ СВЕТА, в узком (наи­более употребительном) смысле — явление огибания лучами света кон­тура непрозрачных тел и, следова­тельно, проникновение света в область геом. тени; в широком смысле — про­явление волновых св-в света в ус­ловиях, близких к условиям применимости представлении геометриче­ской оптики.

В естеств. условиях Д. с. обычно наблюдается в виде нерезкой, раз­мытой границы тени предмета, освещаемого удалённым источником. Наиболее контрастна Д. с. в про­странств. областях, где плотность по­тока лучей претерпевает резкое из­менение (в области каустической по­верхности, фокуса, границы геом. тени и др.). В лабораторных условиях можно выявить структуру света в этих областях, проявляющуюся в чередо­вании светлых и тёмных (или окра­шенных) областей на экране. Иногда эта структура проста, как, напр., при Д. с. на дифракционной решётке, часто очень сложна, напр. в области фокуса линзы. Д. с. на телах с рез­кими границами используется в ин­струментальной оптике и, в частности, определяет предел возможностей оптич. устройств.

Первая элем. количеств. теория Д. с. была развита франц. физиком О. Фре­нелем (1816), к-рый объяснил её как результат интерференции вторичных волн (см. Гюйгенса — Френеля прин­цип). Несмотря на недостатки, метод этой теории сохранил своё значение, особенно в расчётах оценочного ха­рактера.

Метод состоит в разбиении фронта падающей волны, обрезанного краями экрана, на зоны Френеля. Считается,



Рис. 1. Дифракц. кольца при прохождении света: слева — через круглое отверстие, в к-ром укладывается чётное число зон; спра­ва — вокруг круглого экрана.


что на экране вторичные световые волны не рождаются и световое поле в точке наблюдения опреде­ляется суммой вкладов от всех зон. Если отверстие в экране оставляет открытым чётное число зон (рис. 1), то в центре дифракц. картины полу­чается тёмное пятно, при нечётном числе зон — светлое. В центре тени от круглого экрана, закрывающего не слишком большое число зон Фре­неля, получается светлое пятно. Ве­личины вкладов зон в световое поле в точке наблюдения пропорциональны площадям зон и медленно убывают с ростом номера зоны. Соседние зоны вносят вклады противоположных зна­ков, т. к. фазы излучаемых ими волн противоположны.

Результаты теории О. Френеля по­служили решающим доказательством волновой природы света и дали ос­нову теории зонных пластинок. Раз­личают два вида Д. с.— д и ф р а к-

172


ц и ю Френеля и дифрак­цию Фраунгофера в зави­симости от соотношения между раз­мерами тела b, на к-ром происходит дифракция, и величиной зоны Фре­неля (z) (а следовательно, в зависи­мости от расстояния z до точки на­блюдения). Метод Френеля эффекти­вен лишь тогда, когда размер отвер­стия сравним с размером зоны Фре­неля: b ~ (z) (дифракция в сходя­щихся лучах). В этом случае неболь­шое число зон, на к-рые разбивается сферич. волна в отверстии, опреде­ляет картину Д. с. Если отверстие в экране меньше зоны Френеля (b<<(z), дифракции Фраунгофера), как, напр., при очень удалённых от экрана наблюдателя и источника света, то можно пренебречь кривизной фронта волны, считать её плоской и картину дифракции характеризовать угловым распределением интенсивности пото­ка. При этом падающий параллельный пучок света на отверстии становится расходящимся с углом расхо­димости  ~ /b. При освещении щели параллельным монохроматич. пучком света на экране получается ряд тёмных и светлых полос, быстро убывающих по интенсивности. Если свет падает перпендикулярно к пло­скости щели, то полосы расположены симметрично относительно центр. по­лосы (рис. 2), а освещённость меняется вдоль экрана периодически с изменением , обращаясь в нуль при углах , для к-рых sin=m/b (m=1, 2, 3, . . .).



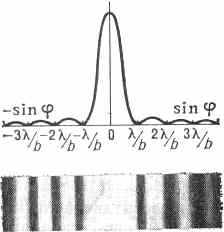
Рис. 2. Дифракция Фраунгофера на щели.


При промежуточных зна­чениях  освещённость достигает макс. значений. Гл. максимум имеет место при m=0 и sin=0, т. е. =0. С умень­шением ширины щели центр. светлая полоса расширяется, а при данной ширине щели положение минимумов и максимумов зависит от , т. е. рас­стояние между полосами тем больше, чем больше . Поэтому в случае белого света имеет место совокупность со­ответствующих картин для разных цветов; гл. максимум будет общим для всех  и представляется в виде белой полоски, переходящей в цветные по­лосы с чередованием цветов от фио­летового к красному.

В матем. отношении дифракция Фраунгофера проще дифракции Фре­неля. Идеи Френеля математически

воплотил нем. физик Г. Кирхгоф (1882), к-рый развил теорию гра­ничной Д. с., применяемую на практике. Однако в его теории не учитываются векторный характер све­товых волн и св-ва самого материала экрана. Математически корректная теория Д. с. на телах требует решения сложных граничных задач рассеяния эл.-магн. волн, имеющих решения лишь для частных случаев.

Первое точное решение было полу­чено нем. физиком А. Зоммерфельдом (1894) для дифракции плоской волны на идеально проводящем клине. На больших по сравнению с  расстояниях от острия клина результат Зоммерфельда предсказывает более глубокое проникновение света в область тени, чем это следует из теории Кирхгофа.

Дифракц. явления возникают не только на резких границах тел, но и в протяжённых системах. Такая объ­ёмная Д. с. обусловливается крупномасштабными по сравнению с  неоднородностями диэлектрич. про­ницаемости среды. В частности, объ­ёмная Д. с. происходит при дифрак­ции света на ультразвуке, в голограм­мах в турбулентной среде и нелиней­ных оптич. средах. Часто объёмная Д. с., в отличие от граничной, неот­делима от сопутствующих явлений отражения и преломления света. В тех случаях, когда в среде нет резких границ и отражение играет незначит. роль в характере распро­странения света в среде, для дифракц. процессов применяют асимптотич. ме­тоды теории дифференциальных ур-ний. Для таких приближённых методов, к-рые составляют предмет диффузионной теории ди­фракции, характерно медленное (на размере Я) изменение амплитуды и фазы световой волны вдоль луча.

В нелинейной оптике Д. с. проис­ходит на неоднородностях показателя преломления, к-рые создаются самим распространяющимся через среду из­лучением. Нестационарный характер этих явлений дополнительно услож­няет картину Д. с., в к-рой кроме углового преобразования спектра из­лучения возникает и частотное преобразование.

• Ландсберг Г. С., Оптика, 5 изд., М. 1976 (Общий курс физики); Б о р н М. Вольф Э., Основы оптики, пер. с англ. 2 изд., М., 1973.

С. Г. Пржибельский

ДИФРАКЦИЯ СВЕТА НА УЛЬТРАЗВУКЕ (акустооптическая дифрак­ция). При распространении света в среде, в к-рой присутствует УЗ волна, происходит дифракция света. Впервые Д. с. на у. была обнаружена П. Дебаем и Ф. Сирсом (США) и одновре­менно Р. Люка и П. Бикаром (Фран­ция) в 1932.

Упругие деформации в звук. волне приводят к периодич. изменению по­казателя преломления и среды, в результате чего в среде возникает структура, аналогичная дифракцион­ной решётке, с периодом, равным длине звук. волны . Если в такой структуре распространяется луч све­та, то в среде, помимо основного (0-го порядка), возникают дифракц. пучки света, характеристики к-рых — нап­равление в пр-ве, поляризация и ин­тенсивность — зависят от параметров звук. поля (частоты и интенсивности УЗ, толщины звук. пучка D), а также от угла 6, под к-рым падает свет на звук. пучок. В результате Доплера эффекта при рассеянии на движу­щейся решётке частота дифрагиров. света отличается от частоты падаю­щего на величину частоты звука.

Интенсивность света в дифракц. максимуме определяется фазовыми сдвигами между волнами, приходя­щими в точку наблюдения из всех точек объёма вз-ствия. При произ­вольном 6 эффективность Д. с. на у. =I_m/I₀ мала (I₀ и I_m — интенсив­ности света в падающем пучке и в дифракц. пучке m-го порядка). Лишь при определённом  световые волны, идущие из разл. точек области вз-ствия, оказываются синфазными и эффек­тивность дифракции возрастает во много раз, т. е. возникает резо­нансная дифракция. Для неё характерна зависимость эффек­тивности от длины L пути, пройден­ного светом в области акустооптич. вз-ствия (длины вз-ствия). При до­статочно большой L интенсивность дифрагиров. света становится срав­нимой с интенсивностью падающего.



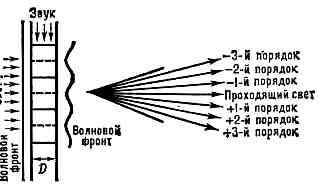
Рис. 1. Схема дифракции Рамана — Ната.


Условия возникновения и характер резонансной Д. с. на у. зависят от соот­ношения между  и , где  — длина волны света. Для НЧ звука (от неск. десятков МГц и ниже), для к-рого справедливо условие L/²<<1, ре­зонансная дифракция имеет место при норм. падении света на звук. пучок (т. н. дифракция Р а м а н а — Н а т а, рис. 1). При этом све­товая волна проходит сквозь звук. пучок, не отражаясь, а периодич. изменение n под действием УЗ при­водит к периодич. изменению фазы прошедшей световой волны. В ре­зультате на выходе из акустич. пучка плоская световая волна оказывается модулированной по фазе: её волновой фронт становится гофрированным. Та­кая волна эквивалентна большому числу плоских волн, распространяю­щихся под малыми углами друг к другу. В соответствии с этим падаю-

173


щий световой луч разбивается на серию лучей, направленных под ма­лыми углами '_m=m/ (m=0, ±1, . . .— порядок дифракции) к направ­лению падающего света. Энергия па­дающего излучения распределяется среди мн. порядков дифракции сим­метрично относительно проходящего света.

Резонансная дифракция на ВЧ зву­ке (на частотах гиперзвука), длина волны к-рого удовлетворяет условию L/²>1, наз. брэгговской ди­фракцией. Она возникает в изо­тропной среде, если свет падает на



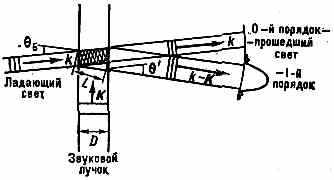
Рис. 2. Схема дифракции Брэгга.

звук. пучок под т. н. углом Брэгга (рис. 2) _Б=arcsin((¹/₂)(/)). В этом

случае отклонение света происходит только в 1-й порядок дифракции: в + 1-й для света, падающего в сто­рону, противоположную распростра­нению звука, или в -1-й, если свет падает в сторону распространения звука. Объяснить дифракцию Брэгга можно тем, что падающая под углом к звук. решётке световая волна ча­стично отражается от неё и интерфе­ренция отражённых лучей определяет интенсивность дифрагиров. света — она максимальна, если разность оп-

выходит из звук. пучка под углом '=_б. Для фиксированной К сущест­вует предельная звук. частота f_макс= 2с/ (с — скорость звука), выше к-рой брэгговская дифракция невоз­можна. Эта частота отвечает отра­жению световой волны назад от звук. решётки.

В анизотропной среде брэгговская дифракция может происходить как с изменением поляризации у дифрагированного света, так и без него. В последнем случае картина ди­фракции аналогична картине брэг­говской дифракции в изотропной среде. При дифракции с изменением поля­ризации брэгговский угол опреде­ляется не только соотношением длин волн света и звука, но и оптич. св-вами среды. Продифрагировавший свет вы­ходит из звук. пучка под углом не равным брэгговскому. Дифракция све­та с данной длиной волны возможна на звук. волнах, частоты .к-рых огра­ничены не только сверху, но и

снизу: f_мин<f<f_макс. Миним. зна­чению частоты f₁ соответствует коллинеарная дифракция, при к-рой све­товые лучи, как падающий, так и дифрагированный, параллельны и рас­пространяются в одну сторону.

С помощью Д. с. на у. определяют­ся хар-ки звук. полей (звук. давление, интенсивность звука и т. п.), измеря­ются поглощение и скорость УЗ, модули упругости 2-го и 3-го поряд­ков, упругооптич. и магнитооптич. св-ва материалов. Д. с. на у. приме­няется в разл. устройствах акустооптики для модуляции и отклонения света, при акустооптич. обработке СВЧ сигналов, для приёма сигналов в УЗ-вых линиях задержки и др.

Дифракция света может происхо­дить не только на вводимой извне звук. волне, но и на собственных упругих колебаниях конденсирован­ных сред (тв. тел, жидкостей) — это т. н. Мандельштама — Бриллюэна рассеяние.

• Ультразвук, М., 1979 (Маленькая энцик­лопедия); Физическая акустика, под ред. У. Мэзона и Р. Терстона, пер. с англ., т. 7, М., 1974, гл. 5; Т а к е р Дж., Р э м п т о н В., Гиперзвук в физике твердого те­ла, пер. с англ., М., 1975; Гуляев Ю. В., Проклов В. В., Шкердин Г. Н., Дифракция света на звуке в твердых телах, «УФН», 1978, т. 124, в. 1, с. 61.

В. М. Левин.

ДИФРАКЦИЯ ЭЛЕКТРОНОВ, см. Дифракция микрочастиц.

ДИФФЕРЕНЦИАЛЬНЫЙ МЕТОД ИЗМЕРЕНИЙ (разностный метод), ме­тод измерений, в к-ром определяют разность между измеряемой и из­вестной физ. величинами. Известную величину чаще всего воспроизводят при помощи меры. Если разность между измеряемой и известной ве­личинами мала, то погрешность из­мерения в основном определяется точ­ностью знания известной величины. Напр., если разность не превышает 0,01 части измеряемой величины, из­мерение её с погрешностью 0,1% внесёт в общий результат погрешность не более 0,001%. Д. м. и. применя­ется при поверке средств измере­ний — сличении поверяемой меры с образцовой (напр., концевых мер дли­ны на компараторе), а также при испытаниях материалов и изделий, основанных на сравнении их с об­разцами. В области линейных изме­рений Д. м. и. наз. относитель­ным методом.

К. П. Широков.

ДИФФУЗИОННАЯ КАМЕРА, прибор, в к-ром можно наблюдать треки заряж. ч-ц, как и в Вильсона камере. Треки в Д. к. создаются каплями жидкости в пересыщенных парах спир­та, дересыщение их достигается за счёт непрерывного потока пара от горячей поверхности у крышки ка­меры к более холодной поверхности у её дна. В отличие от камеры Виль­сона, в Д. к. пересыщение существует постоянно (в нек-ром слое Д. к.), поэтому Д. к. чувствительна к иони­зирующим ч-цам непрерывно. Впер­вые осуществлена амер. физиком А. Лангсдорфом в 1936.

• Ляпидевский В. К., Диффузионная камера, «УФН», 1958, т. 66, в. 1, с. 111.

ДИФФУЗИЯ (от лат. diffusio — рас­пространение, растекание), взаимное проникновение соприкасающихся в-в друг в друга вследствие теплового движения ч-ц в-ва. Д. происходит в направлении уменьшения концент­рации в-ва и ведёт к его равномерному распределению по занимаемому объ­ёму (к выравниванию хим. потенциа­ла). Д. имеет место в газах, жидко­стях и тв. телах, причём диффундиро­вать могут как находящиеся в них ч-цы посторонних в-в, так и собствен­ные ч-цы (самодиффузия). Д. круп­ных ч-ц, взвешенных в газе или жид­кости (напр., ч-ц дыма или суспен­зии), осуществляется благодаря их броуновскому движению. Ниже в ста­тье рассматривается Д. молекул (или атомов).

Наиболее быстро Д. происходит в газах, медленнее — в жидкостях, ещё медленнее — в тв. телах, что обусловле­но характером теплового движения ч-ц в этих средах. Траектория движения каждой ч-цы газа представляет собой ломаную линию, т. к. при столкно­вениях она меняет направление и скорость движения. Поэтому диффу­зионное проникновение значительно медленнее свободного движения. Сме­щение ч-цы L меняется со временем случайным образом, но ср. квадрат его L² за большое число столкновений растёт пропорционально времени С L² ~ Dt; коэфф. пропорциональности D наз. коэфф. Д. Это соотношение, полученное А. Эйнштейном, справед­ливо для любых процессов Д. Для простейшего случая самодиффузии в газах коэфф. Д. может быть определён, если за ср. смещение принять ср. длину свободного про­бега молекулы l. Для газа l=c, где с — ср. скорость движения ч-ц,  — ср. время между столкновениями. Т. о., D~l²/ ~lс (более точно D=¹/₃lc). Коэфф. Д. обратно про­порционален давлению р газа (т. к. l ~ 1/р); с ростом темп-ры Т (при пост. объёме) коэфф. D увеличивается пропорционально Г^1/2, т. к. с ~ T. С увеличением мол. массы D умень­шается.

В жидкостях, в соответствии с характером теплового движения молекул, Д. осуществляется пере­скоками молекул из одного устойчивого положения в другое. Каждый скачок происходит при сообщении молекуле энергии, достаточной для разрыва её связей с соседними моле­кулами и перехода в окружение др. молекул (в новое энергетически вы­годное положение). Ср. перемещение при таком скачке не превышает меж-мол. расстояния. Диффузионное дви­жение ч-ц в жидкости можно рас­сматривать как движение с трением, к нему применимо второе соотношение Эйнштейна: D ~ ukT. Здесь u — по-

174


движность диффундирующих ч-ц, т. е. коэфф. пропорциональности между скоростью ч-цы с и движущей силой F при стационарном движении с тре­нием (с=uF). Если ч-цы сферически симметричны, то u=1/6r, где  — коэфф. вязкости жидкости, r — радиус ч-цы (см. Стокса закон). В жидкости увеличение коэфф. Д. с ростом темп-ры обусловлено «разрыхлением» её струк­туры при нагреве и соответствующим увеличением числа перескоков в еди­ницу времени.

В твёрдом теле могут дей­ствовать неск. механизмов Д.: обмен местами атомов с вакансиями (не­занятыми узлами крист. решётки), перемещение атомов по междоузлиям, одноврем. циклич. перемещение неск. атомов, прямой обмен местами двух соседних атомов и т. д. Первый ме­ханизм преобладает, напр., при об­разовании тв. растворов замещения, второй — тв. растворов внедрения.

Коэфф. Д. в тв. телах крайне чув­ствителен к дефектам крист. решётки, возникшим при нагреве, напряжениях, деформациях и др. воздействиях. Уве­личение числа дефектов (гл. обр. вакансий) облегчает перемещение ато­мов в тв. теле и приводит к росту Д. В тв. телах характерна резкая (экс­поненциальная) зависимость D от Т. Так, коэфф. Д. цинка в медь при повышении Т от 20°С до 300°С воз­растает в 10¹⁴ раз.

ЗНАЧЕНИЕ КОЭФФИЦИЕНТА ДИФФУЗИИ (при атм. давлении)



Для большинства науч. и практич. задач существенно не диффузионное движение отд. ч-ц, а обусловленное им выравнивание концентрации в-ва в первоначально неоднородной среде. Из областей высокой концентрации уходит больше ч-ц, чем из областей низкой концентрации. Через еди­ничную площадку в неоднородной среде проходит за единицу времени безвозвратный поток в-ва в сторону меньшей концентрации — диффузи­онный поток j. Он равен разности между числами ч-ц, пересекающих площадку в том и др. направлениях, и потому пропорционален градиенту концентрации _С (уменьшению кон­центрации С на единицу длины). Эта зависимость выражается зако­ном Ф и к а (1855): j =-D_С. Математически закон Фика аналоги­чен ур-нию теплопроводности Фурье. В основе этих явлений лежит единый механизм мол. переноса: в законе Фика — перенос массы, в ур-нии теплопроводности — энергии (см. Пере­носа явления).

Д. возникает не только при нали­чии в среде градиента концентрации (хим. потенциала). Под действием внешнего электрического поля про­исходит Д. заряженных ч-ц (элек­тродиффузия), действие по­ля тяжести или давления вызы­вает бародиффузию, в нерав­номерно нагретой среде возникает термодиффузия.

Все эксперим. методы определения Д. требуют приведения в контакт диф­фундирующих в-в и анализа их со­става, изменённого в процессе Д. Анализ состава производят химиче­скими, оптическими (по изменению показателя преломления или погло­щения света), масс-спектроскопическими методами, с помощью меченых атомов и т. д.

Д. важна в хим. кинетике и техно­логии. При протекании хим. реакции на поверхности катализатора или од­ного из реагирующих в-в (напр., го­рении угля) Д. может определять скорость подвода др. реагирующих в-в и отвода продуктов реакции, т. е. являться определяющим (лимитиру­ющим) процессом.

Для процессов испарения и кон­денсации, растворения кристаллов и кристаллизации Д. оказывается обыч­но определяющей. Д. газов через пористые перегородки или в струю

пара используется для изотопов раз­деления.

В жидких р-рах Д. молекул рас­творителя через полупроницаемые пе­регородки (мембраны) приводит к возникновению осмотич. давления (см. Осмос), что используется для разде­ления в-в. Д. лежит в основе мн. технологич. и биологич. процессов.

Д. А. Франк-Каменецкий.

ДИФФУЗИЯ НЕЙТРОНОВ, распро­странение нейтронов в в-ве, сопро­вождающееся многократным измене­нием направления и скорости их движения в результате их столкнове­ний с ат. ядрами. Д. н. в среде ана­логична диффузии атомов и молекул в газах и подчиняется тем же законо­мерностям. Быстрые нейтроны (с энер­гией, во много раз большей, чем ср. энергия теплового движения ч-ц сре­ды) при диффузии отдают энергию среде и замедляются. В слабо погло­щающих средах нейтроны приходят в тепловое равновесие со средой (тепловые нейтроны). В безграничной среде тепловой нейтрон диффундирует до тех пор, пока не поглотится одним из ат. ядер.

Диффузия тепловых нейтронов ха­рактеризуется коэфф. диффузии D и ср. квадратом расстояния L²_T от точки образования теплового нейтрона до точки его поглощения: L²_T=6Dt, где t — ср. время жизни теплового нейтрона в среде (табл.). Диффузию быстрых нейтронов характеризуют ср. квадратом расстояния l²_б между точ­кой образования быстрого нейтрона



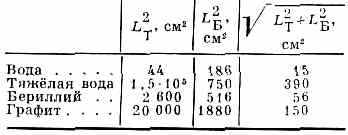
(в яд. реакции или при радиоактив­ном распаде) и точкой его замедления до тепловой энергии.

При диффузии в ограниченной среде нейтрон с большой вероятностью вы­летает за её пределы, если радиус системы мал по сравнению с величиной

(L²_T+L²_Б), и, напротив, нейтрон с большой вероятностью поглощается в среде, если её радиус велик по срав­нению с этой величиной. Д. нейтронов играет существенную роль в работе ядерных реакторов.

• См. лит. при ст. Нейтронная физика.

Ф. Л. Шапиро.

ДИФФУЗИЯ НОСИТЕЛЕЙ, переме­щение носителей заряда в полупро­водниках, обусловленное неоднородностями их концентрации. В резуль­тате Д. н. в ПП возникает электрич. ток плотностью:

j=eD_ngradrn-eD_pgradp,

где е — заряд эл-на, n — концентра­ция эл-нов проводимости, р — дырок, D_n, D_p — соответствующие коэфф. диффузии. Д. в. ПП с монополярной проводимостью (носители одного знака) сопровождается появлением объёмно­го заряда и электрич. поля. В резуль­тате возникает дрейф носителей, на­правленный противоположно Д-н. В условиях равновесия диффузионный и дрейфовый токи взаимно компенси­руются. Д. н. в ПП с биполярной проводимостью, несмотря на наличие носителей обоего знака, также со­провождается возникновением объём­ного заряда, поскольку, как правило, D_nD_p, и при диффузии носители одного знака обгоняют носителей дру­гого знака. При этом также появля­ется электрич. поле, к-рое тормозит более подвижные и ускоряет менее подвижные носители. В результате осуществляется перемещение носите-

175


лей обоих знаков — а м б и п о л я р н а я диффузия, коэфф. к-рой



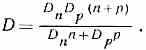
При n>>р DD_p, а при n<_n. Амбиполярная диффузия неравновес­ных носителей явл. причиной Дембера эффекта и Кикоина — Носкова эффекта.

Э. М. Эпштейн.

ДИФФУЗНОЕ ОТРАЖЕНИЕ света, см. в ст. Отражение света.

ДИФФУЗНЫЙ РАЗРЯД, электри­ческий разряд в газе (напр., тлеющий или дуговой) в виде широкого све­тящегося столба. Д. р. формируется при низких давлениях (~10^-1—10мм рт. ст.) и в условиях, когда длина свободного пробега <амбиполярная диф­фузия. Часто термин «Д. р.» употреб­ляется как противопоставление 'контрагированному разряду.

ДИФФУЗОР в гидроаэромеханике, участок проточного канала (трубо­провода), в к-ром происходит тормо­жение потока жидкости или газа. Поперечное сечение Д. может быть круглым, прямоугольным, кольцевым, эллиптическим, а также несиммет­ричным. По своему назначению и геом. форме Д.— устройство, обрат­ное соплу. Вследствие падения ср. скорости v давление р в направлении течения растёт (см. Бернулли урав­нение) и кинетич. энергия потока частично преобразуется в потенциаль­ную. В отличие от сопла, преобразо­вание энергии в Д. сопровождается заметным возрастанием энтропии и уменьшением полного давления. Раз­ность полных давлений на входе и выходе Д. характеризует его гидравлич. сопротивление и наз. потерями. Потерянная часть кинетич. энергии потока затрачивается на образование вихрей, работу против сил трения и необратимо переходит в теплоту. Дви­жение жидкости (газа) в направлении роста давления в потоке, т. е. сущест­вование положит. градиента давления в направлении течения,— осн. отли­чит. свойство Д.

В случае несжимаемой жидкости, а также при дозвуковой скорости газа v₁ перед входом в Д. (v₁а — скорость звука) площадь поперечного сечения канала в силу неразрывности уравнения должна увеличиваться в направлении течения, поэтому дозвук. Д. имеет форму расходящегося канала (рис. 1). При сверхзвук. скорости перед входом в Д. (v₁>а) он имеет форму сходящегося или цилиндрич. канала, в к-ром после торможения ср. скорость становится дозвуковой. Дальнейшее торможение дозвук. ско­рости осуществляется в расходящемся дозвук. Д., присоединённом к сверх­звук. Д. (рис. 2).

Вязкость оказывает решающее влия­ние на течение в Д. В пограничном слое скорость под действием вязкости быстро убывает, обращаясь в нуль на стенке Д. Кинетич. энергия в погра­ничном слое меньше, чем в остальной части потока, а статич. давление в данном поперечном сечении почти постоянно. Т. к. средняя скорость по длине Д. падает, а давление рас­тёт, то в сечении, расположенном на нек-ром расстоянии от входа в Д.,



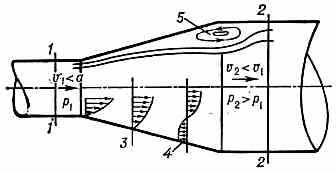
Рис. 1. Дозвук. диффузор круглого сечения. 1 — сечение перед входом в диффузор; 2 — сечение за диффузором; 3 — профиль ско­рости; 4 — возвратное течение; 5 — циркуляц. течение.



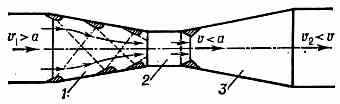
Рис. 2. Сверхзвук. диффузор прямоугольного сечения. 7 — сходящаяся часть; 2 — гор­ловина (цилиндрич. участок); 3 — расходя­щаяся часть.


кинетич. энергия потока вблизи стен­ки недостаточна для того, чтобы пе­реместить жидкость или газ против сил давления, возрастающих в на­правлении потока. Вблизи этого се­чения начинается отрыв потока от стенки и возникает возвратное те­чение. В результате у стенки Д. образуются области циркуляц. дви­жения (рис. 1). Слой жидкости между оторвавшимся от стенки и осн. по­токами неустойчив и периодически свёртывается в вихри, к-рые сносятся вниз по потоку. Место расположения отрыва в Д. зависит от толщины по­граничного слоя, от величины по­ложит. градиента давления, опреде­ляемого геом. формой Д., а также от профиля скорости и степени турбу­лентности потока перед входом в Д. В случае сверхзвук. скорости перед входом в Д. торможение потока осу­ществляется в ударных волнах, взаи­модействующих между собой и отра­жающихся от стенок Д. (пунктир на рис. 2). Давление в потоке, про­шедшем через ударную волну, резко увеличивается, и под воздействием большого положит. градиента дав­ления в местах отражения ударных волн от стенок может происходить отрыв пограничного слоя (штриховка на рис. 2). Потери полного давления при торможении сверхзвук. потока в Д. намного больше, чем при тормо­жении дозвук. потока. Площадь гор­ловины (наиболее узкого поперечного

сечения) сверхзвук. Д. оказывает ре­шающее воздействие на течение и потери в Д.

Д. применяются, когда необходимо затормозить поток жидкости или газа с наименьшими потерями. Они ис­пользуются в газо-, нефте- и воздухо­проводах, в гидравлич. магистралях, в турбомашинах всех типов, в воз­душно-реактивных двигателях, эжек­торах, МГД-генераторах, аэродина­мических трубах, стендах для ис­пытаний ракетных двигателей и др.

Теория течения в Д. недостаточно разработана, его осн. хар-ки и оп­тимальную форму определяют на ос­новании результатов эксперим. иссле­дований и их теоретич. обобщения.

• Абрамович Г. Н., Прикладная га­зовая динамика, 4 изд., М., 1976; Дейч М. Е., Зарянкин А. Е., Газодинамика диффузоров и выхлопных патрубков турбомашин, М., 1970; И д е л ь ч и к И. Е., Справочник по гидравлическим сопротивле­ниям, 2 изд., М., 1975. С. Л. Вишневецкий,

ДИХРОИЗМ (от греч. dichroos — двух­цветный), различная окраска обла­дающих двойным лучепреломлением од­ноосных кристаллов в проходящем свете при взаимно перпендикулярных направлениях наблюдения — вдоль оптич. оси кристалла (т. н. «осевая» окраска) и перпендикулярно к ней («базисная» окраска). Д.— частный случай плеохроизма (многоцветности). Подробнее см. в ст. Плео­хроизм, где разъяснены также тер­мины круговой Д. и линей­ный Д.

ДИЭЛЕКТРИКИ (англ. dielectric, от греч. dia — через, сквозь и англ. electric — электрический), вещества, плохо проводящие электрич. ток. Тер­мин «Д.» введён Фарадеем для обо­значения в-в, в к-рые проникает элект­рич. поле. Д. явл. все газы (неиони­зованные), нек-рые жидкости и тв. тела. Электропроводность Д. по срав­нению с металлами очень мала. Их уд. электрич. сопротивление  — 10⁸— 10¹⁷ Ом•см. Количеств. различие в электропроводности Д. и металлов классич. физика пыталась объяснить тем, что в металлах есть свободные эл-ны, а в Д. все эл-ны связаны с атомами. Электрич. поле не отрывает их от атомов, а лишь слегка смещает. Квант. теория твёрдого тела объ­ясняет разные электрич. св-ва ме­таллов и Д. разл. характером рас­пределения эл-нов по уровням энер­гии. В Д. верхний заполненный эл-нами энергетич. уровень совпадает с верхней границей одной из разрешён­ных зон (в металлах он лежит внутри разрешённой зоны), а ближайшие свободные уровни отделены от за­полненных запрещённой зоной, к-рую эл-ны под действием обычных (не слишком сильных) электрич. полей преодолеть не могут (см. Зонная тео­рия). Действие электрич. поля сво­дится к перераспределению электрон­ной плотности, к-рое приводит к поляризации Д. Резкой границы меж­ду Д. и полупроводниками провести

176


нельзя. В-ва с шириной запрещённой зоны ξ_g<3 эВ условно относят к ПП, а с ξ_g>3эВ — к Д.

Поляризация. Механизмы поляри­зации Д. различны и зависят от ха­рактера хим. связи. Напр., в ионных кристаллах (NaCl и др.) поляризация явл. результатом сдвига ионов друг относительно друга (ионная по­ляризация; рис., а) и деформации электронных оболочек отд. ионов (электронная поляризация).



Рис. Поляризация диэлектриков: а — ион­ная; б — электронная; в — ориентационная.


В кристаллах с ковалентной связью (напр., алмаз) поляризация обуслов­лена гл. обр. смещением эл-нов, осу­ществляющих хим. связь (рис., б). В т. н. полярных Д. (напр., твёрдый H₂S) молекулы или радикалы пред­ставляют собой электрич. диполи, к-рые в отсутствии электрич. поля ориентированы хаотически, а в поле приобретают преимуществ. ориента­цию (рис., в). Такая ориентаци­онная поляризация типична для мн. жидкостей и газов. Сходный механизм поляризации связан с «пере­скоком» под действием электрич. поля отд. ионов из одних положений рав­новесия в другие. Особенно часто такой механизм наблюдается в в-вах с водородной связью, напр. у льда, где ионы водорода имеют неск. поло­жений равновесия.

Поляризацию Д. характеризуют электрич. дипольным моментом единицы объёма



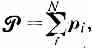
где p_i — дипольные моменты ч-ц (атомов, ионов, молекул), N — число ч-ц в единице объёма (см. Поляризуемость). Вели­чина  зависит от напряжённости электрич. поля E. В слабых полях =E. Коэфф. пропорционально­сти  наз. диэлектрической восприимчивостью. Часто

вместо вектора  пользуются векто­ром электрич. индукции:

D=E+4=E (в системе СГСЭ), (1)

где 6 — диэлектрическая проница­емость. В вакууме =0 и =1 (в системе СГСЭ). Величины  и  — осн. характеристики Д. В анизо­тропных крист. Д. направление  определяется не только направлением поля Е, но и направлением осей сим­метрии кристалла. Поэтому вектор  составляет разл. углы с E в за­висимости от ориентации Е по от­ношению к осям симметрии в кристал­ле. В этом случае  и  явл. тензорами.

Диэлектрики в переменном поле. Если поле E быстро изменяется во времени t, то поляризация Д. не ус­певает следовать за ним. Между ко­лебаниями  и E появляется раз­ность фаз 8. Диэлектрич. проница­емость в этом случае представляют комплексной величиной: ='-i", причем ' и " зависят от частоты перем. электрич. поля . Абс. ве­личина ||=('²+"²) определяет ам­плитуду колебания вектора индукции D, а отношение '/" определяет ди­электрические потери. В пост. элект­рич. поле "=0, а '=.

В перем. электрич. полях высоких частот (оптич. диапазон) св-ва Д. принято характеризовать показате­лями преломления n и поглощения k (вместо ' и "). Первый равен отно­шению скоростей распространения эл.-магн. волн в Д. и в вакууме. Пока­затель поглощения k характеризует затухание эл.-магн. волн в Д. Ком­плексный показатель преломления ра­вен n=n(1+ik); величины n, k, ' и " оказываются связанными соотноше­нием:

n(1+ ik)=('-i") . (2)

Поляризация диэлектриков в отсут­ствии электрич. поля Е. В крист. Д., где ионы разного знака расположены в определённом порядке, поляризация может существовать и в отсутствии электрич. поля. Обычно она не про­является, т. к. создаваемое электрич. поле компенсируется полем свободных зарядов, натекающих на поверхность кристалла извне и изнутри. Нару­шение компенсации, приводящее к врем. появлению электрич. поля в кристалле, происходит в пироэлектриках — при изменении темп-ры кри­сталла и в пьезоэлектриках — при де­формации. Разновидностью пироэлектриков явл. сегнетоэлектрики, в к-рых поляризация может существенно из­меняться (как по величине, так и по направлению) под влиянием внешних воздействий. Поляризация в отсут­ствии поля может наблюдаться также в нек-рых в-вах типа смол и стёкол (см. Электреты).

Электропроводность Д. мала, но отлична от нуля (табл.). Подвижными носителями заряда в Д. могут быть эл-ны и ионы. Электронная проводи­мость в обычных условиях мала по

сравнению с ионной. Ионная прово­димость обусловлена перемещением собств. и примесных ионов. Возмож­ность перемещения ионов по кри­сталлу связана с наличием структур­ных дефектов в кристаллич. решётке. Если, напр., в кристалле есть ва­кансии, то под действием поля сосед­ний ион может занять её, во вновь образовавшуюся вакансию может пе­рейти след. ион и т. д. Перемещение ионов может происходить также по междоузлиям. С ростом темп-ры ион­ная проводимость возрастает. Замет­ный вклад в электропроводность Д. может вносить поверхностная прово­димость (см. Поверхностные явления).

Пробой. Электрич. ток j через Д. пропорционален напряжённости элект­рич. поля Е (закон Ома): j=E, где а — проводимость Д. Однако в до­статочно сильных полях ток нарастает быстрее, чем по закону Ома. При нек-ром критич. значении E_пр на­ступает электрич. пробой Д. Величина E_пр наз. электрической проч­ностью Д. (табл.). При пробое

УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ  И ЭЛЕКТРИЧ. ПРОЧНОСТЬ Е_пр НЕК-РЫХ ТВЁРДЫХ ДИЭЛЕКТРИКОВ



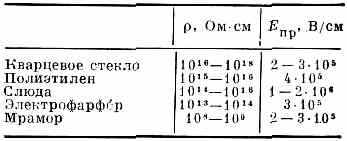
почти весь ток течёт по узкому каналу (см. Шнурование тока).

В твёрдых Д. различают тепловой и электрич. пробой. При тепловом пробое с ростом j растёт темп-pa Д. (Джоулева теплота), что приводит к увеличению числа подвижных носи­телей заряда n и уменьшению . При электрич. пробое с ростом поля Е возрастает генерация носителей под действием поля. В Д. пробою способствуют неизбежные неоднород­ности, т. к. в местах неоднородности поле Е может возрасти.

Плотность тока в шнуре может достигать больших величин. Это мо­жет привести к разрушению Д.: об­разуется сквозное отверстие или Д. проплавляется по каналу; в канале могут протекать хим. реакции; напр., в органич. Д. осаждается углерод, в ионных кристаллах — металл (метал­лизация канала) и т. п.

Электрич. прочность жидких ди­электриков в сильной степени зависит от чистоты жидкости. Наличие при­месей и загрязнений существенно по­нижает Е_пр. Для чистых однородных жидких Д. E_пр близка к E_пр твёрдых Д. Пробой в газе связан с ударной ионизацией и проявляется в виде электрического разряда в газах.

177