Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби, г. Алматы; > С. К. Тлеукенов доктор физико-математических наук, профессор, пгу им. С. Торайгырова, г. Павлодар; > А. М. Мубараков

Вид материала

Учебник

Содержание 3.1.2 Напряженность электрического поля. Поток линий вектора напряженности S в однородном электрическом поле (рисунок - 3.6). Выберем нормаль n

Подобный материал:

• Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 349.17kb.
• Б. А. – доктор юридических наук, профессор Казну им аль-Фараби, 209.21kb.
• Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная, 263.95kb.
• А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор, 1066.25kb.
• Веселаго Виктор Георгиевич, доктор физико-математических наук, профессор мфти, область, 30.58kb.
• Практических: 0 Лабораторных, 16.69kb.
• Практических: 34 Лабораторных, 24.5kb.
• Практических: 0 Лабораторных, 16.63kb.
• Практических: 34 Лабораторных, 20.05kb.
• Практических: 0 Лабораторных, 18.53kb.

3.1.2 Напряженность электрического поля. Поток линий вектора напряженности

Электрические заряды вносят определенные изменения в окружающее их пространство, проявляющееся, в частности, в том, что на другие, внесенные в это пространство электрические заряды, действуют определенные силы. Если в пространстве обнаруживается действие сил на электрические заряды, то говорят, что в нем существует электрическое поле. Поле так же реально, как вещество. Так же, как и вещество, является одним из видов материи, которой присуща масса и определенная энергия.

Электрическое поле изучают с помощью пробного точечного положительного заряда, величина которого своим действием не искажает заметно исследуемое поле. Помещая пробный заряд в различные точки поля, можно определять действующие на него силы, которые не будут равны во всех точках по величине и направлению. Следовательно, действие поля на один и тот же электрический заряд в одной его точке отличается от действия поля в другой ее точке.

Если в одну и ту нее точку электрического поля помещать порознь пробные заряды q₁, q₂, q_n., то действующие силы на эти заряды будут соответственно равны F_1. F₂; F..;; F_n. Оказалось, что отношение F₁/ q₁ = F_2/ q₂ = ..= F_n/q_n. т. е. для данной точки поля величина постоянная и не зависит от величины пробного заряда. Это отношение взято для количественной характеристики поля, обозначено буквой Е и названо напряженностью электрического поля:

Е = F/q.

(3.2)

Напряженность поля Е есть векторная величина; ее направление совпадает с направлением вектора силы F, действующей на положительный заряд. Из определения видно, что напряженность поля является силовой характеристикой поля. Определим напряженность электрического поля простейшего точечного заряда q. Для этого подставим в формулу напряженности из закона Кулона силу, действующую на него со стороны электрического поля:

Е = F/q = q/4πε0εr2.

(3.3).

Анализ данной формулы показывает, что для точечного заряда направление вектора Е совпадает с направлением силы, действующей на положительный заряд, а величина убывает пропорционально квадрату расстоянию от точечного заряда.

Важнейшей задачей электростатики является исследование поля, т. е. нахождение напряженности в каждой точке исследуемого пространства. Если известно электрическое поле произвольных зарядов q₁ и q₂ в отдельности, то естественно поставить вопрос о том, каково будет результирующее поле, образованное этими зарядами. Опыт показывает, что напряженность результирующего электрического поля определяется векторной суммой напряженностей, создаваемых накладывающимися полями. Это называется принципом наложения (суперпозиции) электрических полей.

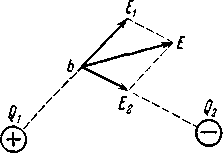
Пусть в нашем примере E₁ — напряженность поля, создаваемая зарядом q₁, в точке b, напряженность же, создаваемая зарядом q₂, в этой же точке пусть будет Е₂ (рисунок - 3.2). На основании принципа суперпозиции результирующая напряженность в точке b равна Е = E₁+ E₂. Принцип суперпозиции справедлив для какого угодно числа полей:

Е = E1+ E2 + + E2 = ∑Ei

(3.4).

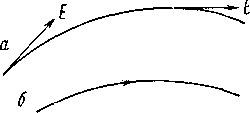
Напряженность электрического поля в различных точках пространства может быть неодинаковой, но в каждой точке поля вектор напряженность имеет определенное направление. Поэтому, электрическое поле можно изобразить графически с помощью системы линий называемых «силовыми линиями». Силовыми линиями называют линию, проведенную в электрическом поле так, что в любой точке касательная к ней совпадает с вектором напряженности (рисунок - 3.3). Силовым линиям приписываются направления электрических сил, действующих на положительные пробные заряды. Так как напряженность в каждой точке поля имеет определенное направление, то силовые линии не могут пересекаться. Силовым линиям приписывают начало у положительных зарядов и конец — у отрицательных. Иногда силовые линии могут уходить в

Рисунок - 3.2	Рисунок - 3.3

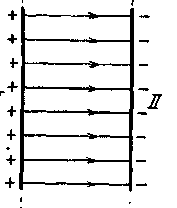
бесконечность или начинаться и кончаться в особых точках поля, в которых напряженность равна нулю. Но никогда силовые линии электростатического поля не замыкаются сами на себя, т. е. не образуют замкнутых петель. Поля, обладающие этими свойствами, называются потенциальными. Для иллюстрации на рисунке - 3.4—3.4 приведены картины силовых линий для некоторых важных частных случаев. Если напряженность поля всюду одинакова по величине и направлению, то поле называется однородным, графически оно изображается системой параллельных силовых линий (рис. 16в).

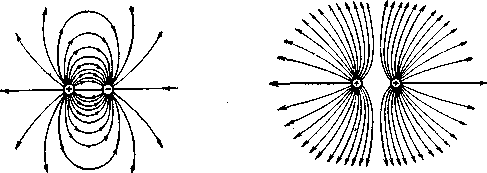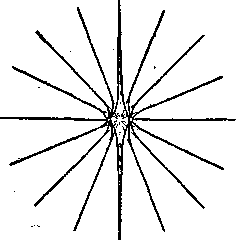а)	б)	в)
Рисунок - 3.4

Электрические явления имеют особую природу и не могут быть объяснены чисто механическими представлениями: изображение полей с помощью силовых линий служит удобным графическим приемом. Чтобы силовые линии отображали величину напряженности в ой или иной точке, условились проводить силовые линии так, чтобы число линий, пронизывающих единицу площади поверхности было пропорционально величине напряженности поля в данном месте. Число силовых линий, пронизывающих данную поверхность, называется потоком силовых линий (Ф_Е), или потоком напряженности поля.

Пусть требуется определить поток, пронизывающий плоскую поверхность S в однородном электрическом поле (рисунок - 3.6). Выберем нормаль n к поверхности, которая составляет угол а с направлением силовых линий. Величина S₀ = S cos α есть проекция

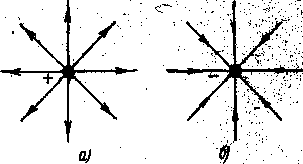Рисунок - 3.5

поверхности S на плоскость, перпендикулярную к направлению силовых линий. Так как через 1 см² площади S₀ проходит Е силовых линий, то весь поток через площадь S₀ будет

ФЕ = ES0 = ES cos α.

(3.5).

Очевидно, такой же поток пронизывает площадку S. Величина Е_n = E cos α есть проекция вектора Е на направление нормали n. Таким образом, поток силовых линий через плоскую поверхность S в однородном поле равен:

ФЕ = Еn S.

(3.6).

Поток силовых линий есть скаляр. Из (18,1) видно, что эта величина может быть положительной и отрицательной. Если силовые линии составляют острый угол с нормалью (cos α > 1), то поток будет положительным. Если этот угол тупой (cos α < 1), то поток отрицателен.

Пусть требуется определить поток силовых линий через произвольно выбранную поверхность в данном неоднородном поле. Эту поверхность можно разбить на бесконечно малые элементы dS, которые можно считать плоскими, а поле возле них - однородным.

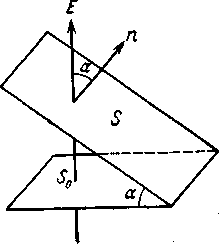Рисунок - 3.6

Поэтому поток через любой элемент такой поверхности равен

dФЕ =EndS.

(3.7).

Полный поток силовых линий через произвольно выбранную поверхность S в любом неоднородном поле равен сумме потоков всех ее элементов:

ФЕ = ∫EndS,

(3.8),

где знак ∫ выражает интегрирование по поверхности S.