А. М. Мубараков

Вид материала

Содержание

2.1.3 Законы идеального газа
Закон Шарля.
Закон Дальтона.
2.3. Первое начало термодинамики

Подобный материал:

1 ... 7 8 9 10 11 12 13 14 ... 48

2.1.3 Законы идеального газа

Законы, управляющие поведением газов, были в свое время открыты опытным путем.

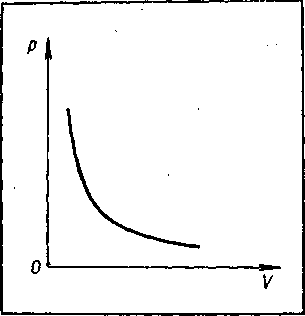
Закон Бойля— Мариотта. Рассмотрим газ, когда его температура поддерживается постоянной. Такие условия называются изотермическими. Если изменение состояния происходит при Т = const, то остальные два параметра (Pи V) ведут себя таким образом, что их произведение остается величиной постоянной:

_PV = const.

(2.13).

Эта формулу называют уравнением изотермы, и выражает закон Бойля – Мариотта. Графически зависимость р от V изображен на рисунке - 2.8. Эти кривые, называемые изотермами, они представляют собой гиперболы.

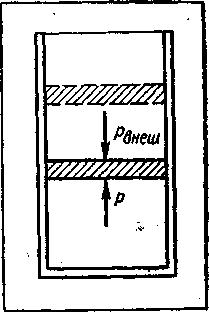
Закон Гей-Люссака. Поместим газ в цилиндр под поршень (рисунок - 2.9.). Пусть на поршень сверху действует атмосферное давление р₀. Это давление по закону Паскаля будет передаваться во все точки газа под поршнем. Если поршень имеет массу т и сечение S, то давление р_внеш внешних сил газ займет такой объем, при котором давление внутри газа станет равным внешнему давлению: р₀. == р_внеш

При квазистатическом нагревании газа под поршнем при постоянном внешнем давлении, как показывает опыт, объем всех без исключения газов увеличивается, а при охлаждении уменьшается. Так же как и для твердых тел, можно ввести коэффициент объемного расширения газов по формуле

α = (1/V₀)_*(V- V₀)/(t-t₀) = (1/V₀)_*(∆V/∆t),

(2.14),

где ∆V = V - V₀ — изменение объема газа при изменении температуры на ∆t = t — t₀,, V и V₀ — объемы при температурах t и t₀. Исследуя на опыте тепловое расширение газов, французский ученый Гей-Люссак открыл, что коэффициент объемного расширения при постоянном давлении у всех газов одинаков и равен 1/273,15 °С ^-1. Из этого закона следует, что объем газа V при температуре t можно найти, зная


Рисунок - 2.8	Рисунок - 2.9

начальный объем газа V₀, при температуре t₀:

V = V₀[1+ α (t — t₀)]

(2.15).

Обычно в качестве начальной температуры берут 0° С, в этом случае V = V₀(l+αt). Как видно из этого уравнения, совокупность состояний, отвечающих одному и тому же давлению, изобразится на графике в координатах V и t прямой линией, отсекающей на оси V отрезок V₀ и имеющей тангенс угла наклона, равный αV₀ (рисунок - 2.10). Такую зависимость поэтому обычно называют линейной. В координатах р и t график изобарического процесса представляет собой прямую линию, параллельную оси t (рисунок - 2.10), называемую изобарой. Закон Гей-Люссака отражает связь между объемом и температурой идеального газа в изобарическом процессе изменения его состояния.

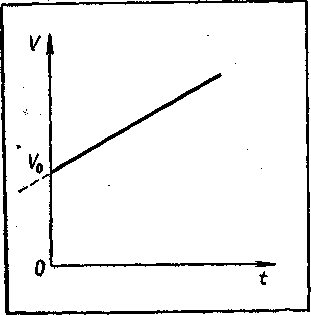Рисунок - 2.10

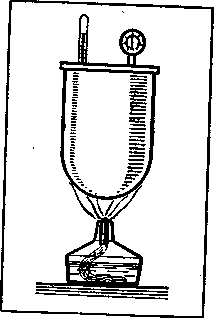
Закон Шарля. Рассмотрим теперь процесс нагревания газа при постоянном объеме, или, как говорят, процесс изохорического нагревания газа. Поместим для этого газ в герметичный сосуд, например в металлический котел с плотно завинчивающейся крышкой (рисунок - 2.11). Будем нагревать газ в котле, измеряя его температуру и давление. Как показывает опыт, давление газа внутри котла увеличивается с ростом температуры. Величину γ, характеризующую изменение давления газа при изменении температуры и называют термическим коэффициентом давления:

γ = 1/p₀ _*(p-p₀)/(t-t₀) = 1/p₀ _*∆p/∆t

(2.16),

где ∆р = p-p₀— изменение давления газа при изменении его температуры на ∆t = t-t₀, р и р₀ — давления газа соответственно при температурах t и t₀. Измеряя давление различных газов при нагревании при постоянном объеме, французский ученый Шарль установил, что термический коэффициент давления для всех газов одинаков и равен 1/273,15 °С ^-1Зная начальное давление р₀ и начальную температуру t₀, из закона, установленного Шарлем, легко найти давление р при температуре t:

р = р₀[1+γ(t-t₀)]

(2.17).

Если за начальную температуру принять 0° С, то р = р₀(t-γt). График изохорического процесса в координатах p и t представляет собой прямую линию, отсекающую на оси р отрезок р₀ и имеющую тангенс угла наклона, равный ур₀ (рисунок - 2.12).

Законы Гей-Люссака и Шарля выглядят гораздо проще, если вместо шкалы Цельсия для температуры ввести шкалу, предложенную английским физиком Кельвином. Связь между температурой Т по шкале Кельвина и температурой t по шкале Цельсия дается формулой

Т= t + 1/α =t + 273,15°.

(2.18).

Шкалу Кельвина называют абсолютной шкалой температур. Законы Гей-Люссака и Шарля при этом примут вид:

V = αV₀T, p = αp_QT,

(2.19),

где V₀ и р₀ — объем и давление газа при температуре T₀=- = 273,15 К.

Равенство коэффициента теплового расширения газа при постоянном


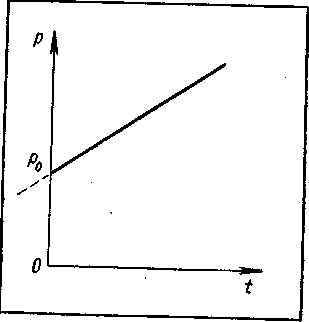Рисунок - 2.11	Рисунок - 2. 12

давлении термическому коэффициенту давлению при постоянном объеме является свойством, присущим только газам. Оно позволяет найти уравнение состояния газов.

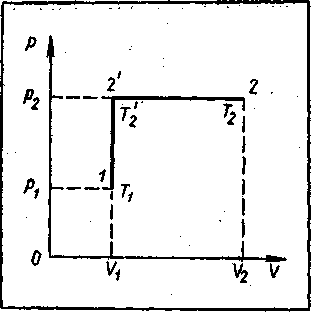
Совершим для этого над газом тепловой процесс, нагревая его сначала при постоянном объеме, а затем при постоянном давлении. График процесса изохорического нагревания в координатах р и V изобразится прямой /, 2', параллельной оси ординат р. Процесс изобарического нагревания изобразится на этом графике прямой 2', 2, параллельной оси абсцисс V (рисунок - 2.13). Обозначим:

- давление, объем и температуру газа в начале теплового процесса через р₁, V_l ,T₁(точка 1)

- в конце процесса изохорического нагревания через р₂, V₁ T '₂ (точка 2')

- и в конце изобарического процесса через р₂, V₂, T₂(точка 2).

Из закона Шарля следует, что отношение давления к абсолютной температуре есть величина постоянная (р/Т₀ = αр₀). Поэтому давление и температура газа в точке 2 связаны с давлением и температурой газа в точке1 соотношением р₂/Т '_{2 =} р₁/Т₁ из которого находим температуру Т '₂в конце изохорического нагревания:

Т '₂=(р_2/р₁ )Т_1.Температура Т'₂ и объем газа V₁ в точке 2' в процессе изобарического нагревания связаны с температурой Т₂ и объемом газа V₂ в точке 2 соотношением

V1/ Т '2 = V2/ Т'2

Подставляя в это уравнение температуру Т'₂= (р₂Т₁)/р₁ , получаем: V₁ р₁/ р₂ Т₁= V₂/ Т'₂. Откуда следует:

V₁р₁/Т₁= V₂р₂/Т₂

Начальное и конечное состояния газа (точки 1 и 2 в данном опыте) были выбраны совершенно произвольно. Можно было бы взять в

Рисунок - 2. 13

качестве начального и конечного состояний другие точки. Процесс перевода газа из состояния 1 в состояние 2 также можно было бы совершить по-иному, нагревая, например, газ сначала изобарически, а затем изохорически. Однако в любом случае можно показать, что начальное (1) и конечное (2) состояния газа всегда связаны между собой соотношением: V₁р₁/Т₁= V₂р₂/Т₂или, по-другому, что в состоянии теплового равновесия для данной массы газа справедливо соотношение рV/Т = const.

Неизвестную постоянную удалось вычислить после того, как итальянским физиком Авогадро был экспериментально установлен закон, что один моль любого газа при давлении в 1 атм и температуре 0° С занимает объем 22,4 л. Подставляя эти данные в найденное соотношение, получили постоянную

рV/Т≈8,3 Дж/моль К

(2.20).

Эту величину обозначают буквой R и называют универсальной газовой постоянной.

Для произвольной массы газа m постоянную легко найти, учитывая, что в состоянии теплового равновесия масса газа распределена равномерно по объему. Если моль газа массой μ занимает объем V_μ., то тот же газ массой m занимает при тех же условиях V = mV_μ/ μ, где V_μ/ μ – объем, занимаемый 1 г вещества. Из уравнения рV_μ/Т = R находим: рμV_μ/ m Т = R, или

pV= (m/μ)RT.

(2.21).

Это уравнение и называют уравнением состояния идеального газа.

Уравнение состояния в форме рV/Т = const было впервые получено Клапейроном, а для произвольной массы газа уравнение состояния в форме pV= (m/μ)RT было записано Менделеевым. Поэтому часто уравнение газового состояния идеального газа называют уравнением Менделеева — Клапейрона.

Следует отметить, что в реальных условиях ни один из газов не подчиняется строго уравнению Менделеева — Клапейрона. Правда, отклонения от закона Менделеева — Клапейрона фактически исчезают для достаточно разреженных газов. Однако при низких температурах и больших плотностях начинаются заметные отклонения от этого закона. То же самое происходит и при достаточно высоких температурах (порядка тысячи и нескольких тысяч градусов) для газов из многоатомных молекул. При этих температурах начинается распад молекул газа на атомы. При еще более высоких температурах начинается распад атомов на электроны и ионы и любой газ перестает подчиняться уравнению Менделеева — Клапейрона, даже при сколь угодно малых плотностях.

Закон Дальтона. В обычных условиях чаще приходится иметь дело не с чистым газом (кислородом, азотом и т. д.), а со смесью нескольких газов. Так, например, воздух состоит из смеси азота, кислорода, углекислого и других газов.

Каждый из газов в смеси вносит свой вклад в давление, создаваемое смесью. Давление, оказываемое какой-либо компонентой смеси на стенки сосуда, когда все другие компоненты газа удалены из объема, называют парциальным давлением. Английский физик Дальтон экспериментально установил, что давление газовой смеси равно сумме парциальных давлений:

р = р₁ + р₂ + . :

(2.22),

а парциальное давление каждой из компонент смеси подчиняется при этом уравнению Клапейрона — Менделеева: р_lV = m₁/μ₁ RT, p₂V = m₂/μ₂ RT и т.д., где V —объем смеси, Т — ее температура, m — масса, a μ_i — молярная масса i-й компоненты смеси.

Уравнение состояния газовой смеси легко найти из закона Дальтона. Для этого нужно подставить в уравнение р =p₁ + p₂+ парциальные давления, найденные из уравнения состояния каждой компоненты p₁ = m₁/μ₁ RT/V, и умножить правую и левую части полученного равенства на объем, т. е.

pV = (m₁/μ₁ + m₂/μ₂ + .)RT

(2.23).

2.2 Распределение Максвелла и Больцмана

2.2.1 Скорости газовых молекул

Основное уравнение кинетической теории газов устанавливает связь между средней кинетической энергией поступательного движения молекул и абсолютной температурой:

m‹v²›/2 = 3/2kT

(2.24).

Тем самым и определяется, что средняя квадратичная скорость молекул которая для данного газа (при данном значении массы молекулы m) зависит только от температуры. Поскольку по уравнению состояния pV — RT, где V — объем, занимаемый молем газа, последнее равенство можно представить в виде: √‹v²› = √3р/ρ, где ρ — плотность газа, равная μ/V. Формула показывает, что средняя квадратичная скорость молекул может быть вычислена из данных измерений чисто макроскопических величин — давления газа и его плотности.

√‹v²› = √3kT/m = √3RT/μ

(2.25).

Большой интерес представляет экспериментальное определение скорости газовых молекул. Первое непосредственное опытное определение скорости газовых молекул было проведено Штерном (1920 г.).Схема опыта представлена на рисунок - 2.14. Источником частиц (в данном случае атомов), скорость которых исследуется, в опыте служила платиновая проволока L, покрытая слоем серебра. Она окружена двумя цилиндрическими диафрагмами, в которых прорезаны узкие щели S_x и S_a так, что проволока и щели лежат в одной вертикальной плоскости. Это устройство помещено внутрь цилиндра Р, на внутренней поверхности которого против щели S₂ имеется мишень — съемная латунная пластинка. Вся эта система помещена под колокол насоса, создающего высокий вакуум (≈10 ^-6 тора), и может вращаться с большой скоростью около оси, вдоль которой натянута проволока L. Пропусканием электрического тока через проволоку L Штерн нагревал ее до температуры, при которой серебро заметно испарялось (1235 К). При этом атомы серебра, скорости которых соответствуют температуре проволоки, вылетают по всем направлениям. Часть атомов проходит через щели S₁ и S₂, которые вырезают из потока атомов узкий, резко очерченный пучок, состоящий из движущихся в одном направлении и не сталкивающихся между собой частиц (такие направленные потоки молекул носят общее название молекулярных пучков).

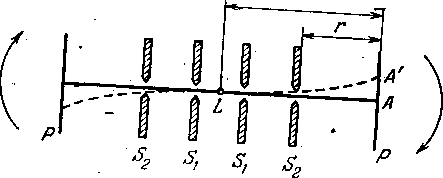Рисунок - 2. 14

Когда вся система неподвижна, атомы серебра, образующие пучок, конденсируются на мишени в месте, обозначенном на рисунке - 2. 14 буквой А, образуя на мишени полоску, являющуюся как бы изображением щели S₂. Но если привести прибор во вращение, атомы пучка попадут уже не в A, а окажутся смещенными относительно А на некоторое расстояние δ (на рисунке δ = АА'). Ведь расстояние r от щели S₂ до мишени атомы, движущиеся со скоростью v, проходят за время t = rlv. Но за это время каждая точка вращающегося цилиндра сместится на расстояние δ, равное 2πηRt, где п — число оборотов цилиндра Р в секунду и R — радиус этого цилиндра: δ = 2πηRt. Подставив сюда вместо t его значение r/v, получаем: δ = 2πηRr/v. При вращении прибора в обратном направлении полоска сместится на такое же расстояние по другую сторону от А. Таким образом на мишени получаются две полоски, разделенные расстоянием 2δ. Это повышает точность измерения δ. Измерив расстояние между полосками, зная п, r и R, вычисляют по последней рабочей формуле скорость атомов v при температуре проволоки.

Измеренные таким образом значения скорости атомов оказались близкими к значениям, вычисленными другими методами. Метод молекулярных пучков, разработанный Штерном, до сих пор широко используется для исследования различных свойств частиц. Опыты Штерна позволяют не только измерить среднюю квадратичную скорость, но и по размытию осадка грубо определить распределение молекул по скоростям.

По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой m в газе, находящемся в состоянии равновесия при Т = const, остается постоянной. Это объясняется тем, что в газе, находящемся в равновесии, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.

При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т. е.

dN(v)/N = f(v)dv,

откуда,

f(v) = dN(v)/N dv.,

Применяя методы теории вероятностей, Максвелл нашел функцию f(v) — закон распределения молекул идеального газа по скоростям:

f(v) = 4π(m₀/2πkT)^3/2v²e^{-m0v2/ 2kT}

(2.26).

Из этой формулы видно, что конкретный вид функции зависит от рода газа (m) и от параметра состояния (Т). График этой функции приведен на рис. 65. Так как при возрастании v множитель exp[-m₀v²/(2kT)] уменьшается быстрее, чем растет множитель v², то функция f(v) достигает максимума при v_B и затем асимптотически стремится к нулю. Кривая асимметрична относительно v_B. Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь более светлой полоски на рисунок - 2.15. Общая площадь фигуры, ограниченной кривой распределения и осью абсцисс, должна быть равна единице, что отражает факт существования самой частицы в этом объеме. Поэтому функция f(v) должна удовлетворять условию нормировки:

∫f(v)dv = 1.

(2.27).

Кривая функции распределения (рисунок - 2. 15) имеет максимум при некотором значении скорости v_в. Это значит, что скорости, близкие к v_в, встречаются у молекул газа чаще других, что вероятности того, что скорость молекулы близка к v_в — наибольшая. Поэтому скорость v_в., которой соответствует максимум кривой распределения Максвелла, называется наиболее вероятной скоростью. Значение этой скорости можно найти, продифференцировав функцию распределения по аргументу v, и приравняв результат нулю. Искомая наиболее вероятная скорость v_в:

v_B = √2kT/m₀=√2RT/μ

(2.28).

Из этой формулы следует, что при повышении температуры максимум функции распределения молекул по скоростям сместится вправо, значение наиболее вероятной скорости становится больше (рисунок - 2.16). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

Зная функцию распределения молекул по скоростям можно найти и другую важную характеристику движения молекул – его среднеарифметическую скорость : =-1/N∫vdN(v) = ∫vf(v)dv. Подставляя сюда f(v) и интегрируя, получим

=√/8/kT/(πm₀) = √8RT/(πμ)

(2.29).

Таким образом, поведение молекул, образующих газа, можно охарактеризовать следующим набором скоростей:

1) наиболее вероятная - v_B = √2kT/m₀=√2RT/μ;

2) среднеарифметическая - =√/8/kT/(πm₀) = √8RT/(πμ) )=1,13 v_B;

3) средняя квадратичная - √‹v²› = √3kT/m = √3RT/μ = 1,22 v_в


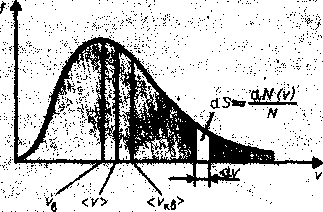Рисунок - 2. 15	Рисунок - 2. 16

Сравнивая выражения для скоростей, находим соотношения между тремя вычисленными скоростями. Средняя квадратичная скорость на 9% больше средней арифметической и на 22% больше наивероятнейшей скорости. Средняя арифметическая скорость оказывается «средней» и в том смысле, что ее численное значение лежит между наивероятнейшей и средней квадратичной скоростями. Как это видно из приведенных цифр, различие между этими тремя скоростями не очень велико.

В равновесном состоянии давление и температура газа одинаковы по всему объему газа. При наличии же внешних сил молекулярные движения приводят к своеобразному распределению молекул в поле этих сил. Рассмотрим, например, газ (воздух), находящийся под действием силы тяжести. Если бы отсутствовало тепловое движение молекул, то все они под действием силы тяжести «упали» бы на Землю, и весь воздух собрался бы тончайшим слоем у поверхности Земли. Если бы отсутствовала сила тяжести, но существовали бы только молекулярные движения, молекулы разлетелись бы по всему мировому пространству. Атмосфера, воздушная оболочка Земли, обязана своим существованием наличию одновременно и теплового движения молекул, и силы притяжения к Земле. При этом в атмосфере устанавливается вполне определенное распределение молекул по высоте.

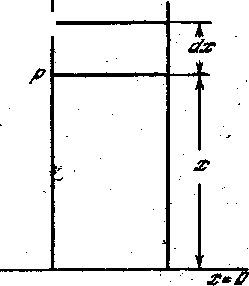
Рассмотрим вертикальный столб воздуха (рисунок - 2.17). Пусть у поверхности Земли, где х = 0, давление равно» р₀, а на высоте х равно р. При изменении высоты на dx давление изменяется на dp. Давление воздуха равно весу вертикального столба воздуха над площадью, равной единице. Поэтому dp равно разности весов столбов воздуха над площадью, равной единице, на высотах х и х + dx: dp = - ρgdx, где ρ плотность воздуха и g — ускорение силы тяжести. Плотность ρ газа равна, очевидно, произведению массы m₀ молекулы на их число п в единице объема: ρ= m₀п. Из кинетической теории известно, что n = p/kT. Следовательно, ρ = m₀p/kT и dp = - mg/kT _*pdx. Произведем разделение переменных dp/p= -( mg/kT)dx. После интегрирования, интересующая нас зависимость давления воздуха от высоты над поверхностью Земли имеет вид:

p = р₀ e ^-(mg/kT)x

(2.30),

или, учитывая, что m = μ/N_а, получаем:

p = р₀ e ^-(^μg^/^RT⁾^x

(2.31).

Это уравнение, устанавливающее закон убывания давления с высотой, называется барометрической формулой. Из уравнения видно, что давление газа убывает с высотой по экспоненциальному закону. Полученная барометрическая формула относится к случаю, когда газ находится под действием силы тяжести.

Так как давление газа, как мы видели раньше, пропорционально числу молекул п в единице объема (р = nkT), то из последней формулы можно найти закон убывания плотности молекул с высотой:

n = n₀ e ^-(^μg^/^RT⁾^x

(2.32),

где п и n₀ — число молекул в единице объема в точках, между которыми разность высот равна х. Эту формулу можно преобразовать, если учесть, что молекула находится в поле силы тяготения Земли (при условии, сто на уровне h=0, Е _пот = 0).

n = n₀ e ^-^mgh^/^kT

(2.33).

Поэтому Л.Больцман показал, что этот закон распределения молекул универсален, имеет место в любом произвольном потенциальном поле внешних сил:

n = n₀ e ^-Еп/^kT

(2.34).

Это соотношение закон распределением Больцмана. Оно позволяет определить долю частиц, которые в условиях теплового равновесия, обладающих заданной энергией Е_пот. Из формулы видно, что эта доля зависит только от температуры. При данной температуре доля молекул, обладающих той или иной энергией, зависит от значения этой энергии и быстро уменьшается с ростом энергии.

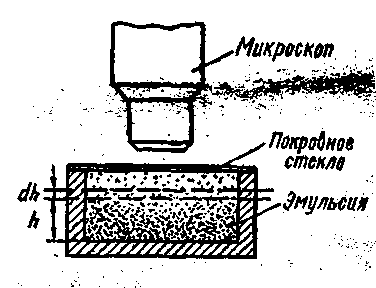
Формула Больцмана была использована Ж Перреном для опытной проверки барометрической формулы и для определения постоянной Больцмана (или, что то же, числа Авогадро). В 1906 г. французский физик Ж. Перрен исследовал распределение по высоте сосуда мельчайших частиц эмульсии смолы гуммигута в воде. Схема опытов Перрена приведена на рисунке - 2.18.

В опытах Ж Перрен изменял: температуру и вязкость среды, а также размер зерен эмульсии. Измерения показали, что концентрация частиц действительно убывает с высотой по экспоненциальному закону, выраженному С помощью микроскопа, установленного вертикально, наблюдалось распределение взвешенных частиц по высоте. Для этого микроскоп фокусировался на слои эмульсии на разных высотах (глубинах). В поле зрения микроскопа оказывались частицы в слое глубиной не более 0,001 мм и совсем не были видны частицы, лежащие выше и ниже. Число частиц в поле зрения было


Рисунок - 2.17	Рисунок - 2.18

невелико, так что их можно было сосчитать. Число это, очевидно, пропорционально числу частиц п в единице объема. Измерения производились многократно, и определялось среднее из многих измерений. Общее число сосчитанных частиц в некоторых сериях опытов достигало многих тысяч. Опыты показали, что при возрастании расстояния h от дна сосуда в арифметической прогрессии концентрация зерен п₀ убывает в геометрической прогрессии.

2.3. Первое начало термодинамики

2.3.1 Работа и энергия в тепловых процессах. Первое начало термодинамики

Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Сказанное позволяет определить общую задачу термодинамики как науки, в которой изучаются свойства макроскопических тел. Термодинамика имеет дело с термодинамической системой — совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией, как между собой, так и с другими телами (внешней средой). Задача термодинамики — определение состояния термодинамической системы. Система может быть в разных равновесных состояниях. Равновесными состояниями называют такие, при которых макроскопические величины, описывающие поведение изолированной системы, остаются неизменными во времени и одинаковыми в пространстве. Состояние системы задается термодинамическими параметрами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно, в качестве параметров, состояния выбирают температуру, давление и объем. Эти параметры являются функциями других параметров. Так, например, объем газа является функцией давления и температуры. Кроме того, во многих задачах нас интересуют такие свойства системы, как внутренняя энергия, энтропия и т. д. Эти величины тоже являются функциями параметров состояния, и их мы будем называть функциями состояния. Следовательно, функцией состояния называется величина, зависящая от параметров состояния: она определена, если даны эти параметры.

Все функции состояния являются «функциями точки», т.е. они вполне определены, если известны координаты точки или параметры состояния на диаграмме. Отсюда вытекают три важных свойства функции состояния.

Если W есть функция состояния, то изменение w зависит только от начальной и конечной точек на диаграмме и не зависит от формы «пути», т. е. не зависит от вида процесса.
Если W = W (x, у, z) есть функция параметров х, у, z, то бесконечно малое изменение dW является полным дифференциалом при бесконечно малых изменениях параметров: dх, dу, dz, где х, у, z — обобщенные параметры состояния, т. е. ими могут быть р, V, Т и т. д.
Для замкнутых процессов (циклов), т. е. таких, когда система из начальной точки после перехода через ряд состояний и вновь возвращается в исходную точку, для функции состояния всегда имеет место: dW = 0. (следствие из 1-го свойства функции состояния: интеграл по z - замкнутому контуру не зависит от вида контура).

Одной из важных функций состояния является внутренняя энергия U. Внутренняя энергия любого тела слагается из кинетической энергии поступательного и вращательного движения молекул, кинетической и потенциальной энергий колебательного движения атомов в молекулах, потенциальной энергии взаимодействия между молекулами и внутримолекулярной энергии (т. е. энергии электронных оболочек атомов и внутриядерной энергии). Кинетическая энергия и потенциальная энергия тела во внешнем силовом поле во внутреннюю энергию тела не входят.

Внутреннюю энергию называют функцией состояния системы, подчеркивая тем самым, что каждому состоянию термодинамической системы однозначно соответствует некоторое значение внутренней энергии. Это означает, что при переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода. Для характеристики этого процесса введено понятие числа степеней свободы — числа независимых переменных (координат), полностью определяющих положение системы в пространстве.

Молекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения (i = 3). При этом энергию вращательного движения можно не учитывать. В классической механике молекула двухатомного газа в первом приближении рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью. Такая система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Таким образом, двухатомный газ обладает пятью степенями свободы (i = 5). Трехатомная и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных (i = 6). Независимо от общего числа степеней свободы молекул три степени свободы всегда поступательные.

В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы

<ε>= i/2kT

(2.35),

где i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы:

i=i_пост+i_вращ + 2i_колеб

(2.36).

В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы. Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия, отнесенная к одному молю газа, будет равна сумме кинетических энергий N_А молекул:

U= i/2kTN_a= i/2m/μRT

(2.37).

ЗдесьU - внутренняя энергия для произвольной массы m газа, где μ — молярная масса этого газа. Таким образом, для идеального газа внутренняя энергия U пропорциональна температуре Т. Из приведенной формулы видно, что для изменения температуры газа нужно изменить его внутреннюю энергию. При изменении внутренней энергии изменится состояние тела, оно будет расширяться или сжиматься и приведет в механическое движение окружающие его тела. Работа А', совершаемая внешними силами над системой, должна быть численно равна и противоположна по знаку работе А, совершаемой при этом самой системой над внешней средой; или, как обычно говорят, «против внешних сил»: А' = - А.

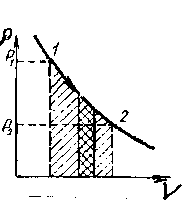
Происходящий обмен энергией между системами может происходить в разных процессах, например, адиабатного взаимодействия. Пусть сначала он находится в равновесном состоянии (рисунок - 2.10). Будем считать заданными первоначальные параметры газа р, V, Т, т. Если уменьшить внешнее давление на малую величину dp, то газ начнет расширяться, причем работа расширения (против внешних сил) равна: dA=(p+dp)dV≈pdV>0. Эту работу принято считать положительной. Она может совершаться за счет изменения внутренней энергии газа, уменьшающейся на величину: dU = - dA<0. Газ при этом охлаждается. Элементарная работа определяется площадью заштрихованного участка. Суммарная работа численно равна площади, ограниченной кривой 1, 2, ординатой р₂, отрезком оси абсцисс (V₂, Vi) и ординатой р_.. Эта работа положительна при обходе контура по часовой стрелке.

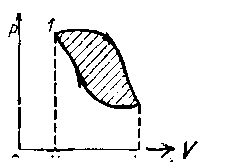
В случае кругового процесса работа будет определяться площадью фигуры внутри замкнутой кривой. После перехода системы из состояния 1 в состояние 2 и обратно ∆U. системы равно нулю, но работа отлична от нуля.Она характеризуется площадью фигуры и зависит от способа, которым осуществляется процесс (рисунок - 2.20). Следовательно, работа, производимая системой, есть характеристика процесса; но она не может быть термодинамической величиной или функцией состояния системы, а является функцией процесса: работа - функция процесса.

В общем, возможны два различных способа изменения внутренней энергии термодинамической системы при ее взаимодействии с внешними телами: путем совершения работы и путем теплообмена.

Благодаря взаимодействию между частицами вещества энергия беспорядочного движения может передаваться от одного тела к другому.


Рисунок - 2.19	Рисунок - 2.20

Это отражается на тепловых свойствах тел. Энергия, сообщаемая системе в форме теплоты, непосредственно идет на увеличение энергии беспорядочного движения частиц системы (атомов, молекул и т. п.), т.е. на увеличение внутренней энергии системы. Частицы тела с более высокой температурой обладают в среднем большей кинетической энергией теплового движения, чем частицы тела, имеющего меньшую температуру. Поэтому частицы первого тела, сталкиваясь с частицами второго тела, передают им часть своей кинетической энергии. В результате интенсивность теплового движения частиц первого тела и его внутренняя энергия уменьшаются, а интенсивность теплового движения частиц второго тела и его внутренняя энергия увеличиваются. Соответственно температура первого тела постепенно понижается, а второго — повышается. Когда температуры тел выравниваются, средние значения кинетической энергии теплового движения частиц в обоих телах также становятся одинаковыми. При этом теплообмен между телами прекращается, так как при столкновениях частиц энергия с равной вероятностью передается как от первого тела второму, так и в обратном направлении. Отсюда следует, что теплота неразрывно связана с процессом передачи энергии, является функцией процесса.

Итак, в отличие от внутренней энергии системы, являющейся однозначной функцией состояния этой системы, теплота и работа имеют смысл только в связи с процессом изменения состояния системы. Они являются энергетическими характеристиками этого процесса. В реальных условиях оба способа передачи энергии системе (в форме работы и в форме теплоты) сопутствуют друг другу:

dU = dQ + dА'

(2.38).

Этот вид уравнения отражает тот факт, что изменение внутренней энергии системы может происходит по двум причинам: - за счет получения или отдачи системой теплоты(dQ) и за счет совершения работы (dA). Если учитывать возможность различных знаков величин , входящих в это уравнение (dА' = - dА.), то его можно написать в виде:

dQ = dU + dA

(2.39).

Данное соотношение отражает собой закон сохранения и превращения энергии в термодинамике. Формулировка первого начала термодинамики выглядит следующим образом: энергия изолированной системы есть величина постоянная. Очевидно, первое начало налагает строгое, ограничение на все процессы в изолированной системе: если затрачивается бесконечно малое количество теплоты dQ и совершается бесконечно малая работа dА, то изменение внутренней энергии тоже бесконечно мало и равно dU.

Blog

Содержание

2.1.3 Законы идеального газа