Программа дисциплины Прикладная статистика Семестры 5,6
| Вид материала | Программа дисциплины |
СодержаниеСодержание курса. |
- Рабочая программа дисциплины «статистика» сд. 01., 398.81kb.
- Программа дисциплины Теория вероятностей и математическая статистика Семестры, 13.32kb.
- Прикладная Статистика, 1137.98kb.
- Программа дисциплины теория вероятностей и математическая статистика, 50.07kb.
- Рабочая программа учебной дисциплины «Прикладная математическая статистика» Уровень, 346.52kb.
- Рабочая программа дисциплины теория игр и исследование операций направления 010400, 185.05kb.
- Программа к государственному экзамену для студентов специальности 061800, 67.22kb.
- Рабочая программа дисциплины прикладная математика (Наименование дисциплины), 188.06kb.
- Рабочая программа дисциплины, 270.7kb.
- Рабочая программа дисциплины для студентов магистратуры, обучающихся по направлению, 120.54kb.
Направление 010100 Математика
Профили. Общий, специализация: Математические методы в экономике.
Программа
дисциплины Прикладная статистика
Семестры 5,6
Цели и задачи курса. Цель курса - ознакомление с методами сбора, обработки и интерпретации данных, планированием эффективных и информативных экспериментов, принятием решений в условиях неопределенности и прогнозированием с использованием компьютерной техники и специализированных программных средств.
Статистические методы используются в технике, экономике, медицине, экономике, при анализе социальных явлений.
Содержание курса. Выборочный метод. Первичная обработка данных. Точечные оценки параметров. Критерии качества оценки: несмещенность оценки состоятельность оценки ,эффективность оценки. Неравенство Рао-Крамера. Основные оценки, используемые в приложениях: оценки среднего,оценки вариации, ассиметрия и эксцесс. Типичные распределения, используемые в статистике: нормальное распределение; распределение
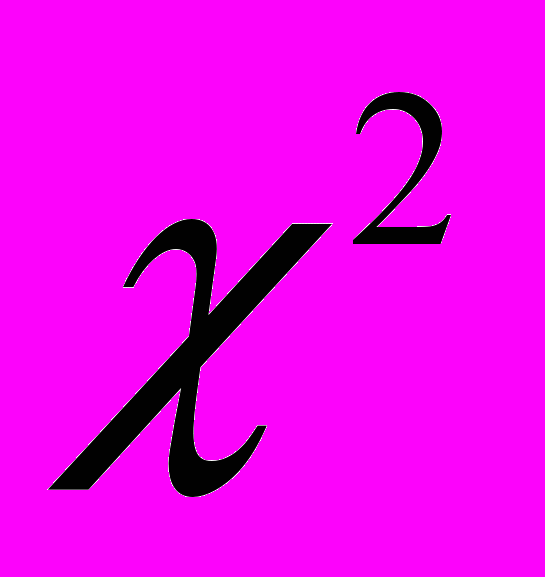- Пирсона; t-распределение Стьюдента; распределение Фишера. Доверительные интервалы: доверительные интервал для математического ожидания: доверительный интервал для дисперсии. Проверка статистических гипотез. Ошибка 1ого и 2ого рода. Лемма Неймана-Пирсона.Типичные задачи проверки гипотез о мат.ожиданиях. Однофакторный дисперсионный (расширенный) анализ (ANOVA). Критерии Кохрана, Бартлетта. Критерий Крускала-Уоллиса. Критерии согласия: критерий χ2-Пирсона; критерий Колмогорова-Смирнова. Проверка однородности выборок. Двухвыборочный критерий Смирнова. Ранговые критерии сдвига. Критерий Манна-Уитни (Вилкоксона). Ранговые критерии парных наблюдений: критерии знаков, знаковых ранговых сумм. Выявление связей между признаками: выявление связей для качественных признаков, критерий 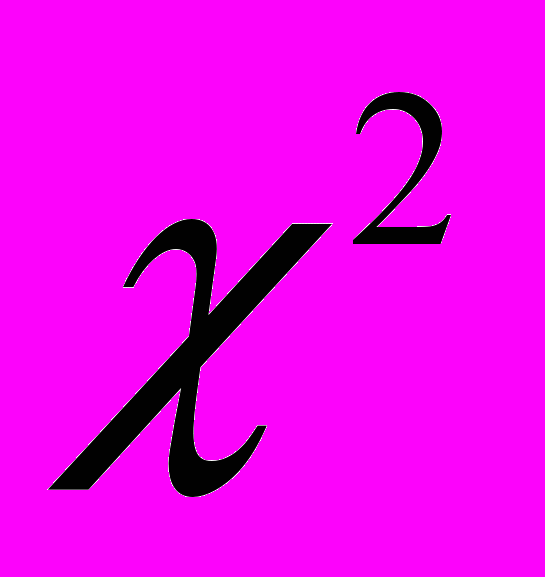-Пирсона; выявление связей для порядковых признаков, критерий Спирмена. Критерий Кендалла. Выявление связей для количественных признаков. Элементы регрессионного анализа: простая линейная регрессия, метод наименьших квадратов для простой регрессии, коэффициент детерминации; стандартные нелинейные модели. Классическая и обобщенная модель Кобба-Дугласа. Множественная линейная модель и МНК.Исправленный коэффициент детерминации. Оценкикачества регрессионной модели в целом. Теорема Гаусса-Маркова. Методы многомерного статистического анализа. Регрессионный анализ: Мультиколлинеарность Ложная корреляция. Частные коэффициенты корреляции. Выявление гетероскедастичности. Автокорреляция в остатках. Критерий Дарбина-Уотсона. Выбор модели оптимальной сложности. Тесты Акайка и Шварца. Фиктивные переменные. Линейные регрессионные модели с переменной структурой. Logit и Probit модели. Метод главных компонент. Элементы факторного анализа. Кластерный анализ.Элементы дискриминантного анализа. Временные ряды. Выделение детерминированной составляющей МНК. Анализ остатков. Белый шум. Адаптивные методы. ARIMA