Личностно ориентированный подход в обучении математике
| Вид материала | Документы |
- Самигуллина Лилия Равилевна учитель физики и информатики моу катмышской сош. Методическая, 32.14kb.
- Методика преподавания русского языка Пособие для учителя, 361.78kb.
- Методические рекомендации личностно ориентированный компетентностный подход к обучению, 26.27kb.
- Личностно – ориентированный подход как основа дифференциации обучения информатики, 91.65kb.
- Личностно-ориентированный подход в обучении физике, 133.53kb.
- План проведения педсовета: Рефлексирование педагогами собственного опыта и знаний, 88.57kb.
- Задачи: Использование личностно-ориентировочных форм, методов и приемов в воспитательной, 309.28kb.
- Открытая школа особый тип учебного заведения. Контингент у нас, действительно,, 94.27kb.
- В. А. Ткаченко моу «Октябрьская сош белгородского района Белгородской области» учитель, 63.58kb.
- Тема: «Личностно ориентированный подход в образовании», 132.1kb.
Личностно ориентированный подход в обучении математике
учитель математики Слободская Т.Г.
стаж работы: 19 лет
Ни для кого не секрет, что математика сложный предмет, который требует плодотворного труда. Математику нельзя выучить («зазубрить»), ее надо понять! А как понять предмет, если он кажется ученику скучным, уроки однообразными. Вот здесь и нужна педагогическая находчивость, которая имеет одну цель – заинтересовать . Появление интереса к предмету можно добиться путем применения новых, современных инновационных технологий в обучении.
В последние годы большинство педагогических коллективов страны настойчиво осваивают теоретические основы и технологию использования ЛОО в учебно – воспитательном процессе. Чем это вызвано?
1. Динамическое развитие общества требует формирования в человеке не столько социально – типичного, сколько ярко индивидуального, позволяющего человеку оставаться самим собой в постоянно изменяющемся социуме.
2. Психологи и социологи отмечают произошедшие в последнее десятилетие существенные изменения в личностном развитии детей. В исследованиях отмечается, что нынешним учащимся свойственны прагматичность мыслей и действий, раскрепощённость и независимость, а эти перемены, в свою очередь, требуют применения новых подходов и технологий во взаимодействии учителя и ученика.
3. Современная школа остро нуждается в гуманизации отношений детей и взрослых, в демократизации школьной жизни.
Личностно ориентированные технологии ставят в центр своей образовательной системы личность обучаемого, обеспечение комфортных, бесконфликтных условий развития, реализацию ее природных потенциалов. Учащийся в этой технологии не просто субъект, но субъект приоритетный; он – цель образовательной системы, а не средство достижения чего – либо отвлеченного.
ЛОТ характеризуются гуманистической и психотерапевтической направленностью и имеют целью разностороннее, свободное и творческое развитие учащегося, формирования у него положительной «Я» - концепции. ЛОО открывает новые потенциальные подходы и тенденции в решении вопросов «чему» и «как» учить сегодня.
Во-первых, содержание обучения рассматривается как средство развития личности, а не как самодавлеющая цель;
во-вторых, обучение ведется прежде всего обобщенным знаниям, умениям и навыкам и способам мышления; осуществляется объединение, интеграция различных дисциплин;
в- третьих, достигается вариативность и диффененциация обучения на основе деятельностного подхода;
в-четвертых, активно используется положительная стимуляция учения.
На личностно ориентированном уроке создается та учебная ситуация, когда не только излагаются знания, но и раскрываются, формируются и реализуются личностные особенности учащихся. На таком уроке господствует эмоционально положительный настрой учащихся на работу, урок становится более интересным, привлекательным, результативным. Учитель не просто создает благожелательную творческую атмосферу, но и постоянно обращается к субъектному опыту школьников, т.е. опыту их собственной жизнедеятельности. И, наконец, самое важное – он признает самобытность и уникальность каждого обучаемого.
^ Особенности личностно ориентированного урока
1. Конструирование дидактического материала разного типа , вида и формы, определение цели, места и времени его использования на уроке.
2. Продумывание учителем возможностей для самостоятельного проявления учеников. Предоставление им возможности задавать вопросы, высказывать оригинальные идеи и гипотезы.
3. Организация обмена мыслями, мнениями, оценками. Стимулирование учащихся к дополнению и анализу ответов товарищей.
4. Использование субъектного опыта и опора на интуицию каждого ученика. Применение трудных ситуаций, возникающих по ходу урока, как области применения знаний.
5. Стремление к созданию успеха для каждого обучаемого.
6. Побуждение учащихся к поиску альтернативной информации при подготовке к уроку.
7. Продуманное чередование видов работ, типов заданий, что уменьшает утомляемость учащихся.
8. Проведение наблюдений за школьниками.
Одна из широко используемых мною технологий является технология уровневой дифференциации. Теоретическое обоснование этой технологии основывается на том, что различия основной массы учащихся по уровню обучаемости сводится прежде всего ко времени, необходимому ученику для усвоения учебного материала. Изучались способности учеников в ситуации, когда время на изучение материала не ограничивалось и были выделены такие категории:
- малоспособные, которые не в состоянии достичь заранее намеченного уровня знаний и умений даже при больших затратах учебного времени;
- талантливые ( около 5% ), которым нередко по силам то, с чем не могут справиться все остальные;
- учащиеся, составляющие большинство ( около 90% ), чьи способности к усвоению знаний и умений зависят от затрат учебного времени.
Если каждому ученику отводить необходимое ему время, соответствующее его личным способностям и возможностям, то можно обеспечить гарантированное освоение базисного ядра учебной программы. Для этого нужны школы с уровневой дифференциацией, в которых ученический поток делится на подвижные по составу группы, овладевающие программным материалом на материале ( государственный стандарт ) базовом, вариативном ( творческом ( уровнях.
^ Организационная модель такой школы включает 3 вида дифференциации обучения.
1. Комплектирование классов однородного состава с начального этапа обучения ( на основе диагностики характеристик личности и уровня овладения общеучебными навыками ).
2. Внутриклассная дифференциация в среднем звене ( на основе отбора групп для раздельного обучения на разных уровнях ).
3. Профильное обучение в основной школе и старших классах.
На своих уроках я провожу повторительно – обобщительные уроки, на которых учащиеся класса делятся на несколько небольших групп – от 3 до 6 человек. Каждая группа получает свое задание ( задания могут быть одинаковыми для всех групп, если в группе оказались и сильные и слабые ученики, или дифференцированными). Внутри каждой группы между ее участниками распределяются роли. Процесс выполнения задания в группе осуществляется на основе обмена мнениями. Выработанные в группе решения обсуждаются всем классом.
Для такой работы характерно непосредственное взаимодействие и сотрудничество между учащимися, которые, таким образом, становятся активными субъектами собственного учения. А это принципиально меняет в их глазах смысл и значение учебной деятельности.
Считаю, что преимущества групповой работы в том, что ученик учится высказывать, отстаивать собственное мнение, прислушиваться к мнению других, сопоставлять, сравнивать свою точку зрения с точкой зрения других. Вырабатываются навыки наблюдения за действиями других, самоконтроль, формируется критическое мышление. А групповое обсуждение , дискуссия оживляют активность учащихся. Надо отметить , что учащиеся со средними способностями одинаково хорошо усваивают учебный материал как при фронтальной, так и групповой формах. Этот слой составляет основную массу школьников. У сильных учащихся на первом месте по продуктивности стоит индивидуальная работа, т.к. при решении заданий более высокого уровня сложности у них возникают вопросы, на которые они хотели бы получить грамотный и исчерпывающий ответ. А слабым учащимся больше импонирует групповая форма работы.
Организация групповой работы меняет функции учителя. Если на традиционном уроке он передает знания в готовом виде, то здесь он должен быть организатором, режиссером урока, соучастником коллективной деятельности. Его действия должны сводиться к следующему:
- Объяснение цели предстоящей работы
- Разбивка учащихся на группы
- Раздача заданий для групп
- Контроль за ходом групповой работы
- Попеременное участие в работе групп, но без навязывания своей точки зрения, а наоборот побуждая к активному поиску решений
- После отчета групп о выполненном задании учитель делает выводы, обращает внимание на типичные ошибки, дает оценку работе учащихся
Приведу несколько примеров применение различных видов дифференцированных работ.
Способ реализации.
Выделяется 3 типологические группы учащихся.
^ 1 группа (первый уровень)- учащиеся с минимальным уровнем знаний и умений.
2 группа (второй уровень)- учащиеся с хорошим уровнем знаний и умений.
3 группа (третий уровень)- учащиеся с хорошей математической подготовкой, проявляющие повышенный интерес к изучению предмета.
^ Формы реализации.
ГД- групповая дифференцированная работа учащихся.
ИД- индивидуальная дифференцированная работа учащихся.
При ГД форме деятельности на уроке организуется отчет каждой типологической группы.
При ^ ИД форме проверяется и оценивается работа каждого ученика.
Цели, реализуемые в каждой группе.
1группа
1.Ликвидация пробелов в знаниях и умениях.
2.Пробуждения интереса к предмету путем использования игровых элементов, занимательных и логических задач наряду с систематической организацией самостоятельной работы учащихся на уроке и дома.
3.Развитие навыков и умений осуществлять самостоятельную деятельность по образцу и в сходных ситуациях, воспроизводить изученный материал, решенную задачу.
4.Доведение учащихся до минимального уровня усвоения знаний и способов деятельности.
2 группа
1.Создание соответствующих условий, повторение, ликвидация пробелов, актуализация знаний для успешного изучения новой темы.
2.Развитие и закрепления интереса к математике и к учебной деятельности, выполняемой в процессе обучения математики.
3.Формирование навыков учебного труда , умение самостоятельно работать над задачей.
4.Доведение учащихся до хорошего уровня усвоения знаний и способов деятельности.
3группа.
1.Расширение и углубление знаний, формирование умений решать задачи повышенной сложности.
2.Развитие устойчивого интереса к предмету, углубление представлений о роли математики в жизни, науке, технике.
3.Развитие умений самостоятельно работать с учебной и научно-популярной литературой, элементов творчества.
4.Доведение учащихся до более высокого уровня усвоения знаний и способов деятельности.
1.ГД на этапе изучения темы „ Произведение суммы и разности
двух одночленов”.
1. Выполните умножение и проанализируйте полученные результаты для
каждого примера.
1 вариант.
а) (х+7)(х-7); б) (2а+5в)(2а-5в);
в) (4х+6у)(4х-6у); г) (2х+3у)(2х-3у).
Образец: (х+7)(х-7)= х·х+7·х-7·х-7 ·7=х²-49.
Выполните аналогично остальные примеры и заполните таблицу.
| ^ Что дано? | Что получилось? | Как получилось? |
| (х+7)(х-7) | Х²- 49 | Х ·Х-7 ·7 |
| (2а+5в)(2а-5в) | | |
| (4х+6у)(4х-6у) | | |
| (2х+3у)(2х-3у) | | |
2 вариант.
а) (5х+2у)(5х-2у); б) (2а+0,3с)(2а-0,3);
в) (
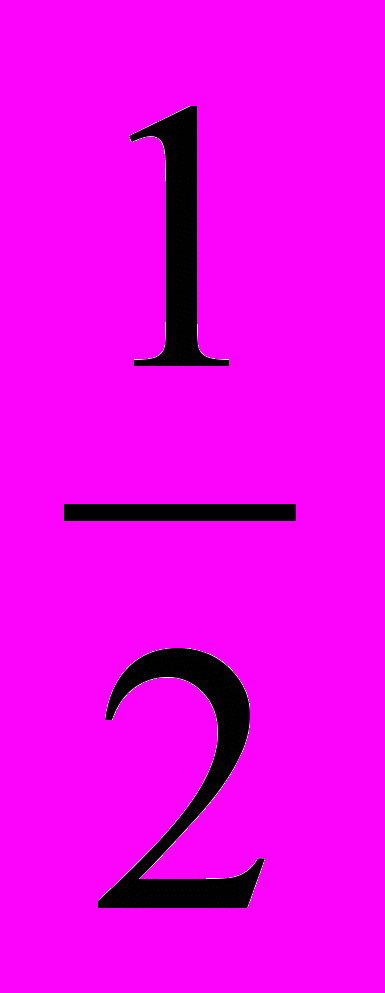 +2в)(
+2в)(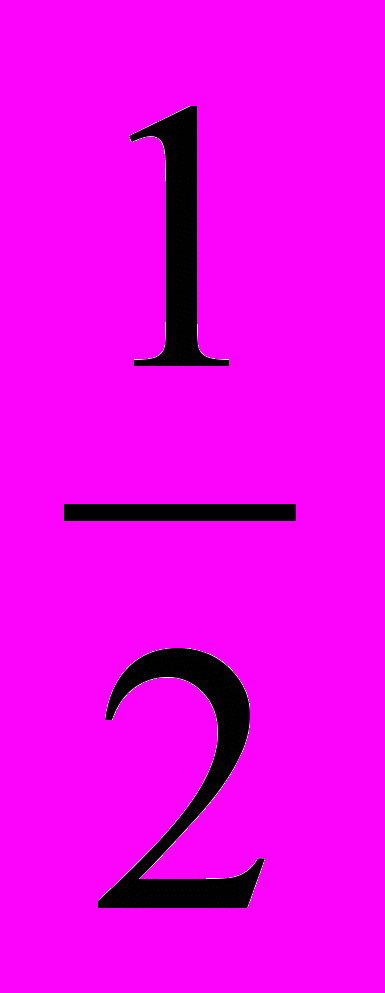 -2в).
-2в).3 вариант.
а) (3х+4у)(3х-4у); б) (0,5а+3в)(0,5а-3в);
в) (2/5х+4/7у)(2/5x-4/7у).
^ 2. Используя результаты задания 1 , не выполняя умножения, напишите
сразу ответ.
1 вариант.
а) (а + в)(а - в); б) (4х+5у)(4х-5у);
в) (6у+7)(6у-7).
2вариант.
а) (а + в)(а - в); б) (4х+5у)(4х-5у);
в) (2а+0,5в)(2а-0,5в).
3 вариант.
а) (а + в)(а – в); б) (7х+8у)(7х-8у);
в) (0,3а+0,4в)(0,3а-0,4в).
3. Подставьте вместо * пропущенные данные так, чтобы получилось верное
тождество.
1 вариант.
а) (х+5)(х-5)= * ; б) (3+а)( * )=9-а².
2 вариант.
а) (7р+2с)(7р-2с)= * ; б) ( * )( * )=81-а².
3 вариант.
а) (3а+2в) * =9а²-4в²; б) ( * )( * )=4х²-25у².
1 вариант.
а) Запишите полученное тождество ( а – в )( а + в )=…
б) Прочтите правило в учебнике.
2 вариант.
а) Запишите полученное тождество;
б) Чему равно произведение суммы и разности двух одночленов?
в) Как найти произведение суммы и разности двух одночленов?
3 вариант.
а) Запишите полученное тождество;
б) Сформулируйте правило устно.
^ 2. ИД на этапе проверки знаний и умений по теме „Производная”.
1) Найти производную функции:
1 вариант
а)f(x)=3x²-12x+1+cos x ; б) f(x)=x²· tg x; в) f(x)=
 .
.2 вариант
а) f(x)=2x⁵+x³+7x-3+
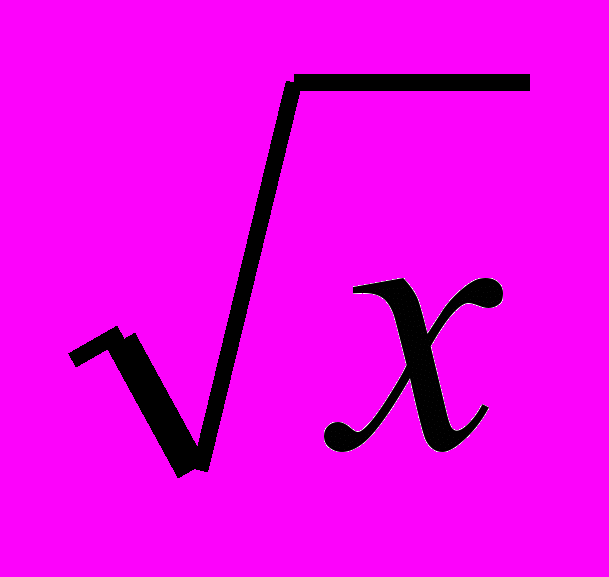 ; б) f(x)=x² ln x; в) f(x)=cos (x²-4x).
; б) f(x)=x² ln x; в) f(x)=cos (x²-4x).3 вариант
а) f(x)=sin(2x²-3x+1); б) f(x)=sin³(2-3x); в) f(x)=
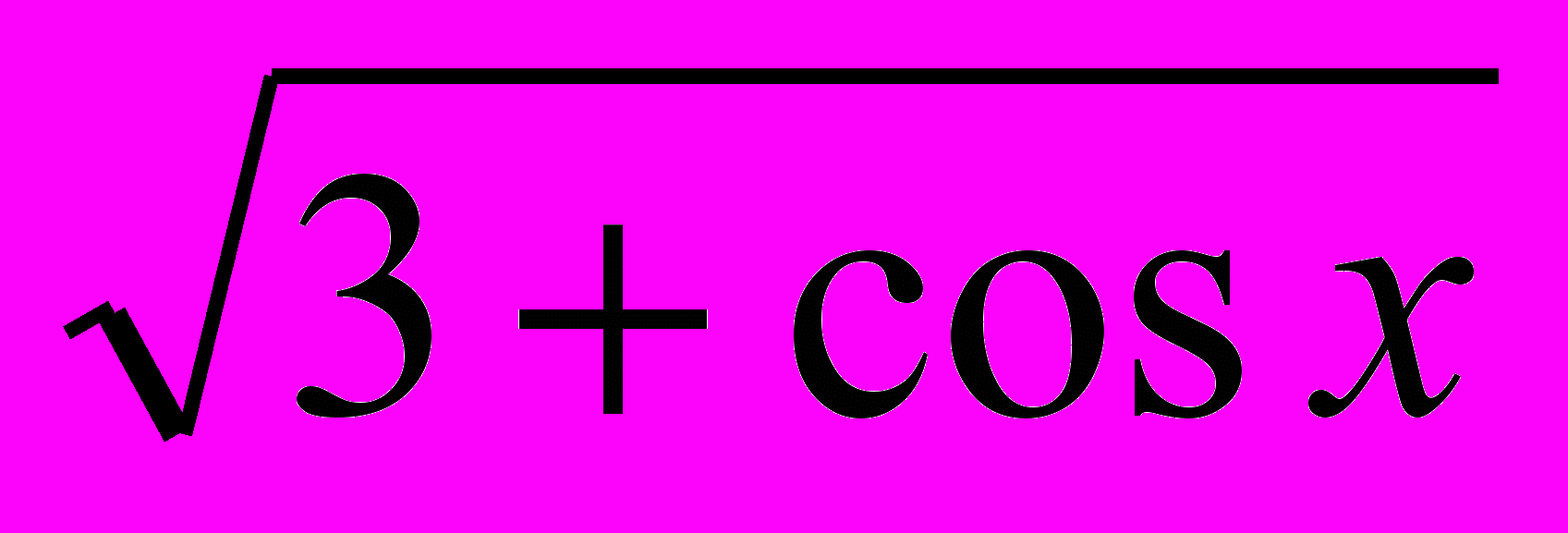 .
.2) Найти промежутки возрастания функции:
1 вариант
f(x)=2x³-3x²+5 .
2 вариант
f(x)=x⁶+3x⁴-9x² .
3 вариант
f(x)=
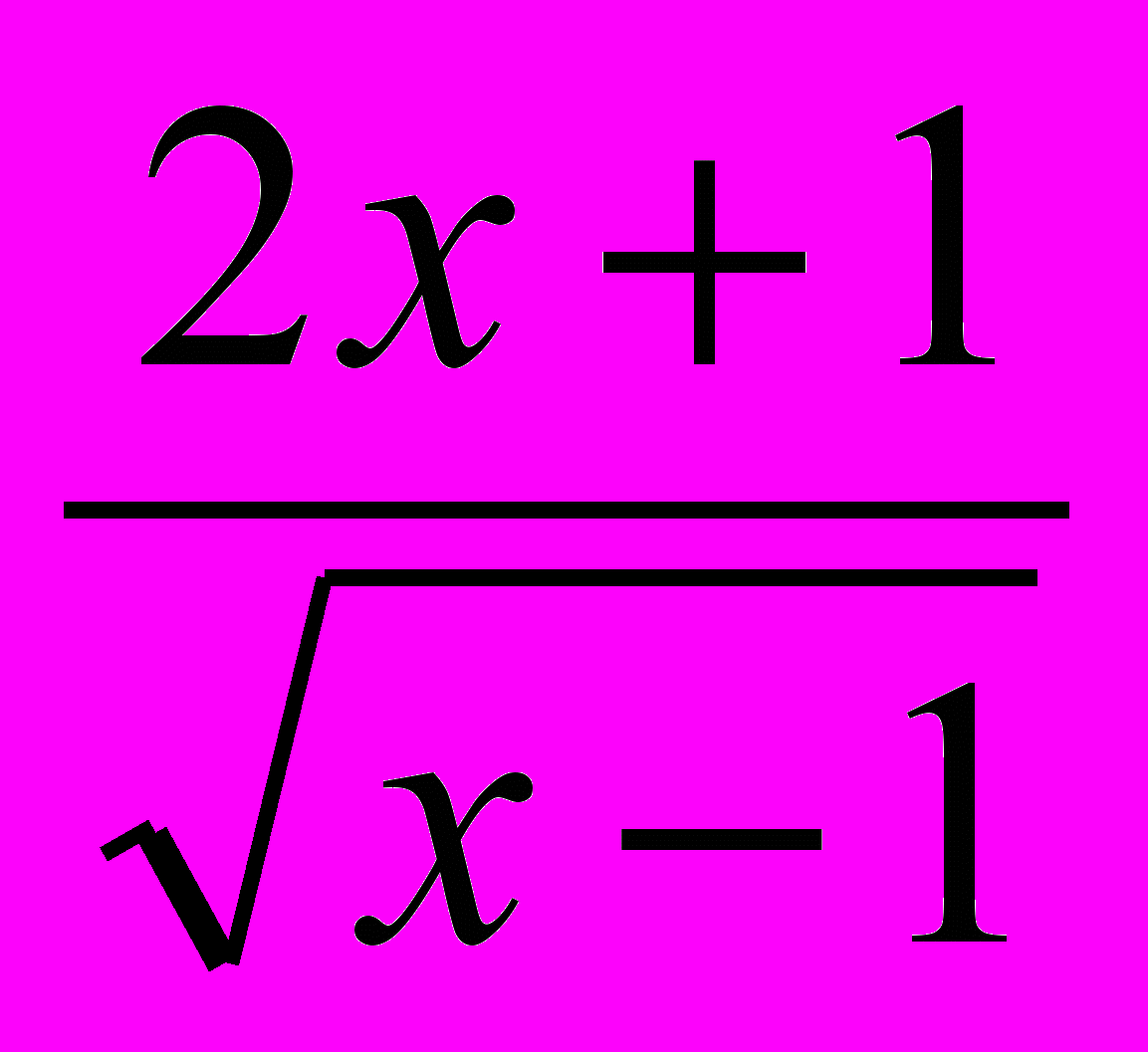 .
.3) Найти точки экстремума функции:
1 вариант
f(x)=2x³-3x²-1 .
2 вариант
f(x)=2x³-
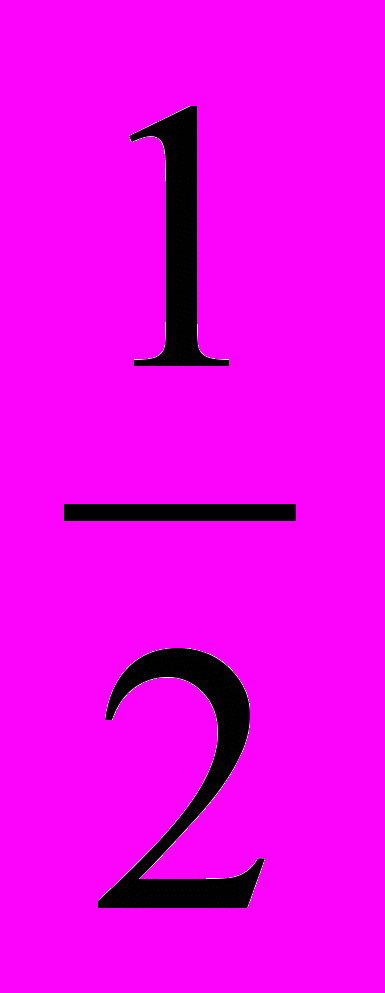 x⁴-8 .
x⁴-8 .3 вариант
f(x)=x⁵-5x⁴+3 .
4) Найти наименьшее значение функции на промежутке, если
1 вариант
f(x)=3x²+18x+7 на [-5; -1] .
2 вариант
f(x)=x⁴-
 +1 на [-1; 1] .
+1 на [-1; 1] .3 вариант
f(x)=
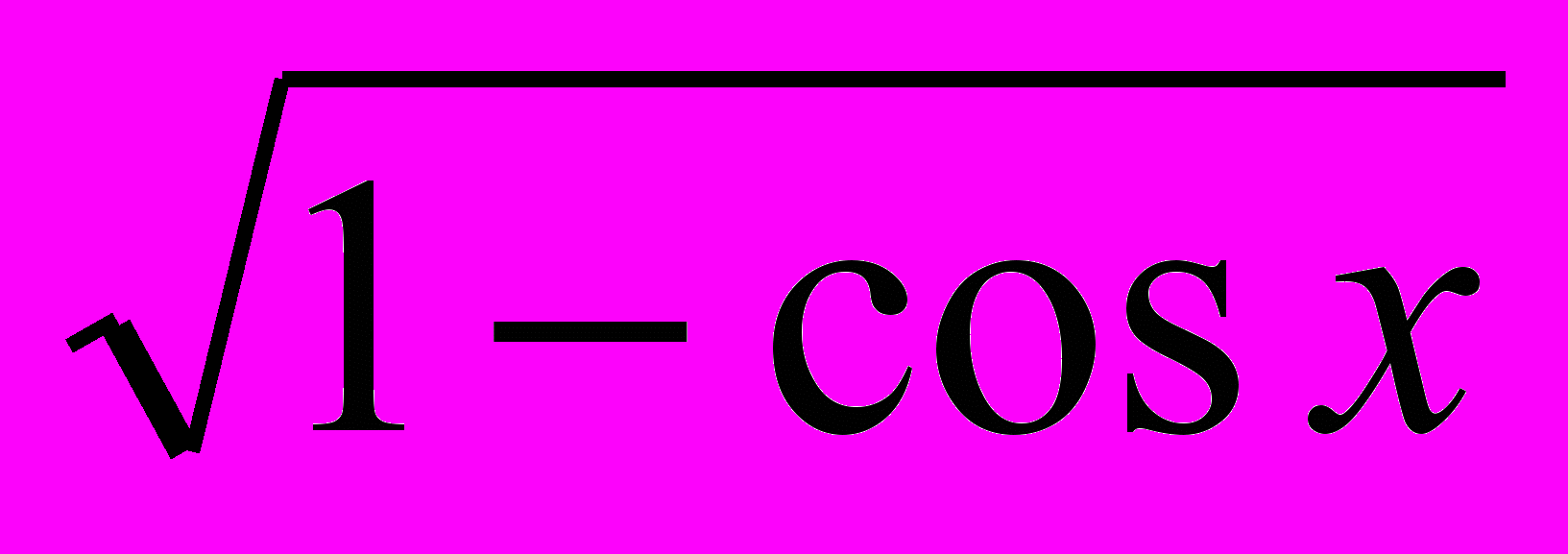 на [- π/2 ; π/2 ] .
на [- π/2 ; π/2 ] .5) Решить задачу.
1 вариант
Тело движется по прямой так, что расстояние S от начальной точки изменяется по закону S(t), где t-время движения в секундах . Найти скорость тела через t секунд, если S(t)=5t+0,5t², t=4c.
2 вариант
Закон движения точки определяется формулой Х(t)=3cos 2t .При каких t ускорение точки положительно?
3 вариант
Скорость V точки, двигающейся прямолинейно, и пройденный ею путь Х связаны уравнением V=
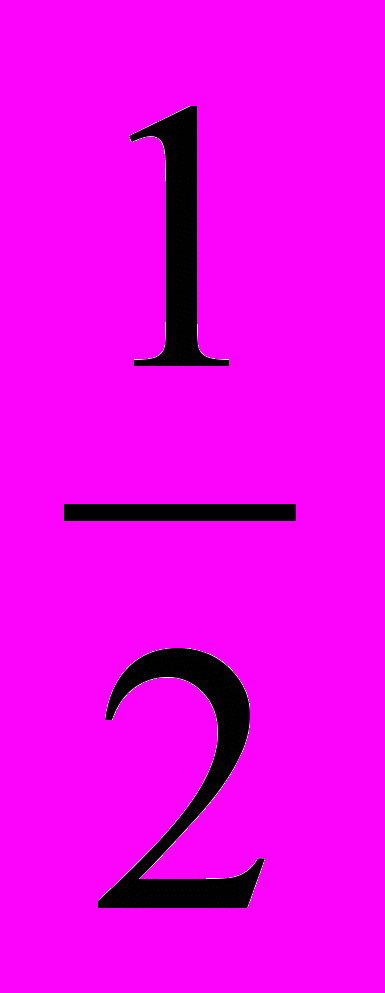 x² .Найдите ускорение движения точки в тот момент, когда значение х=4.
x² .Найдите ускорение движения точки в тот момент, когда значение х=4.6) Найдите угловой коэффициент касательной к графику функции f(x) в его точке с абсциссой х:
1 вариант
f(x)=3x²+2x-5 ,x₀=2 .
2 вариант
f(x)=4 cos x +3,x₀=- π/3 .
3 вариант
f(x)=
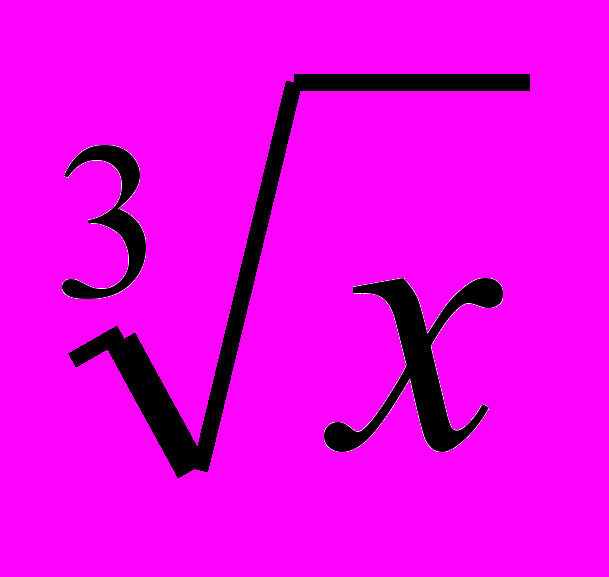 ,x₀=8 .
,x₀=8 .
