Лекция №6. Координаты и проекции Данные реального мира, отображаемые в гис, можно рассматривать с учетом трех аспектов: пространственного, временного и тематического

Вид материала

Лекция

Содержание 6.1. Определение положения точек на поверхности Земли Плоские декартовы координаты Плоские полярные координаты 6.2. Координатные данные 6.3.. Номенклатура и разграфка топографических карт 6.4.Проекции и проекционные преобразования Конические проекции (konical projection). Азимутальные проекции (azimuthal projection). Цилиндрические проекции (cylindrical projection). Поликонические проекции Видоизмененная простая полнконнческая проекция. Псевдоцилиндрические проекции. Проекция Гаусса-Крюгера. Х всех точек имеют положительное значение. Координаты Y 6.5.Система реальных географических координат 6.6.Плоские системы координат 6.7.Картографические проекции Свойства проекций Равноплощадные проекции Проекции истинного направления ... Полное содержание

Подобный материал:

• Лекция №10. Инструментальные средства гис лекция №10. Инструментальные средства гис, 499.17kb.
• Кинематика материальной точки, 36.75kb.
• Рассуждения по поводу имперско-региональных понятий, 507.22kb.
• Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
• Лекция №7. Атрибутивная информация Лекция №7. Атрибутивные данные в гис, 283.92kb.
• 3 Виды поверхностеЙ и их проекции, 84.24kb.
• Лекция 1) гис как специализированная информационная система. Структура информационных, 78.1kb.
• Отчет по проекту «Трехмерная компьютерная модель и гис-проект университетского городка, 127.67kb.
• План 1 Введение 2 Глава 4 Теоретические аспекты изучения пространственного восприятия, 348.28kb.
• План учебных занятий по курсу «Физика». 9 класс (4 часа в неделю), 72.35kb.

Лекция №6. Координаты и проекции

Данные реального мира, отображаемые в ГИС, можно рассматривать с учетом трех аспектов: пространственного, временного и тематического.

Пространственный аспект связан с определением местоположе­ния, временной - с изменениями объекта или процесса с течением вре­мени, в частности от одного временного среза до другого. Примером временных данных служат результаты переписи населения. Тематический аспект обусловлен выделением одних признаков объекта и исключением из рассмотрения других.

Все измеримые параметры моделей геоинформационных данных подпадают под одну из этих характеристик: место, время, предмет. Затруднительно исчерпывающим образом описать сразу все три эти ха­рактеристики. Поэтому при построении моделей данных на основе на­блюдений явлений реального мира один параметр считают "неизмен­ным", изменения другого "задаются" и при этом "измеряют" изменения третьего параметра.

Зафиксировав географическое положение и изменяя время, можно получить временные ряды данных. Зафиксировав время и изменяя гео­графическое положение, получаем данные по профилям.

В большинстве технологий ГИС для определения места используют один класс данных - координаты, для определения параметров времени и тематической направленности - другой класс данных -атрибуты.

Однако прежде чем рассмотреть два основных класса данных в ГИС, необходимо рассмотреть методы определения местоположения точек объектов на поверхности Земли.
^

6.1. Определение положения точек на поверхности Земли

Координатные данные, составляющие один из основных классов геоинформационных данных, используют для указания местоположения на земной поверхности.

Поверхность Земли имеет сложную форму. При общей площади ее поверхности 510 млн. км² 71 % приходится на дно морей и океанов и 29 % - на сушу. Это дает основание считать, что земная поверхность состоит из двух резко отличающихся морфологических элементов - материков и океанов.

С учетом того что поверхность вод Мирового океана занимает почти 3/4 поверхности Земли, за общую фигуру земли принимают тело, ограниченное поверхностью воды океанов. Такая поверхность называется уровненной. Потенциал силы тяжести на ней имеет одно и то же значение. Другими словами, эта поверхность везде перпендикулярна отвесной линии, т.е. везде горизонтальна.

Можно построить семейство горизонтальных поверхностей. Поверхность, которая совпадает с поверхностью Мирового океана в состоянии покоя и равновесия и продолжена под материками, образует фигуру, принятую в геодезии за общую фигуру Земли, называемую геоид.

С помощью методов дистанционного зондирования удалось установить, что Земля имеет грушевидную форму. В качестве математической модели Земли применяют эллипсоид, который в геодезии принято называть референц-эллипсоидом. В СССР до 1946 г. использовался эллипсоид, полученный Ф. Бесселем. В 1946 г. для обязательного использования был введен эллипсоид, вычисленный в ЦНИИГАиК в 1940 г. под руководством Ф.Н. Красовского при участии А. А. Изотова.

Для отображения положения точек поверхности на плоскости используют различные математические модели поверхности и различные системы координат. На практике применяют два основных типа координат: плоские и сферические Реже применяют криволинейные или полярные.

Выбор системы координат зависит от размеров исследуемых участков поверхности, как следствие, от влияния кривизны Земли. При изображении небольших участков Земли часть уровненной поверхности можно принять за плоскость. Такими участками будут участки до 20 км длиной и площадью до 400 км². В этих случаях применимы плоские координаты.

^ Плоские декартовы координаты определяются заданием двух осей. При этом обычно координата Х указывает на восток, Y - на север. Задают масштабные отрезки. Упорядоченная пара (X, Y) определит положение точки в заданной системе.

^ Плоские полярные координаты используют расстояние от начала координат (r) и угол () от фиксированного направления. Направление обычно фиксируется на север, а угол отсчитывается по часовой стрелке от него. Полярные координаты удобны при проведении измерений от какой-либо заданной точки, например когда используются данные таких источников, как радарные съемки.

При необходимости учета кривизны Земли применяют пространственные системы координат. Для определения географической системы координат (разновидности сферической системы) введем следующие понятия:

• плоскость земного экватора - проходит через центр Земли перпендикулярно к оси вращения;
  

• плоскость географического (астрономического) меридиана - проходит через ось вращения Земли и отвесную линию в точке земной поверхности;
  

• меридиан — линия пересечения плоскостей географических меридианов с земной поверхностью;
  

• параллель - линия, образованная пересечением плоскости, параллельной плоскости земного экватора, с поверхностью Земли.
  
• Положение точки определяется широтой ( ) и долготой ().
  
• Широта - это угол между линией, соединяющей точку и центр земли и главным экватором.. Она изменяется от -90 ° (южный полюс) до +90 ° (северный полюс).
  

• Долгота - это угол в плоскости экватора между меридианом точки и главным (нулевым) меридианом, проходящим через Гринвич (Англия). Она изменяется от-180° (западная долгота) до+180° (восточная дол­гота).
  

Основными понятиями этой системы координат являются:

• меридиан - линия постоянной долготы; параллель - линия постоянной широты;
  

• большой круг - воображаемый круг на земной поверхности, образованный плоскостью, проходящей через центр земного шара;
  

• малый круг - воображаемый круг на земной поверхности, образованный плоскостью, не проходящей через центр земного шара.
  

Рассмотренные системы координат носят в большей степени теоре­тический характер. На практике используют более широкий набор систем координат [2]: геоцентрические, топоцентрические, полярные геодезические, эллиптические и др.
^

6.2. Координатные данные

Геометрически информация, содержащаяся на карте, может быть определена как совокупность наборов точек, линий, контуров и площа­дей, имеющих метрические значения, отражающие трехмерную реаль­ность. Эта информация образует класс координатных данных ГИС.
^

6.3.. Номенклатура и разграфка топографических карт

Поскольку основой интеграции данных в ГИС является географическая информация, необходимо рассмотреть понятия разграфка и номенклатура топографических карт.

• Разграфкой называется разделение топографических карт на листы.
  

• Номенклатура - это система обозначений отдельных листов топо­графических карт. Общегеографические карты делятся на три вида:
  

• обзорные (масштаб 1 : 1 000 000 и мельче);
  

• обзорно-топографические (масштаб 1: 100 000 - 1 : 1 000 000);
  

• топографические (масштаб 1: 100 000 и крупнее),
  

Обзорно-топографические карты составляются по картам более крупных масштабов.

Топографические карты составляются по результатам съемок территорий и отличаются детальностью изображения местности. Это многолистные карты, т.е. на каждом листе отображается часть территории, а в совокупности на всех листах содержится полное отображение. Строго говоря, криволинейная часть поверхности отображаемой на листе карты соответствует некоей криволинейной трапеции. Поэтому для обозначения определенных листов карты используют термин трапеция.

В основу разграфки топографических карт положен лист карты масштаба 1 : 1000000. Для составления карты такого масштаба изображение земной поверхности разбивается на 60 колонн (двухугольников), начиная от Гринвичского меридиана через 6° (рис.4.3).



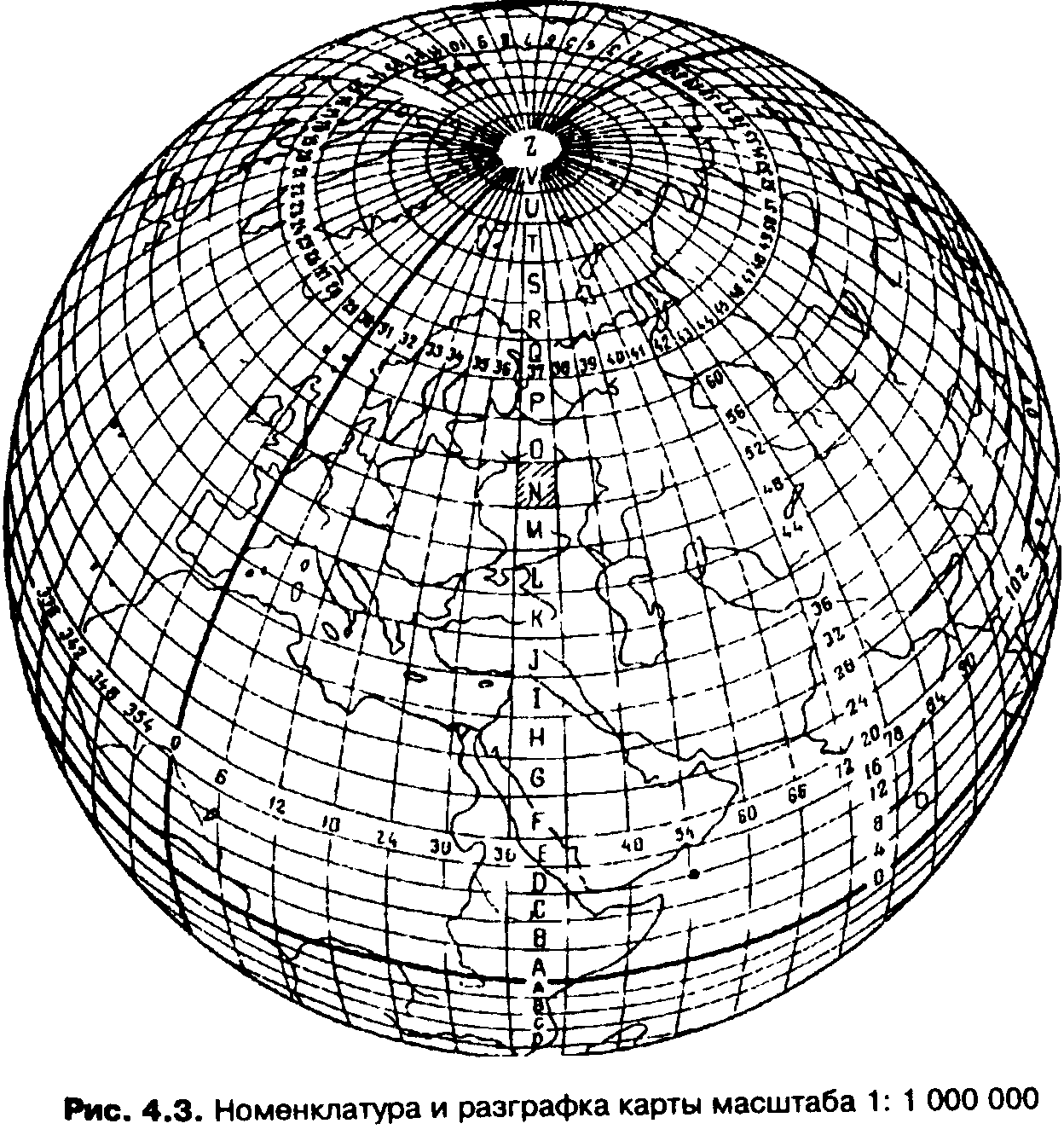
Рис. 4.3. Номенклатура и разграфка карты масштаба 1: 000 000

Двуугольники нумеруются арабскими цифрами от 1 до 60 на восток от 180°. Возможна нумерация от 0°. В этом случае двуугольники называ­ют не колоннами, а зонами. Нумерация зон от колонн отличается на 30 еди­ниц. Например, колонна с номером 40 соответствует зоне с номером 10.

Таким образом колонны и зоны делят земной шар по меридианам. Па­раллелями через 4° по широте изображение земной поверхности делится на ряды, обозначаемые буквами латинского алфавита к северу и югу от эк­ватора (см. рис. 4.3) . Таким делением по меридианам и параллелям опре­деляется номенклатура листа карты масштаба 1 : 1 000 000 (миллионной).

Номенклатура каждого листа включает букву ряда и номер колон­ны. Так, лист, на котором показывается г. Москва, имеет номенклатуру N-37, что соответствуют 52 - 56° широты и 36- 42° долготы. Номенкла­тура сдвоенных или счетверенных листов карты складывается из обо­значений широтного пояса и соответственно двух или четырех колонн. Номенклатура листов карт более крупных масштабов связана с но­менклатурой листов миллионной карты. Так, лист карты масштаба 1 : 500 000 (рис. 4.4) составляет 1/4 листа миллионной карты и обозна­чается добавлением прописной буквы А, Б, В, Г к номенклатуре листа миллионной карты, например М-37-Б.




Рис. 4.4. Номенклатура листов карт масштабов 1:500 000 и 1:300 000

Лист карты масштаба 1 : 300 000 составляет 1/9 листа миллионной карты и обозначается римскими цифрами от 1 до IX, расположенными перед номенклатурой миллионного листа, например 1-N-37 (см. рис. 4.4). Лист карты масштаба 1 : 200 000 (рис. 4.5) составляет 1/36 листа миллионной карты и обозначается римскими цифрами от 1 до XXXVI, расположенными после номенклатуры миллионного листа, например N-37-1.

N-37

1	11	III	IV	V	VI
VII					XII
XIII					XVIII
XIX					XXIV
XXV					XXX
XXXI	XXXII	XXXIII	XXXIV	XXXV	XXXVI

О - N-37-1

Рис. 4.5. Номенклатура листов карты масштаба 1: 200 000

Лист карты масштаба 1 : 100 000 (рис. 4.6) составляет 1/144 листа миллионной карты и обозначается арабскими цифрами от 1 до 144, рас­положенными после номенклатуры миллионного листа, например N-37-143.

Номенклатура листов карт более крупных масштабов строится на основе листа карты масштаба 1 : 100 000, подобно тому, как строились номенклатуры рассмотренных выше карт на основе листа миллионной карты.

Так, лист карты масштаба 1 : 50 000 составляет 1/4 листа карты мас­штаба 1: 100 000 и обозначается добавлением прописной буквы А, Б, В, Г к номенклатуре листа карты стотысячного масштаба ( рис. 4.7, а), на­пример N-37-144-А.

N-37

1											12
13											24
25											36
37											48
49											60
61											72
73											84
85											96
97											108
109											120
121											132
133										0	144

0 - N-37-143

Рис. 4.6. Номенклатура листов карты масштаба 1: 100 000

Лист карты масштаба I : 50 000 содержит 4 листа карты масштаба 1: 25 000, которые обозначаются добавлением строчных букв а, б, в, г к номенклатуре листа карты пятидесятитысячного масштаба (см. рис. 4.7, a), например N-37-144-B-6.

Лист карты масштаба 1 : 25 000 содержит 4 листа карты масштаба 1: 10 000, которые обозначаются добавлением арабских цифр 1, 2, 3, 4 к номенклатуре листа карты двадцатипятитысячного масштаба (см. рис. 4.7, а), например N-37-144-B-a-l.

Лист карты масштаба 1 : 100 000 содержит 256 листов карты масш­таба 1: 5 000, которые обозначаются добавлением арабских цифр от 1 до 256 к номенклатуре листа карты стотысячного масштаба (см. рис. 4.7, a), например N-37-144-(255).





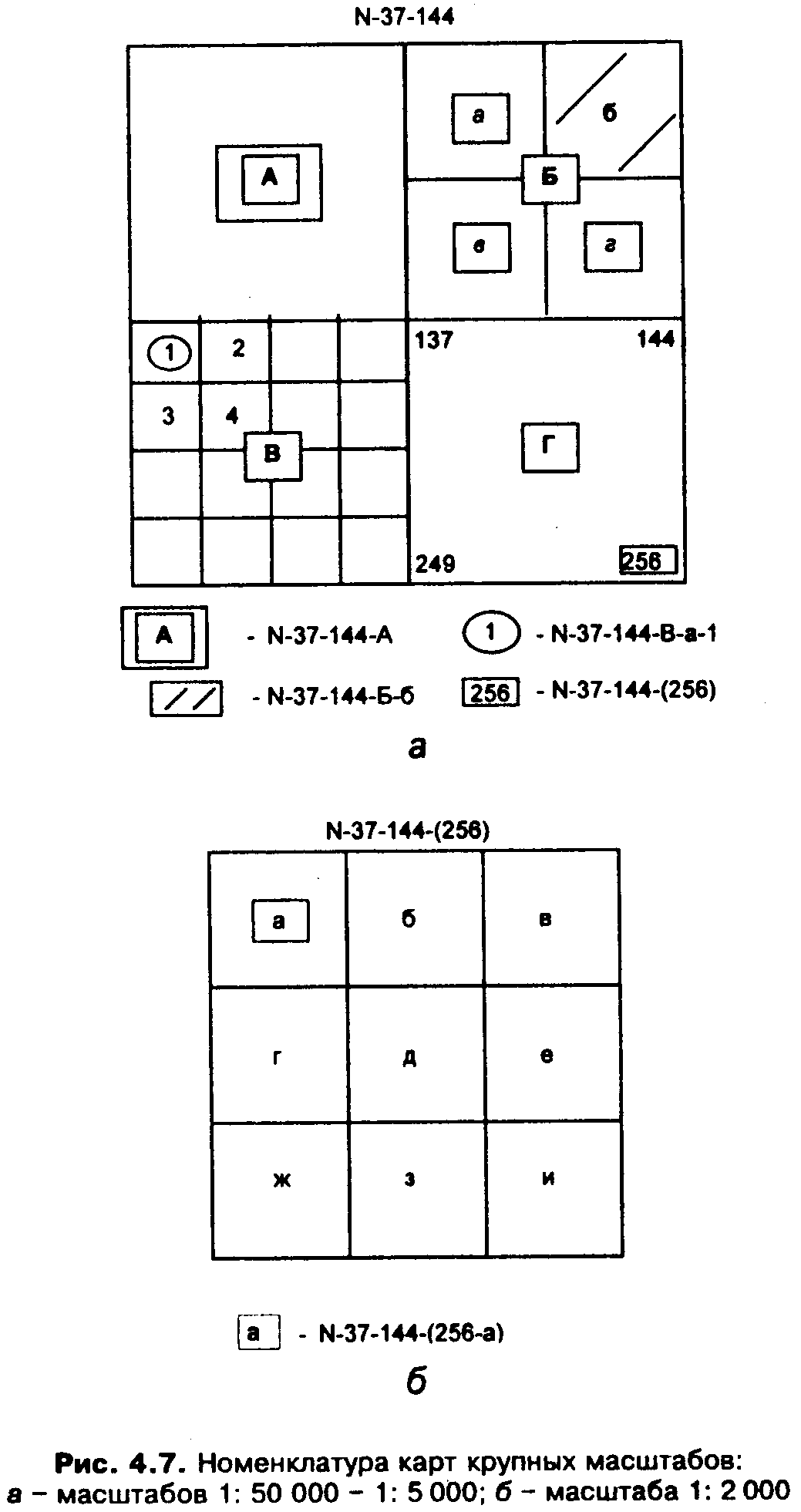
Рис. 4.7. Номенклатура карт крупных масштабов: а – масштабов 1: 50 000 – 1: 5 000; б – масштаба 1: 2 000



Номенклатура листа карты масштаба 1:2 000 образуется на основе де­ления листа карты 1: 5 000 на 9 частей. Каждый лист обозначается путем добавления строчных букв русского алфавита а, б. в, г, д. е, ж, з, и к номен­клатуре пятитысячного масштаба (рис. 4.7, б), например N-37-144-(256-а).

^

6.4.Проекции и проекционные преобразования

Координаты точек пространственных объектов используют для ука­зания местоположения объектов на земной поверхности. Поверхность Земли имеет сложную форму. При составлении карт пространственное положение точек отображается в плоском (двухмерном) представлении. Для отображения положения точек поверхности на плоскости применя­ют различные математические модели поверхности, задающие различ­ные картографические проекции.

Проекция – это математическая модель, преобразующая места расположения объектов на поверхности Земли в их места расположения на двумерной поверхности. Некоторые из картографических поверхностей сохраняют точность площади, расстояния или направления.

Группа математических процедур ГИС, осуществляющая переход от одной картографической проекции к другой или от пространствен­ной системы к картографической проекции, носит название проекционных преобразований. Эта группа реализуется методами моделиро­вания, образуя единый блок. В этот блок входят и различные процедуры обработки пространственных данных для получения новых проекций на основе исходных. Эти процедуры включают и простые операции пе­ресчета координат пространственных объектов (поворота, смещения, масштабирования и т. п.), более сложные (связанные, например, с "ук­ладкой" объектов в систему опорных точек) и самую сложную подгруп­пу операций (трансформация картографических проекций).

Число проекционных преобразований в блоках моделирования ГИС различно: в системе ER Mapper их свыше 700, в ГеоГраф - около трех десятков, а в некоторых настольных системах (DeskTop GIS) их нет вообще.

Рассмотрим наиболее общие классы проекционных преобразований [2] для решения задач в ГИС.

Преобразования картографических проекций применяют для перехода от исходной (хранимой в базе данных) картографической композиции к за­даваемой пользователем. В частности, когда цифровая карта (слой), выпол­ненная в известной проекции и соответствующая ее теоретическим коор­динатам, должна быть преобразована в географические координаты либо в другую картографическую проекцию.

Достоинством моделирования в ГИС является возможность трансформирования космического (или аэро-) снимка непосредственно в картографическую проекцию, минуя построение фотограмметрической модели или традиционное фотограмметрическое трансформирование сним­ков. Эта возможность предоставляется в пакетах ГИС, в первую очередь связанных с обработкой данных дистанционного зондирования.

Выделение подгруппы преобразования проекций связано с необхо­димостью интеграции данных из различных картографических источ­ников с разнородной математической основой. Карты могут отличаться моделью Земли, примененной при создании карты; картографической проекцией; системой координат, привязанной к используемой модели Земли.

Технологически для проекционных преобразований в ГИС необхо­димо создать файл описания картографической проекции и выбрать ис­ходный файл. Из набора типов преобразований выбирают необходимое, задают требуемые параметры, и проекционное преобразование осуще­ствляется автоматически путем создания новой картографической про­екции в заданном слое и соответствующем файле.

Проекционные преобразования требуют рассмотрения различных классов проекций, применяемых для создания карт[2]. Картографичес­кие проекции классифицируют по различным признакам, например в зависимости от характера и размера искажений.

Равноугольные проекции (conformai projection) сохраняют без иска­жений углы и формы малых объектов, но в них резко деформируются длины и площади объектов. В математике такие преобразования назы­вают конформными.

Равновеликие проекции (equivalente projection) не искажают пло­щадей, но в них искажены углы и формы объектов. Первый вид проек­ций приемлем для прокладки маршрутов транспортных средств, второй - для определения площадей и землепользования.

Произвольные проекции (arbitrary projection) имеют искажения углов, площадей и длин, но эти искажения распределены по карте, например, так, что минимальные искажения имеются в центральной части и возрастают к краям. Среди произвольных проекций выделяют равнопромежуточные (equidistant projection), в которых искажения длин отсутствуют по одному из направлений: вдоль меридиана или вдоль параллели.

^ Конические проекции (konical projection). По характеру искажений конические проекции могут быть различными. Наибольшее распростране­ние получили равноугольные и равнопромежуточные проекции.

Образование конических проекций можно представить как проек­тирование земной поверхности на боковую поверхность конуса, опре­деленным образом ориентированного относительно земного шара (эл­липсоида) (рис. 5.1, а). В прямых конических проекциях оси земного шара и конуса совпадают. При этом конус берется или касательный, или секущий.

После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость (рис. 5.1, б). При проектировании по методу линейной перспективы получаются перспек­тивные конические проекции, обладающие только промежуточными свойствами по характеру искажений.

Другой метод образования конических проекций - аналитический. В его основу положены уравнения проекций, вытекающие из их опреде­ления и формулы общей теории искажений. В конических проекциях имеются две постоянные проекции ее и с. Постоянная а равняется синусу широты стандартной параллели или, что то же самое, синусу угла при вершине конуса.

В зависимости от размеров изображаемой территории в конических проекциях принимаются одна или две параллели, вдоль которых сохра­няются длины без искажений. Одна параллель (касательная) принима­ется при небольшом протяжении по широте; две параллели (секущие) – при большом протяжении для уменьшения уклонений масштабов от еди­ницы. В литературе их называют стандартными параллелями.

Коническая проекция данной группы вполне определяется, если за­даны постоянные проекции или любые величины, с ними связанные. Это могут быть широты стандартных или крайних параллелей. В после­днем случае, например, может быть дополнено условие, чтобы масшта­бы на крайних параллелях и на параллели с наименьшим масштабом были равны по абсолютной величине.

^ Азимутальные проекции (azimuthal projection). В них параллели (альмукантараты) изображаются концентрическими окружностями, а меридианы (вертикалы) - пучком прямых, исходящих из центра (рис. 5.2, а).






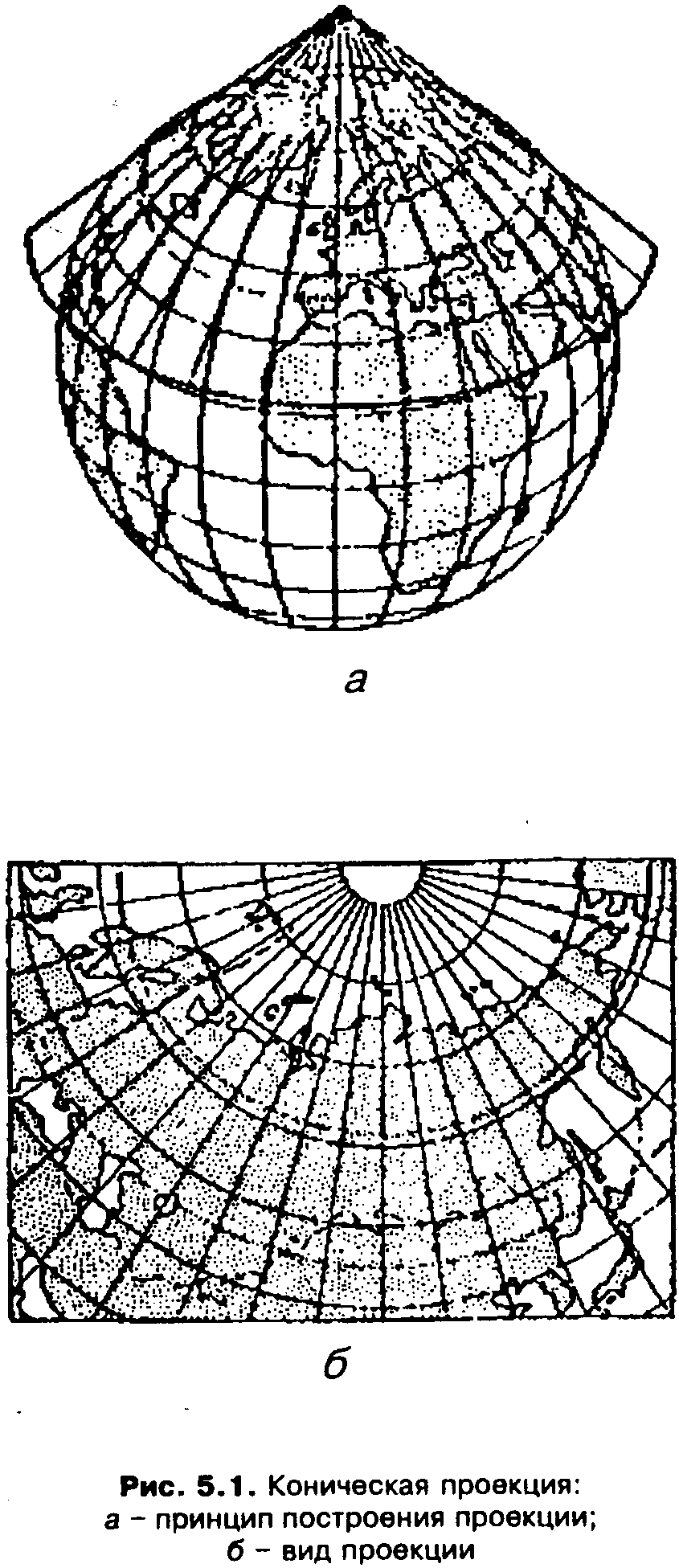
Рис. 5.1. Коническая проекция: а – принцип построения проекции; б – вид проекции

Рис. 5.2. Азимутальная проекция: а – принцип построения проекции; б – вид проекции







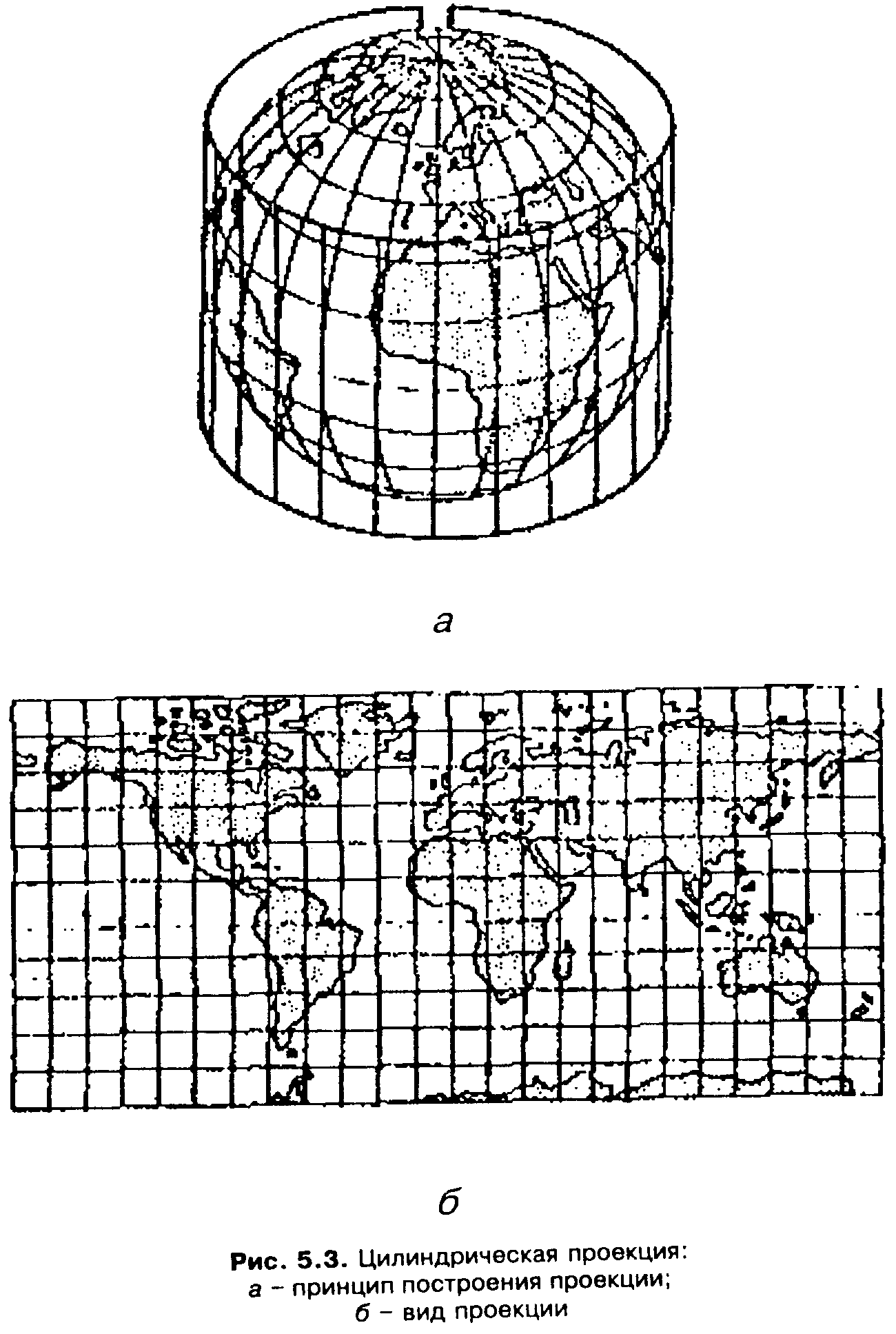
Рис. 5.3. Цилиндрическая проекция: а – принцип построения проекции; б – вид проекции



Углы между меридианами проекции равны соответствующим раз­ностям долгот. Промежутки между параллелями определяются при­нятым характером изображения (равноугольным или другим) или спо­собом проектирования точек земной поверхности на картинную плос­кость.

Нормальная сетка азимутальных проекций ортогональна. Их мож­но рассматривать как частный случай конических проекций, в кото­рых a=1 (альфа=1).

Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор кото­рой зависит от расположения территории. Меридианы и параллели в косых и поперечных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.

В зависимости от искажений азимутальные проекции подразделя­ются на равноугольные, равновеликие и с промежуточными свойства­ми. В проекции масштаб длин может сохраняться в точке или вдоль од­ной из параллелей (вдоль альмукантарата). В первом случае предпола­гается касательная картинная плоскость, во втором - секущая. В пря­мых проекциях формулы даются для поверхности эллипсоида или шара (в зависимости от масштаба карт), в косых и поперечных - только для поверхности шара (рис.5.2, б).

^ Цилиндрические проекции (cylindrical projection). В прямых ци­линдрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг дру­гу. Таким образом задается прямоугольная сетка цилиндрических про­екций (рис. 5.3, а).

Промежутки между параллелями пропорциональны разностям дол­гот. Промежутки между меридианами определяются принятым характе­ром изображения или способом проектирования точек земной поверх­ности на боковую поверхность цилиндра. Из определения проекций следует, что их сетка меридианов и параллелей ортогональна. Цилинд­рические проекции можно рассматривать как частный случай коничес­ких при (х=0 (вершина конуса в бесконечности).

По свойствам изображения проекции могут быть равноугольными, равновеликими и произвольными. Применяются прямые, косые и попе­речные цилиндрические проекции в зависимости от расположения изоб­ражаемой области. В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой.

Существуют разные способы образования цилиндрических проек­ций. Наглядным представляется проектирование земной поверхности на боковую поверхность цилиндра (рис. 5.3, а), которая затем разверты­вается на плоскости [2] (рис.5.3, б). Цилиндр может быть касательным к земному шару или секущим его. В первом случае длины сохраняются по экватору, во втором - по двум стандартным параллелям, симметрич­ным относительно экватора.

Цилиндрические проекции применяются при составлении карт мелких и крупных масштабов - от общегеографических до специаль­ных. Так, например, аэронавигационные маршрутные полетные карты чаще всего составляются в косых и поперечных цилиндрических равно­угольных проекциях (на шаре).

В прямых цилиндрических проекциях одинаково изображаются одни и те же участки земной поверхности вдоль линии разреза - по восточ­ной и западной рамкам карты (дублируемые участки карты) и обеспечи­вается удобство чтения по широтным поясам (например, на картах рас­тительности, осадков) или по меридианальным зонам (например, на кар­тах часовых поясов).

Косые цилиндрические проекции при широте полюса косой сис­темы, близкой к полярным широтам, имеют географическую сетку, дающую представление о сферичности земного шара. С уменьшени­ем широты полюса кривизна параллелей увеличивается, а их протя­жение уменьшается, поэтому уменьшаются и искажения (эффект сфе­ричности).

В прямых проекциях полюс показывается прямой линией, по дли­не, равной экватору, но в некоторых из них (проекции Меркатора, Уэтча) полюс изобразить невозможно. Полюс представляется точкой в косых и поперечных проекциях. При ширине полосы до 4,5° можно использовать касательный цилиндр, при увеличении ширины поло­сы следует применять секущий цилиндр, т.е. вводить редукционный коэффициент.

^ Поликонические проекции (policonic projection). В них паралле­ли изображаются дугами эксцентрических окружностей с центрами на среднем (прямолинейном) меридиане или его продолжении, а меридиа­ны - кривыми, симметричными относительно среднего меридиана (рис. 5.4).



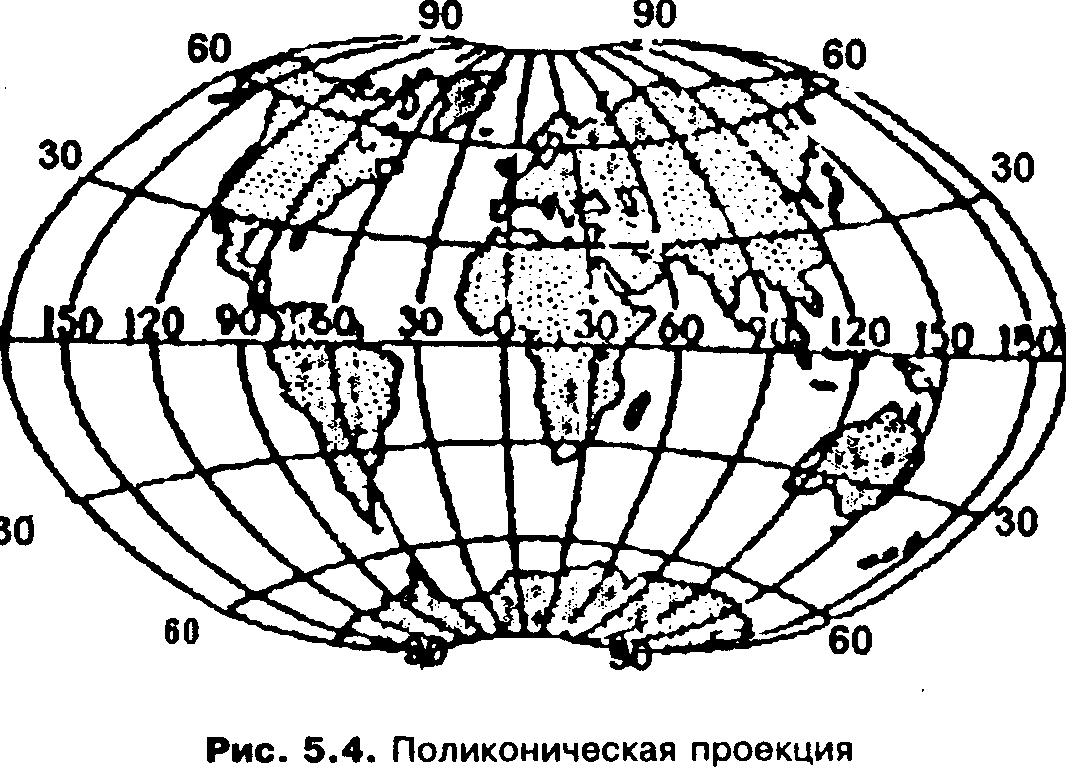
Рис. 5.4. Поликоническая проекция

Частным случаем поликонических проекций являются собственно поликонические проекции, для которых принимаются дополнительные условия, и круговые проекции с меридианами в виде дуг эксцентричес­ких окружностей.

К поликоническим проекциям в широком понимании относятся про­екция Таича (определялась аналитически) и проекции Гинзбурга (полу­чены численными методами).

^ Видоизмененная простая полнконнческая проекция. Она при­меняется как многогранная. Земная поверхность, принимаемая за по­верхность эллипсоида вращения, делится линиями меридианов и парал­лелей на трапеции.

При рассмотрении данной проекции учтем особенности ее приме­нения при создании карты масштаба 1:1 000 000.

Трапеции изображаются на отдельных листах в одной и той же про­екции (для карты масштаба 1:1 000 000 - в видоизмененной простой поликонической).

Листы международной карты мира масштаба 1:1 000 000 имеют определенные размеры сторон трапеций: по меридианам -4°, по парал­лелям - 6°; на широте от 60 до 76° листы сдваивают, они имеют размеры по параллелям 12°; выше 76° листы счетверяют, их протяжение по па­раллелям - 24°.

Применение проекции как многогранной определяет необходимость введения номенклатуры - системы обозначения отдельных листов.

Для карты масштаба 1:1 000 000 установлено обозначение трапеций по широтным поясам в направлении от экватора к полюсам буквами латинского алфавита (А, В, С, D и т.д.) и по колоннам - арабскими циф­рами (1, 2, 3, 4 и т.д.), которые считают от меридиана с долготой 180° (по Гринвичу) против часовой стрелки.

Номенклатура сдвоенных и счетверенных листов карты складыва­ется из обозначений широтного пояса и соответственно двух или четы­рех колонн.

Отметим особенности видоизмененной простой поликониче'кой проекции и распределение искажений б пределах отдельных листов карты масштаба 1:1 000 000.

Меридианы изображаются прямыми линиями. Длина двух мериди­анов, отстоящих от среднего на ±2° по долготе (на ±4° на сдвоенных листах и на ±8° на счетверенных), искажений не имеет.

Крайние параллели каждого листа (северная и южная) являются ду­гами окружностей, центры этих параллелей находятся на среднем мери­диане, длина их не искажается.

Для построения внутренних параллелей используют способ Хинкса, т. е. проводят эти параллели через точки, полученные путем деления всех меридианов на четыре равные части.

Картографическая сетка строится через 1 ° по широте и по долготе, на сдвоенных листах - по долготе через 2°, на счетверенных - через 4°. Таким образом, все листы карты масштаба 1:1 000 000 имеют пять па­раллелей и семь меридианов.

Криволинейные меридианы простой поликонической проекции заменяются в видоизмененной поликонической проекции прямыми, соединяющими соответствующие точки крайних параллелей, поэто­му масштабы на внутренних параллелях будут меньше единицы.

Минимальный масштаб получают на средней параллели каждого листа карты. Для карты масштаба 1 : 1 000 000 искажение длины сред­ней параллели каждого листа Vn-0,06%.

Масштабы по меридианам и параллелям для этой карты могут быть приняты за экстремальные (а и Ь), так как сетка проекции практически ортогональна. На каждом листе имеются четыре точки, в которых от­сутствуют искажения всех видов; эти точки находятся на пересечении крайних параллелей листа с меридианами, удаленными от среднего на 2° к западу и востоку.

Максимальное искажение площади Vp находится в середине листа, оно имеет знак минус и может достигать -0,14 %. Изоколы нулевых искажений площади имеют вид кривых, проходящих через точки, в которых отсутствуют искажения, и вытянутых вдоль крайних меридианов.

Достоинством видоизмененной простой поликонической проекции, применяемой как многогранная, является небольшая величи­на искажений. Анализ в пределах листа карты показал, что искажения длин не превышают 0,10 %, площади -0,15 %, углов - 5' и являются практически неощутимыми. Недостаток этой проекции - появле­ние разрывов при соединении листов по меридианам и параллелям.

^ Псевдоцилиндрические проекции. В прямых псевдоцилиндрических проекциях параллели изображаются в виде прямых параллельных линий, меридианы - в виде кривых (дуг, синусоид, гипербол, парабол, эллипсов и т.д.) , симметричных относительно среднего прямолиней­ного меридиана (рис.5.5).



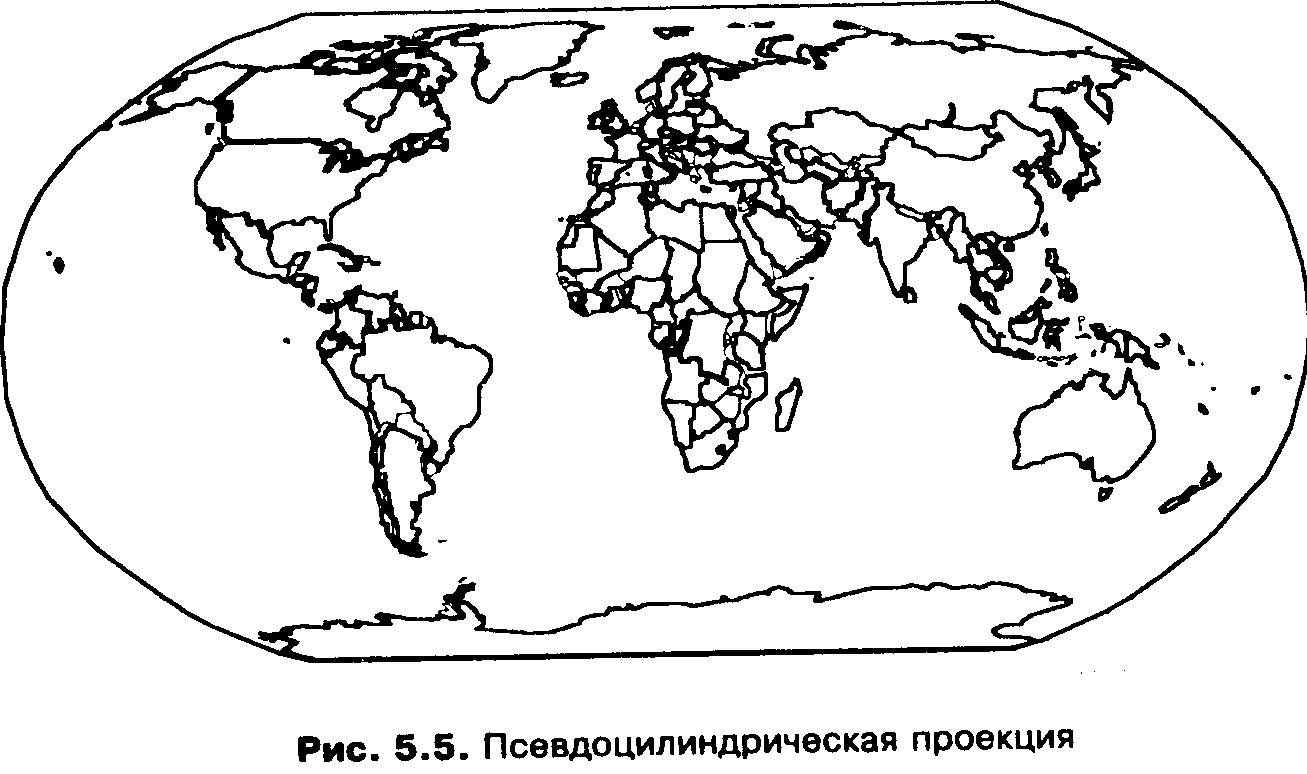
Рис. 5.5. Псевдоцилиндрическая проекция

Промежутки между параллелями определяются принятым законом изображения земной поверхности на плоскости. Промежутки между меридианами в равновеликих проекциях пропорциональны разностям долгот, в других проекциях они могут убывать или, значительно реже, воз­растать от среднего меридиана к востоку и западу.

Полюс в псевдоцилиндрических проекциях изображается точкой или полярной линией, длина которой устанавливается или получается из зада­ния. Поэтому сетка меридианов и параллелей не ортогональна, в силу чего эти проекции не могут быть равноугольными.

При рассмотрении цилиндрических проекций как частного случая псевдоцилиндрических проекций, когда меридианы изображаются пря­мыми параллельными линиями, ортогональными к параллелям, цилин­дрическую равноугольную проекцию Меркатора можно считать равно­угольной псевдоцилиндрической проекцией.

Из-за неортогональности сетки экстремальные масштабы не совпа­дают с направлением меридианов и параллелей, за исключением сред­него меридиана и экватора.

Псевдоцилиндрические проекции в основном применяются для изображения всей земной поверхности или значительных ее частей в мелких масштабах, поэтому земная поверхность принимается за по­верхность шара с радиусом R. Эти проекции имеют две оси симмет­рии - экватор и средний меридиан нормальной сетки. Косые и попе­речные псевдоцилиндрические проекции используются крайне редко.

^ Проекция Гаусса-Крюгера. К.Ф. Гаусс в 1820 - 1830 гг. разра­ботал "двойную" равноугольную проекцию, сохраняющую длины на среднем меридиане. Л.Крюгер в 1912и 1919 гг. предложил способ непосредственного отображения эллипсоида взамен определения, указанного двойной проекцией, и эту проекцию стали называть про­екцией Гаусса-Крюгера (Gauss - Kruger projection). Она была приня­та в СССР ( на эллипсоиде Бесселя) в 1928 г. для всех геодезических и топографических работ. В ней создавали топографические карты масштабов крупнее 1:500 000, а с 1939 г. проекция Гаусса-Крюгера стала применяться и для карты масштаба 1:500 000.

В апреле 1946 г. постановлением правительства были утверждены размеры референц-эллипсоида Красовского и новые исходные даты, характеризующие систему координат 1942 г.

Проекция Гаусса-Крюгера не является строго равноугольной, так как при ее получении использовано разложение в такой ряд, для которо­го выполняется только одно из условий Коши-Римана.

При введении в уравнение проекции еще одного дополнительного члена ряда начинает выполняться второе условие, а первое, которое со­хранялось ранее, не выполняется.

Проекция при сохранении в ее формулах достаточного количества (7-8) членов является практически равноугольной, поэтому можно счи­тать, что в ней соблюдаются условия ортогональности сетки и равен­ства масштабов.

В проекции Гаусса-Крюгера поверхность эллипсоида на плоскости отображается по меридианным зонам, ширина которых равна 6° (для карт масштабов 1:500000-1:10 000) и 3° (для карт масштабов 1:5 000 -1: 2 000) (рис. 5.6, a).

Меридианы и параллели изображаются кривыми, симметричными относительно осевого меридиана зоны и экватора, однако их кривизна настолько мала, что западная и восточная рамки карты показаны пря­мыми линиями.

Параллели, совпадающие с северной и южной рамками карт, изоб­ражаются прямыми на картах крупных масштабов (1:2 000 - 1:50 000), на картах мелких масштабов - кривыми. Начало прямоугольных коор­динат каждой зоны находится в точке пересечения осевого меридиана зоны с экватором (рис. 5.6, б).

В России принята нумерация зон, отличающаяся от нумерации колонн карты масштаба 1:1 000 000 на тридцать единиц, т. е. крайняя западная зона с долготой осевого меридиана 1=21° имеет номер 4, к востоку номера зон возрастают. Номер зоны N и долгота осевого меридиана 1° в градусах свя­заны между собой равенством L°= 6N-3.

Территория России находится в северном полушарии, поэтому ко­ординаты ^ Х всех точек имеют положительное значение. Координаты Y имеют отрицательные значения левее осевого меридиана и положитель­ные правее его (рис. 5.6, б ). Чтобы исключить из обращения отрица­тельные координаты и облегчить пользование прямоугольными коорди­натами на топографических картах, ко всем координатам Y добавляют постоянное число 500 000 м (см. рис. 5.6, б). Для указания зоны, к кото­рой относятся координаты, к значению Y слева приписывают номер зоны. Например, запись координаты Y" 30 786 543м означает, что точка нахо­дится в 30-й зоне, ее реальная координата равна 786 000 - 500 000 = 286 543 м, т.е она расположена правее осевого меридиана 30-й зоны. Запись координаты Y= 8 397 720 м означает, что точка находится в 8-й зоне, ее реальная координата равна 397 720 - 500 000 = 102 280 м, она расположена левее осевого меридиана 8-й зоны.

Изоколы в проекции Гаусса-Крюгера имеют вид овалов, вытянутых вдоль осевого меридиана; в пределах отдельных листов карт они имеют вид прямых. Максимальные искажения в каждой зоне будут при значе­ниях широт 0° и ±3°, в этих точках они достигают ^пи»=0,14 %.

На расстоянии около 200 км по обе стороны от осевого меридиа­на и параллельно ему находятся две изоколы с нулевыми иска­жениями длин. При дальнейшем удалении от осевого меридиана масштаб длин становится больше единицы и достигает максиму­ма на пересечении крайних меридианов зоны с экватором (Vmax = +0,05 %).






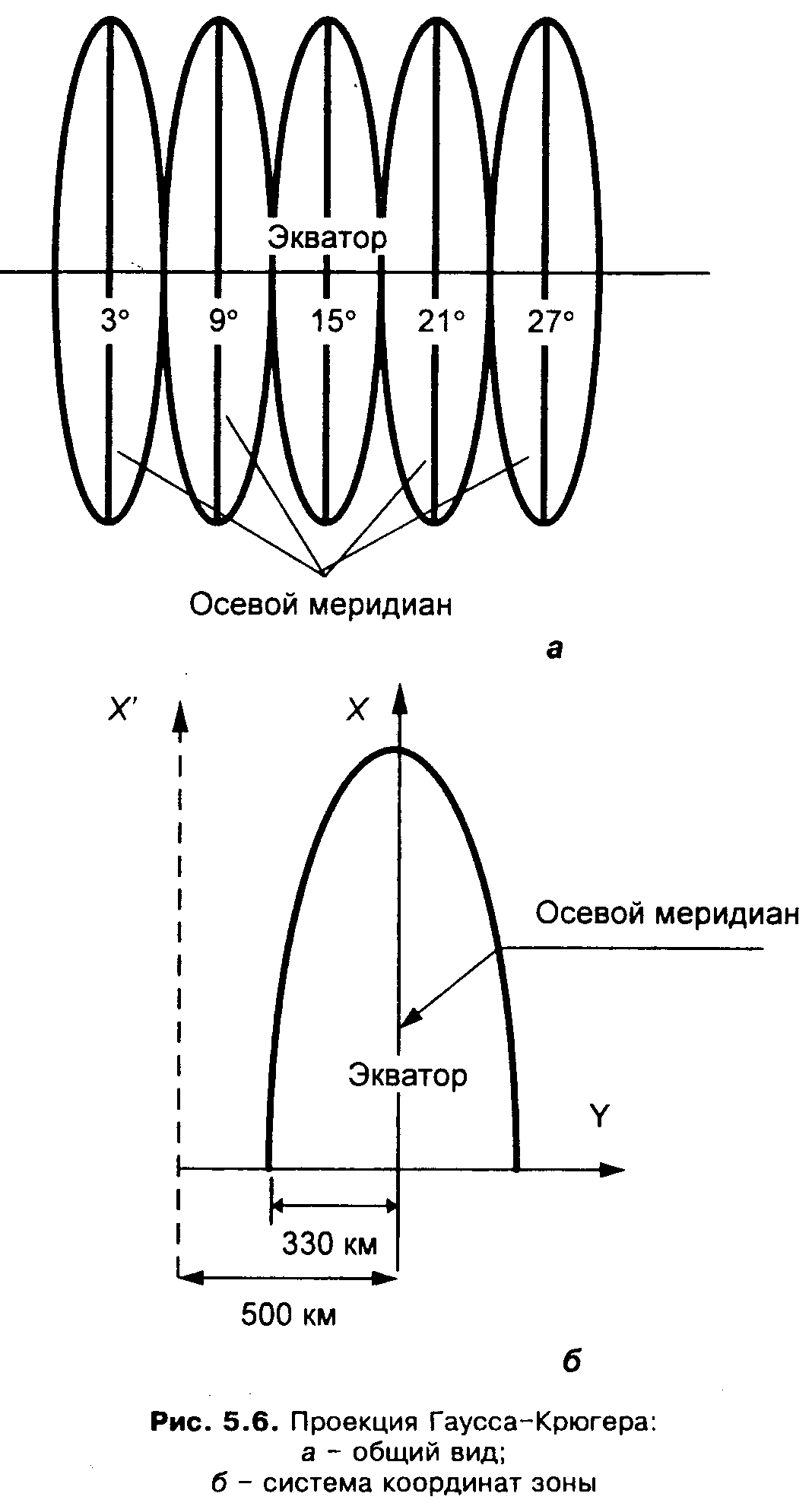
Рис. 5.6. Проекция Гаусса – Крюгера: а – общий вид; б – система координат зоны



Осевые меридианы трехградусных зон совпадают попеременно то с осевыми меридианами шестиградусных зон, то с крайними меридиана­ми этих зон.

Во многих странах применяют для составления топографичес­ких карт универсальную поперечно-цилиндрическую проекцию Меркатора (UTM) в шестиградусных зонах. Эта проекция близка по сво­им свойствам и распределению искажений к проекции Гаусса-Крюгера, но на осевом меридиане каждой зоны масштаб М=0,9996, а не единица. Проекция UTM получается двойным проектированием: эллипсоида на шар, а затем шара - на плоскость в проекции Меркатора.

Достаточно полное описание перечня проекций приведено в [2] . Важно отметить, что существует различие между проекцией, с которой работает пользователь, и проекцией исходной карты. Для мелкомасш­табных карт существенно различие картографических проекций. Про­цесс трансформации картографических данных из одной проекции в другую требует знания параметров проекции источника и производной проекции, известных из курсов математической картографии и теории картографических проекций и справочных изданий.

Пересчет координат может быть представлен как решение обратной задачи математической картографии, т.е. преобразования прямоуголь­ных координат в географические, а вслед за нею - прямой задачи с ис­пользованием уравнения производной проекции либо непосредствен­ного пересчета данных из проекции в проекцию, минуя приведение к системе географических координат.

При неизвестных функциональных зависимостях, определяющих соответствие географических и условных координат, можно воспользо­ваться методами трансформации по сети опорных точек с известными координатами. В этом случае возникает проблема оптимального выбора аппроксимирующей функции. Наличие координатной основы - обяза­тельное требование трансформационных преобразований.

Программные средства ГИС содержат различные блоки преобразо­вания, включающие различные проекции: равновеликую коническую Алберса, азимутальную равнопромежуточную, коническую равнопромежуточную, гномоническую, равновеликую азимутальную Ламберта, кони­ческую равноугольную Ламберта, Меркатора, цилиндрическую Милле­ра, косую Меркатора (Hotine), ортографическую, полярную стереогра­фическую, поликоническую, синусоидальную, стереографическую, поперечную Меркатора, универсальную поперечную Меркатора (UTM), Гринтена.

На практике использование модулей трансформации проекций может быть осложнено отсутствием параметров проекции карты-источника.

При определении проекций исходной карты рекомендуют пользо­ваться атласом для отечественных карт [4] и для зарубежных [17].

Для топографических карт в отличие от мелкомасштабных нет тако­го разнообразия проекций, однако имеется разнообразие моделей Зем­ли и географических систем координат.

Специфика российского рынка геоинформационных технологий определяет проблемы проекционных преобразований в России. Одна из серьезных проблем связана с использованием отечественной картогра­фической информации, имеющей значительные отличия от аналогич­ной иностранной. Как правило, иностранные программные средства не поддерживают напрямую распространенные в нашей стране проекции, а информацию о типе проекции и ее параметрах получить довольно сложно.

Другая проблема состоит в том, что широко распространенные в России разнообразные методы работы с пространственными данными не получили признания или не имеют аналогов за рубежом и нуждаются в анализе и классификации.

^

6.5.Система реальных географических координат

Большинство карт изображают координатные данные, используя одну из принятых глобальных систем координат, например, Универсальную поперечную Меркатора (UTM), Коническую равноплощадную Альберта или полярную стереографическую. Проекция используется для обеспечения взаимосвязи между местоположением на карте и истинным местоположением на земной поверхности.

Наиболее привычной системой описания положения в пространстве является система широт и долгот. Эта система может использоваться для определения местоположения точек в любом месте на земной поверхности.

Широта и долгота являются угловыми величинами, измеренными от центра земли до точки на земной поверхности. Широта может быть северная и южная, долгота – западная и восточная. Картографическая сетка (сетка широт и долгот) может быть наложена на земную поверхность, чтобы географически описать местоположение. Линии долготы называются меридианами и начинаются и заканчиваются на Северном и Южном полюсе. Линии широты называются параллелями и охватывают земной шар параллельными кольцами.

Широта и долгота традиционно измеряются в градусах, минутах и секундах. Широта равная 0 гр. Располагается на экваторе, +90 гр. - На Северном полюсе, -90 гр. – на Южном полюсе. На долготе, равной 0, расположен начальный меридиан, который начинается на Северном полюсе, проходит через Гринвич и заканчивается на Южном. Долгота положительна до 180 гр., если двигаться к востоку от Гринвича, и отрицательна, если двигаться к Западу от . Гринвича.

Однако широта и долгота являются географической описательной системой, а не двумерной (плоской) системой координат. Меридианы в этой системе сходятся в полюсах и расходятся при движении к экватору. Т.о., длина одного градуса долготы будет различной в зависимости от широты, на которой она измерена. Например, 1 гр. Долготы на экваторе по длине равен 111 км, но длина 1 гр. На полюсах стремится к нулю. Итак, в этой системе координат измеряются углы от центра земли, а не расстояние на земной поверхности, она не является плоской системой координат.
^

6.6.Плоские системы координат

Плоские системы координат (частот называемые Декартовыми) обладают некоторыми свойствами, которые делают их пригодными для представления реальных географических координат на карте:

• Имеется два измерения: x измеряет расстояние в горизонтальном направлении, а y измеряет расстояние в вертикальном направлении
  
• Меры длин, углов и площадей остаются постоянными по всем измерениям
  
• Существуют различные математические формулы для отображения сферической поверхности земли на плоскую двумерную поверхность.
  

ГИС, как и плоские карты, используют различные плоские координатные системы для картографирования земной поверхности. Каждая из используемых координатных систем базируется на определенной картографической проекции.
^

6.7.Картографические проекции

Поскольку поверхность земли является сфероидом, для создания плоской карты сферической поверхности необходимо использовать математические преобразования. Эти математические преобразования обычно называют картографическими проекциями.

!!!Поскольку каждая базовая карта хранится в конкретной проекции, необходимо определить проекцию базовой карты перед вводом ее в систему.

Необходимо иметь в виду:

• Любое двумерное представление земной поверхности всегда вносит искажения в некоторые параметры либо в форму, площадь, расстояние или направление.
  
• Различные проекции вносят различные искажения
  
• Характеристики каждой проекции делают ее удобной для некоторых приложений и непригодной для других.
  

Проекция	Характеристики	Карты
Меркатора	Форма: сохраняется Площадь: Определенные искажения Расстояния: Искажения возрастают по направлению к полюсам Направление: Некоторые искажения	Навигационные карты Карты часовых поясов
UTM не используется для изображения очень больших территорий	Форма: Сохраняется Площадь: Искажения возрастают при удалении от центрального меридиана Расстояния: то же, что и для площади Направление: некоторые искажения	Серия трапецеидальных карт в масштабе 1:250 000 (зоны в 1гр. по широте и 2 гр. по долготе)
Поперечная Меркатора	Форма: Сохраняется Площадь: Определенные искажения Расстояния: некоторые искажения Направление: некоторые искажения
Коническая равноплощадная Альбера	Форма: Некоторые искажения Площадь: сохраняется Расстояния: некоторые искажения Направление: некоторые искажения
Коническая равноугольная Ламберта	Форма: Сохраняется Площадь: некоторые искажения Расстояния: некоторые искажения Направление: некоторые искажения	Базовые государственные карты

^ Свойства проекций

Конформные проекции

Конформные проекции сохраняют локальную форму. Линии градусной сетки на глобусе – перпендикулярны. Чтобы сохранить углы, описывающие пространственные отношения, конформное проекция должна представить сетку линий, пересекающихся под 90 градусов.

^ Равноплощадные проекции

Равноплощадные проекции сохраняют область.

Эквидистантные проекции.

Эквидистатные карты сохраняют расстояния между некоторыми точками.

^ Проекции истинного направления

Наикратчайший путь между двумя точками на кривой поверхности (Земля) – это единственный сферический эквивалент прямой линии на плоскости.


^ Типы проекций

Математическое выражение, которое систематически проецирует место с поверхности сферы на соответствующую позицию на плоской поверхности называется картографической проекцией.

Первый шаг в проецировании с одной поверхности на другую состоит в создании одной или более контактных точек. Каждая точка называется точкой касательной. Плоская проекция касается глобуса только в одной точке. Касание глобуса конусом или цилиндром происходит по линии.

Искажение проекции увеличивается с увеличением расстояния от точки контакта.

^ Конические проекции

Большинство конических проекций касаются глобуса вдоль линии широты. Эта линия называется стандартной параллелью для данной проекции. Меридианы проецируются на коническую поверхность, соединясь в вершине.

Цилиндрические проекции

Цилиндрическая проекция должна иметь одну линию касания или две секущих линии. Меркаторская проекция – одна из наиболее общих цилиндрических проекций. Экватор – обычно линия его касания. Меридины геометрически проецируются на цилиндрическую поверхность

Планарные (плоские) проекции

Другие проекции