Урок по теме «Линейная функция»

Вид материала

Урок

Содержание 3) Исторический экскурс. 4) Выполнение практических заданий. Применение имеющихся знаний к решению новых задач. 1 вариант 2 вариант 7) Домашняя работа. Выставление оценок.

Подобный материал:

• Домашнее задание: лекция, тест 6 по теме «Линейная функция» (с сайта ), построить графики, 56.95kb.
• Урок по теме: "Условная функция в Excel", 153.87kb.
• Урок в 8-м классе по теме: "Тепловой баланс. Решение задач", 94.3kb.
• Доклад Абсолютная величина, 29.68kb.
• Тематическое планирование по теме: «Функция», 64.78kb.
• S: Функция выявления закономерностей исторического развития это функция, 1125.29kb.
• Урок по теме: «Мотивация как функция менеджмента», 24.69kb.
• Программа для аттестационных испытаний по дисциплине: «математический анализ и линейная, 77.58kb.
• Урок геометрии в 8 классе по теме «Площади многоугольников», 52.25kb.
• План урока Вступление Закрепление и обобщение изученного материала. Составление плана, 86.07kb.

Обобщающий урок по теме « Линейная функция»

Цели урока:

1. Обучающие:
   

• Систематизировать, расширить и углубить знания, умения и навыки учащихся, связанные с понятиями линейной функции и ее графика; взаимного расположения графиков линейной функции на координатной плоскости
  
• повторение и закрепление понятий и определений: функция, график, независимая переменная, зависимая переменная, линейная функция, функция прямой пропорциональности,
  
• умение выполнять построения графиков по формуле;
  
• умение применять графический и алгебраический методы.
  

2. Развивающие:
   

• развитие познавательного интереса к алгебре;
  
• развитие логического
  
• мышления; активизация внимания учащихся;
  
• формирование потребности приобретения знаний.
  

3. Воспитывающие: воспитание дружеских отношений в коллективе, положительной мотивации к изучению предмета, аккуратности, добросовестности и чувство ответственности.
   

Оборудование: плакат с изображением графиков линейных функций с одинаковыми и с разными коэффициентами; компьютерное сопровождение (слайды к уроку); тесты; рабочие тетради

Ход урока:

1. Организационный момент: учитель сообщает тему, план и цели урока.
   
2. Устная работа – теоретическая разминка. Презентация.
   

Вопросы:

1) Какая функция называется линейной? Область определения и область значения линейной функции? (показ слайдов 2 из 9)

2) При каком условии линейная функция становиться прямой пропорциональностью? (показ слайдов 3 из 9)

3) Что является графиком линейной функции и прямой пропорциональности? Как построить график линейной функции (прямой пропорциональности)? Чем обусловлено различие графиков этих функций? (показ слайдов 3 из 9)

4)Среди указанных функций выделите такие, графиками которых является прямая: у = - 3х + 12;

у = х² - 3; у = 3х³ + 4; у = 5; у = - 4х; у = ¾ х+ 1; у = - 0,5х; у = - 2; у = - 3 + х?

Назовите те функции, графики которых: а) проходят через начало координат; б) параллельны оси абсцисс? (показ слайдов 4 из 9)

5) Функция задана формулой у=2х-3. Найдите значение функции, если значение аргумента равно 3; -3; 0. Найдите значение аргумента, если известно значение функции: у=2х - 3 равно -5; 0. (показ слайдов 5 из 9)

6) Определите, проходит ли график функции, заданной формулой у=1,2х - 7 через точку с координатами? А(100; 113), В(- 10; 5) (показ слайдов 5 из 9)

7) Как, не выполняя построения, определить, каким (острым или тупым) является угол наклона графика с положительным направлением оси абсцисс? В какой точке график пересекает ось ординат? (показ слайдов 6 из 9)

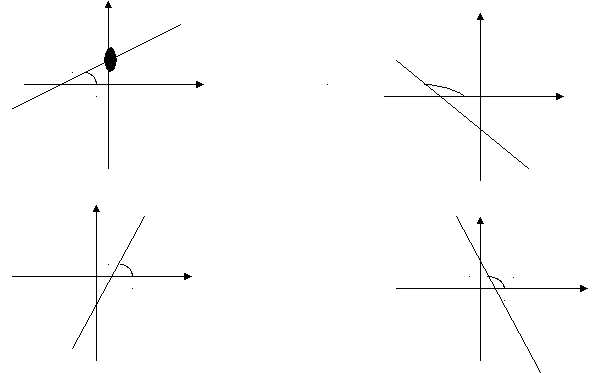у к>0 у к<0


х х


к>0

у у к<0

х

х


8) По графику определить знаки к и b ? (показ слайдов 7 из 9)



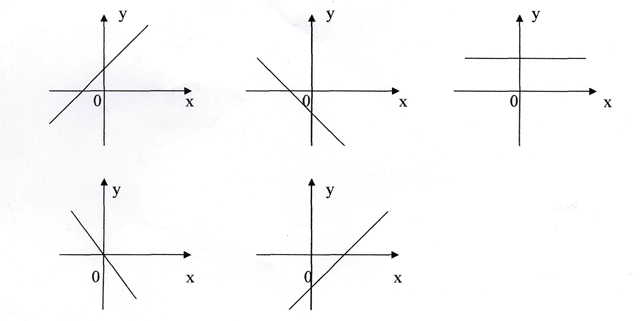
19) В построении графиков функций, заданных формулами у =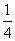х; у =-3х+2; у = 2х-1, допущены ошибки. Найдите эти ошибки и объясните, как правильно построить. (показ слайдов 8 из 9)

у
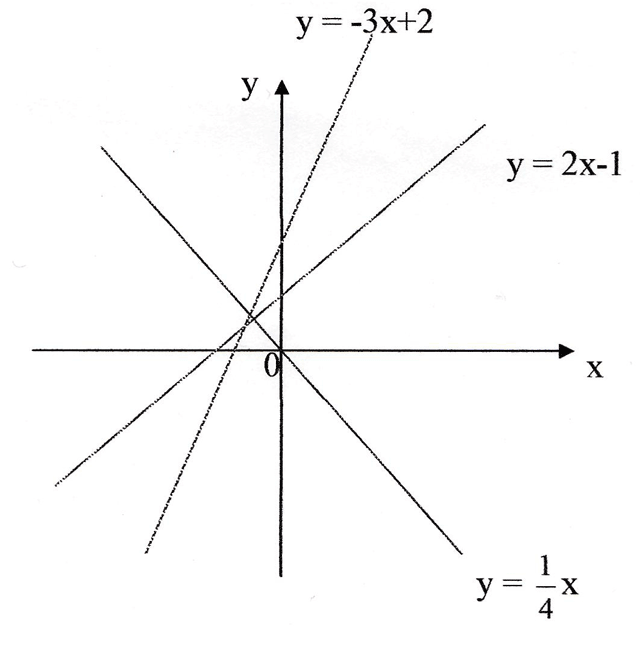
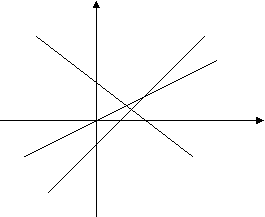Ответ:

у=2х-1

у=1/4х


х

у= -3х+2


^ 3) Исторический экскурс. (показ слайдов 9 из 9)

Знакомство с великим французским математиком Рене Декартом (1596г.-1650г.)

Декарт был крупнейшим философом и математиком своего времени. Декарт ввел систему координат, которой пользуются и сейчас.

Он установил соответствия между числами и отрезками на прямой, таким образом ввел алгебраический метод в геометрию. Появилась возможность изображать зависимость величин графически на координатной плоскости, числа -отрезками.

Это был совершенно новый метод, отличавшийся красотой, изяществом и простотой.

^ 4) Выполнение практических заданий. Применение имеющихся знаний к решению новых задач. ( задания на карточке)

1) Построить график линейной функции у=3(х+6). Написать формулу прямой пропорциональности, график которой параллелен графику линейной функции.

2) Найти координаты точек пересечения функций у = 10х-8 и у = -3х+5.

3) Задайте формулой линейную функцию, если известен угловой коэффициент к = 2.

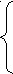
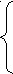2х, если х ≥ 0 3, если х < 0

4)Построить графики функций а) у = б) у =

½ х, если х < 0 х + 3, если х ≥ 0

5)Построить графики функций, содержащих знак модуля.

а) У= I х I

б) У= - I х I

в) У= I х I + 2

г) У= I х I -2

Ответы:




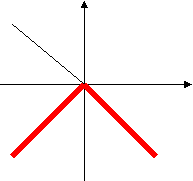
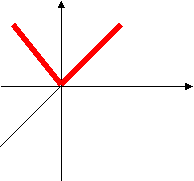
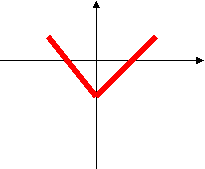у у

а) б)

х

х





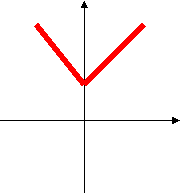
у у


г)

в) х

2

-2

х


5) Самостоятельная работа. ( материал для самостоятельной работы отпечатан ( бумажный носитель ЦОР), у каждого на столе, таблицы и графики приготовлены для подстановки или для выполнения чертежа)

^ 1 вариант 2 вариант

1. Определи числа k и b в заданных линейных функциях:

функция k b 1 f(x)=3x 2 3 h(x)=4-x

функция k b 1 v(x)=2-x 2 u(x)=-5+х 3 m(x)=4x

2. Заполни таблицу и построй график линейной функции, заданной формулой:
а) f(x)=-2x+3; а) ) f(x)=7-x

x	-2	-1	0	1	2
f(x)

? Какая линия получается при построении графика линейной функции?
? Сколько точек достаточно, чтобы построить такую линию?

3. На рисунке изображён график функции y=f(x). Не заполняя таблицы, построй графики функций y=g(x) и y=h(x).

а) f(x)=x/2, g(x)=x/2+4, h(x)=x/2–3	а) f(x)=–x+5, g(x)=–x, h(x)=–x–1

4. Для каждой из записанных здесь формул найди соответствующий график на рисунке:
1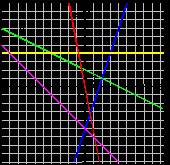. y = –5x,
1. y = –x –5,
2. y = 3х-5,
2. y = 4


6)Запутанный след (творческое задание). (для тех, кто быстро сделает самостоятельную работу)

На листах ( на каждой парте) записаны рассказы, необходимо найти ошибки, парная работа, ответы на отдельных листах, выдаётся после выполнения для самопроверки)

Текст: Понятие функция появилось до нашей эры. Функции бывают различные. Линейную функцию можно задать формулой у= кх +вх. Область определения множество положительных чисел. Графиком линейной функции является прямая, обязательно проходящая через начало координат.

Ответ: Понятие функция появилось в XVII веке. Функции бывают различные. Линейную функцию можно задать формулой у = кх +в. Область определения множество действительных чисел. Графиком линейной функции является прямая.

^ 7) Домашняя работа. Выставление оценок.

Сильным учащимся составить сказку, где главная героиня линейная функция.

Учащиеся, знания которых оцениваются в « 3» балла, составляют кроссворд (количество слов от 8 до 10).

Общее задание: Построить графики функции:

у=х-3; у= -х+3; у= I х I - 4; у= I х I +3.

8) Подведение итогов.

1. Анализ действий, выполненных на уроке:

• вспомнили определение линейной функции;
  
• рассмотрели всевозможные эскизы графиков в зависимости от коэффициента и свободного члена;
  
• вспомнили навык построения графика линейной функции и составление формулы по координатам двух точек;
  
• вспомнили навык нахождения значения аргумента и значения функции; определения принадлежности точки графику функции;
  
• вспомнили взаимное расположение графиков линейной функции и прямой пропорциональности;
  

2. Расширение кругозора.

• – Оказывается, что наши знания по данной теме можно применить при построении графиков функции с модулями, а также при построении графика функции вида:
  

У= 3х, если х≥0

1/3х, если х<0