Доклад Абсолютная величина

Вид материала

Доклад

Подобный материал:

• Задачи курса : вооружить учащихся системой знаний по теме «Абсолютная величина»: сформировать, 323.97kb.
• Доклад Абсолютная величина и динамика роста основных средств характеризует экономический, 43.22kb.
• Понятийно-терминологический словарь Абсолютная магнитная проницае­мость среды, 176.32kb.
• Тема: Литосфера. Форма рельефа земной коры, 18.52kb.
• Абсолютная погрешность измерения, 125.99kb.
• Командир электромеханической боевой части подводного атомохода это уважаемый человек,, 26.53kb.
• 2 Этнокультурная ситуация в Балаково (К. С. Мокин), 402.77kb.
• Стратегическими целями предприятия в области финансов являются обеспечение его ликвидности, 52.14kb.
• Доклад директора победителя пнпо 2006 года моу «мелекесская средняя общеобразовательная, 512.65kb.
• Вопрос Межъязыковые соотносительные лексико-семантические категории. Абсолютная и относительная, 19.97kb.

Доклад

Абсолютная величина





График вещественной функции





Модуль | z | и другие характеристики комплексного числа | z |

Абсолю́тная величина́ или мо́дуль, обозначается 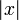. В случае вещественного аргумента — непрерывная кусочно-линейная функция, определённая следующим образом:



Обобщением этого понятия является модуль комплексного числа 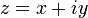, также иногда называемый абсолютной величиной^[ Он определяется по формуле:



Основные свойства

С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина 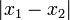означает расстояние между точками и 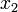и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.

Вещественные числа

• Область определения: .
  
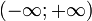• Область значений: .
  
• Функция чётная.
  
• Функция дифференцируема всюду, кроме нуля. В точке x = 0 функция претерпевает излом.
  

Комплексные числа

• Область определения: вся комплексная плоскость.
  
• Область значений: .
  
• Модуль как комплексная функция не дифференцируема ни в одной точке, поскольку условия Коши-Римана не выполнены.
  

Алгебраические свойства

Для любых 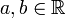имеют место следующие соотношения:

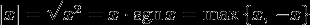• (см. Функция sgn(x)).
  
• 
  
• .
  

Как для вещественных, так и для комплексных 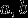имеют место соотношения:

• , причём | a | = 0 тогда и только тогда, когда .
  
• | − a | = | a | .
  
• .
  
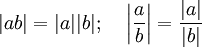• (неравенство треугольника).
  
• .
  
• .
  
• .
  
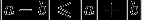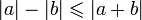• , если существует.
  

История

Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.

Обобщение

Обобщением понятия модуля можно считать норму элемента многомерного векторного пространства, обозначаемую 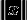. Норма вектора в евклидовом пространстве иногда тоже называется модулем. По аналогии с модулем разности чисел, норма разности двух векторов является мерой близости между ними. В отличие от модуля числа, норма вектора может определяться различными способами, однако в случае одномерного пространства норма вектора пропорциональна (часто и равна) модулю его единственной координаты.