М. К. Аммосова рабочая программа
| Вид материала | Рабочая программа |
- М. К. Аммосова Институт физической культуры и спорта рабочая программа, 343.46kb.
- М. К. Аммосова Педагогический институт рабочая программа, 237.42kb.
- М. К. Аммосова Педагогический институт Рабочая программа, 162.88kb.
- М. К. Аммосова Педагогический институт рабочая программа, 133.8kb.
- М. К. Аммосова Медицинский институт рабочая программа, 722.74kb.
- М. К. Аммосова Кафедра философии Рабочая программа, 160.43kb.
- М. К. Аммосова программа к урса строение вещества для государственных университетов, 197.97kb.
- М. К. Аммосова Педагогический институт Кафедра педагогики дошкольного воспитания рабочая, 88.09kb.
- М. К. Аммосова программа курса физика для государственных университетов Специальность, 335.55kb.
- М. К. Аммосова рабочая программа, 165.41kb.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Якутский государственный университет им. М.К. Аммосова
РАБОЧАЯ ПРОГРАММА
по курсу «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»
Специальность 351400 - «прикладная информатика в экономике»
Форма обучения: дневная
Якутск 2001
Составители: к.ф-м.н., доцент М.П.Григорьев
К.ф-м.н., доцент Н.А.Романова
Дифференциальные уравнения широко используются в вариационном исчислении, оптимальном управлении, геометрии и топологии, уравнениях математической физики и др. Теория дифференциальных уравнений применяется в непрерывных моделях экономики, где независимым переменным является время. Такие модели достаточно эффективны при исследовании эволюции экономических систем на длительных интервалах времени; они являются предметом исследования экономической динамики. Цель дисциплины - выработать у студентов глубокие знания основ теории обыкновенных дифференциальных уравнений, умение применять эти знания при исследовании и решении конкретных дифференциальных уравнений и систем, встречающихся в различных областях естествознания, экономики. Лекционный курс сопровождается упражнениями, при помощи которых у студентов вырабатываются навыки решения конкретных задач.
1. ^ ВЫПИСКА ИЗ УЧЕБНОГО ПЛАНА
Объем работы студента из учебного плана специальности 351400 -«прикладная информатика в экономике» составляет 140 часов, в том числе
аудиторных занятий - 68,
самостоятельной работы- 72.
1.2. Требования стандарта по дисциплине
Студент должен свободно ориентироваться в основных разделах дисциплины:
- дифференциальные уравнения первого порядка, разрешенные относительно производной;
- дифференциальные уравнения первого порядка, не разрешенные относительно производной;
- дифференциальные уравнения высших порядков, допускающих понижение порядка;
- линейные дифференциальные уравнения с постоянными коэффициентами;
- линейные системы дифференциальных уравнений с постоянными коэффициентами;
- Цели дисциплины
Целью дисциплины является:
- Формирование у студента прочных знаний основ теории обыкновенных дифференциальных уравнений;
- Закрепление навыков интегрирования в квадратурах основных типов дифференциальных уравнений и систем;
- Воспитание у студента умения применять методы теории дифференциальных уравнений в прикладных задачах;
- Воспитание у студента культуры мышления;
- Развитие у студента математической культуры и интуиции;
- Привитие студенту навыков самостоятельной работы над изучением литературы по дифференциальным уравнениям и ее приложениям.
Вопросы к зачету
^ 1. Дифференциальные уравнения первого порядка,
разрешенные относительно производной
1. Какие уравнения называются дифференциальными? дифференциальными уравнениями первого порядка?
2. Что называется решением дифференциального уравнения? В каких видах могут быть заданы решения?
3. Какую геометрическую интерпретацию можно дать самому дифференциальному уравнению
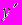 =(x,y)? Его решению?
=(x,y)? Его решению?4. Каковы основные формы задания уравнения первого порядка, разрешенного относительно производной?
5. Что такое интегральная кривая?
6. Что такое изоклина? Напишите уравнение изоклины нуля и бесконечности. Может ли изоклина быть одновременно быть его интегральной кривой? Если да, то приведите пример.
7. В чем состоит задача Коши для уравнения первого порядка, разрешенного относительно производной? При каком условии она имеет решение? При каких условиях это решение будет заведомо единственным?
8. Геометрическая интерпретация теоремы существования и единственности.
9. Привести пример нарушения единственности решения задачи Коши.
10. Дать определение общего решения. Как решается задача Коши при помощи общего решения?
11. Дать определение частого решения. Как оно может быть связано с формулой общего решения?
12. Какое решение называется особым? Как оно может быть связано с формулой общего решения? Как найти кривые, подозрительные на особое решение, по самому дифференциальному уравнению? В каком случае дифференциальное уравнение заведомо не имеет особых решений?
13. Что такое особая точка дифференциального уравнения? Как по виду правой части уравнения установить у него наличие особых точек?
14. Как интегрируются уравнения с разделенными и разделяющимися переменными?
15. Найти решение уравнения 3y 2
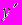 + 16x = 2xy 3 при х .
+ 16x = 2xy 3 при х .16. Какое уравнение называется однородным? Как оно интегрируется?
17. Какому условию должна удовлетворять функция (x,y), чтобы уравнение
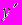 =(x,y), было однородным?
=(x,y), было однородным?18. Какое уравнение называется линейным? При каком условии задача Коши имеет единственное решение?
19. Найти общее решение линейного уравнения через заданные функции, входящие в уравнение.
20. Может ли график ненулевого решения линейного однородного уравнения пересекает ось Ох или касается ее? Может ли линейное уравнение иметь особое решение?
21. Как найти общее решение неоднородного линейного уравнения, если известно одно частное решение?
22. Найти решение уравнения
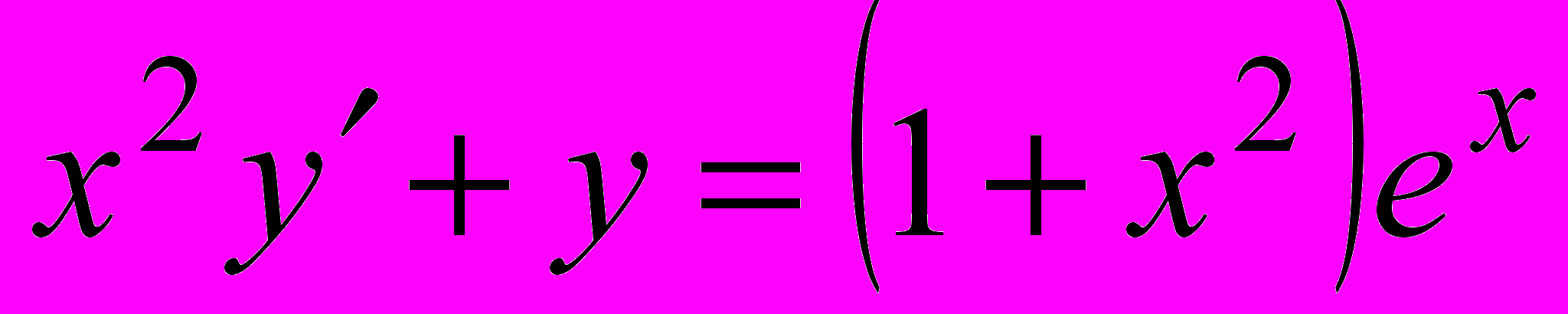 , удовлетворяющее условию:
, удовлетворяющее условию:  при
при 
 .
.23. Найти ограниченность решения при
 0 уравнения
0 уравнения 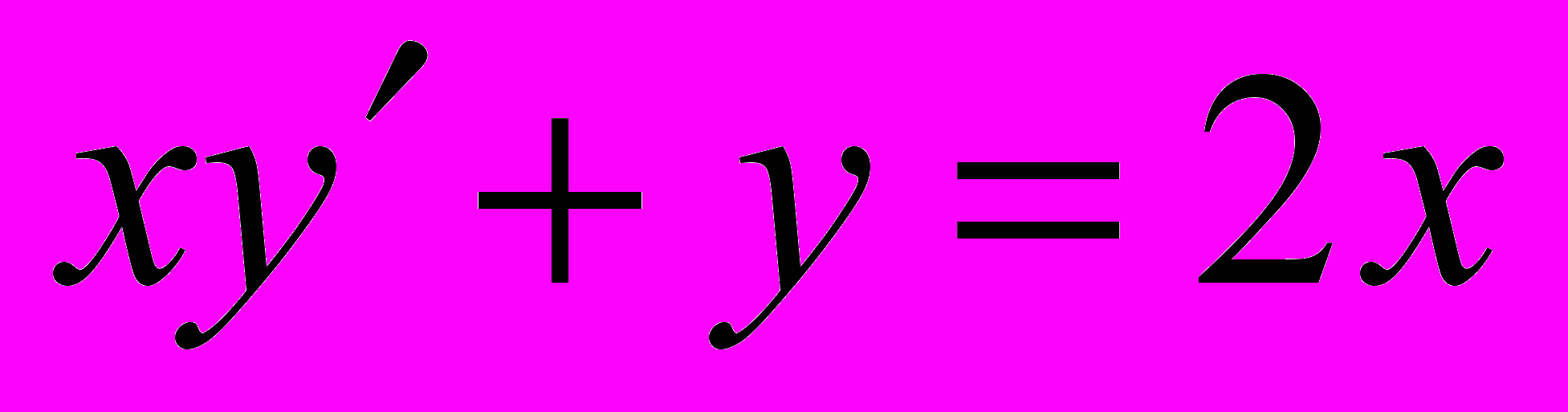 .
.24. Как интегрируется уравнение Бернулли? При каком условии y = 0 будет решением, когда это решение является частным и когда особым?
25. При каком условии уравнение
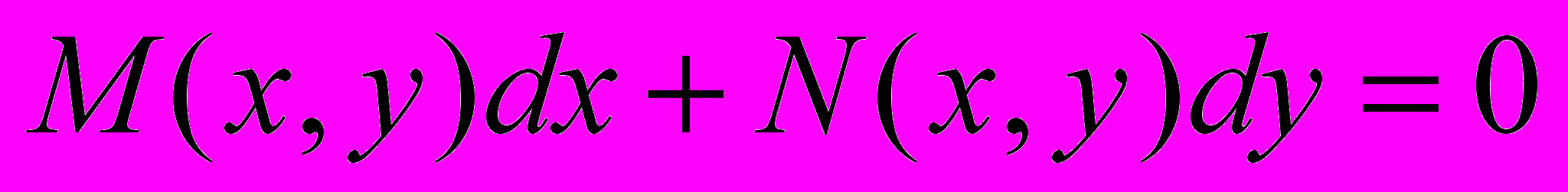 является уравнением в полных дифференциалах? Какой вид имеет его общий интеграл?
является уравнением в полных дифференциалах? Какой вид имеет его общий интеграл?26. Как по виду уравнения в полных дифференциалах написать его решение задачи Коши с начальными данными x 0, y 0?
24. В чем состоит метод интегрирующего множителя? При каком условии существует интегрирующий множитель, зависящий: а) только от х; б) только от y?
25. С помощью метода последовательных приближений найти решения уравнений:
а)
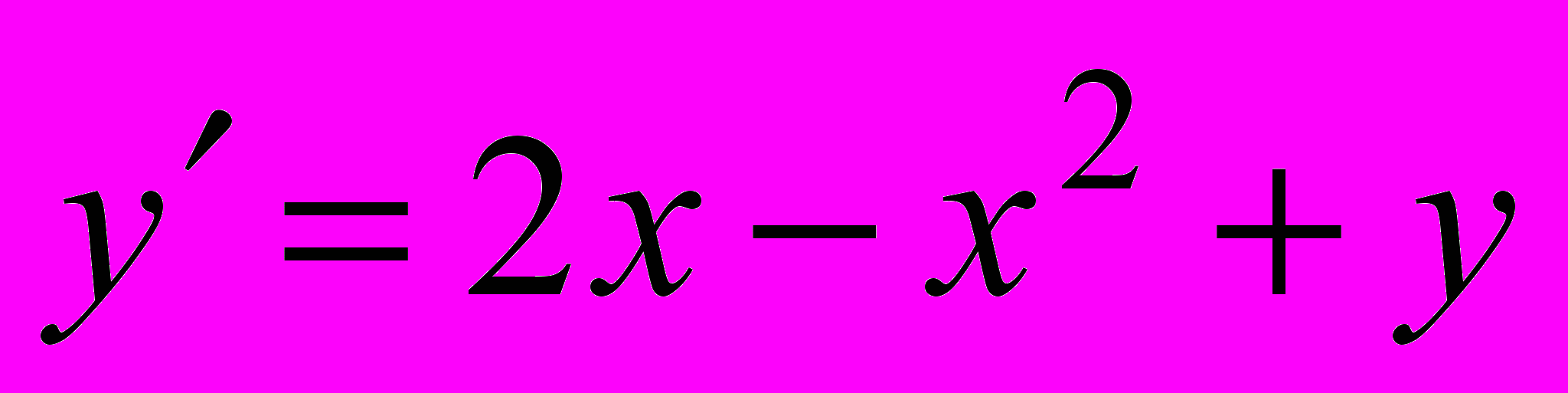 , y(0) = 1; б)
, y(0) = 1; б) 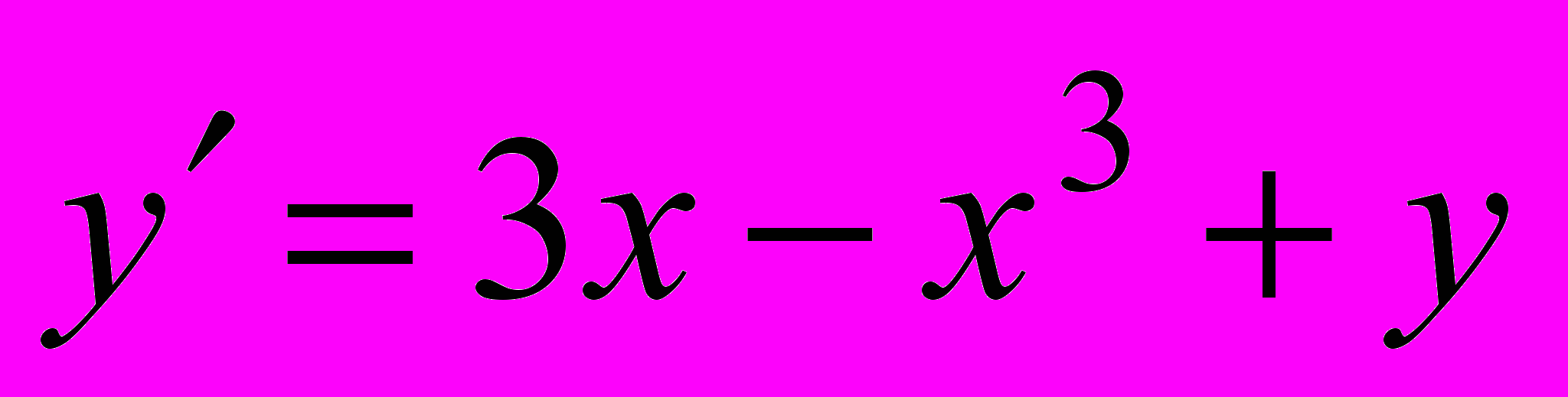 , y(0) = 3.
, y(0) = 3.26. Доказать по виду уравнений, что они не имеют особых решений:
а)
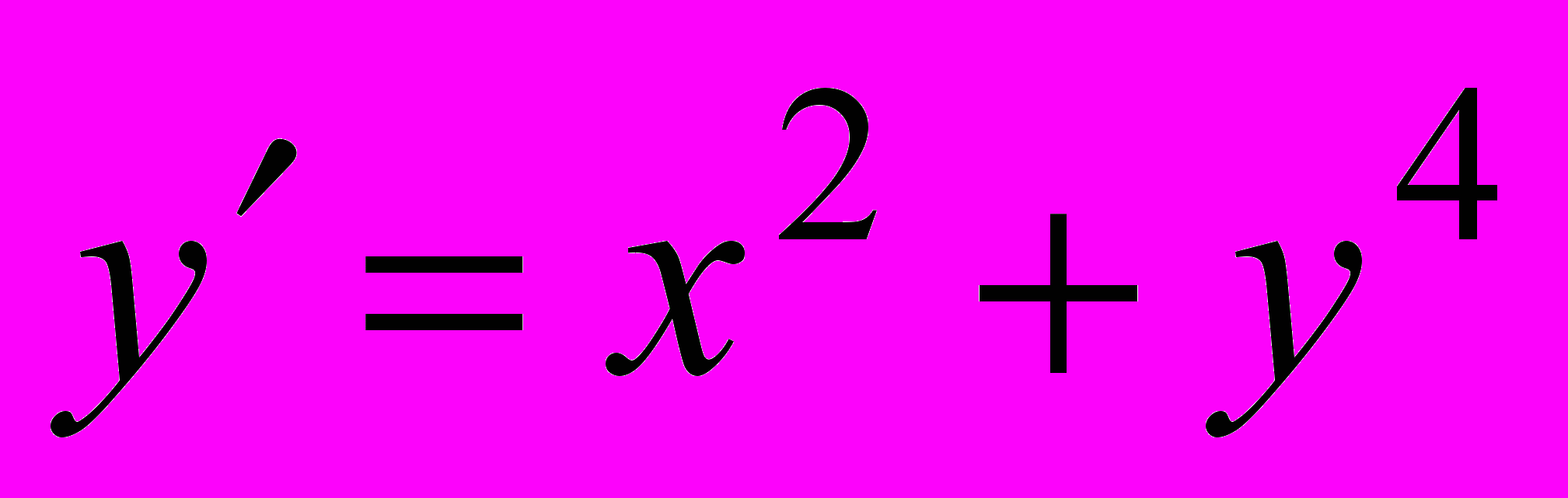 б)
б) 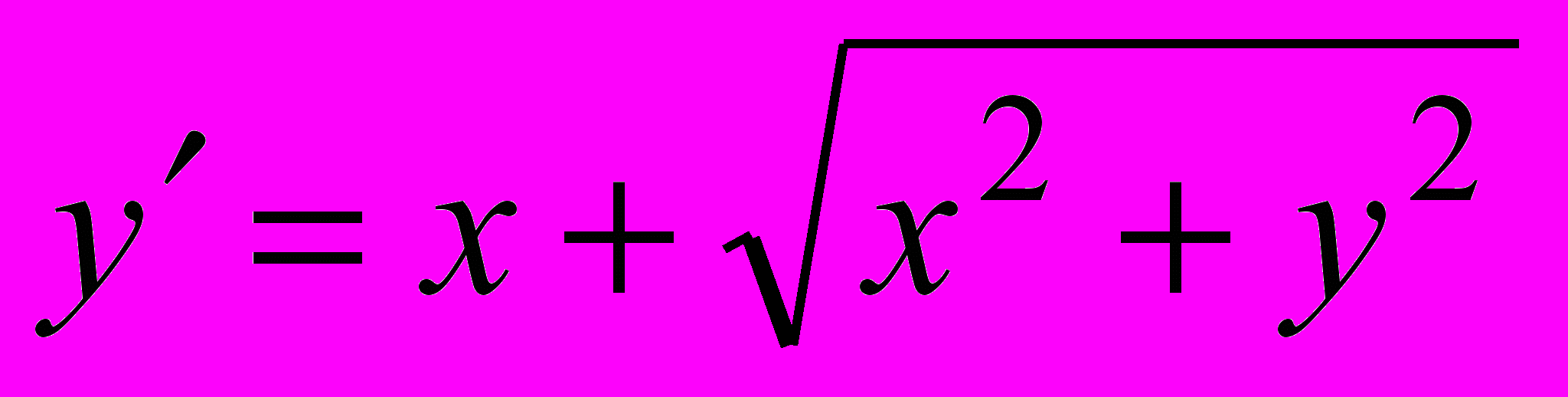 .
.27. Определить тип каждого из следующих уравнений и указать метод интегрирования его: а)
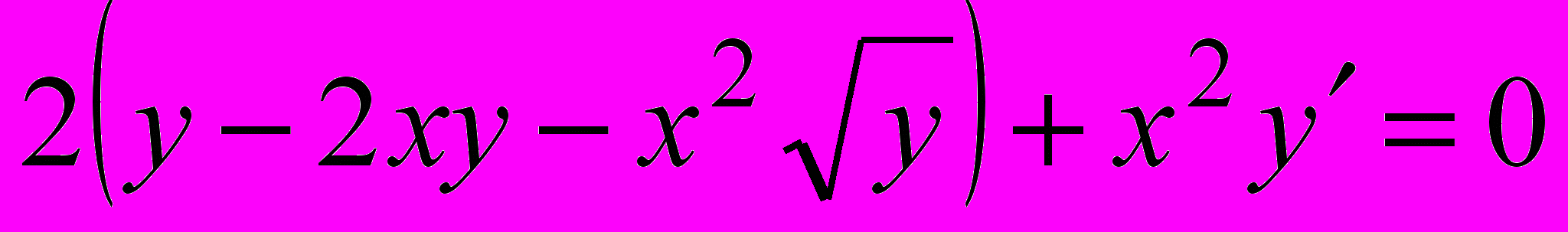 б)
б) 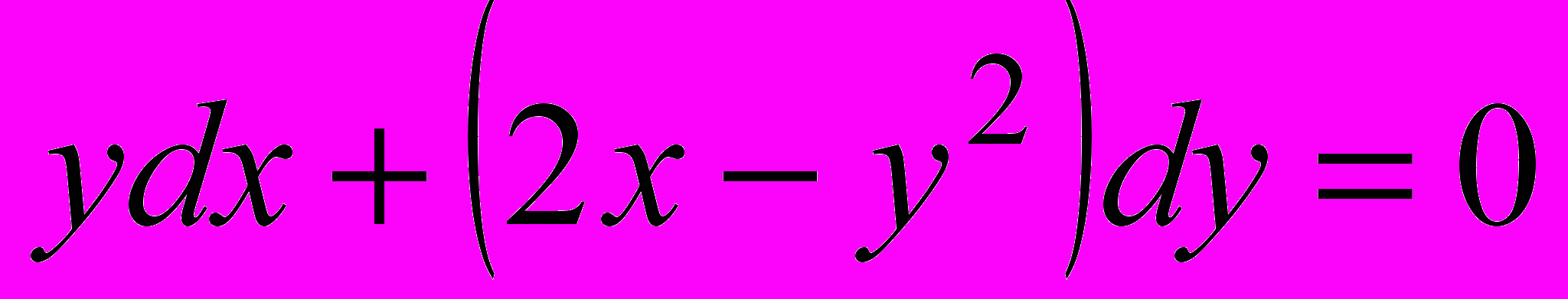 .
.^ 2. Дифференциальные уравнения первого порядка,
не разрешенные относительно производной
1. Какой вид имеет общее решение уравнения первого порядка, не разрешенные относительно производной?
2. В чем состоит отличие поля направлений, определяемого уравнением, не разрешенного относительно производной, от поля направлений, определяемого уравнением, разрешенного относительно производной?
3. Могут ли интегральные кривые пересекаться между собой? Могут ли касаться друг друга?
4. Как ставиться задача Коши для уравнения первого порядка, не разрешенного относительно производной?
5. Что такое частное решение?
6. Какое решение называется особым? Как найти кривые, подозрительные на особые решения, по самому дифференциальному уравнению?
7. Какой вид имеет общий интеграл уравнения
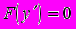 ?
?8. Как интегрируется уравнение, не содержащее искомой функции?
9. Как интегрируется уравнение, не содержащее независимой переменной?
10. Какой вид имеет уравнение Лагранжа?
11. Какой вид имеет уравнение Клеро? Чем оно отличается от уравнения Лагранжа?
12. Как интегрируется уравнение общего вида, разрешенное относительно искомой функции или независимой переменой?
^ 3. Линейные дифференциальные уравнения n-го порядка
1. В каком интервале существует решения линейного уравнения?
2. Почему линейное уравнение не имеет особых решений?
3. Может ли график ненулевого решения однородного линейного уравнения второго порядка касаться оси Ох? Может ли пересекать ось Ох?
4. Какие решения однородного линейного уравнения называются линейно-независимыми? Привести пример.
5. Какие решения однородного линейного уравнения называются линейно-зависимыми?
Привести пример.
6. Исследовать на линейно зависимость функции:
1) x+1 , x
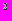 +1 , 2x
+1 , 2x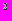 +x ; 2) 1+x , 2-x
+x ; 2) 1+x , 2-x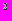 , x
, x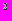 +2x ;
+2x ;7. Что такое фундаментальная система решений? Может ли нулевое решение входить в состав фундаментальной системы решений?
8. Как построить общее решение однородного линейного уравнения, если известно фундаментальная система решений? В какой области определено общее решение?
9. Как решить задачу Коши при помощи формулы общего решение?
10. Как построить Л.О.У, используя данную по ФСР?
11. Как найти общее решение неоднородного линейного уравнения, если известно одно частное решение его и общее решение соответствующего однородного уравнения ?
12. В чем состоит метод Эйлера интегрирования однородных линейных уравнений с постоянными коэффициентами? Как зависит структура фундаментальной системы решений от вида корней характеристического уравнения? В какой области определено общее решение?
13. В каких случаях и в каком виде может быть найдено частное решение неоднородного линейного уравнения методом неопределенных коэффициентов?
14. В чем состоит метод Лагранжа нахождения частного решения неоднородного линейного уравнения?
15. Какие уравнения называются уравнениями гармонического колебания (частота, амплитуда, период).
^
Линейная система дифференциальных уравнений
1. Какой общий вид имеет линейная система? Когда она называется однородной? Неоднородной?
2. В чем состоит задача Коши для линейной системы?
3. При каком условии задачи Коши для линейной системы имеет единственное решение?
4. Почему линейная система не имеет особых решений?
5. Как найти общее решение неоднородной линейной системы, если известно одно частное решение ее и общее решение соответствующей однородной системы ?
6. В чем состоит метод Лагранжа нахождения общего решения неоднородной линейной системы?
7. В чем состоит метод Эйлера интегрирования однородных линейных систем с постоянными коэффициентами ? Как зависит структура фундаментальной системы решений от вида характеристического уравнения?
8. Как судить об устойчивости ( неустойчивости ) нулевого решения однородной линейной системы с постоянными коэффициентами по характеристическим числам этой системы?
9. Как проводится исследование на устойчивость по первому приближению?
10. Исследовать на устойчивость нулевое решение систем уравнений :
1)
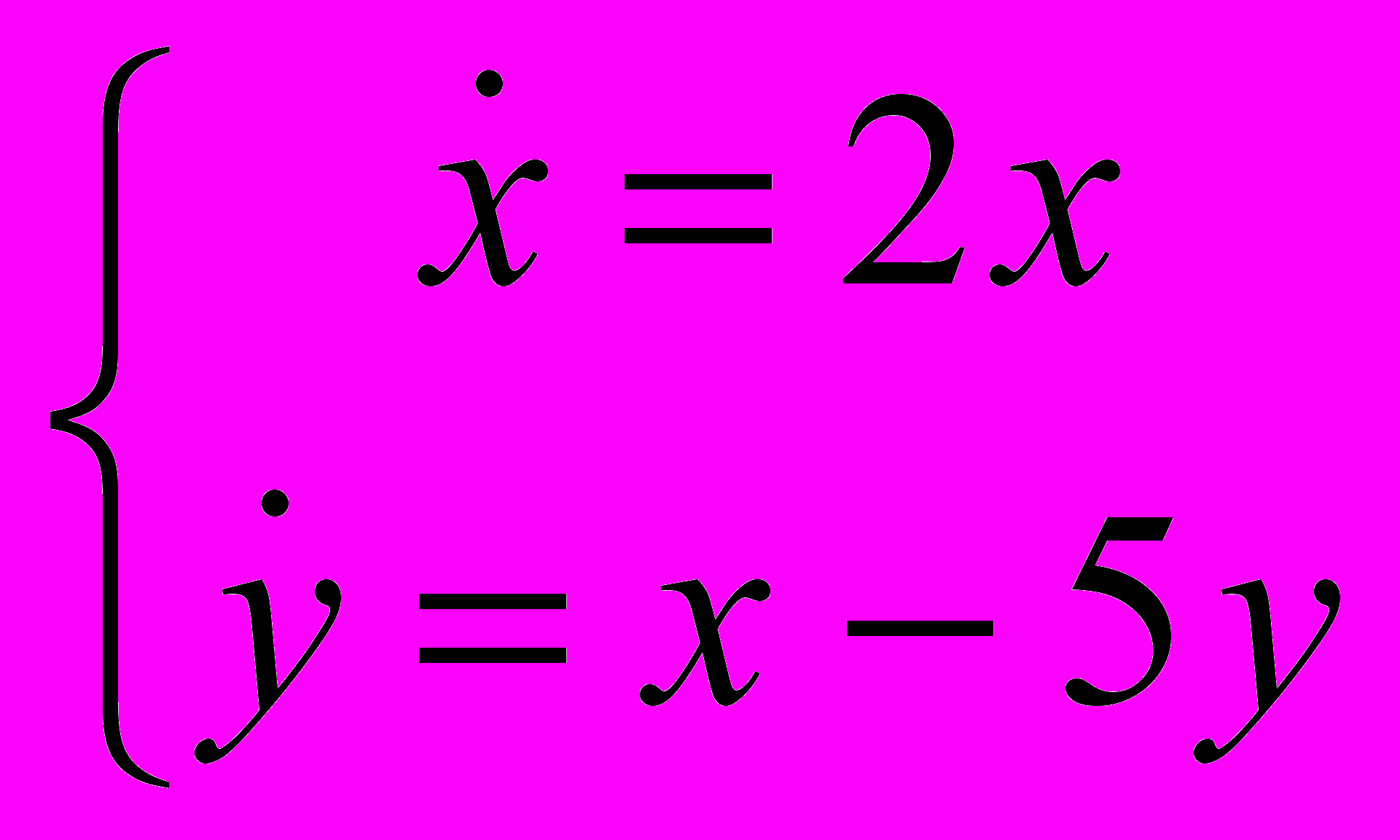 ; 2)
; 2) 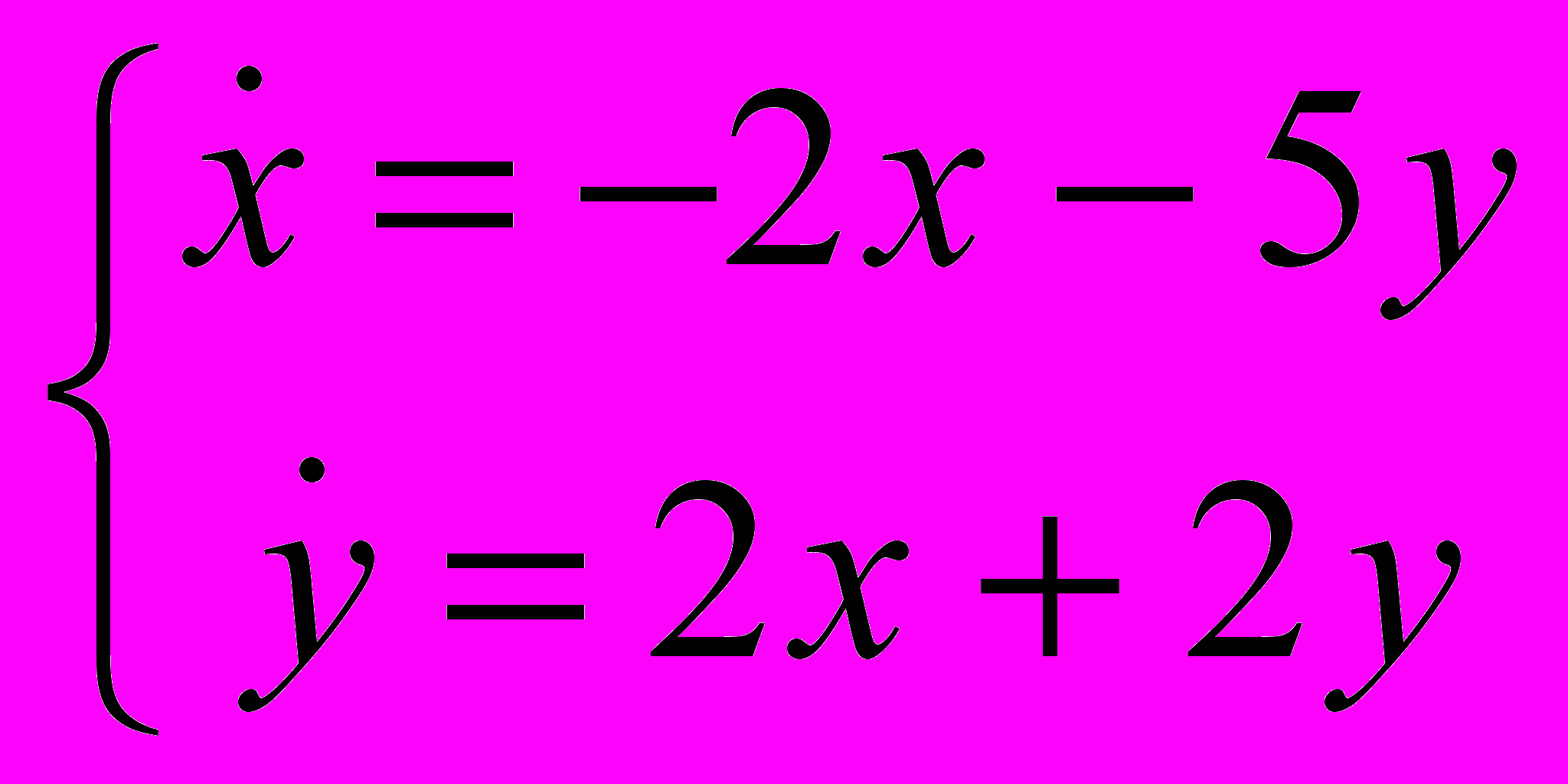 ; 3)
; 3)  ;
;11. Исследовать поведение фазовых кривых систем уравнений :
1)
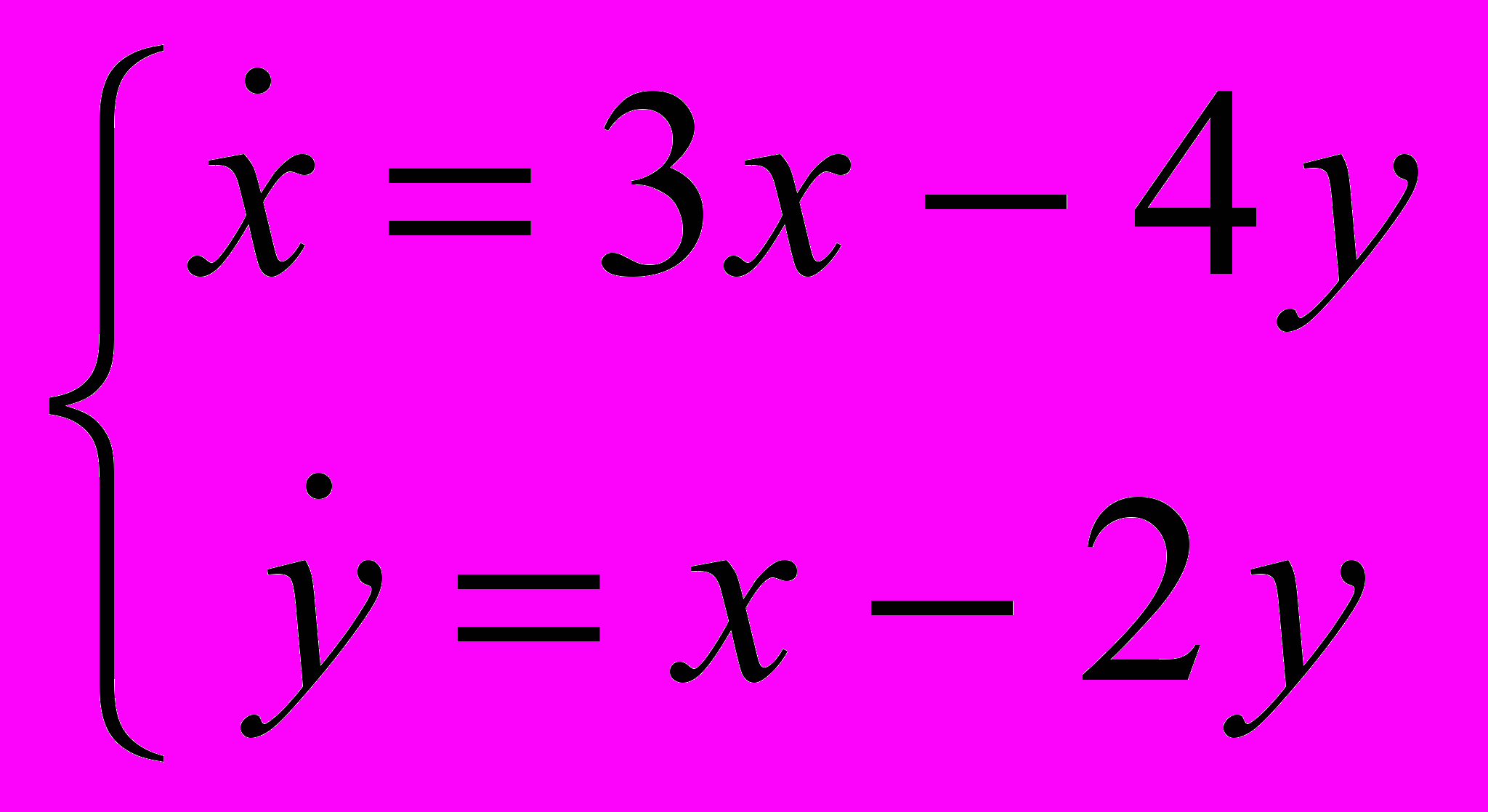 2)
2)  3)
3) 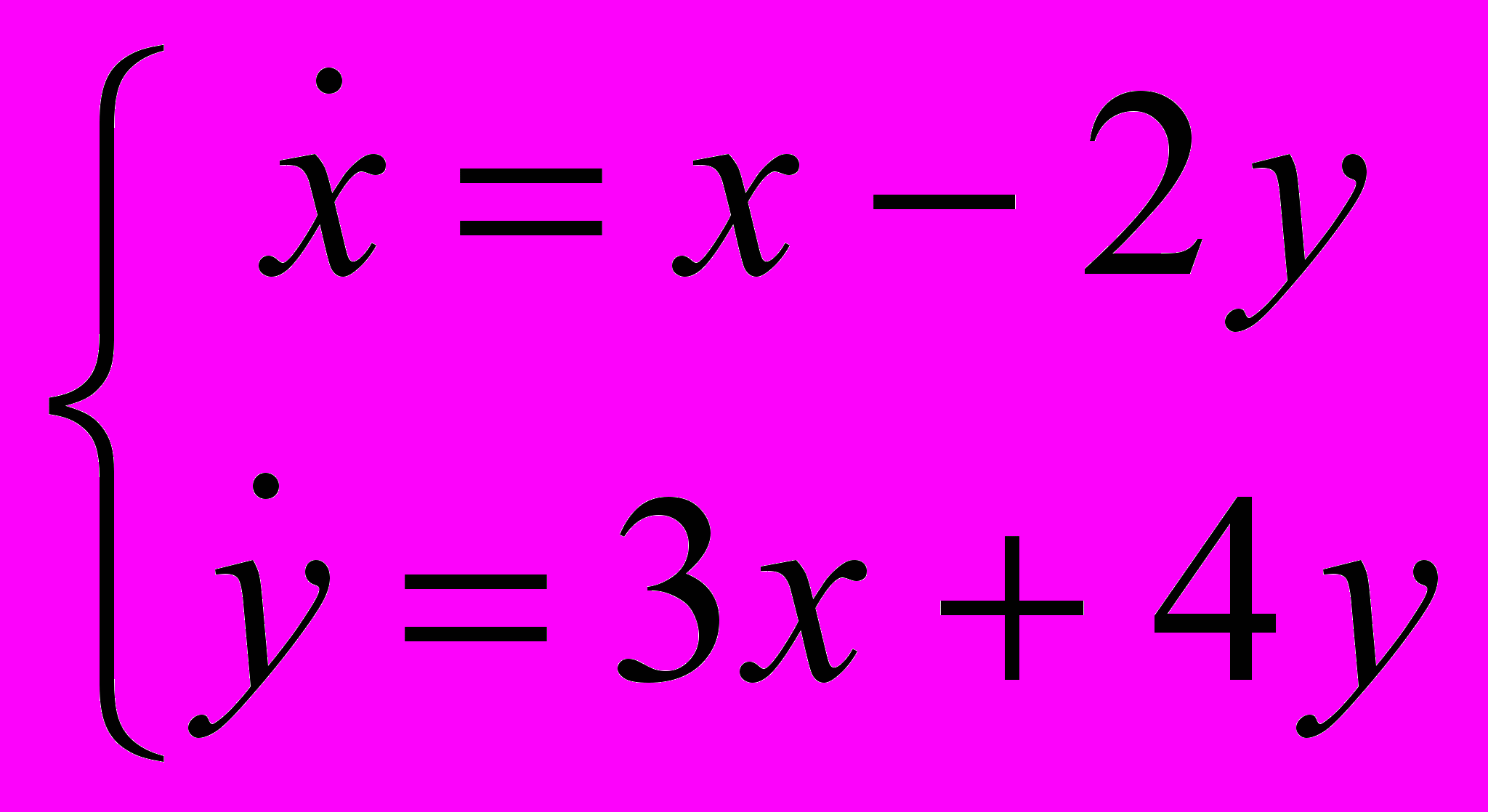
Решить систему уравнений
12.
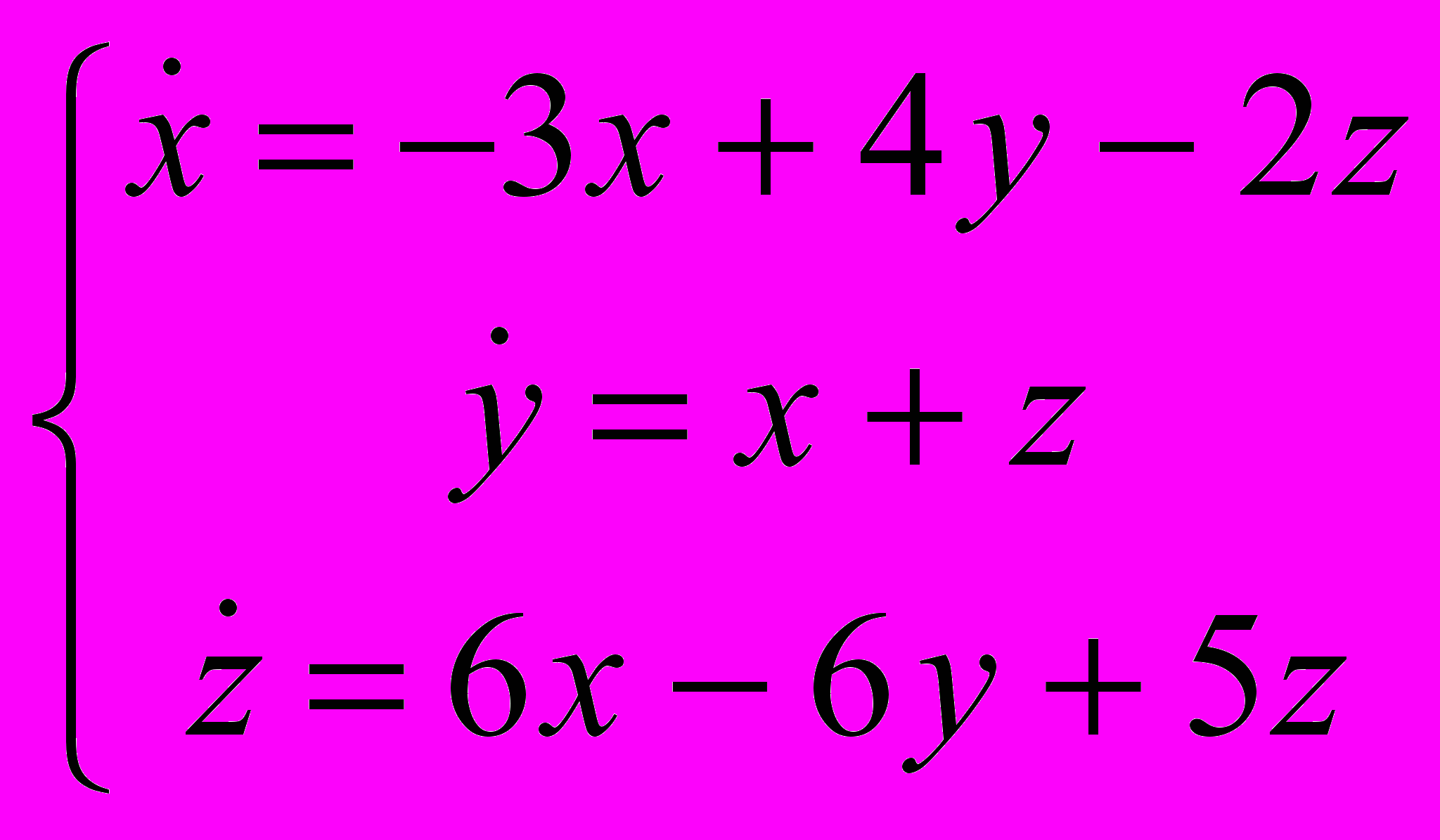 19.
19. 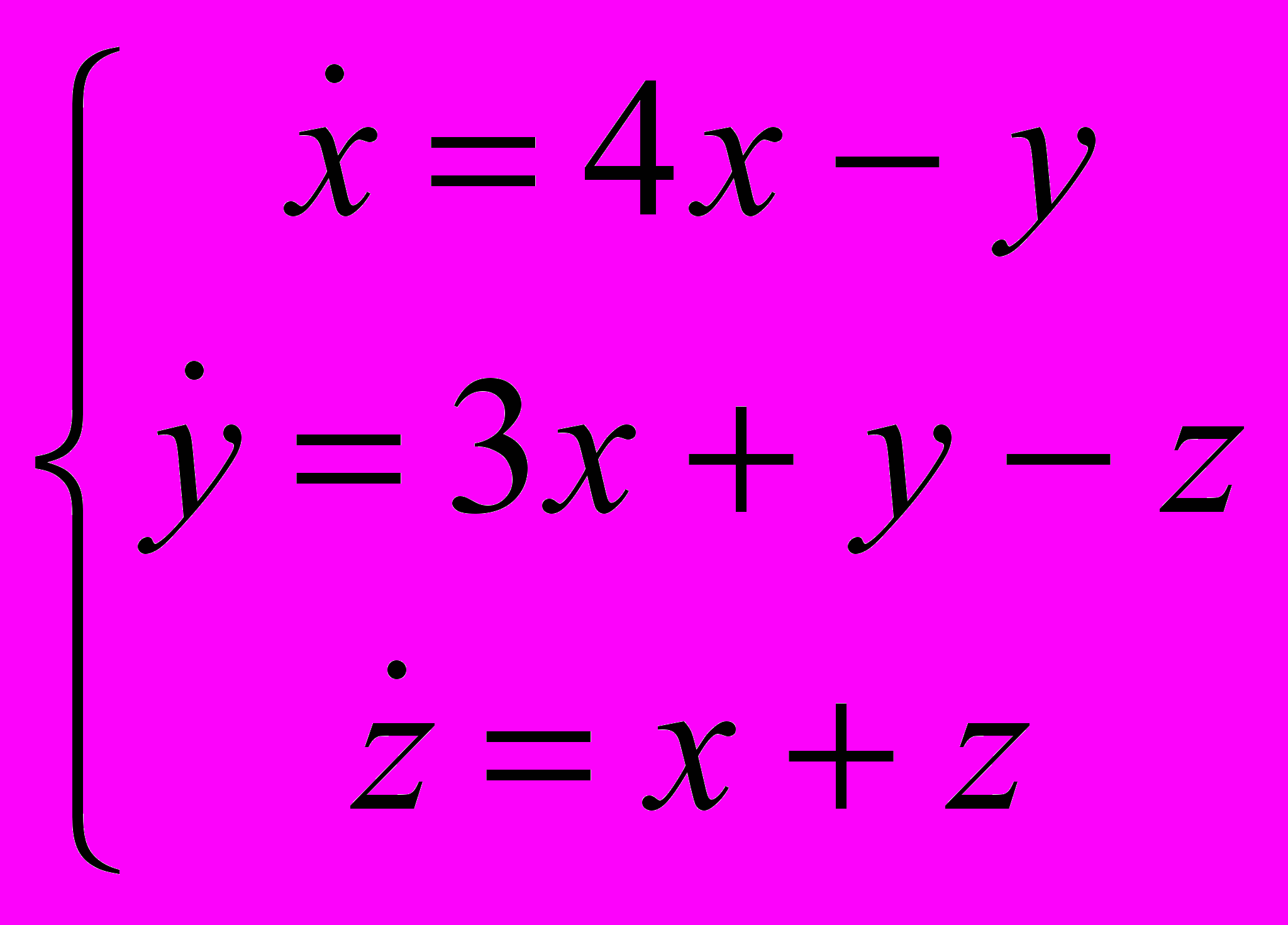
13.
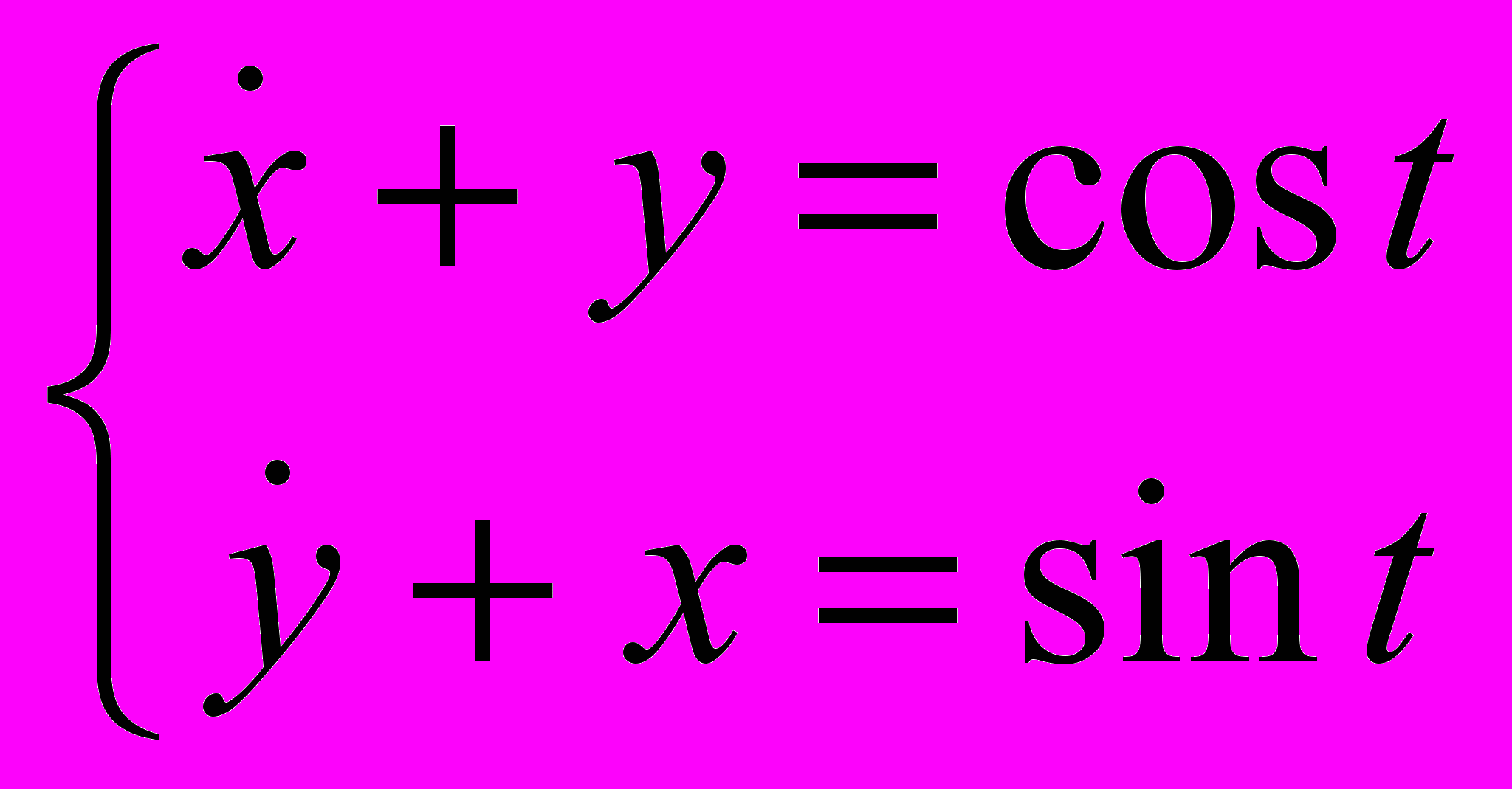 21.
21. 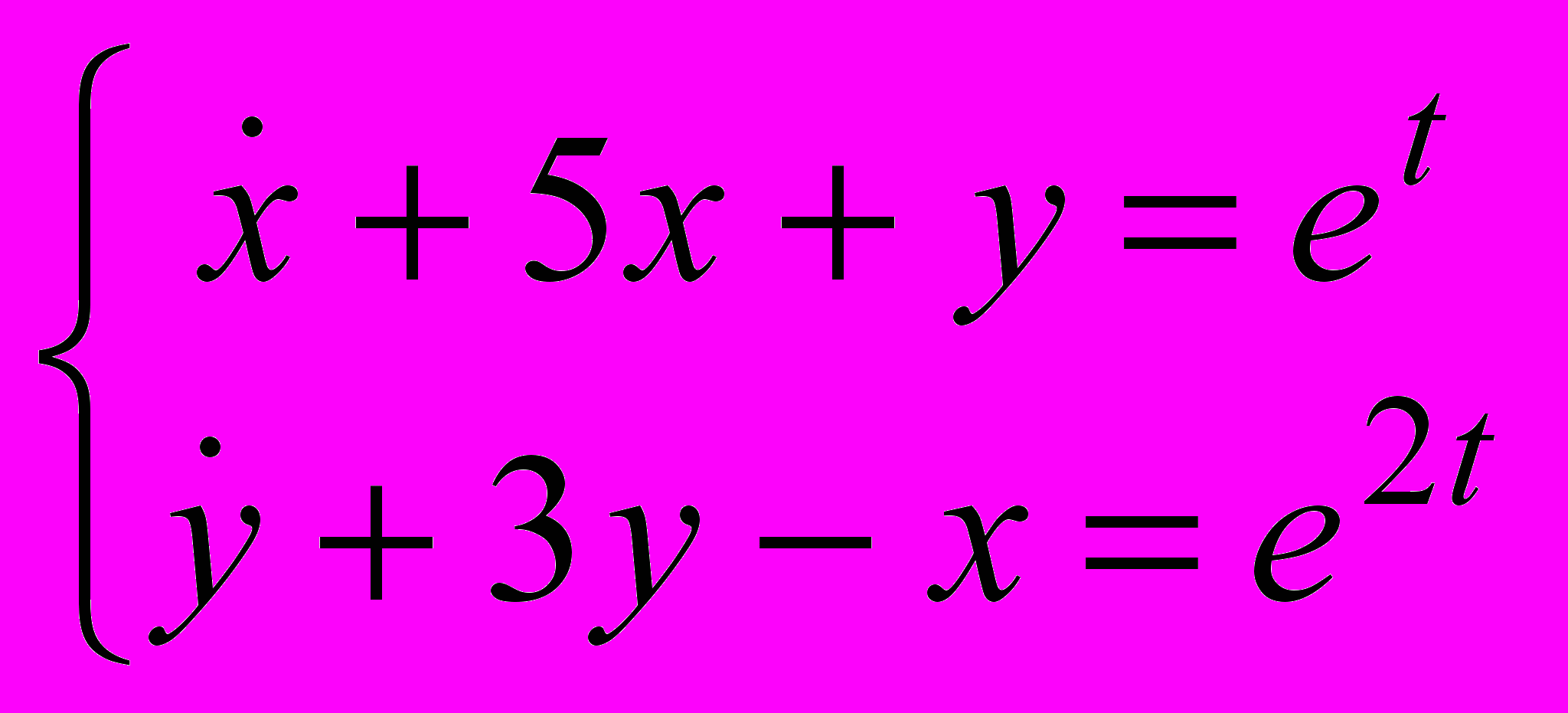
14. Записать в векторной форме систему уравнений

15. Записать систему уравнений по координатно
 , где A=
, где A=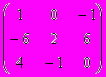
Литература
Основная:
1. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. –
М. : Наука, Физматлит, 1998.
- Матвеев Н.М. Обыкновенные дифференциальные уравнения. «Специальная литература». Санкт-Петербург, 1996
- Есипов А.А., Л.И.Сазонов, В.И.Юдович. Дифференциальные уравнения. Москва, «Вузовская книга». 2001.
- Матвеев Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям. Санкт-Петербург, 2002.
Дополнительная:
- Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. - Минск: ВШ, 1974.
- Еругин Н.П. Книга для чтения по общему курсу дифференциальных уравнений. - Минск: Наука и техника, 1972.
- Бибиков Ю.Н. Общий курс обыкновенных дифференциальных уравнений. - М.: Наука, 1986.
- Богданов Ю.С. Дифференциальные уравнения. - Минск: ВШ., 1983.
- Арнольд В.И. Обыкновенные дифференциальные уравнения. - Наука, 1984.
- Замков О.О. и др. Математические методы в экономике. 1998.
- Кремер Н.Ш. Высшая математика для экономистов. 1998.
- Степанов В.В. Курс дифференциальных уравнений. - М.: Физматгиз, 1959.
- Понтрягин Л.С. Обыкновенные дифференциальные уравнения - М. : Наука, 1982.
- Петровский И.Г. Лекции по теории дифференциальных уравнений. - М. : Изд-во МГУ, 1984.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям. - М.: Наука, 1976.
Пособия:
- Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения. Примеры и задачи. - М. : ВШ, 1989.
- Есипов А.А., Сазонов Л.И., Юдович В.И. Руководство к решению задач по обыкновенным дифференциальным уравнениям. - Ростов-на-Дону: Изд-во Ростов. ун-та, 1989.
- Матвеев Н.М. Дифференциальные уравнения. - Минск: ВШ., 1976.
- Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. - Мир, 1986.
- Григорьев М.П., Софронов Е.Т. Сборник заданий по обыкновенным дифференциальным уравнениям n-го порядка. - Якутск: Изд-во ЯГУ, 1989.
- Григорьев М.П., Софронов Е.Т. Сборник заданий по курсу обыкновенных дифференциальных уравнений. (Линейные уравнения, особые точки). - Якутск, 1991.
- Григорьев М.П., Софронов Е.Т. Дифференциальные уравнения. - Якутск: Изд-во ЯГУ,1988.
- Григорьев М.П., Софронов Е.Т. Линейные дифференциальные уравнения высших порядков в примерах и задачах. - Якутск: Изд-во ЯГУ, 1991.
- Григорьев М.П., Софронов Е.Т. Задания по курсу «Обыкновенные дифференциальные уравнения». - Якутск: Изд-во ЯГУ, 1985.
- Григорьев М.П., Софронов Е.Т. Специализированные задачи по обыкновенным дифференциальным уравнениям.- Якутск: Изд-во ЯГУ,1988.
