Geum.ru

Модуль по выбору для специализации 1

Вид материалаДокументы

Содержание


Модуль по выбору для специализации 1
Модуль по выбору для специализации 2
Казахский язык
Модуль по выбору для специализации 4
Модуль по выбору для специализации 5
Модуль по выбору для специализации 6
Модуль по выбору для специализации 7
Модуль по выбору для специализации 8
Подобный материал:
  1   2   3   4

ЕНУ им. Л.Н. Гумилева

Каталог элективных модулей

по специальности 6М060100 – Математика

Факультет Механико – математический

прием 2011 года


Наименование специальности/ специализации
Цикл дисциплины
Дисциплина
Семестр
Кафедра разработчик
Описание дисциплины

(1.Краткое содержание

2. Компетенции

3. Постреквизиты)
Пререквизиты дисциплины
ФИО, ученая степень, звание преподавателя
кол-во кредитов
кол-во кредитов ECTS

код

название

^ Модуль по выбору для специализации 1

6М060100 – Математика /для всех специализаций
БД
IYaPTs 5205
Иностранный язык для профессиональных целей
2
Кафедра иностран-ных языков
1. Говорение: владение устной профессиональной речью – диалогической и монологической в варьирующихся ситуациях, связанных с профессиональной деятельностью, ситуациях повседневного общения и общественно-политического характера. Письмо: развитие навыков реферирования, аннотирования, навыков написания тезисов, докладов, резюме на иностранном языке Углубление и развитие приобретенных в бакалавриате умений и навыков для практического владения разговорно-бытовой речью и языком специальности для активного применения иностранного языка как в повседневном так и в профессиональном общении. Лексика: овладение лексикой повседневного, общенаучного и профессионального характера – не менее 5000 единиц (включая 500 терминов профилирующей специальности). содержания. Перевод: умение работать с со словарями, а также справочной литературой по специальности.

IYa 5202 Иностранный язык



2
6

^ Модуль по выбору для специализации 2

6М060100 – Математика /для всех специализаций
БД
DKYa 5206
Деловой казахский язык
2
Кафедра практического казахского языка
1. Расширение лексического минимума общеупотребительных слов и словосочетаний, овладения грамматическими формами и конструкциями на уровне их употребления в речи. Овладение лексическим и терминологическим минимумом по специальности. Построение различных типов речевой деятельности: беседа, опис ание, информирование. Грамматические формы и конструкции в коммуникативном, функциональном аспектах.

Репродуцирование адаптированных и продуцирование несложных прагматических текстов, диалогических и монологических, в устной и письменной форме, на темы, актуальные для социально-бытовой.

^ Казахский язык:

- уровень (элементарный): Республика Казахстан. Природа моего края. Экология. Охрана природы. Праздники, традиции, обычаи и обряды народов Республики Казахстан.

- уровень: В мире искусства. Молодежь -будущее страны. Человек в современном мире.

- уровень. Функционирование казахского языка в Казахстане. Образование - условие прогресса. Моя специальность. Наука и современные технологии.

- уровень. Стили речи: понятие, функции, сфера употребления. Научный стиль речи, его особенности. Лексика научного стиля речи.

Терминологическая лексика казахского языка. Морфология научного стиля. Синтаксис научного стиля речи.

- уровень: текст как единица обучения связной речи. Типы монологической речи. Понятие о монологической речи. Развитие навыков монологической речи на материале текстов по специальности.
KYa 1102 Каз.яз.



2
6

Модуль по выбору для специализации 3

6М060100 – Математика / 1. Теория операторов,

2. Спектральная теория операторов,

3.Мультипликаторы в весовых пространствах гладких функций и их приложения
БД
TMP 5207
Теория метрических пространств
1
ФиПМ

Оспанов К.Н.
1. Метрические и топологические пространства. Линейные нормированные пространства. Гильбертово пространство Представление гильбертовых пространств в виде ортогональной суммы подпространств. Основные теоремы в полных метрических пространствах. Линейные функционалы и операторы. Банахово пространство линейных операторов. Сопряженный оператор. Сопряжен-ный оператор в гильбертовом пространстве. Теорема Банаха-Штейнхауса. Спектр оператора. Резольвента. Пространства основных и обобщенных функций. Восстановление функции по производной. Теорема Гильберта-Шмидта.

2. Знать свойства метрических пространств и с помощью метрики исследовать различные операторы в бесконечномерном пространстве.

3. Теория линейных операторов. Условия ограниченности интегральных и матричных операторов.
MA 1(2)201 Мат.анализ I-IV

FA 3301 Функц. анализ.
Ойнаров Р.О., д.ф.-м.н., проф.; Кусаинова Л.К., д.ф.-м.н., проф.; Тлеуханова Н.Т., д.ф.-м.н., проф.; Ибатов А.И., к.ф.-м.н., доцент
4
12

6М060100 – Математика / Качественные свойства решений квазилинейных дифференциальных уравнений
БД
TKO 5208
Теория конечномерных операторов
1
ФиПМ

Оспанов К.Н.
1. Линейные функционалы и операторы. Операторы в конечномерных пространствах и их свойства. Непрерывность линейных операторов. Пространства линейных ограниченных операторов.

2. Развить навыки исследования операторов в конечномерном пространстве, изучить общие методы теории конечномерных операторов.

3. Элементы качественного анализа полулинейного дифференциального уравнения второго порядка
MA 1(2)201 Мат.анализ I-IV

FA 3301 Функц. анализ.
Ойнаров Р.О., д.ф.-м.н., проф.
4
12

6М060100 – Математика / Дифференциальные уравнения
БД
KZDU 5209
Краевые задачи для дифференциальных уравнений.
1
ФиПМ

Оспанов К.Н.
1. Дифференциальные уравнения с переменными коэффициентами. Постановка краевых задач. Собственные значения и собственные функции одномерной задачи Штурма-Лиувилля, их свойства. Интегральные уравнения в пространствах суммируемых функций. Приведение краевых задач к изучению интегральных уравнений. Альтернативы Фредгольма. Случаи разделенных и общих ядер.

2. Магистрант должен уметь свести краевые задачи для дифференциальных уравнений к эквивалентному интегральному уравнению в классах разрывных функций и применить теорию Фредгольма.

3. Сингулярные диф. уравнения.
DU 2205 Диф. ур-я
Оспанов К.Н., д.ф.-м.н., проф.; Байбурин М.М., к.ф.-м.н., доцент; Бияров Б.Н., к.ф.-м.н.
4
12

6М060100 – Математика / Мультипликативные преобразования рядов Фурье и преобразований Фурье, их приложения
БД
TRFPF 5210
Тригонометрические ряды Фурье и преобразования Фурье
1
ФиПМ

Оспанов К.Н.
1. Коэффициенты Фурье, ряды Фурье. Тригонометрические ряды Фурье. Свойства. Достаточные признаки сходимости. Преобразования Фурье. Свойства. Теорема Котельникова.

2. Выпускник должен владеть современными методами функциональных пространств, приложением в теории ортогональных рядов, аппаратом теории интерполяции, уметь применять полученные знания в научно-исследовательской работе.

3. Гармонический анализ, теория ортогональных рядов.
MA 1(2)201 Мат.анализ I-IV

DA 2307 Действ.анализ

FA 3301 Функц. анализ.
Нурсултанов Е.Д., д.ф.-м.н., проф.; Тлеуханова Н.Т., д.ф.-м.н., проф.;

Сарыбекова Л.О., PhD-доктор
4
12

6М060100 – Математика / Функциональные пространства, интерполяционные методы и их приложения
БД
DPON 5211
Дискретные пространства и основные неравенства в них
1
ФиПМ

Оспанов К.Н.
1. Дискретные пространства Лебега, Лоренца. Свойства. Неравенства Гельдера (обобщения), Минковского (обобщения), Юнга, Юнга-О’Нейла, Харди-Литллвуда-Пэли. Различные обобщения, уточнения.

2. Выпускник должен владеть современными методами функциональных пространств, различных неравенств в них, аппаратом теории интерполяции, уметь применять полученные знания в научно-исследовательской работе.

3. Гармонический анализ, теория ортогональных рядов
MA 1(2)201 Мат.анализ I-IV

DA 2307 Действ.анализ

FA 3301 Функц. анализ.
Тлеуханова Н.Т., д.ф.-м.н., проф.;

Сарыбекова Л.О., PhD-доктор
4
12

6М060100 – Математика / Функциональные пространства с различными ортогональными базисами и их приложения
БД
RUH 5212
Ряды Уолша и Хаара
1
ВМиММ, Бокаев Н.А.
1. Определения и свойства систем Уолша и Хаара. Коэффициенты Фурье. Сходимость рядов Фурье-Уолша и Фурье-Хаара в различных пространствах. Прямые и обратные теоремы для наилучших приближений. Ряды Фурье-Уолша от непрерывных функций. Сходимость и расходимость ряда Фурье-Уолша на множестве. Абсолютная сходимость рядов Фурье- Уолша. Аналоги теорем Бернштейна, Саса, Харди-Литлвуда. Ряды Уолша и Хаара с монотонными коэффициентами. Суммирование рядов Фурье- Уолша.

2. Магистрант должен владеть современными методами теории ортогональных рядов, аппаратом рядов Уолша и Хаара, уметь применять полученные знания в научно-исследовательской работе.

3. Теория ортогональных рядов, теория рядов и интегралов Фурье, обработка сигналов.
MA 1(2)201 Мат.анализ I-IV

FA 3301 Функц. анализ.
Каримов С.К., к.ф.-м.н., доц.;

Сулейменова З.Р., к.ф.-м.н., доцент
4
12

6М060100 – Математика / Алгебра и теория чисел
БД
AL 5213
Алгебры Ли
1
АиГ

Козыбаев Д.Х.
1. Аксиоматика и примеры алгебр Ли. Алгебры дифференцирований. Универсальные обертывающие алгебры. Свободные алгебры Ли. Разрешимые и нильпотентные алгебры Ли. Полупростые алгебры Ли. Полная приводимость.

2. Магистрант должен владеть современными методами построения базисов свободных алгебр Ли, уметь применять полученные знания в научно-исследовательской работе.

3. Полупростые алгебры Ли, теория неасоциативных алгебр.
Alg1(2) 1202 Алгебра I, II,

Умирбаев У.У., д. ф.-м.н., профессор, Абуталипова Ш.У., к.ф.-м.н.
4
12

6М060100 – Математика / математическая логика
БД
UA 5214
Универсальная алгебра
1
АиГ

Козыбаев Д.Х.
1. Основы теории множеств. Алгебры. Классические алгебры: группы, кольца, поля, модули, решетки, булевы алгебры. Изоморфизмы, гомоморфизмы и конгруэнции. Подалгебры, фактор-алгебры, прямые и фильтрованные произведения. Свободные алгебры. Многообразия и квазимногообразия алгебр. Дистрибутивные, модулярные и полудистрибутивные (квази) многообразия

2. Магистрант должен владеть основными свойствами свободных алгебр, Уметь применять теоремы Биркгоффа, Мальцева в научно-исследовательской работе

3. Теория решеток, теория универсов
Alg1(2) 1202 Алгебра I, II, DMML 2204 Дискретная математика и математическая логика

Нуракунов А.М., к. ф.-м.н., профессор, Байсалов Е.Р., к.ф.-м.н., доцент
4
12

6М060100 – Математика

БД
OTI 5215
Общая теория интегрирования


1
ФиПМ

Оспанов К.Н.
1. Численное интегрирование функции одной переменной: метод прямоугольников, метод трапеций, метод Симпсона. Мера и интеграл Лебега. Теория рядов Фурье. Теория сравнений. Теория алгебраической теории чисел. Класс Коробова как модельный случай. Оценка снизу Шарыгина. Подход школы Коробова. Теорема Темиргалиева: случай 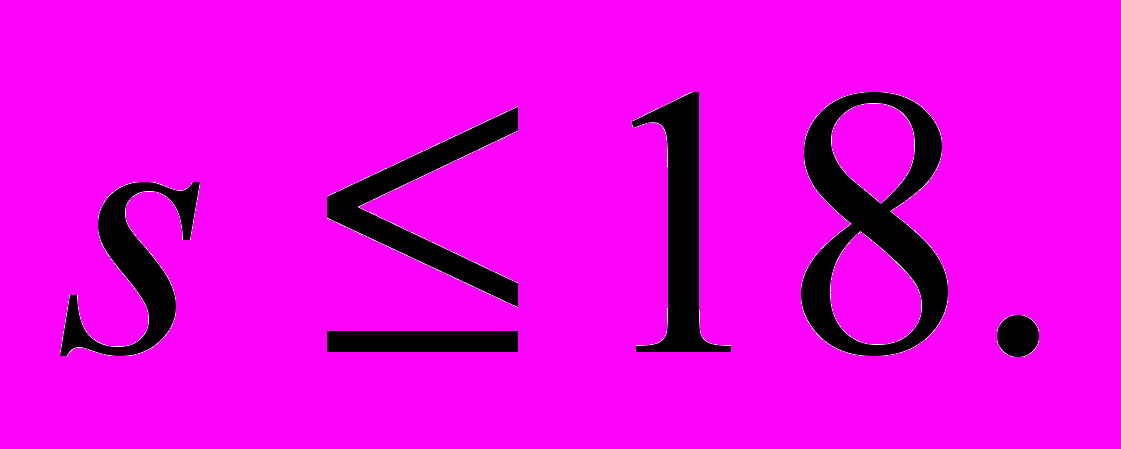Подход Воронина: случай произвльной размерности. Подход Баилова-Темиргалиева: случай произвольной размерности.

2. Магистрант должен знать теория алгебраических чисел, разные подходы к разным случаям, должен владеть общей теорией численного интегрирования.

3. Основные вычислительные агрегаты численного анализа, компьютерный (вычислительный) поперечник, предельная погрешность неточной информации, задачи восстановления в классах бесконечно гладких функции, равномерно распределенные сетки.
MA 1(2)201 Мат.анализ I-IV
TFDP 3301 Теор. функц. дейст. пер.
Темиргалиев Н.Т., д.ф.-м.н., проф.;
4
12

^ Модуль по выбору для специализации 4

6М060100 – Математика / Теория операторов
ПД
LNАKP 5303
Линейный и нелинейный анализ в конечномерном пространстве
2
ФиПМ

Оспанов К.Н.
1. Линейные пространства. Линейные отображения линейных пространств. Общая теория. Евклидовы пространства. Линейные операторы в евклидовом пространстве. Билинейные и эрмитово билинейные функционалы. n - мерное пространство. Дифференциальное исчисление функции многих переменных. Интегральное исчисление функции многих переменных. Криволинейные и поверхностные интегралы. Основные интегральные формулы анализа. Теория поля. Интегралы, зависящие от параметра. Линейные нормированные пространства. Ортогональные системы. Ряды Фурье. Приближение функций полиномами. Интеграл Фурье. Обобщенные функции. Дифференцируемые многообразия и дифференциальные формы. Интеграл Лебега.

2. Умение исследовать операторы в конечномерном пространстве по средствам алгебры и математического анализа.

3. Теория метрических пространств. Теория линейных операторов.

MA 1(2)201 Мат.анализ I-IV

Alg 1202 Алгебра I-II

TMP 5207 Теория метрических пространств
Ойнаров Р.О., д.ф.-м.н., проф.
4
12

6М060100 – Математика / Качественные свойства решений квазилинейных дифференциальных уравнений
ПД
MFA 5304
Методы функционального анализа
2
ФиПМ

Оспанов К.Н
1. Понятие метрического пространства. Метрика. Примеры метрических пространств. Понятия компактности, плотности множеств, сходимости. Полные метрические пространства. Пространства . Общие теоремы о непрерывности интегральных операторов. Операторы типа потенциала. Нелинейные интегральные операторы. Условия непрерывности интегральных операторов. Дифференцирование нелинейных операторов.

2. Умение применять методы функционального анализа в исследовании качественных свойств дифференциальных уравнений.

3. Вариационный метод исследования оссциляторных свойств полулинейных дифференциальных уравнений второго порядка.
MA 1(2)201 Мат.анализ I-IV

FA 3301 Функц. анализ
Ойнаров Р.О., д.ф.-м.н., проф.
4
12

6М060100 – Математика / Дифференциальные уравнения
ПД
LUBP 5305
Линейные уравнения в банаховом пространстве
2
ФиПМ

Оспанов К.Н.
1. Уравнение с замкнутым оператором и с плотной областью определения в банаховом пространстве. Сопряженное уравнение в банаховом пространстве. Априорные оценки. Уравнения с конечным дефектом. Нетеровы уравнения, индекс. Фредгольмовы уравнения. Переопределенные уравнения. Неопределенные уравнения. Интегральные уравнения. Дифференциальные уравнения.

2. Магистрант должен владеть современными методами теории уравнений в линейном нормированном пространстве, уметь доказать разрешимость уравнений с оператором с замкнутой областью значений.

3. Спектральная теория линейных операторов.
MA 1(2)201 Мат.анализ I-IV

FA 3301 Функц. анализ
Оспанов К.Н., д.ф.-м.н., проф.
4
12

6М060100 – Математика /

Спектральная теория операторов


ПД
TFP 5306
Теория функциональных пространств
2
ФиПМ

Оспанов К.Н
1.В курсе изучаются общие методы построения пространств гладких функций и вопросы соотношений между ними. Приводятся теоремы вложения и компактности пространств гладких функций.

2. Умение применять методы функционального пространств в решении краевых задач для дифференциальных уравнений.

3. Теория разделимости операторов..
FA 3301 Функц. анализ
Оспанов К.Н., д.ф.-м.н., проф.; Кусаинова Л.К., д.ф.-м.н., проф.
4
12

6М060100 – Математика / Мультипликативные преобразования рядов Фурье и преобразований Фурье, их приложения
ПД
TM 5307
Теория мультипликаторов
2
ФиПМ

Оспанов К.Н.
1. Мультипликаторы рядов Фурье. Теоремы Марцинкевича, Хермандера. Мультипликаторы преобразования Фурье. Теоремы Михлина, Лизоркина. Функциональные пространства. Мультипликаторы в конкретных пространствах.

2. Выпускник должен владеть современными методами теории ортогональных рядов, аппаратом теории интерполяции, мультипликаторов рядов Фурье и преобразований Фурье, уметь применять полученные знания в научно-исследовательской работе.

3. Теория ортогональных рядов, спектральная теория операторов.
MA 1(2)201 Мат.анализ I-IV

DA 2307 Действ. анализ FA 3301 Функц. анализ

Тлеуханова Н.Т., д.ф.-м.н., проф.;

Сарыбекова Л.О., PhD-доктор
4
12