Geum.ru

Вопросы по курсу «Дифференциальные уравнения»

Вид материалаДокументы
Подобный материал:
Вопросы по курсу «Дифференциальные уравнения»,

2-ой семестр 2010-2011 уч. года.

  1. Зависимые и независимые интегралы системы дифференциальных уравнений (СДУ).
  2. Сведение СДУ к равносильному уравнению и обратная задача.
  3. Теорема Пикара для СДУ.
  4. Следствия из теоремы Пикара.
  5. Теорема о непрерывной зависимости решения СДУ от параметров.
  6. Теорема о непрерывной зависимости решения СДУ от начальных условий.
  7. Теорема о существовании общего решения СДУ.
  8. Теорема о степени гладкости решения СДУ.
  9. Теорема об интегральной непрерывности решения СДУ.
  10. Лемма Адамара.
  11. Теорема о дифференцируемости решения СДУ по параметру.
  12. Дифференцируемость решения СДУ по начальным данным.
  13. Лемма об элементарной мажоранте.
  14. Теорема о существовании голоморфного решения СДУ.
  15. Системы уравнений в симметрической форме.
  16. Линейная СДУ и её свойства.
  17. Фундаментальная матрица линейной СДУ и ее свойства.
  18. Линейная неоднородная СДУ. Общее решение и решение в форме Коши.
  19. Теорема о существовании голоморфного решения линейной системы.
  20. Понятие о сопряжённой системе уравнений. Самосопряжённая система.
  21. Представление фундаментальной матрицы в случае, когда матрица системы перестановочна со своим интегралом (случай Лаппо-Данилевского).
  22. Интегрирование линейной стационарной системы с помощью матрицы .
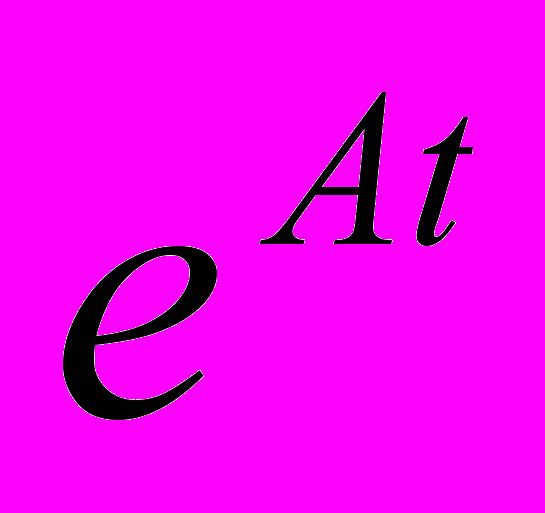  23. Особые точки. Узел и седло.
  24. Особые точки. Центр и фокус.
  25. Особые точки. Вырожденный и дикритический узел.
  26. Особые точки. Случай нулевых собственных чисел.
  27. Особые точки. Нелинейный случай.
  28. СДУ с периодическими коэффициентами. Теорема Ляпунова – Флоке.
  29. Периодические решения уравнения 2-го порядка. Случай единственного периодического решения.
  30. Периодические решения уравнения 2-го порядка. Семейства периодических решений.
  31. Случай отсутствия периодических решений у уравнения 2-го порядка.
  32. Метод малого параметра. Нерезонансный случай.
  33. Метод малого параметра. Резонансный случай. Резонанс n-го рода.
  34. Метод малого параметра. Автономный случай.
  35. Метод малого параметра. Построение решения задачи Коши.
  36. Понятие о предельном цикле.
  37. Линейные однородные уравнения в частных производных.
  38. Линейные неоднородные уравнения в частных производных.


Литература.

  1. Матвеев Н. М. Методы интегрирования обыкновенных дифференциальных уравнений.
  2. Еругин Н. П. Книга для чтения по общему курсу диф. уравнений.
  3. Петровский И. Г. Лекции по теории обыкновенных диф. уравнений.
  4. Понтрягин Л.С. Обыкновенные диф. уравнения.
  5. Степанов В.В. Курс диф. уравнений.
  6. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление.



Лектор О. Н. Чижова