2. Построение математических моделей по экспериментальным данным

Вид материала

Задача

Содержание 2.2. Идентификация моделей с помощью регрессионного метода Методы применяются для линейных по идентифицируемым параметрам моделям Минимизируемой функцией ошибки (разности между прогнозируемой моделью и данными эксперимента) при регрессионном анализе является 2.2.1. Идентификация статических линейных систем 2.2.2. Идентификация нелинейных систем 2.2.3. Достоверность (адекватность) регрессионной модели 2.3. Построение моделей идентификации поисковыми методами K – константа скорости. Решение этого уравнения при следующих начальных условиях: у=1

Подобный материал:

• План изучения дисциплины № п/п, 155.57kb.
• Лекция №8 Построение математических моделей технологических объектов и систем аналитическим, 98.99kb.
• Изучение математических функций с использованием км-школы в VII-VIII классах, 166.32kb.
• Шейчекова Марина Евгеньевна, 10А класс Научный Кулигина Анна Леонидовна, учитель информатики, 18.75kb.
• Тема: Построение математических моделей как предварительный этап алгоритмизации. Цель, 110.57kb.
• Рецензи я, 16.05kb.
• Название Лекция-семинар: Построение математических моделей целочисленного линейного, 64.42kb.
• Исследование математических моделей, 9.9kb.
• 1. Введение Основы анализа данных. Методология построения моделей сложных систем. Модель, 399.94kb.
• Утверждаю, 89.56kb.

2. Построение математических моделей по экспериментальным данным


2.1. Постановка задачи идентификации


Задача идентификации формулируется следующим образом. Пусть в результате каких либо экспериментов над объектом замерены его входные X=(х₁, х ₂,…х_n) и выходные переменные Y=(y₁, y₂,…y_m) как функции времени. Требуется определить вид (структуру) и параметры некоторого оператора Â, ставящего в соответствие переменные X и Y.








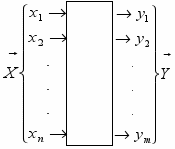
В реальных условиях переменные и замеряются с погрешностьюи.Чаще всего эти погрешности считаются некоррелированными и аддитивными с полезной информацией, т.е. имеют вид


x_i=x_i^ист± (i=1,2…n)

y_j=y_j^ист± (j=1,2…m)


Различают задачи идентификации в широком (структурная идентификация) и узком смысле (параметрическая идентификация) соответственно. В первом случае неизвестна структура и параметры оператораÂ, во втором – лишь параметры этого оператора.

Таким образом, задача идентификации модели тесно связана с проведением эксперимента и обработкой экспериментальных зависимостей.

Задача параметрической идентификации сводится к отысканию таких оценок параметров математической модели Â, которые обеспечивают в каком либо смысле близость расчетных и экспериментальных значений выходных переменных при одинаковых входных . Отметим, что в общем случае необходимы измерения «m» компонент вектора , которые могут производиться при «к» повторениях эксперимента при «l» дискретных отметках времени (если идентифицируемый объект функционирует во времени). В качестве критериев количественной меры близости модели и оригинала чаще всего используются максимальные δ_у, средние m_у и среднеквадратичные δ_у величины погрешностей рассогласования расчетных и экспериментальных значений у_рi и у_эi, соответственно, т.е

d _у = max | у_рi – у_эi|

m_у = 1/Nå ( у_рi – у_эi ), (2.1)

,

где: i = 1, 2…, N = m + l + k - номер опыта по измерению компоненты у_эi

Таким образом, задача параметрической идентификации сводится к минимизации одной из функций вида (2.1). Для минимизации могут быть использованы известные численные методы решения экстремальных задач.

Обилие существующих методов идентификации отражает разнообразие используемых математических моделей и методов их исследования. Очевидно, что идентифицировать модель детерминированного, линейного, стационарного процесса (модель считается стационарной, если её параметры либо постоянные, либо меняются медленно по сравнению со временем, необходимым для их идентификации) известной размерности, с одним входом – существенно проще, чем аналогичного стохастического процесса неизвестного порядка и степени стационарности.


^ 2.2. Идентификация моделей с помощью регрессионного метода


Регрессионный анализ представляет собой классический статистический метод. Благодаря своим широким возможностям регрессионные методы давно и успешно используются в инженерной практике. В последнее время в связи с развитием и внедрением быстродействующих ЭВМ они широко используются для идентификации моделей, в том числе для идентификации динамических, многомерных процессов, систем диагностики и управления в реальном масштабе времени. Регрессионный анализ основывается на двух главных принципах.

1. ^ Методы применяются для линейных по идентифицируемым параметрам моделям. Структура математической модели процесса представляется функцией вида:

, (2.2)


где а_i – i-тый оцениваемый параметр; f_i- i-тая известная функция, - вектор входных воздействий, y – выходная переменная.

Возможно представление идентифицируемой модели в следующей форме:

(2.3)


где а_i, b_j – оцениваемые параметры; f_iи - априори известные (заданные) функции. После несложных математических преобразований на основе этих функций можно формировать невязки, линейно зависящие от идентифицируемых параметров а_i, b_j.

На практике, чаще всего в качестве f_iи выбираются степенные функции, а соответственно выражения (2.2) и (2.3) являются полиномиальными, либо дробно-рациональными зависимостями. При этом точность описания достигается увеличением числа членов полинома, обеспечивающих их сходимость к реальному процессу. Заметим, что получающаяся модель практически никогда не соответствует физической сущности моделируемого реального процесса, его истинному виду, однако инженерная простота вычислений, удобство практического использования модели, возможность получения результата без «особых размышлений» служит основной причиной широкого распространения на практике регрессионных методов.

Естественно, и в этом случае с помощью удачно выбранного вида полинома можно существенно сократить размер модели, а значит и трудоемкость вычислительного процесса, как при идентификации, так и при использовании модели.

2. ^ Минимизируемой функцией ошибки (разности между прогнозируемой моделью и данными эксперимента) при регрессионном анализе является сумма квадратов ошибок. Благодаря этому удается применить метод наименьших квадратов, математический аппарат которого предельно прост, а вычислительные методы сводятся к методам линейной алгебры.

Регрессионные модели могут быть как линейными, так и нелинейными с любым числом входов и выходов.


^ 2.2.1. Идентификация статических линейных систем

с несколькими входами


Пусть необходимо идентифицировать систему с «n» входами x₁, x₂,…x_n и одним выходом y. Представим структуру модели в виде линейного алгебраического уравнения вида:

y=a₀ + a₁ x₁+ a₂ x₂+…+ a_nx_n , (2.4)

где a₀, a₁,..a_n - параметры модели, подлежащие идентификации. В результате идентификации мы должны получить вектор оценок истинного вектора . Этому вектору будет соответствовать оценка значения выходной величины .

Для определения значений произведем N последовательных измерений величины у, соответствующих в определенном смысле произвольным набором величин х_i (i=1,2,…n). В результате получим вектор . По N наборам входных величин х_i (i=1,2,…n) будет соответственно N оценок выходных величин




(2.5)



Разница характеризует погрешность каждой модели в каждом из N измерений. Суммарную погрешность будем характеризовать величиной:

(2.6)

Определение оценок производят из условия минимума величины суммарной погрешности J. Таким образом, основой идентификации регрессионными методами служит метод наименьших квадратов. Используя аппарат математического анализа, оценка вектора должна удовлетворять необходимому условию экстремума


(i=0,1,2,…n) (2.7)

Уравнения (2.7) позволяют построить вычислительный процесс идентификации вектора на основе N групп измерений y и . Для получения эффективных и несмещенных оценок * необходимо, чтобы N >> n. Если N= n+1, то в оценке шум измерений не будет сглажен, окажет негативное влияние и случайность наборов . Мерой ошибки регрессионной модели обычно служит величина среднеквадратичного отклонения . С увеличением N уменьшается флуктуация , ее величина и является определяющей для выбора N в рамках принятой структуры модели.

К обсуждаемому типу линейных моделей простым преобразованием сводятся применяемые на практике мультипликативные модели. Действительно, модель типа


(2.8)


с помощью логарифмирования и замены у=lnW, x_i=lnZ_i (i = 1, 2, …m) приводится к виду y=. Зависимости (2.8) широко используются при построении моделей по эмпирическим данным в гидравлике, термодинамике, обработке металлов давлением и т.д. Можно сказать, что и другие типы нелинейных регрессионных моделей, в конечном итоге, сводятся к зависимостям (2.4).


^ 2.2.2. Идентификация нелинейных систем


Если величина среднеквадратичного отклонения идентифицируемой системы слишком велика, значит, структура модели неудовлетворительна и необходимо учитывать нелинейные члены алгебраического полинома. Рассмотрим порядок идентификации параметров нелинейной системы второго порядка с одним выходом у и входами Z₁, Z₂,… Z_n.


(2.9)


Обозначим переменные Z_i и произведения Z_i Z_j переменных в выражении (2.9) через новые переменные х_i (i=1, 2,…m). С учетом этого, выражение (2.9) можно записать в виде:


, (2.10)

что совпадает с (2.4).

Для большинства систем 20% факторов определяют 80% свойств. Поэтому в процессе идентификации несущественные параметры, влияние которых на величину среднеквадратичного отклонения мало, отсеивают. Тем самым определение значений постоянных коэффициентов в (2.9) и в эквивалентном ему выражении (2.10) представляет собой процесс структурно-параметрической идентификации.


^ 2.2.3. Достоверность (адекватность) регрессионной модели

Обычно мерой ошибки регрессионной модели служит стандартное (среднеквадратичное) отклонение _. Для процессов, подчиняющихся закону нормального распределения, приблизительно 66% точек находится в пределах одного стандартного отклонения от модели и 95% точек в пределах двух стандартных отклонений.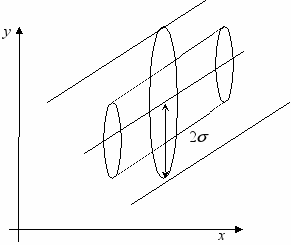


Стандартное отклонение – важный показатель для решения вопроса о достоверности модели. Большая ошибка может означать, что модель не соответствует процессу, который послужил источником экспериментальных данных. Однако большая ошибка модели может быть вызвана и другой причиной: большим разбросом данных измерений. В этом случае, возможно, потребуется взять большее количество выборок.

Для характеристики среднего разброса относительно линии регрессии применяют дисперсию адекватности:

; f – число степеней свободы.

Проверка значимости (качества предсказания) множественного уравнения регрессии можно осуществить на основе F-критерия Фишера. Вычисляют дисперсию среднего:

.


Вычисляют так называемую остаточную дисперсию (дисперсию адекватности):


.


Сравнивают с числом степеней свободы в числителе , в знаменателе . Считают, что уравнение регрессии предсказывает результаты опытов лучше среднего, если F достигает или превышает границу значимости при выбранном уровне значимости р (обычно принимают р = 1 – q = 5 %, q – вероятность предсказания). Другими словами, F – критерий Фишера показывает во сколько раз уравнение регрессии предсказывает результаты опытов лучше,чем среднее «у».

^ 2.3. Построение моделей идентификации поисковыми методами


При нелинейной параметризации дело обстоит сложнее. Приходится решать систему нелинейных уравнений. Для этого можно использовать методы последовательного приближения.

Предположим, что y (функция отклика) – доля химического вещества А, оставшаяся к моменту времени x₁ в результате реакции типа А→В. Зависимая переменная y удовлетворяет дифференционному уравнению (известно из литературы): , где ^ K – константа скорости. Решение этого уравнения при следующих начальных условиях: у=1 при х=0 имеет вид: у= exp (-К х₁); K зависит от абсолютной температуры х₂ следующим образом:

К= b₁ ехр (-b₂ / х₂) , b₁ – предэкпоненциальный множитель, b₂ – энергия активации. Модель процесса

(2.11)

нелинейна по параметрам b₁, b₂ .



Если ввести то





Начальные (нулевые) значения параметров b₁⁰,b₂⁰ могут быть получены методом линеаризации:

ln у = - b₁х₁ ехр ( -b₂ / х₂); ln у (- ln у) = ln b₁ - b₂ / х₂ + ln х₁ или

, где , , , .

Поисковые методы идентификации. В этих методах принятый критерий невязки (показатель качества идентификации) формируется из выходных характеристик объекта и его идентифицируемой модели и минимизируется с помощью численных методов. Итерационный процесс изменения вектора идентифицируемых параметров определяется используемым алгоритмом (методом) поиска и текущей ситуацией.