Устаревшая ед частотного интервала. Названа в честь франц физика Ф. Савара (F. Savart). 1 С

Вид материала

Документы

Содержание С квант. точки зрения, С. э. объяс­няется изменением импульса фотонов при вз-ствии излучения с в-вом. На­личие у потока фотонов Самоиндуцированная про­зрачность Самосогласованное поле Паули принцип Самостоятельный разряд Самостягивающийся разряд Рис. 1. Траектории лучей: о — при фоку­сировке светового пучка обычной линзой, б — при самофокусировке в нелинейной среде, в — в Рис. 2. Траектории лучей: а — при расфо­кусировке светового пучка рассеивающей (отрицательной) линзой, б — при самодефо­кусировк Рис. 3. Самоотклонение светового пучка на­встречу поперечному движению нелинейной дефокусирующей среды (n А. П. Сухорукое. Саха формула 1 — неподвижный клин из правовращающего кварца; 2 Сверхвысокие частоты Сверхзвуковая скорость Рис. 1. Конус возму­щений СО и конус влияния АОВ. Рис. 2. Обтекание сверх­звуковым потоком: а — стенок с изломом, б — выпуклой искривлённой стенки. Рис. 3. Обтекание сверхзвуковым потоком: а — клина, б — затупленного тела. Подъём­ная сила) Рис. 4. Схема обтекания стреловидного крыла. Ди­намика разреженных газов) ... Полное содержание

Подобный материал:

• Синдром удлинённого интервала qt и проблемы безопасности психофармакотерапии, 109.2kb.
• Товариство з обмеженою, 119.57kb.
• Н. Г. Чернышевского кафедра теоретической и математической физики рабочая программа, 152.3kb.
• Программа по физике для 10-11 классов общеобразовательных, 75.87kb.
• Татьяна Евгеньевна Зыкова. Сюных лет ему была интересна литература, 95.59kb.
• Электронная газета в рамках «Дня науки», посвященного Году российской космонавтики, 85.16kb.
• Лекция Логические основы компьютеров , 369.25kb.
• Игра ) Имя известного ученого, в честь которого названа самая популярная программа, 21.91kb.
• Физика биологических систем, 39.45kb.
• Динамика культурных процессов в современной России, 39.45kb.

С

САВАР, устаревшая ед. частотного интервала. Названа в честь франц. физика Ф. Савара (F. Savart). 1 С. равен интервалу частот с таким от­ношением f₂/f₁ граничных частот интервала, что lg|f₂/f₁|=0,001; при этом f₂/f₁=1,0023. 1 С.=3,32•10^-3 октавы=3,98 цента. С. применялся для измерения интервалов высоты звука.

САДОВСКОГО ЭФФЕКТ, возникно­вение механич. вращательного момента у тела, облучаемого эллиптически поляризованным светом. Как показал впервые А. И. Садовский (1898), эллиптически поляризованная свето­вая волна обладает моментом импульса (моментом количества движения), к-рый она и передаёт телу, поглощаю­щему её или изменяющему состояние её поляризации. Напр., когда на крист. пластинку в ¹/₄ длины волны падает световая волна, п о л я р и з о в а н н а я по к р у г у, появляется вра­щат. момент, стремящийся повернуть пластинку в сторону вращения эл.-магн. векторов эл.-магн. волны; при падении п л о с к о п о л я р и з о в а н н о г о света на такую же пла­стинку появляется момент вращения, действующий в обратную сторону.

651


Величина вращат. момента, возникаю­щего под действием поляризов. света, прямо пропорц. длине волны излу­чения и плотности эл.-магн. энергии в падающем пучке (яркости светового лучка). Несмотря на то что С. э. очень мал, он наблюдался на опыте как для видимого света, так и в сантиметро­вом диапазоне волн (впервые амер. учёным Р. Бетом в 1935—36). С по­явлением лазеров, излучение к-рых имеет большую плотность энергии, стало возможным наблюдать значи­тельную величину вращательного мо­мента.

Доказательство существования С.э. явилось указанием на то, что к вз-ствию эл.-магн. излучения с в-вом применим закон сохранения момента кол-ва движения. Впоследствии это положение стало неотъемлемой частью квант. теории таких вз-ствий, позво­лило описать мн. особенности процес­сов излучения и поглощения света атомами и молекулами, предсказать и открыть др. эффекты (см., напр., Оп­тическая ориентация).

^ С квант. точки зрения, С. э. объяс­няется изменением импульса фотонов при вз-ствии излучения с в-вом. На­личие у потока фотонов момента им­пульса связано с тем, что при эллип­тич. поляризации вероятности ориен­тации спина фотона в направлении его движения и навстречу ему неодина­ковы.

САМОДИФФУЗИЯ, частный случай диффузии в чистом в-ве или р-ре пост. состава, при к-ром диффундируют собственные ч-цы в-ва. При С. атомы, участвующие в диффузионном дви­жении, обладают одинаковыми хим. св-вами, но могут различаться, напр., ат. массой (см. Изотопы). За процес­сом С. можно наблюдать, применяя радиоакт. изотопы или анализируя изотопный состав при помощи масс-спектрометров. Изменение концент­рации данного изотопа в рассматри­ваемом объёме в-ва в зависимости от времени описывается обычными ур-ниями диффузии, а скорость процесса характеризуется соответствующим коэфф. С. Диффузионные перемеще­ния ч-ц тв. тела могут приводить к изменению его формы и к др. явле­ниям, если на образец длительно действуют силы поверхностного натя­жения, тяжести, упругие, электрич. силы и т. д. При этом может наблю­даться сращивание двух пришлифов. образцов одного и того же в-ва, спе­кание порошков, растягивание тел под действием подвешенного к ним груза (диффузионная ползучесть ма­териалов) и т. д. Изучение кинетики этих процессов позволяет определить коэфф. С. в-ва.

• См. лит. при ст. Диффузия.

САМОИНДУКЦИЯ, возникновение эдс индукции в проводящем контуре при изменении в нём силы тока; частный случаи электромагнитной ин­дукции. При изменении тока в контуре меняется поток магн. индукции через поверхность, ограниченную этим кон­туром, в результате чего в нём возбуж­дается эдс С. Направление эдс С. определяется Ленца правилом, т. е. при увеличении в цепи силы тока эдс С. препятствует его возрастанию, а при уменьшении тока — его убыванию. Т. о., С. подобна явлению инерции в механике. Эдс С. e_z пропорц. скорости изменения силы тока i и индуктив­ности L контура: e_z=Ldi/dt.

В электрич. цепи, содержащей постоянную эдс, при замыкании цепи сила тока за счёт эдс С. устанавлива­ется не мгновенно, а через нек-рый промежуток времени, при выключении источника ток не прекращается мгно­венно; возникающая при размыкании цепи эдс С. может во много раз превы­сить эдс источника. В цепи перем. тока вследствие С. сила тока в ка­тушке, обладающей индуктивностью, отстаёт по фазе от напряжения на концах катушки на /2 (см. Перемен­ный ток).

Явление С. играет важную роль в электротехнике и радиотехнике. Бла­годаря С. происходит перезарядка конденсатора, соединённого последо­вательно с катушкой индуктивности (см. Колебательный контур), в ре­зультате в контуре возникают сво­бодные эл.-магн. колебания.

• Калашников С. Г., Электриче­ство, 4 изд., М., 1977 (Общий курс физики).

Г. Я. Мякишев.

^ САМОИНДУЦИРОВАННАЯ ПРО­ЗРАЧНОСТЬ, эффект пропускания ко­ротких мощных когерентных импуль­сов света резонансно поглощающими средами. При С. п. глубина проник­новения импульса в среду значительно превосходит обычную длину погло­щения света в среде, а скорость его распространения, как правило, зна­чительно меньше групповой скорости света в среде. С. п. наблюдается, когда длительность импульса света меньше времени релаксации, а интен­сивность его превышает нек-рое поро­говое значение. При выполнении этих условий световой импульс любого вида после прохождения в среде определён­ной длины приходит в стационарное состояние, в к-ром длительность, энер­гия и форма его остаются неизмен­ными. Стационарный импульс имеет симметричную форму; в течение пер­вой его половины резонансные атомы переводятся из осн. состояния в воз­буждённое, в течение второй половины импульса происходит обратный про­цесс. Если энергия падающего на среду импульса достаточна для пере­вода в возбуждённое состояние всех атомов в области его влияния, то та­кой импульс придёт в стационарное состояние; в противном случае затухнет. Этим и определяется поро­говое значение интенсивности падаю­щего импульса.

• См. лит. при ст. Фотонное эхо, Нели­нейная оптика.

А. В. Андреев.

^ САМОСОГЛАСОВАННОЕ ПОЛЕ, ус­реднённое поле сил вз-ствия с данной ч-цией всех др. ч-ц квантовомеханич. системы. Задача вз-ствия многих ч-ц очень сложна, при её решении поль­зуются приближёнными методами расчёта. Один из наиб. распростра­нённых приближённых методов квант. механики основан на введении С. п., позволяющего свести задачу многих ч-ц к задаче одной ч-цы, движущейся в среднем С. п., создаваемом всеми др. ч-цами. Разл. варианты введения С. п. отличаются способом усреднения вз-ст­вия. Метод С. п. широко применяется для приближённого описания состоя­ний многоэлектронных атомов, моле­кул, тяжёлых ядер, эл-нов в металле, системы спинов в ферромагнетике и т. Д.

В квантовомеханич. системе многих взаимодействующих ч-ц движение любой ч-цы сложным образом взаимо­связано (коррелировано) с движе­нием всех остальных ч-ц системы. Вследствие этого каждая ч-ца не на­ходится в определённом состоянии и не может быть описана своей (одночастичной) волновой функцией. Состоя­ние системы в целом описывается волн. ф-цией, зависящей от координатных и спиновых переменных всех ч-ц системы. В методе С. п. для прибли­жённого описания системы вводят волн. ф-ции для каждой ч-цы системы; при этом вз-ствие с др. ч-цами прибли­жённо учитывается введением поля, усреднённого по движениям осталь­ных ч-ц системы (по их одночастичным волн. ф-циям). Одночастичные волн. ф-ции, с одной стороны, явл. решением Шрёдингера уравнения для одной ч-цы, движущейся в ср. поле, создаваемом др. ч-цами, с другой — определяют ср. потенциал поля, в к-ром движутся ч-цы. Термин «С. п.» связан с этим согласованием.

Простейший метод введения С. п. (в котором определяются не волно­вые функции, а плотность распреде­ления частиц в пространстве) — м е т о д Т о м а с а — Ф е р м и, предложен­ный английским физиком Л. Тома­сом (1927) и итальянским физиком Э. Ферми (1928). В многоэлектронных атомах ср. потенциал, действующий на данный эл-н, изменяется достаточно медленно. Поэтому внутри объёма, где относит. изменение потенциала невелико, находится ещё много эл-нов, и эл-ны, к-рые подчиняются Ферми — Дирака статистике, можно рассмат­ривать как вырожденный ферми-газ (см. Вырожденный газ). При этом дей­ствие всех остальных эл-нов на дан­ный можно заменить действием нек-рого центрально-симметричного С. п., к-рое добавляется к полю ат. ядра. Это поле подбирают так, чтобы оно было согласовано с распределением ср. плотности заряда (пропорц. рас­пределению ср. плотности эл-нов в атоме), т. к. потенциал электрич. поля связан с распределением заряда Пуас­сона уравнением. Ср. плотность эл-нов

652


в свою очередь рассматривается как плотность вырожденного идеального ферми-газа, находящегося в этом ср. поле, и связана с ним через Ферми энергию. Это означает, что выбор ср. потенциала поля должен быть «само­согласованным». На основе С. п. То­маса — Ферми удалось объяснить порядок заполнения электронных оболочек в атомах, а следовательно, и периодич. систему элементов. Этот метод применим также в теории тяжё­лых ядер. Он позволяет объяснить порядок заполнения нуклонами яд. оболочек; при этом, кроме центрально-симметричного С. п., нужно учиты­вать С. п., вызванное вз-ствием орбит. движения нуклонов с их спином (спин-орбитальное взаимодействие).

Другой, более точный, метод вве­дения С. п.— метод Хартри (предложен в 1927 англ. физиком Д. Хартри). В этом методе волн. ф-цию многоэлектронного атома пред­ставляют приближённо в виде произ­ведения волн. ф-ций отд. эл-нов, соот­ветствующих разл. квант. состояниям эл-нов в атоме. Такому распределению эл-нов отвечает нек-рое ср. С. п., к-рое зависит от выбора одноэлектронных ф-ций, а эти ф-ции в свою очередь зависят от ср. поля. Одноэлектронные волн. ф-ции выбирают из условия минимума ср. энергии, что обеспечи­вает наилучшее приближение для выбранного типа волн. ф-ций. С. п. в этом случае получаются с помощью усреднения по орбит. движениям всех др. эл-нов и для разл. состояний эл-нов в атоме оказываются различными. Волн. ф-ции эл-нов определяются теми же ср. потенциалами, что и озна­чает их самосогласованность.

В методе Хартри не учитывается ^ Паули принцип, из к-рого следует, что полная волн. ф-ция эл-нов в атоме должна быть антисимметричной. Более совершенный метод введения С. п. даёт Хартри — Фока ме­тод (В. А. Фок, 1930), к-рый исходит из волн. ф-ции (эл-нов в атоме) пра­вильной симметрии в виде определи­теля из одноэлектронных орбит. волн. ф-ций, что обеспечивает выполне­ние принципа Паули. Одноэлектронные ф-ции находят, как и в методе Хартри, из минимума ср. энергии. При этом получается С. п. с усредне­нием, в к-ром учитывается корреляция орбит. эл-нов, связанная с их обменом (см. Обменное взаимодействие).

Кроме простой обменной корреля­ции возможна корреляция пар ч-ц с противоположно направленными спинами; в случае притяжения такая корреляция приводит к образованию коррелированных пар ч-ц (связанных пар). Обобщение метода Хартри — Фока, учитывающее эту корреляцию, было сделано Н. Н. Боголюбовым (1958); обобщённый метод приме­няется в теории сверхпроводимости и в теории тяжёлых ядер.

В теории металлов также пользу­ются понятием «С. п.». В рамках этой теории принимается, что эл-ны метал­ла движутся независимо друг от друга в С. п., создаваемом всеми ионами крист. решётки и остальными эл-нами. В простейших вариантах теории это поле считается известным. Наиб. совершенный способ введения С. п. в теории металлов даёт т. н. метод псевдопотенциала, применяемый для щелочных и щёлочноземельных ме­таллов (в этом случае С. п. не явля­ется потенц. полем).

Др. примером самосогласования в физике тв. тела явл. своеобразное поведение эл-на в ионном непрово­дящем кристалле. Эл-н своим полем поляризует окружающую среду, причём поляризация, связанная со смещением ионов, создаёт потенц. яму, в к-рую попадает сам эл-н. Такое самосогласованное состояние эл-на и диэлектрической среды наз. поляроном.

Исторически первым вариантом С. п. было т. н. мол. поле, введённое в 1907 франц. физиком П. Вейсом для объяснения ферромагнетизма. Вейс предположил, что магн. момент каж­дого атома ферромагнетика находится ещё во внутр. мол. поле, к-рое само пропорц. магн. моменту и, т. о., само­согласовано. В действительности же это поле выражает на языке самосог­ласованного приближения квант. обменное вз-ствие. Обменное вз-ствие данного спина со всеми остальными спинами заменяется действием нек-рого эффективного мол. поля (оно вво­дится самосогласованным образом).

• Хартри Д. Р., Расчеты атомных структур, пер. с англ., М., I960; Бого­любов Н. Н., Толмачев В. В., Ш и р к о в Д. В., Новый метод в теории сверхпроводимости, М., 1958, с. 122—26; Харрисон У., Псевдопотенциалы в тео­рии металлов, пер. с англ., М., 1968, гл. 1; С м а р т Дж., Эффективное поле в теории магнетизма, пер. с англ., М., 1968, гл. 3; Тябликов С. В., Методы квантовой теории магнетизма, 2 изд., М., 1975, гл. 6; Киржниц Д. А., Полевые методы тео­рии многих частиц, М., 1963; С л э т е р Дж., Методы самосогласованного поля для моле­кул и твердых тел, пер. с англ., М., 1978.

Д. Н. Зубарев.

^ САМОСТОЯТЕЛЬНЫЙ РАЗРЯД, электрич. ток в газе, не требующий для своего поддержания действия внеш. ионизатора. С. р. образуется при достаточно высоком напряжении на электродах, когда начавшийся раз­ряд создаёт необходимые для его поддержания ионы и эл-ны (см. также Электрические разряды в газах).

^ САМОСТЯГИВАЮЩИЙСЯ РАЗРЯД, то же, что контрагированний разряд. САМОФОКУСИРОВКА СВЕТА, кон­центрация энергии световой волны в нелинейной среде, показатель прелом­ления n к-рой растёт с увеличением интенсивности светового поля. Под действием светового пучка (простран­ственно ограниченной световой волны) нелинейная среда становится оптичес­ки неоднородной и в ней возникает искривление лучей (нелинейная рефракция). Если n увеличива­ется с ростом напряжённости Е электрич, поля световой волны, то лучи, изгибаясь, концентрируются в обла­сти большей интенсивности — среда становится объёмной собирающей нелинейной линзой, фокус к-рой на­ходится на нек-ром расстоянии f_нл от входа пучка в среду (рис. 1, а).



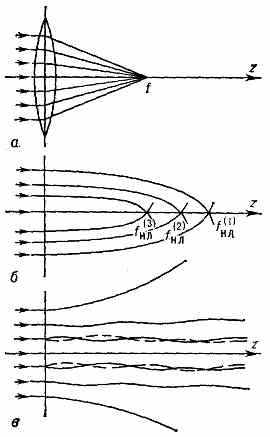
^ Рис. 1. Траектории лучей: о — при фоку­сировке светового пучка обычной линзой, б — при самофокусировке в нелинейной среде, в — в нелинейном диэлектрич. волно­воде.


Световой пучок с поперечным радиу­сом d фокусируется на расстоянии

f_нлd(n₀/_нл)^1/2, (1)

где n₀ — показатель преломления вне пучка, _нл — перепад показа­теля преломления в пучке. Показатель преломления n среды может увеличи­ваться с ростом поля Е из-за измене­ния нелинейной поляризации среды, высокочастотного Керра эффекта, электрострикции, нагрева и др. (см. Нелинейная оптика). С. с. наступает, если нелинейная рефракция подав­ляет неизбежную дифракц. расходи­мость пучка (см. Дифракция света)

нл/n₀>²_р (2)

(_р — угол дифракц. расходимости). Это происходит, когда фокусное рас­стояние f_нл меньше протяжённости зоны дифракции Френеля. Для вы­полнения неравенства (2) требуется мощность пучка, превышающая нек-рую критич. величину. По мере при­ближения к фокусу лучи всё более искривляются (С. с. носит характер лавинообразный), и концентрация по­ля в нелинейном фокусе значительно сильнее, чем при обычной фокусиров­ке линзой. С. с. может привести к световому пробою, способствовать развитию процессов вынужденного рас­сеяния света и др. нелинейных про­цессов.

653


Вслед за первым фокусом при С. с. мощного пучка может появиться ряд последующих — возникает многофокусовая структура. Число фокусов растёт с увеличением мощности источ­ника, и они приближаются ко входу в нелинейную среду (рис. 1, б). В слу­чае коротких световых импульсов фо­кусы могут двигаться с околосвето­выми скоростями (n_нл становится функцией времени).

Пучок, несущий критич. мощность, сохраняет свою форму в нелинейной среде, к-рая превращается в стационар­ный диэлектрич. волновод (рис. 1, в).

Явление С. с. теоретически было предсказано Г. А. Аскарьяном (1962) и впервые наблюдалось Н. Ф. Пилипецким и А. Ф. Рустамовым (1965).

В самофокусирующей среде может развиться специфич. неустойчивость, приводящая к т. н. мелкомасштабной С. с. В световом пучке большой мощ­ности пространств. флуктуации (ма­лые возмущения) экспоненциально нарастают, в результате чего пучок ещё до фокуса разбивается на отд. нити. Для устранения мелкомасш­табной С. с. в активной среде лазеров применяются пространств. фильтры и др. устройства, сглаживающие амп­литудные профили пучков.

Если показатель преломления среды уменьшается с ростом интенсивности света, то имеет место обратное явле­ние — с а м о д е ф о к у с и р о в к а с в е т о в ы х п у ч к о в (нелиней­ное расплывание пучков, рис. 2). Наиболее распространена тепловая дефокусировка, обусловленная умень­шением n вследствие расширения в-ва при его нагреве светом.

В нелинейной среде, движущейся перпендикулярно световому пучку (конвективные потоки жидкостей и газов и др.), возникает самоотклонение света от заданного направления.



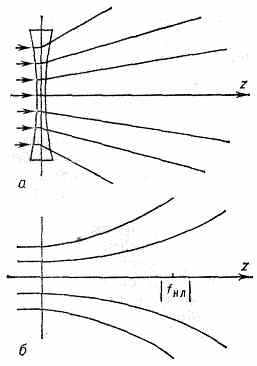
^ Рис. 2. Траектории лучей: а — при расфо­кусировке светового пучка рассеивающей (отрицательной) линзой, б — при самодефо­кусировке в нелинейной среде.




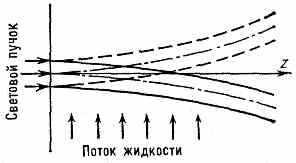
^ Рис. 3. Самоотклонение светового пучка на­встречу поперечному движению нелинейной дефокусирующей среды (n_Iнл<0, сплошные линии) и по движению нелинейной самофо­кусирующей среды (n_нл>0, пунктирные линии).


Угол самоотклонения зависит от мощ­ности пучка, скорости поперечного движения среды и инерционности не­линейного механизма изменения пока­зателя преломления (рис. 3). С. с. и самодефокусировка наблюдаются в конденсированных средах и газах (в т. ч. в воздухе и в плазме). Критич. мощность может составлять малую величину вплоть до долей Вт.

• Ахманов С. А., С у х о р у к о в А. П., Хохлов Р. В., Самофокуси­ровка и дифракция света в нелинейной среде, «УФН», 1967, т. 93, в. 1, с. 19; Луго­вой В. Н., Прохоров A.M., Теория распространения мощного лазерного излу­чения в нелинейной среде, там же, 1973, т. ill, в. 2, с. 203; Аскарьян Г. А., Эффект самофокусировки, там же.

^ А. П. Сухорукое.

САНТИ... (от лат. centum — сто), при­ставка к наименованию ед. физ. ве­личины для образования наименова­ния дольной единицы, равной 1/100 от исходной. Сокр. обозначение с. Пример: 1 см (сантиметр) = 0,01 м.

САПФИР (греч. sappheiros, от др.-евр. саппир — синий камень), при­родный и синтетич. монокристалл корунда, Аl₂O₃, синяя или голубая окраска к-рого обусловлена одноврем. присутствием примесей Ti и Fe. В фи­зике и технике назв. «С.» («лейкосапфир») укоренилось за бесцветными синтетич. монокристаллами Аl₂О₃, содержащими ~0,0001% примесей. Точечная группа симметрии 3m, плот­ность 3,93 г/см³, T_пл=2040°С, мол. м. 101,94, твёрдость по шкале Мооса 9. Прозрачен в ИК области (до  ~ 6,5 мкм), оптически анизотропен, хороший проводник гиперзвука, ди­электрик. Применяется для изготов­ления «окон» в вакуумной аппаратуре, оптич. фильтров и световодов. Ис­пользуется в микроэлектронике как подложка для изготовления интег­ральных и гибридных схем, перспек­тивен для звукопроводов и УЗ линий

задержки.

Н. В. Переломоеа.

^ САХА ФОРМУЛА определяет степень а термической ионизации в газе (т. е. отношение числа ионизов. атомов к общему числу всех атомов). Получена инд. физиком М. Сахой в 1920 для описания процессов в атмос­ферах звёзд. С. ф. выведена из общих термодинамич. соображений, относит­ся к слабоионизов. газу в состоянии равновесия термодинамического и имеет вид:



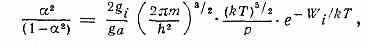
где р — давление газа, W_i — энергия ионизации его атомов, g_a и g_i — ста­тистические веса нейтр. атома и иона, m — масса эл-на. С. ф. справедлива лишь приближённо, т. к. при её вы­воде предполагается наличие только трёх сортов ч-ц: нейтральных атомов, однократно заряж. ионов и эл-нов, т. е. не учитываются многократная ионизация, возбуждение атомов и присутствие примесей. Не учиты­вается также и вз-ствие газа со стен­ками, при к-ром возможны ионизация газа эл-нами, испускаемыми горячей стенкой, и поверхностная ионизация. Несмотря на столь ограничивающие допущения, С. ф. применима во мн. случаях, когда <<1.

Л. А. Сена.

САХАРИМЕТР, поляризационный при­бор для определения содержания са­хара (реже — др. оптически активных веществ) в р-рах по измерению угла вращения плоскости поляризации (ВПП) света, пропорц. концентрации р-ра. Компенсация ВПП в С., в отличие от поляриметра, производится линейно перемещающимся кварцевым клином (рис.). Применение кварцевого ком­пенсатора позволяет освещать С. белым светом, т. к. кварц и сахар обладают почти одинаковой враща­тельной дисперсией. (При измерении концентрации др. в-в, напр. камфары, их освещают монохро­матическим светом определённой



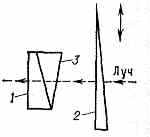
Кварцевый компенсатор: ^ 1 — неподвижный клин из правовращающего кварца; 2 — подвижный клин из левовращающего кварца, соединённый со шкалой (её нулевая от­метка соответствует поло­жению клина, при к-ром действия обоих кварцевых клиньев скомпен­сированы); 3 — клин из стекла (подклинок), вводимый для того, чтобы луч света, проходя через кварцевые клинья, не изменял своего направления.

длины волны.) Отсчёт угла вращения ведётся по линейной шкале, непосред­ственно указывающей процентное содержание сахара в р-ре. Как и в поляриметрах, в С. при компенсации происходит уравнивание яркостей двух половин поля зрения, регистри­руемое визуально или фотоэлектри­чески.

Во мн. современных С. с поляри­зационной модуляцией света кварцевый компенсатор и шкала свя­заны со следящей системой и компен­сация измеряемого ВПП осуществля­ется автоматически.

• Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); Шишловский А. А., Прикладная физиче­ская оптика, М., 1961.

САХАРИМЕТРИЯ, метод определения концентрации р-ров оптически ак­тивных веществ (гл. обр. Сахаров, откуда назв. метода), основанный на

654


зависимости вращения плоскости поля­ризации от концентрации р-ра. С. применяется в пищевой и химико-фармацевтич. пром-сти.

^ СВЕРХВЫСОКИЕ ЧАСТОТЫ (СВЧ), область радиочастот от 300 МГц до 300 ГГц, охватывающая дециметро­вые волны, сантиметровые волны и миллиметровые волны (см. Радиовол­ны).

^ СВЕРХЗВУКОВАЯ СКОРОСТЬ, ско­рость движения среды или тела в среде, превышающая скорость звука в дан­ной среде.

СВЕРХЗВУКОВОЕ ТЕЧЕНИЕ, тече­ние газа, при к-ром в рассматриваемой области скорости v его ч-ц больше местных значений скорости звука а. С изучением С. т. связан ряд важных практич. проблем, возникающих при создании самолётов, ракет и арт. сна­рядов со сверхзвуковой скоростью полёта, паровых и газовых турбин, высоконапорных турбокомпрессоров, аэродинамических труб для получе­ния потоков со сверхзвуковой скоро­стью и др. (См. также Диффузор, Сопло, Струя.)

Особенности сверхзву­кового течения. С. т. газа имеют ряд качеств. отличий от дозву­ковых течений. Поскольку слабое воз­мущение в газе распространяется со скоростью звука, влияние слабого изменения давления, вызываемого помещённым в равномерный сверхзву­ковой поток источником возмущений (напр., телом), не может распростра­няться вверх по потоку, а сносится вниз по потоку со скоростью v > а, оставаясь внутри т. н. конуса возму­щений COD, или конуса Маха (рис. 1). В свою очередь, на данную точку О потока могут оказывать влияние сла­бые возмущения, идущие только от источников, расположенных внутри



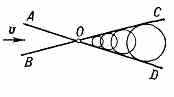
^ Рис. 1. Конус возму­щений СО и конус влияния АОВ.

конуса АОB с вершиной в данной точке и с тем же углом при вершине, что и у конуса возмущений, но обращённого противоположно ему. Если устано­вившийся поток газа неоднороден, то области возмущений и области влия­ния ограничены не прямыми круглыми конусами, а коноидами — конусоидными криволинейными поверхностя­ми с вершиной в данной точке.

При установившемся С. т. вдоль стенки с изломом (рис. 2, а) возмуще­ния, идущие от всех точек линии излома, ограничены огибающей кону­сов возмущений плоскостью, наклонённой к направлению потока под углом , таким, что sin=a/v₁, где v₁ — скорость набегающего пото­ка. Вслед за этой плоскостью поток поворачивается, расширяясь внутри угловой области, образованной пучком плоских фронтов возмущений (ха­рактеристик), до тех пор, пока не ста-



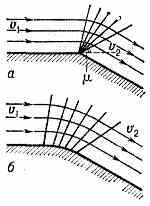
^ Рис. 2. Обтекание сверх­звуковым потоком: а — стенок с изломом, б — выпуклой искривлённой стенки.


нет параллельным направлению стен­ки после излома. Если стенка между двумя прямолинейными участками искривляется непрерывно (рис. 2, б), то поворот потока происходит посте­пенно в последовательности прямых хар-к (волн разрежения), исходящих из каждой точки искривлённого уча­стка стенки. В этих течениях, наз. те­чениями Прандтля — Майера, пара­метры газа постоянны вдоль прямых хар-к.

Волны сжатия, вызывающие повы­шение давления, и волны разрежения, понижающие давление в газе, имеют разный характер. Волна разрежения распространяется со скоростью звука. Волна, вызывающая повышение дав­ления, распространяется со скоро­стью, большей скорости звука, и мо­жет иметь очень малую толщину (по­рядка длины свободного пробега моле­кул). При многих теор. исследова­ниях её заменяют поверхностью раз­рыва — т. н. ударной волной, или скачком уплотнения. При прохожде­нии газа через ударную волну его ско­рость, давление, плотность, энтропия меняются разрывным образом — скачком.

При обтекании сверхзвуковым пото­ком клина (рис. 3, а) поступат. те­чение вдоль боковой поверхности кли­на отделяется от набегающего потока




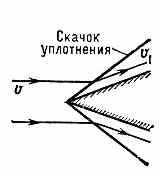
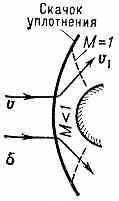
^ Рис. 3. Обтекание сверхзвуковым потоком: а — клина, б — затупленного тела.


плоским скачком уплотнения, иду­щим от вершины клина. При углах раскрытия клина, больших нек-рого предельного, скачок уплотнения ста­новится криволинейным, отходит от вершины клина и за ним появля­ется область с дозвуковой скоростью течения газа. Это характерно для сверхзвукового обтекания тел с тупой головной частью (рис. 3, б).

При обтекании сверхзвуковым пото­ком пластины (см. рис. 2 в ст. ^ Подъём­ная сила) под углом атаки, меньшим того, при к-ром скачок отходит от передней кромки пластины, от её передней кромки вниз идет плоский скачок уплотнения, а вверх — течение раз­режения Прандтля — Майера.


В ре­зультате на верхней стороне пластины давление ниже, чем под пластиной; вследствие этого возникает подъёмная сила и сопротивление, т. е. Д'Аламбера— Эйлера парадокс не имеет мес­та. Причиной того, что при сверхзву­ковой скорости обтекания идеальным газом тела испытывают сопротивле­ние, служит возникновение скачков уплотнения и связанное с ними уве­личение энтропии газа. Чем большие возмущения вызывает тело в газе, тем интенсивнее ударные волны и тем боль­ше сопротивление движению тела. Для уменьшения сопротивления крыльев, связанного с образованием голов­ных ударных волн, при сверхзвуко­вых скоростях пользуются стреловид­ными (рис. 4) и треугольными крылья-



^ Рис. 4. Схема обтекания стреловидного крыла.


ми, передняя кромка к-рых образует острый угол  с направлением ско­рости v набегающего потока. Аэроди­намически совершенной формой (т. е. формой с относительно малым сопро­тивлением давления) при С. т. явл. тонкое, заострённое с концов тело, движущееся под малыми углами атаки. При движении тел с умеренной сверх­звуковой скоростью (когда скорость полёта превосходит скорость звука в небольшое число раз) производимые ими возмущения давления и плотности газа и возникающие скорости движе­ния ч-ц газа малы, что позволяет поль­зоваться линейными ур-ниями дви­жения сжимаемого газа для определе­ния аэродинамич. хар-к профилей крыла, тел вращения и др.

Для расчёта С. т. около тел враще­ния и профилей не малой толщины, внутри сопел ракетных двигателей, сопел аэродинамич. труб и в др. случаях С. т. пользуются численными методами.

Течения с большой сверхзвуковой (гиперзвуковой) скоростью (v>>а) обладают нек-рыми особыми св-вами. Полёт тел в газе с гинерзвуковой ско­ростью связан с ростом до очень больших значений темп-ры газа вблизи поверхности тела, что вызывается мощ­ным сжатием газа перед головной частью движущегося тела и выделе­нием теплоты вследствие внутр. тре­ния в газе, увлекаемом телом при по­лёте. Поэтому при изучении гиперзву­ковых течений газа необходимо учиты­вать изменение св-в воздуха при высо­ких темп-рах: возбуждение внутр. сте­пеней свободы и диссоциацию молекул газов, составляющих воздух, хим.

655


реакции (напр., образование окиси азо­та), возбуждение эл-нов и иониза­цию. В задачах, в к-рых существенны явления мол. переноса,— при расчёте поверхностного трения, тепловых по­токов к обтекаемой газом поверхно­сти и её темп-ры — необходимо учиты­вать изменение вязкости и тепло­проводности воздуха, а в ряде случа­ев — диффузию и термодиффузию компонент воздуха.

В нек-рых условиях гиперзвукового полёта на больших высотах (см. ^ Ди­намика разреженных газов) процессы, происходящие в газе, нельзя считать термодинамически равновесными. Ус­тановление термодинамич. равнове­сия в движущейся «частице» (т. е. очень малом объёме) газа происходит не мгновенно, а требует определённо­го времени — т. н. времени релакса­ции, к-рое различно для разл. процес­сов. Отступления от термодинамич. равновесия могут заметно влиять на процессы, происходящие в погранич­ном слое (в частности, на величину тепловых потоков от газа к телу), на структуру скачков уплотнения, на распространение слабых возмущений и др. явления. Так, при сжатии воздуха в головной ударной волне легче всего возбуждаются поступат. степени сво­боды молекул, определяющие темп-ру воздуха; возбуждение колебат. сте­пеней свободы требует большего времени. Поэтому темп-ра воздуха и его излучение в области за ударной волной могут быть намного выше, чем по расчёту, не учитывающему релакса­цию колебат. степеней свободы.

При очень высокой темп-ре (~3000— 4000 К и более) в воздухе присутству­ют достаточно большое кол-во иони­зов. ч-ц и свободные эл-ны. Хорошая электропроводность воздуха вблизи тела, движущегося с большой сверх­звуковой скоростью, открывает воз­можность использования эл.-магн. воздействий на поток для изменения сопротивления тела или уменьшения тепловых потоков от горячего газа к телу. Она же затрудняет проблему ра­диосвязи с летательным аппаратом из-за отражения и поглощения радиоволн ионизов. газом, окружающим тело. Нагревание воздуха при сжатии его перед головной частью движущегося с гиперзвуковой скоростью тела может вызывать мощные потоки лучистой анергии, частично передающейся телу и вызывающей дополнит. трудности при решении проблемы его охлажде­ния.

Если скорость набегающего потока во много раз превосходит скорость звука, то при малых возмущениях скорости изменения давления и плот­ности уже не будут малыми и необхо­димо пользоваться нелинейными ур-ниями даже при изучении обтекания тонких, заострённых тел. Для гипер­звуковой аэродинамики существенна :

роль нелинейных эффектов, в резуль­тате чего представления аэродинамики умеренных сверхзвуковых скоростей, касающиеся характера сил и моментов, действующих на летательные аппара­ты, их устойчивости и управляемости при гиперзвуковых скоростях полёта, становятся неприменимыми. Так, при очень больших значениях Маха числа М оказывается, что давление в набе­гающем на тело потоке становится пренебрежимо малым по сравнению с давлением в области течения за удар­ной волной, возникающей перед телом, а энтальпией набегающего потока можно пренебречь сравнительно с его кинетич. энергией. При таких усло­виях течение за ударной волной пере­стаёт зависеть от числа М набегаю­щего потока (см. Автомодельное тече­ние). В этом состоит принцип стабили­зации течения около тел при гиперзву­ковых скоростях, причём стабилиза­ция течения около тупых тел наступает при меньших значениях числа М, чем около тонких, заострённых тел (рис. 5).



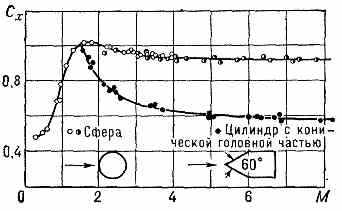
^ Рис. 5. Значения коэфф. сопротивления сфе­ры и цилиндра с конич. головной частью; начиная с М=4 эти значения перестают заметно изменяться.


Важным результатом теории гипер­звукового обтекания тонких, заострён­ных тел под малым углом атаки явл. т. н. закон плоских сечений, согласно к-рому при движении тонкого тела в покоящемся газе с гиперзвуковой скоростью ч-цы газа почти не испы­тывают продольного смещения, т. е. движение ч-ц происходит в плоскостях, перпендикулярных направлению дви­жения тела (рис. 6). Из закона плоских сечений следует закон подобия, к-рый позволяет, напр., пересчиты­вать параметры движения, получен­ные для одного тела вращения при определённом числе М, на случай обте­кания других тел с тем же распределе­нием относит. толщины по длине, для к-рых произведение М сохраняет од­но и то же значение ( — наибольшее значение относит. толщины тела).




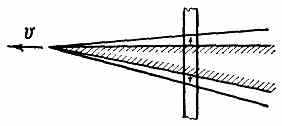
^ Рис. 6. Схема к объяснению закона плоских сечений.


• Кочин Н. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, 4 изд., ч. 2, М., 1963; Липман Г. В., Р о ш к о А., Элементы газовой динамики, пер. с англ., М., 1960; Чёрный Г. Г., Течения газа с большой сверхзвуковой ско­ростью, М., 1959.

Г. Г. Чёрный.

^ СВЕРХНОВЫЕ ЗВЁЗДЫ, звёзды, вспышки (взрывы) к-рых сопровож­даются полным энерговыделением ~10⁵¹ эрг. При всех др. звёздных вспышках выделяется значительно меньше энергии, напр. при вспышках т. н. новых звёзд — до 10⁴⁶ эрг. С. з. в осн. делятся на два типа (I и II). Из наблюдений более 400 внегалактич. С. з. и исследования ок. 100 галактич. туманностей — остатков вспышек

(разлетающихся оболочек) С. з. уста­новлены след. ср. свойства С. з. I типа: светимость в максимуме блеска ~3•10⁴³ эрг/с, полная энергия эл.-магн. излучения ~ 4•10⁴⁹ эрг, кине­тич. энергия оболочки, сброшенной звездой при взрыве, ~ 5•10⁵⁰ эрг, масса оболочки М— 0,05—0,5 М_солн (М_солн=2•10³³ г). У С. з. II типа те же хар-ки соответственно равны: 4•10⁴² эрг/с, 1•10⁴⁹ эрг, 1•10⁵¹ эрг, М>5М_солн. Кроме кривых блеска, к-рые позволяют оценить первые две из приведённых величин, С. з. различа­ются характером спектров. У С. з. I типа спектры тепловые, планковские (см. Планка закон излучения), с очень широкими и глубокими линиями поглощения ионизов. металлов и нейтрального гелия, их доплеровское смещение соответствует движению в-ва со скоростью ~10⁴ км/с. В спект­рах С. з. II типа наблюдаются яркие водородные линии, к-рых вовсе нет у С. з. I типа. Частота вспышек С. з. мала и довольно неопределённа — в одной галактике (типа нашей) про­исходит одна вспышка С. з. за 10— 100 лет. Но в нашей Галактике вспыш­ки С. з. фиксируются реже. Послед­няя С. з. вспыхнула в Галактике и наблюдалась в 1604 (всего зафиксиро­вано 6 галактич. С. з.). Галактич. остатки С. з.— волокнистые туман­ности, к-рые явл. источниками ра­диоизлучения. В трёх из них найдены пульсары — вращающиеся нейтрон­ные звёзды.

Развитие теории С. з. пошло в двух направлениях. Первое из них основы­вается на наблюдат. данных и решает задачу о законе энерговыделения, массе и структуре предсверхновой звезды. Наилучшее согласие с кри­выми блеска и спектрами С. з. дости­гается при решении радиационной гидродинамич. задачи сброса и высве­чивания оболочки для С. з. I типа при предположении о малом нач. радиусе звезды R<R_солн=7•10¹⁰ см и медленном законе выделения энер­гии с характерным временем 10 дней, а для С. з. II типа — при радиусе до взрыва R~10³—104 R_солн (звезда-сверх­гигант) и быстром (даже мгновенном) выделении энергии. О массах М сбро­шенных оболочек и полной энергии

656


взрыва теория не даёт столь опре­делённых выводов, но приведённые выше оценки М и энергии взрыва по­лучены именно этим методом и сопо­ставлены с данными наблюдений остат­ков вспышек С. з.

Др. направление теории С. з. за­нимается более фундам. проблемой -природой взрыва С. з. Тем самым оно включается в общую теорию эволюции звёзд. С энергетич. точки зрения вспышка С. з. может быть обус­ловлена либо термоядерным взрывом (энергия, связанная с массой покоя звезды М_солнc²=2•10⁵⁴ эрг, а запас термоядерной энергии составляет 0,1 — 1 % этой величины), либо гравитацион­ным коллапсом (при образовании в результате коллапса нейтронной звезды освобождается 10⁵³—10⁵⁴ эрг), либо, наконец, комбинацией обоих этих механизмов. Теория связывает вспышки С. з. с окончанием эволюции довольно массивных звёзд (М3 — 4M_солн), у к-рых в центр. области прошли термоядерные реакции «го­рения» водорода и гелия и образова­лось углеродно-кислородное ядро (СО-ядро). Окончат. судьба звезды зависит от массы СО-ядра М_со. В мас­сивных СО-ядрах (М_со>1,4М_солн), характерных для звёзд с массой М8—10М_солн, продолжается спокойное термоядерное «горение» углерода и др. более тяжёлых элементов, приво­дящее к образованию у звезды желез­ного ядра (Fe-ядра) массой М_Fe~1—3M_солн. В конце концов такая звезда коллапсирует, порождая нейт­ронную звезду или чёрную дыру. Рас­чёт в этом случае оставляет совсем мало надежды на сброс оболочки с пара­метрами, соответствующими явлению С. з. Иным образом эволюционируют звёзды с менее массивными СО-ядрами (M_CO1,4M_солн), окружёнными водородо-гелиевыми оболочками. Вместо горения углерода в них сначала про­исходит охлаждение за счёт нейтрин­ных потерь, затем постепенное увели­чение массы М_CO вплоть до 1,4M_солн благодаря сгоранию гелия в узком слое на поверхности СО-ядра и при­соединению продуктов реакции к ядру. Увеличение массы ядра вызывает повышение его плотности  и темп-ры до значений в центре: 3•10⁹ г/см³, Т 3•10⁸ К. При таких условиях либо происходит термоядерный угле­родный взрыв, к-рый приводит к полному разлёту всей звезды с харак­терным для С. з.. энерговыделением, либо развивается гравитац. коллапс. Второй путь развития возможен при значит. потерях энергии с испускае­мыми звездой нейтрино и нейтронизации продуктов горения углерода -элементов т. н. железного пика, т. е. близких по ат. массе к ⁵⁶Fe. Коллапс более вероятен, если нач. плотность в центре звезды превышает 8•10⁹ г/см³. В отличие от коллапса звёзд с массив­ным СО-ядром, у звёзд с M_CO<1,4M_солн

получается сброс оболочки, хотя и с недостаточно большим энерговы­делением 10⁵⁰ эрг. Коллапс заканчи­вается образованием нейтронной звез­ды с массой ~1,4M_солн. Т. о., вспышки С. з. удаётся объяснить, по меньшей мере качественно, как взрывы не очень массивных звёзд, у к-рых в ходе эволюции сформировалось сверхплот­ное СО-ядро с массой M_CO1,4M_солн. При этом вариант полного разлёта в-ва звезды может отвечать С. з. II типа, а вариант коллапса со сбро­сом оболочки — С. з. I типа. Большую роль во взрыве С. з. I типа должны играть вращение и магн. поле, энер­гия к-рых может увеличивать полную энергию сброшенной оболочки до наб­людаемого значения ~10⁵¹ эрг. Эволюц. теория С. з. обоих типов вполне согласуется с упомянутой выше тео­рией кривых блеска С. з., если при­нять во внимание обмен массой в тес­ных двойных системах или к.-н. др. механизм значит. изменения массы у предсверхновой звезды. Для взрыва С. з. I типа важна предварительная (на всех предшествующих стадиях эволюции) потеря большой доли мас­сы из внеш. слоев, так что предсверхновая звезда I типа должна представ­лять собой почти голое СО-ядро с M_CO ~1,4M_солн. Для вспышки С. з. II типа, в соответствии с выводами теории С. з., не характерны значит. потери массы в ходе эволюции.

С. з., особенно II типа, выбрасы­вают в межзвёздное пр-во большие кол-ва углерода, кислорода и элемен­тов «железного пика», к-рые в присут­ствии свободных нейтронов участвуют впоследствии в образовании более тя­жёлых элементов (см. Нуклеосинтез). С др. стороны, в окрестностях G. з. I типа создаются условия для нейт­ринного нуклеосинтеза и ускорения ч-ц (рождения космических лучей). Вра­щающаяся нейтронная звезда с силь­ным магн. полем в остатках С. з. I ти­па проявляет себя в дальнейшем как радиопульсар или рентг. пульсар в зависимости от возраста и окру­жающих условий.

• Шкловский И. С., Сверхновые звезды и связанные с ними проблемы, 2 изд., М., 1976; Псковский Ю. П., Новые и сверхновые звезды, М., 1974; Итоги науки и техники. Сер. Астрономия, т. 21 —Вспыш­ки на звездах, М., 1982.

^ В. С. Имшенник.

СВЕРХПРОВОДИМОСТЬ, свойство мн. проводников, состоящее в том, что их электрич. сопротивление скачком падает до нуля при охлаждении ниже определённой критич. темп-ры Т_к, характерной для данного материала. С. обнаружена у более чем 25 металлич. элементов, у большого числа сплавов и интерметаллич. соединений, а также у нек-рых ПП и полимеров. Рекордно высоким значением Т_к (ок. 23 К) обла­дает соединение Nb₃Ge (см. Сверхпро­водники).

Основные явления. Скачкообразное исчезновение сопротивления ртути при понижении темп-ры впервые наблюдал голл. физик X. Камерлинг-Оннес (1911) (рис. 1). Он пришёл к выводу, что ртуть при T=4,15 К переходит в новое состояние, к-рое было названо сверхпроводящим. Несколько позднее Камерлинг-Оннес обнаружил, что электрич. сопротивление ртути восста­навливается при Т<Т_к в достаточно сильном магн. поле (см. Критическое магнитное поле Н_к). Падение сопротивления до нуля происходит на про­тяжении очень узкого интервала темп-р, ширина к-рого для чистых образцов составляет 10^-3—10^-4 К и возрастает при наличии примесей и др. дефектов структуры.




^ Рис. 1. Зависимость сопротивления R от темп-ры Т для Hg и для Pt. Ртуть при T=4,15 К переходит в сверхпроводящее состояние. R_0°С — значение R при 0°С.


Отсутствие сопротивления в сверх­проводящем состоянии с наибольшей убедительностью демонстрируется опытами, в к-рых в сверхпроводящем кольце возбуждается ток, практически не затухающий. В одном из вариантов опыта используются два кольца из сверхпроводящего металла. Большее из колец неподвижно закрепляется, а меньшее концентрически подвеши­вается на упругой нити таким обра­зом, что когда нить не закручена, плос­кости колец образуют между собой нек-рый угол. Кольца охлаждаются в присутствии магн. поля ниже темп-ры Т_к, после чего поле выключается. При этом в кольцах возбуждаются токи, вз-ствие между к-рыми стремится уменьшить первоначальный угол меж­ду плоскостями колец. Нить закручи­вается, а наблюдаемое постоянство угла закручивания показывает, что токи в кольцах явл. незатухающими. Опыты такого рода позволили уста­новить, что сопротивление металла в сверхпроводящем состоянии меньше, чем 10^-20 Ом•см (сопротивление чи­стых образцов Cu или Ag составляет ок. 10^-9 Ом•см при темп-ре жидкого гелия). Однако сверхпроводник не явл. просто идеальным проводником. В 1933 нем. физики В. Мейснер и Р. Оксенфельд установили, что слабое магн. поле не проникает в глубь сверхпроводника независимо от того, было ли поле включено до или после перехода металла в сверхпроводящее состояние. В отличие от этого, идеаль­ный проводник (т. е. проводник с исчезающе малым сопротивлением) дол­жен захватывать пронизывающий его магн. поток (рис. 2, а, б, в).

Выталкивание магн. поля из сверх­проводящего образца (Мейснера эф­фект) означает, что в присутствии внеш. магн. поля такой образец ведёт

657




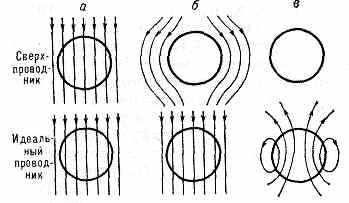
^ Рис. 2. Распределение магн. поля около сверхпроводящего шара и около шара с ис­чезающим сопротивлением (идеальный про­водник): а — при Т>Т_к; б — при Т<Т_к, внеш. поле H_вн0; в — при Т<Т_к, Н_вн=0.


себя, как идеальный диамагнетик той же формы с магнитной восприим­чивостью =1/4. В частности, если образец имеет форму длинного сплош­ного цилиндра, а внеш. поле Н одно­родно и параллельно оси цилиндра, то магн. момент, отнесённый к единице объёма, М=-Н/4. Это примерно в 10⁵ раз больше по абс. величине, чем для металла в норм. состоянии. Эф­фект Мейснера связан с тем, что при Н<H_к в поверхностном слое (тол­щиной 10^-5—10^-6 см) сверхпрово­дящего цилиндра появляется круговой незатухающий ток, сила к-рого как раз такова, что магн. поле этого тока компенсирует внеш. поле в толще сверхпроводника.

По своему поведению в достаточно сильных полях сверхпроводники подразделяются на две большие груп­пы, т. н. сверхпроводники 1-го и 2-го рода. Кривые намагничивания М(Н), типичные для каждой из этих групп, приведены на рис. 3 и 4. Нач.



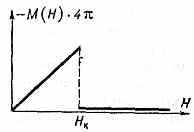
Рис. 3. Кривая намагничивания сверхпроводников 1-го рода. Образ­цы — цилиндриче­ские, длинные: намагничивающее поле на­правлено вдоль оси цилиндра (в этих усло­виях устранены эффекты размагничивания).



Рис. 4. Кривая намагничивания сверхпро­водников 2-го рода, полученная в тех же ус­ловиях, что и на рис. 3.


прямолинейный участок кривых на­магничивания, где М=-H/4, соот­ветствует интервалу значений H, на к-ром имеет место эффект Мейснера. Дальнейший ход кривых М(Н) для

сверхпроводников 1-го и 2-го рода су­щественно различается.

Сверхпроводники 1-го рода теряют С. в поле Н=Н_к, когда поле скачком проникает в металл и он во всём объёме переходит в норм. состояние. При этом уд. магн. момент также скачком уменьшается в 10⁵ раз. Критич. полю можно дать простое термодинамич. истолкование. При темп-ре Т<Т_к и в отсутствии магн. поля свободная энергия (см. Гельмгольца энергия) в сверхпроводящем состоянии F_c ниже, чем в нормальном F_н. При включении поля свободная энергия сверхпроводника возрастает на величину H²/8, равную работе намагничивания, и при Н=Н_к срав­нивается с F_н (в силу малости магн. момента в норм. состоянии F_н практи­чески не изменяется при включении поля). Т. о., поле H_к определяется из условия:

F_c+H²_к/8=F_н. (1)

Критич. поле Н_к зависит от темп-ры: оно максимально при T=0 и монотонно убывает до нуля при Т  Т_к.



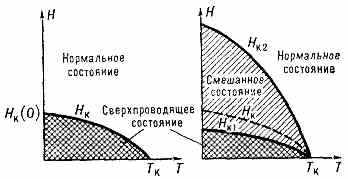
Рис. 5. Фазовая диаграмма для сверхпро­водников 1-го и 2-го рода.


На рис. 5 приведена фазовая диаграм­ма на плоскости (Н, Т). Заштрихо­ванная область, ограниченная кривой Н_к(Т), соответствует сверхпроводя­щему состоянию. По измеренной за­висимости Н_к (Т) могут быть рассчи­таны все термодинамич. хар-ки сверх­проводника 1-го рода. В частности, из ф-лы (1) непосредственно получается (при дифференцировании по темп-ре) выражение для теплоты фазового перехода Q в сверхпроводящее состоя­ние:



где ^ S — энтропия ед. объёма. Знак Q таков, что теплота поглощается сверх­проводником при переходе в норм. состояние. Поэтому, если разрушение С. магн. полем производится при адиабатич. изоляции образца, то последний будет охлаждаться. В действительно­сти скачкообразный характер фазо­вого перехода в магн. поле (рис. 3) наблюдается только в случае длинного цилиндра в продольном поле. При произвольной форме образца и др. ориентациях поля переход оказыва­ется растянутым по нек-рому интер­валу значений H: он начинается при Н<Н_к и заканчивается, когда поле

во всех точках образца превысит H_к. В этом интервале значений  сверх­проводник 1-го рода находится в т. н. промежуточном состоянии. Он рас­слаивается на чередующиеся области норм. и сверхпроводящей фаз, при­чём так, что поле в норм. фазе вблизи границы раздела параллельно этой границе и равно H_к. По мере увели­чения поля возрастает доля норм. фазы и происходит уменьшение магн. момента образца.

С магн. св-вами сверхпроводников тесно связаны и особенности протека­ния в них тока. В силу эффекта Мей­снера ток явл. поверхностным, он сосредоточен в тонком слое, определяе­мом глубиной проникновения магн. поля. Когда ток достигает нек-рой критич. величины, достаточной для создания критич. магн. поля, сверх­проводник 1-го рода переходит в промежуточное состояние и приобре­тает электрич. сопротивление.

Картина разрушения сверхпроводи­мости магн. полем у сверхпроводни­ков 2-го рода сложнее. Даже в случае цилиндрич. образца (рис. 4) в продоль­ном поле происходит постепенное уменьшение магн. момента на протя­жении значит. интервала полей от H_{к., 1} — ниж. критич. поля, когда оно начинает проникать в толщу образца, и до верх. критич. поля H_{к, 2}, при к-рой происходит полное разрушение сверх­проводящего состояния. В большинст­ве случаев кривая намагничивания такого типа необратима (наблюдается магн. гистерезис). Поле H_{к, 2} часто оказывается весьма большим; достигая сотен тысяч эрстед. Термодинамич. критич. поле H_к, определяемое соот­ношением (1), для сверхпроводников 2-го рода не явл. непосредственно наб­людаемой хар-кой. Его можно рассчи­тать, исходя из найденных опытным путём значений свободной энергии в норм. и сверхпроводящем состояниях в отсутствии магн. поля. Вычисленное таким способом значение H_к попадает в интервал между H_{к, 1} и H_{к, 2}. Т. о., проникновение магн. поля в сверх­проводник 2-го рода начинается уже в поле, меньшем чем H_к, когда условие равновесия (1) ещё нарушено в пользу сверхпроводящего состояния. Свя­зано это с поверхностной энергией границы раздела норм. и сверхпрово­дящей фаз. В случае сверхпроводников 1-го рода эта энергия положительна, так что появление поверхности разде­ла требует энергетич. затрат. Это существенно ограничивает степень расслоения в промежуточном состоя­нии. Аномальные магн. св-ва сверх­проводников 2-го рода можно качественно объяснить, если принять, что в этом случае поверхностная энергия отрицательна. Именно к такому выводу приводит совр. теория сверхпроводимости. При отрицат. поверхностной энергии уже при H