М. К. Аммосова институт математики и информатики рабочая программа
| Вид материала | Рабочая программа |
- М. К. Аммосова Институт математики и информатики рабочая программа, 31.65kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 219.2kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 460.29kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 247.89kb.
- М. К. Аммосова Институт математики и информатики Кафедра математической экономики рабочая, 71.2kb.
- М. К. Аммосова Институт математики и информатики Кафедра информатики и вычислительного, 59.79kb.
- М. К. Аммосова институт математики и информатики рабочая программа, 100.1kb.
- М. К. Аммосова институт математики и информатики рабочая программа, 98.66kb.
- М. К. Аммосова институт математики и информатики рабочая программа, 199.63kb.
- М. К. Аммосова институт математики и информатики рабочая программа, 78.16kb.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ЯКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМ. М.К. АММОСОВА
ИНСТИТУТ МАТЕМАТИКИ И ИНФОРМАТИКИ
РАБОЧАЯ ПРОГРАММА
курса
«Линейная алгебра и геометрия»
(наименование курса)
Для государственных университетов
Направление 510100 - Математика
(шифр, название)
Степень - бакалавр математики
Якутск 2003
Составители: доцент Гурзо Г.Г.,
ассистент Иванова А.О.,
старший преподаватель Антонен А.И.
(уч. ст., уч. зв., должн., ФИО)
^
Рабочая программа утверждена на заседании кафедры алгебры и геометрии
“ “ _________________ 2003 г. протокол № _____
Зав. кафедрой: Никитина Е.С.
Рабочая программа утверждена на заседании методкомиссии ИМиИ
“ “ _________________ 2003 г. протокол № _____
Председатель методкомиссии ИМиИ: Афанасьева В.И.
Рабочая программа утверждена на заседании научно – методического совета ЯГУ
“ “ _________________ 2003 г. протокол № _____
Председатель научно – методического совета ЯГУ: Яковлева А.Н.
^ Выписка из учебного плана (ОПД.Ф.04)
Объем работы студентов (в часах) из учебного плана направления 510100 - Математика составляет 200 часов, в том числе:
- лекций - 72;
- лабораторных занятий - 90;
- аудиторных занятий - 162;
- СРС - 38.
^ Распределение часов по семестрам
| Вид занятий | Семестры | Всего | |
| II (18 нед.) | III (18 нед.) | ||
| Аудиторные | 90 | 72 | 162 |
| Лекционные | 36 | 36 | 72 |
| Лабораторные | 54 | 36 | 90 |
| СРС | 18 | 20 | 38 |
| Итого | 108 | 92 | 200 |
| Форма контроля | Экзамен | Экзамен | |
^ Недельная нагрузка по семестрам
| Вид занятий | Семестры | |
| II | III | |
| Аудиторные | 4 | 4 |
| Лекционные | 2 | 2 |
| Лабораторные | 3 | 2 |
^ 1. ТРЕБОВАНИЯ К ОБЯЗАТЕЛЬНОМУ МИНИМУМУ СОДЕРЖАНИЯ
ОСНОВНОЙ ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ ПОДГОТОВКИ
БАКАЛАВРА МАТЕМАТИКИ ПО СПЕЦИАЛЬНОСТИ510100 - Математика
^ ДИСЦИПЛИНА - ЛИНЕЙНАЯ АЛГЕБРА И ГЕОМЕТРИЯ
Векторные пространства: линейная зависимость векторов; размерность и базис векторного пространства; координаты вектора в заданном базисе; изоморфность векторных пространств одинаковой конечной размерности; подпространства векторного пространства; линейная оболочка и ранг системы векторов; пересечение и сумма подпространств; прямая сумма; линейные функции; сопряженное пространство; дуальный базис; линейные отображения векторных пространств, их задание матрицами; ядро и образ линейного отображения; условие существования обратного отображения; линейные операторы; действия над ними; матрицы оператора в различных базисах; инвариантные подпространства; собственные векторы и собственные значения; характеристический многочлен линейного оператора; теорема Гамильтона-Кэли. Жорданова клетка: корневые пространства; разложение в прямую сумму; теорема о жордановой нормальной форме матрицы линейного оператора в комплексном и в вещественном пространстве; единственность жордановой нормальной формы; необходимое и достаточное условие диагонализируемости матрицы; полилинейные функции на векторном пространстве: общее понятие о тензорах; координаты тензора; переход от одной системы координат к другой; задание тензоров типа /2,0/ (билинейных функций) матрицей; квадратичные и эрмитовы формы; приведение симметрических билинейных форм к каноническому виду; закон инерции; положительно определенные формы; критерий Сильвестра; свертка тензора; симметрические и кососимметрические тензоры; операция симметрирования и альтернатирования; внешнее умножение; внешняя алгебра; связь с определителями; ориентация конечномерного векторного пространства. Евклидовы и унитарные векторные пространства: длина вектора и угол между векторами; неравенство Коши-Буняковского; ортонормированные базисы; процесс ортогонализации; ортогональные и унитарные матрицы; примеры; изоморфность унитарных пространств одинаковой размерности; соответствие между билинейными формами и линейными операторами; линейный оператор, сопряженный к данному; симметрические и эрмитовы линейные операторы; их спектр; существование собственного ортонормированного базиса; приведение квадратичной (эрмитовой) формы к главным осям; ортогональные и унитарные линейные операторы; канонический базис для них. Аффинные (точечные) пространства: системы координат; плоскости в аффинном пространстве; их задание системами линейных уравнений; расстояние между точками евклидова пространства; расстояние от точки до плоскости; объем в евклидовом пространстве; объем параллелепипеда и определитель Грама; аффинные отображения: их запись в координатах: разложение аффинного преобразования в произведение сдвига и преобразования, оставляющего на месте точку; геометрический смысл определителя аффинного преобразования; движение евклидова пространства; классификация движений; теоретико-групповая точка зрения на геометрию; аффинная и евклидова геометрия; квадрики (гиперповерхности второго порядка) в аффинном пространстве: классификация квадрик в аффинной и евклидовой геометриях; невырожденные центральные квадрики; асимптотические направления; геометрические свойства главных осей эллипсоида; проективное пространство произвольной размерности, различные модели: однородные координаты; аффинные карты проективного пространства; проективные преобразования и проективная группа; квадрики в проективном пространстве, их квалификация.
2. ТРЕБОВАНИЯ СТАНДАРТА К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКА ПО СПЕЦИАЛЬНОСТИ 510100 – Математика
Бакалавр математики отвечает следующим требованиям:
- Имеет целостное представление о процессах и явлениях, происходящих в неживой и живой природе, понимает возможности современных научных методов познания природы и владеет ими на уровне, необходимом для решения задач, имеющих естественнонаучное содержание и возникающих при выполнении профессиональных функций;
- Способен продолжить обучение в магистратуре и по специальности, в соответствии с п.1.3., вести профессиональную деятельность в иноязычной среде (требование рассчитано на реализацию в полном объеме через 10 лет);
- Владеет культурой мышления, знает его общие законы, способен в письменной и устной речи правильно (логически) оформить его результаты;
- Умеет на научной основе организовать свой труд, владеет компьютерными методами сбора, хранения и обработки (редактирования) информации, применяемые в сфере его профессиональной деятельности;
- Способен в условиях развития науки и изменяющейся социальной практики к переоценке накопленного опыта, анализу своих возможностей, умеет приобретать новые знания, обучаться в магистратуре, использовать другие формы обучения, включая самостоятельные и информационно образовательные технологии;
- Понимает сущность и социальную значимость своей будущей профессии, основные проблемы дисциплин, определяющих конкретную область его деятельности, видит их взаимосвязь в целостной системе знаний;
- Способен к проектной деятельности в профессиональной сфере на основе системного подхода, умеет строить и использовать модели для описания и прогнозирования различных явлений, осуществлять их качественный и количественный анализ;
- Способен поставить цель и сформулировать задачи, связанные с реализацией профессиональных функций, умеет использовать для их решения методы изученных им наук;
- Готов к кооперации с коллегами и работе в коллективе, знаком с методами управления, умеет организовать работу исполнителей, находить и принимать управленческие решения в условиях различных мнений, знает основы педагогической деятельности;
- Методически и психологически готов к изменению вида и характера своей профессиональной деятельности, работе над междисциплинарными проектами;
- Способен к совершенствованию своей профессиональной деятельности в области математики.
^ 3. ПРИНЦИПЫ И ЦЕЛИ
3.1. Принципы построения курса
3.1.1. Данный курс разработан в соответствии с Государственным образовательным стандартом высшего профессионального образования по специальности 510100 – Математика;
3.1.2. В рабочей программе выделяется ядро курса (линейные пространства, квадратичные и билинейные формы, линейные преобразования линейных пространств, евклидовы пространства);
3.1.3. Курс имеет практическую направленность: лабораторные – 90 ч., самостоятельная работа – 38 ч.;
3.1.4. Программа предполагает индуктивное построение курса;
^ 3.2. Цели курса
| № | Содержание |
| Студент должен иметь представление о | |
| | Инвариантных множителях, элементарных делителях, минимальном многочлене матрицы, теореме Гамильтона-Кэли. |
| | Полилинейных функциях на векторном пространстве, общем понятии тензора, свертке тензора, внешней алгебре. |
| | Расстоянии между точками евклидова пространства, расстоянии от точки до плоскости. |
| Студент должен знать | |
| | Определение квадратичной и билинейных форм, их рангов, эквивалентных квадратичных и билинейных форм, конгруэнтных билинейных форм, распадающейся и положительно определенной квадратичной формы, сигнатуру канонического и нормального видов форм, сигнатуры, положительного и отрицательного индексов матриц, связь матриц эквивалентных форм и конгруэнтных симметрических билинейных форм. Свойства эквивалентных форм. |
| | Доказательства основной теоремы теории квадратичных форм, закона инерции, основной теоремы о распадающихся формах, теорем о положительно определенных формах (критерий Сильвестра). |
| | Определение 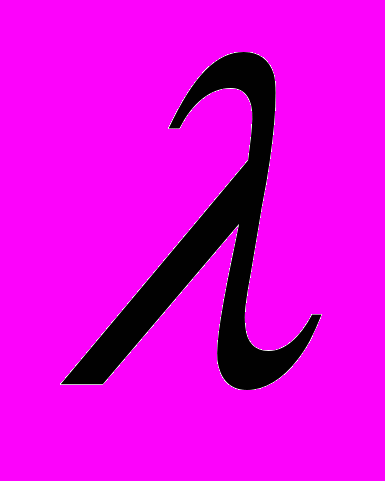 - матрицы, эквивалентных матриц, канонического вида, унимодулярной матрицы, элементарных матриц, подобных матриц, жордановой матрицы - матрицы, эквивалентных матриц, канонического вида, унимодулярной матрицы, элементарных матриц, подобных матриц, жордановой матрицыТипы элементарных преобразований, критерий эквивалентности 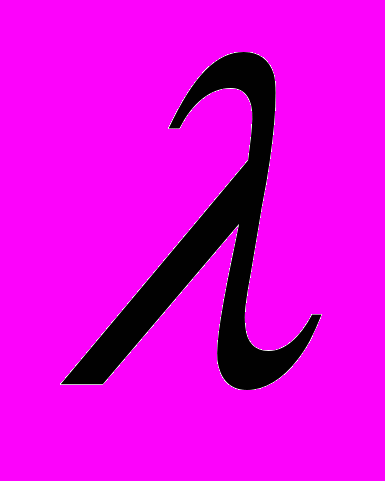 -матриц, основную теорему о подобии матриц, свойства унимодулярных матриц, критерий приводимости матрицы к жордановой нормальной форме. -матриц, основную теорему о подобии матриц, свойства унимодулярных матриц, критерий приводимости матрицы к жордановой нормальной форме. |
| | Доказательства теоремы о существовании и единственности канонической матрицы, II критерий эквивалентности 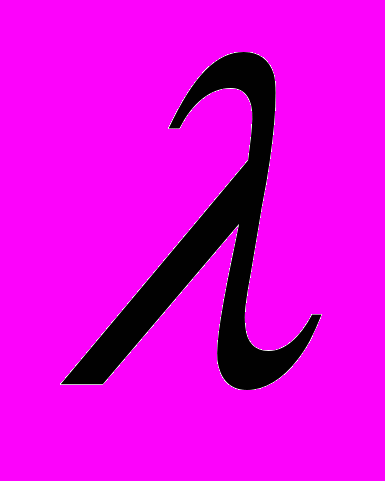 -матриц. -матриц. |
| | Аксиоматическое определение линейного пространства, базы и размерности, линейно зависимой системы векторов, изоморфных пространств, линейно зависимой системы векторов, изоморфных пространств, подпространства, суммы и пересечения подпространств, прямой суммы, линейного преобразования, неособенного линейного преобразования, дефекта ранга линейного преобразования, собственных векторов линейного преобразования, подпространств инвариантных, относительно преобразования, линейного преобразования, линейного многообразия. Формулировки теорем о размеренности суммы подпространств, о ранге линейного преобразования. Доказательство того, что ядро и область значений линейного преобразования это инвариантные подпространства, что сумма ранга и дефекта равна размерности пространства. Необходимые и достаточные условия приводимости матрицы линейного преобразования к диагональному виду, условия существования обратного отображения. |
| | Аксиоматическое определение скалярного произведения в евклидовом и унитарном пространстве. Определение ортонормированного базиса, ортогонального и симметрического преобразования. Условия изоморфизма евклидовых пространств, свойства ортогональных матриц, ортогональных и симметрических преобразований. Процесс ортогонализации, неравенство Коши - Буняковского. |
| Студент должен уметь | |
| | Приводить квадратичную и билинейную формы к нормальному виду и находить невырожденные линейные преобразования, приводящие форму к этому виду. Определить эквивалентность форм, положительную определенность, представлять распадающуюся форму в виде произведения линейных форм. |
| | Находить канонический вид 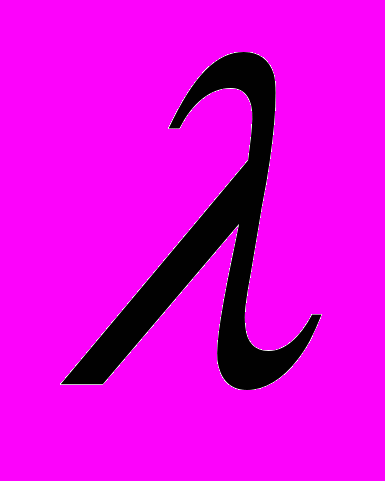 - матриц, определять эквивалентность - матриц, определять эквивалентность 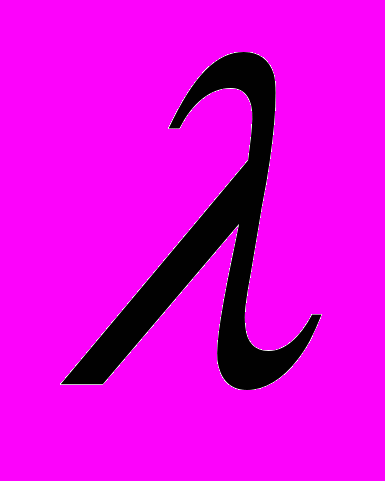 - матриц, подобие матриц, находить жорданову нормальную форму матрицы. - матриц, подобие матриц, находить жорданову нормальную форму матрицы. |
| | Находить базу и размерность пространства, матрицу перехода от одного базиса к другому, распознавать является ли заданное преобразование линейным. Находить ядро и область значений, дефект и ранг линейного преобразования, заданного в некотором базисе матрицы, его собственные векторы. Выполнять действия над линейными преобразованиями (сложение, умножение, умножение на число). Находить строку координат вектора в заданном базисе, базис суммы и пересечения подпространств. |
| | Находить длину вектора и угол между векторами, ортогональное дополнение подпространств, собственный ортонормированный базис, приводить квадратичные формы к главным осям, находить преобразование для пары форм (одна из которых положительно определена), приводящее одну из них к каноническому, а другую к нормальному виду. Определять, является ли данное преобразование ортогональным или симметрическим. |
^ 7. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- Гурзо Г.Г., Скрябин А.В. Квадратичные и билинейные формы, Якутск 1997
- Гурзо Г.Г., Антонен А.И. Полиномиальные матрицы, 1998
- Гурзо Г.Г. Лабораторные задания по теме «Линейные пространства», Якутск, 1995
- Гурзо Г.Г, Антонен А.И. Лабораторные занятия по теме "Линейные преобразования линейных пространств". Якутск, 1996
- Гурзо Г.Г, Скрябин А.В. Лабораторные занятия по теме "Евклидовы пространства". Якутск, 1996
- Курош А.Г. Курс высшей алгебры. М.: Наука, 1986 *
- Мальцев А.И. Основы линейной алгебры. М.: Наука, 1975с *
- Проскуряков И.В. Сборник задач по линейной алгебре. *
- Петрова В.Т. Лекции по алгебре и геометрии. – М., 1999
- Иванова А.О., Неустроева Т.К., Гурзо Г.Г., Бочарова И.Н. Методические указания и контрольные задания по алгебре и теории чисел находится в печати типографии ЯГУ, 2000 и в электронной библиотеке СИТИМ в виде pdf-файлов
- Антонен А.И., Бочарова И.Н., Дмитриев И.Г., Гурзо Г.Г., Иванова А.О., Неустроева Т.К. «Методические указания для студентов заочного отделения 1 курса МПО Электронная библиотека «Ситим» (http://www.sitim.sitc.ru), Якутск 2002
- Глухов М.М, Солодовников А.С. Задачник-практикум по высшей алгебре. М.: Просвещение, 1969
Примечание: * отмечена основная литература.
^ 8. КОНТРОЛИРУЮЩИЕ МАТЕРИАЛЫ
Экзаменационные вопросы
Модуль 1. Квадратичные и билинейные формы.
Модуль 2. Полиномиальные матрицы.
- Квадратичные формы. Основная теорема.
- Конгруэнтные и эквивалентные билинейные формы. Приведение симметрических билинейных форм к каноническому виду. Связь матриц конгруэнтных и эквивалентных билинейных форм.
- Закон инерции.
- Распадающиеся квадратичные формы.
- Свойства положительно определенных квадратичных форм.
- Критерий Сильвестра.
- Теорема о существовании канонической
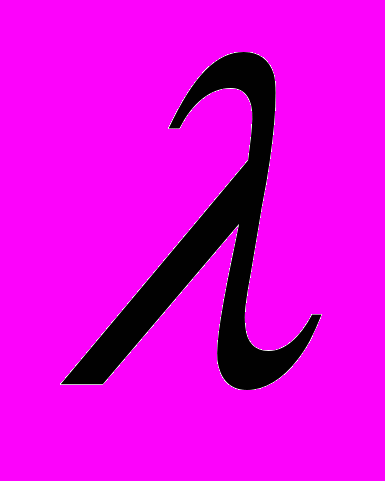 -матрицы.
-матрицы.
- Теорема о единственности канонической матрицы.
- Унимодулярные матрицы и их свойства.
- 2-ой критерий эквивалентности
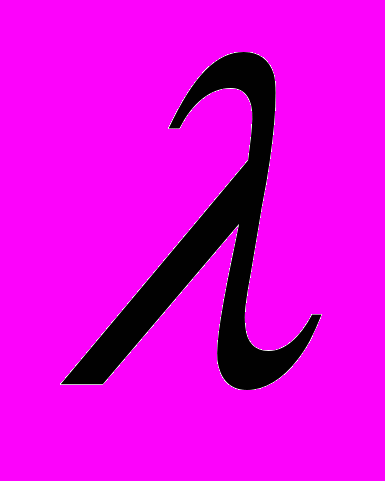 -матриц. Подобие матриц, свойства подобных матриц.
-матриц. Подобие матриц, свойства подобных матриц.
- Основная теорема о подобии матриц.
- Жорданова нормальная форма. Теорема о приведении матрицы к жордановой нормальной форме.
Модуль 3. Векторные пространства.
Модуль 4. Евклидовы и унитарные векторные пространства.
- Определение n-мерного векторного пространства. Линейная зависимость векторов. Теорема о том, что все базы n-мерного векторного пространства состоят из одинакового количества векторов.
- Основная теорема.
- Линейные пространства. Изоморфизм линейных пространств. Свойства изоморфного отображения.
- Теорема о том, что каждый вектор пространства единственным образом представляется как линейная комбинация векторов базиса.
- Невырожденность матрицы перехода. Связь координат одного и того же вектора в разных базисах.
- Пересечение и сумма линейных подпространств.
- Теорема о размерности суммы двух подпространств.
- Теорема о прямых суммах подпространств.
- Линейные многообразия.
- Линейные преобразования линейных пространств. Действия над линейными преобразованиями.
- Матрица линейного преобразования. Формула нахождения координат образа вектора при линейном преобразовании.
- Связь между матрицами линейного преобразования в разных базах.
- Теорема о существовании и единственности линейного преобразования, переводящего линейно независимые векторы в произвольные.
- Область значений и ядро линейного преобразования. Теоремы об их размерностях.
- Теорема о том, что образы и прообразы линейных пространств опять являются линейными пространствами.
- Неособенные линейные преобразования. Необходимое и достаточное условие для того, чтобы линейное преобразование было неособенным.
- Ранг линейного преобразования. Теорема о ранге произвольного линейного преобразования.
- Инвариантные подпространства.
- Теорема о прямой сумме инвариантных подпространств.
- Собственные векторы и собственные значения линейного преобразования. Теорема о том, что собственными значениями линейного преобразования служат действительные характеристические корни линейного преобразования, и только они.
- Спектр. Теорема о матрице линейного преобразования в базе, состоящей из собственных векторов.
- Простой спектр. Диагональный вид матрицы линейного преобразования с простым спектром.
- Теорема о том, что характеристический многочлен любого линейного преобразования не зависит от выбора базиса.
- Аксиоматическое определение евклидова пространства. Теорема о превращении любого линейного пространства в евклидово.
- Неравенство Коши - Буняковского.
- Длина вектора и угол между векторами.
- Теорема о том, что всякое евклидово пространство обладает ортогональными базами.
- Ортогональная система векторов. Процесс ортогонализации.
- Ортонормированная система векторов. Теорема о том, что всякое евклидово пространство обладает ортонормированными базами.
- Необходимое и достаточное условие для того, чтобы база евклидова пространства была ортонормированной.
- Теорема о том, что всякая ортогональная система ненулевых векторов является линейно независимой.
- Ортогональное дополнение. Теорема о представлении евклидова пространства в виде прямой суммы подпространства
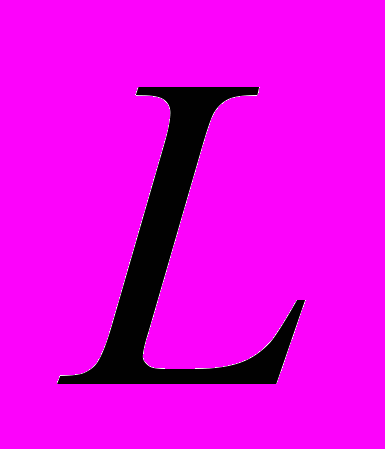 и его ортогонального дополнения.
и его ортогонального дополнения.
- Ортогональная проекция вектора на подпространство и ортогональная составляющая вектора относительно подпространства.
- Изоморфизм евклидовых пространств. Теорема.
- Ортогональные матрицы. Свойства ортогональных матриц.
- Необходимое и достаточное условие для того, чтобы матрица была ортогональной.
- Теорема о матрице перехода от ортонормированной базы евклидова пространства к любой другой его ортонормированной базе.
- Ортогональные преобразования евклидовых пространств. Утверждения о них.
- Свойства ортогональных преобразований.
- Симметрические преобразования и их свойства.
- Утверждения о симметрических преобразованиях.
- Теорема о характеристических корнях симметрического преобразования.
- Необходимое и достаточное условие для того, чтобы линейное преобразование евклидова пространства было симметрическим.
- Приведение квадратичных форм к главным осям. Теорема о существовании ортогональной матрицы, приводящей симметрическую матрицу к диагональной.
- Теорема о приведении действительной квадратичной формы к главным осям.
- Теорема о коэффициентах канонического вида квадратичной формы, к которому она приводится с помощью ортогонального преобразования.
- Теорема о собственных векторах симметрического преобразования, относящихся к различным собственным значениям.
- Пары форм. Теорема о существовании невырожденного линейного преобразования, одновременно приводящего действительную положительную определенную квадратичную форму
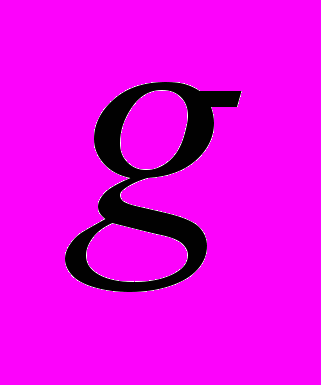 к нормальному виду и произвольную действительную форму
к нормальному виду и произвольную действительную форму 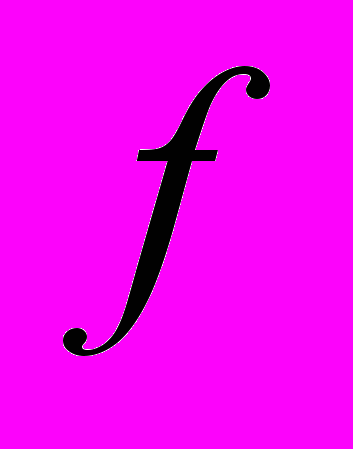 - к каноническому.
- к каноническому.
Вопросы коллоквиумов
Модуль 1. Квадратичные и билинейные формы.
- Квадратичные формы. Основная теорема.
- Конгруэнтные и эквивалентные билинейные формы. Приведение симметрических билинейных форм к каноническому виду. Связь матриц конгруэнтных и эквивалентных билинейных форм.
- Закон инерции.
- Распадающиеся квадратичные формы.
- Свойства положительно определенных квадратичных форм.
- Критерий Сильвестра.
Модуль 2. Полиномиальные матрицы.
- Теорема о существовании канонической
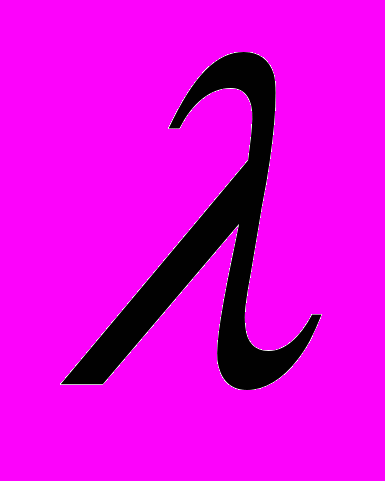 -матрицы.
-матрицы.
- Теорема о единственности канонической матрицы.
- Унимодулярные матрицы и их свойства.
- 2-ой критерий эквивалентности
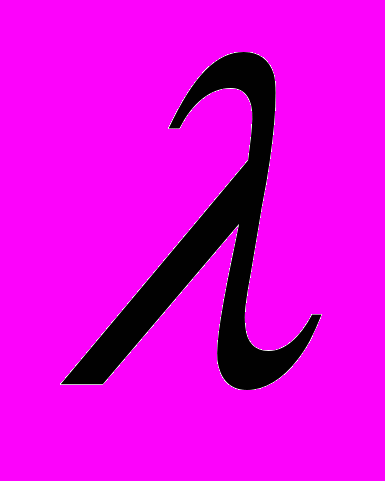 -матриц. Подобие матриц, свойства подобных матриц.
-матриц. Подобие матриц, свойства подобных матриц.
- Основная теорема о подобии матриц.
- Жорданова нормальная форма. Теорема о приведении матрицы к жордановой нормальной форме.
Модуль 3. Векторные пространства.
Линейные пространства
- Определение n-мерного векторного пространства. Линейная зависимость векторов. Основная теорема. Утверждения об эквивалентных системах векторов.
- Определение линейного пространства. Конечномерные линейные пространства. Теорема о том, что все базы конечномерного линейного пространства состоят из одинакового количества векторов.
- Теорема о том, что любую линейно независимую систему векторов можно дополнить до базы всего пространства.
- Изоморфизм линейных пространств. Свойства.
- Теорема о том, что каждый вектор пространства единственным образом представляется как линейная комбинация векторов базиса.
- Невырожденность матрицы перехода. Связь координат одного и того же вектора в разных базах.
- Пересечение и сумма линейных подпространств. Теорема о размерности суммы двух подпространств.
- Прямая сумма подпространств. Теорема о прямых суммах подпространств.
Линейные преобразования линейных пространств
- Определение линейного преобразования. Действия над линейными преобразованиями.
- Матрица линейного преобразования. Формула для нахождения координат образа вектора при линейном преобразовании.
- Связь между матрицами линейного преобразования в разных базах.
- Теорема о существовании и единственности линейного преобразования, переводящего линейно независимые векторы в произвольные.
- Область значений и ядро линейного преобразования. Теоремы об их размерностях.
- Теорема о том, что образы и прообразы линейных пространств снова являются линейными пространствами.
- Неособенные линейные преобразования. Необходимое и достаточное условие для того, чтобы линейное преобразование было неособенным.
- Ранг линейного преобразования. Теорема о ранге произвольного линейного преобразования.
- Инвариантные подпространства. Теорема о том, что ядро и область значений линейного преобразования являются инвариантными подпространствами относительно любого линейного преобразования.
- Теорема о прямой сумме инвариантных подпространств.
- Собственные векторы и собственные значения линейного преобразования. Теорема о том, что собственными значениями линейного преобразования служат действительные характеристические корни линейного преобразования и только они.
- Спектр. Теорема о матрице линейного преобразования в базе, состоящей из собственных векторов.
- Простой спектр. Диагональный вид матрицы линейного преобразования с простым спектром.
- Теорема о том, что характеристический многочлен любого линейного преобразования не зависит от выбора базиса.
Модуль 4. Евклидовы и унитарные векторные пространства.
- Аксиоматическое определение евклидова пространства. Теорема о превращении любого линейного пространства в евклидово.
- Неравенство Коши – Буняковского. Длина и угол между векторами.
- Ортогональная система векторов. Процесс ортогонализации.
- Теорема о том, что всякое евклидово пространство обладает ортогональными базами.
- Ортонормированная система векторов. Теорема о том, что всякое евклидово пространство обладает ортонормированными базами.
- Необходимое и достаточное условие для того, чтобы база евклидова пространства была ортонормированной.
- Теорема о том, что всякая ортогональная система ненулевых векторов является линейно независимой.
- Ортогональное дополнение. Теорема о представлении евклидова пространства в виде прямой суммы подпространства L и его ортогонального дополнения.
- Ортогональная проекция вектора на подпространство и ортогональная составляющая вектора относительно подпространства.
- Изоморфизм евклидовых подпространств. Теорема.
- Ортогональные матрицы. Свойства ортогональных матриц.
- Необходимое и достаточное условие для того, чтобы матрица была ортогональной.
- Теорема о матрице перехода от ортонормированной базы евклидова пространства к любой другой его ортонормированной базе.
- Ортогональные преобразования евклидовых пространств. Свойства ортогональных преобразований утверждения о них.
- Симметрические преобразования евклидовых пространств. Свойства симметрических преобразований и утверждения о них.
- Теорема о характеристических корнях симметрического преобразования.
- Необходимое и достаточное условие для того, чтобы линейное преобразование евклидова пространства было симметрическим.
- Теорема о существовании ортогональной матрицы, приводящей симметрическую матрицу к диагональному виду.
- Теорема о приведении действительной квадратичной формы к главным осям.
- Теорема о коэффициентах канонического вида квадратичной формы, к которому она приводится с помощью ортогонального преобразования.
- Теорема о собственных векторах симметрического преобразования, относящихся к различным собственным значениям.
- Пары форм. Теорема о существовании невырожденного линейного преобразования, одновременно приводящего действительную положительно определенную квадратичную форму g к нормальному виду и произвольную действительную квадратичную форму f – к каноническому виду.
