Geum.ru

М. К. Аммосова Институт математики и информатики рабочая программа

Вид материалаРабочая программа

Содержание


Распределение часов по видам занятий
Принципы и цели
Примерные варианты зачетной контрольной работы
Х(w) - случайная величина, заданная на вероятностном пространстве (W,Á,P). Доказать, что функция 5½Х
Подобный материал:
Якутский государственный университет им. М.К. Аммосова
Институт математики и информатики



РАБОЧАЯ ПРОГРАММА


специального курса

«Дополнительные главы теории вероятностей»

специализации

«Математическое моделирование (стохастических процессов)»

направления

510200 – Прикладная математика


Якутск 2004




Составитель: Мынбаева Г.У., к.ф.-м.н., доцент кафедры высшей математики ИМИ


1. ВЫПИСКА ИЗ УЧЕБНОГО ПЛАНА


Объем работы студента (в часах) из учебного плана направления 510200 – Прикладная математика составляет часов.

Распределение часов по видам занятий


Виды занятий
5 семестр (18 недель)

Лекционные
18

Практические
18

Индивидуальные
-

Самостоятельная работа



Всего



Форма контроля
зачет




  1. ПРИНЦИПЫ И ЦЕЛИ



    1. Принципы построения программы
  • курс имеет как теоретическую, так и практическую направленность (50% аудиторных занятий – лекции, 50% – практические занятия);
  • курс предполагает изложение теоретического материала на основе аксиоматики Колмогорова; введение основных понятий курса сопровождается примерами и краткими историческими справками.



    1. Цели курса

Целями курса являются:
  • повторение основных понятий теории множеств и теории мер;
  • углубленное изучение таких разделов теории вероятностей как аксиоматика Колмогорова, случайная величина, функция одной случайной величины, случайный вектор, распределение суммы, произведения и частного двух случайных величин, характеристическая функция.


Примерные варианты зачетной контрольной работы:


Вариант 1.

1. Вероятностное пространство (W,Á,P) представляет собой отрезок [0;1] с s-алгеброй борелевских подмножеств и мерой Лебега. Описать s-алгебру, порожденную случайной величиной Х, если X=.

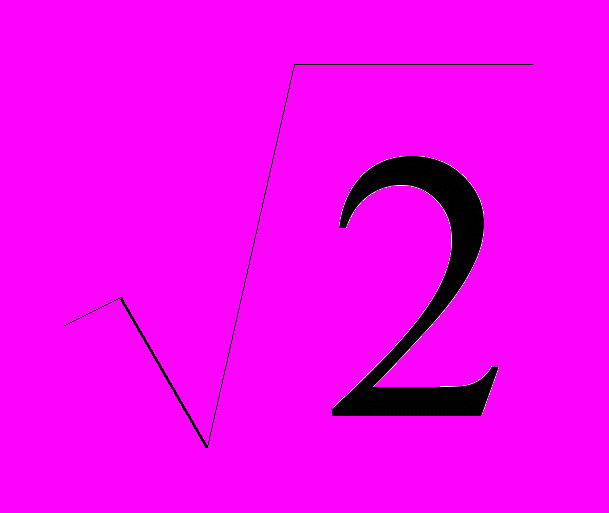2. Пусть Х(w) - случайная величина, заданная на вероятностном пространстве (W,Á,P). Доказать, что функция 5½Х(w)½+4 будет случайной величиной.

3. Независимые случайные величины Х и Y имеют распределение с плотностью 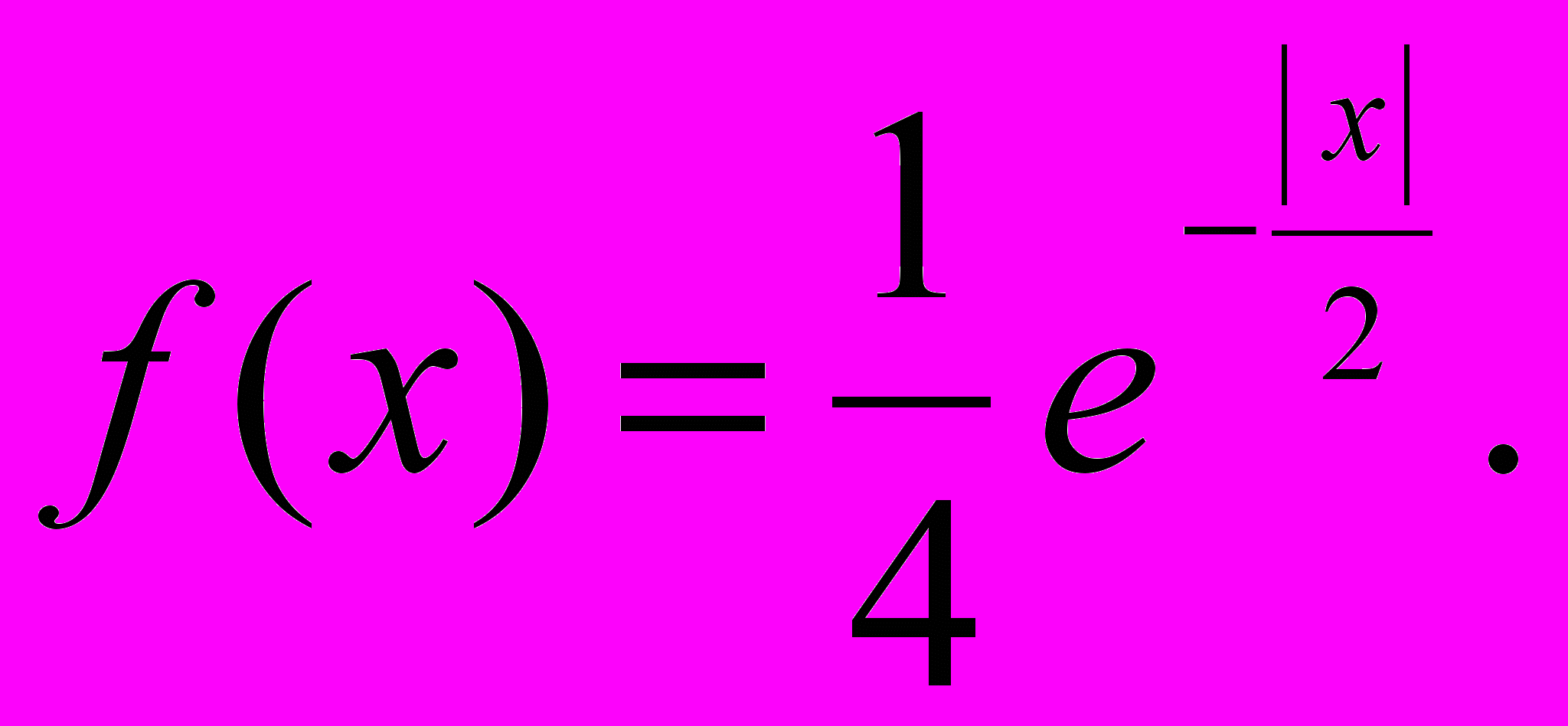Найти плотность распределения случайной величины X+Y.

Вариант 2.

1. Пусть Х(w) - случайная величина, заданная на вероятностном пространстве (W,Á,P). Доказать, что множество {w: x1 £ X(w) £ x2}, xiÎR, является случайным событием.

2. Вероятностное пространство (W,Á,P) представляет собой отрезок [0;1] с s-алгеброй борелевских подмножеств и мерой Лебега. Описать s-алгебру, порожденную случайной величиной Х, если



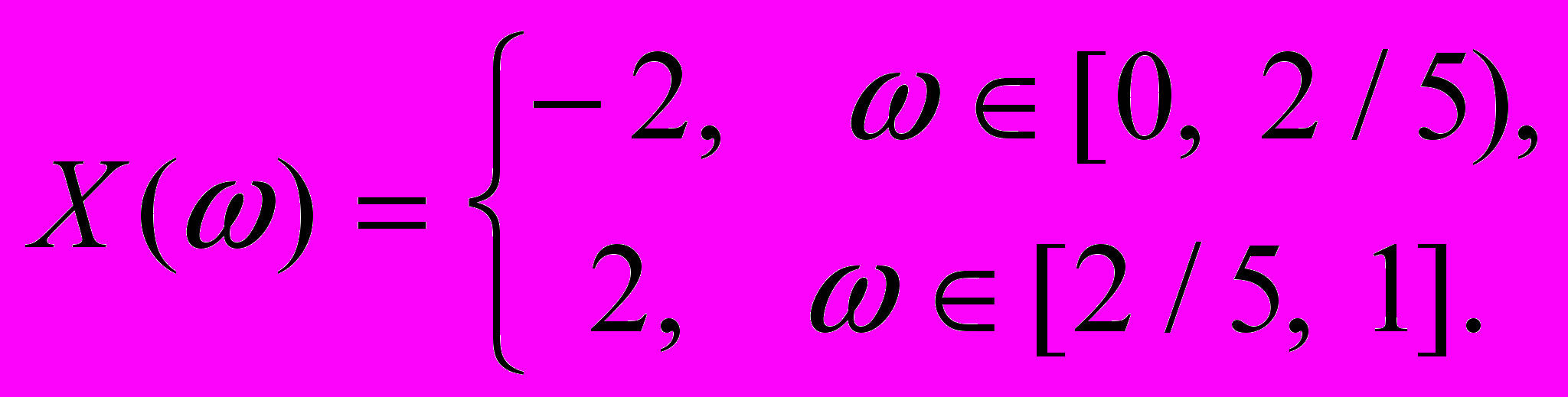
3. Независимые случайные величины Х и Y имеют распределение Коши с параметрами (m;а)=(1;1):

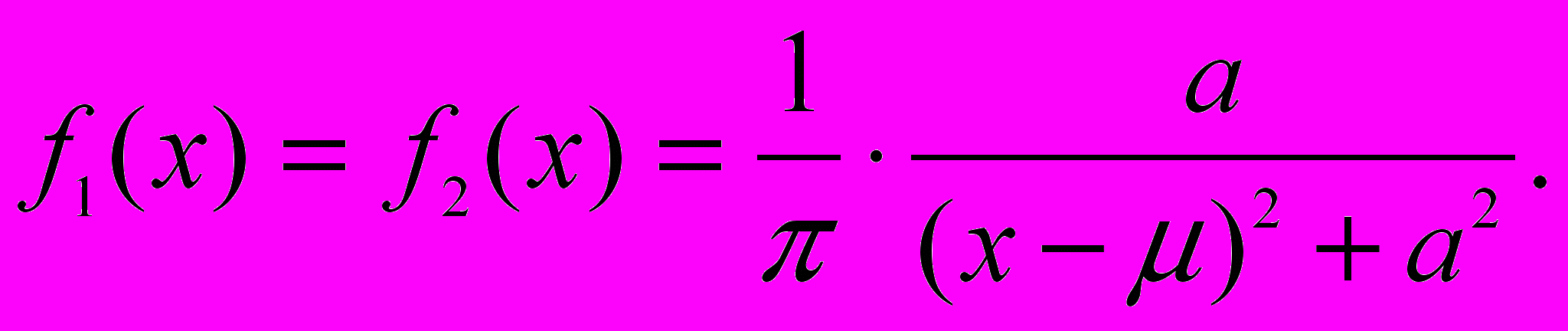
Доказать, что случайная величина X+Y имеет распределение Коши с параметрами (2;2).


Основная литература


  1. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1999.
  2. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика.- Киев: Выща школа, 1988.
  3. Вентцель Е.С. Теория вероятностей. – М.: Высшая школа, 1999.
  4. Печинкин А.В., Тескин О.И., Цветкова Г.М. Теория вероятностей.- М.: Изд-во МГТУ им Н.Э.Баумана, 2001 г.
  5. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. Под ред. Свешникова А.А.- М.: Наука, 1970.
  6. Прохоров А.В., Ушаков В.Г, Ушаков Н.Г. Задачи по теории вероятностей. Основные понятия, предельные теоремы, случайные процессы. – М.: Наука, 1986.