М. К. Аммосова институт математики и информатики рабочая программа

Вид материала

Рабочая программа

Содержание Рабочая программа утверждена на заседании кафедры алгебры и геометрии Выписка из учебного плана (ОПД.Ф.02) Распределение часов по семестрам Недельная нагрузка по семестрам Требования к обязательному минимуму содержания Дисциплина - алгебра 3. Принципы и цели 3.2. Цели курса Р многочлена, правильной рациональной и простейшей в поле Р 7. Рекомендуемая литература 8. Контролирующие материалы Модуль 3. Определители n-го порядка. Модуль 4. Комплексные числа Модуль 5. Матрицы и системы линейных уравнений

Подобный материал:

• М. К. Аммосова Институт математики и информатики рабочая программа, 31.65kb.
• М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 219.2kb.
• М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 460.29kb.
• М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 247.89kb.
• М. К. Аммосова Институт математики и информатики Кафедра математической экономики рабочая, 71.2kb.
• М. К. Аммосова Институт математики и информатики Кафедра информатики и вычислительного, 59.79kb.
• М. К. Аммосова институт математики и информатики рабочая программа, 100.1kb.
• М. К. Аммосова институт математики и информатики рабочая программа, 98.66kb.
• М. К. Аммосова институт математики и информатики рабочая программа, 190.99kb.
• М. К. Аммосова институт математики и информатики рабочая программа, 78.16kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ЯКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМ. М.К. АММОСОВА

ИНСТИТУТ МАТЕМАТИКИ И ИНФОРМАТИКИ

РАБОЧАЯ ПРОГРАММА

курса

«Алгебра »

(наименование курса)


Для государственных университетов

Направление 510100 – Математика

(шифр, название)


Степень – бакалавр математики


Якутск 2003


Составители: доцент Гурзо Г.Г.,

ассистент Иванова А.О.,

старший преподаватель Антонен А.И.

(уч. ст., уч. зв., должн., ФИО)

Рабочая программа утверждена на заседании кафедры алгебры и геометрии

“ “ _________________ 2003 г. протокол № _____

Зав. кафедрой: Никитина Е.С.

Рабочая программа утверждена на заседании методкомиссии ИМиИ

“ “ _________________ 2003 г. протокол № _____

Председатель методкомиссии ИМиИ: Афанасьева В.И.

Рабочая программа утверждена на заседании научно – методического совета ЯГУ

“ “ _________________ 2003 г. протокол № _____

Председатель научно – методического совета ЯГУ: Яковлева А.Н.


Выписка из учебного плана (ОПД.Ф.02)


Объем работы студентов (в часах) из учебного плана направления 510100 – Математика составляет 250 часов, в том числе:

– аудиторных занятий – 162;

– СРС – 88.

Распределение часов по семестрам

Вид занятий	Семестры		Всего
	I (18 нед.)	IV (18 нед.)
Аудиторные	90	72	162
Лекционные	36	36	72
Лабораторные	54	36	90
СРС	44	44	88
Итого	134	116	250
Форма контроля	Экзамен	Экзамен

Недельная нагрузка по семестрам

Вид занятий	Семестры
	I	IV
Аудиторные	5	4
Лекционные	2	2
Лабораторные	3	2

1. ТРЕБОВАНИЯ К ОБЯЗАТЕЛЬНОМУ МИНИМУМУ СОДЕРЖАНИЯ
   

ОСНОВНОЙ ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ ПОДГОТОВКИ БАКАЛАВРА МАТЕМАТИКИ ПО СПЕЦИАЛЬНОСТИ 510100 - Математика

ДИСЦИПЛИНА - АЛГЕБРА


Понятие группы, кольца и поля; поле комплексных чисел; кольцо многочленов; деление многочленов с остатком; теорема Безу; кратность корня многочлена, ее связь со значениями производных; разложение многочлена на неприводимые множители над полями комплексных и действительных чисел; формулы Виета; наибольший общий делитель многочленов, его нахождение с помощью алгоритма Евклида; кольцо многочленов от нескольких переменных; симметрические многочлены. Группа подстановок; четность подстановки; циклические группы; разложение группы на смежные классы по подгруппе; теорема Лагранжа. Системы линейных уравнений; свойства линейной зависимости; ранг матрицы; определители, их свойства и применение к исследованию и решению систем линейных уравнений; кольцо матриц и группа невырожденных матриц. Векторные пространства; базис и размерность; подпространства; сумма и пересечение подпространств; прямые суммы; билинейные и квадратичные формы; приведение квадратичной формы к нормальному виду; закон инерции; положительно определенные квадратичные формы; критерий Сильвестра; ортонормированные базисы и ортогональные дополнения; определители Грамма и объем параллелепипеда. Линейные операторы; собственные векторы и собственные значения; достаточные условия приводимости матрицы линейного оператора к диагональному виду; понятие о жордановой нормальной форме; самосопряженные и ортогональные (унитарные) операторы; приведение квадратичной формы в евклидовом пространстве к каноническому виду. Аффинные системы координат; линейные многообразия, их взаимное расположение; квадрики (гиперповерхности второго порядка); их аффинная и метрическая классификация и геометрические свойства; Примеры групп преобразований: классические линейные группы, группа движений и группа аффинных преобразований, группы симметрии правильных многоугольников и многогранников в трехмерном пространстве; классификация движений плоскости и трехмерного пространства.


2. ТРЕБОВАНИЯ СТАНДАРТА К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКА ПО СПЕЦИАЛЬНОСТИ 510100 – Математика


Бакалавр математики отвечает следующим требованиям:

1. Имеет целостное представление о процессах и явлениях, происходящих в неживой и живой природе, понимает возможности современных научных методов познания природы и владеет ими на уровне, необходимом для решения задач, имеющих естественнонаучное содержание и возникающих при выполнении профессиональных функций;
   
2. Способен продолжить обучение в магистратуре и по специальности, в соответствии с п.1.3., вести профессиональную деятельность в иноязычной среде (требование рассчитано на реализацию в полном объеме через 10 лет);
   
3. Владеет культурой мышления, знает его общие законы, способен в письменной и устной речи правильно (логически) оформить его результаты;
   
4. Умеет на научной основе организовать свой труд, владеет компьютерными методами сбора, хранения и обработки (редактирования) информации, применяемые в сфере его профессиональной деятельности;
   
5. Способен в условиях развития науки и изменяющейся социальной практики к переоценке накопленного опыта, анализу своих возможностей, умеет приобретать новые знания, обучаться в магистратуре, использовать другие формы обучения, включая самостоятельные и информационно образовательные технологии;
   
6. Понимает сущность и социальную значимость своей будущей профессии, основные проблемы дисциплин, определяющих конкретную область его деятельности, видит их взаимосвязь в целостной системе знаний;
   
7. Способен к проектной деятельности в профессиональной сфере на основе системного подхода, умеет строить и использовать модели для описания и прогнозирования различных явлений, осуществлять их качественный и количественный анализ;
   
8. Способен поставить цель и сформулировать задачи, связанные с реализацией профессиональных функций, умеет использовать для их решения методы изученных им наук;
   
9. Готов к кооперации с коллегами и работе в коллективе, знаком с методами управления, умеет организовать работу исполнителей, находить и принимать управленческие решения в условиях различных мнений, знает основы педагогической деятельности;
   
10. Методически и психологически готов к изменению вида и характера своей профессиональной деятельности, работе над междисциплинарными проектами;
    
11. Способен к совершенствованию своей профессиональной деятельности в области математики.
    

3. ПРИНЦИПЫ И ЦЕЛИ


3.1. Принципы построения курса


3.1.1. Данный курс разработан в соответствии с Государственным образовательным стандартом высшего профессионального образования по специальности 510100 – Математика;

3.1.2. В рабочей программе выделяется ядро курса (матрицы и системы линейных уравнений, многочлены от одного неизвестного);

3.1.3. Курс имеет практическую направленность: лабораторные – 90 ч., самостоятельная работа – 88 ч.;

3.1.4. Программа предполагает индуктивное построение курса;


3.2. Цели курса

№	Содержание
Студент должен иметь представление о
	Декартовом произведении множеств; n–ой декартовой степени множества; n–арной операции определенной на множестве А со значением во множестве В; универсальных алгебрах и подалгебрах, группоидах, квазигруппах, лупах; отображениях алгебр, об изоморфизме, гомоморфизме, эндоморфизме, автоморфизме.
	О том, что корни n–ой степени из единицы образуют группу относительно операции умножения; первообразных корнях и их свойствах.
	Равенстве строчного и столбцового ранга; главных и свободных неизвестных системы; основной теореме теории систем линейных уравнений (про главные неизвестные); аддитивной группе матриц, о мультипликативной группе невырожденных матриц, о кольце квадратных матриц; представлении любой невырожденной квадратной матрицы в виде произведения элементарных матриц.
Студент должен знать
	Понятие отображения множества А во множество В, определение сюръективного, инъективного, биективного отображений, произведения отображений, необходимое и достаточное условия существования произведения отображений, обратного отображения; теорему об ассоциативности произведения отображений. Определение полугруппы, группы, кольца, поля.
	Определение перестановки, подстановки, инверсии, четной, нечетной перестановки, декремента, транспозиции; доказательства теорем о транспозициях, о декременте.
	Формулу Муавра, формулу извлечения корней n–ой степени из комплексного числа, записанного в тригонометрической форме.
	Определение определителя, минора, дополнительного минора, алгебраического дополнения, условия равенства нулю определителя; свойства определителя; теоремы о разложении определителя по элементам строки, теорему Лапласа, следствие из теоремы Лапласа.
	Определение ранга матрицы, основные типы элементарных преобразований, элементарных матриц, связь элементарных преобразований с умножением на элементарные матрицы. Матричную форму записи системы линейных уравнений, равносильные системы уравнений. Знать необходимые и достаточные условия, совместности и определенности системы линейных уравнений, свойства произведения матриц (ассоциативность, коммутативность). Доказательство теоремы Кронекера–Капели, теоремы о существовании и единственности обратной матрицы, о ранге и об определителе произведения матриц
	Определение корня многочлена, неприводимого в поле Р многочлена, правильной рациональной и простейшей в поле Р дроби. Формулировку теоремы о выражении НОД через исходные многочлены, следствие из нее о взаимно простых многочленах, основной теории алгебры и ее следствие, связь коэффициентов многочлена с его корнями, доказательство теоремы алгоритм деления с остатком, доказательство того, что последний остаток отличный от нуля в алгоритме Евклида есть НОД многочленов 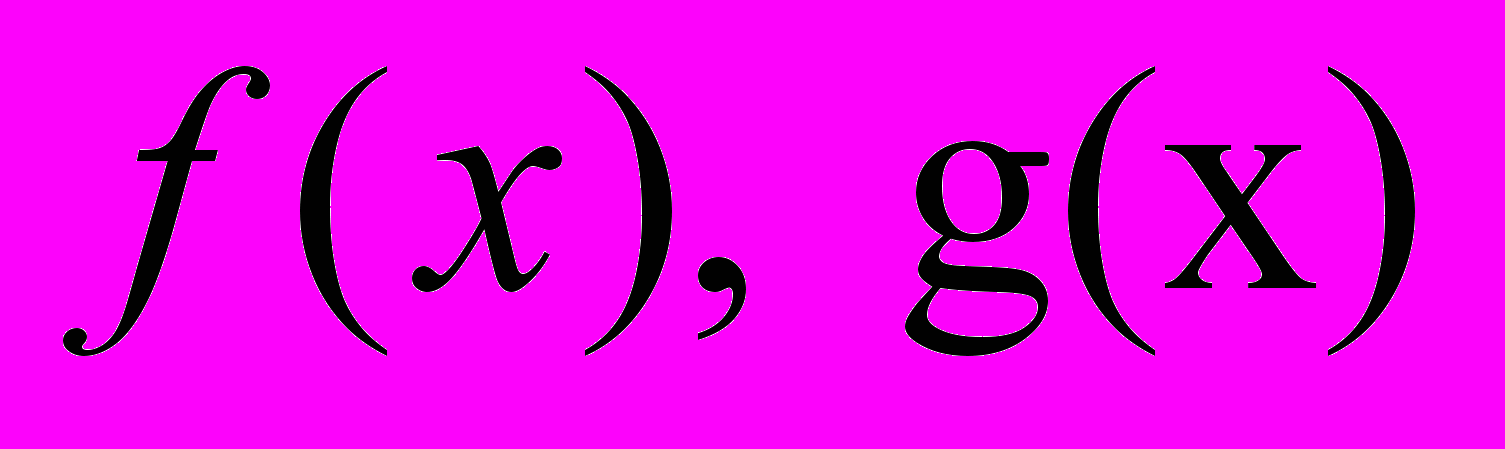, теоремы Безу и ее следствия, теоремы о рациональных корнях целочисленных многочленов, о выражении симметрического многочлена через элементарные симметрические многочлены.
	Определение циклической группы, подгруппы, нормальной подгруппы, классов смежности, фактор – группы, группы подстановок, коммутатора, коммутанта, центра группы, нормализатора элемента классической линейной группы, группы движений, группы симметрий правильных многоугольников и многогранников в 3–х мерном пространстве; доказательство теорем Лагранжа, Кэли.
Студент должен уметь
	Определять вид отображения одного множества в другое; определять вид алгебры по множеству с совокупностью определенных на нем операций.
	Определять четность перестановки и подстановки, разлагать подстановку в произведение независимых циклов и в произведение транспозиций, решать уравнения вида АХ=В, ХА=В, АХВ=С в подстановках; вычислять определители 2, 3, 4 … порядков, вычислять определители треугольных матриц, вычислять определители сведением их к треугольному виду, методом рекуррентных соотношений, вычислять определитель Вандермонда. Решать системы по правилу Крамера.
	Представлять комплексное число в тригонометрической форме, выполнять действия сложения, вычитания, умножения, деления, извлечения корня квадратного для комплексных чисел, записанных в алгебраической форме, т.е. в виде a+i*b; выполнять действия умножения, деления, возведения в степень, извлечения корня n–ой степени для комплексных чисел, записанных в тригонометрической форме.
	Вычислять ранг матрицы с помощью окаймляющих миноров и приведением к ступенчатому виду, исследовать системы линейных уравнений на совместность; решать системы линейных уравнений, находить фундаментальную систему решений у однородной системы линейных уравнений; находить обратную матрицу с помощью формулы и с помощью элементарных преобразований, решать матричные уравнения типа АХВ=С.
	Находить НОД двух и более многочленов; многочлены U(x) и V(x), такие что f(x) U(x)+g(x) V(x)=d(x); находить рациональные корни целочисленных многочленов; выражать симметрические многочлены через элементарные; определять число действительных корней многочлена; представлять рациональную дробь в виде суммы простейших.
	Определять порядок элемента группы, порядок класса сопряженности. Разлагать группу на классы смежности, находить подгруппы, строить фактор – группы, определять число абелевых групп указанного порядка с точностью до изоморфизма. Находить группу подстановок, изоморфную данной конечной группе.

7. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Глухов М.М, Солодовников А.С. Задачник–практикум по высшей алгебре. М.: МГЗПИ, 1969 *
   
2. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп *
   
3. Кострикин А.И. Введение в алгебру. – М.: Наука, 1977 *
   
4. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1968 *
   
5. Проскуряков И.В. Сборник задач по линейной алгебре. – М.: Наука, 1970 *
   
6. Скорняков Л.А. Элементы алгебры. – М.: Наука, 1986 *
   
7. Фадеев Д.К, Соминский И.С. Сборник задач по высшей алгебре. *
   
8. Петрова В.Т. Лекции по алгебре и геометрии. – М., 1999
   
9. Гурзо Г.Г. Индивидуальные задания по теме "Универсальные алгебры". – Якутск, 1991
   
10. Гурзо Г.Г. Индивидуальные задания по теме "Многочлены". – Якутск, 1994
    
11. Гурзо Г.Г., Бочарова И.Н. Лабораторные задания по теме "Матрицы и системы линейных уравнений". – Якутск, 1994
    
12. Гурзо Г.Г., Бочарова И.Н. Перестановки и подстановки. – Якутск, 1999
    
13. Иванова А.О., Антонен А.И., Бочарова И.Н., Гурзо Г.Г., Неустроева Т.К. Сборник задач для проведения контрольных работ по курсу высшей алгебры находится в печати типографии ЯГУ, 1999
    
14. Гурзо Г.Г., Иванова А.О., Неустроева Т.К. Определители (индивидуальные задания) находится в печати типографии ЯГУ, 2000 и в электронной библиотеке СИТИМ в виде pdf-файлов
    
15. Иванова А.О., Неустроева Т.К., Гурзо Г.Г., Бочарова И.Н. Методические указания и контрольные задания по алгебре и теории чисел находится в печати типографии ЯГУ, 2000 и в электронной библиотеке СИТИМ в виде pdf-файлов
    
16. Гурзо Г.Г., Иванова А.О. Комплексные числа (индивидуальные задания) находится в печати типографии ЯГУ, 2000 и в электронной библиотеке СИТИМ в виде pdf-файлов
    
17. Антонен А.И., Бочарова И.Н., Дмитриев И.Г., Гурзо Г.Г., Иванова А.О., Неустроева Т.К. «Электронное учебное пособие «Алгебра» Электронная библиотека «Ситим»; Якутск 2001
    
18. Антонен А.И., Бочарова И.Н., Дмитриев И.Г., Гурзо Г.Г., Иванова А.О., Неустроева Т.К. «Методические указания для студентов заочного отделения 1 курса МПО Электронная библиотека «Ситим» (http://www.sitim.sitc.ru), Якутск 2002
    

Примечание: * отмечена основная литература.


8. КОНТРОЛИРУЮЩИЕ МАТЕРИАЛЫ

Экзаменационные вопросы.

I семестр

1. Отображения множеств. Виды отображений. Произведение отображений. Ассоциативность произведения отображений. Существование обратных отображений. Некоммутативность произведения отображений.
   
2. Понятие о n–арной операции, об универсальных алгебрах. Группоиды, полугруппы, квазигруппы, лупы, группы, кольца, поля. Примеры указанных алгебр. Подалгебры. Примеры конечных и бесконечных алгебр. Конечные и бесконечные поля. Бесконечность множества числовых полей.
   
3. Доказать, что подстановки из n символов образуют группу относительно умножения.
   
4. Группы корней n–ой степени из единицы.
   
5. Кольца и группы вычетов.
   
6. Поле комплексных чисел. Действия над комплексными числами в алгебраической и тригонометрической формах. Формула Муавра. Корни n–ой степени из единицы.
   
7. Теоремы о подстановках и перестановках (весь 3 параграф).
   
8. Матрицы и их элементарные преобразования. Ступенчатая матрица. Теорема о том, что каждую матрицу конечным числом элементарных преобразований строк можно привести к ступенчатому виду.
   
9. Эквивалентные системы линейных уравнений. Теорема о том, что если от расширенной матрицы одной системы можно перейти к расширенной матрице другой системы с помощью конечного числа элементарных преобразований строк, то соответствующие системы линейных уравнений эквивалентны.
   
10. Определитель n–го порядка и его свойства.
    
11. Теорема о произведении минора на его алгебраическое дополнение.
    
12. Теорема о разложении определителя по элементам некоторой строки.
    
13. Теорема Лапласа.
    
14. Теорема об определителе матрицы с нулями в правом верхнем углу.
    
15. Определитель Вандермонда.
    
16. Вычисление определителей методом рекуррентных соотношений.
    
17. Определитель треугольной матрицы.
    
18. Ранг матрицы. Теорема о ранге ступенчатой матрицы. Теорема о неизменности ранга матрицы при транспонировании, при элементарных преобразованиях.
    
19. Теорема Кронекера – Капелли.
    
20. Теорема о необходимом и достаточном условии, чтобы совместная система от n неизвестных имела единственное решение.
    
21. Действия над матрицами, ассоциативность умножения матриц. (АВ)=ВА.
    
22. Главные и свободные неизвестные. Основная теорема теории систем линейных уравнений.
    
23. Диагональные матрицы, умножение произвольной матрицы на диагональную. Связь элементарных преобразований над матрицей с умножением на элементарные матрицы.
    
24. Теорема о ранге произведения матриц.
    
25. Теорема об определителе произведения матриц.
    
26. Обратная матрица. Теорема о существовании и единственности обратной матрицы. Два способа нахождения обратной матрицы.
    
27. Правило Крамера.
    
28. Многочлены n-ой степени от одного неизвестного, действия над многочленами. Кольцо многочленов.
    
29. Теорема. Алгоритм деления с остатком.
    
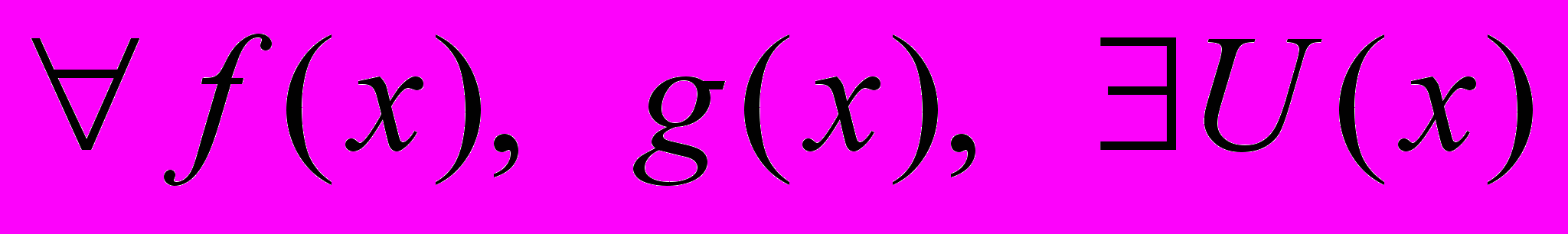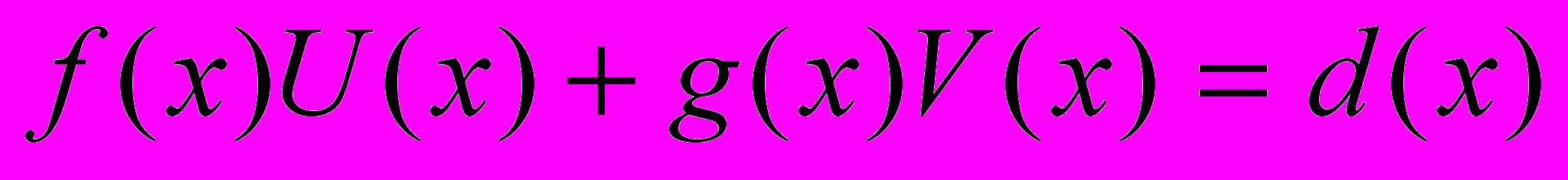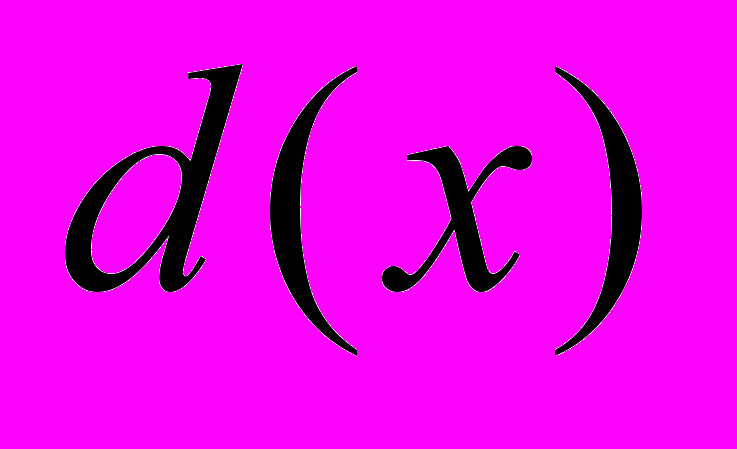30. НОД двух и нескольких многочленов. Алгоритм Евклида. Теорема о том, что такие, что , где =НОД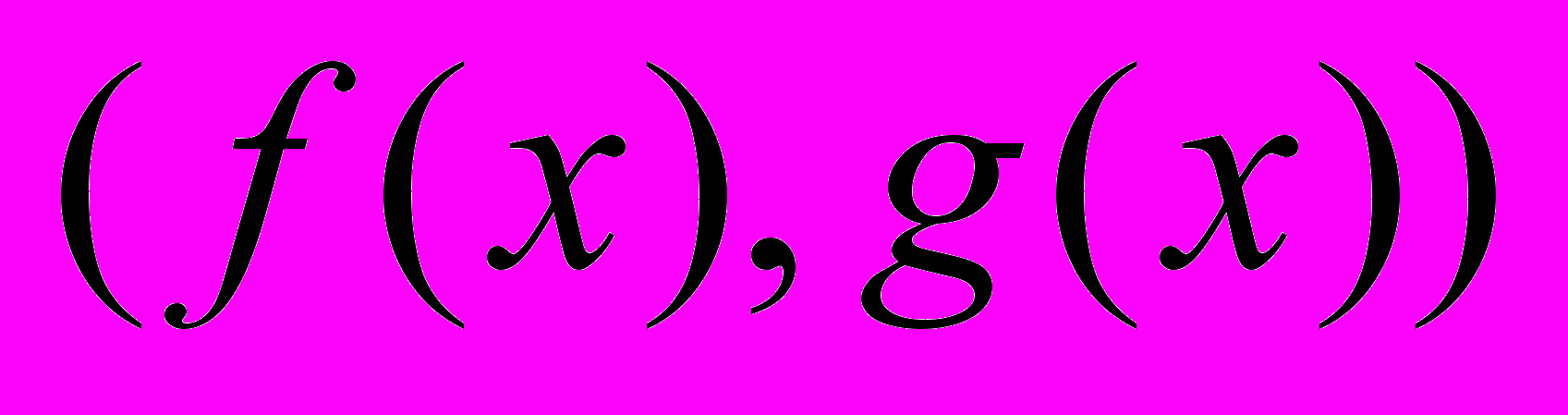. Ее следствия.
    
31. Корни многочленов. Схема Горнера. Теорема Безу и ее следствия.
    
32. Кратные корни. Теорема о понижении кратности корня при дифференцировании.
    
33. Основная теорема алгебры (без доказательства) и ее следствия.
    
34. Теоремы о рациональных корнях целочисленных многочленов.
    
35. Приводимость многочленов над полем P. Критерий Эйзенштейна.
    
36. Разложение многочлена на неприводимые множители.
    
37. Рациональные дроби. Простейшие дроби. Теорема о разложении правильной рациональной дроби в сумму простейших. Теорема единственности.
    
38. Кольцо симметрических многочленов. Основная теорема теории симметрических многочленов. Теорема единственности.
    

Экзаменационные вопросы.

IV семестр.

1. Истоки развития групп.
   
2. Определения группы. Их равносильность. Примеры.
   
3. Отображения групп. Изоморфизм групп. Примеры. Неизоморфизм аддитивной группы рациональных чисел и мультипликативной группы положительных рациональных чисел.
   
4. Возведение в целую степень элементов группы. Порядок элемента. Утверждения о нем.
   
5. Понятие подгруппы. Примеры. Критерий определения подгрупп. Утверждения о подгруппах.
   

6. Порождающие множества в группах. Примеры.
   
7. Теорема Кэли. Таблица Кэли для групп. Свойства расположения элементов группы в этой таблице. Примеры.
   
8. Циклические подгруппы и группы. Теорема о подгруппах циклических групп, ее необратимость.
   
9. Смежные классы по подгруппе. Свойства. Индекс подгруппы в группе.
   
10. Теорема Лагранжа, её следствия. Необратимость утверждения о порядках подгрупп.
    
11. Инвариантные подгруппы. Примеры. Инвариантность подгрупп индекса 2.
    
12. Фактор – группа по инвариантной подгруппе. Примеры.
    
13. Классы сопряженных элементов. Свойства. Теорема об инвариантных подгруппах.
    
14. Гомоморфизмы групп. Свойства гомоморфизма. Теорема о ядре гомоморфизма. Гомоморфизм группы на фактор – группу. Естественный гомоморфизм. Теорема о гомоморфизмах.
    
15. Нормализатор элемента. Теорема о порядке класса сопряженности. Примеры применения данной теоремы в практических задачах.
    
16. Центр группы. Свойства. Примеры. Теорема о группах с нетривиальным центром.
    
17. Коммутатор пары элементов и его свойства. Строение коммутанта. Инвариантность коммутанта. Утверждение о коммутанте абелевых групп. Примеры совпадения группы и её коммутанта.
    
18. Теорема Галуа о простоте группы A₅. Следствия. Неразрешимые группы и неразрешимость уравнения в радикалах.
    
19. Декартово произведение групп. Утверждения о них. Критерий разложимости группы в произведение групп меньшего порядка.
    
20. Конечные абелевы группы. Теорема о цикличности или разложимости абелевых p–групп. Основная теорема об абелевых группах. Подсчет числа попарно неизоморфных абелевых групп данного порядка.
    
21. Группы симметрий правильных многогранников.
    

Вопросы коллоквиумов

Модуль 2. Перестановки и подстановки

1. Теорема о числе различных перестановок из n символов.
   
2. Теорема о транспозиции в перестановке.
   
3. Теорема о расположении всех n! Перестановок из n символов.
   
4. Теорема о разложении подстановки в произведение транспозиций.
   
5. Теорема о декременте подстановки.
   

Модуль 3. Определители n-го порядка.

1. Метод рекуррентных соотношений.
   
2. Определитель Вандермонда.
   
3. Теорема Лапласа.
   
4. Теорема об определителе матрицы с нулями в правом верхнем углу.
   
5. Теорема о произведении минора на его алгебраическое дополнение.
   
6. Теорема о разложении определителя по элементам некоторой его строки.
   
7. Свойства определителя n-го порядка.
   

Модуль 4. Комплексные числа

1. Вывод формул умножения и деления комплексных чисел, записанных в тригонометрической форме.
   
2. Две теоремы о первообразных корнях n-ой степени из единицы.
   
3. Вывод формулы Муавра.
   
4. Вывод формулы для извлечения корня n-ой степени из комплексного числа.
   
5. Доказать, что корни n-ой степени из единицы образуют группу относительно операции умножения.
   

Модуль 5. Матрицы и системы линейных уравнений

1. Теорема о том, что если от матрицы А можно перейти к матрице В с помощью конечного числа элементарных преобразований строк, то соответствующие системы линейных уравнений эквивалентны.
   
2. Теорема о том, что любую матрицу можно привести к ступенчатому виду с помощью конечного числа элементарных преобразований строк.
   
3. Теорема о ранге ступенчатой матрицы.
   
4. Теорема о неизменности ранга матрицы при а) транспонировании; б) при выполнении конечного числа элементарных преобразований строк.
   
5. Необходимое и достаточное условие для того, чтобы совместная система линейных уравнений была определенной.
   
6. Теорема Кронекера – Капелли.
   
7. Доказать: а) ассоциативность умножения матриц; б) (А_*В)’=В’_*А’.
   
8. Основная теорема теории систем линейных уравнений.
   
9. Теорема о ранге произведения матриц.
   
10. Теорема о существовании и единственности обратной матрицы.
    
11. Вывод формулы для нахождения обратной матрицы.
    
12. Связь элементарных преобразований с умножением на элементарные матрицы.
    
13. Определитель произведения матриц.
    
14. Правило Крамера.
    

Модуль 6. Многочлены от одного неизвестного.

1. Многочлены n-ой степени от одного неизвестного, действия над многочленами. Кольцо многочленов.
   
2. Теорема. Алгоритм деления с остатком.
   
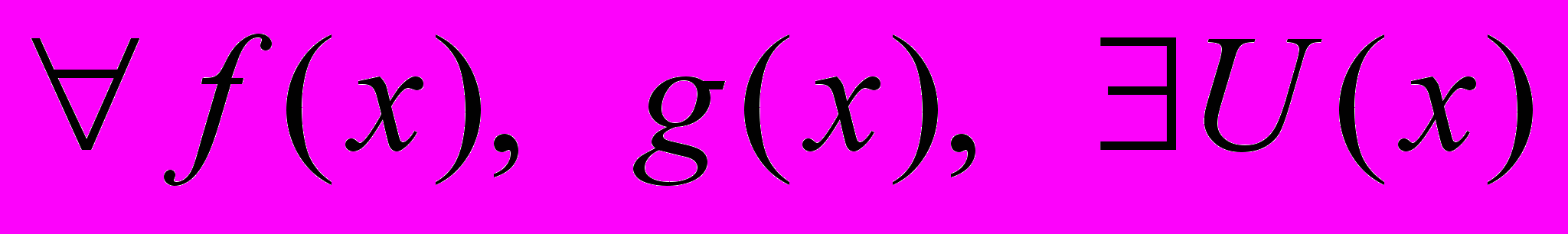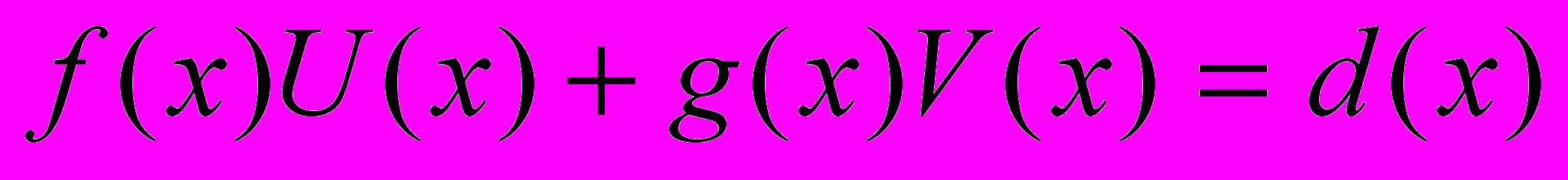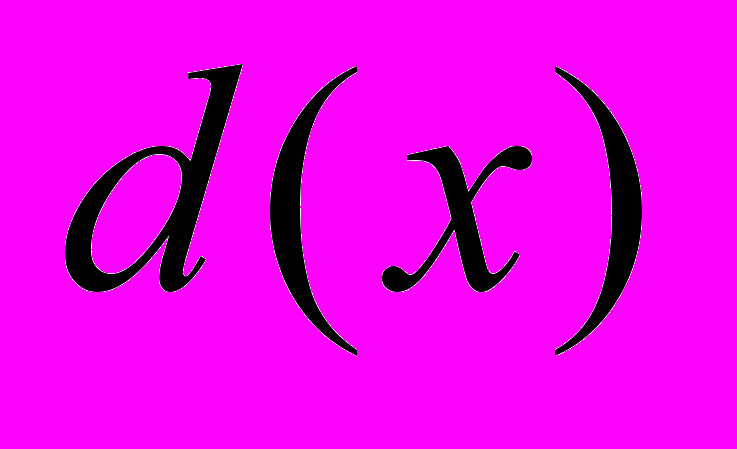3. НОД двух и нескольких многочленов. Алгоритм Евклида. Теорема о том, что такие, что , где =НОД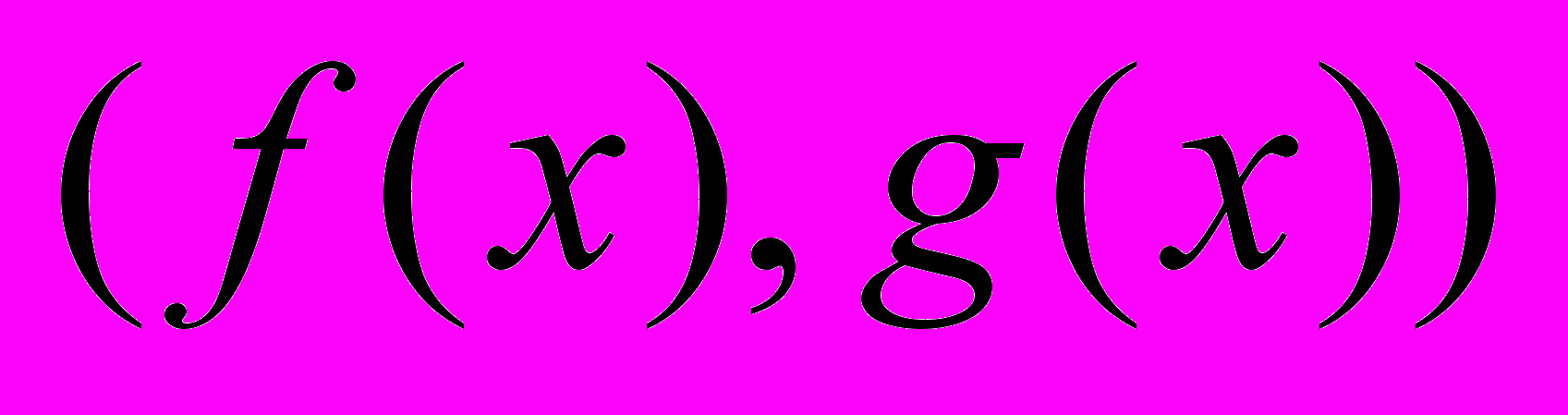. Ее следствия.
   
4. Корни многочленов. Схема Горнера. Теорема Безу и ее следствия.
   
5. Кратные корни. Теорема о понижении кратности корня при дифференцировании.
   
6. Основная теорема алгебры (без доказательства) и ее следствия.
   
7. Теоремы о рациональных корнях целочисленных многочленов.
   
8. Приводимость многочленов над полем P. Критерий Эйзенштейна.
   
9. Разложение многочлена на неприводимые множители.
   
10. Рациональные дроби. Простейшие дроби. Теорема о разложении правильной рациональной дроби в сумму простейших. Теорема единственности.
    
11. Кольцо симметрических многочленов. Основная теорема теории симметрических многочленов. Теорема единственности.
    

Модуль 7. Элементы теории групп.

1. Определения группы. Их равносильность. Примеры.
   
2. Отображения групп. Изоморфизм групп. Примеры.
   
3. Возведение в целую степень элементов группы. Порядок элемента. Утверждения о нем.
   
4. Понятие подгруппы. Примеры. Критерий определения подгрупп. Утверждения о подгруппах.
   

5. Порождающие множества в группах. Примеры.
   
6. Теорема Кэли. Таблица Кэли для групп. Свойства расположения элементов группы в этой таблице. Примеры.
   
7. Циклические подгруппы и группы. Теорема о подгруппах циклических групп, ее необратимость.
   
8. Смежные классы по подгруппе. Свойства. Индекс подгруппы в группе.
   
9. Теорема Лагранжа, её следствия. Необратимость утверждения о порядках подгрупп.
   
10. Инвариантные подгруппы. Примеры. Инвариантность подгрупп индекса 2.
    
11. Фактор – группа по инвариантной подгруппе. Примеры.
    
12. Классы сопряженных элементов. Свойства.
    
13. Теорема об инвариантных подгруппах.
    
14. Гомоморфизмы групп. Свойства гомоморфизма. Теорема о ядре гомоморфизма.
    
15. Гомоморфизм группы на фактор – группу. Естественный гомоморфизм. Теорема о гомоморфизмах.
    
16. Нормализатор элемента. Теорема о порядке класса сопряженности.
    
17. Центр группы. Свойства. Примеры. Теорема о группах с нетривиальным центром.
    
18. Коммутатор пары элементов и его свойства. Строение коммутанта. Инвариантность коммутанта. Утверждение о коммутанте абелевых групп.
    
19. Теорема Галуа о простоте группы A₅. Следствия. Неразрешимые группы и неразрешимость уравнения в радикалах.
    
20. Декартово произведение групп. Утверждения о них. Критерий разложимости группы в произведение групп меньшего порядка.
    
21. Конечные абелевы группы. Теорема о цикличности или разложимости абелевых p–групп.
    
22. Основная теорема об абелевых группах. Подсчет числа попарно неизоморфных абелевых групп данного порядка.