В. Г. Уткин Кандидат философских наук, доцент логика (краткие тексты лекций) Москва 2004 содержание введение 1 Предмет формальной логики. Логические закон

Вид материала

Содержание

Основные виды умозаключений
Полная индукция
Неполная индукция
4. Доказательство: логическая структура.
Правила относительно тезиса
Второе правило
Правила относительно оснований
Третье правило
Правила относительно демонстрации
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА Учебная литература
Популярная литература

Подобный материал:

1 2 3

Суждения свойства носят название категорических, поскольку информация в них передается в категорическом виде. Общая форма таких суждений может быть выражена определенными схемами: «S есть Р» или « S не есть Р». Буква «S» в данном случае используется для обозначения субъекта суждения. Субъект суждения - это понятие о предмете суждения. Буква «Р» обозначает предикат суждения. Предикат - это понятие о признаке предмета суждения. «S и Р» называются терминами суждения.

Кроме этих обозначений, в рассматриваемой схеме присутствует связка «есть» (или «не есть»). Может также иметь место и квантор (знак общности), который выражается словами «все», «всякий», «каждый», «ни один». Например: «Все люди смертны».

Простые категорические суждения делятся на различные виды, предложенные еще Аристотелем.¹³

Во-первых, в зависимости от качества связки, выделяют утвердительные и отрицательные категорические суждения. В утвердительных суждениях указывается на принадлежность предмету определенных признаков. Например: «Защита Отечества есть священный долг каждого гражданина». В отрицательных суждениях указывается на отсутствие у предметов определенных признаков. Например: «Ни один карась не является хищной рыбой». Такое деление категорических суждений в логике называется делением по качеству.

-------------------------------------------------------------------------------------------------------------------

11. См.: Кондаков Н.И. Введение в логику. - М.:Наука,1967.-С.38.

12. См.: Подробно о сложных суждениях см.: М.Г. Дегтярёв, С.А.Хмелевская Логика. - М: «PerSe», 2003.

13. См.: Маковельский А.О. История логики. - М. .-Наука, 1967.-С. 106

11

Во-вторых, в зависимости от того, идет ли речь в суждении об одном предмете, о некоторых предметах определенного класса или же обо всех предметах данного класса, суждения делятся на единичные, частные и общие. Такое деление суждений в логике получило название деления по количеству.

Поскольку в каждом категорическом суждении содержится и количественная и качественная определенность характеристик предмета мышления, то в логике используется объединенная классификация категорических суждений по количеству и качеству.¹⁴

В соответствии с этой классификацией выделяются четыре типа категорических суждений: общеутвердительные, частноутвердителъные, общеотрицательные и частноотрицательные, которые обозначаются буквами А, I , Е. 0. Утвердительные суждения обозначаются двумя первыми гласными буквами латинского слова «affirmo», что в переводе на русский язык означает «утверждаю». Отрицательные суждения обозна-чены гласными буквами латинского слова «nego», что означает «отрицаю».

Суждение А имеет общую схему: «Все S есть Р». Например: «Все студенты институ-та являются спортсменами». Суждение I имеет вид: «Некоторые S есть Р». Например: "Некоторые студенты института являются спортсменами». Суждение Е, в свою очередь, может быть представлено схемой: «Ни одно S не есть Р.».Например: «Ни один студент института не является спортсменом». Наконец, суждение 0 имеет вид: «Некоторые S не есть Р». Например: «Некоторые студенты института не являются спортсменами».

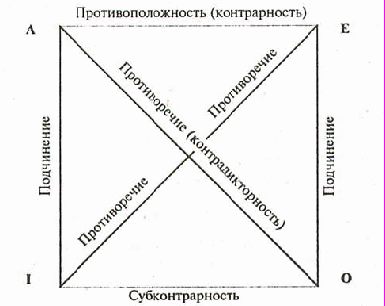
Между рассмотренными типами категорических суждений имеют место различные отношения. В общем, виде их можно представить как отношение противоречия (контрадикторности), отношение противности (контрарности), отношение подпротивности (субконтрарности) и отношение подчинения.

Если в одном из двух суждений что-либо утверждается (отрицается) о каком-то предмете мышления (или о каком-то классе предметов), а в другом суждении то же самое, в то же время и в одном и том же отношении отрицается (утверждается) о том же предмете (или некоторых предметах того же класса), то такие суждения называются противоречащими (контрадикторными). Так, противоречащими суждениями будут следующие: «Все селитры растворяются в воде» и «Некоторые селитры не растворяются в воде» или «Студент Иванов И.И. сегодня сдал зачёт по логике» и «Студент Иванов И.И. сегодня не сдал зачёт по логике». Противоречащие суждения отличаются тем, что они не могут быть одновременно ни оба истинными, ни оба ложными. Одно из них всегда истинно, другое - столь же всегда ложно,

Противными (контрарными) называются такие два суждения, в одном из которых что-либо утверждается (отрицается) обо всех предметах рассматриваемого класса, а в другом одновременно и в одном и том же отношении то же самое отрицается (утверждается) либо обо всех предметах рассматриваемого класса, либо о некоторых предметах этого же класса. Например, противными будут следующие суждения: «Все студенты - отличники

Учебы» и « Ни один студент не является отличником учебы». Из приведенного примера видно, что противные суждения не могут быть одновременно истинными, но они могут быть одновременно ложными.

Если в одном из двух суждений что-либо утверждается о некоторых предметах определенного класса, а в другом - это же самое в одно и то же время и в одном и том же отношении отрицается о тех же предметах того же самого класса, то такие суждения называются подпротивными (субконтрарными). Например: «Некоторые студенты знают теорему Гаусса» и «Некоторые студенты не знают теорему Гаусса». Субконтрарные суждения отличаются тем, что могут быть оба одновременно истинными, но не могут быть одновременно ложными.

Наконец, подчиненными называются такие суждения, в одном из которых что-либо утверждается (отрицается) обо всех предметах определенного класса, а в другом - то же самое, в одно и то же время и в одном и том же отношении утверждается (отрицается) о некоторых, предметах того же самого класса.

-------------------------------------------------------------------------------------------------------------------

14. См: Гетманова А.Д. Логика. - М «ОМЕГА-Л», 2003.-с.63

12

Например, подчиненными являются суждения: «Все студенты умеют пользоваться ЭВМ» и «Некоторые студенты умеют пользоваться ЭВМ» или «Ни один студент не умеет пользоваться ЭВМ» и «Некоторые студенты не умеют пользоваться ЭВМ» Общее суждение здесь называется подчиняющим, частное - подчиненным.

Рассмотрев приведенные примеры, можно легко убедиться, что если подчиняющее суждение, истинно, то истинно и суждение подчиненное. Если подчиняющее суждение ложно, то подчиненное суждение может быть как истинным, так и ложным. Если известно, что истинно подчиненное суждение, то подчиняющее суждение может быть как истинным, так и ложным. Наконец, если подчиненное суждение ложно, то подчиняющее суждение также всегда ложно.

Рассмотренные отношения между категорическими суждениями в логике принято изображать при помощи «логического квадрата», который был предложен для этого византийским политическим деятелем, писателем, ученым и философом Михаилом Пселлом (1018 - ок. 1096 гг.). Квадрат представляет собой диаграмму, показывающую тип отношений между основными категорическими суждениями (см. рис. 1).

Р

ис.1

2.5. Модальность суждений

Наряду с делением суждений по количеству и качеству, Аристотель осуществлял их деление еще по одному основанию, а именно - по модальности.¹⁵ Под модальностью в логике понимается выраженное в суждении отношение говорящего к самому, высказыванию, либо к действительности, о которой говорится в этом высказывании. В этом смысле Аристотель выделял три типа суждений: суждения, говорящие о простом бытии, суждения, говорящие о необходимом бытии и суждения, говорящие о возможном бытии. Такое деление Аристотель объясняет как бы состояниями бытия, считая, что оно может быть действительным, возможным и необходимым.

Действительные суждения в литературе по логике иногда называются ассерторическими, суждения необходимости - аподиктическими, а суждения возможности - проблематическими.

-------------------------------------------------------------------------------------------------------------------

15. См.: Маковельский А.О. История логики. - М.:.Наука, 1967.-С.108.

13

Модальные суждения могут быть как простыми, так и сложными. Рассмотрение сложных модальных суждений выходит за пределы нашего внимания. Простыми же модальными суждениями называются такие, в которых связь между субъектом и предикатом выражается при помощи модальных операторов. Модальные операторы (М)- это модальные слова, такие, например, как «должен», «возможно», «необходимо», «вероятно» и другие. Структура модальных суждений выглядит следующим образом: «М ( S есть Р )» или «М ( S не есть Р )».

В настоящее время в модальной логике в основном рассматриваются алетические, эпистемические, деонтические, аксиологические и временные модальности.

Алетическая модальность (термин «элетический» - греческого происхождения и означает необходимость) представляет собой выраженную в терминах необходимости или возможности информацию либо о характере логической связи между субъектом и предикатом суждения, либо о реальной зависимости отражаемых терминами суждения явлений. Примером суждения с алетической модальностью может служить следующее: "На Марсе, возможно, есть жизнь».

Эпистемическая модальность (от греческого слова «эпистеме» - несомненное, достоверное знание) - это содержащаяся в суждении информация о характере принятия и степени обоснованности знания. В качестве суждений с эпистемической модальностью могут выступать следующие: «Верю, что скоро здесь будет город», «Доказано, что сумма углов треугольника равна 180 градусов», «Не опровергнуто, что Земля имеет шарообразную форму» и др.

Деонтическая модальность (также греческий термин, означающий обязанность) - это выраженное в суждении при помощи различных терминов побуждение к конкретным действиям. Например: «Студент обязан соблюдать правила поведения в институте», «На экзамене запрещено пользоваться шпаргалками» и др.

Аксиологическая модальность - это выражение определенности в отношении характера оценки информации, содержащейся в суждении. Например: «Хорошо, что мы не опоздали на занятия», «Плохо, что вылет самолета задерживается», «Студент Иванов знает матема-тику лучше, чем студент Петров» и т.д.

Временная модальность - это содержащаяся в суждении информация о последователь-ности наступления событий, а так же о континуальности или дискретности их протяжен-ности. В качестве примеров суждений с временной модальностью можно привести следующие: «Он всегда приходит вовремя», «Петров финишировал раньше Иванова» и др.

В логике принято выделять сильные и слабые характеристики модальности. Сильными являются положительная («М (S есть Р)») и отрицательная («М (S не есть P)») характеристики. Слабая характеристика представляет собой отрицание сильной (« не- M (S есть Р)») или «Не-М (S не есть Р)».

Например, для аксиологической модальности, эти характеристики можно показать на следующем примере: «Хорошо, что сегодня идет дождь»; «Хорошо, что сегодня нет дождя». Эти суждения являются сильными характеристиками аксиологической модальности. Суждения «Нехорошо, что сегодня идет дождь» и «Нехорошо, что сегодня нет дождя» являются слабыми характеристиками аксиологической модальности.

В целом модальность суждений изучается в модальной логике, которая имеет различные разделы.

Завершая характеристику суждения, необходимо отметить, что оно играет значительную роль в процессе мышления. Такой вывод уже позволяет сделать анализ определения суждения и многообразия видов суждений. Однако суждения сами по себе важны еще и тем, что из них складываются умозаключения.

14

^ ОСНОВНЫЕ ВИДЫ УМОЗАКЛЮЧЕНИЙ

В самом широком смысле, в логике под умозаключением понимается такая форма мышления, в которой из одного или нескольких связанных между собой суждений при помощи определенных правил осуществления вывода получается новое суждение.

Всякое умозаключение имеет общую логическую структуру, включающую в себя три основных элемента:

а) исходное знание, выражающееся в посылках умозаключения;

б) обосновывающее знание, выражающееся в правиле умозаключения, по которому устанавливается отношение между посылками (либо посылка трансформируется непосредственно в вывод умозаключения);

в) выводное знание, выражающееся в выводе умозаключения.

Формально схему умозаключения можно представить следующим образом:

А равно Б.

Б равно В.

----------------------------------

Следовательно, А равно В.

В этой схеме суждения «А равно Б» и «Б равно В» являются посылками. Обосновывающим знанием будет правило, которое гласит: «Если два предмета равны в каком-либо отношении, третьему, то они равны в этом же отношении между собой». Суждение «А равно В» является выводом умозаключения.

По своей форме умозаключения делятся на различные виды. Наиболее общим является их деление на дедуктивные, индуктивные и умозаключения по аналогии.

Дедуктивное умозаключение

Дедуктивное умозаключение – это форма логического мышления, в которой из некоторого исходного знания определенной степени общности, получается новое знание, меньшей степени общности.

Например:

Все студенты института – юристы

Петров - студент института

---------------------------------------------

Петров – юрист.

Простейшим видом дедуктивного умозаключения является простой категорический силлогизм (от греческого слова sillogismos - рассуждение, вывод, умозаключение), представляющий собой рассуждение, в котором две посылки, связывающие субъекты

(подлежащие) и предикаты (сказуемые) объединены общим, (средним) термином, обеспечивающим «замыкание» понятий (терминов) в заключении (выводе). Например:

Все жидкости (М)- упруги (Р).

Вода (S) - жидкость (М).

-----------------------------------------------

Следовательно, вода (S) упруга (Р).

Здесь «S» - это меньший термин умозаключения, «Р» больший, а «М» - средний термин. Посылка, в которой содержится больший термин, называется большей посылкой. Посылка, содержащая меньший термин, называется меньшей. Вывод называется заключением.

В процессе повседневного общения мы вместо простого категорического силлогизма чаще пользуемся сокращенными силлогизмами (энтимемами). Энтимема - это такой силлогизм, - в котором опущена либо одна из посылок, либо заключение. Так, например,

авторы книги «Наука убеждать: логика и риторика в вопросах и ответах», в качестве примера энтимемы приводят утверждение французского драматурга Пьера Бомарше (1732 - 1799гг.): «Так как ум нельзя унизить, ему мстят».

15

Для того чтобы восстановить простой категорический силлогизм из данной энтимемы следует знать, что заключением в энтимеме является та часть утверждения, которая стоит

после слов «итак», «следовательно», «потому что», «так как», «ибо» и др.

Зная заключение, несложно определить термины простого категорического силлогизма: восстановим простой категорический силлогизм, получим следующее умозаключение:

Мстят тому чего (кого) нельзя унизить.

Уму - мстят.

--------------------------------------------------

Следовательно, ум нельзя унизить.

Наряду с рассмотренными разновидностями дедуктивных умозаключений существуют и другие. Все дедуктивные умозаключения, как уже было отмечено, отличаются направленностью знания или вывода от большей степени общности - к меньшей. Однако общие знания тоже ведь откуда-то берутся. Методом получения таких знаний является индукция.

Индуктивное умозаключение

Индуктивным называется такое умозаключение, в котором из посылок, содержащих знание определённой степени общности, мы получаем вывод, содержащий знание большей степени общности.

Примером индуктивного умозаключения может служить следующее:

Натриевая селитра растворяется в воде.

Калиевая селитра растворяется в воде.

Кальциевая селитра растворяется в воде.

Аммиачная селитра растворяется в воде.

Больше селитр нет.

Все селитры растворяются в воде.

Индуктивное умозаключение имеет общую структуру, которая включает в себя:

исходное знание - это знание, полученное опытным путем о ряде предметов или явлений определенного класса (или обо всех предметах или явлениях этого класса), которые имеют одинаковые признаки. В приведенном примере это информация о том, что каждая из селитр растворяется в воде;
обосновывающее знание - это опытное знание о предметах, принадлежащих к рассматриваемому классу. В нашем примере - это утверждение о том, что селитр больше нет;
заключение - это вывод, полученный в результате изучения существенных признаков предметов или явлений целого класса;

В логике выделяются два вида индукции - полная и неполная.

^ Полная индукция возможна лишь тогда, когда число обобщаемых однородных фактов точно известно и сравнительно невелико. Иными словами, в данном случае, мы имеем возможность осуществить изучение всех предметов рассматриваемого класса без исключения. Поэтому вывод, полученный в результате полной индукции всегда содержит в себе достоверное знание. Выше приведенное умозаключение, обосновывающее растворяемость селитр в воде, как раз и представляет собой пример полной индукции.

^ Неполная индукция - это умозаключение, в котором, вывод делается на основании изучения не всех, а только части предметов рассматриваемого класса. Понятно, что к такому виду индукции мы прибегаем тогда, когда число предметов рассматриваемого класса нам точно неизвестно или же когда число однородных фактов настолько велико, что рассмотрение каждого из них не представляется возможным.

Неполная индукция делится на научную и популярную. Научная индукция имеет место тогда, когда вывод обо всех предметах определенного класса делается на основании установления внутренних причинно-следственных связей (или познания необходимых признаков) части предметов.

Необходимые признаки или внутренние причинно-следственные связи присущи всем предметам определенного класса.

16

Поэтому если такие признаки и связи определены правильно, то совершенно определенно можно утверждать, что вывод полученный в результате рассуждения будет содержать в себе достоверное знание. Так, примером умозаключения полученного методом научной индукции будет, утверждение о том, что теплый воздух поднимается вверх.

Никто никогда не нагревал весь воздух, чтобы убедиться в этом. Но эксперименты, состоящие в нагревании частей воздуха в различных его объемах, показали, что в результате повышения температуры происходит разрежение воздуха и он становится легче своего исходного состояния.

Популярная индукция представляет собой умозаключение, в котором вывод обо всех предметах определенного класса делается на основании изучения лишь некоторых предметов этого класса, при условии отсутствия противоречивых случаев. Например, вывод о том, что все сороки имеют белый бок, получен посредством популярной индукции. Никто никогда не наблюдал одновременно всех сорок, чтобы установить этот факт. Но, тем не менее, никто пока еще не встречал сороку, у которой был бы красный, синий или другого цвета бок. Вместе с тем, это отнюдь не означает, что такого и впредь не может произойти. Многие выводы, полученные путем популярной индукции, со временем были опровергнуты (например, о том, что все лебеди белы, или о том, что все металлы тонут в воде и др.). Поэтому вывод, полученный в результате популярной индукции, всегда содержит лишь вероятностное знание.

Умозаключение по аналогии

Одним из самых древних и распространенных видов умозаключений является умозаключение по аналогии. Это такое умозаключение, в котором вывод о принадлежности предмету определенного признака (свойства, отношения) делается на основании сходства этого предмета в существенных признаках с другими предметами.

Общую форму умозаключения по аналогии можно условно изобразить следующей схемой:

Предмет А имеет признаки а, в, с, х.

Предмет В имеет признаки а, в, с.

-------------------------------------------------------

Вероятно, что предмет В имеет признак х.

Аналогия может быть строгой и нестрогой. Строгая аналогия имеет место тогда, когда признаки сходства предметов связаны с переносимым признаком внутренней необходимой связью. Применение строгой аналогии широко распространено в научных исследованиях и в математических доказательствах. В качестве примера, иллюстрирующе-го вариант ее использования, можно привести формулировку признаков подобия треуголь-ников: «Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны». Строгая аналогия дает достоверное знание.

Нестрогая аналогия имеет место в том случае, когда между признаками сходства предметов и самим предметом, на который переносится признаки, отсутствует непосредственная конкретная связь. Примером нестрогой аналогии является перенесение признаков модели корабля, полученных в результате экспериментов с моделью в бассейне на реальный строящийся корабль и др.

Рассмотренные основные виды умозаключений (дедуктивные, индуктивные и умозаключения по аналогии) играют в процессе мышления важную роль. Умозаключение как форма логического мышления позволяет уже связывать различные суждения по определенным правилам и делать вывод из них, в котором содержится новое знание.

17

^ 4. ДОКАЗАТЕЛЬСТВО: ЛОГИЧЕСКАЯ СТРУКТУРА.

ОСНОВНЫЕ ВИДЫ И ПРАВИЛА.

То, что мы познаем при помощи органов чувств, представляет собой очевидное знание. Это знание не подлежит особому доказательству.

Вместе с тем, во многих случаях человеку приходится доказывать истинность различного рода суждений, выводов, научных положений, которые непосредственно не опираются на опыт, на результаты чувственного познания.. Можно сказать, что доказа-тельству подлежит любое выводное знание. Истинность такого знания должна быть обоснована при помощи других, независящих от него (с точки зрения истинности) положений. Причем истинность этих положений и выводов также, должна быть доказана.

Обоснование истинности или ложности какого-либо знания осуществляется посредством доказательства, которое является мощным средством формирования научно-обоснованных убеждений.

Таким образом, доказательство представляет собой совокупность логических приемов обоснования истинности (или ложности) какого-либо положения с помощью других истинных и связанных с ним положений.

4.1. Логическая структура и основные

виды доказательства

С точки зрения своей формы, любое доказательство всегда имеет определенную струк-туру, которая включает в себя три элемента: тезис, основания (аргументы) и демонстра-цию (способ доказательства).

Тезисом доказательства принято называть суждение, истинность (или ложность) которого необходимо доказать. Если мы доказали истинность тезиса, то он считается оправданным. Если же доказана его ложность, то тезис считается опровергнутым.

Основаниями доказательства (аргументами) называются все положения, на которые опирается доказательство. Иными словами, это приводимые истинные положения для оправдания (или опровержения) тезиса.

Все положения, которые могут выступать в качестве аргументов в логике принято делить на четыре группы. Первую группу аргументов составляют единичные достоверные факты. Доказательство истинности (или ложности) какого-либо положения при помощи конкретных, действительных, достоверных фактов относится к разряду наиболее обоснованных. Вторая группа аргументов - это определения основных понятий конкретной науки. Они считаются истинными и составляют теоретический фундамент определенной науки и, следовательно, могут быть использованы в качестве аргументов. В третью группу входят аксиомы и постулаты. Они представляют собой суждения, которые приняты в качестве истинных без доказательства в силу того, что прошли испытание на истинность в ходе многовековой практики людей. Четвертая группа аргументов - это доказанные ранее положения (законы, теоремы и т.д.) науки. Поскольку их истинность уже доказана, постольку они могут рассматриваться в качестве аргументов.

Демонстрация (способ доказательства) представляет собой логическое рассуждение, связывающее тезис доказательства с его основаниями и выводящее из последних утверждение об истинности (или ложности) доказываемого тезиса. Иначе говоря, демонстрация - это цепь умозаключений, посылками которых являются основания доказа-тельства, а последним заключением - доказываемый тезис.

В традиционной логике выделяются различные виды доказательств. Доказательство может осуществляться с целью оправдания, или же с целью опровержения тезиса. В первом случае мы имеем доказательство как оправдание тезиса (или просто доказа-тельство), во втором - доказательство как опровержение тезиса (или просто опроверже-ние).

Когда применяется первый вид доказательства, то необходимо подбирать такие аргументы, которые показывают истинность выдвинутого тезиса.

18

Если же используется второй вид - необходимо иметь основания, свидетельствующие о ложности тезиса.

По форме своей доказательства делятся на прямые и косвенные.

Прямыми доказательством называется такое, которое основывается на определенных несомненных (истинных) началах, из которых по правилам, и законам логики выводится тезис.

Косвенным доказательством называется такое, в котором истинность тезиса обосновывается посредством опровержения положения, противоречащего тезису. Такое положение носит название антитезиса. Косвенное доказательство применяется в том случае, когда прямое доказательство по каким-либо причинам невозможно.

4.2. Правила доказательства. Основные

ошибки в доказательстве.

Для того чтобы доказательство приводило к желаемому результату необходимо знать и соблюдать правила его осуществления. Авторы известной «Логики Пор-Рояля», вышедшей в свет впервые еще в 1662 году отмечали, что: «Для того чтобы доказательство было истинным, требуется, во-первых, чтобы в материи доказательства не было ничего, кроме достоверного и несомненного, и, во-вторых, чтобы не было никаких погрешностей в форме доказательства.»¹⁶ Выполнение этих требований реализуется через соблюдение правил доказательства.

В логике принято выделять три группы правил доказательства, соответствующих трем элементам его структуры:

а) правила относительно тезиса;

б) правила относительно аргументов;

в) правила относительно формы доказательства,

^ Правила относительно тезиса. Первое из них гласит, что тезис должен быть точно, четко и ясно сформулированным. Это требование означает, что в процессе формирования тезиса должны быть выполнены следующие условия. Во-первых, необходимо полностью исключить возможность неоднозначного (двусмысленного) толкования положения, выступающего в качестве тезиса. Во-вторых, необходимо уточнить количественную характеристику объема понятий, входящих в тезис.

^ Второе правило гласит, что тезис на протяжении всего доказательства должен оставаться одним и тем же. Если правило нарушается, то возникает логическая ошибка, которая называется «подменой тезиса». Это весьма распространенная ошибка. Суть ее состоит в том, что в процессе, доказательства нарушается закон тождества, когда отождествляются нетождественные понятия или суждения. Иначе говоря, если дискуссия разворачивается вокруг одного выдвинутого тезиса, а затем в процессе, его доказательтва рассуждения направляются на другой тезис, который может быть связанным с первым, но не доказывает его истинности, то в данном случае, несомненно, имеет место подмена тезиса. Такая ситуация часто встречается в научных дискуссиях, когда при оценке значения результатов работы исследователя разворачивается спор относительно нравственных качеств последнего.

^ Правила относительно оснований (аргументов) доказательства.

Первое правило требует, чтобы аргументы в доказательстве были истинными и не противоречили друг другу. Нарушение этого правила может привести к логической ошибке, которая называется «основным заблуждением». Она состоит в том, что для дока-зательства истинности (или ложности) тезиса, используются ложные аргументы. Это весьма опасная ошибка, поскольку если аудитория или оппоненты не знают о ложности оснований, то они могут быть введены в заблуждение. Доказательство в этом случае может выглядеть безупречным: демонстрация может быть правильной, а тезис будет логически вытекать из аргументов.

------------------------------------------------------------------------------------------------------------------

А Арно и П.Николь. Логика, или Искусство мыслить. - М.:Наука, 1991.-С. 331.

19

Второе правило требует, чтобы истинность аргумента была доказана независимо от тезиса. Если это правило нарушается, то возникает «круг в доказательстве».

Суть этой ошибки состоит в том, что истинность какого-либо доказываемого положения (тезиса) обосновывается посредством того же самого положения, которое еще должно быть доказано.

^ Третье правило гласит, что аргументы должны быть достаточным основанием для доказательства тезиса. Нарушение этого правила приводит к тому, что при доказательстве устанавливается связь между суждениями, имеющими различное содержание. Например, если тезис «Этот человек бежит», мы будем обосновывать утверждением «На улице сильный мороз», то этого явно будет недостаточно. Между этими событиями может быть связь, но тезис не вытекает в данном случае из аргумента. Ведь человек может бежать совсем по другой причине.

^ Правила относительно демонстрации. Их составляют правила осуществления различ-ных умозаключений, которые используются при построении доказательства. Нарушение этих правил может привести к возникновению целого ряда логических ошибок. Наиболее распространенными из них являются «поспешное обобщение», «ложное следование» и ошибка, которая называется «от сказанного с условием к сказанному безусловно».

Логическая ошибка «поспешное обобщение» состоит в том, что в структуре доказа-тельства оказываются «выброшенными» целые звенья демонстрации. Например, когда при осуществлении полной индукции подвергаются рассмотрению не все элементы данного класса и, в силу этого, признак, по которому делается вывод, оказывается неверно определенным. В качестве иллюстрации можно привести следующее умозаключение:

Железо - твердое тело.

Серебро - твердое тело.

Золото - твердое тело.

. Железо, серебро,и золото– металлы.

--------------------------------------------------------------

Следовательно, все металлы - твердые тела.

В доказательствах, основанных на дедукции, «поспешное обобщение» может возникать при использовании энтимем.

Если в ходе доказательства утверждается логическая связь между основаниями и заключением, а на самом деле ее быть не может, то возникает логическая ошибка «ложное следование».

Она встречается в доказательствах, построенных, как правило, на условных умозаключениях, посылками которых являются невыделяющие суждения (т.е. такие, в которых утверждается, что- то, о чем говорится в основании, достаточно, но не необходимо для существования того, о чем говорится в следствии, а то о чем говорится в следствии, необходимо, но, недостаточно для существования того, о чем говорится в основании). В качестве примера такого суждения можно привести следующее: «Если я хочу хорошо знать логику, то мне необходимо купить учебник по логике». Наличие учебника является достаточным условием хорошего знания этой дисциплины. Но оно не является необходимым. Можно хорошо знать логику и, не имея учебника. В то же время, можно ее не знать и при наличии такового.

Логическая ошибка «от сказанного с условием к сказанному безусловно» возникает в том случае, когда аргумент, истинный только с учетом определенного времени отношения, места или меры приводится в качестве безусловного, верного во всех случаях.¹⁷ Так, если снотворное полезно для больного бессонницей в небольших дозах, в которых оно помогает больному уснуть то, в больших дозах оно может причинить ему непоправимый вред.

Нарушение отмеченных правил может привести и к возникновению других ошибок. Но, как вполне справедливо считали авторы «Логики Пор-Рояля», «...маловероятно, чтобы человек среднего ума, мало-мальски рассудительный, допустил другие ошибки, особенно в умозрительных материях».¹⁸

^{----------------------------------------------------------------------------------------------------------------------------------------------------------------------}

17. См.: Гетманова Д.Д. Логика. - М. «ОМЕГА-Л», 2003.-с.200

18. См.: А.Арно и П.Николь. Логика, или искусство мыслить.- М.:Наука, 1991.-С. 332.

20

Подводя итог сказанному о доказательстве, можно сделать вывод, что оно не является какой-то определенной формой мышления. Это совокупность логических приемов использования различных форм логического мышления в соответствии с определенными правилами для обоснования истинности или ложности какого-либо утверждения. Поскольку сфера применения, доказательства весьма велика, постольку знание основ его осуществления представляется чрезвычайно необходимым условием эффективного общения.

21

ЗАКЛЮЧЕНИЕ.

Теория логики, или логическое знание развивается не обособленно, а во взаимной связи с практикой. Сфера практической деятельности человека сегодня значительно расширилась, что оказало существенное влияние на развитие логики. Это развитие осуществляется, прежде всего, в силу того, что логика обнаруживает все новые и новые области своего применения. Возникновение в конце ХIХ - начале XX вв. математической логики в сущности можно рассматривать как закономерный результат интенсивной разработки логического знания.

Благодаря бурному развитию математической логики, сегодня уже сложились самостоятельные области логического знания. К ним относятся многозначная логика, модальная логика, теория логического следования, деонтическая логика и целый ряд других теоретических направлений.. Все эти области знания сегодня принято называть неклассической логикой. Однако основу этих логических теорий составляет традиционная классическая логика, рассмотрению азов которой и посвящено настоящее пособие.

Содержание кратких текстов лекций не исчерпывает всего объема знаний, составляющих основы формально-логической теории, поскольку пособие подготовлено в соответствии с тем количеством учебных часов, которое выделяется для изучения логики в институте. В связи с этим, представляется, что заинтересованный читатель не остановится на предложенном в настоящем издании материале и обратит свое внимание на список литературы, приведенный в конце пособия.

Изучение указанной литературы позволит не только уверенно овладеть общими основами формальной логики, но и получить достаточно содержательные знания по конкретным вопросам формально-логической теории. Такие знания, с одной стороны, будут способствовать повышению уровня общей культуры студента, а с другой помогут ему успешно сформировать у себя высокие профессиональные качества.

22

^

Учебная литература

Гетманова А.Д. Логика. М., 2002.

Гетманова А.Д. Словарь и задачник по логика. М., 1998.

Гетманова А.Д. Учебник по логике. М., 2001.

Горский Д.П., ИвинА. А, Никифоров А.Л. Краткий словарь по логике М 1991.

Ивлев Ю.В. Логика. М., 2002.

Кириллов В.И., Старченко А.А. Логика. М., 2002.

Светлов В.А. Практическая логика. С.-Петербург, 1995.

Свинцов В.И. Логика. М., 1987.

Уемов А. И. Основы практической логики. Одесса, 1997.

Упражнения по логике. М., 1990.

Яшин Б.Л. Сборник задач и упражнений по логике. М., 1996.

^

Blog

В. Г. Уткин Кандидат философских наук, доцент логика (краткие тексты лекций) Москва 2004 содержание введение 1 Предмет формальной логики. Логические закон

Содержание

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Учебная литература

Популярная литература