Электронное научное издание «Труды мэли: электронный журнал»

Вид материала

Содержание

Подобный материал:

Электронное научное издание «Труды МЭЛИ: электронный журнал»

Курбатский С. Н. − аспирант МЭЛИ

Прогнозирование временных рядов как инструмент увеличения эффективности управления предприятием

Прогнозирование разнообразных экономических показателей широко применяется в управлении предприятием. Наиболее часто прогнозирование применяется:

в инвестиционной деятельности предприятия (прогнозируют курсы акций, курсы валют, различные индексы и т.д.);
в планировании (например, можно прогнозировать продажи в следующем периоде);
в логистике (прогнозирование применяют для определения запасов и т.д.).

Так же прогнозирование различных показателей рынка нашло свое применение в маркетинге. Наиболее часто прогнозирование используют для решения следующих маркетинговых задач:

прогнозирование спроса;
прогнозирование изменения рыночных цен;
прогнозирование емкости рынка;
прогнозирование результатов работы предприятия;
прогнозирование поведения других игроков рынка;
прогнозирование эффективности рекламных компаний;
прогнозирование влияния различных внешних факторов на спрос, продажи и т.д.

Прогноз служит основой создания маркетинговой программы и производственного плана. Его цель – дать наиболее вероятные альтернативные пути развития исследуемого рынка при заданном уровне знаний и закладываемых предпосылках. Следовательно, прогнозирование спроса представляет собой исследование будущего (возможного) спроса на товары (услуги) в целях обоснования инвестиций, а также производственных планов.

Принимая то или иное управленческое решение, менеджер использует различную информацию, в том числе прогнозы различных рыночных показателей. Но часто за место прогноза, какого либо рыночного показателя используются предыдущие значения временного ряда этого показателя, и менеджер, изучив историю ряда, экстраполирует этот ряд и на основании этих данных принимает решение. Такая ситуация связана с тем что алгоритмы прогнозирования сложны и не обеспечивают требуемой точности, поэтому и используется экспертный метод прогнозирования.

Предлагаемая далее методология прогнозирования временных рядов позволит при минимальных временных затратах спрогнозировать практически любой рыночный показатель при этом обеспечить необходимую точность прогнозирования.

Основным вопросом прогнозирования рыночных показателей является: «Можно предсказать рынок?» и «С какой точностью можно предсказать рыночные показатели?». В начале прошлого века считалось, что изменение рыночных показателей носит случайный характер и попытки прогнозирования этих показателей схожи с азартной игрой на деньги. Однако в 80-х годах появилась теории динамического хаоса. Эта теория построена на противопоставлении хаотичности и стохастичности (случайности). По мнению Хорофаса Д.Н. (D.N. Chorafas), одного из исследователей зависимостей в поведении рынка: «Хаотические ряды только выглядят случайными, но, как детерминированный динамический процесс, вполне допускают краткосрочное прогнозирование. Область возможных предсказаний ограничена по времени горизонтом прогнозирования, но этого может оказаться достаточно для получения реального дохода от предсказаний. И тот, кто обладает лучшими математическими методами извлечения закономерностей из зашумленных хаотических рядов, может надеяться на большую норму прибыли - за счет своих менее оснащенных собратьев» [5].

Согласно Александру Элдеру (A.EIder) [3], известному специалисту по техническому анализу (по своей предыдущей специальности – психотерапевту), поведение рыночного сообщества имеет много аналогий с поведением толпы, характеризующимся особыми законами массовой психологии. Влияние толпы упрощает мышление, нивелирует индивидуальные особенности и рождает формы коллективного, стадного поведения, более примитивного, чем индивидуальное. В частности, стадные инстинкты повышают роль лидера, вожака. Ценовая кривая, по Элдеру, как раз и является таким лидером, фокусируя на себе коллективное сознание рынка. Такая психологическая трактовка поведения рыночной цены обосновывает применение теории динамического хаоса. Частичная предсказуемость рынка обусловлена относительно примитивным коллективным поведением игроков, которые образуют единую хаотическую динамическую систему с относительно небольшим числом внутренних степеней свободы.

Так же огромную роль в доказательстве предсказуемости рыночных показателей сыграли российские ученые А. Ежов и С. Шумский. Используя нейросетевое программирование для предсказания показателей финансовых рынков, они показали предсказуемость исследуемых рядов и также привели примеры полезного использования данных предсказаний.

Я полностью согласен с Александром Элдером, рынок это сложная динамическая система, поведение которой можно описать используя математические модели, а следовательно можно прогнозировать состояние рынка используя эти модели. Конечно, рынок это очень сложная система, и, соответственно, математическая модель, описывающая рынок, должна быть очень сложна, поэтому раньше было сложно создавать такие модели, но современная наука дает нам новые инструменты, позволяющие создавать более сложные модели. Например, нейросетевой подход, предложенный А. Ежовым и С. Шумским, позволяет создавать сложные динамические нелинейные модели, которые могут с достаточной точностью прогнозировать основные рыночные показатели.

Далее будет приведена методология прогнозирования экономических показателей рынка, используя нейросетевое программирование, и методология использования этих прогнозов для управления предприятием.

Нейросетевой подход позволяет давать более точные прогнозы, нежели технический анализ, затрачивая при этом меньше временных ресурсов и обладая большей наглядностью.

Среди достоинств нейросетевого подхода можно выделить основные преимущества:

Нейросетевой анализ позволяет строить нелинейные модели, в то время как технический анализ преимущественно оперирует линейными моделями. Использование нелинейных моделей позволяет с большей точностью описать рынок, а, следовательно, увеличить точность прогноза.
Нейросетевой анализ, в отличие от технического, не предполагает никаких ограничений на характер входной информации. Это могут быть как индикаторы данного временного ряда, так и сведения о поведении других рыночных инструментов.
В отличие от технического анализа, основанного на общих рекомендациях, нейросети способны находить оптимальные для данного инструмента индикаторы и строить по ним оптимальную опять же для данного ряда стратегию предсказания. Более того, эти стратегии могут быть адаптивны, меняясь вместе с рынком, что особенно важно для молодых активно развивающихся рынков, в частности, российского.

Из недостатков нейросетевого моделирования можно отметить следующий. Нейросетевое моделирование в чистом виде базируется лишь на данных, не привлекая никаких априорных соображений. Имеющихся данных может не хватить для обучения, размерность потенциальных входов может оказаться слишком велика. Но есть методы, позволяющие бороться с данным недостатком и получать точные прогнозы при небольшом количестве данных.

Задача прогнозирования временных рядов предъявляет определенные пребывания к информационным маркетинговым системам (ИМС). Эти требования необходимы для возможности работы алгоритмов предсказания:

Все экономические показатели, различные признаки и другие данные должны храниться в хранилище данных в одинаковом временном масштабе.
Необходима возможность получения экономических показателей и признаков в различных временных масштабах (например: день, неделя, месяц, год).
ИМС должна корректно работать с временной шкалой, необходимо наличие функций, учитывающих количество дней, количество рабочих дней, количество выходных, рабочих часов в периоде времени.
Необходимо наличие функций математической статистики для работы с временными рядами (например: корреляция, энтропия, кросс-энтропия и т.д.).
Необходимы средства для кодирования и нормирования значений временных рядов.
ИМС должна иметь удобный интерфейс и средства для визуализации временных рядов и их прогнозов.

Если ИМС соответствует приведенными выше требованиям, то маркетолог, используя приведенную дальше методологию, сможет подобрать данные для прогнозирования, определить степень прогнозируемости временного ряда, построить и обучить оптимальную нейросетевую модель для прогнозирования и использовать данную модель для прогнозирования временного ряда. Для создания нейросетевой модели необходимо использовать нейросетевые пакеты, широко представленные на рынке программного обеспечения. Схема прогнозирования с использованием нейросетевого подхода представлена на рис. 1.

Для динамических систем доказана следующая теорема Такенса. Если временной ряд порождается динамической системой, т.е. значения X_t есть произвольная функция состояния такой системы, существует такая глубина погружения d (примерно равная эффективному числу степеней свободы данной динамической системы), которая обеспечивает однозначное предсказание следующего значения временного ряда [6]. Таким образом, выбрав достаточно большое d можно гарантировать однозначную зависимость будущего значения ряда от его d предыдущих значений:

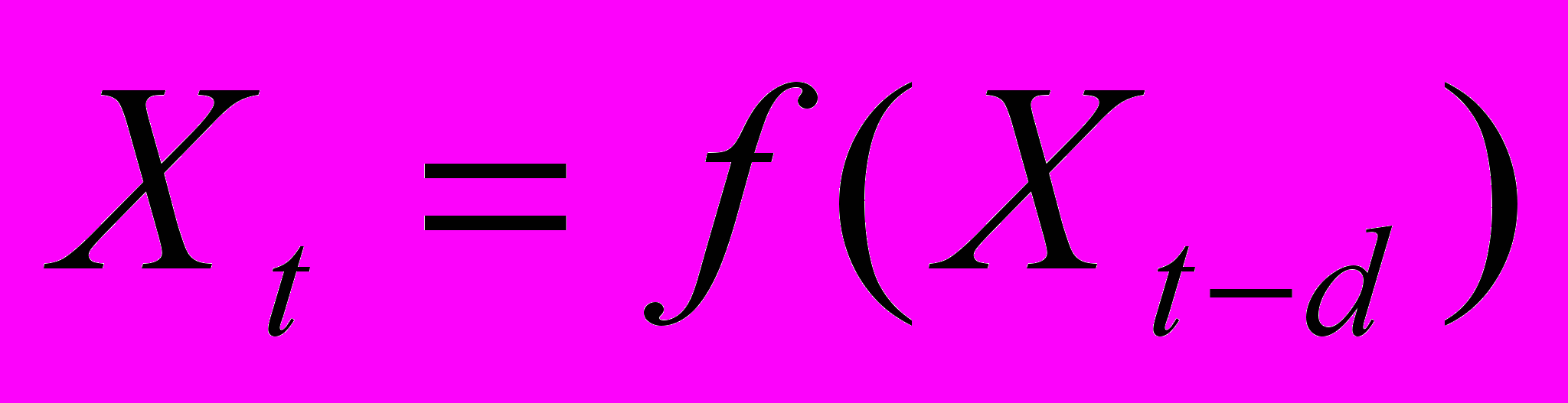, т.е. предсказание временного ряда сводится к задаче интерполяции функции многих переменных. Нейросеть далее можно использовать для восстановления этой неизвестной функции по набору примеров, заданных историей данного временного ряда.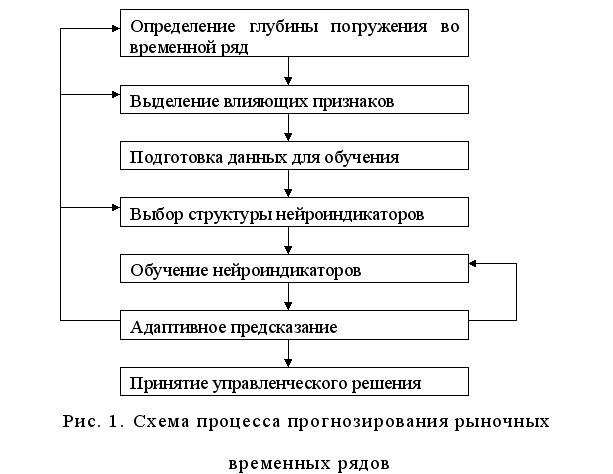

Напротив, для случайного ряда знание прошлого ничего не дает для предсказания будущего. Поэтому, согласно теории эффективного рынка, разброс предсказываемых значений ряда на следующем шаге при погружении в лаговое пространство не изменится.

Метод погружения позволяет количественно измерить предсказуемость реальных финансовых инструментов, т.е. проверить или опровергнуть гипотезу эффективности рынка. Согласно последней, разброс точек по всем координатам лагового пространства одинаков (если они – одинаково распределенные независимые случайные величины). Напротив, хаотическая динамика, обеспечивающая определенную предсказуемость, должна приводить к тому, что наблюдения будут группироваться вблизи некоторой гиперповерхности

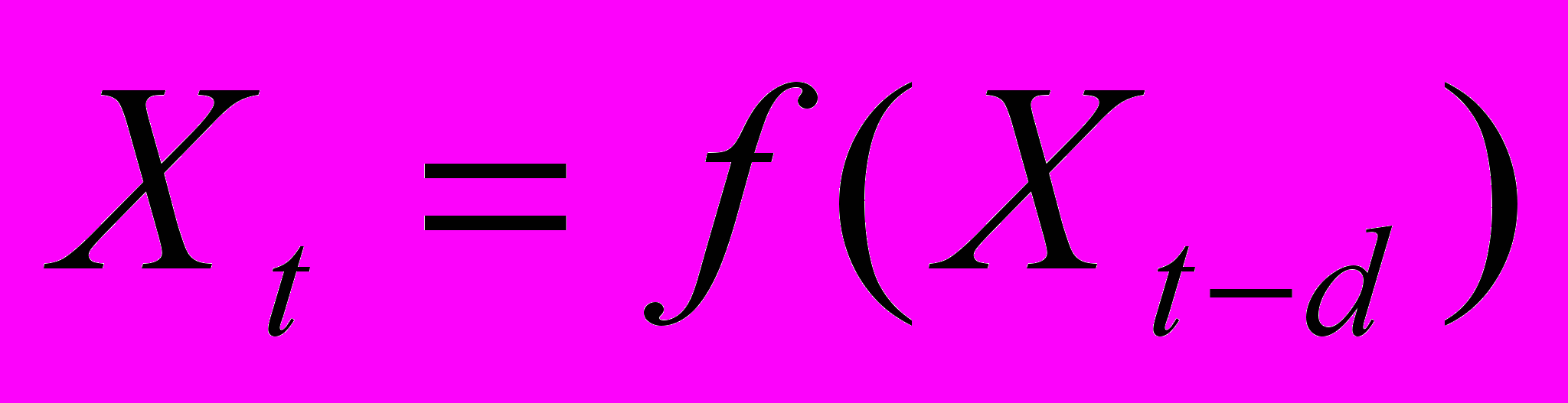, т.е. экспериментальная выборка формирует некоторое множество размерности меньшей, чем размерность всего лагового пространства.

Н

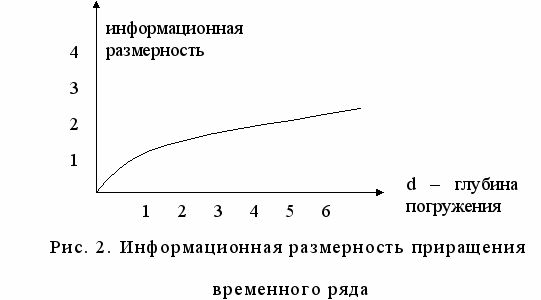
аиболее распространенным методом для определения размерности множества является box-counting. Таким образом, если посчитать информационную размерность интересуемого временного ряда, получим график, подобный показанному на рис. 2.

Из графика видно, что информационная размерность растет с увеличением глубины погружения, однако эта зависимость не прямо пропорциональная, что свидетельствует о наличии некоторой предсказуемой составляемой в данном временном ряде. Хотя здесь нельзя говорить о полностью детерминированной хаотической динамике, так как график информационной размерности с ростом глубины погружения не входит в насыщение, которое зафиксировало бы существование замкнутой детерминированной системы. То есть во временном ряде присутствует и случайная составляющая. Если бы временной ряд состоял из случайных значений, тогда информационная размерность была бы прямо пропорциональна глубине погружения.

Заметим, что теоретическая предсказуемость вовсе не гарантирует достижимость практически значимого уровня предсказаний. Количественную оценку предсказуемости конкретных рядов дает измерение кросс-энтропии, также возможное с помощью методики box-counting.

Кросс-энтропия:

.

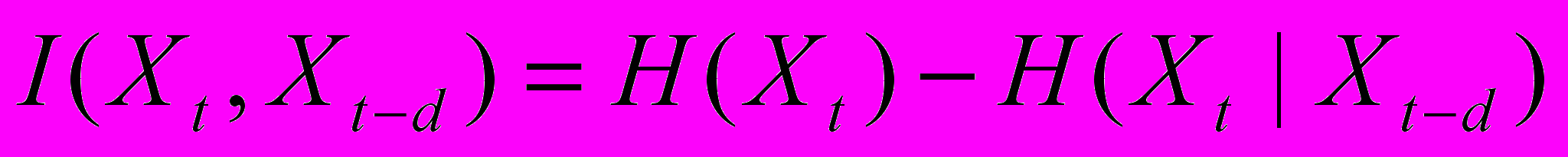Следует также отметить, что увеличение глубины погружения положительно влияет на предсказуемость лишь до определенного предела, при увеличении глубины погружения выше данного предела происходит понижение предсказуемости. Это означает, что размерность лагового пространства d велика для данного количества примеров.

Довольно часто временные ряды предсказывают лишь на основании прошлых значений данного временного ряда (например, курсы акций или курсы валют), но есть возможность использовать для прогнозирования дополнительную информацию. Например, увеличение затрат на рекламу приведет к увеличению продаж в последующих месяцах, или планируемое снижение цен тоже может привести к увеличению продаж, или прогнозируемая жара стимулирует сбыт прохладительных напитков. Таких факторов, влияющих на интересующие нас временные ряды, множество, причем многими из этих факторов предприятие может управлять, и если использовать эту информацию, то можно улучшить точность прогноза.

В качестве примера можно рассмотреть, какие основные факторы влияют на временной ряд продаж кровельных материалов в московском регионе:

Несомненно, основной фактор – это сезонный. Продажи сильно зависят от времени года, продажи максимальны летом и минимальны зимой.
Так же на продажи кровельных материалов влияет погода, к примеру, если зимой не будет снега и будет достаточно тепло, то продажи будут гораздо выше, чем в морозную погоду.
Еще один влияющий фактор - это цена кровельных материалов в исследуемой фирме, точнее даже не цена, а отношение цены к среднерыночной цене.
Так же на продажи будет влиять количество рекламы, даваемой данной фирмой, или затраты на рекламу.

Конечно же, существуют и другие факторы, влияющие на продажи кровельных материалов, но выше перечислены факторы, которые влияют в большей степени. Попробуем разобраться, как влияют эти факторы. Понятно, что влияние этих факторов довольно сложный вид и вряд ли это влияние можно описать с помощью простых линейных математических моделей. Это влияние имеет динамический характер, к примеру если увеличить затраты на рекламу, это даст увеличение продаж не только в этом месяце, но и отразится в последующих месяцах. Использование нейросетевых моделей позволяет использовать информацию из этих факторов, чтобы увеличить точность прогноза. Временные значения этих признаков, закодированные определенным образом, также подаются на входы нейросети аналогично значениям исследуемого ряда. В данном случае функция нейросети будет выглядеть как

.

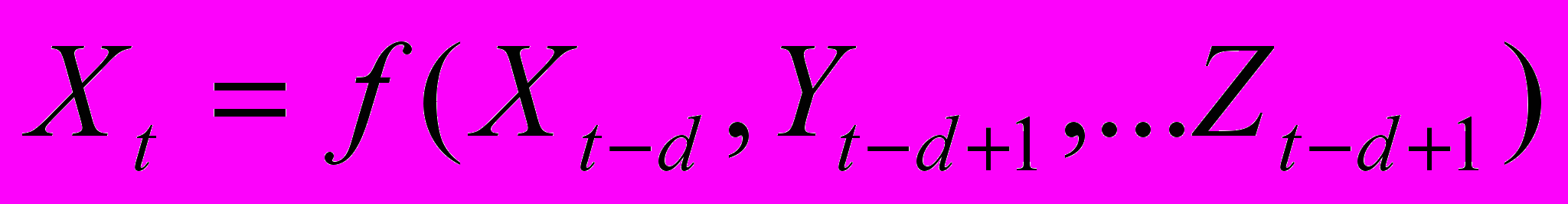Чтобы понять, насколько сильно данный фактор влияет на изучаемый временной ряд и стоит ли его использовать для построения прогноза, можно рассчитать корреляцию этих рядов - при большой корреляции этот фактор следует использовать. Также можно построить несколько сетей - одни с учетом данного фактора, другие – без учета, и сравнить их точность.

Ключевым для повышения качества предсказаний является эффективное кодирование входной информации. Это особенно важно для труднопредсказуемых временных рядов.

В качестве входов и выходов нейросети не следует выбирать сами значения временного ряда, которые мы обозначим

. Действительно значимыми для предсказаний являются изменения значений временного ряда. Поскольку эти изменения, как правило, гораздо меньше по амплитуде, чем сами значения, между последовательными значениями отсчетов имеется большая корреляция, т.е. наиболее вероятное значение временного ряда в следующий момент равно его предыдущему значению: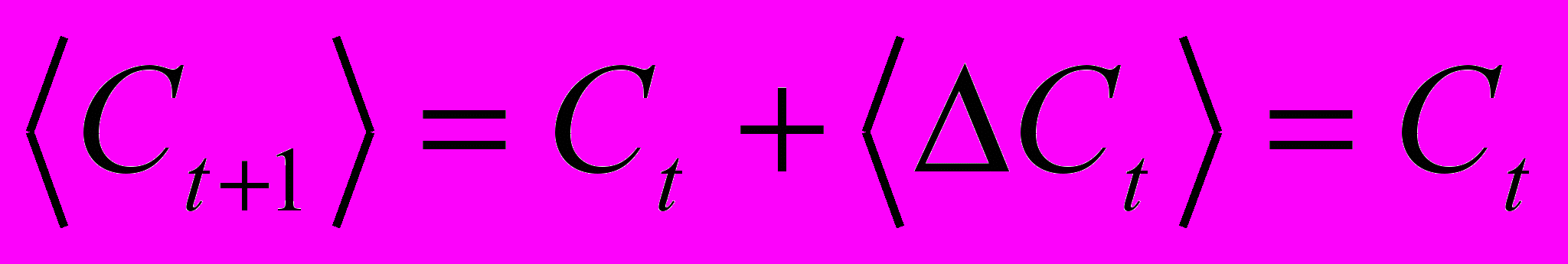

. Между тем, как это уже неоднократно подчеркивалось, для повышения качества обучения следует стремиться к статистической независимости входов, то есть к отсутствию подобных корреляций.

Поэтому в качестве входных переменных логично выбирать наиболее статистически независимые величины, например, изменения значений

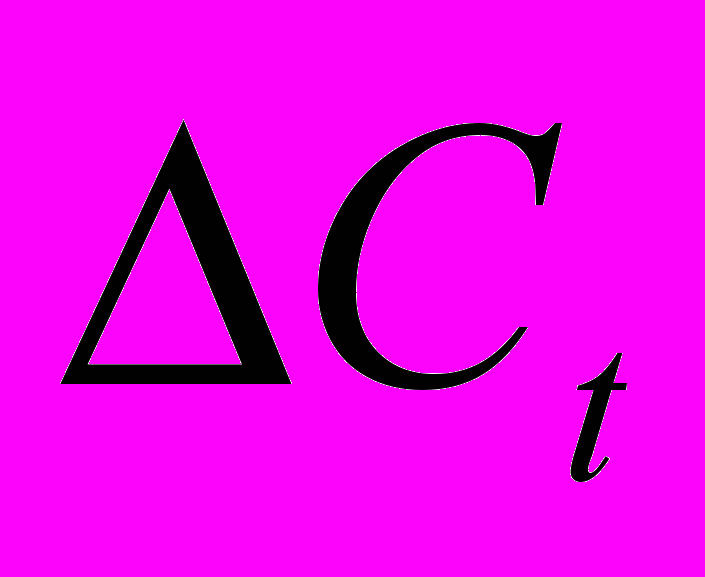или логарифм относительного приращения

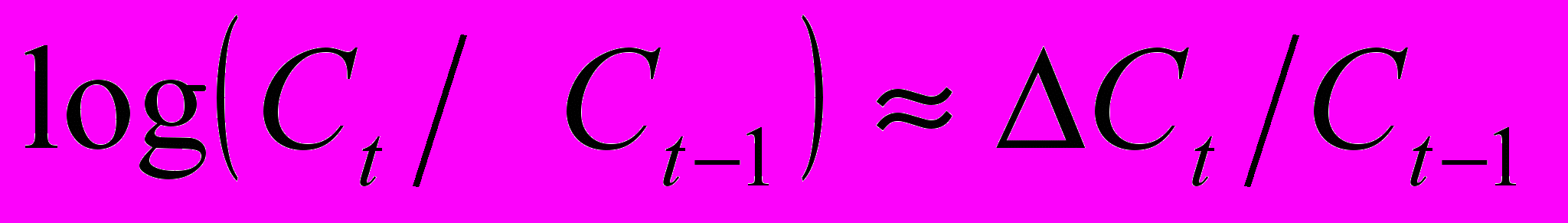. Последний выбор хорош для длительных временных рядов, когда уже заметно влияние долгосрочных изменений временного ряда (как например, инфляция). В этом случае простые разности в разных частях ряда будут иметь различную амплитуду, так как фактически измеряются в различных единицах. Напротив, отношения последовательных отсчетов не зависят от единиц измерения, и будут одного масштаба, несмотря на изменение единиц измерения. В итоге, большая стационарность ряда позволит использовать для обучения большую историю и обеспечит лучшее обучение.

Отрицательной чертой погружения в лаговое пространство является ограниченный «кругозор» сети. Технический анализ же, напротив, не фиксирует окно в прошлом, и пользуется подчас весьма далекими значениями ряда. Утверждается, что для большинства рядов максимальное и минимальное значения ряда даже в относительно далеком прошлом оказывает влияние на будущие значения ряда. Недостаточно широкое окно погружения в лаговое пространство не способно предоставить такую информацию, что, естественно, снижает эффективность предсказания. С другой стороны, расширение окна до таких значений, когда захватываются далекие экстремальные значения ряда, повышает размерность сети, что в свою очередь приводит к понижению точности нейросетевого предсказания - уже из-за разрастания размера сети.

Выходом из этой ситуации являются альтернативные способы кодирования прошлого поведения ряда. Весьма перспективным инструментом здесь может оказаться вейвлетное разложение (wavelet decomposition). Оно эквивалентно по информативности лаговому погружению, но легче допускает такое сжатие информации, которое описывает прошлое с избирательной точностью.

Иногда складывается ситуация, когда число примеров не достаточно для обучения сети, то есть, не накоплена информация о характере поведения ряда. В данном случае можно применить метод искусственных примеров. Суть метода заключается в том, что ряд растягивают по оси времени, тем самым добавляя новые примеры для обучения.

Часто в качестве признаков (входов нейросети) используют различного рада индикаторы, которые применяются для предсказания в техническом анализе, но многочисленность этих эмпирических признаков затрудняет пользование ими.

Так же можно использовать качественные индикаторы в качестве входов нейросети, только их надо первоначально закодировать. Разработка структуры нейросети, а также выбор типа нейросети является основной задачей, от которой во многом зависит точность предсказания. Для предсказания временных рядов используют нейросети с радиально базисной функцией (RBF) и многослойный персептрон (MLP). К преимуществам RBF над MLP можно отнести:

RBF может моделировать произвольную нелинейную функцию лишь с помощью одного промежуточного слоя, при этом сложность функции определят количество нейронов в промежуточном слое.
RBF не склона попадать в локальные минимумы, за счет этого обучается на порядок быстрее, чем MLP.

К недостаткам RBF можно отнести:

неумение экстраполировать результаты (при удалении от обучающего множества значение функции отклика быстро спадает до нуля), в то время как сеть MLP выдает более определенное решение для отклоняющихся данных.
RBF более ресурсоемкая, чем сеть MLP.
RBF требует большего числа обучающих примеров, чем сеть MLP.

Для определения оптимальной структуры сети можно воспользоваться автоматическим конструктором, который присутствует во многих программных пакетах, работающих с нейросетями. Конструктор переберет несколько нейросетей и выдаст сети, которые обладают наименьшей ошибкой на тестовых данных.

В литературе имеются свидетельства улучшения качества предсказаний за счет использования нейросетей с обратными связями. Такие сети могут обладать локальной памятью, сохраняющей информацию о более далеком прошлом, чем то, что в явном виде присутствует во входах. Однако нейросети с обратной связью не достаточно изучены.

Из-за случайности в выборе начальных значений синаптических весов, предсказания сетей, обученных на одной и той же выборке, будут, вообще говоря, разниться. Этот недостаток (элемент неопределенности) можно превратить в достоинство, организовав комитет нейро-экспертов, состоящий из различных нейросетей. Разброс в предсказаниях экспертов даст представление о степени уверенности этих предсказаний, что можно использовать для правильного выбора стратегии игры.

Легко показать, что среднее значений комитета должно давать лучшие предсказания, чем средний эксперт из этого же комитета. Пусть ошибка i -ого эксперта для значения входа x равна

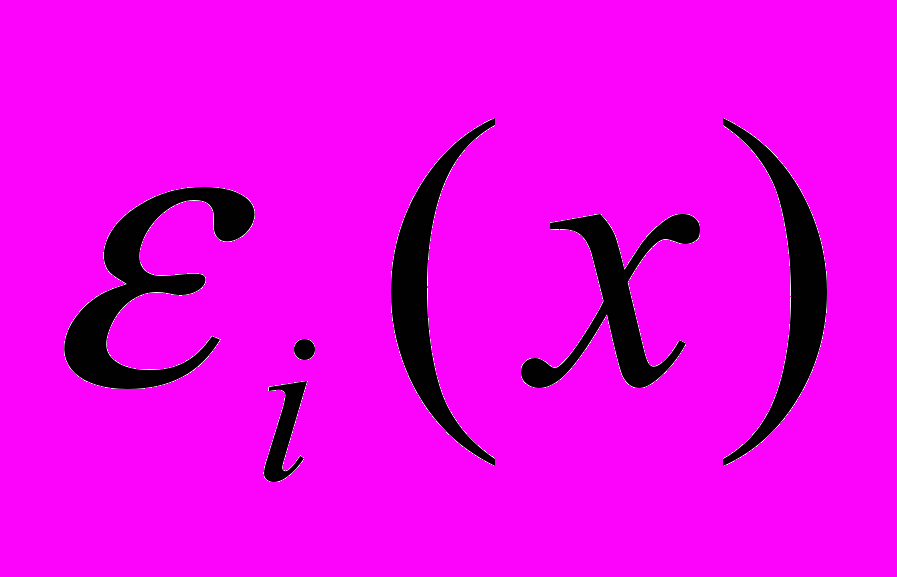. Средняя ошибка комитета всегда меньше среднеквадратичной ошибки отдельных экспертов в силу неравенства Коши:

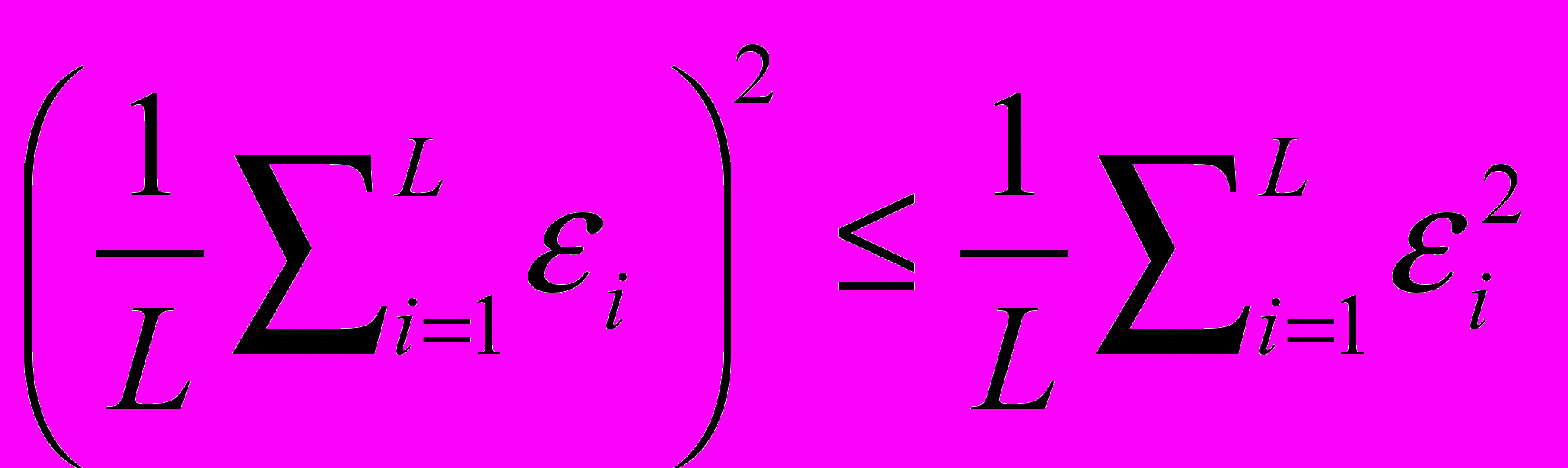. Причем, снижение ошибки может быть довольно заметным. Так, если ошибки отдельных экспертов не коррелируют друг с другом, т.е.

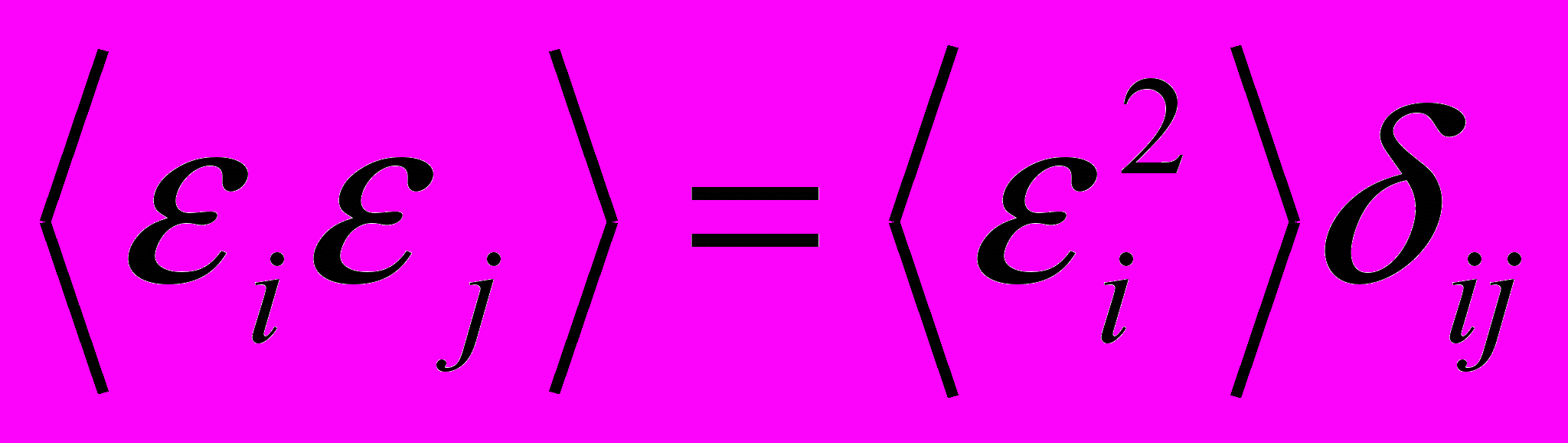, то среднеквадратичная ошибка комитета из L экспертов в

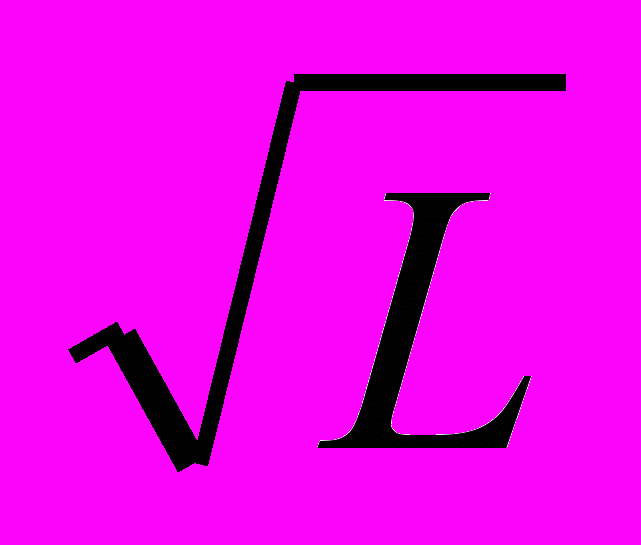раз меньше, чем средняя индивидуальная ошибка одного эксперта.

Можно пойти еще дальше и вместо среднего использовать взвешенное мнение сетей-экспертов. Веса выбираются адаптивно, максимизируя предсказательную способность комитета на обучающей выборке. В итоге, хуже обученные сети из комитета вносят меньший вклад и не портят предсказания.

Процедура обучения отдельных нейросетей стандартна. Имеющиеся примеры разбиваются на три выборки: обучающая, валидационная и тестовая. Первая используется для обучения, вторая - для выбора оптимальной архитектуры сети и/или для выбора момента остановки обучения. Наконец, третья, которая вообще не использовалась в обучении, служит для контроля качества прогноза обученной нейросети. Процедуру обучения сетей можно периодически повторять при накоплении определенного количества новых примеров.

В составе ИМС, в соответствии с данной методологией, возможно создание мощного инструмента для прогнозирования различных маркетинговых показателей. Данные прогнозы будут использованы при принятии управленческих решений, что позволит добиться более эффективного управления предприятием.
^

Список литературы

Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление. - М.: Мир, 1974.
Дюк В., Самойленко А. - Data Mining: учебный курс. - СПб: Питер, 2001.
Ежов А.А., Шумский С.А. Нейрокомпьютеринг и его применение в экономике и бизнесе - М.: Диалог-МИФИ, 1998.
Льюис К.Д. Методы прогнозирования экономических показателей. / Пер. с англ. - М.: Финансы и статистика, 1986.
Chorafas D.N. Chaos Theory in the Financial Markets, Probus Publishing, 1994.
Sauer T., Yorke, J.A., Casdagli, M. “Embedology”. Journal of Statistical Physics, 1991, 65, 579-616.
Weigend, A. and Gershenfield, eds. Times series prediction: Forecasting the future and understanding the past, Addison-Wesley, 1994.

Курбатский С.Н .Прогнозирование временных рядов как инструмент увеличения эффективности управления предприятием

Blog

Электронное научное издание «Труды мэли: электронный журнал»

Содержание

Курбатский С. Н. − аспирант МЭЛИ

Прогнозирование временных рядов как инструмент увеличения эффективности управления предприятием

Список литературы