Ольга Анатольевна Белимова Ответственный за выпуск: зам директора по учебно-методической работе Александр Александрович Петрухин Данные методические указания

Вид материала

Методические указания

Содержание Методические указания. Метод отбора Собственно-случайная выборка Механическая выборка Типический отбор. Серийный отбор. Комбинированный отбор. Многоступенчатым называется отбор Основные понятия Вопросы для самопроверки Ряды динамики. Методические указания. Абсолютный прирост Темп прироста Средний темп прироста Основные понятия Методические указания. Агрегатный индекс физического объема Основные понятия Вопросы для самопроверки ... Полное содержание

Подобный материал:

• К выполнению курсовой работы по дисциплине «Микроэкономика» для студентов II курса, 1508.71kb.
• Замураева Лариса Евгеньевна; Киселица Елена Петровна; Шумилова Юлия Александровна., 823.59kb.
• Светлана Ивановна Бессонова Ответственный редактор : зав кафедрой менеджмента, профессор,, 592.42kb.
• Н. В. Олейникова м 90 Актуальные проблемы музыкального образования, 97.8kb.
• Задачи, мероприятия Сроки Ответственный   Утверждение плана работы, решение организационных, 131.83kb.
• План учебно-методической работы школы на 2008-2009 уч год Ответственный: Зам директора, 192.28kb.
• Дерюгин Александр Александрович, Иванов Александр Владимирович, методические указания, 307.43kb.
• Ащеулова Зинаида Николаевна, зам директора по вр, Головко Тамара Семёновна, зам директора, 743.19kb.
• Методические объединения создаются, реорганизуются и ликвидируются директором Центра, 46.33kb.
• Профессионального образования и развитие рынка образовательных услуг для учащихся, 103.77kb.

Тема 5. Выборочное наблюдение.

Выборочное наблюдение как важнейший источник статистической информации. Основные способы формирования выборочной совокупности. Определение необходимого объема выборки. Малая выборка.

^ МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Под выборочным наблюдением понимается такое несплош­ное наблюдение, при "котором статистическому обследованию (наблюдению)' подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ста­вит перед собой задачу - по обследуемой части дать характери­стику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.

Предельная ошибка выборки определяется следующим образом.



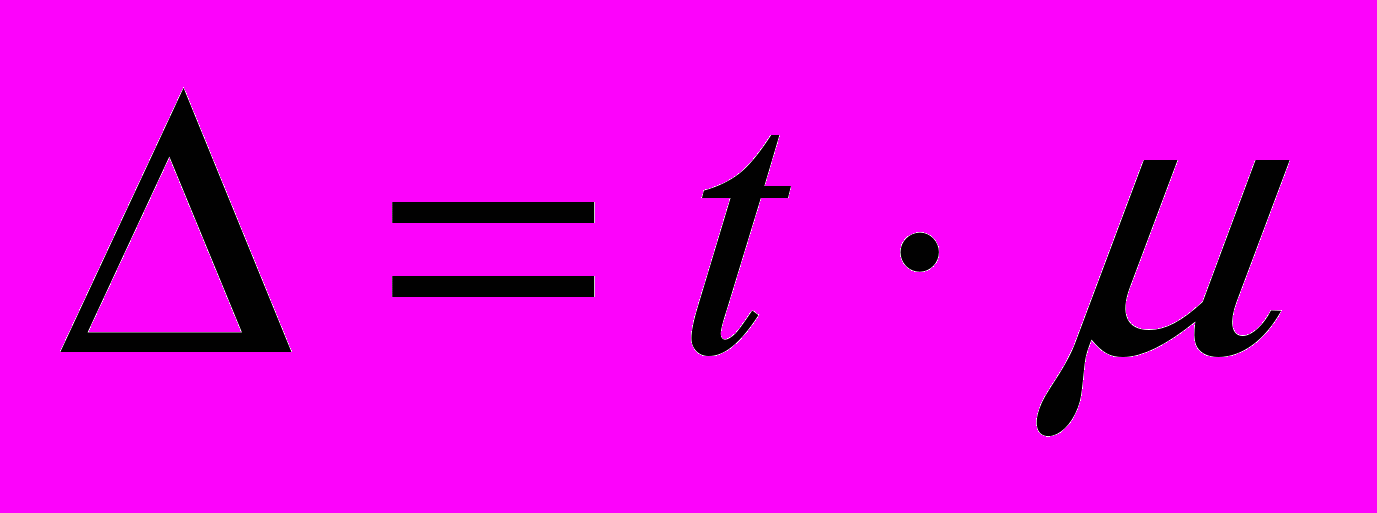
где: - средняя ошибка выборки

t- коэффициент доверия (его значение берется из таблицы).

Средняя ошибка выборки рассчитывается:

для повторного метода:



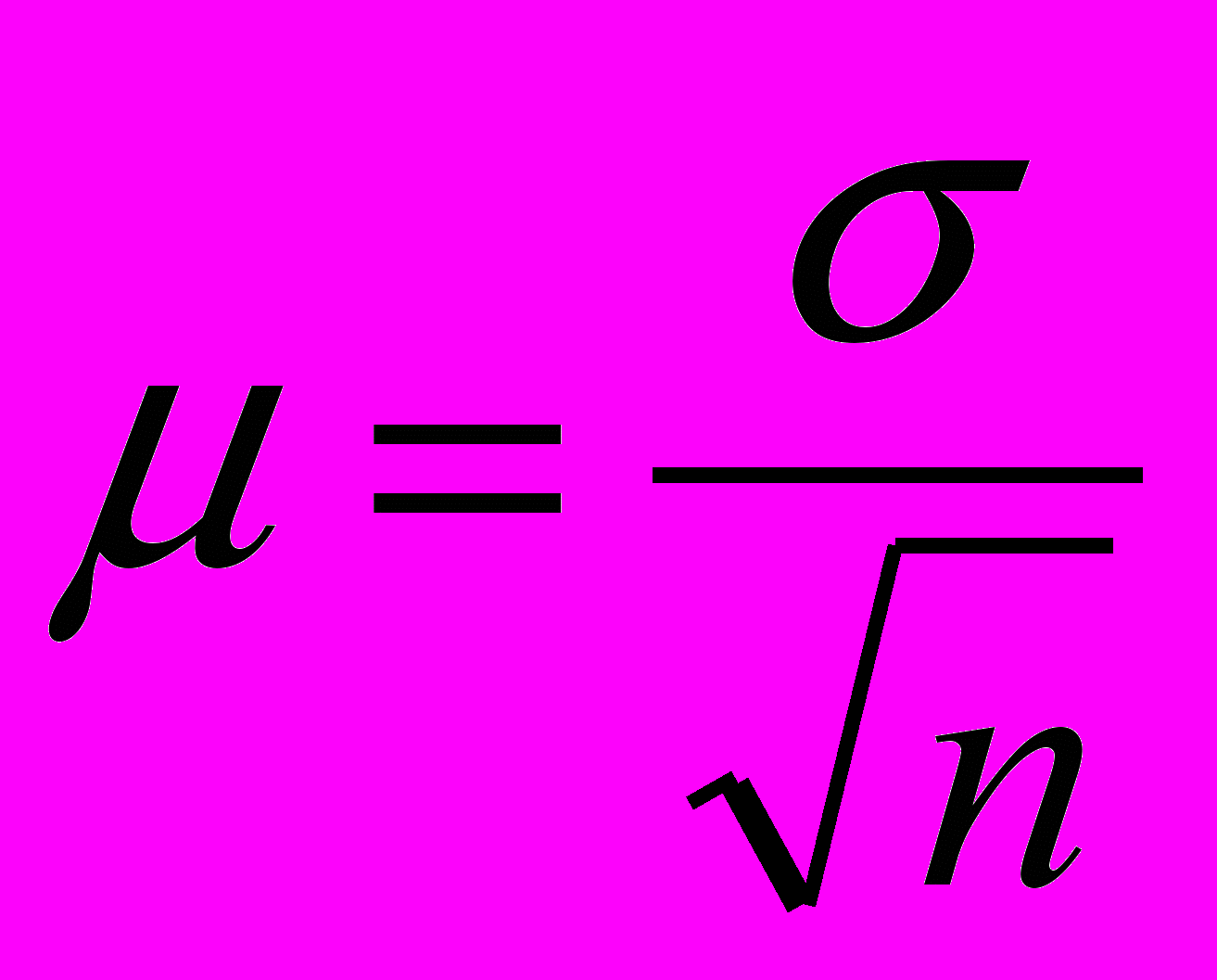
для бесповторного метода



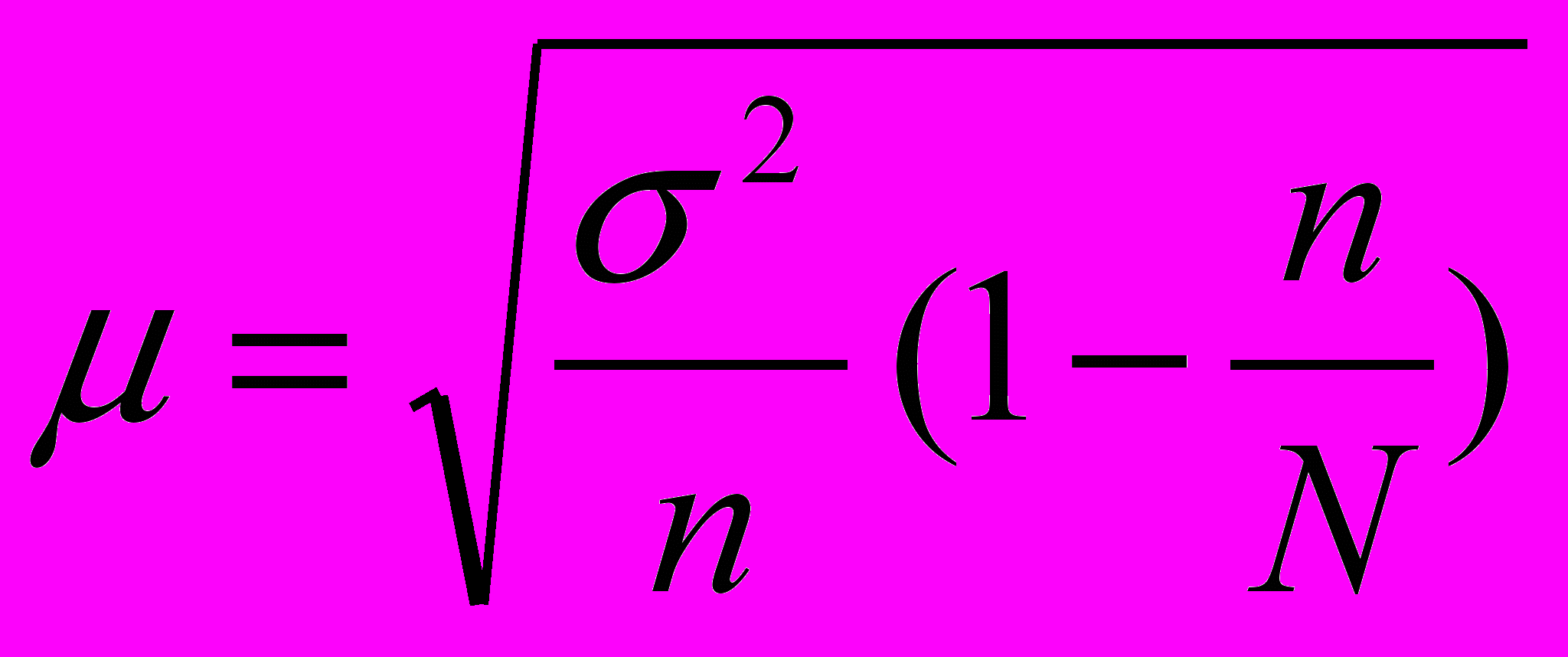
где N- объем генеральной совокупности

n- объем выборочной совокупности

Однако данные формулы применяются только для собственно-случайной выборки, для других способов отбора существуют свои формулы.

Расчет средней и предельной ошибки выборки позволяют определить возможные пределы, в которых находится характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:



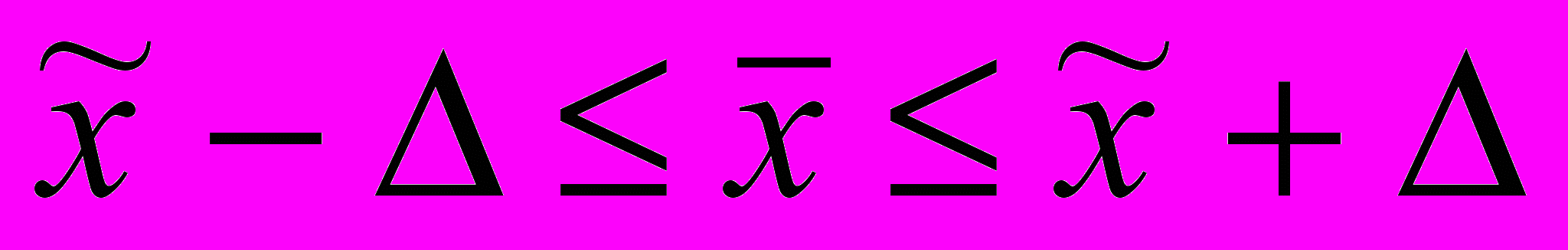
Для определений объема выборки необходимо также воспользоваться формулами соответственно способа и метода отбора.

^ Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.

Бесповторным называется такой отбор, при котором попав­шая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.

При повторном отборе попавшая в выборку единица пост регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшей процеду ре отбора. При этом методе отбора объем генеральной совокупности на всем протяжении процедуры выборки остается неизменным, что обусловливает постоянную вероятность попадания в выборку всех единиц совокупности.

Способ отбора определяет конкретный механизм или проце­дуру выборки единиц из генеральной совокупности. В практике выборочных обследований наибольшее распространение получи­ли следующие выборки:

• собственно-случайная;

• механическая;

• типическая;

• серийная;

• комбинированная.

^ Собственно-случайная выборка заключается в отборе еди­ниц из генеральной совокупности наугад или наудачу, без ка­ких-либо элементов системности

Собственно-случайный отбор может быть как повторным, так и бесповторным. После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предель­ная ошибки выборки.

^ Механическая выборка применяется в случаях, когда гене­ральная совокупность каким-либо образом упорядочена, т. е. имеется определенная последовательность в расположении еди­ниц (табельные номера работников, списки избирателей, теле­фонные номера респондентов, номера домов и квартир и т. п

Для проведения механической выборки устанавливается про­порция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей. Так, если из совокупности в 500 000 единиц предполагается получить 2%-ную вы­борку, т. е. отобрать 10 000 единиц, то пропорция отбора составляет

Для определения средней ошибки механической выборки используется формула средней ошибки при собственно-случай­ном бесповторном отборе

^ Типический отбор. Этот способ отбора используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп.

^ Серийный отбор. Данный способ отбора удобен в тех случа­ях, когда единицы совокупности объединены в небольшие груп­пы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объеди­нения. Сущность серийной выборки заключается в собственно-случайном либо механическом отборе серий, внутри которых производится сплошное обследование единиц.

Поскольку внутри групп (серий) обследуются все без исклю­чения единицы, средняя ошибка серийной выборки (при отбо­ре равновеликих серий) зависит от величины только межгруп­повой (межсерийной) дисперсии

^ Комбинированный отбор. В практике статистических обсле­дований помимо рассмотренных выше способов отбора приме­няется и их комбинация. Так, например, можно комбинировать типическую и серийную выборки, когда серии отбираются в установленном порядке из нескольких типических групп. Воз­можна также комбинация серийного и собственно-случайного отборов, при которой отдельные единицы отбираются внутри серии в собственно-случайном порядке. Ошибка такой выборки определяется ступенчатостью отбора.

^ Многоступенчатым называется отбор, при котором из гене­ральной совокупности сначала извлекаются укрупненные груп­пы, потом - более мелкие и так до тех пор, пока не будут ото­браны те единицы, которые подвергаются обследованию.

^ Основные понятия: выборочное наблюдение, выборочная совокупность, ошибка выборочного наблюдения, индивидуальный отбор, групповой отбор, комбинированный отбор, виды выборки, малая выборка.

^ Вопросы для самопроверки:

1. В чем преимущества выборочного метода исследования коммерческой деятельности в сравнении с другими вида­ми статистического наблюдения на рынке товаров и ус­луг?
   
2. Что такое "ошибка репрезентативности"? Каковы факто­ры ее возникновения при использовании выборочного метода изучения коммерческой деятельности?
   
3. Из каких последовательных этапов складывается закон­ченное выборочное изучение объектов коммерческой дея­тельности?
   
4. В чем отличия между способами повторного и бесповтор­ного отбора единиц изучаемой статистической совокупно­сти в выборку? Каковы особенности формул расчета ошиб­ки выборки при изучении коммерческой деятельности?
   
5. В чем отличия показателей "средней" и "предельной" ошиб­ки выборки, значение "коэффициента доверия"? Каковы особенности его применения в определении доверительных интервалов при осуществлении выборочного изучения ком­мерческой деятельности?
   

Тема 6. ^ Ряды динамики.

Понятие и классификация рядов динамики. Показатели измерения уровней ряда. Компоненты ряда динамики. Виды трендовой компоненты и проверка гипотезы о существовании тенденции. Методы расчета среднегодовых уровней. Приведение рядов динамики к одному основанию. Определение общей тенденции динамических рядов методом простой средней, аналитического выравнивания и скользящей средней. Расчет показателей сезонности.

^ МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Начиная изучение темы, необходимо обратить внимание на классификацию рядов динамики, различия между ними, так как отнесение ряда динамики, к тому или иному виды имеет важное значение для их изучения. Выбор соответствующих приемов и способе анализа определяется характером исходных данных и зависит от задач исследования.

В зависимости от способа выражения уровней (в виде абсолютных, относительных и средних величин) ряды динами­ки подразделяются на ряды абсолютных, относительных и средних величин. В зависимости от того, выражают уровни ряда состояние явления на определенные моменты време­ни (на начало месяца, квартала, года и т. п.) или его величину за определенные интервалы времени (например, за сутки месяц, год и т. п.), различают соответственно моментные и ин­тервальные ряды. Ряды динамики могут быть с равноотстоя­щими (по времени) уровнями и неравноотстоящими (по време­ни) уровнями.

Анализ скорости и интенсивности развития явления во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнения уровней между собой. К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста. При этом принято сравниваемый уровень называть отчетным, а уровень, с которым производят сравнение, - базисным.

^ Абсолютный прирост (у) характеризует размер увеличения (ли уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выра­жает абсолютную скорость роста.

Если уровень ряда сравнивается с предыдущим для данного ряда, то абсолютные приросты будут цепными. Если с постоянным (базисным) для данного ряда, то абсолютные приросты будут базисными.

Показатель интенсивности изменения уровня ряда в зависи­мости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или тем­пом роста(Т_р). Иными словами, коэффициент роста и темп роста представляют собой две формы выражения интенсивности изме­нения уровня.

Темп роста определяется отношение одного уровня ряда к другому. Он также может быть цепным или базисным.

Наряду с темпом роста можно рассчитать показатель ^ Темп прироста(Т_пр)., характеризующий относительную скорость изменил уровня ряда в единицу времени. Темп прироста есть отношение абсолютного прироста к уровню ряда, принятого за базу или рассчитывается как разность темпа роста за минусом 100% Если темп роста всегда положительное число, то темп прироста может быть положительным, отрицательным и равным нулю

В статистической практике часто вместо расчета и анализ темпов роста и прироста рассматривают абсолютное значение одного процента прироста |%|. Оно представляет собой одну со­тую часть базисного уровня и в то же время - отношение абсо­лютного прироста к соответствующему темпу прироста.

Средний уровень ряда динамики (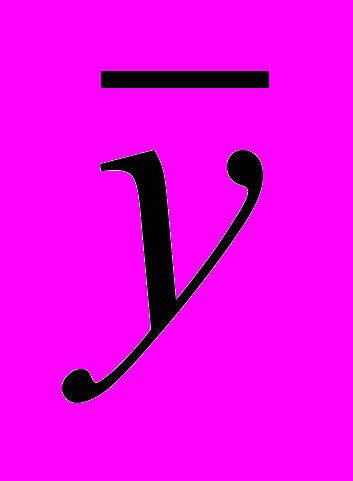) рассчитывается по сред­ней хронологической. Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов с равно­стоящими уровнями средний уровень находится по формуле средней арифметической простой, а для неравноотстоящих - по средней арифметической взвешенной.

Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста, оказывающий, во сколько раз в среднем за единицу времени изменился уровень динамического ряда.



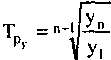
^ Средний темп прироста не может быть определен непосред­ственно на основании последовательных темпов прироста или показателей среднего абсолютного прироста. Для его вычисле­ния необходимо вначале найти средний темп роста, а затем уменьшить его на единицу, или 100%

Влияния эволюционного характера - это изменения, опреде­ляющие некое общее направление развития, как бы многолет­нюю эволюцию, которая пробивает себе дорогу через другие систематические и случайные колебания. Такие изменения дина­мического ряда называются тенденцией развития, или трендом.


^ Основные понятия: ряд динамики, уровень ряда динамики, хронологическая средняя, абсолютный прирост, средняя хронологическая, темп роста, темп прироста, абсолютное значение одного процента прироста, средний абсолютный прирост, средний темп роста, средний тем прироста, тренд, механическое сглаживание, аналитическое выравнивание, экстраполяция.

Вопросы для самопроверки:

1. Какое значение имеют ряды динамики в статистических исследованиях?

2. Какие виды рядов динамики различают?

3. Какие существуют формы средних уровней в рядах дина­мики (в зависимости от их вида)?

5. Как привести ряд динамики к сопоставимому виду

6. Какие Вы знаете методы определения общей тенденции развития явления во времени (их положительные и отрица­тельные особенности)? В чем ее сущность?

7. Как находятся индексы сезонности при различных методах определения тренда? В чем их сущность?


Тема 7. Индексы.

Понятие экономических индексов. Классификация индексов. Индивидуальные и общие индексы. Средние индексы. Индексы структурных сдвигов. Индексы пространственно-территориального сопоставления. Свойства индексов Ласпейреса и Паше. Идеальный индекс Фишера. Индексы-дефляторы. Индексы переменного и постоянного состава, их взаимосвязь. Факторный анализ.

^ МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Эта тема— одна из важнейших тем курса общей теории статистики. Уяснение сущности, общих правил и принципов построения индексных показателей позволит правильно при­менять их в конкретных экономико-статистических анализах. Индивидуальный индекс характеризует изменение во времени отдельных элементов той или иной совокупности, сводный – изменение социально-экономического явления, состоящего из непосредственно несоизмеримых элементов.

Основными вопросами построения общих индексов яв­ляются: выбор весов и соизмерителей конкретных индексов. Общие индексы являются индексами постоянного состава. Общие индексы качественных показателей (цен, себестоимос­ти, производительности труда и т.д.) строятся с постоянными весами отчетного периода, индексы количественных показа­телей (количества выпущенной продукции, физического объ­ема товарооборота) — с постоянными соизмерителями базис­ного периода.

При изучении агрегатных форм индексов необходимо понять, почему они являются основной формой общего ин­декса. В каждом агрегатном индексе важно выделить индек­сируемую величину и вес, понять роль каждой из этих вели­чин. Так, например, агрегатный индекс цен продукции — ин­декс качественного состава определяется по следующей фор­муле:

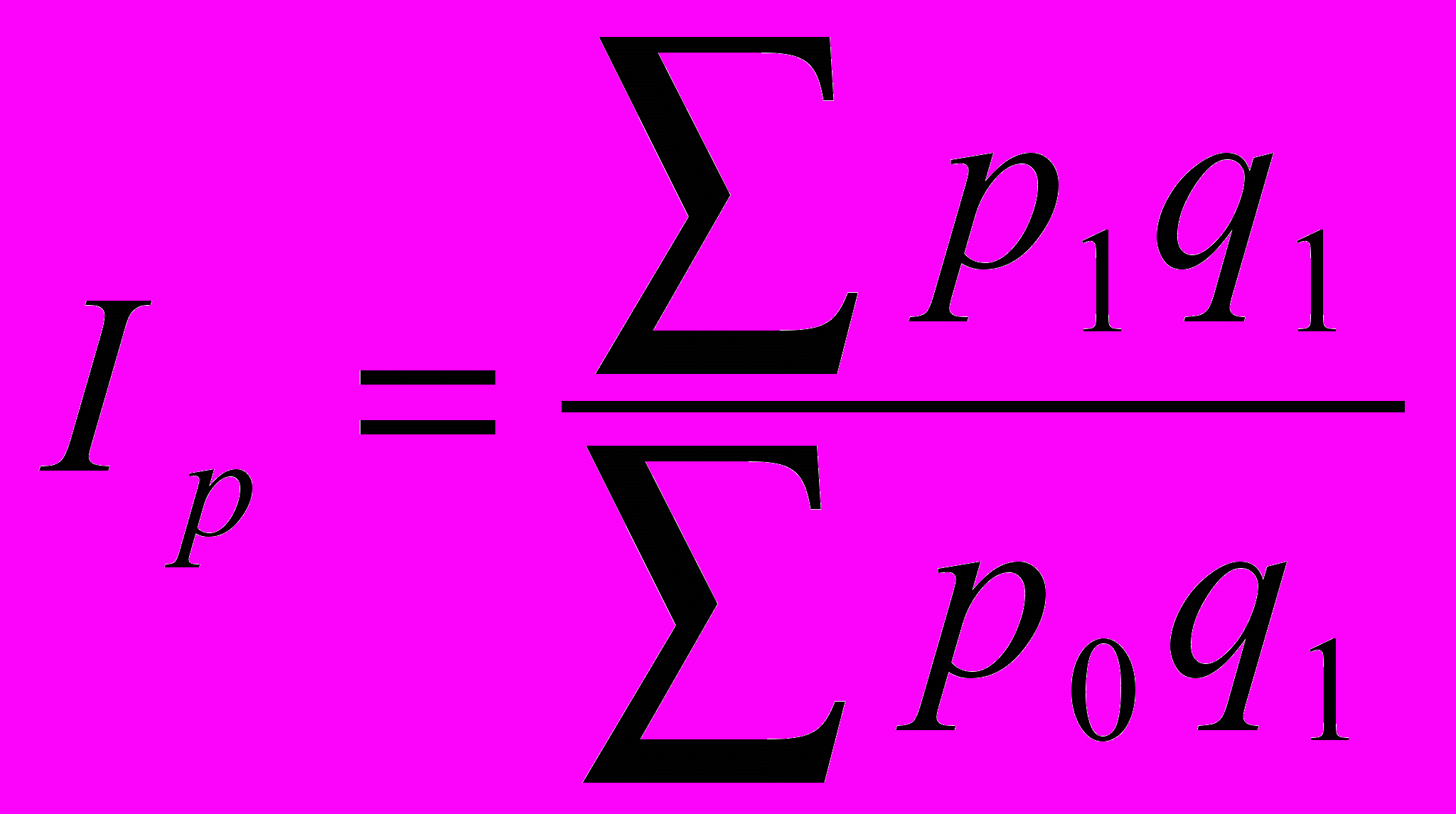. где


I_p - индекс цен

р — цена каждого вида продукции, руб.;

q — количество каждого вида проданной продукции в натуральных единицах;

о — базисный период,

1 — отчетный период.

^ Агрегатный индекс физического объема — индекс коли­чественного состава находится по формуле:



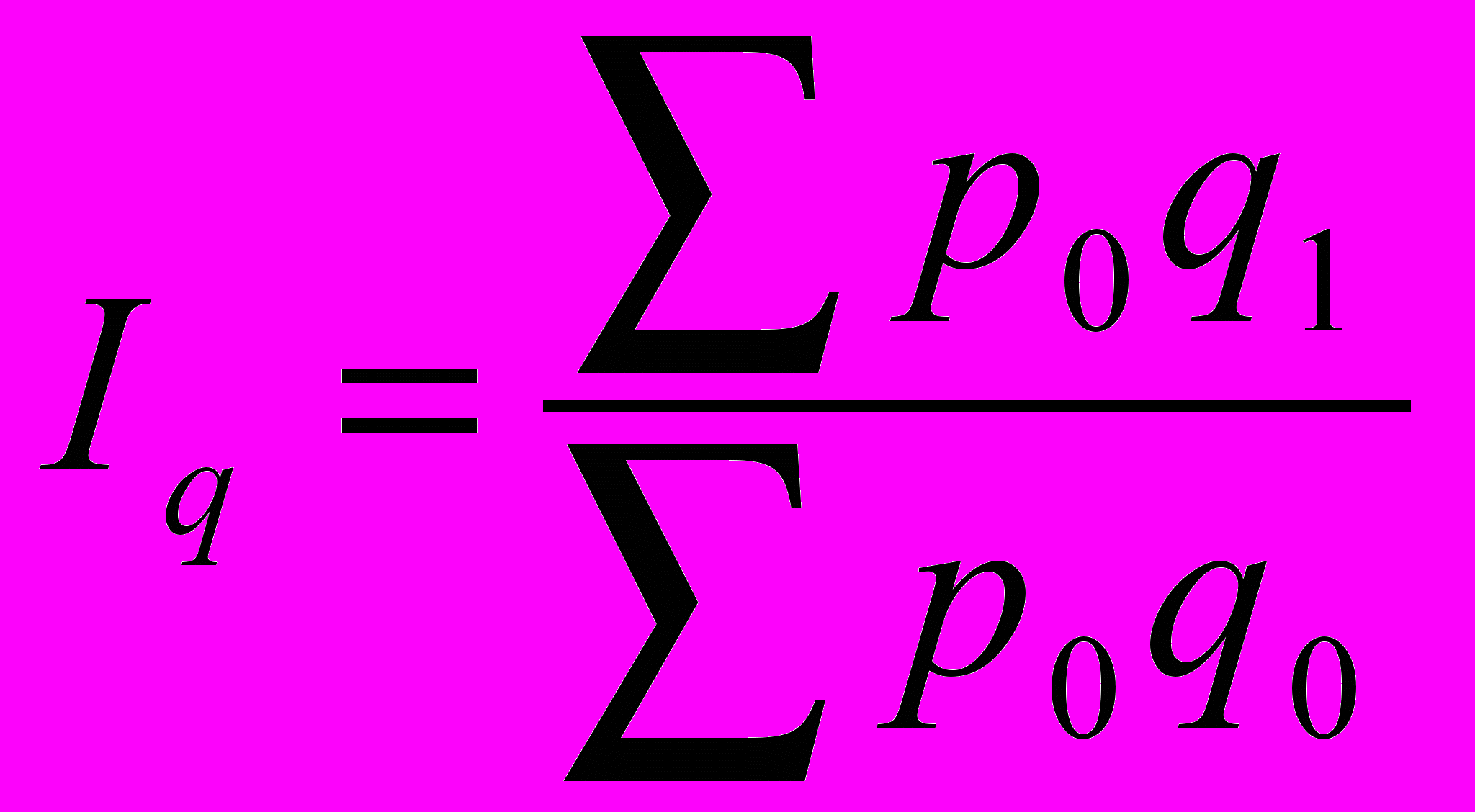
Существует взаимосвязь между индексами качественно­го и количественного состава:



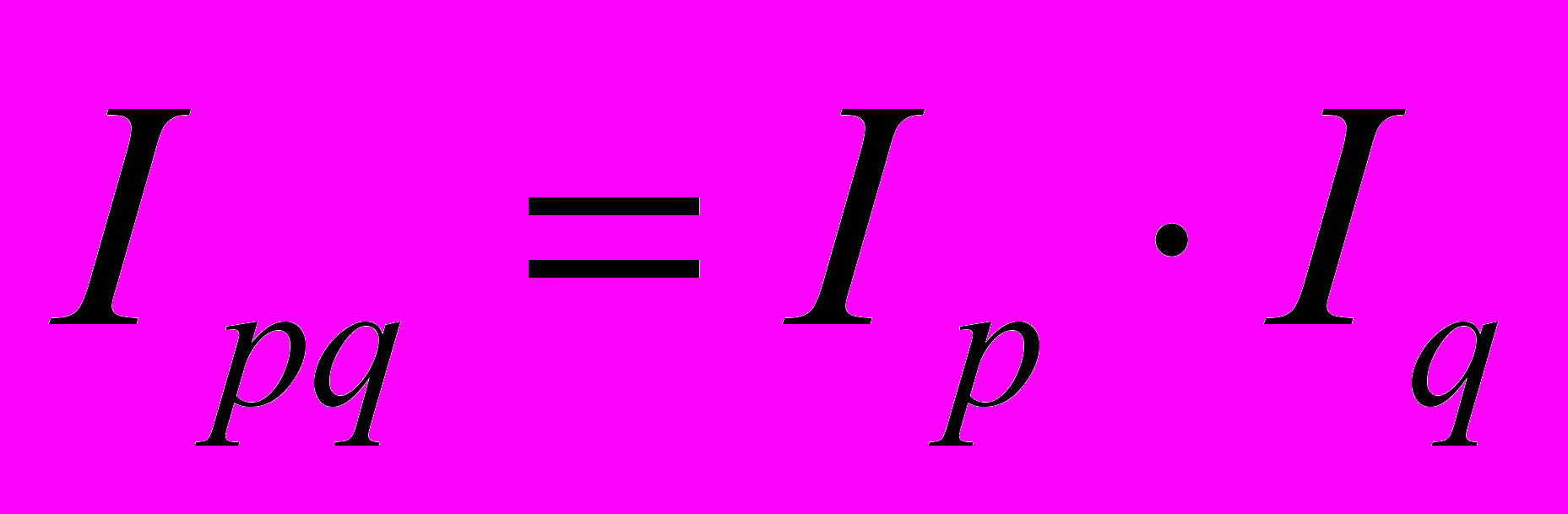
Индексная взаимосвязь дополняется факторной взаимо­связью индексов, которая выявляет роль отдельных факторов в изменении сложного несоизмеримого явления. Факторная взаимосвязь определяется как разность между числителем и знаменателем каждого вышеуказанного индекса, то есть:



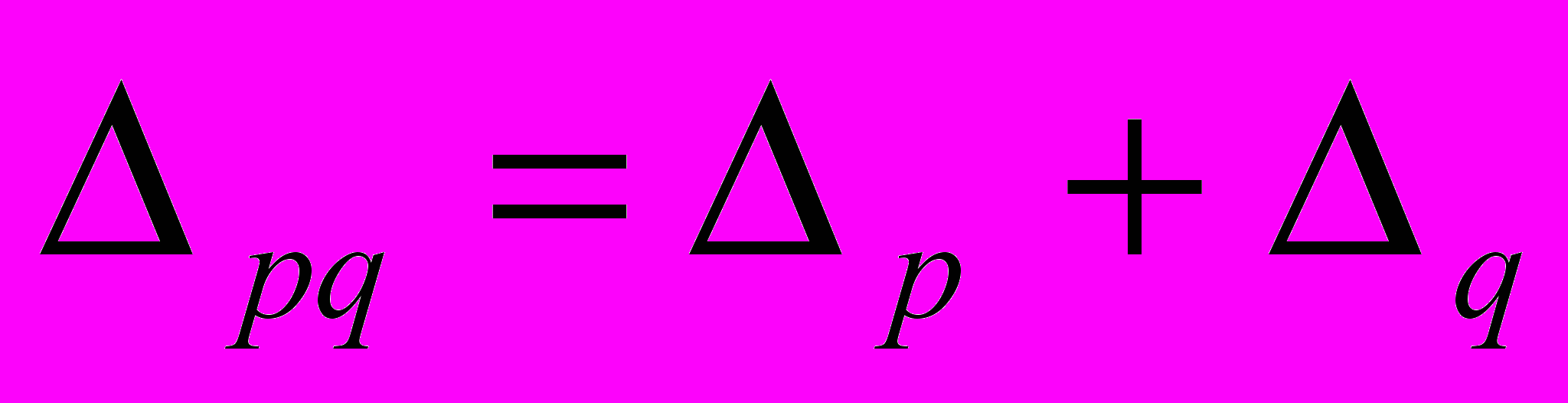
или




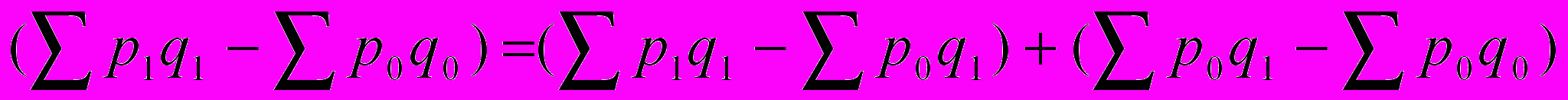
Следует уяснить, что только индексы качественного со­става измеряют экономический эффект, то есть, в нашем слу­чае Iр — индекс цен. Так, если Iр > 1, то р > 0 руб. — значит, в отчетном периоде по сравнению с базисным цены на продукцию повысились, и на сумму р, произошел перерас­ход денежных средств у населения (или у потребителя). В слу­чае, если Iр < 1, то, р < 0 руб. — значит в отчетном периоде по сравнению с базисным цены на продукцию снизились. На сумму р произошла экономия денежных средств у населе­ния (или у потребителя).

Другой формой общих индексов являются средние фор­мы индексов. Они тождественны агрегатным формам индек­сов качественного и количественного состава. Так, средне-гармонический индекс цен (себестоимости) тождественны агрегатному индексу цен (себестоимости), а среднеарифмети­ческий индекс физического объема — агрегатному индексу физического объема. Эти формы индексов применяются в том случае, когда исходные данные не позволяют использовать агрегатные формы индексов.

Среднегармонический индекс цен равен:



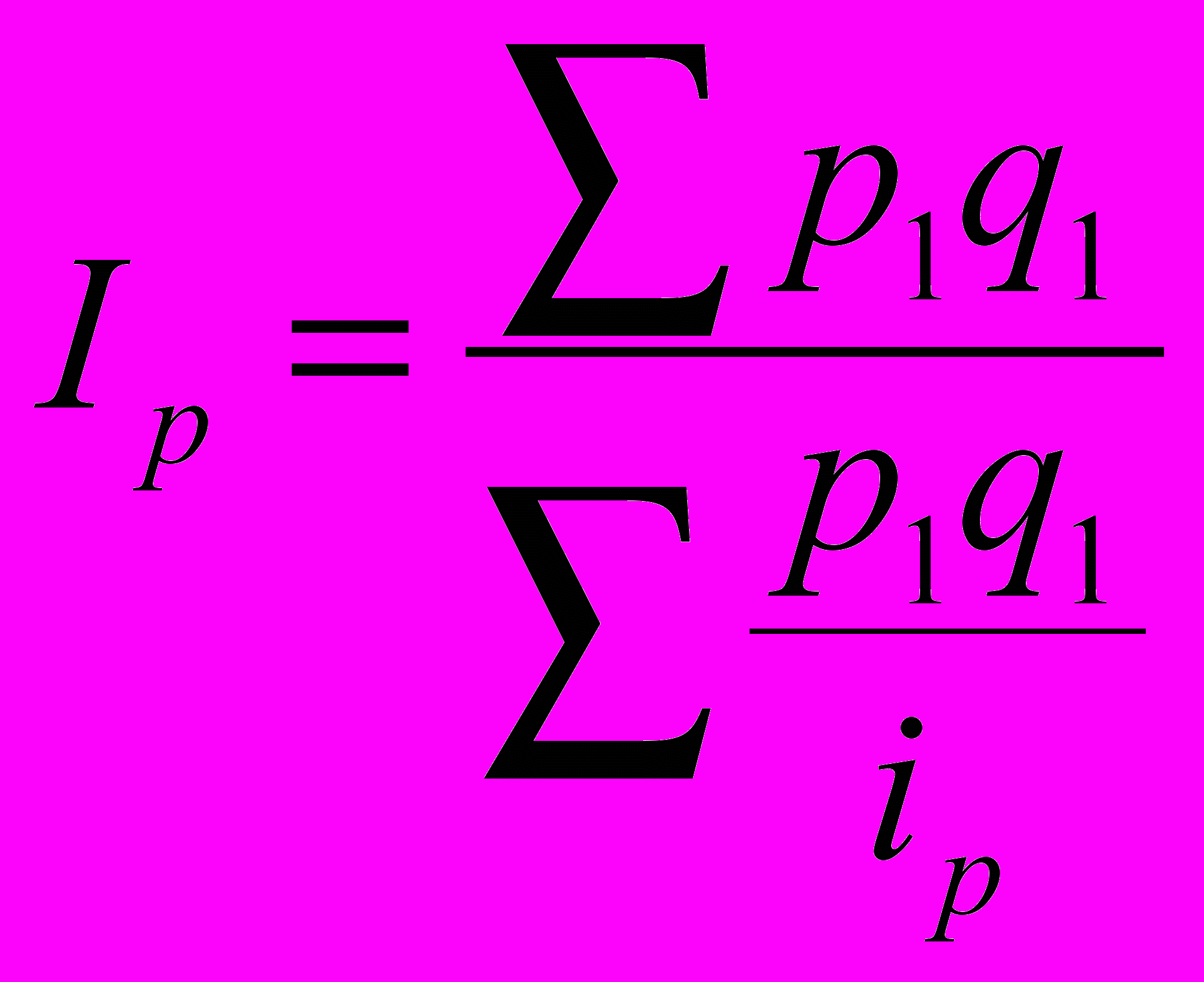
р и q — цена (руб.) и количество (в натуральном вы­ражении) каждого вида продукции;

i_p= 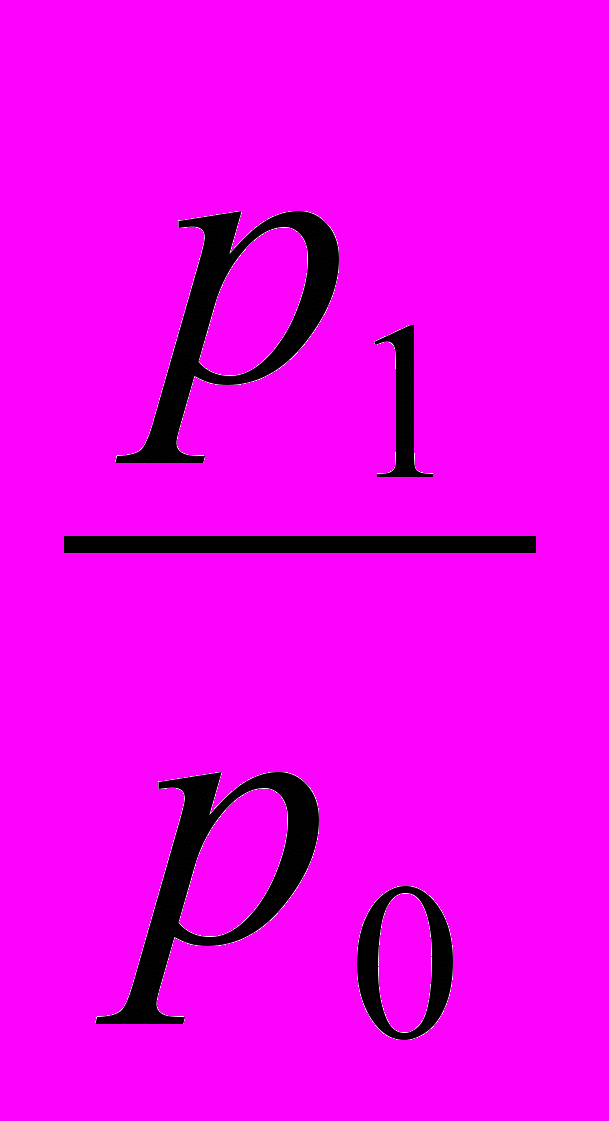-индивидуальный индекс цен (индекс цен на каждый вид реализованной продукции);

знаменатель дроби — условная стоимость реализованной продукции в отчетном периоде при неизменных, ба­зисных ценах продукции.

Среднеарифметический индекс физического объема равен:



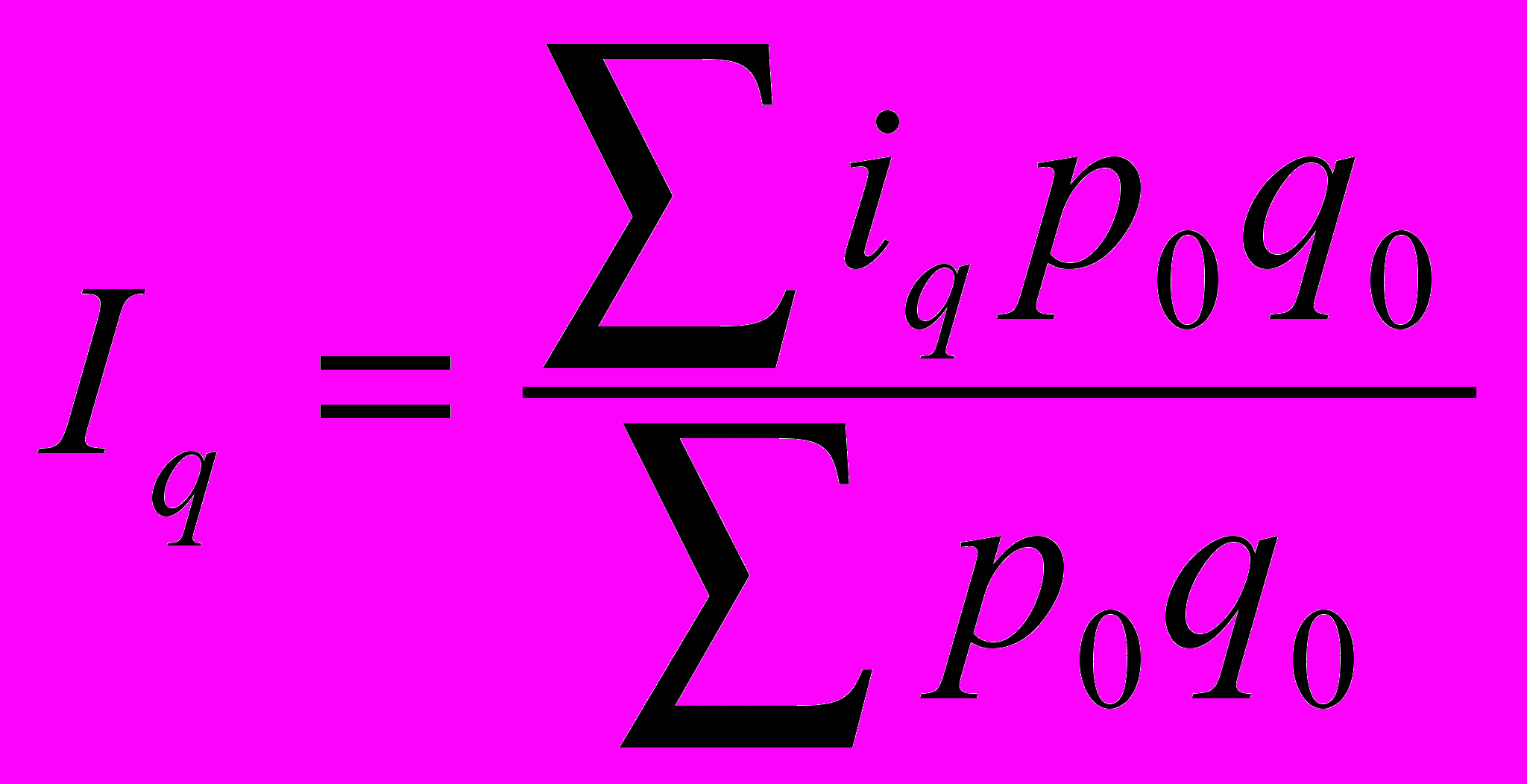
i_q=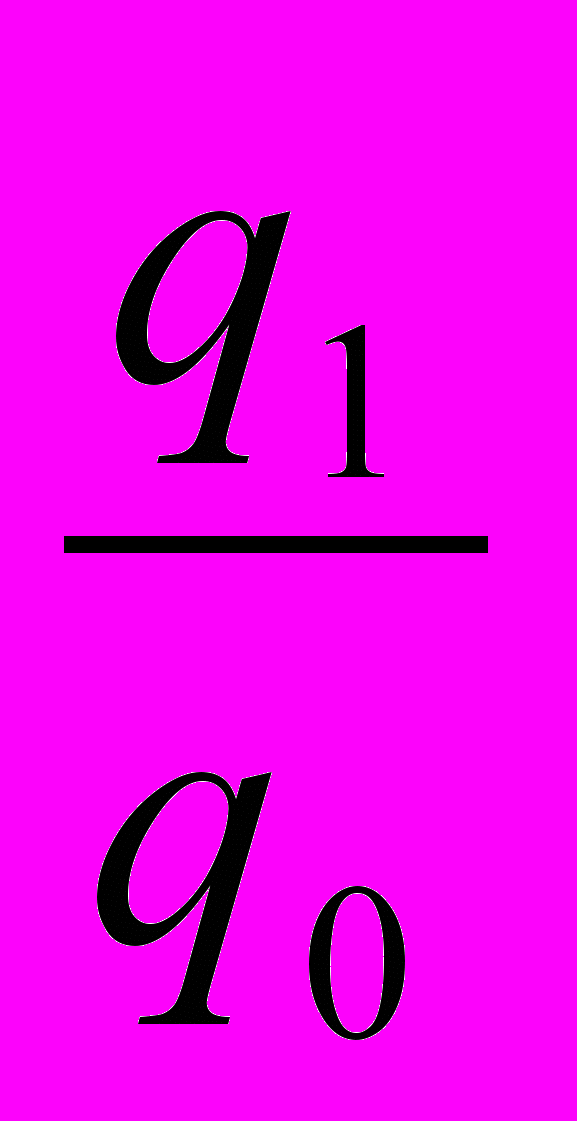— индивидуальный индекс физического объема каждого вида изделия.

Числитель дроби — условная стоимость продукции отчетного пе­риода при базисных ценах.

Экономический смысл этого индекса аналогичен агре­гатному индексу физического объема продукции.


^ Основные понятия: индекс, индивидуальный индекс, сводный индекс, агрегатный индекс, вес индекса, средний индекс, система базисных индексов, система цепных индексов, индекс переменного состава, индекс постоянного состава, индекс структурных сдвигов, территориальные индексы, индексы дефляторы.

^ Вопросы для самопроверки:

1. Каковы роль и задачи индексного метода в изучении коммер­ческой деятельности на рынке товаров и услуг?
   
2. На каких методологических принципах базируется получение обобщающих статистических индексов в оценке показателей коммерческой деятельности на рынке товаров и услуг?
   
3. Какова роль "весов" в построении индексов и в чем их значе­ние в индексном отношении? Какие основные методологичес­кие принципы положены в основу определения общих индек­сов?
   
4. В чем отличие между индексами с постоянными и перемен­ными весами? Каковы цели их применения в изучении ком­мерческой деятельности на рынке товаров и услуг?
   
5. При каких условиях возможен пересчет цепных индексов фи­зического объема товарооборота в базисные индексы?
   
6. Чем отличаются индексы переменного и постоянного состава и для каких целей они используются в изучении коммерчес­кой деятельности?
   

Тема 8. ^ Основные понятия корреляционного и регрессионного анализа.

Причинность, регрессия, корреляция. Парная регрессия на основе метода наименьших квадратов и метода группировок. Множественная регрессия. Оценка существенности связи. Принятие решения на основе управления регрессии. Собственно-корреляционные параметрические методы изучения связи. Оценка существенности корреляции.

^ МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Исследование объек­тивно существующих связей между явлениями - важнейшая задача теории статистики.

Социально-экономические явления представляют собой ре­зультат одновременного воздействия большого числа причин. При изучении этих явлений необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.

В основе первого этапа статистического изучения связей лежит качественный ана­лиз явления, связанный с анализом его природы методами эко­номической теории, социологии, конкретной экономики.

Второй этап - построение модели связи. Он базируется на методах статистики: группировки, средних величин, таблиц и т. д. Третий последний этап - интерпретация результатов, вновь свя­зан с качественными особенностями изучаемого явления. Статис­тика разработала множество методов изучения связей, выбор кон­кретного из которых зависит от цели исследования и от постав-. ленной задачи. Связи между признаками и явлениями, ввиду их большого разнообразия, классифицируются по ряду оснований. Признаки по их значению для изучения взаимосвязи делятся на два класса. Признаки, обусловливающие изменение других, свя­занных с ними признаков, называют факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называют результативными. Связи между явлениями и их признаками классифицируются по степени тесноты, по на­правлению и по аналитическому выражению В статистике различают функциональную связь, и стохасти­ческую зависимость. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.

Если причинная зависимость проявляется не в каждом от­дельном случае, а в общем, среднем при большом числе наблю­дений, то такая зависимость называется стохастической. Част­ным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативно­го признака обусловлено изменением факторных признаков.

По степени тесноты связи различают количественные крите­рии оценки тесноты связи.

По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений фак­торного признака происходит увеличение или уменьшение зна­чений результативного. По аналитическому выражению выделяют связи прямоли­нейные (или просто линейные) и нелинейные (криволиней­ные). Если статистическая связь между явлениями приближен­но выражена уравнением прямой линии, то ее называют линей­ной связью; если же она выражена уравнением какой-либо кривой линии (параболы, гиперболы: степенной, показательной, экспоненциальной и т. д.), то такую связь называют нелинейной или криволинейной

Для выявления наличия связи, ее характера и направления в статистике используются методы: приведения параллельных данных, аналитических группировок, графический, корреляции и регрессии.

Метод приведения параллельных данных основан на со­поставлении двух или нескольких рядов статистических вели­чин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере.

Парная регрессия характеризует связь между двумя призна­ками: результативным и факторным. Аналитически связь между ними описывается уравнениями:

прямой

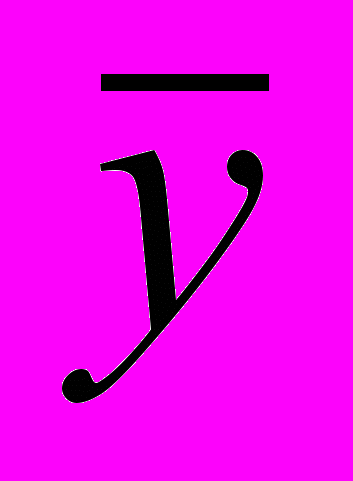
параболы 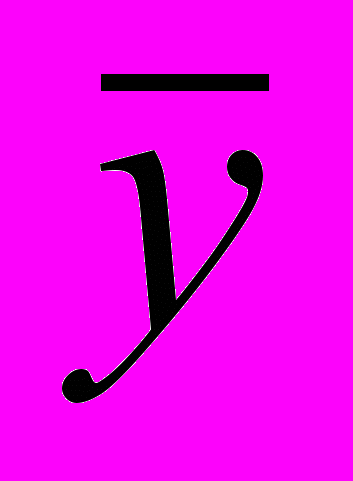= а₀ + а₁х+а₂х

гиперболы 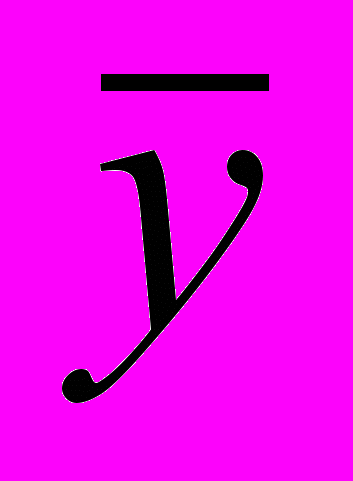= а₀ + а₁;

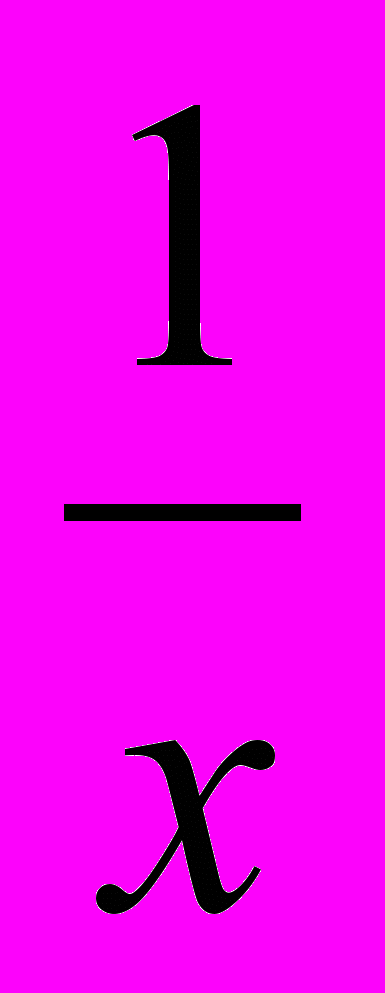Множественная (многофакторная) регрессия. Изучение связи между тремя и более связанными между собой признака­ми носит название множественной (многофакторной) регрес­сии.

Изменение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений.

Теснота связи при линейной зависимости измеряется с помо­щью линейного коэффициента корреляции. В статистической теории разработаны и на практике приме­няются различные модификации формул расчета данного коэф­фициента.


^ Основные понятия: признак, причинно-следственные отношения, результативный признак, факторный признак, функциональная связь, стохастическая связь, корреляционная связь, прямая связь, обратная связь, линейная связь, нелинейная связь, корреляции, регрессионный анализ, парная регрессия, множественная регрессия, коэффициент эластичности, коэффициент детерминации, линейный коэффициент корреляции, корреляционные отношения, множественный коэффициент корреляции, частный коэффициент корреляции.

^ Вопросы для самопроверки:

1. Какие виды связи изучаются статистикой между показате­лями коммерческой деятельности?
   
2. В чем состоит отличие между функциональной и корреля­ционной связью социально-экономических явлений?
   
3. Какие основные методологические вопросы решаются при изучении корреляционной связи показателей коммерчес­кой деятельности? Как используется при этом метод науч­ной абстракции?
   
4. Из каких основных этапов состоит законченное статисти­ческое изучение корреляционной зависимости показателей коммерческой деятельности?
   
5. Каковы условия признания типичными полученных в ана­лизе параметров уравнения регрессии? Какова при этом роль t-критерия Стьюдента?