Geum.ru

Кафедра психологии

Вид материалаДокументы

Содержание


Распределение индивидуальных различий
Нормальное распределение
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   46
Глава 2 РАСПРЕДЕЛЕНИЕ ИНДИВИДУАЛЬНЫХ

РАЗЛИЧИЙ

В повседневной речи часто можно слышать, что кто-то «обладает» какой-то способностью, а кто-то — нет. Джонс умеет писать, Смит — нет. У Елены есть талант к музыке, у Дорис — к рисованию, у Дика — к математике, у Сэма — к руководству. Такие характеристики основаны на произвольных утверждениях, продиктованных практическими потребностями. Чтобы избрать, например, музыку в качестве своей профессии или просто в качестве серьезного увлечения, индивид должен обладать минимальным музыкальным талантом. Если степень его музыкальных способностей находится ниже этого минимума, его не считают «музыкальной личностью». Для нас стало привычным, описывая индивида, говорить о его выдающихся способностях и дарованиях и просто-напросто игнорировать те его качества, в которых он показывает средние результаты. Поэтому мы называем м-ра Блэка творчески мыслящим человеком, м-с Вентворт — хорошей собеседницей, а м-ра До человеком спортивным. Мы обычно не отзываемся о м-ре Блэке как о посредственном спортсмене, о м-с Вентворт как о не очень творческой личности и о м-ре До как о малоинтересном собеседнике!

Каждый день мы сталкиваемся с резкими качественными различиями людей. Однако при ближайшем рассмотрении оказывается, что все индивиды обладают всеми качествами и что по степени обладания каждым конкретным качеством их можно распределить вдоль длинной шкалы. Иными словами, люди не укладываются в четко разграниченные категории. Различия между людьми — вопрос степени. В этом смысле можно сказать, что индивидуальные различия носят скорее количественный, чем качественный характер.

Можно возразить, что существует по крайней мере несколько характеристик, которыми человек либо обладает, либо не обладает, и что в этом отношении мы все же можем говорить о

2 Дифференциальная психология

34 Дифференциальная психология

качественных различиях. Классическим примером этого может являться потеря зрения или слуха. В этом случае соответствующее качество либо присутствует у человека, либо отсутствует у* него: он видит или не видит; слышит или не слышит. Но это также оказывается чисто условным и житейским разделением. Каждый, кто посещает школу для слепых, знает, что существуют разные степени слепоты и что не все те, кого называют слепыми, абсолютно ничего не видят. Бытовое определение слепоты — это всего лишь некая степень недостаточности зрения, слишком серьезная, чтобы вести нормальный образ жизни. То же самое справедливо для глухоты и любого другого сенсорного нарушения. Между эмпирически определяемым «нормальным» зрением или слухом и тем, что называется слепотой или глухотой, находится множество промежуточных степеней. Необходимо добавить, что если зрение находится на нулевой отметке, уровне полной слепоты, то это вовсе не противоречит количественному подходу к индивидуальным различиям. Из последнего следует, что промежуточные степени встречаются гораздо чаще, чем простое наличие или отсутствие какого-либо качества.

^ РАСПРЕДЕЛЕНИЕ ИНДИВИДУАЛЬНЫХ РАЗЛИЧИЙ

Поскольку индивидуальные различия в обозначенном выше смысле носят количественный характер, возникает вопрос, как различные степени каждого качества распределяются среди людей. Происходит ли распределение индивидов равномерно по всему ряду этих степеней, или они как бы группируются вокруг одного или нескольких пунктов? Какова относительная частота проявления различных степеней? На эти вопросы лучше всего отвечать, анализируя частотные распределения и графики частоты.

Подобно другим методам статистики, частотное распределение представляет собой суммирование и обработку количественных данных, которые производятся для понимания общей картины и выявления существенных тенденций. Результаты тестирования или любые другие серии измерений группируются в классы, и все случаи, лежащие внутри каждого класса, заносятся в таблицу. Таблица 1 представляет собой пример та-

распределение индивидуальных различий 3 5

кого частотного распределения. В ней приводятся результаты тестирования 1000 студентов колледжа на умение применять код, в котором необходимо было один набор бессмысленных слогов заменить на другой. Данные, показывающие количество правильно замененных за две минуты слогов, находились в интервале от 8 до 52. Они были сгруппированы по интервалам (по 4 пункта в каждом), начиная с 52—55 на верхней точке распределения и заканчивая 8—11 на нижней. Колонка под названием «частота» в таблице 1 показывает количество людей, чьи результаты лежат в этих интервалах. Например, показатели, находящиеся в пределах 52 и 55, зафиксированы только у одного человека, значения между 48 и 51 — тоже у одного, а значения между 44 и 47 — у двадцати и так далее. Очевидно, что результаты данного теста гораздо легче увидеть при помощи такого распределения, чем рассматривая лист, содержащий 1000 первичных результатов.

Еще удобнее иметь дело с показателями частотного распределения, если изобразить их графически. Рисунок 2 представляет данные таблицы 1 в графической форме. На горизонтальной оси даны результаты, сгруппированные в интервалы; числа на вертикальной оси означают количество случаев внутри каждого интервала.

График сделан в двух формах, которые обычно широко используются. Одна графическая форма называется полигоном частот, в котором число индивидов внутри каждого интервала обозначено точкой, расположенной напротив центра интервала; последовательность точек затем была соединена прямыми линиями. Другая графическая форма образуется прямыми колонками, или прямоугольниками, основаниями которых служат интервалы высота каждой колонки зависит от числа случаев в данном интервале. Такая графическая форма называется гистограммой. Если взглянуть, например, на интервал 44—47 в таблице 1, то можно найти 20 случаев результирующих значений, находящихся в его пределах. Соответственно на рисунке 2 точка ставится на пересечении проекции от 20 и проекции центра интервала 44—47. Мы получаем одну из точек, необходимых для построения частотного полигона. В гистограмме те же 20 случаев представлены колонкой 44—47 интервала, ограниченной сверху проекцией числа 20, находящегося на вертикальной оси.

36 Дифференциальная психология *

Таблица 1 Частотное распределение данных 1000 студентов колледжа, тестирование умения применять код. (Данные из Анастази, 2, с. 34.)

Класс—интервал
Частота

52-55 48-51 44-47 40-43 36-39 32-35 28-31 24-27 20-23 16-19 12-15 8-11
1

1

20 73 156 328 244 136 28

8

3

2




N = 1000



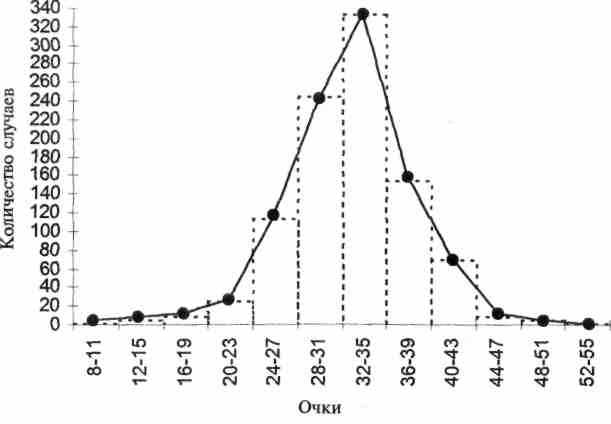
Рис. 2. График распределения: полигон частот и гистограмма. (Данные из таблицы 1.)

Распределение индивидуальных различий 3 7

Мы можем продолжить описание группы, определив ее центральную тенденцию. Если мы захотим получить наиболее типичное значение, которое характеризовало бы группу в целом, то необходимо определение главной тенденции. Одним из наиболее известных способов является вычисление средней величины, получаемой при сложении всех показателей и делении полученной суммы на число случаев. Такая величина называется средним арифметическим.

Другим способом определения главной тенденции, часто используемым в психологии, является медианный. Если все результирующие значения расположить по порядку в соответствии со своей величиной, то медианой будет результат, расположенный ровно посередине ряда. Для больших групп гораздо легче вычислить медиану непосредственно на основе частотного распределения. В этом случае медианная точка разделяет распределяемое множество таким образом, что половина случаев будет находиться выше нее, а другая половина — ниже. Еще одним способом измерения главной тенденции, иногда встречающимся в психологических исследованиях, является определение моды, или наиболее часто встречающегося показателя. Его так же можно найти на основе частотного распределения, выявив ту точку интервала, которая имеет самую большую частоту. Заметим, что мода соответствует самой высокой точке графика. Для распределения, данного в таблице 1 и на рисунке 2, среднеарифметическое значение составляет 32,37, медианное — 32,46 и значение моды — 33,5.

^ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Читатель наверняка уже обратил внимание на особенности распределения, представленного в таблице 1 и на рисунке 2. Большинство случаев расположены в центре ряда, а приближаясь к крайним значениям, происходит долгий плавный спад. На графике нет разрывов — нет классов, которые были бы отделены друг от друга. Кроме этого, график по обе стороны симметричен; это означает, что если его разделить вертикальной линией по центру, то получившиеся две половинки окажутся примерно одинаковыми. Такой график распределения своей формой похож на коло-

кол, это так называемое «нормальное распределение», которое чаще всего встречается при измерениях индивидуальных различий. В своем идеальном виде нормальное распределение изображено на рисунке 3.

Понятие нормального распределения в статистике используется уже давно. Вероятность какого-либо события представляет собой частоту его наступления, зафиксированного очень большим количеством наблюдений. Эта вероятность представляет собой определенное соотношение, точнее, дробь, числителем которой является ожидаемый результат, а знаменателем — все возможные результаты. Таким образом, вероятность, или шансы, того, что две монеты выпадут одной и той же стороной, например решкой, будет один к четырем, или '/4. Это следует из того факта, что существует всего четыре возможные комбинации выпадения монет РР, РО, ОР, ОО, где Р — решка, а О — орел. Одна из четырех, РР, означает выпадение только решек. Вероятность выпадения двух орлов будет также составлять '/4, а вероятность выпадения решки какой-либо одной монеты при выпадении орла другой составит один к двум, или '/2. Даже если число монет увеличить, скажем, до 100, и количество возможных комбинаций станет очень большим, то

мы по-прежнему сможем математически определить вероятность возникновения каждой комбинации, например, выпадения всех решек или 20 решек и 80 орлов. Эти вероятности, или ожидаемую частоту выпадений, можно изобразить графически описанным выше методом. Если число монет будет очень велико, то построенный график окажется колокольной формы, то есть графиком нормального распределения.

На рисунке 4 можно найти теоретический и фактический



0 1 2 3 4 5 6 Количество выпадений решек

Рис. 4. Теоретическое (пунктир, линия) и фактически наблюдаемое (сплошная линия) распределение количества выпадений решек в 128 случаях подбрасывания шести монет. (Данные из Гилфорда, 10, с. 119.)



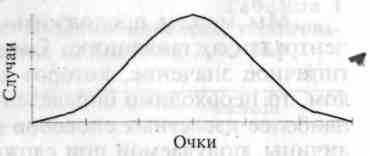
Рис. 3. График нормального распределения

Распределение индивидуальных различий 3 9

графики, показывающие количество выпадения решек в 128 случаях подбрасывания шести монет. При каждом броске число решек, естественно, может варьироваться от 0 до 6. Чаще всего будет выпадать комбинация из трех решек (и трех орлов). Частота возрастает или понижается, когда число решек становится меньше или больше трех. На рисунке 4 теоретически вычисленные вероятности обозначены пунктирной линией, в то время как реальная частота, полученная в результате 128 последовательных подбрасываний шести монет, начерчена непрерывной линией. Необходимо заметить, что ожидаемые и фактически полученные результаты достаточно близки друг к другу. Чем больше количество наблюдений (или бросков), тем больше вероятность их совпадения.

Чем большее количество монет подбрасывается, тем ближе будет график теоретически ожидаемого распределения к графику нормальной вероятности. Говорят, что результаты, получаемые при подбрасывании монет или бросании игральных костей, зависят от «случайности». Под этим подразумевается, что результат определяется большим количеством независимых факторов, влияние которых учесть невозможно. Высота, с которой бросают монету или игральную кость, ее вес и размер, подкрутка, которую делает бросающий, и многие другие подобные факторы определяют в каждом отдельном случае, какой стороной упадет монета. График нормального распределения был впервые построен математиками Лапласом и Гауссом в связи с исследованиями ими игры случая, распределения отклонений в наблюдениях и других типов случайных изменений.

Уже в девятнадцатом веке бельгийский статистик Адольф Кутелет первым применил понятие нормального распределения к исследованию качеств человека (ср. 4). Кутелет обратил внимание на то, что определенные измерения роста, объема грудной клетки армейских призывников распределялись в соответствии с графиком вероятности колокольной формы. На основании сходства этого графика с данными человеческой изменчивости, он построил теорию, согласно которой такая человеческая изменчивость имеет место, когда природа стремилась воплотить «идеал», или норму, но в силу различных обстоятельств потерпела неудачу. Иными словами, человеческий рост, вес, уровень интеллектуального развития зависят от огромного количества не-

40 Дифференциальная психология

зависимых факторов, так что конечный результат окажется распределенным в соответствии с теорией вероятности. Опыт Куте-лета по применению графика нормального распределения был переосмыслен и развит Гальтоном, чей вклад в дифференциальную психологию уже обсуждался нами в главе 1. У Гальтона график нормального распределения получил широкое и разнообразное применение, многие наработки были связаны с кванти-фикацией и преобразованием данных, касающихся как индивидуальных, так и групповых различий.

Определить, является ли распределение, воспроизведенное в таблице 1 и на рисунке 2, «нормальным» можно путем применения соответствующих математических процедур. Несмотря на незначительные отклонения, этот график не отличается существенно от графика нормального распределения. Таким образом, мы можем сделать вывод, что его расхождение с нормой находится в пределах ожидаемых флуктуации, и считать его графиком нормального распределения. Многие распределения, открытые в дифференциальной психологии, так же соответствуют математическим вариантам нормального распределения, особенно когда они получаются в результате применения тщательно сконструированных измерительных приборов на больших репрезентативных выборках. В остальных случаях распределение может соответствовать нормальному лишь приблизительно. Оно может

представлять собой некую непрерывность и быть более или менее симметричным, отражая то, что большинство индивидов находятся в центре ряда, а ближе к крайним значениям их количество постепенно и плавно снижается.

На рисунках 5—10 мы видим примеры графиков распределения, отражающих широкое разнообразие свойств человека. Эти распределения



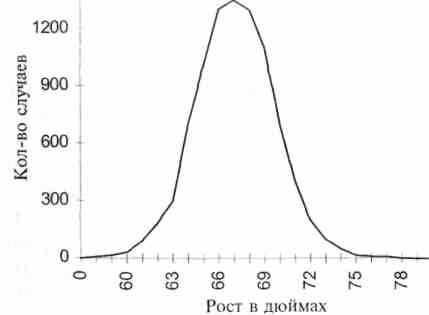
Рис. 5. Распределение роста у 8585 коренных

англичан. (Данные из Юля

и Кенделла, 34, с. 95.)



41

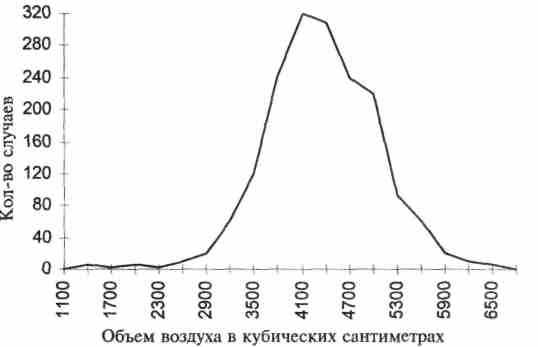
Рис. 6. Распределение качества, связанного с возможностями легких, у 1633 студентов мужского колледжа. (Данные из Харриса и др., 12, с. 94.)

были выбраны специально, потому что они основаны на больших репрезентативных выборках, большинство из которых включало в себя 1000 и более случаев. Два графика, построенные для меньших групп, приводятся для того, чтобы показать распределение физиологических и личностных характеристик в таких областях, где данные для больших групп сравнительно скудные.

Пример распределения слабоструктурированного качества дан на рисунке 5, который показывает рост в дюймах 8585 коренных англичан. Можно заметить, что график практически совпадает с математически нормальным графиком. На рисунке 6 представлен частотный график более функционального, физиологического качества, связанного с возможностями легких. Это измеряющийся в кубических сантиметрах объем воздуха, который выдувается из легких после максимально глубокого вдоха. Необходимые для построения графика измерения были сделаны на 1633 студентах мужского колледжа. Общее соответствие нормальному графику здесь так же очевидно.

Рисунок 7 связан с физиологическими измерениями, которые, как считается, имеют отношение к эмоциональным и личностным свойствам. На нем показано распределение показателей 87 детей по данным композиционного измерения автономного баланса. Высокие результаты в этом исследовании показывают функциональное преобладание парасимпатического от-

42 Дифференциальная психология

дела периферической нервной системы; низкие значения — функциональное преобладание ее симпатического отдела. Для психологов периферическая нервная система представляет особый интерес, он связан с той ролью, которую она играет в эмоциональном поведении.

График, представленный на рисунке 8 иллюстрирует распределение результатов теста на скорость и точность восприятия. Результатом является общее число вычеркнутых за одну минуту букв А на пестром листе. Этот тест считается просто тестом на внимание и восприятие, хотя скорость и координация движений здесь тоже имеют значение. В этой связи мож-



Показатель автономного баланса

Рис. 7. Распределение значений оценок

автономного баланса у 87 детей в

возрасте от 6 До 12 лет. (Данные из

Уингера и Эллингтона, 33, с. 252.)



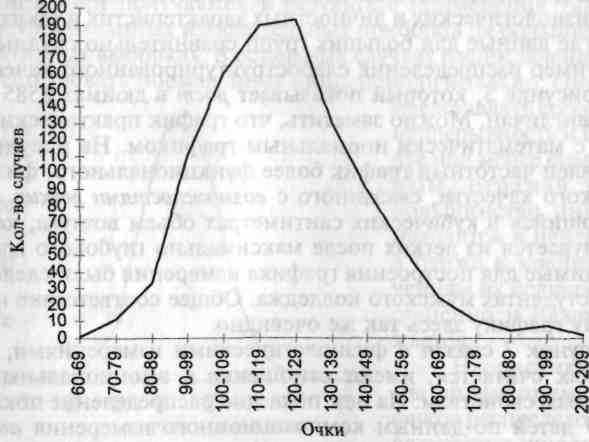
Рис. 8. Количество вычеркнутых за одну минуту букв А 1000 студентами колледжа. (Данные из Анастази, 2, с. 32.)



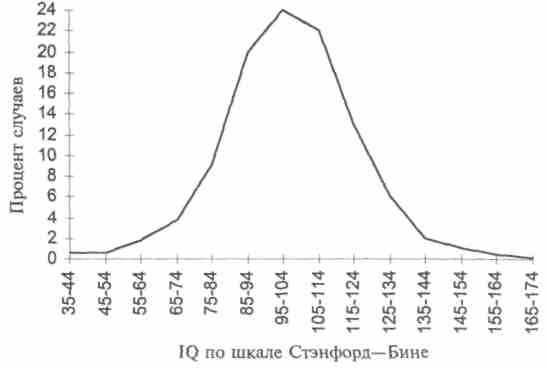
Рис. 9. Измерение IQ репрезентативной выборки, состоящей из 2904 детей в

возрасте от 2 до 18 лет, по шкале Стэнфорд—Бине.

(Данные от Термена и Меррилла, 27, с. 37.)

но вспомнить данные теста на простое научение, зафиксированные в таблице 1 и на рисунке 2. Этот тест требовал применения кода, состоявшего из парных, не имеющих смысла слогов. Оба теста предлагались одной и той же группе, состоящей из 1000 студентов колледжа, и оба дали распределения, лежащие в пределах ожидаемых математических значений нормального графика.

На рисунке 9 мы видим типичные результаты применения интеллектуального теста в условиях большой выборки. Она показывает распределение IQ (Стэнфорд—Бине, редакция 1937 года) 2904 детей в возрасте от 2 до 18 лет. График показывает, что в наибольшем проценте случаев IQ испытуемых находится в пределах среднего интервала, от 95 до 104 баллов. Процент постепенно снижается до 1, поскольку IQ лишь очень малого числа детей находится в пределах между 35 и 44 и между 165 и 174 баллами. В данное распределение не включались данные по находящимся в интернатах слабоумным детям, выборка была также ограничена и по ряду других параметров. Так, в нее вошли только белые американцы с несколько преувеличенной (по сравнению с реальным населением страны) пропорцией городских жителей. Большую часть выборки составили учащиеся начальной



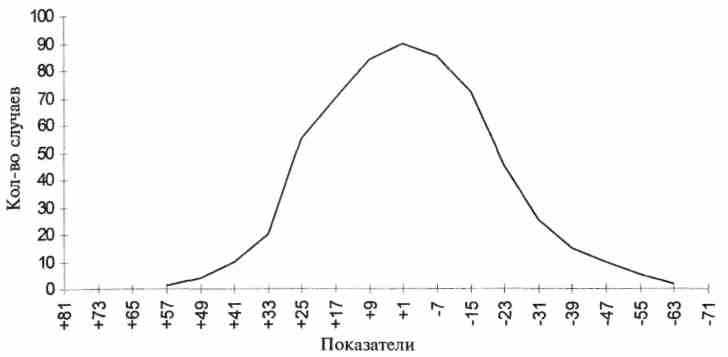
Рис. 10. Распределение 600 учениц колледжа по результатам теста Оллпорта на доминирование-подчинение. (Данные из Рагглзаи Оллпорта, 24, с. 520.)

школы, и хотя организаторы стремились к тому, чтобы обеспечить полноценное участие в тестировании групп старших и самых младших возрастов, их число едва ли соответствовало числу тестируемых учащихся начальной школы. Отметим, что весь ряд IQ для целостной популяции, на самом деле, как свидетельствуют данные, полученные разными исследователями, простирается от значений, близких к 0, до значений, несколько превышающих 200.

В качестве последней иллюстрации рассмотрим рисунок 10, содержащий распределение результатов широко используемого личностного опросника. График показывает распределение 600 учениц колледжа по результатам теста Оллпорта на доминирование-подчинение. Целью этого личностного опросника было исследование стремления индивида доминировать над другими членами группы в повседневной жизни или подчиняться им. Рисунок 10 показывает, что, несмотря на биполярное определение качества (противопоставление доминирования и подчинения), большинство результатов испытуемых располагаются вокруг середины шкалы и распределение приближается к нормальному. Иными словами, биполярное наименование качества не должно вводить нас в заблуждение, что индивидов можно классифицировать на доминирующих и подчиняющихся. Как и дру-

I

Распределение индивидуальных различий 4 5

гие измеряемые свойства человека, данное личностное качество имеет множество степеней проявления; и при этом большинство людей относятся к промежуточным типам.