Специальная математика
| Вид материала | Конспект |
Содержание3.4. Особенности минимизации автомата Мура 3.5. Переход от автомата Мура к автомату Мили и наоборот |
- Направления работы семинара, 152.43kb.
- «Математика. Прикладная математика», 366.03kb.
- Программа подраздела «Философские проблемы математики», 94.9kb.
- Рабочая программа по курсу «Специальная педагогика и специальная психология» на 5 курсе, 94.48kb.
- Специальная обработка, 1624.5kb.
- Расшифровка : Математика, 146.94kb.
- Abramson Family Cancer Research Institute University of Pennsylvania (usa) Роль апоптоза, 15.2kb.
- Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
- Пангеометризм и математическая мифология, 956.71kb.
- Строительство. Система производственного контроля. Часть, 84.92kb.
3.4. Особенности минимизации автомата Мура
Минимизация автомата Мура отличается первым шагом. Здесь в классы одно-эквивалентных попадают состояния, отмеченные одинаковыми выходными сигналами.
А В


| | y1 | y2 | y2 | y2 | y2 | y2 | y2 |
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| x1 | 2/B | 3/B | 5/B | 3/B | 4/B | 7/B | 3/B |
| x2 | 1/А | 1/А | 1/А | 1/А | 1/А | 1/А | 1/А |
| | y1 | y2 |
| | A | B |
| x1 | B | B |
| x2 | А | А |
3.5. Переход от автомата Мура к автомату Мили и наоборот
Автоматы Мура и Мили отличаются функцией выходов.
y(t) = (q(t)) – для автомата Мура
и
y(t) = (q(t-1), x(t)) – для автомата Мили
Переход от автомата Мура к автомату Мили заключается в построении таблицы переходов. Построение состоит в подстановке выходных сигналов, отмечающих состояния в расширенной таблице переходов, вместо состояний, в которые автомат переходит. Тем самым, если говорить в терминах графов, выходные сигналы от состояний сдвигаются на стрелки, которые в эти состояния заходят.
А таблица переходов автомата Мили получается из расширенной таблицы переходов автомата Мура отбрасыванием первой строки.
х1
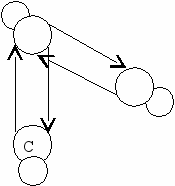 | y1 | y3 | y2 |
| A x2 | A | B | C |
| x1 | A | B | A |
| x x1 x1 B x3 2 | B | B | C |
| x x3 3 | C | A | C |
y2
y3
x2
x2
x3






y1
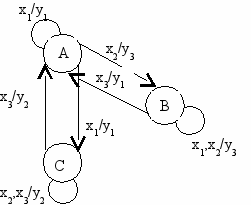
| Т.П. | A | B | C |
| x1 | A | B | A |
| x2 | B | B | C |
| x3 | C | A | C |
| Т.В. | A | B | C |
| x1 | y1 | y3 | y1 |
| x2 | y3 | y3 | y2 |
| x3 | y2 | y1 | y2 |
П
x1
ереход от автомата Мили к автомату Мура.
| Т qixj yij bij .П. | q1/b0 | q2 | q3 |
| x1 | q1/b11 | q3/b21 | q2/b31 |
| x2 | q2/b12 | q1/b22 | q3/b32 |
| Т.В. | q1 | q2 | q3 |
| x1 | y3 | y1 | y2 |
| x2 | y4 | y5 | y6 |
| | | y3 | y4 | y1 | y5 | y2 | y6 |
| | b0 | b11 | b12 | b21 | b22 | b31 | b32 |
| x1 | b11 | b11 | b21 | b31 | b11 | b21 | b31 |
| x2 | b12 | b12 | b22 | b32 | b12 | b22 | b32 |
Теорема : (Глушкова)
Таким образом доказана конструктивная теорема, что для произвольного автомата Милли может быть построен эквивалентный ему автомат Мура имеющий не более
n * m + 1 состояний, где n - число входных сигналов, m - число состояний исходного автомата Милли.
