Специальная математика

Вид материала

Конспект

Содержание 3.2. Примеры автоматов

Подобный материал:

• Направления работы семинара, 152.43kb.
• «Математика. Прикладная математика», 366.03kb.
• Программа подраздела «Философские проблемы математики», 94.9kb.
• Рабочая программа по курсу «Специальная педагогика и специальная психология» на 5 курсе, 94.48kb.
• Специальная обработка, 1624.5kb.
• Расшифровка : Математика, 146.94kb.
• Abramson Family Cancer Research Institute University of Pennsylvania (usa) Роль апоптоза, 15.2kb.
• Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
• Пангеометризм и математическая мифология, 956.71kb.
• Строительство. Система производственного контроля. Часть, 84.92kb.

3.2. Примеры автоматов

Замечание. Для удобства восприятия и сокращения описания будем говорить об автоматах как об автоматических роботоподобных устройствах, хотя на самом деле это, как уже было сказано, лишь математические модели, преобразующие входные слова в выходные и не имеющие дела с физическими сущностями, вроде монет, билетов и т.п.

Пример 1 (автомат Мили):

Построить (синтезировать) автомат, на вход которого могут поступать в любой последовательности и, возможно, с повторениями монеты (как в добрые старые времена) 1; 2 и 3 копейки. Автомат продает билет, если сумма опущенных монет равна 3. В случае превышения суммы автомат возвращает деньги.

Входной алфавит в описании задан явно: Х = {1, 2, 3}.

Выходной алфавит будет содержать буквы (сигналы): Б – выдает билет, В – возвращает деньги, Н – ничего не выдает (это такой специфический выходной сигнал). То есть У = {Б, В, Н}.

Можно представить автомат в виде графа, где вершины представляют состояния, а к каждой стрелке приписана пара входной сигнал/выходной сигнал. То есть размеченные стрелки отражают функции переходов и выходов.




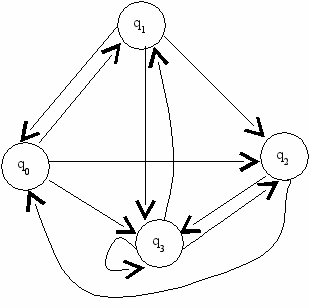
3/В 1/Н 1/Н


2/Б 1/Н


2/Н


3/Б 1/Б 2/Н


2/В 3/Б


От представления автомата в виде графа можно очевидным образом перейти к его табличному представлению, которое также однозначно определяет автомат. Табличное представление предпочтительно для автоматов с большим числом состояний и при представлении автоматов в компьютере.


Можно построить для данного автомата таблицы

переходов

Т.П.	q0	q1	q2	q3
1 f	q1	q2	q3	q1
2	q2	q3	q0	q2
3	q3	q0	q0	q3

и


выходов

Т.В.	q0	q1	q2	q3
1 	Н	Н	Б	Н
2	Н	Б	В	Н
3	Б	В	В	Б

Пример 2 (автомат Мура).

Построить автомат, на вход которого могут поступать монеты 1, 2, 3 коп. Автомат выдает сигнал “чет”, если поступившая сумма в данный момент четная и “нечет”, если наоборот.

2

1,3



1,3

2

Ч

Н



чет нечет


Это автомат Мура. Поэтому выходные сигналы приписаны не стрелкам, а к состояниям, которыми они однозначно определяются. Табличное представление сводится к одной таблице – расширенной таблице переходов. В ней добавляется верхняя строка, позволяющая приписать выходные сигналы состояниям.

- выходные сигналы - состояния	Чет	Нечет
	Ч	Н
1	Н	Ч
2	Ч	Н
3	Н	Ч