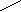Специальная математика

Вид материала

Конспект

Содержание 4.5. Алгоритм Краскала Теорема Кэли

Подобный материал:

• Направления работы семинара, 152.43kb.
• «Математика. Прикладная математика», 366.03kb.
• Программа подраздела «Философские проблемы математики», 94.9kb.
• Рабочая программа по курсу «Специальная педагогика и специальная психология» на 5 курсе, 94.48kb.
• Специальная обработка, 1624.5kb.
• Расшифровка : Математика, 146.94kb.
• Abramson Family Cancer Research Institute University of Pennsylvania (usa) Роль апоптоза, 15.2kb.
• Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
• Пангеометризм и математическая мифология, 956.71kb.
• Строительство. Система производственного контроля. Часть, 84.92kb.

4.4. Деревья

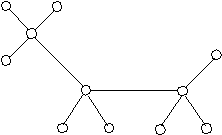
Дерево - это связный граф без циклов. Можно дать другое определение дерева или вывести его из первого. Дерево – это граф, между любой парой вершин которого существует единственная цепь.


Теорема: В графе типа дерева с n вершинами n-1 ребер.

Доказательство. Для графа, состоящего лишь из одной вершины, это соотношение выполняется. Пусть оно выполняется и для графа с n-1 вершинами, тогда добавление новой дуги приводит к добавлению и одной вершины, что сохраняет соотношение.


П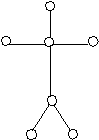римеры деревьев.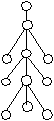





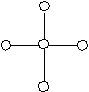
Лесом называется граф, состоящий из нескольких компонент связности, каждая из которых является деревом.

Диаметром для графов типа дерева является максимальное расстояние между его вершинами.

. Определим для каждой вершины ее расстояние от самого удаленного листа Минимальное число - радиус, эта вершина корневая (центральная).

В любом дереве существует одна или две (смежные) корневые вершины


4 4


4

4

2 3

-Диаметр 4.


3 3 4 4


4 3 3 4




Диаметр: 5

Радиус : 3


5 5 4 4 4 4 5 5

4.5. Алгоритм Краскала

Пусть дан полный граф. Ребрам приписаны штрафы. На основе этого графа строят дерево, имеющее минимальный суммарный штраф.

Для этого на каждом шаге выбирают ребро, имеющее минимальный штраф и не образующее цикл с уже выбранными ребрами.

.


Пример.




2 3 5 5

6


4 4 8 6


6


Жирными линиями выделено минимальное дерево

Теорема Кэли для раскрашенных деревьев.

Для n вершин существует n^n-2 различных помеченных деревьев.

Например, существует 16 различных деревьев с четырьмя вершинами.

1 2 3 4



4 3 2 1

4 вершины  4^{4 - 2} = 16 различных помеченных деревьев

1 2 3

4