Учебно-методический комплекс учебной дисциплины ен. Ф. 01 Математика (аналитическая геометрия и линейная алгебра)
| Вид материала | Учебно-методический комплекс |
- Учебно-методический комплекс для специальности 080111 Маркетинг Москва 2009, 497.47kb.
- Рабочая программа учебной дисциплины линейная алгебра и аналитическая геометрия уровень, 426.51kb.
- Лекции, час, 202.55kb.
- Рабочая программа учебной дисциплины ен. Ф. 01. Аналитическая геометрия и линейная, 148.75kb.
- Линейная алгебра и аналитическая геометрия, 103.33kb.
- Рабочая программа дисциплины (модуля) «Линейная алгебра и аналитическая геометрия», 275.82kb.
- Учебно-методический комплекс учебной дисциплины Геометрия Специальность 032100., 183.68kb.
- Правительство Российской Федерации Государственное образовательное бюджетное учреждение, 416.73kb.
- Рабочая программа по дисциплине б 2 математика. Алгебра и геометрия шифр и название, 370.36kb.
- Рабочая программа «Механика и основы механики сплошных сред» Специальность 010400 физика,, 141.09kb.
3. Содержание учебной дисциплины
3.1 Содержание лекционного курса
| № лек. | Тема лекции | Содержание лекции | Вид контроля |
| 1 | Комплексные числа | Понятие комплексного числа. Арифметические действия с комплексными числами. Комплексно-сопряженные числа. Геометрическое изображение комплексного числа. Тригонометрическая форма комплексного числа. | Самостоятельная работа |
| 2 | Матрицы | Определение и виды матриц. Транспонированная матрица. Сложение матриц. Умножение матрицы на число. Линейная зависимость матриц. | Самостоятельная работа |
| 3 | Элементарные матрицы | Правило суммирования Эйнштейна. Умножение матриц. Элементарные преобразования. Элементарные матрицы. | Самостоятельная работа |
| 4 | Ранг матрицы | Вырожденные и невырожденные матрицы. обратная матрица. Ранг матрицы. Основные теоремы о ранге матрицы. | Самостоятельная работа |
| 5 | Определители | Определители II и III порядков. Определитель матрицы n-го порядка. | Самостоятельная работа |
| 6 | Свойства определителей | Свойства определителей. Дополнительная подматрица. Дополнительный минор. Алгебраическое дополнение. Вычисление обратной матрицы с помощью определителя. | Самостоятельная работа |
| 7 | Системы линейных уравнений | Определение и виды систем линейных уравнений. Системы линейных уравнений с m=n. Правило Крамера. | Самостоятельная работа |
| 8 | Теорема Кронекера-Капелли | Теорема Кронекера-Капелли. Общее правило нахождения решений. Приведенная система линейных уравнений. Общее решение системы линейных уравнений. | Контрольная работа по темам лекций 1 - 8 |
| 9 | Векторы и линейные операции над ними | Определение вектора и линейные операции над ними. Свойства линейных операций над векторами. Линейная зависимость векторов. Геометрический смысл линейной зависимости. Базис. | Самостоятельная работа |
| 10 | Системы координат | Декартова (аффинная) система координат. Деление отрезка в данном отношении. Декартова прямоугольная система координат. Полярная система координат. Цилиндрическая и сферическая системы координат. Параллельный перенос ПСК на плоскости. Поворот ПСК в плоскости. | Самостоятельная работа |
| 11 | Умножение векторов | Скалярное произведение векторов. Законы скалярного произведения векторов. Скалярное произведение векторов в координатной форме. Проекция вектора на произвольную прямую. Ориентация прямой, плоскости и пространства. Площадь ориентированного параллелограмма, объем ориентированного параллелепипеда. | Самостоятельная работа |
| 12 | Векторное и смешанное произведение векторов | Векторное произведение двух векторов. Законы векторного произведения. Векторное произведение двух векторов в координатной форме. Векторно-векторное произведение трех векторов. Векторно-скалярное (смешанное) произведение трех векторов. Свойства смешанного произведения трех векторов. | Самостоятельная работа |
| 13 | Прямые линии и плоскости | Параметрическое уравнение прямой. параметрическое уравнение плоскости. Прямая линия на плоскости. | Самостоятельная работа |
| 14 | Векторные уравнения прямой и плоскости | Векторные уравнения прямой и плоскости. Условия параллельности плоскостей и прямых на плоскости. Уравнение прямой в пространстве. | Самостоятельная работа |
| 15 | Линии второго порядка. Парабола. Эллипс | Линии второго порядка. Парабола. Директориальное свойство параболы. Касательная к параболе. Оптическое свойство параболы. Линии второго порядка. Эллипс. Фокальное и директориальное свойства эллипса. Касательная к эллипсу. Оптическое свойство эллипса. | Самостоятельная работа |
| 16 | Линии второго порядка. Гипербола | Линии второго порядка. Гипербола. Фокальное и директориальное свойства гиперболы. Касательная к гиперболе. Оптическое свойство гиперболы. Уравнения гипербол, эллипсов и парабол отнесенные к вершине. Уравнения гипербол, эллипсов и парабол в полярных координатах. | Контрольная работа по темам 9-16 |
| 17 | Линии второго порядка. Общая теория | Общее понятие о линии второго порядка. Преобразование коэффициентов при параллельном переносе ПСК. Преобразование коэффициентов при повороте ПСК. Понятие инварианта. Основные инварианты линии второго порядка. | Самостоятельная работа |
| 18 | Упрощение линии второго порядка | Центр линии второго порядка. Преобразование к центру. Стандартное упрощение любого уравнения линии второго порядка путем поворота осей ПСК. Упрощение уравнения центральной линии второго порядка. | Самостоятельная работа |
| 19 | Упрощение линии второго порядка без определенного центра | Упрощение линии второго порядка без определенного центра. Классификация линий второго порядка. | Домашняя контрольная работа по темам 17-19 |
| 20 | Поверхности второго порядка | Цилиндрические поверхности. Конусы второго порядка. Эллипсоиды, гиперболоиды и параболоиды. | Самостоятельная работа |
| | II семестр | | |
| 1 | Определение и аксиомы линейного пространства | Определение и аксиомы линейного пространства. Примеры линейных пространств. Элементарные следствия из аксиом линейного пространства. линейная зависимость. Базис. | Самостоятельная работа |
| 2 | Замена базиса | Замена базиса. Формулы перехода к новому базису. Формулы последовательного перехода к новому базису. Преобразование координат вектора при замене базиса. | Самостоятельная работа |
| 3 | Операции над линейными пространствами | Ориентация линейного пространства. Линейное подпространство. Линейная оболочка. Сумма и пересечение подпространств. | Самостоятельная работа |
| 4 | Линейные преобразования | Линейные преобразования. Матрица линейного преобразования. Линейные отображения. координатная запись отображений. Изоморфизм. | Самостоятельная работа |
| 5 | Действия над операторами | Изменение матрицы линейного отображения при замене базиса. Канонический вид матрицы линейного отображения. Сумма отображений. умножение линейного отображения на число. произведение отображений. | Самостоятельная работа |
| 6 | Задача о собственных векторах | Инвариантные подпространства. Собственные подпространства. Характеристическое уравнение. | Самостоятельная работа |
| 7 | Свойства собственных подпространств | Основные теоремы о характеристическом многочлене. Свойства собственных подпространств. Комплексные характеристические числа. приведение матрицы преобразования к диагональному виду. | Самостоятельная работа |
| 8 | Линейные функции | Определение и примеры линейных функций. сопряженное пространство. | Самостоятельная работа |
| 9 | Билинейная и квадратичная функции | Билинейная функция. Матрица билинейной функции. Квадратичная линейная функция (форма). | Самостоятельная работа |
| 10 | Полуторалинейные функции | Ранг и индекс квадратичной формы. Закон инерции квадратичной формы. Критерий Сильверста. полуторалинейные функции. | Самостоятельная работа |
| 11 | Евклидовы пространства | Определение евклидова пространства и его примеры. Основные метрические понятия: длина вектора; угол между векторами; теорема Пифагора; неравенства треугольника. Выражение скалярного произведения через координаты сомножителей. | Самостоятельная работа |
| 12 | Ортогональные базисы | Ортогональные базисы. Ортогональные матрицы. Ортогональное дополнение подпространства. | Самостоятельная работа |
| 13 | Метод ортогонализации Грамма-Шмидта | Ортогональные проекции. Метод ортогонализации Грамма-Шмидта. QR – разложение. | Самостоятельная работа |
| 14 | Линейные преобразования вещественного евклидова пространства | Преобразование, сопряженное к данному. Самосопряженное преобразование. Ортогональное преобразование. Произвольное невырожденное линейное преобразование вещественного евклидова пространства. | Самостоятельная работа |
| 15 | Линейные преобразования комплексного евклидова пространства | Эрмитово преобразование. Унитарное преобразование. Произвольное линейное преобразование комплексного евклидова пространства. | Самостоятельная работа |
3.2 Содержание практических занятий
| № занят. | Тема практического занятия | Содержание практического занятия | Вид контроля |
| 1 | Комплексные числа | Действия над комплексными числами. Тригонометрическая форма комплексного числа. Решение задач [16] №№ 1 - 53 | Самостоятельная работа |
| 2 | Матрицы | Сложение и умножение матриц. Элементарные действия над матрицами. Обратная матрица. Решение задач [15] №№ 1.3 – 1.34 | Самостоятельная работа |
| 3 | Определители | Вычисление определителей матриц. Обратная матрица. Решение задач [15] №№ 3.1 – 3.10 | Самостоятельная работа |
| 4-5 | Системы линейных уравнений | Решение систем линейных уравнений методом Крамера. Нахождение фундаментальных и общих решений. Решение задач [15] №№ 3 – 10, 12, 14 | Самостоятельная работа; контрольная работа |
| 6-7 | Векторная алгебра | Вычисление скалярного, векторного и смешанного произведения векторов. Деление отрезка в данном отношении. Решение задач [2] №№ 1.4, 1.6, 1.10, 1.13, 1.14, 1.17, 1.18, 2.1, 2.4, 2.6, 2.7, 2.8, 2.10, 2.14, 2.34, 3.1, 3.6, 3.8, 3.19, 3.23, 4.1, 4.4 | Самостоятельная работа |
| 8-12 | Прямая на плоскости, плоскость и прямая в пространстве | Решение стандартных задач: прямая на плоскости, плоскость и прямая в пространстве Решение задач [2] №№ 5.7, 5.8, 5.9, 5.10, 5.11, 5.15, 5.23, 5.27(1), 5.36, 5.47, 6.16, 6.17, 6.18, 6.19, 6.20, 6.21, 6.22, 6.25(4), 6.27(2), 6.29, 6.30, 6.47(1), 6.49, 6.52(3), 6.53(2), 6.54(2), 6.62(1,4), 6.63, 6.64 , 6.72 | Самостоятельная работа |
| 13-14 | Линии второго порядка | Решение задач, связанных с каноническими уравнениями линий второго порядка. Решение задач [2] №№ 7.22, 7.23, 7.25(1,4), 7.26(1), 7.35, 7.40, 7.51, 7.62(2), 8.1; [10] 657, 658, 646, 647, 562 ,653 | Самостоятельная работа; контрольная работа |
| 15-16 | Общее уравнение линии второго порядка | Приведение общего уравнения линии второго порядка к каноническому виду Домашняя контрольная работа №3 | Самостоятельная работа |
| | II семестр | | |
| 1-2 | Линейные пространства | Базис, размерность, линейная оболочка. Сумма и пересечение подпространств. Решение задач [2] №№ 20.14(2,5), 20.16, 20.17(3), 20.23(6), 20.33, 21.4(2), 21.7(5), 21.8, 21.9 | Самостоятельная работа |
| 3-4 | Линейные операторы | Ядро, множество значений, матрицы линейных отображений и преобразований Решение задач [2] №№ 23.26(2,3), 23.28(3), 23.29(3,4), 23.30(2,3), 23.56(1,2), 23.57(1,2), 23.58(а,б), 23.60(2), 23.62(1,3,5), 23.67(1,2), | Самостоятельная работа |
| 5-6 | Собственные значения и собственные векторы линейных операторов | Вычисление собственных значений и собственных векторов линейных операторов. Решение задач [2] №№ 24.20(2,3,4), 24.30(3,4,5), [18] №№ 1(1-7), 2(1-8) | Самостоятельная работа |
| 7 | Линейные функции | Примеры линейных функций. Вычисление коэффициентов линейных функций. Вычисление сопряженного базиса. Решение задач [2] №№ 31.8, 31.10, 31.19, 31.29, 31.31(2), | Самостоятельная работа |
| 8-9 | Билинейные и квадратичные формы | Билинейные и квадратичные формы в вещественном линейном пространстве. Билинейные и квадратичные функции в комплексном пространстве. Решение задач [2] №№ 32.1(4), 32.3(7), 32.7(2,5), 32.8(7,9), | Самостоятельная работа |
| 10-11 | Евклидовы пространства | Скалярное произведение с матрицей Грамма. Ортогональные проекции. Метод ортогонализации Грамма-Шмидта. [18] №№ 1(1,2), 2(1-4), 3(а-г), 4, 5 | Самостоятельная работа |
| 12 | Линейные операторы в унитарном пространстве | Самосопряженные и ортогональные преобразования. Линейные преобразования унитарного пространства. [18] №№ 1, 2(1-2), 3(1-5), 4, 5, 6(1-3), 7(1-2), 8, 9, 10 | Самостоятельная работа |
4. Методические материалы и рекомендации для преподавателя
Основным методом изучения тем, вынесенных в лекционный курс, является информационно-объяснительный метод с элементами проблемных ситуаций и заданий студентам. На практических занятиях основным является поисковый метод, связанный с решением различных типов задач.
Средствами обучения является базовый учебник, дополнительные пособия для организации самостоятельной работы студентов, демонстрационные материалы, компьютерные обучающие программы, сборники задач.
Приемами организации учебно-познавательной деятельности студентов являются приемы, направленные на осмысление и углубление предлагаемого содержания и приемы, направленные на развитие аналитико-поисковой и исследовательской деятельности.
Важно четко представлять структуру курса, уметь выделить в каждом разделе основные, базовые понятия, обозначенные минимумом содержания, определенного государственным образовательным стандартом.
Изложение теории курса опирается на следующие понятия и факты, изучаемые в курсе аналитической геометрии и линейной алгебры:
- матрица,
- ранг матрицы.
- определители и их свойства,
- системы однородных и неоднородных уравнений,
- прямые и плоскости,
- линии и поверхности второго порядка,
- линейные пространства,
- линейные операторы,
- евклидовы пространства.
Понятия и факты, изучаемые в курсе аналитической геометрии и линейной алгебры, применяются в последующих разделах геометрии, а также в других учебных дисциплинах:
в математическом анализе
- метод координат,
- полярная, цилиндрическая и сферическая системы координат,
- уравнения линий второго порядка в прямоугольной декартовой и полярной системах координат,
- уравнения поверхностей второго порядка;
в алгебре
- векторные пространства,
- аффинное и евклидово пространства,
- понятие группы, примеры групп;
в физике
- векторы,
- операции над векторами,
- прямая линия,
- линии и поверхности второго порядка.
4.1. Примерный перечень контрольных вопросов
к зачету и экзамену.
I семестр
- Комплексные числа. Сложение и вычитание комплексных чисел.
- Умножение и деление комплексных чисел.
- Комплексно-сопряженное число. Степень мнимой единицы.
- Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
- Определение и виды матриц. Транспонированная матрица.
- Сложение матриц. Умножение матрицы на число.
- Линейная зависимость матриц.
- Символ
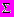 . Правило суммирования Эйнштейна.
. Правило суммирования Эйнштейна.
- Умножение матриц.
- Элементарные преобразования. Элементарные матрицы.
- Вырожденные и невырожденные матрицы.
- Обратная матрица.
- Ранг матрицы.
- Основные теоремы о ранге матрицы.
- Определители II и III порядков.
- Определитель матрицы n-го порядка.
- Свойства определителей (1-4). Алгебраическое дополнение.
- Свойства определителей (5-10).
- Вычисление обратной матрицы с помощью определителя.
- Определение и виды систем линейных уравнений.
- Системы линейных уравнений с m=n. Правило Крамера.
- Теорема Кронекера-Капелли. Общее правило нахождения решений СЛУ.
- Приведенная система линейных уравнений. Общее решение СЛУ.
- Определение вектора и линейные операции над векторами.
- Линейная зависимость векторов.
- Базис. Системы координат.
- Деление отрезка в данном отношении.
- Полярная, цилиндрическая и сферическая системы координат.
- Преобразование координат. Параллельный перенос ПСК на плоскости.
- Преобразование координат. Поворот ПСК на плоскости.
- Скалярное произведение векторов. Законы скалярного произведения векторов.
- Проекция вектора на произвольную прямую.
- Ориентация прямой, плоскости и Пространства. Площадь ориентированного параллелограмма, объем ориентированного параллелепипеда.
- Векторное произведение двух векторов.
- Векторно-векторное произведение трех векторов.
- Смешанное произведение трех векторов и его свойства.
- Параметрическое уравнение прямой. Параметрическое уравнение плоскости.
- Прямая линия на плоскости.
- Векторные уравнения прямой и плоскости.
- Условия параллельности плоскостей и прямых на плоскости.
- Уравнение прямой в пространстве.
- Парабола. Директориальное свойство параболы.
- Касательная к параболе. Оптическое свойство параболы.
- Эллипс. Фокальное свойство эллипса.
- Директориальное свойство эллипса.
- Касательная к эллипсу. Оптическое свойство эллипса.
- Гипербола. Фокальное свойство гиперболы.
- Директориальное свойство гиперболы. Уравнение касательной к гиперболе. Оптическое свойство гиперболы.
- Уравнения гипербол, эллипсов и парабол отнесенные к вершине.
- Уравнения эллипсов, парабол и гипербол в полярных координатах.
- Общее понятие о линии второго порядка. Преобразование коэффициентов при параллельном переносе и повороте ПСК.
- Понятие инварианта. Основные инварианты линии второго порядка.
- Центр линии второго порядка. Преобразование к центру.
- Стандартное упрощение любого уравнения линии второго порядка путем поворота ПСК.
- Упрощение уравнения центральной линии второго порядка.
- Упрощение уравнения линии второго порядка без определенного центра.
- Цилиндрические поверхности.
- Конусы второго порядка.
- Эллипсоиды и гиперболоиды (тип 12 - тип 15).
- Параболоиды (тип 16 - тип 17).
II семестр
1. Определение, аксиомы и примеры линейного пространства.
2. Элементарные следствия из аксиом линейного пространства.
3. Линейная зависимость.
4. Базис.
5. Формулы перехода к новому базису. Формулы последовательного перехода к новому базису.
6. Преобразование координат вектора при замене базиса.
7. Ориентация линейного n-мерного линейного пространства.
8. Линейное подпространство. Линейная оболочка.
9. Сумма и пересечение подпространств.
10. Линейные преобразования.
11. Матрица линейного преобразования.
12. Линейные отображения. Определение и примеры.
13. Координатная запись отображений.
14. Изоморфизм линейных пространств.
15. Изменение матрицы линейного отображения при замене базиса.
16. Канонический вид матрицы линейного отображения.
17. Сумма отображений. Умножение линейного отображения на число.
18. Произведение отображений.
19. Линейные преобразования. Умножение линейных преобразований.
20. Инвариантные подпространства.
21. Собственные подпространства.
22. Характеристическое уравнение. Основные теоремы о характеристическом многочлене.
23. Свойства собственных подпространств.
24. Комплексные характеристические числа.
25. Приведение матрицы преобразования к диагональному виду.
26. Определение и примеры линейных функций.
27. Сопряженное пространство.
28. Билинейная функция.
29. Матрица билинейной функции.
30. Квадратичные линейные формы.
31. Ранг и индекс квадратичной формы.
32. Полуторалинейные функции.
33. Определение евклидова пространства и его примеры.
34. Основные метрические понятия (длина вектора, угол между векторами, неравенство Коши-Буняковского).
35. Терема Пифагора. Неравенство треугольника.
36. Выражение скалярного произведения через координаты сомножителей. Матрица Грама.
37. Ортогональные базисы.
38. Ортогональные матрицы.
39. Ортогональное дополнение подпространства.
40. Ортогональные проекции. Метод ортогонализации Грама-Шмидта.
41. Преобразование, сопряженное к данному.
42. Самосопряженное преобразование.
43. Ортогональное преобразование.
44. Произвольное невырожденное линейное преобразование вещественного евклидова пространства.
45. Эрмитово преобразование.
46. Унитарное преобразование.
47. Произвольное линейное преобразование комплексного евклидова пространства.
4.2. Примерный вариант контрольной работы №1 по курсу
1. Вычислить
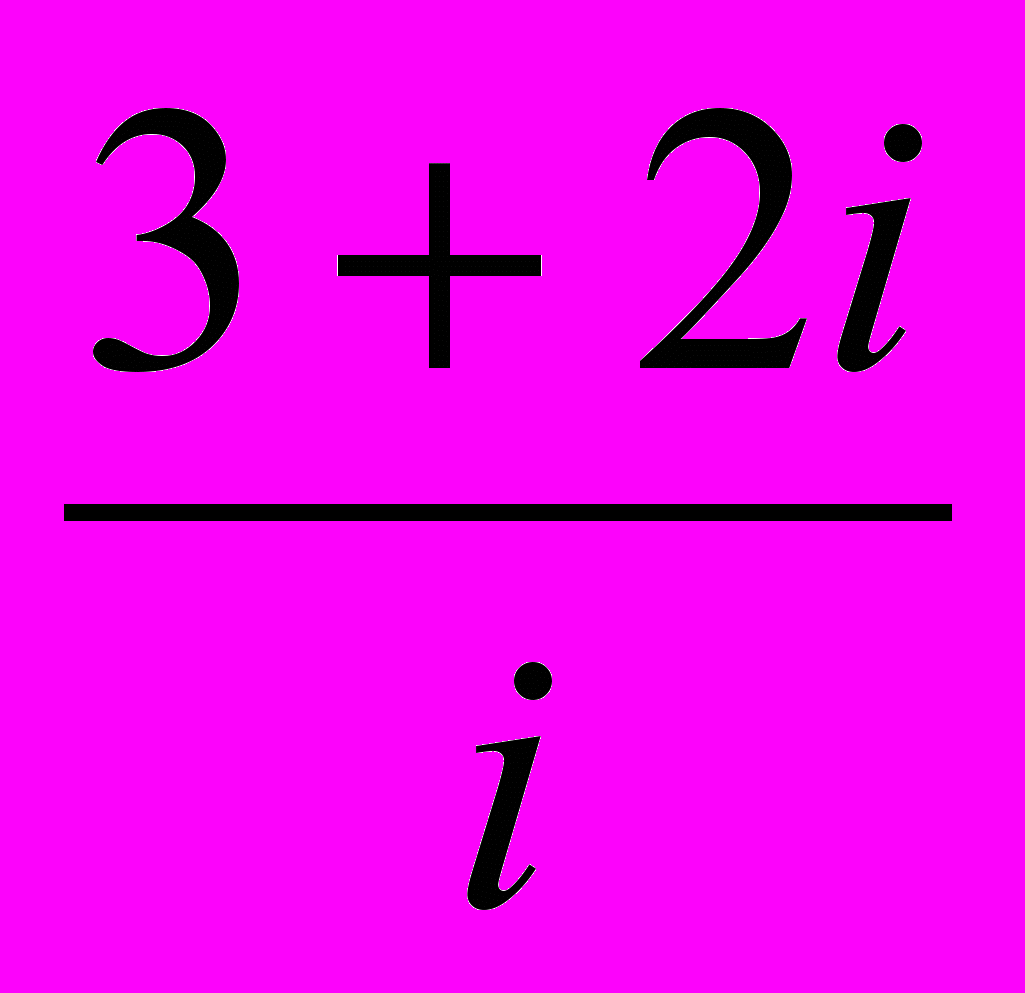 .
.2. Найти общее решение системы
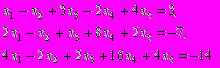
- Найти матрицу, обратную данной
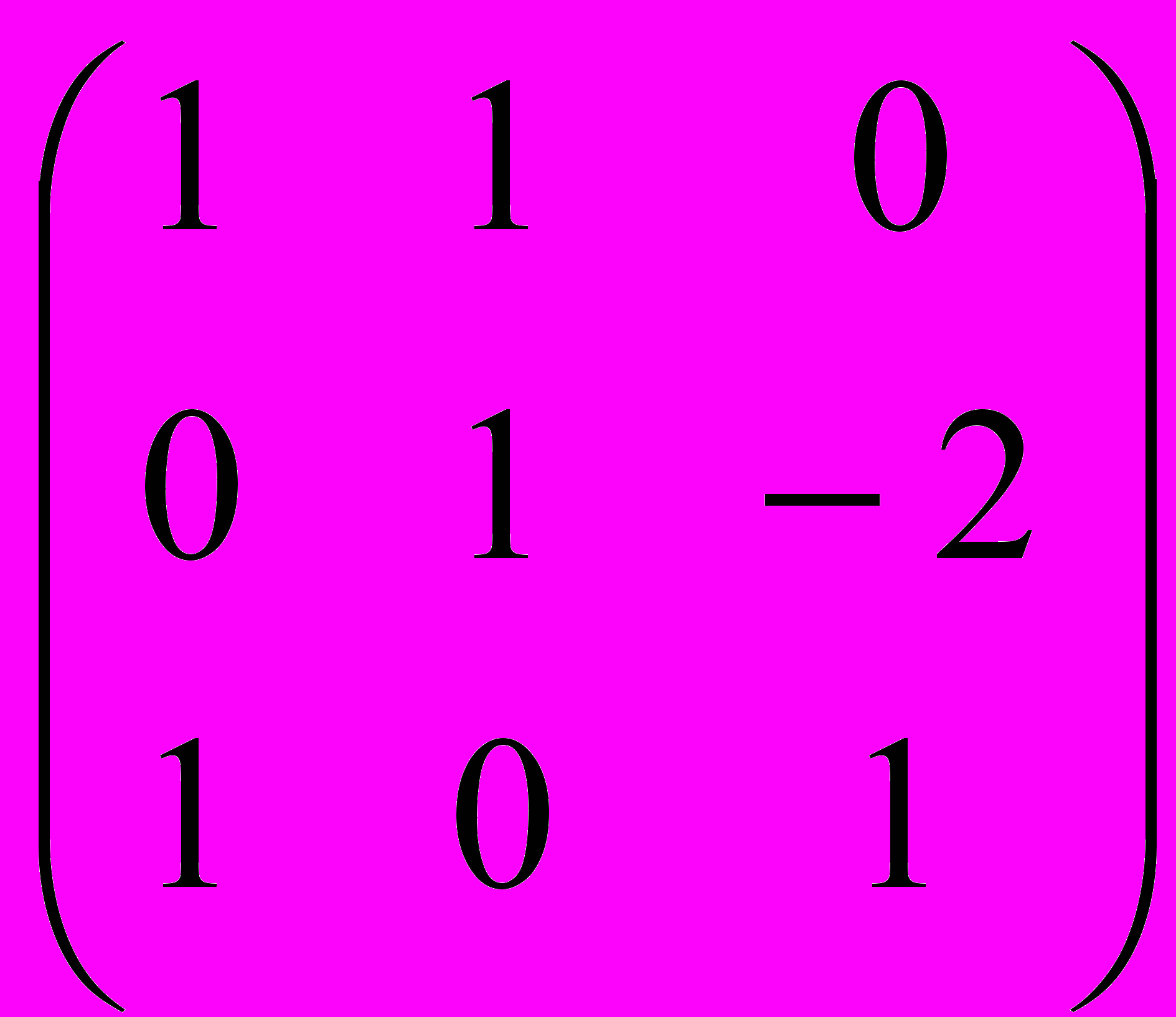 .
.
- Даны матрицы
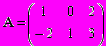 и
и 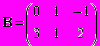 .
.
Найти матрицу
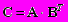 .
.- Вычислить определитель матрицы
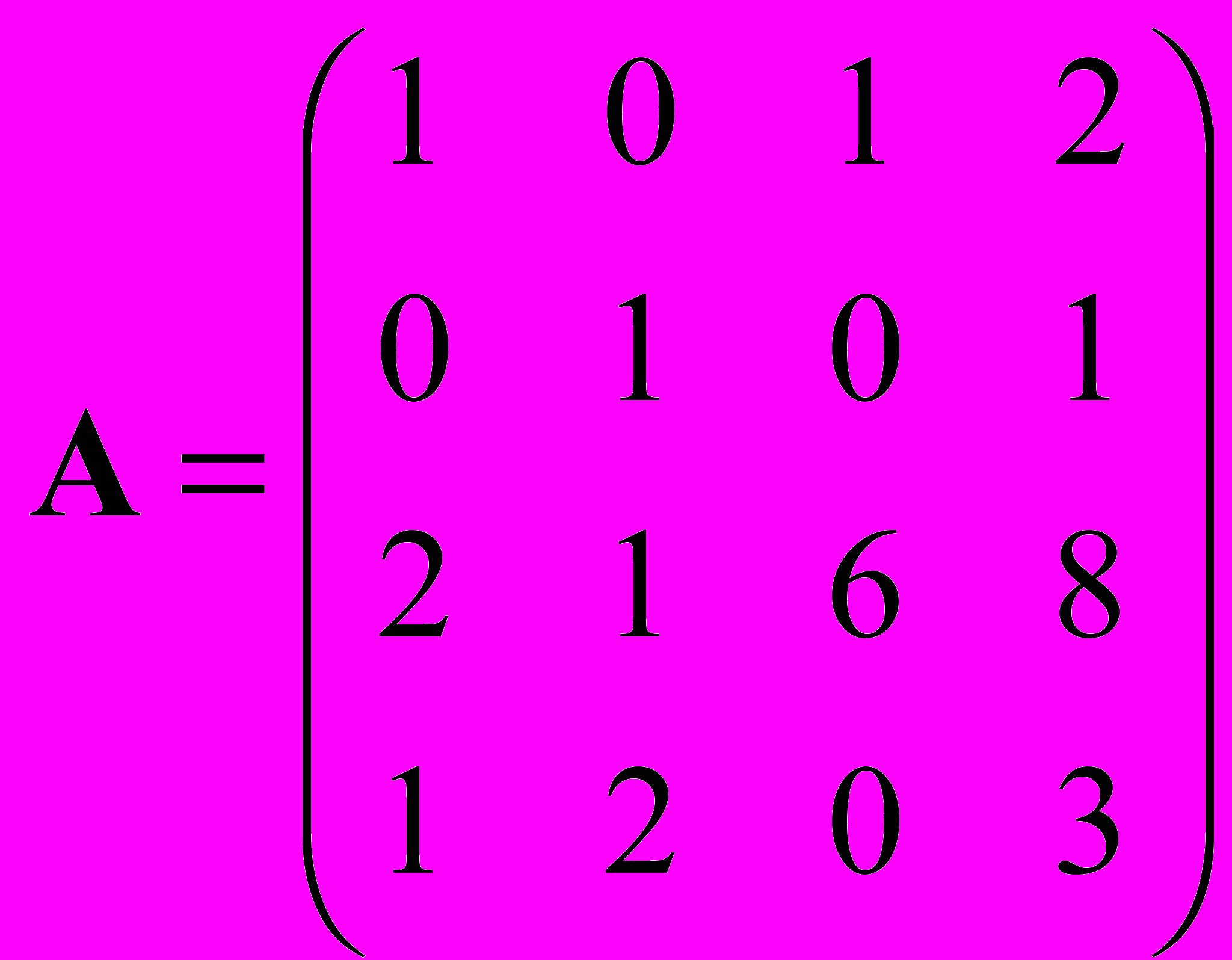 .
.
Примерный вариант контрольной работы №2 по курсу
1. Записать векторное уравнение прямой
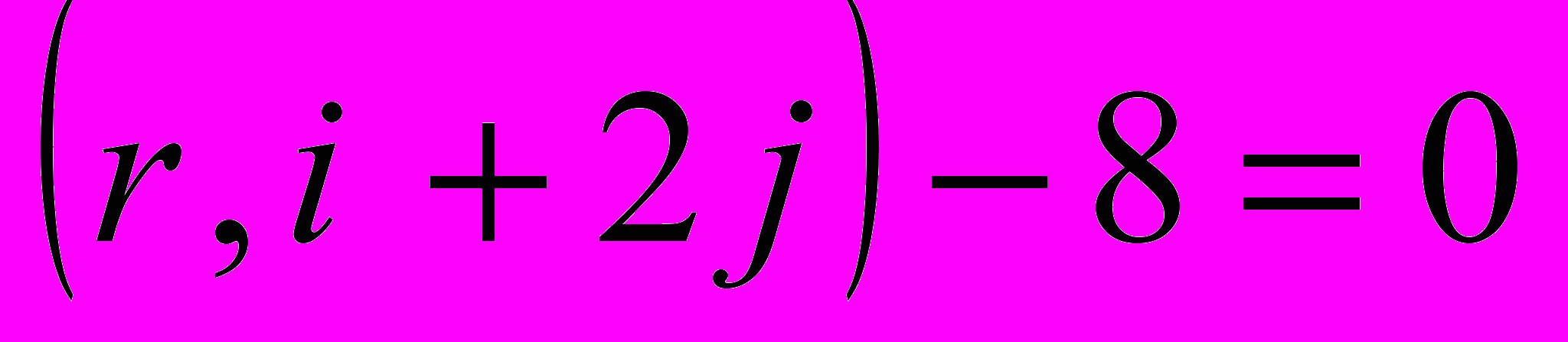
в общей форме.
2. Через точку
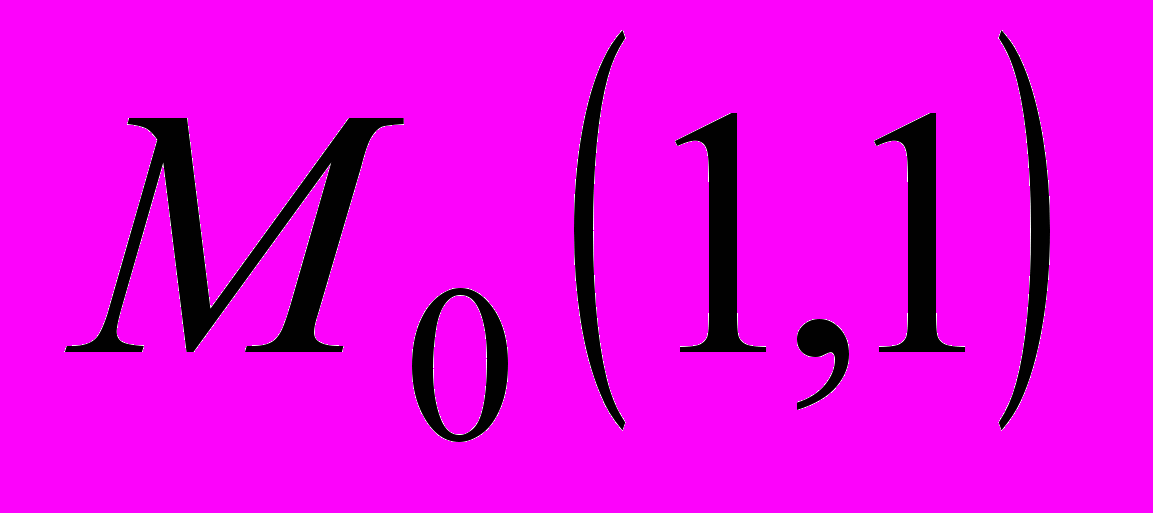 провести прямую, параллельную
провести прямую, параллельнуюпрямой
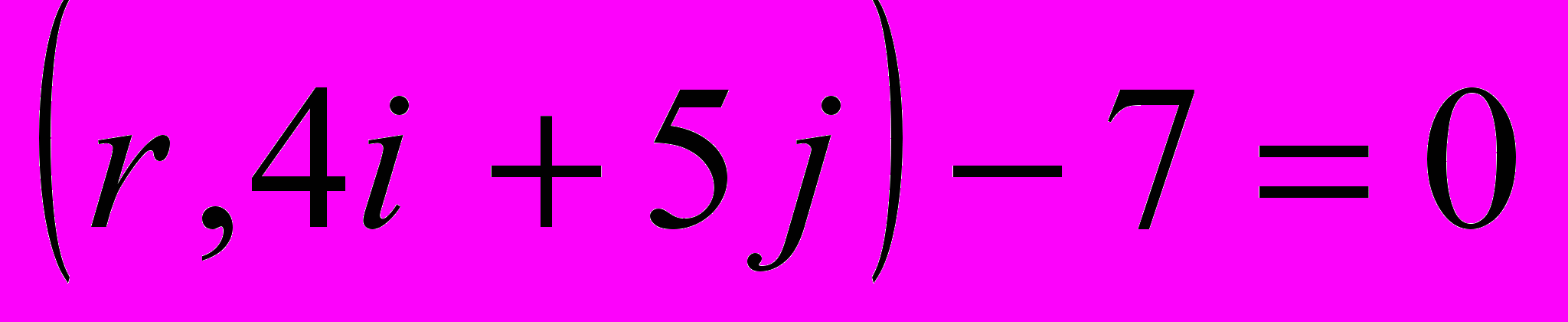 .
.3. Написать уравнение прямой, проходящей через точки
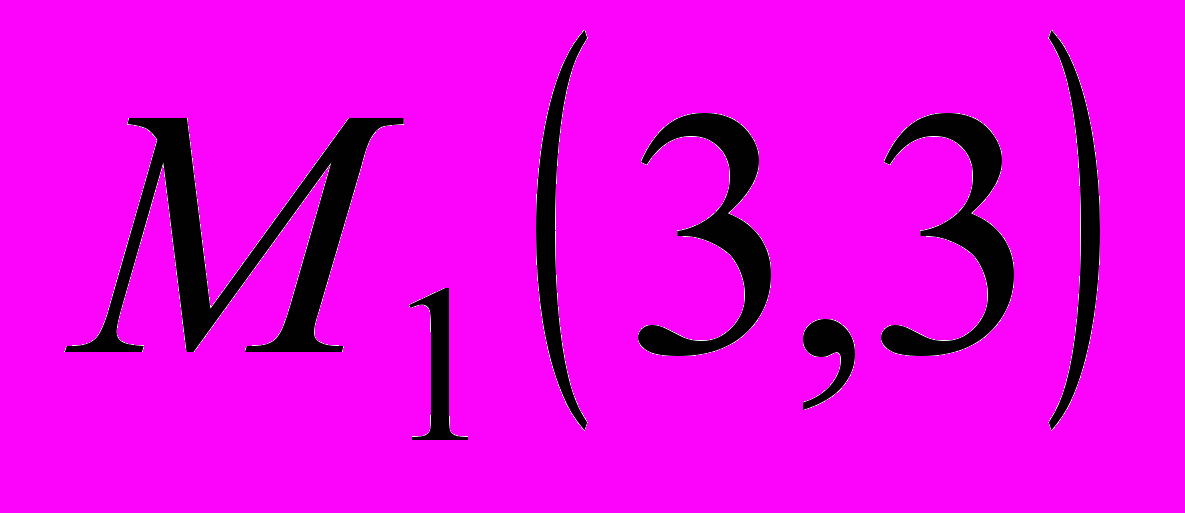 и
и 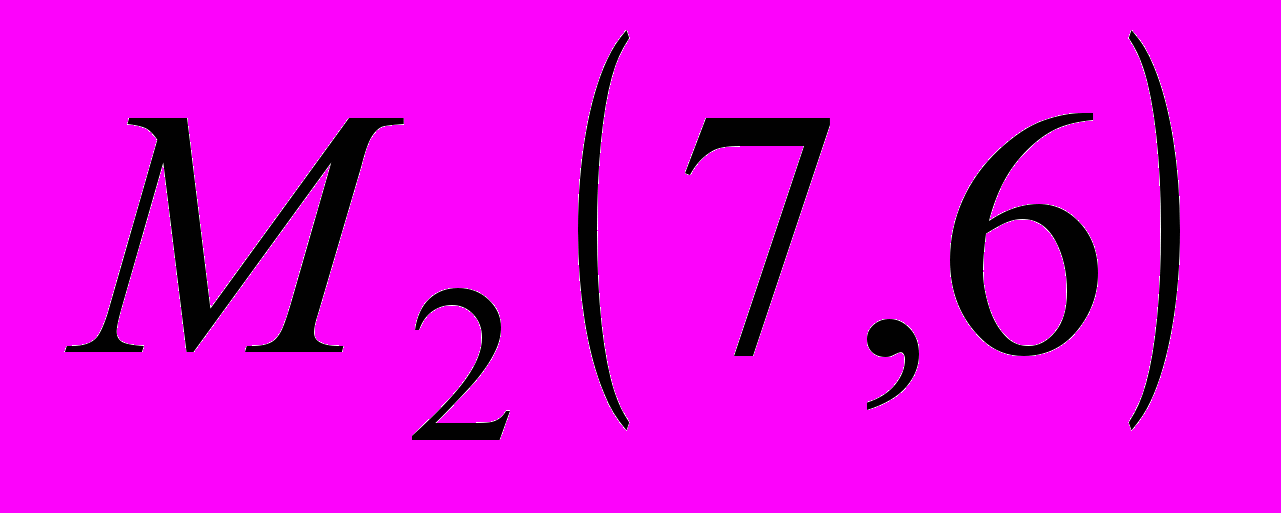 .
.4. Вычислить расстояние от точки
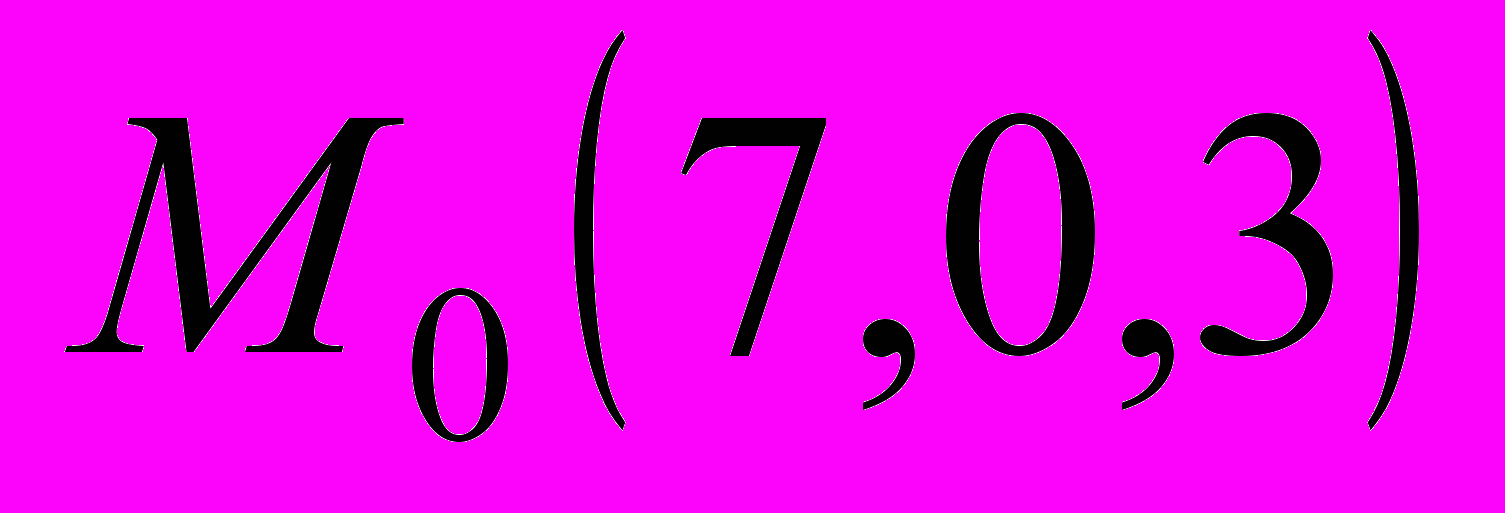 до плоскости
до плоскости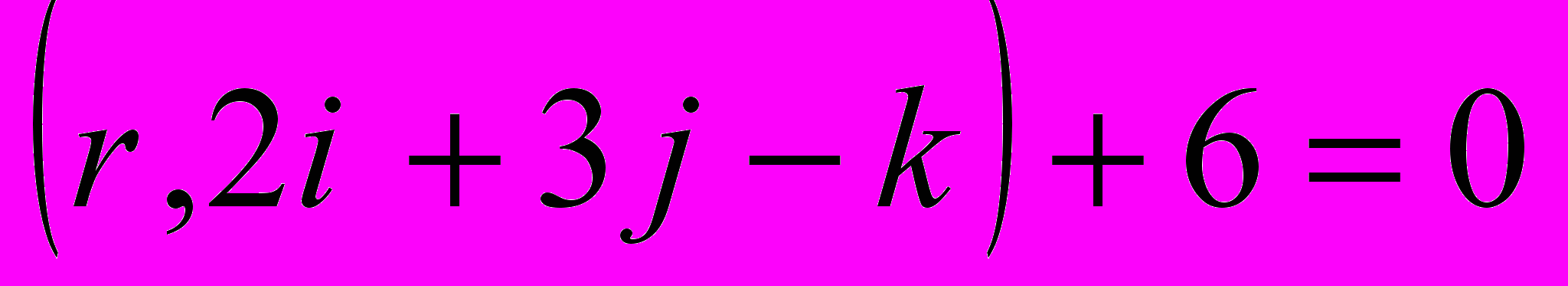 .
.5. Найти угол между прямой
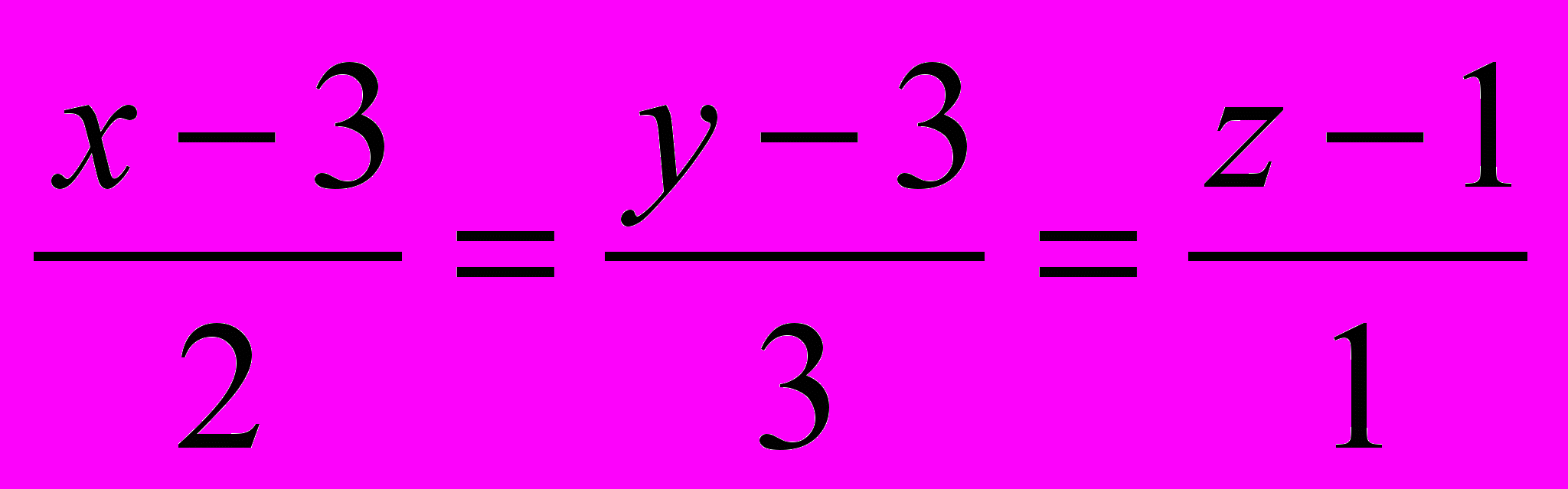 и плоскостью
и плоскостью 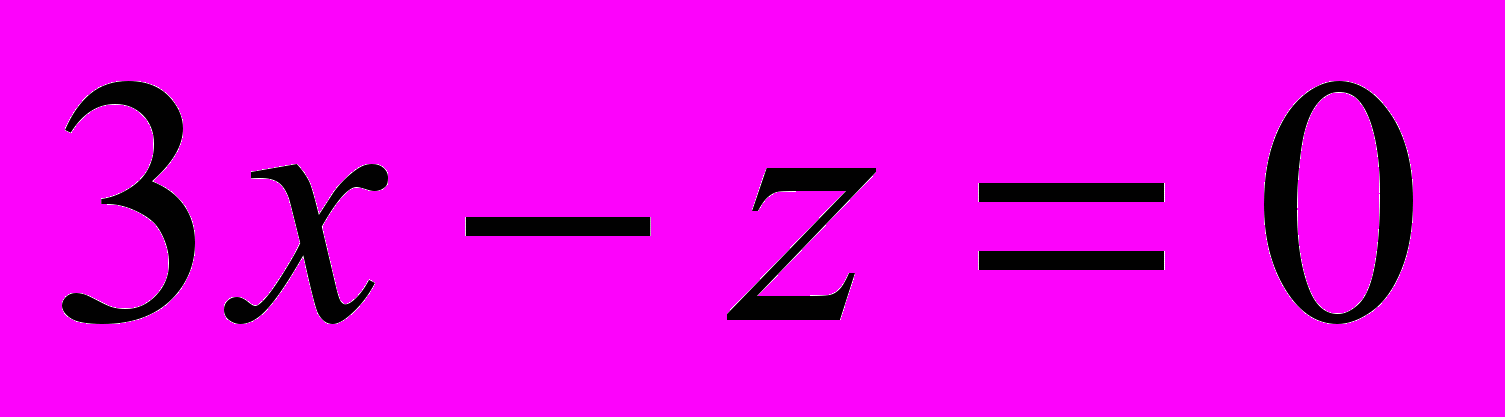 .
.6. Определить фокусы эллипса
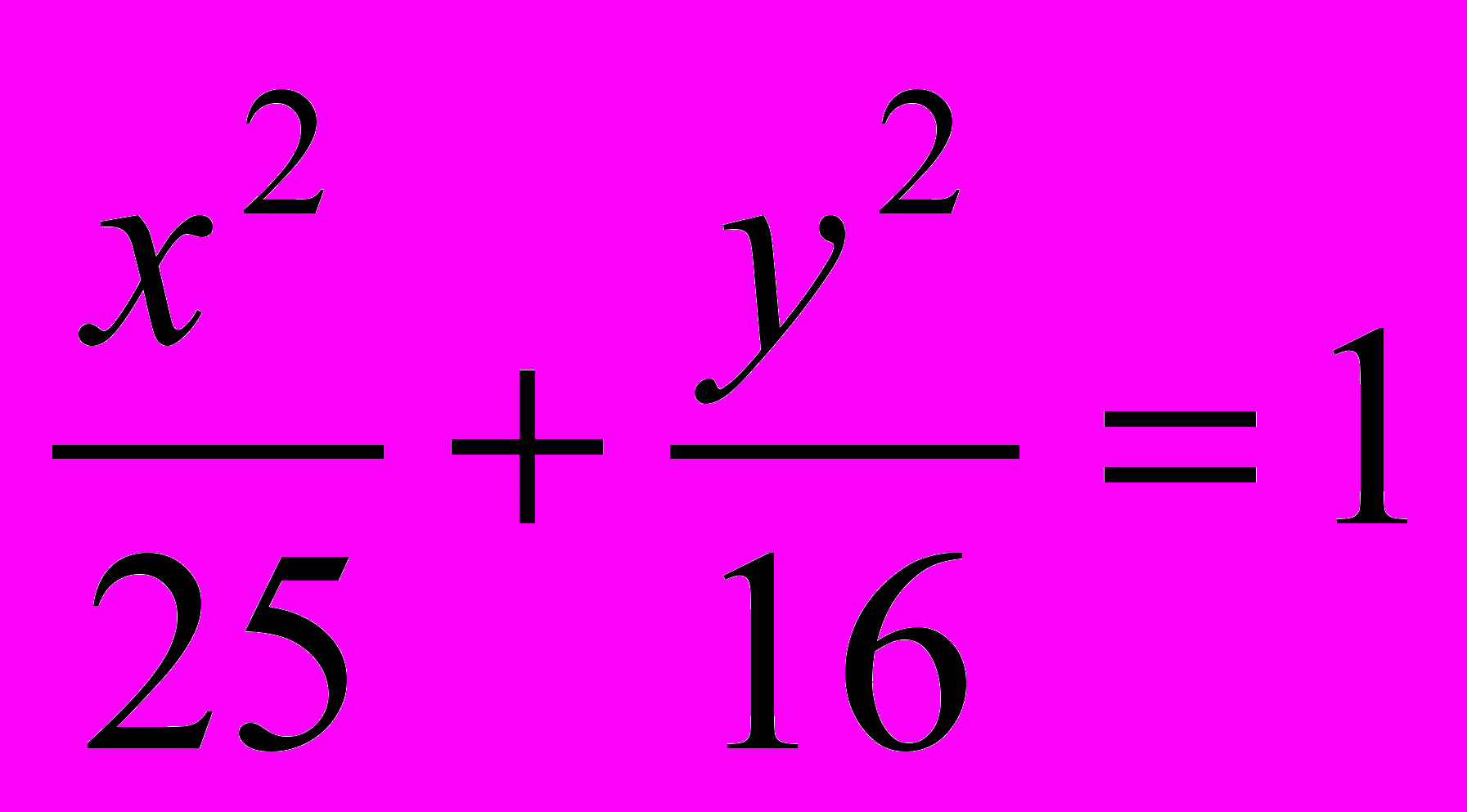 .
.Домашняя контрольная работа №3 по курсу
Исследовать и построить линию второго порядка
1.
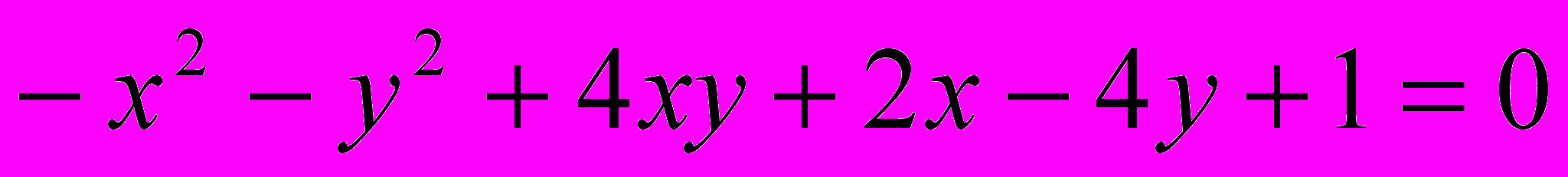 .
.2.
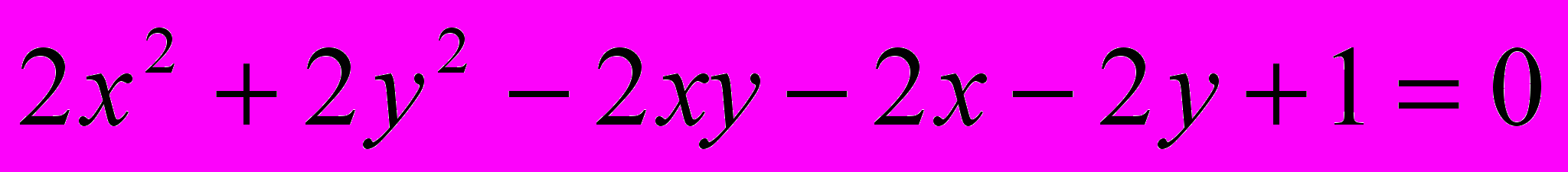 .
.3.
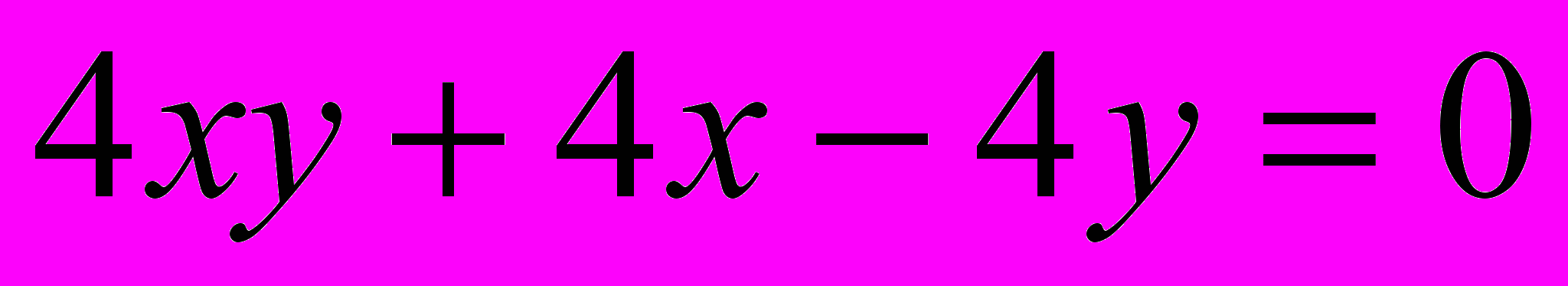 .
.4.
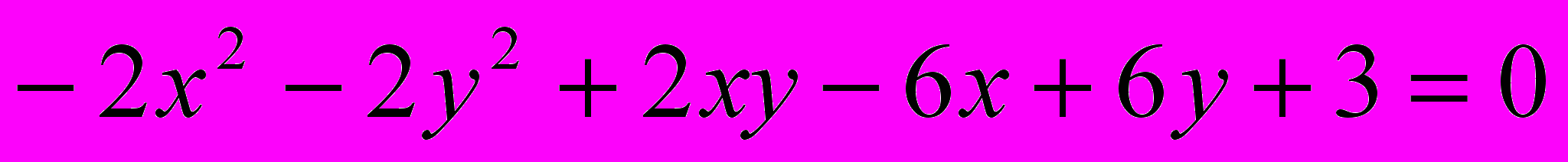 .
.5.
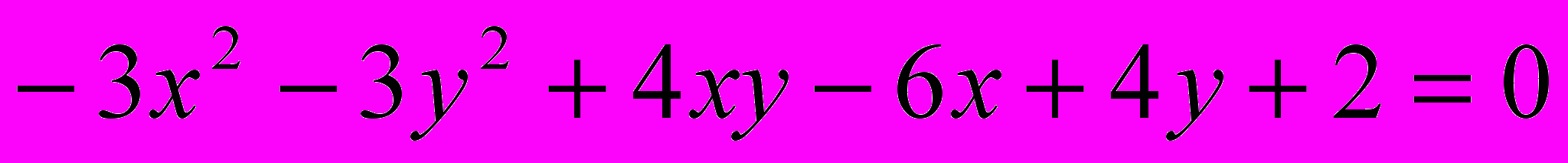 .
.6.
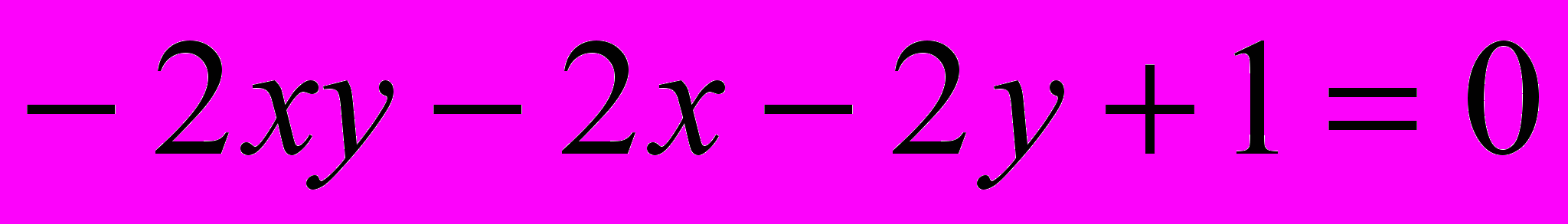 .
.7.
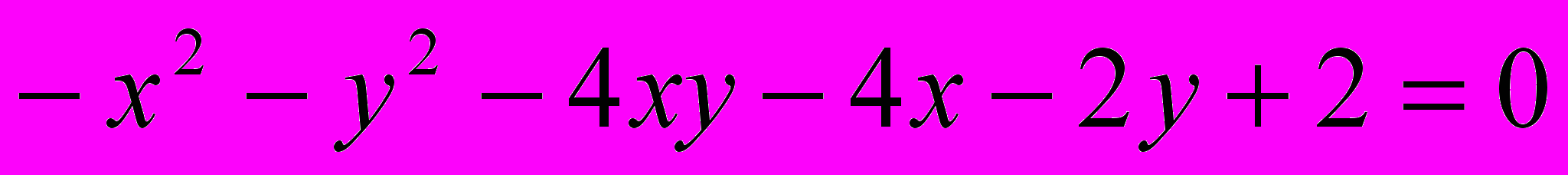 .
.8.
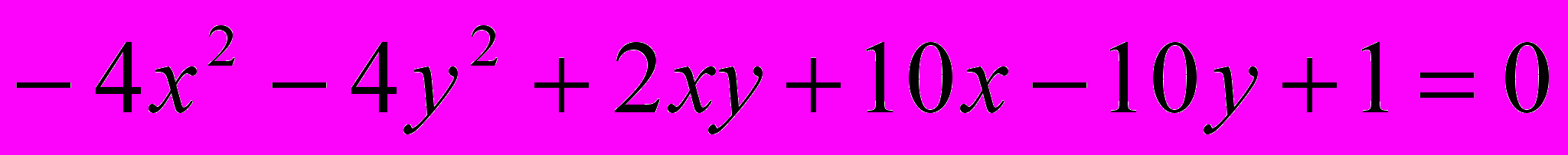 .
.9.
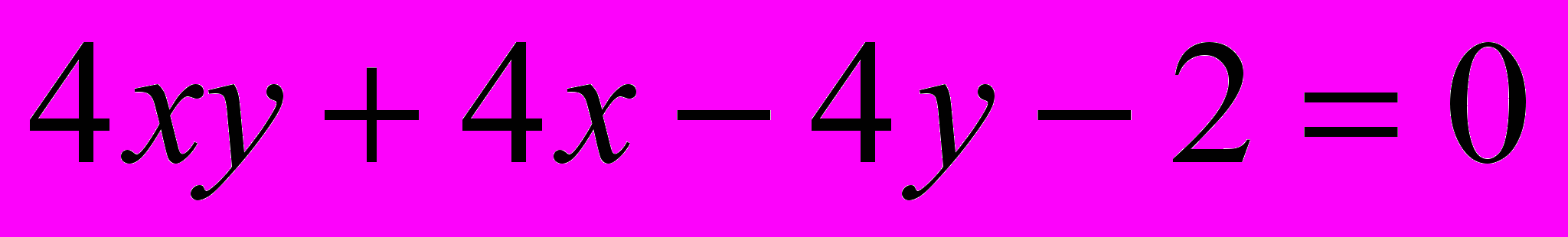 .
.10.
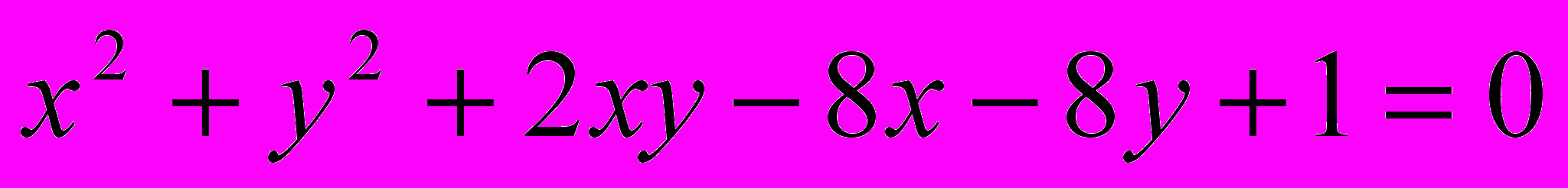 .
.11.
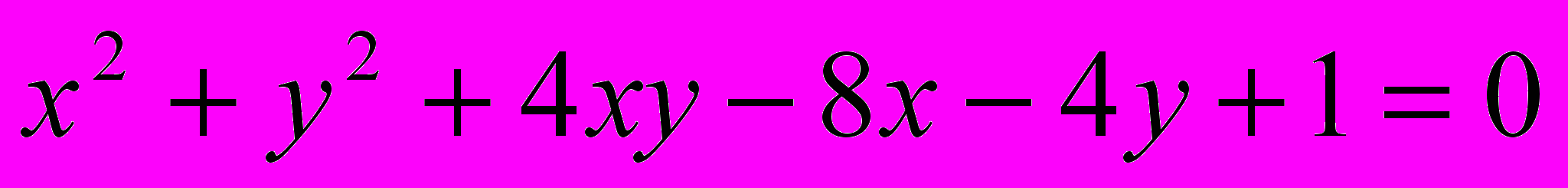 .
.12.
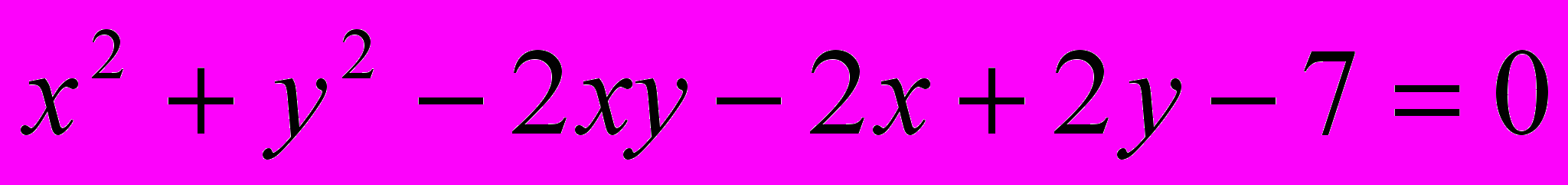 .
.13.
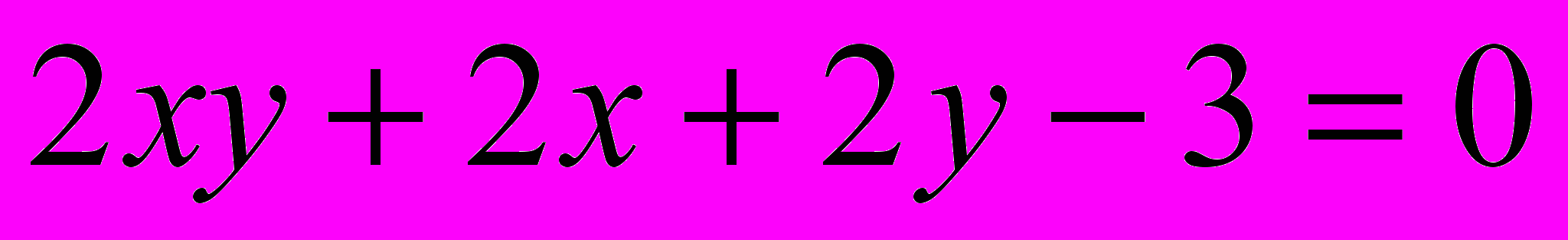 .
.14.
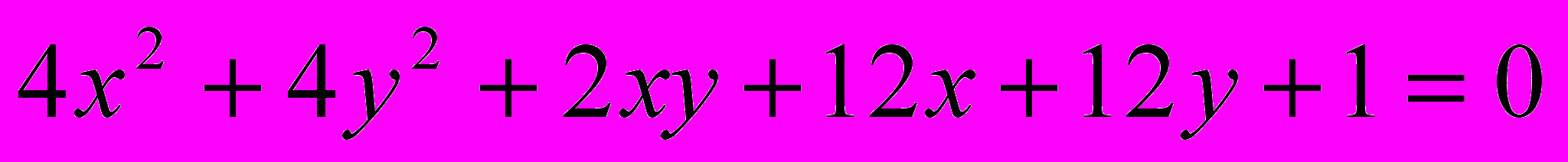 .
.15.
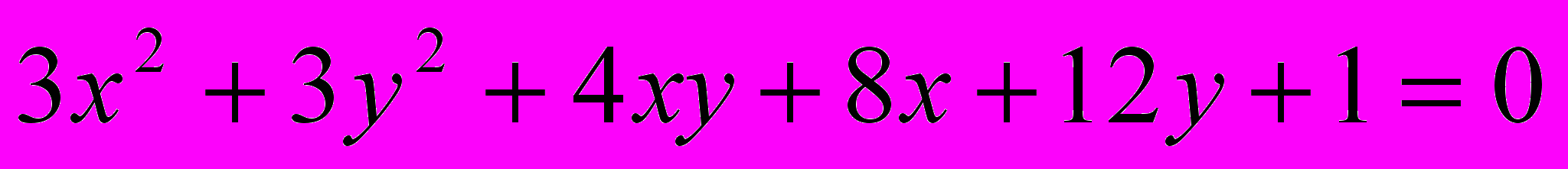 .
.16.
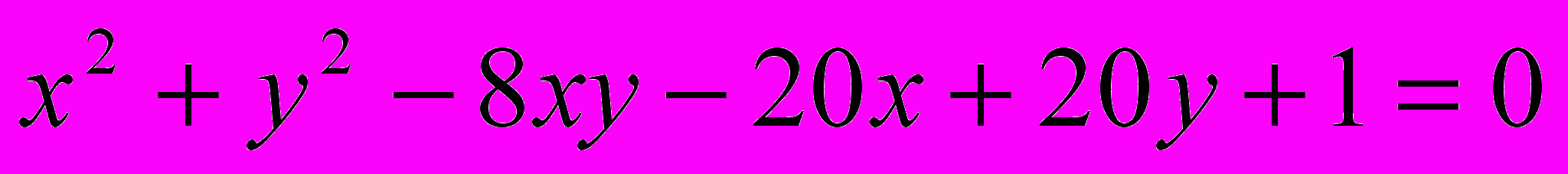 .
.17.
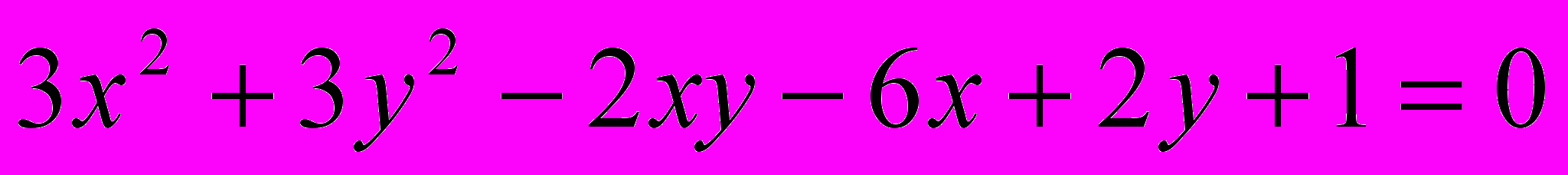 .
.18.
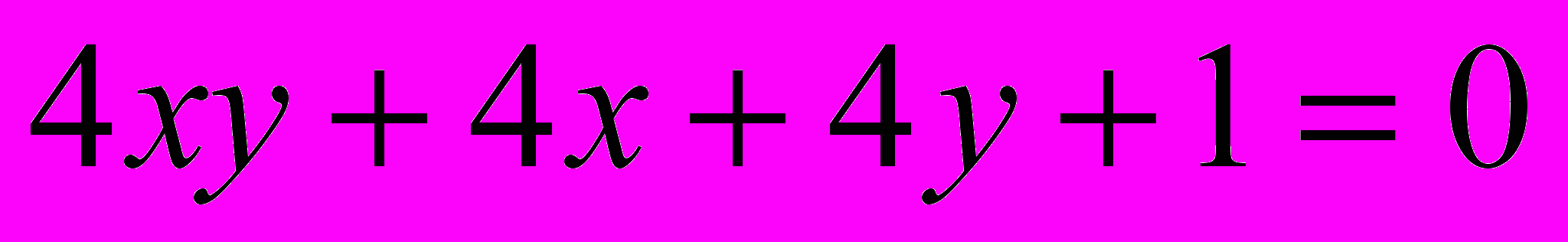 .
.19.
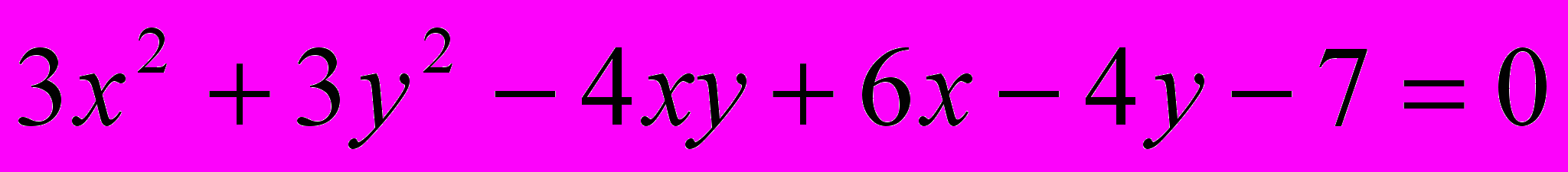 .
.20.
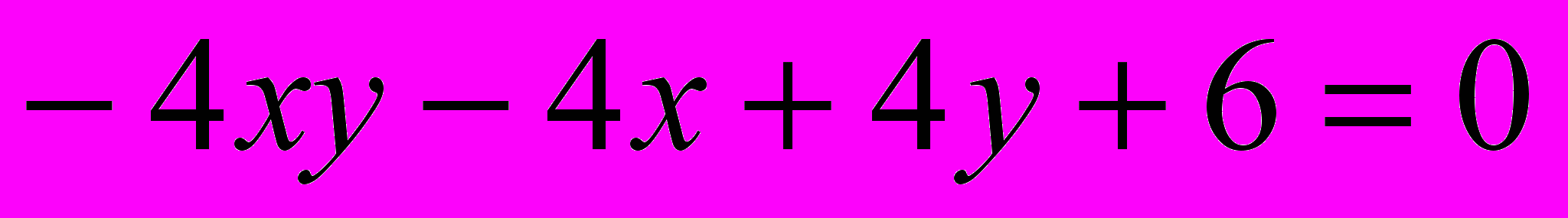 .
.21.
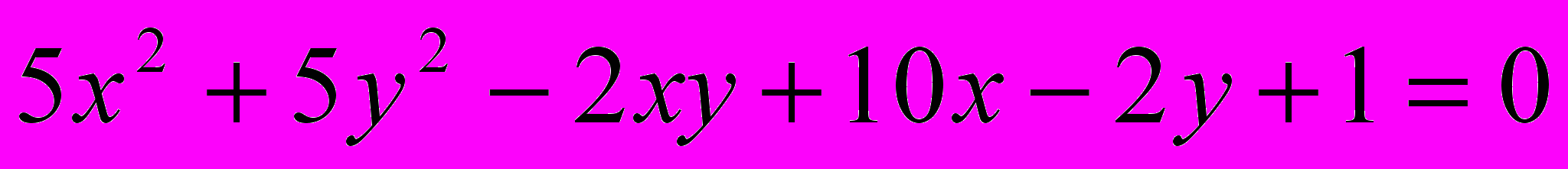 .
.22.
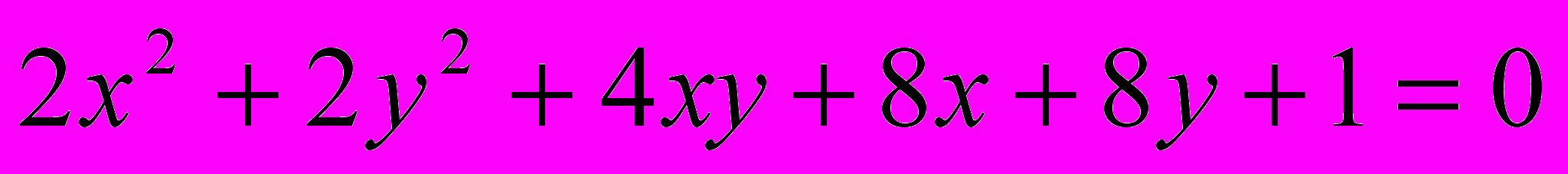 .
.23.
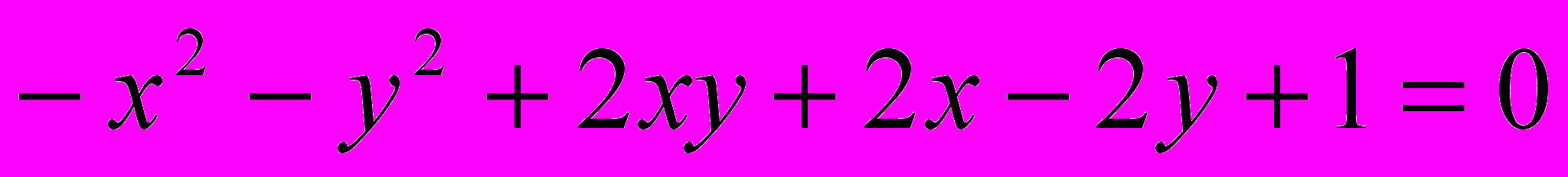 .
.24.
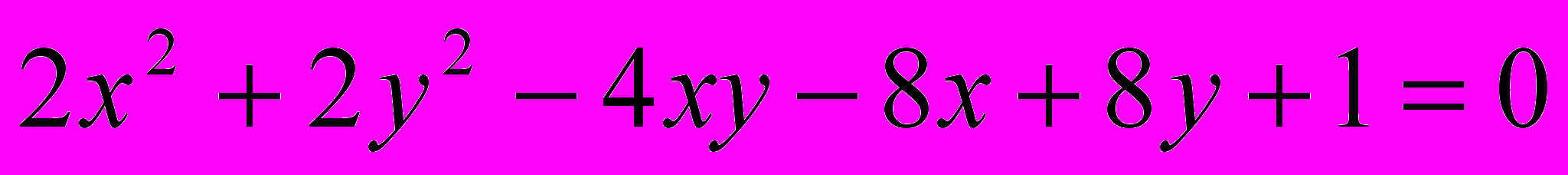 .
.25.
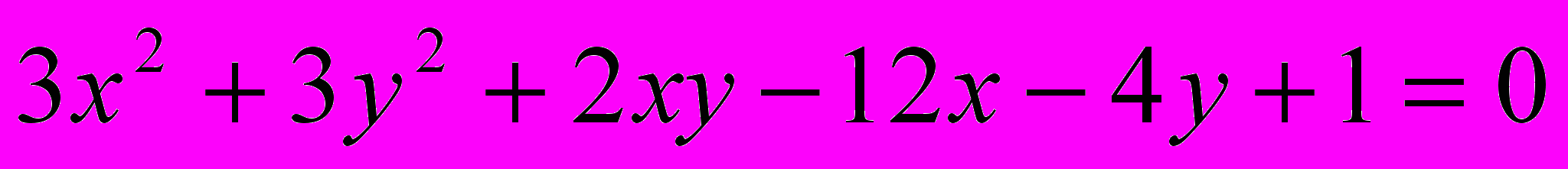 .
.26.
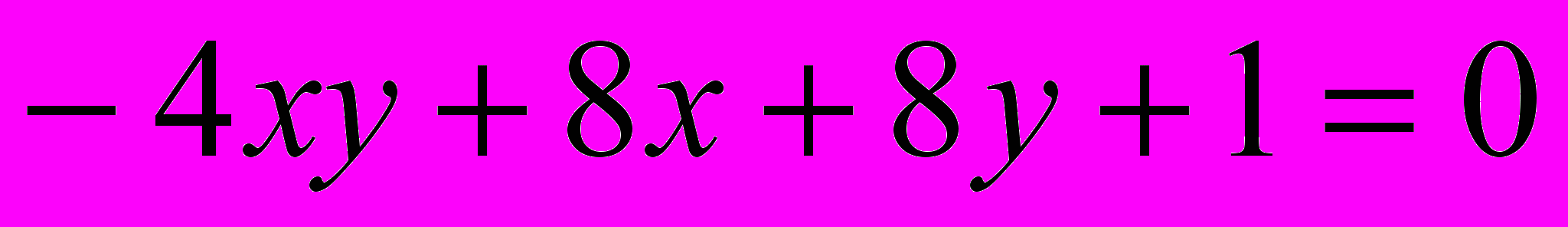 .
.27.
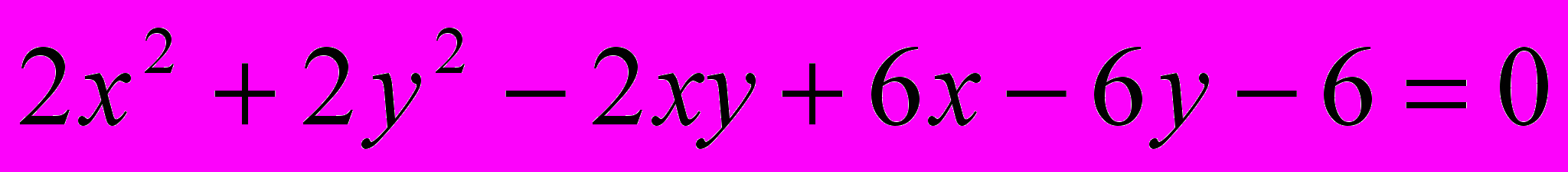 .
.28.
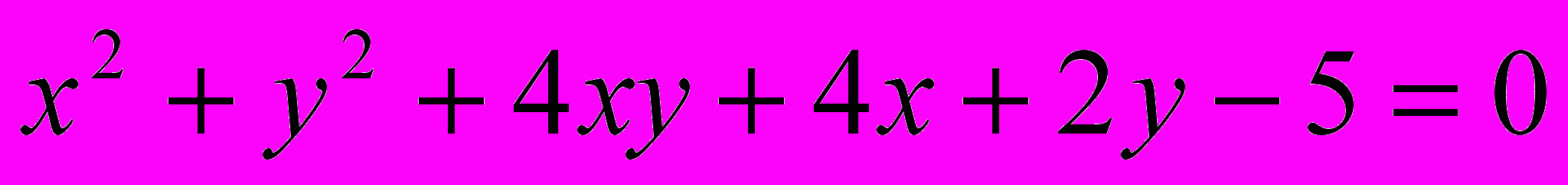 .
.29.
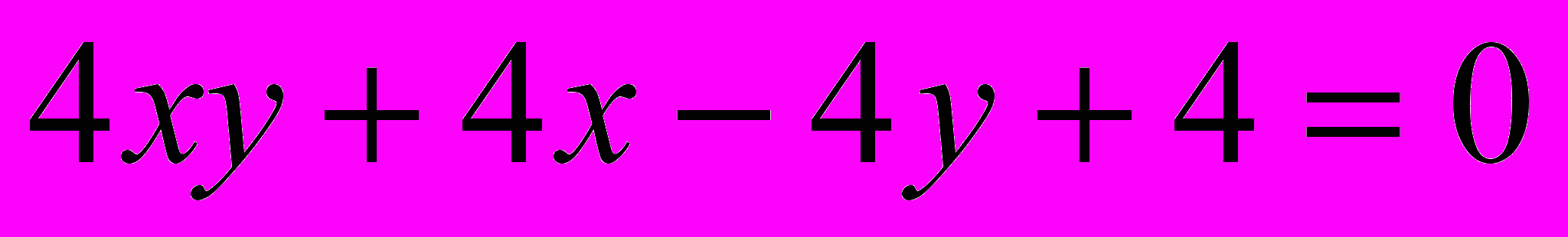 .
.30.
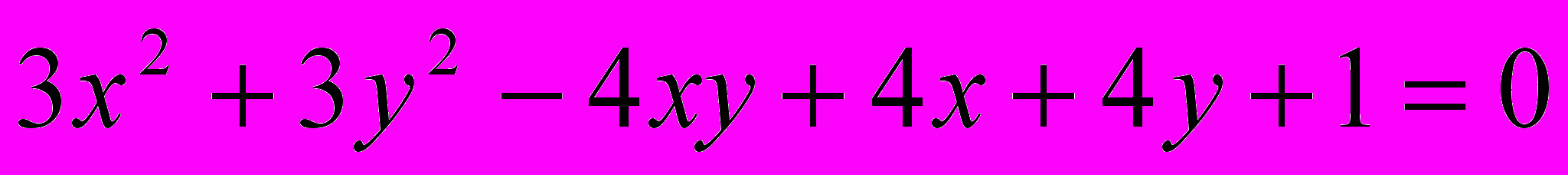 .
.