Geum.ru

I. Гетероскедастичность Как определяется условие независимости ошибок регрессионной модели

Вид материалаДокументы

Содержание


Институт международных экономических отношений
Подобный материал:

Семестр 5

I. Гетероскедастичность

    1. Как определяется условие независимости ошибок регрессионной модели?
    2. Какие требования предъявляются к распределению ошибок наблюдения в классической модели регрессии?
    3. Как определяется условие гомоскедастичности в регрессионной модели?
    4. Как определяется условие гетероскедастичности в регрессионной моде­ли?
    5. Какими свойствами обладают коэффициентов регрессии при наличии гетероскедастичности?
    6. Какими свойствами обладают оценки коэффициентов регрессии, если условие гомоскедастичности удовлетворено?
    7. Каким требованиям должны удовлетворять остатки в хорошо подобранной модели?
    8. С помощью каких тестов можно проверить гипотезу о гомоскедастичности регрессион-ных остат­ков?
    9. Какая гипотеза проверяется в тесте Голдфелда-Квандта для обнаружения гетероскедастич-ности?
    10. Какой статистический критерий используется в тесте Голдфелда-Квандта?
    11. Какая гипотеза проверяется в тесте Спирмена для обнаружения гетероскедастичности?
    12. Какой статистический критерий используется в тесте Спирмена?



II. Устранение гетероскедастичности

    1. С помощью каких тестов можно установить характер зависимости дисперсии ошибок от регрессоров?
    2. Какая гипотеза проверяется в тесте Бреуша-Пагана для обнаружения гетероскедастичности?
    3. Какой статистический критерий используется в тесте Бреуша-Пагана?
    4. Какая гипотеза проверяется в тесте Глейзера для обнаружения гетероскедастичности?
    5. Какой статистический критерий используется в тесте Глейзера?
    6. Почему следует устранять гетероскедастичность?
    7. Какими свойствами обладают оценки коэффициентов регрессии, полученные по методу взвешенных наименьших квадратов при устранении гетероскедастичности?
    8. Метод взвешенных наименьших квадратов требует оценки преобразованного уравнения регрессии. Содержит ли это уравнение свободный член?
    9. Как нужно преобразовать наблюдаемые значения, чтобы устранить гетероскедастичность по методу взвешенных наименьших квадратов?
    10. Почему метод взвешенных наименьших квадратов позволяет получить более эффективные оценки, чем обычный метод наименьших квадратов?



III. Автокорреляция

    1. Какая предпосылка классической теории регрессии нарушается при наличии автокорреляции ошибок регрессии?
    2. Что означает автокорреляция ошибок регрессии?
    3. Какие существуют виды автокорреляции ошибок регрессии? Как часто эти виды автокорреляции встречаются в экономических задачах?
    4. Что такое положительная автокорреляция?
    5. Что такое отрицательная автокорреляция?
    6. Какими свойствами обладают оценки коэффициентов регрессии, полученные по методу наименьших квадратов при отсутствии автокорреляции ошибок регрессии и при выполнении всех остальных предпосылок классической теории регрессии?
    7. Какими свойствами обладают оценки коэффициентов регрессии, полученные по методу наименьших квадратов при наличии автокорреляции ошибок регрессии?
    8. Какие причины приводят к автокорреляции ошибок регрессии?

IV. Устранение автокорреляции.

    1. С помощью какого теста можно установить наличие автокорреляции ошибок регрессии?
    2. Какая гипотеза проверяется в тесте Дарбина-Уотсона?
    3. Какие значения принимает критерий Дарбина-Уотсона?
    4. Напишите формулу связи критерия Дарбина-Уотсона с выборочным коэффициентом корреляции между соседними ошибками регрессии.
    5. Какое неравенство выполняется для критерия Дарбина-Уотсона d, если автокорреляция ошибок регрессии отсутствует?
    6. Какое неравенство выполняется для критерия Дарбина-Уотсона d, если существует положительная автокорреляция?
    7. Какое неравенство выполняется для критерия Дарбина-Уотсона d, если существует отрицательная автокорреляция?
    8. Почему следует устранять автокорреляцию ошибок регрессии?
    9. Смысл поправки Прайса-Уинстона.
    10. При каких условиях можно применять тест Дарбина-Уотсона?

V. Временной ряд.

  1. Что называют временным рядом?
  2. Какие компоненты можно выделить во временном ряду?
  3. Что характеризует тренд временного ряда?
  4. Что характеризует сезонная компонента временного ряда?
  5. Что характеризует циклическая компонента временного ряда?
  6. Что характеризует случайная компонента временного ряда?
  7. Какие существуют модели временного ряда? Каковы их особенности?
  8. Что подразумевается под автокорреляцией уровней временного ряда?
  9. Что называют автокорреляционной функцией временного ряда?
  10. Что называют коррелограммой временного ряда?
  11. Какие компоненты содержит временной ряд, если для него оказался наиболее высоким коэффициент автокорреляции 1-го порядка?
  12. Какие компоненты содержит временной ряд, если для него оказался наиболее высоким коэффициент автокорреляции порядка τ (τ > 1)?
  13. Какие компоненты содержит временной ряд, если для него все коэффициенты автокорреляции оказались не значимы?

VI. Тренд и сезонная компонента.

  1. Что означает выравнивание временного ряда?
  2. Что означает аналитическое выравнивание временного ряда?
  3. Дайте определение белого шума.
  4. Что моделирует белый шум?
  5. Какие функции используют при аналитическом выравнивании временного ряда?
  6. Напишите границы доверительного интервала для среднего значения .
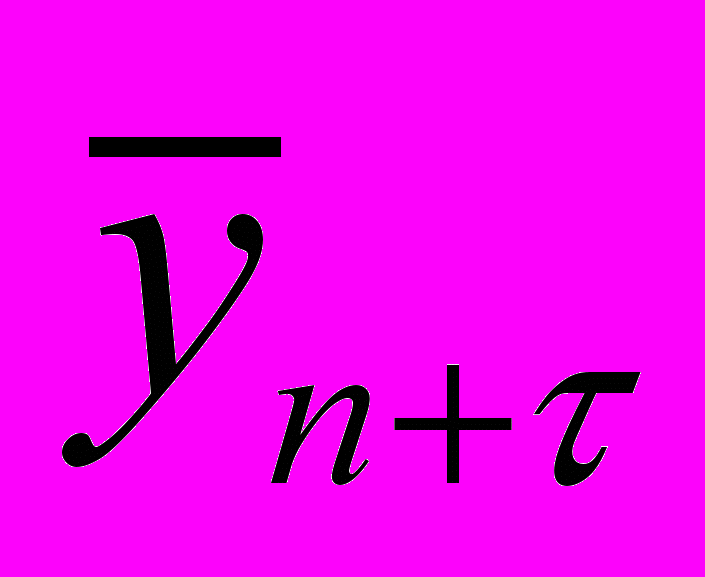  7. С какой целью применяют метод скользящей средней?
  8. Напишите уравнение аддитивной модели временного ряда.
  9. Напишите уравнение мультипликативной модели временного ряда.
  10. В чём состоит корректировка средних сезонных компонент в аддитивной модели временного ряда?
  11. В чём состоит корректировка средних сезонных компонент в мультипликативной модели временного ряда?
  12. Как устраняют сезонную компоненту S из исходных уровней ряда Y в аддитивной модели временного ряда?
  13. Как устраняют сезонную компоненту S из исходных уровней ряда Y в мультипликативной модели временного ряда?

VII. Модели с лагами.

    1. Какая переменная называется лаговой?
    2. Какую модель называют моделью с лагами?
    3. Какую модель называют динамической моделью?
    4. Дайте определение краткосрочного мультипликатора.
    5. Дайте определение долгосрочного мультипликатора.
    6. Дайте определение среднего лага.
    7. Какие из величин в модели полиномиальных лагов записывают в виде полиномов степени т?
    8. Запишите полином степени т, который используют в модели полиномиальных лагов.
    9. Дайте определение медианного лага.
    10. Какие причины приводят к наличию лаговых переменных в эконометрических моделях?
    11. Какие причины затрудняют построение обычным МНК качественной модели с распределены-ми лагами?
  1. VIII. Модель Койка. Модель авторегрессии.



  1. В какую модель преобразуется модель геометрических лагов после преобразования Койка?
  2. Какие из величин в модели геометрических лагов записывают в виде прогрессии?
  3. Запишите геометрическую прогрессию, которую используют в модели геометрических лагов.
  4. Какая модель называется авторегрессионной?
  5. Какой из параметров модели авторегрессии является краткосрочным мультипликатором?
  6. Что характеризует долгосрочный мультипликатор в модели геометрических лагов?
  7. Каковы свойства оценок параметров авторегрессионной модели по МНК?
  8. Сформулируйте основную идею метода инструментальной переменной для оценки модели авторегрессии.
  9. Для каких моделей тест Дарбина-Уотстона не позволяет определить наличие автокорреляции остатков регрессии?



IX. Модели временного ряда. Модель частичной корректировки. Модель адаптивных ожиданий.

  1. Какой ряд называется стационарным?
  2. Напишите уравнение авторегрессионной модели порядка р.
  3. Напишите уравнение модели скользящей средней порядка q.
  4. Напишите уравнение авторегрессионной модели скользящей средней порядков 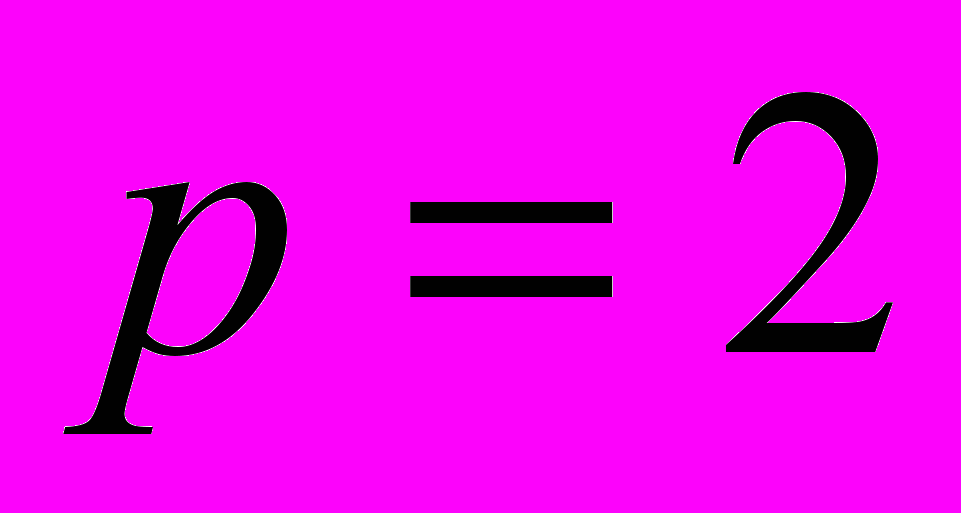и .
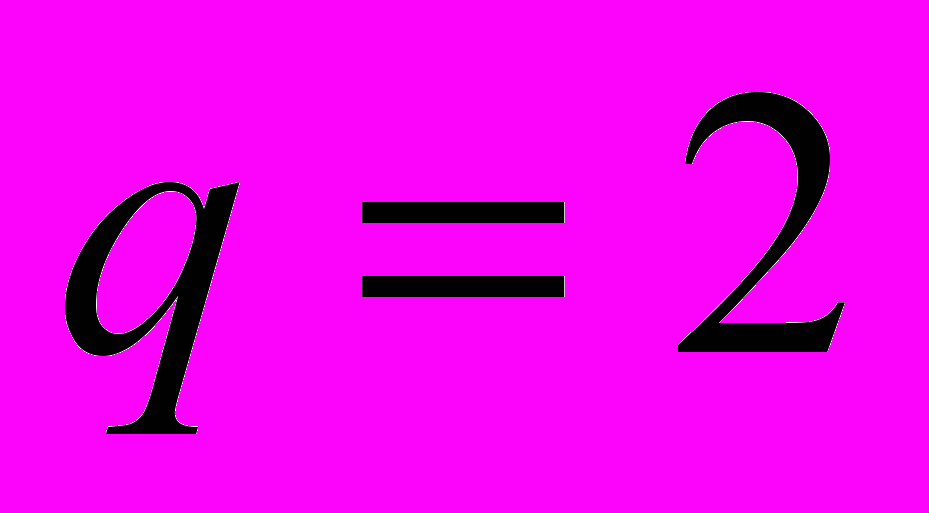  5. Какую модель называют моделью частичной корректировки?
  6. Какие значения принимает коэффициент корректировки? Какой смысл имеют его значения?
  7. Какую модель называют моделью адаптивных ожиданий?

Какие значения принимает коэффициент ожидания? Какой смысл имеют его значения?

X. Системы одновременных уравнений.

  1. Дайте определение эндогенной переменной.
  2. Дайте определение экзогенной переменной.
  3. Дайте определение предопределённой переменной.
  4. Дайте определение системы одновременных уравнений.
  5. Что такое поведенческие уравнения? В чём состоит их отличие от уравнений-тождеств?
  6. Что называют структурной формой системы одновременных уравнений?
  7. Что называют приведённой формой системы одновременных уравнений?
  8. Какие свойства имеют оценки структурных параметров при оценивании структурной модели по методу наименьших квадратов? В чём причина этих свойств?
  9. Какие преимущества имеют приведённые уравнения системы по сравнению со структурными регрессионными уравнениями?
  10. Какова суть косвенного метода наименьших квадратов?
  11. Из каких действий состоит алгоритм косвенного метода наименьших квадратов?
  12. Какие свойства будут иметь оценки структурных параметров, если для их оценивания применить косвенный метод наименьших квадратов?

XI. Идентификация системы одновременных уравнений

  1. Какое структурное уравнение называют идентифицируемым? Неидентифицируемым? Сверхидентифицируемым?
  2. Сформулируйте необходимое условие идентификации.
  3. Какой метод используют для оценки структурных параметров идентифицируемой системы?
  4. Какой метод используют для оценки структурных параметров сверхидентифицируемой системы?
  5. Что нужно предпринять для оценки структурных параметров неидентифицируемой системы?
  6. Какие соотношения выполняются для числа структурных параметров п и числа приведённых параметров 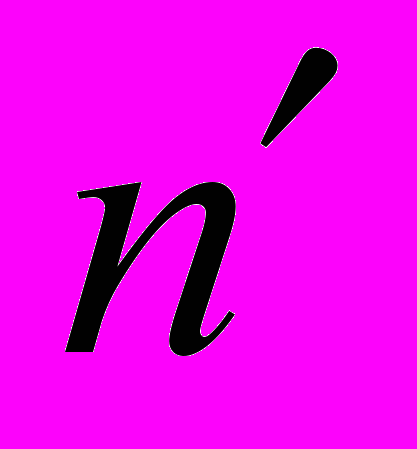системы одновременных уравнений, если система идентифицируема? Неидентифицируема? Сверхидентифицируема?
  7. Из каких действий состоит алгоритм двухшагового метода наименьших квадратов?
  8. Какие свойства будут иметь оценки структурных параметров, если для их оценивания применить двухшаговый метод наименьших квадратов?
  9. В каком случае применение двухшагового метода наименьших квадратов будет эффективным?

ИНСТИТУТ МЕЖДУНАРОДНЫХ ЭКОНОМИЧЕСКИХ ОТНОШЕНИЙ


Вопросы к экзамену по курсу "Эконометрика", 5-й семестр.

  1. Гетероскедастичность, её последствия. Графический анализ остатков.
  2. Обнаружение гетероскедастичности по тесту ранговой корреляции Спирмена.
  3. Обнаружение гетероскедастичности по тесту Голдфельда – Квандта.
  4. Обнаружение гетероскедастичности по тесту Глейзера.
  5. Обнаружение гетероскедастичности по тесту Бреуша – Пагана.
  6. Метод взвешенных наименьших квадратов. Устранение гетероскедастич-ности.
  7. Положительная и отрицательная автокорреляция, её последствия. Графический метод обнаружения автокорреляции.
  8. Авторегрессионная модель 1-го порядка зависимости ошибок регрессии.
  9. Обнаружение автокорреляции по критерию Дарбина-Уотсона.
  10. Обобщенный метод наименьших квадратов устранения автокорреляции: ρ – известно; ρ – неизвестно, процедура Кохрейна-Оркатта.
  11. Временной ряд. Компоненты временного ряда. Модели временных рядов.
  12. Автокорреляция уровней временного ряда.
  13. Аналитическое выравнивание временного ряда. Прогнозирование на основе моделей временного ряда.
  14. Метод скользящей средней.
  15. Определение сезонной компоненты в аддитивной модели временного ряда.
  16. Определение сезонной компоненты в мультипликативной модели временного ряда.
  17. Лаги в экономических моделях. Модели с распределённым лагом.
  18. Модель полиномиальных лагов (метод Алмона).
  19. Модель геометрических лагов (преобразование Койка).
  20. Оценивание авторегрессионных моделей.
  21. Обнаружение автокорреляции ошибок в авторегрессионных моделях.
  22. Модели стационарного временного ряда: . Модель нестационарного временного ряда .
  23. Модель частичной корректировки.
  24. Модель адаптивных ожиданий.
  25. Примеры систем одновременных уравнений для моделирования экономических процессов. Структурная и приведенная формы системы одновременных уравнений.
  26. Косвенный метод наименьших квадратов.
  27. Проблема идентификации модели. Необходимое условие идентифицируемости.
  28. Оценивание параметров структурной модели системы одновременных уравнений. Сверхидентифицируемость. Неидентифицируемость
  29. Двухшаговый метод наименьших квадратов.
  30. Применение функции ЛИНЕЙН.
  31. Применение инструмента РЕГРЕССИЯ из ПАКЕТА АНАЛИЗА.
  32. Применение Мастера диаграмм для построения корреляционного поля, уравнения регрессии, вычисления коэффициента детерминации и построения линии регрессии.


Составил вопросы: зав. кафедрой математики и информатики Евсеев В.Н.