Пример построения регрессионной модели

Вид материала

Документы

Подобный материал:

• I. Гетероскедастичность Как определяется условие независимости ошибок регрессионной, 94.43kb.
• М. Н. Узяков Проблемы построения межотраслевой модели, 310.25kb.
• Аудит общественного здания образец аудита, 1221.73kb.
• Дискретных Марковских Цепей) в анализе данных. Пример применения. (лекция, 7.29kb.
• Методические указания по выбору темы и написанию курсовых проектов по дисциплине «Эконометрика, 22.45kb.
• Г. Р. Серебряков опыт построения динамической межотраслевой равновесной модели российской, 330.44kb.
• Аннотация гридасов В. М., Подгайко Н. В. Модель расчета коэффициента дисконтирования, 218.5kb.
• Лекция Проектирование бд. Архитектура построения субд, 419.57kb.
• Холлифорд, 2689.99kb.
• Особенности автоматизации банковской деятельности, 565.54kb.

Пример построения регрессионной модели


Однофакторная линейная модель имеет вид: .

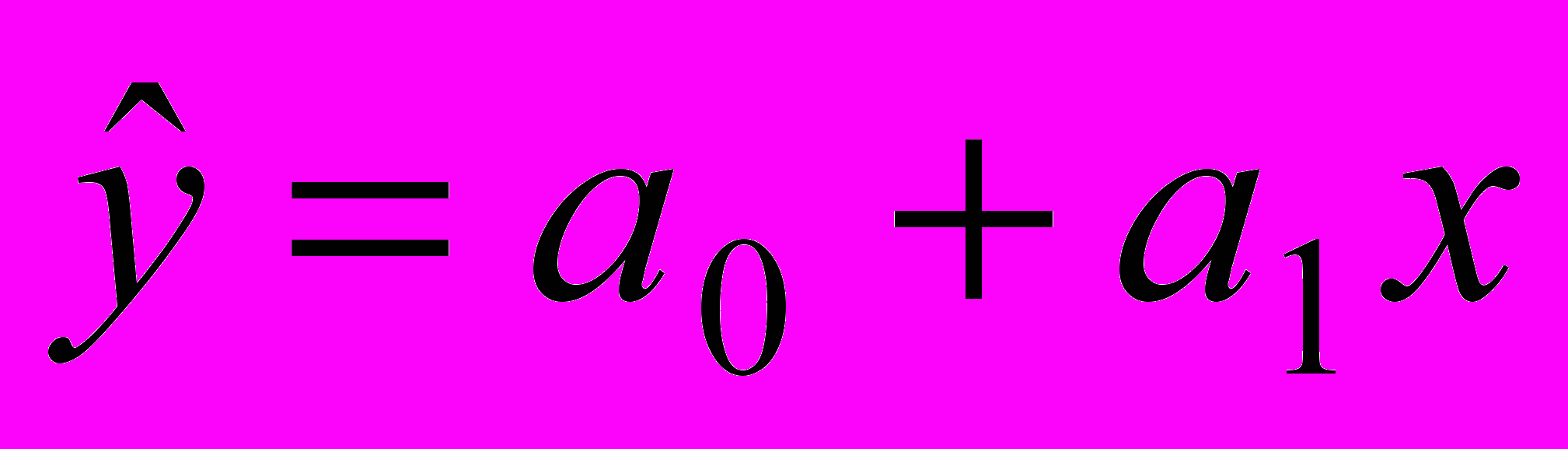1). Для нахождения коэффициентов 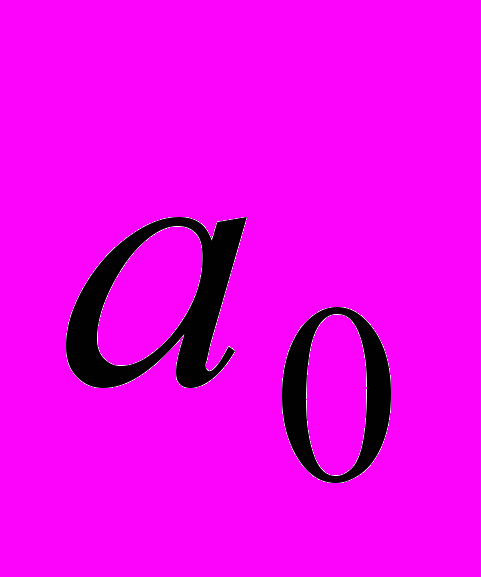и 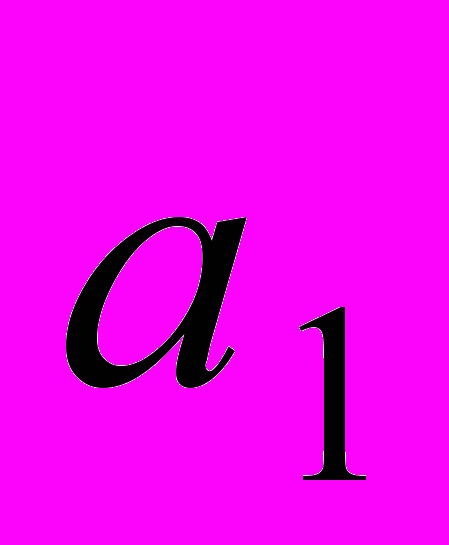применим метод наименьших квадратов:

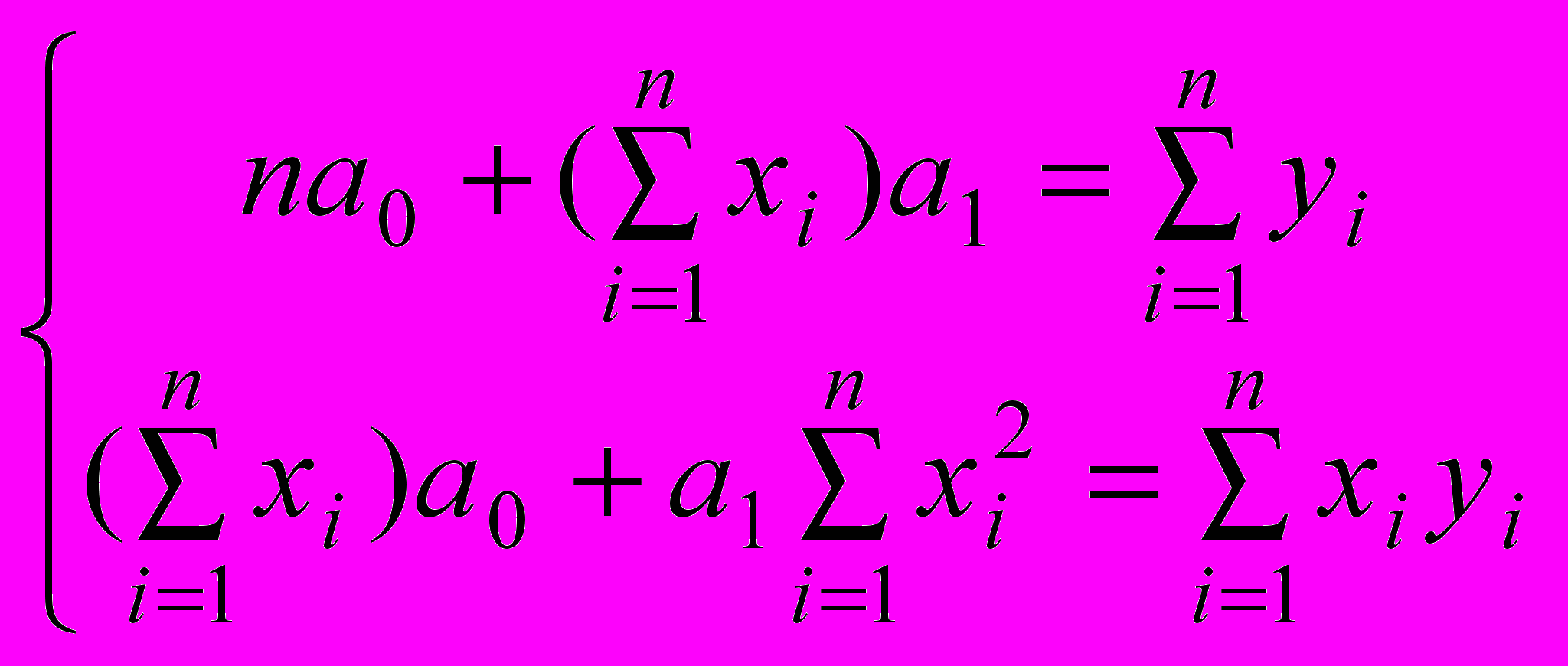(1)


где n – число опытов;

- факторный признак;

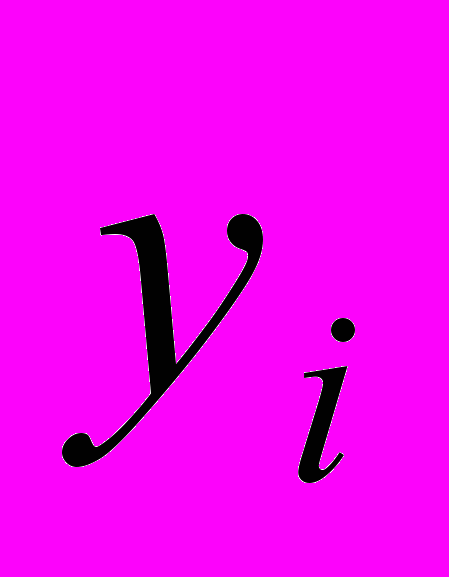- результативный признак.


Если после решения системы (1), коэффициент 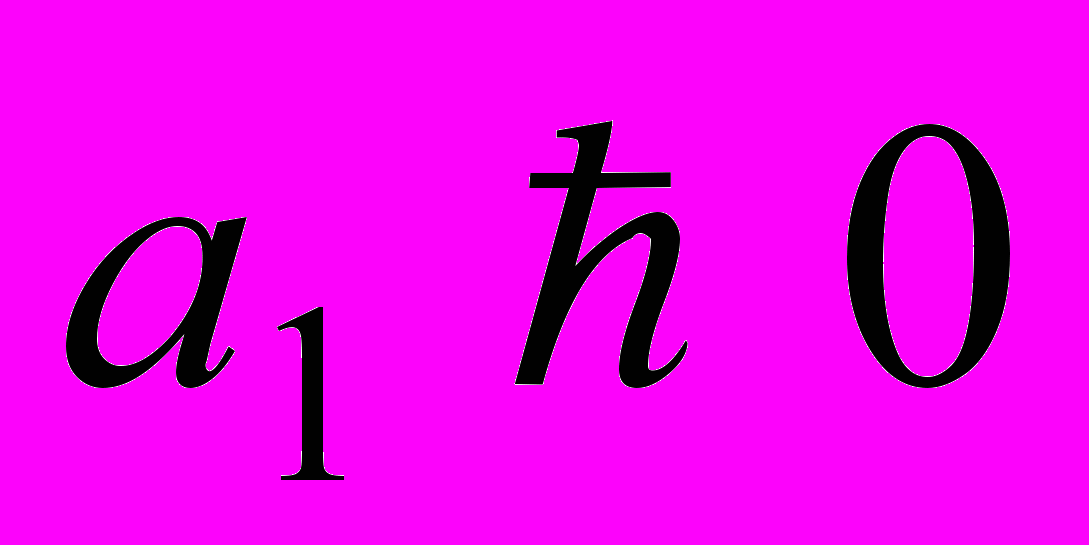, то связь между х и у является прямой.


2). Теснота этой связи определяется коэффициентов корреляции:

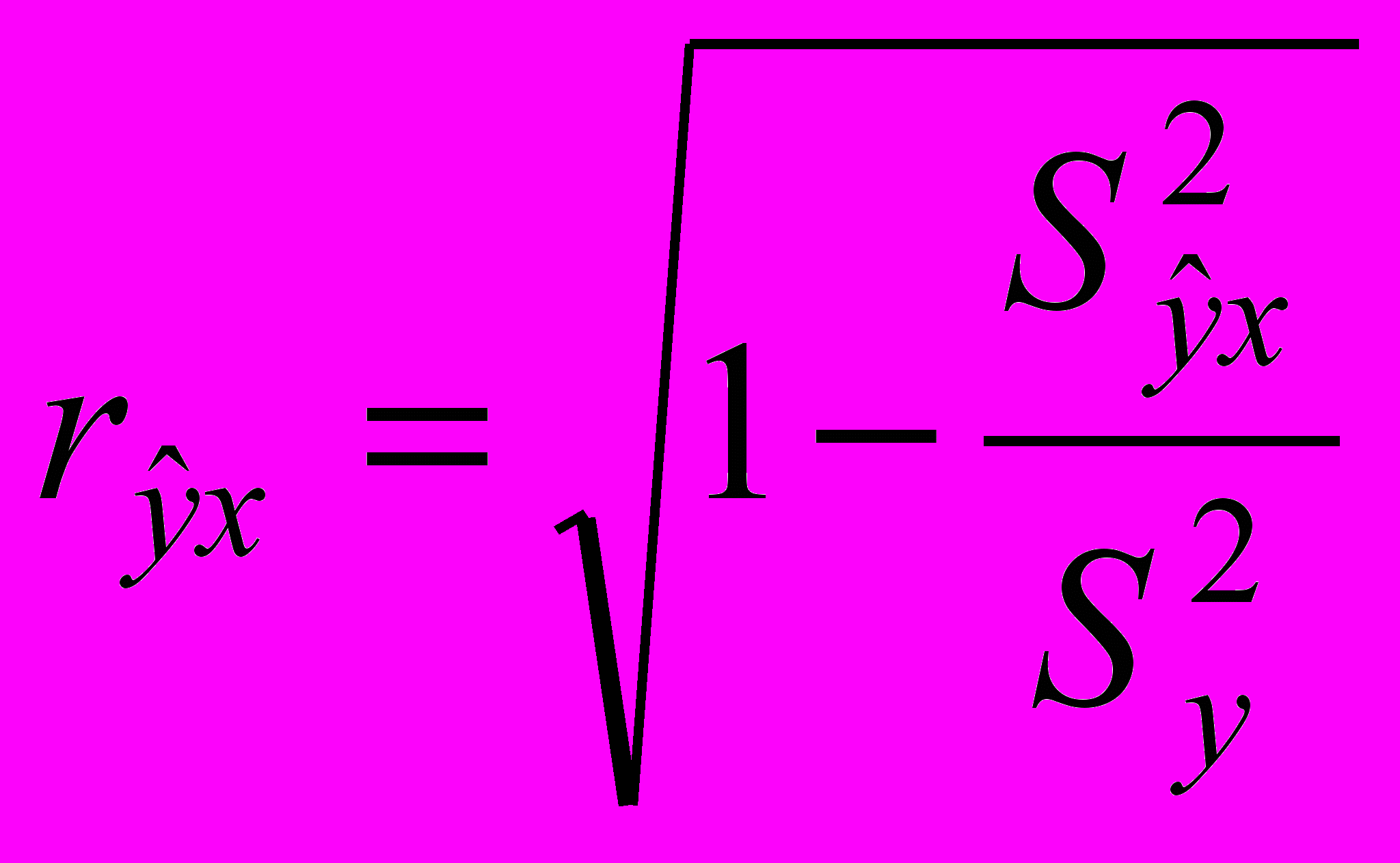. (2)

Коэффициент корреляции находится в интервале от 0 до 1. Чем ближе коэффициент корреляции к единице, тем теснее связь между результативным и факторным признаками.

Средняя квадратическая ошибка выборки:

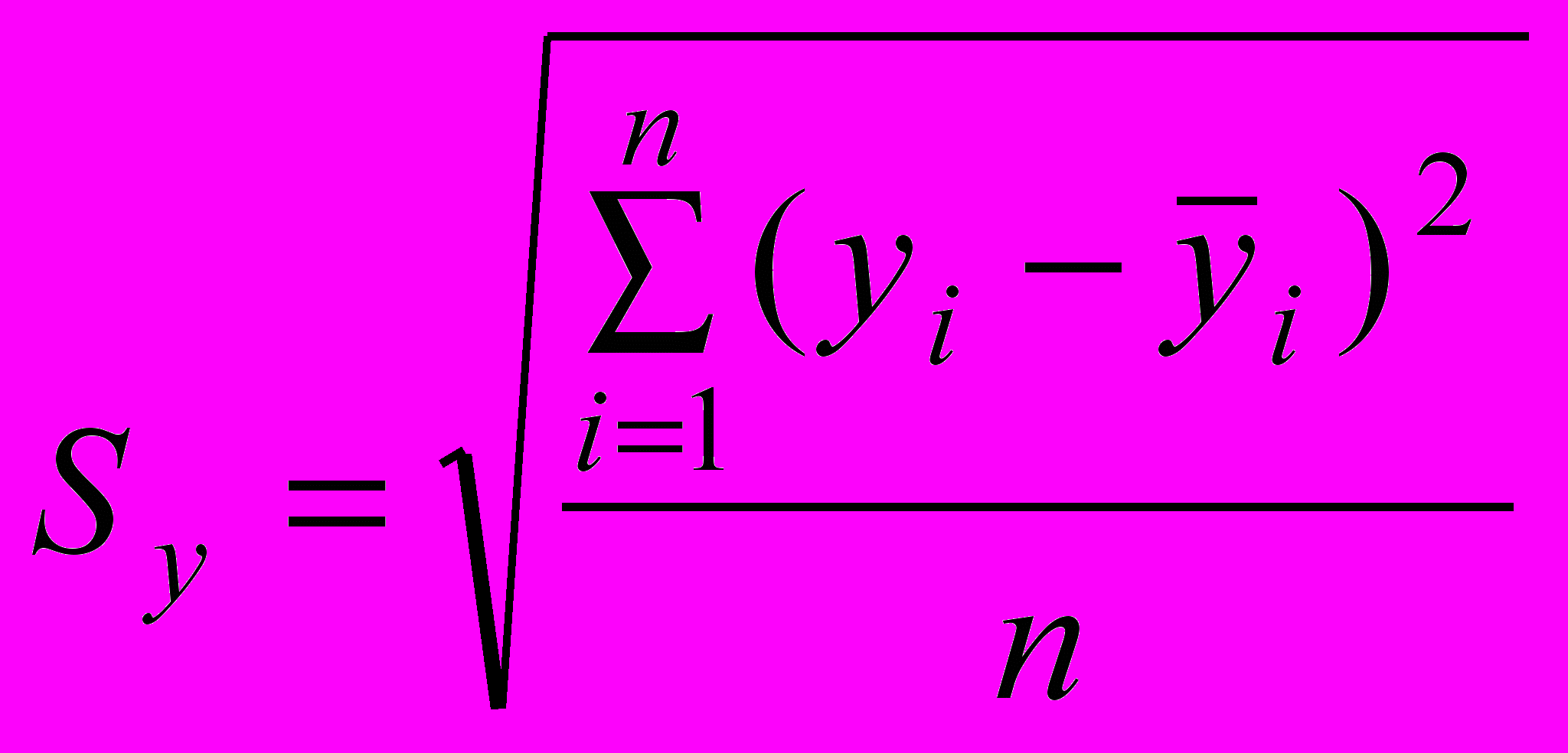, (3)

где 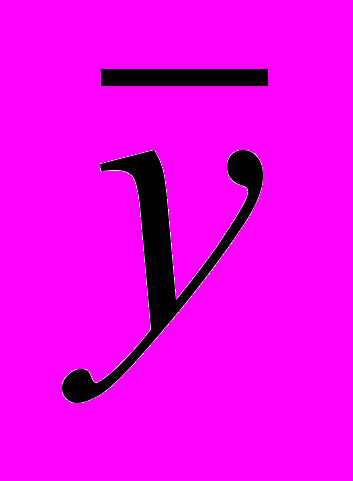- среднее арифметическое значение. Рассчитывается по формуле:

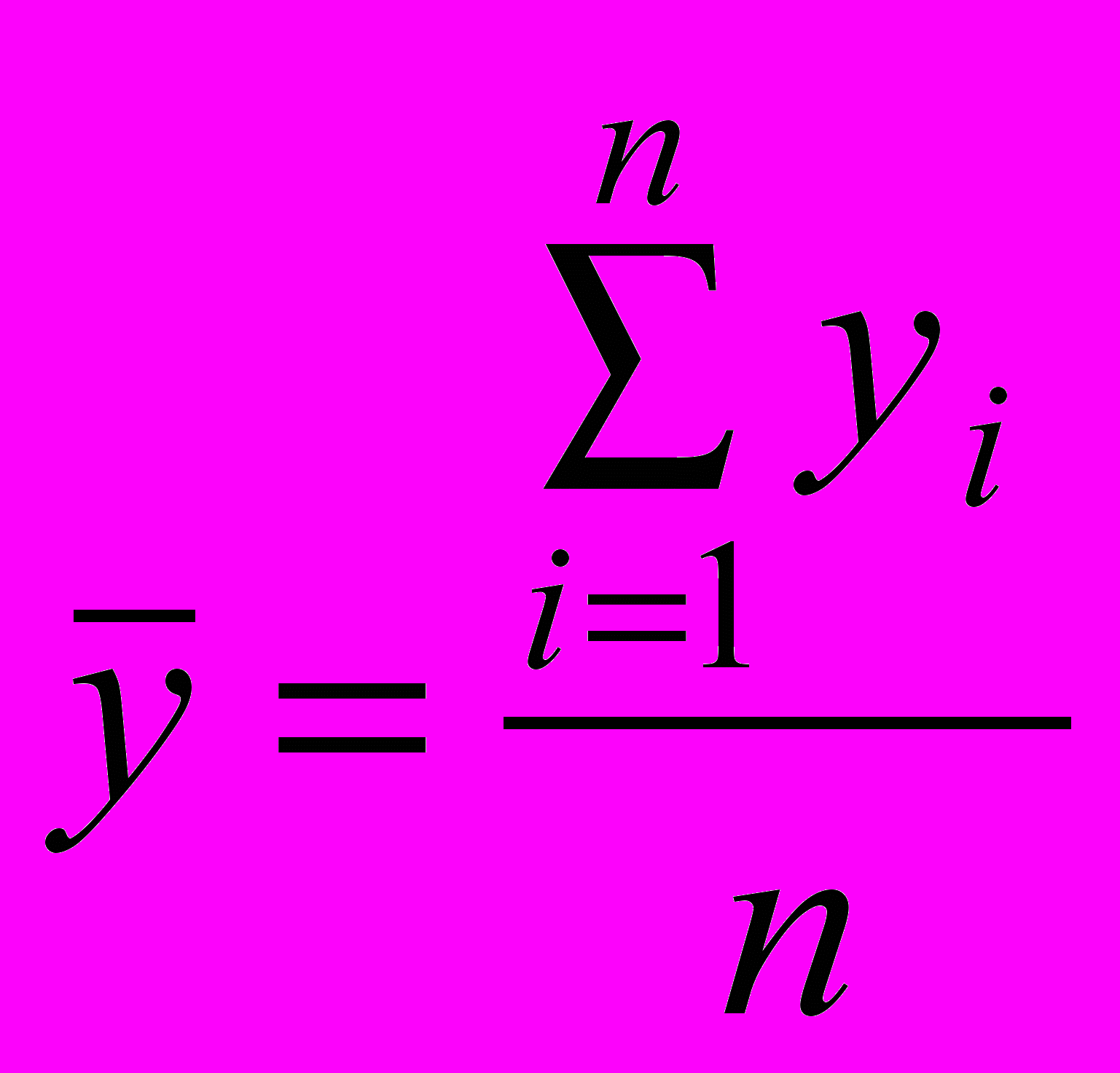. (4)

Средняя квадратическая ошибка уравнения регрессии:

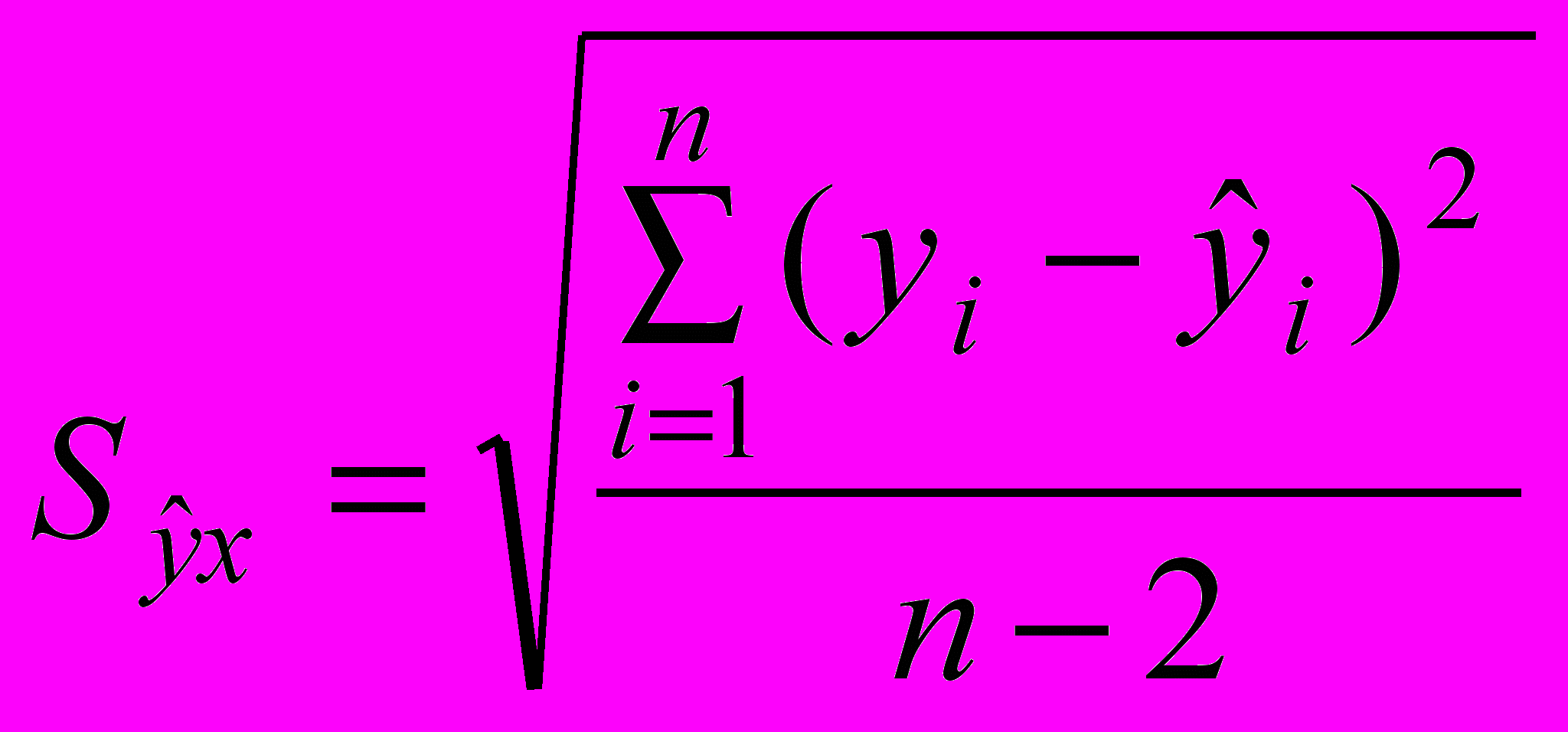. (5)


3). Коэффициент детерминации показывает долю изменения результативного признака под воздействием факторного признака: .


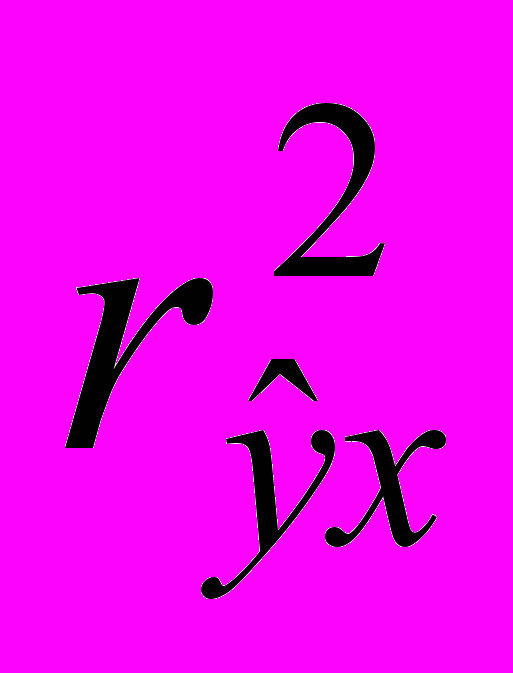4). Коэффициент эластичности показывает, на сколько процентов изменятся результативный признак при изменении факторного признака на 1%. Коэффициент эластичности рассчитывается по формуле:

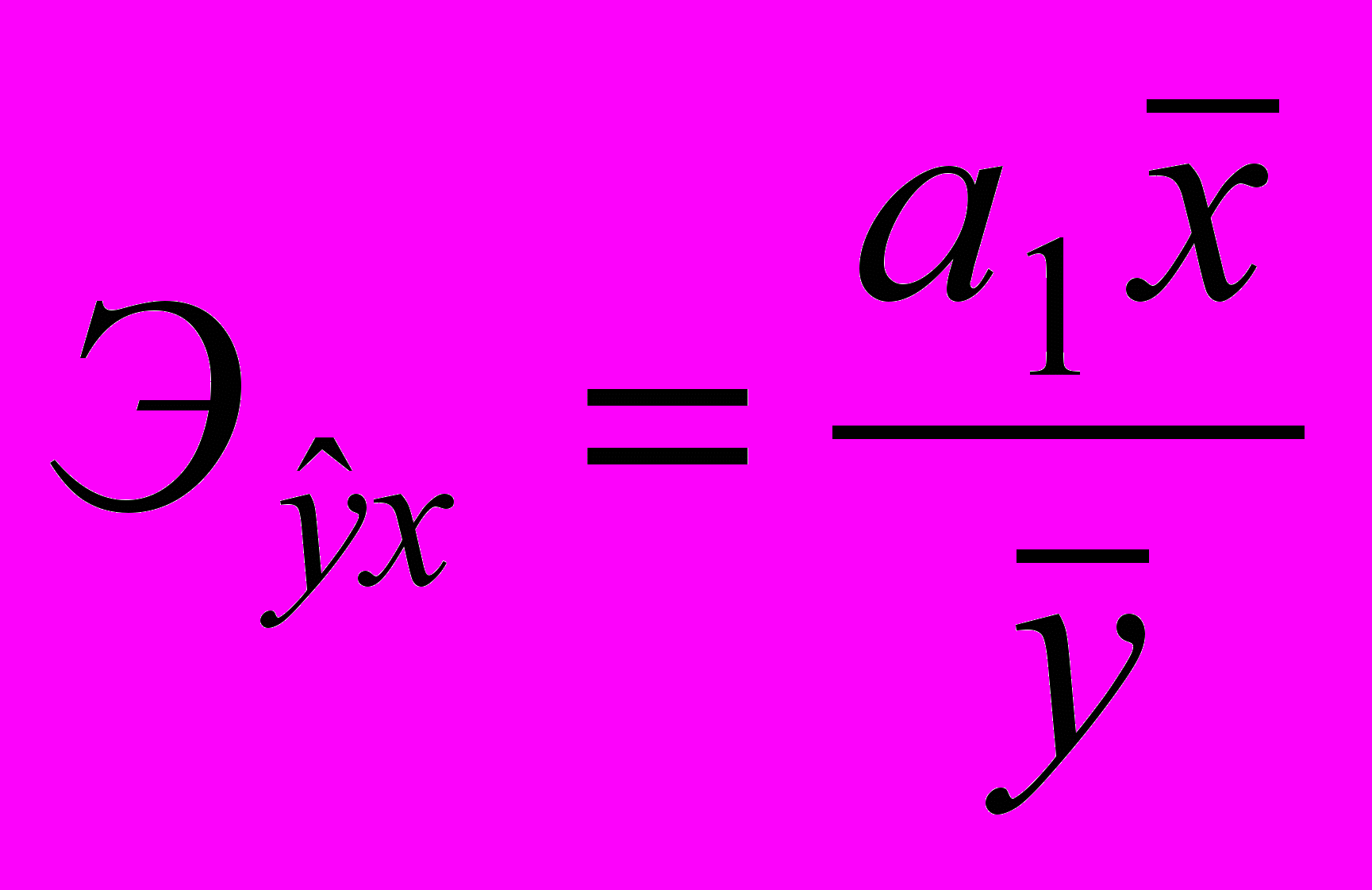, (6)

где 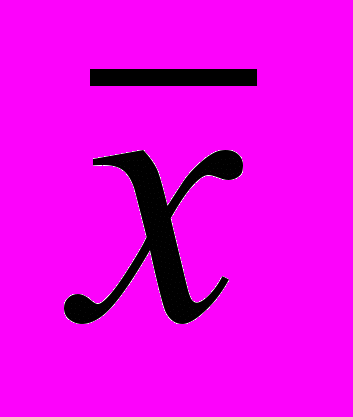- среднее арифметическое значение факторного признака,

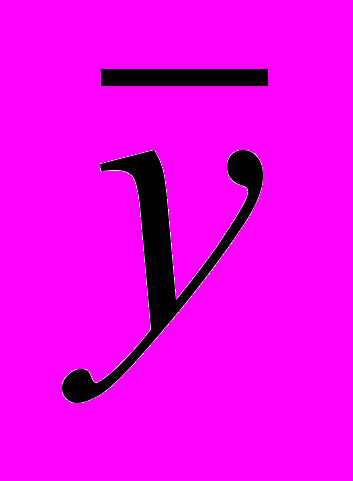- среднее арифметическое значение результативного признака.

5). Бетта - коэффициент показывает, на сколько изменится результативный признак, если изменится факторный:

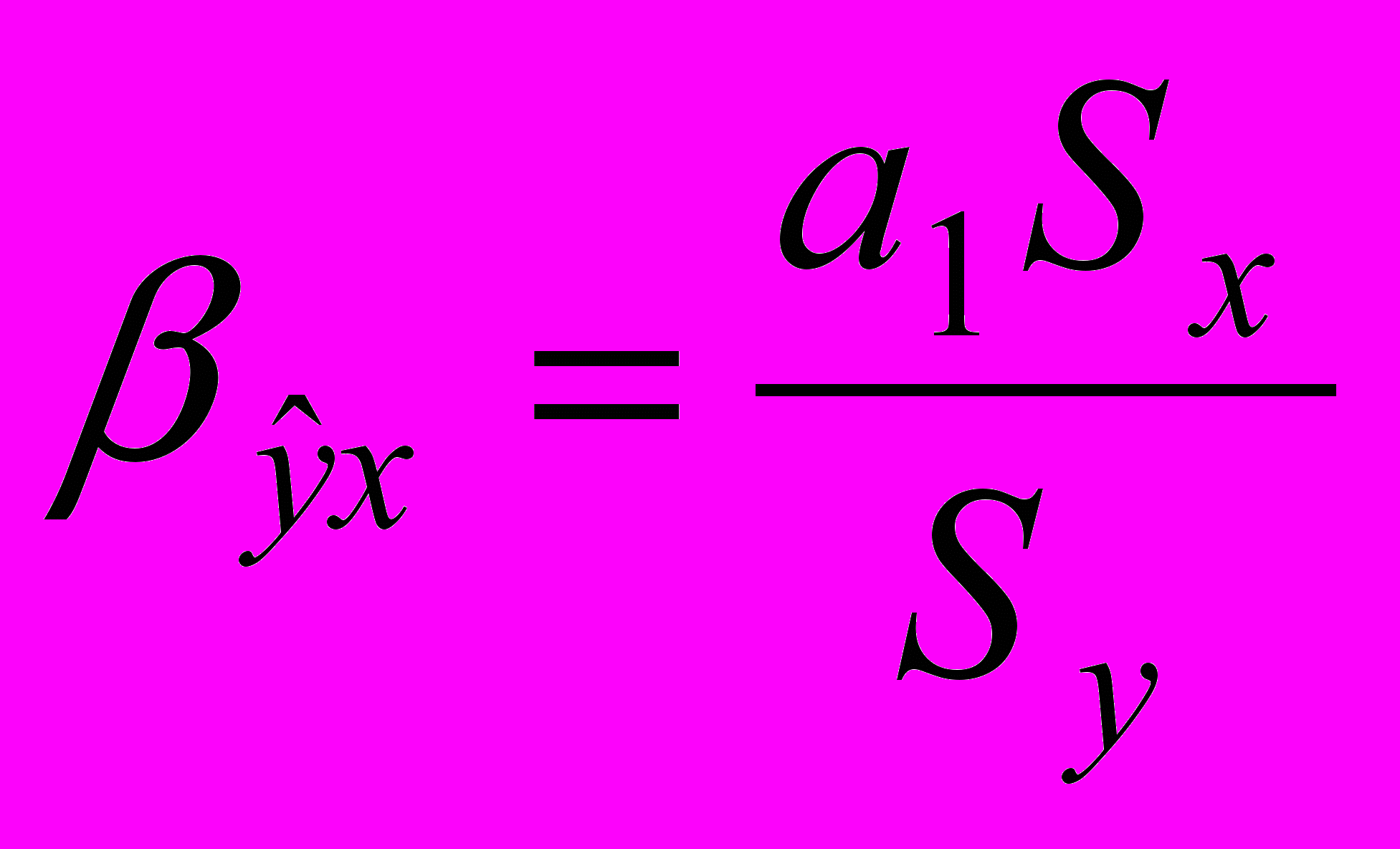, (7)

где 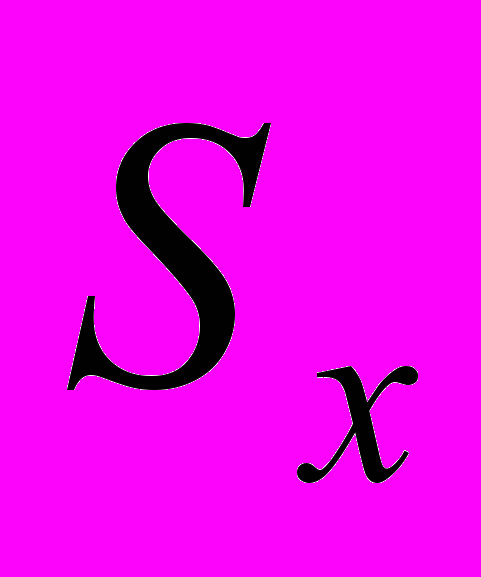, 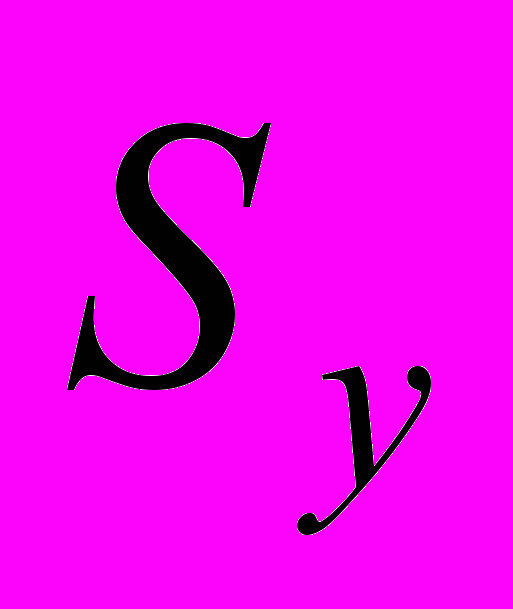- средние квадратические ошибки выборки.


6). Средняя по модулю относительная ошибка аппроксимации:

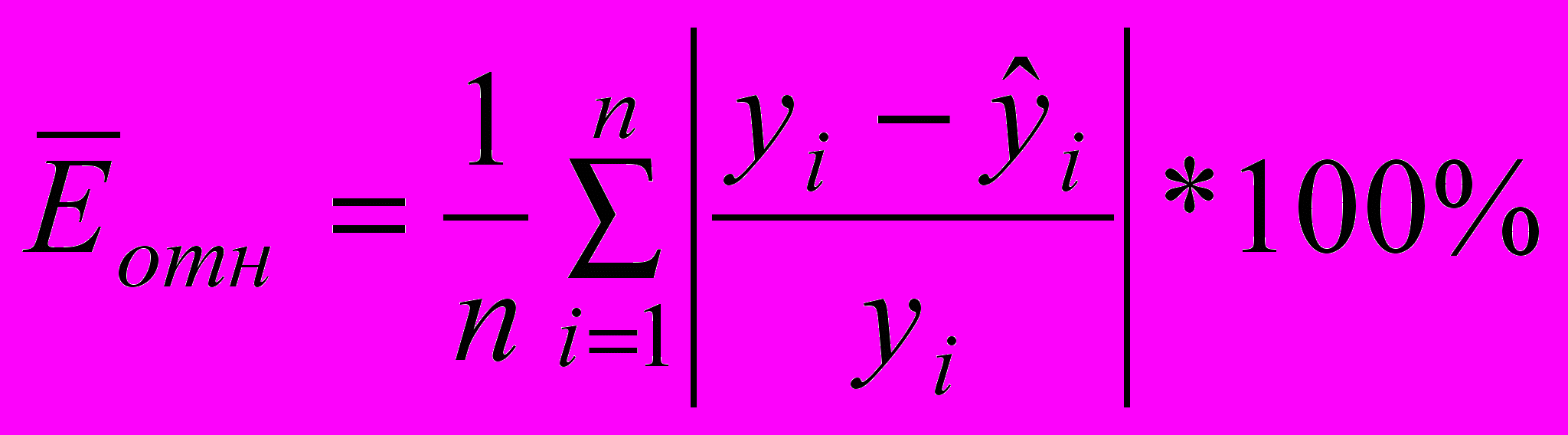. (8)


7). Среднее квадратическое отклонение:

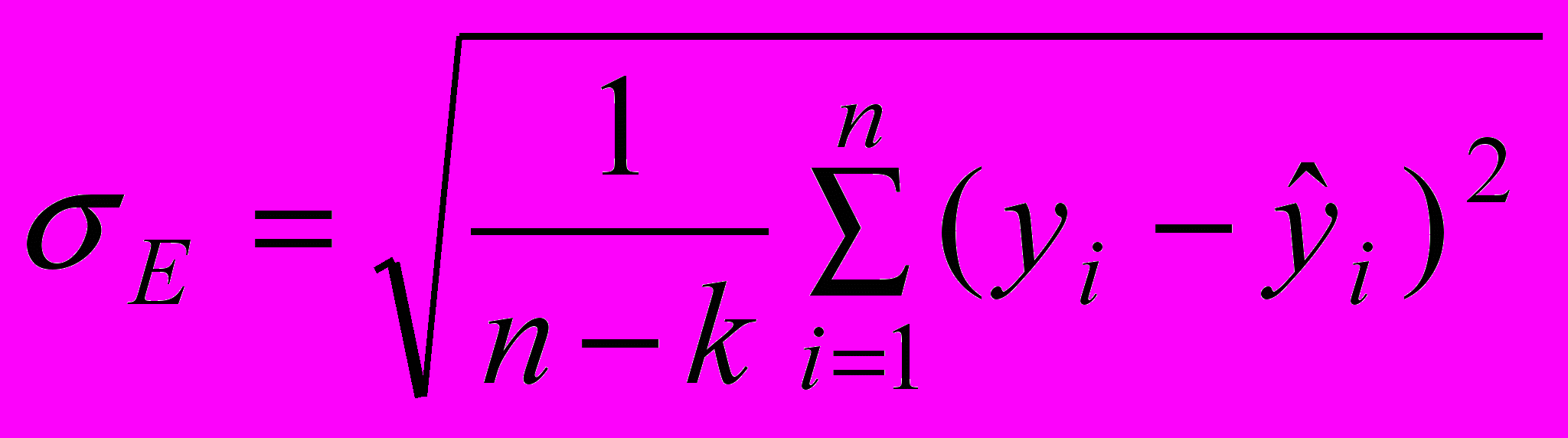, где к – количество признаков. (9)