Лекция 12. Элементы квантовой механики
| Вид материала | Лекция |
- 14. Элементы квантовой статистики и зонной теории твердого тела, 460.81kb.
- Основы квантовой механики, 33.02kb.
- Спецкурс для студентов 6-го курса Объем учебной нагрузки: 24 час лекции, 34.24kb.
- Развитие теоретической физики в ХХ веке шло под флагом зарождения, развития и становления, 110.96kb.
- Будем пытаться строить модель сознания в духе математики квантовой механики, 181.49kb.
- Спецкурс для студентов 5-го и 6-го курсов Объем учебной нагрузки: 48 час лекции, 80.81kb.
- Элементы квантовой механики и физики атомов, молекул, твердых тел, 156.85kb.
- Элементы квантовой механики Атом Резерфорда – Бора и гипотеза де Бройля Ядерная модель, 38.71kb.
- Программа учебной дисциплины вариационные методы в физике (спецкурс, дисциплины, 147.31kb.
- Физические основы механики, 237.04kb.
Лекция 12. Элементы квантовой механики
12.1. Соотношение неопределенностей
Современная трактовка корпускулярно-волнового дуализма может быть выражена словами: для атомного объекта существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна - частица.
Существует критерий, показывающий в каких случаях можно ограничиться классическими представлениями. Этот критерий связан с постоянной Планка ħ. Анализ причин существования этого предела, который называют принципом неопределенности, провел В. Гейзенберг (1927). Количественные соотношения, выражающие этот принцип в конкретных случаях, называют соотношениями неопределенностей. Наиболее важными являются два соотношения.
Первое из них ограничивает точности одновременного измерения координаты (х, у, z) и соответствующих проекций импульса частицы (px, py, pz), причем неопределенности этих величин удовлетворяют условию:
| ∆x ∆px ≥ ћ ∆y ∆py ≥ ћ ∆z ∆pz ≥ ћ | (12.1) |
(В точных соотношениях слева под ∆x и ∆px и других координат и импульсов должны пониматься среднеквадратичные отклонения от средних величин, а справа - ћ/2. Так как для принципиальных вопросов важно знать лишь порядок величины, то можно не пользоваться точными соотношениями.)
Второе соотношение устанавливает неопределенность измерения энергии, ∆E, за данный промежуток времени ∆t:
| ∆E·∆t ≥ ћ | (12.2) |
Первое из этих двух соотношений утверждает, что если положение частицы, например, по оси X известно с неопределенностью ∆x, то в тот же момент проекцию импульса частицы на эту же ось можно измерить только с неопределенностью ∆px ≈ ћ/(∆x). Заметим, что эти ограничения не касаются одновременного измерения координаты частицы по одной оси и проекции импульса — по другой: величины х и ру, у и рг и т. д. могут иметь одновременно точные значения. Таким образом, для микрочастицы не существует состояний, в которых ее проекция импульса и координата на этой же оси проекций имели бы одновременно точные значения. Не возможно одновременно точно определить координату и соответствующую ей проекцию импульса. Это ограничение не связано с несовершенством методов измерения или измерительных приборов, а является следствием специфики микрообъектов, а именно их двойственной корпускулярно-волновой природы
Соотношения неопределенностей связывают между собой пары динамических переменных. В классической механике такие пары величин называются канонически сопряженными.
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку величины меньше постоянной Планка ћ, называется принципом неопределенности Гейзенберга.
Энергия и время являются канонически сопряженными величинами. Согласно второму соотношению (12.2) для измерения энергии с погрешностью ∆E необходимо время, не меньшее, чем ∆t ≈ ћ/(∆E). То есть из-за конечности времени жизни атомов в возбужденном состоянии энергия возбужденных состояний атомов не является точно определенной, а потому соответствующий энергетический уровень характеризуется конечной шириной.
Соотношение неопределенностей указывает, в какой мере можно пользоваться понятиями классической механики применительно к микрочастицам, то есть является квантовым ограничением применимости классической механики к микрообъектам.
Соотношение неопределенностей (12.1) является одним из фундаментальных положений квантовой теории. Одного этого соотношения достаточно, чтобы получить ряд важных результатов, в частности:
Соотношение неопределенностей позволяет объяснить тот факт, что электрон не падает на ядро атома, а также оценить размеры простейшего атома и минимальную возможную энергию электрона в таком атоме.
Пусть частица «заперта» в одномерной области размером l. При нахождении возможного значения минимальной энергии Eмин частицы мы обычно считаем, что импульс частицы по порядку величины равен его неопределенности, т. е. р ~ ∆р. Чтобы понять, почему это так, представим себе, что частица в этой области имеет энергию Е > Eмин. Тогда ее импульс может быть представлен как р = <р> + ∆р. Теперь начнем мысленно уменьшать энергию Е, а значит и импульс <р>. При этом ∆р не меняется, поскольку ∆р ≈ ћ/l согласно соотношению (12.1). Когда Е станет равной Eмин, величина <р> обратится в нуль и останется только ∆р. Эту величину и принимают за р. Теперь перейдем к важному примеру атома водорода.
Точное положение электрона в данном атоме запрещено принципом неопределенности: был бы бесконечно большой разброс в его импульсе. Поэтому для оценки наименьшей возможной энергии Eмин электрона в кулоновском поле ядра можно положить разброс расстояний электрона от ядра ∆r≈rи ∆р ≈ р. Тогда согласно (12.1) р ≈ ћ/r, и энергия Е может быть представлена как
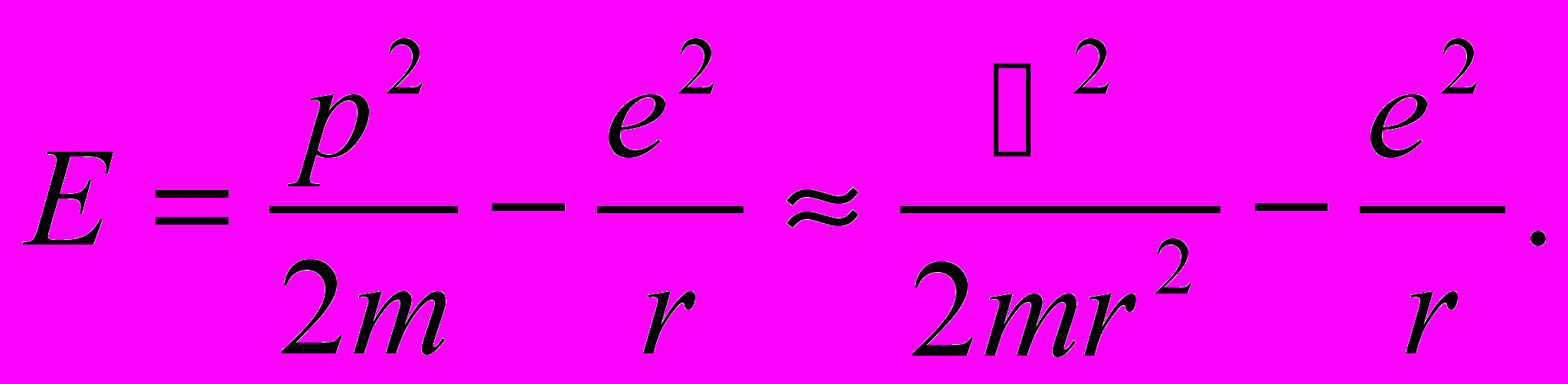 | (12.3) |
Значение r, при котором Е = мин, можно найти, приравняв производную dE/dr к нулю:
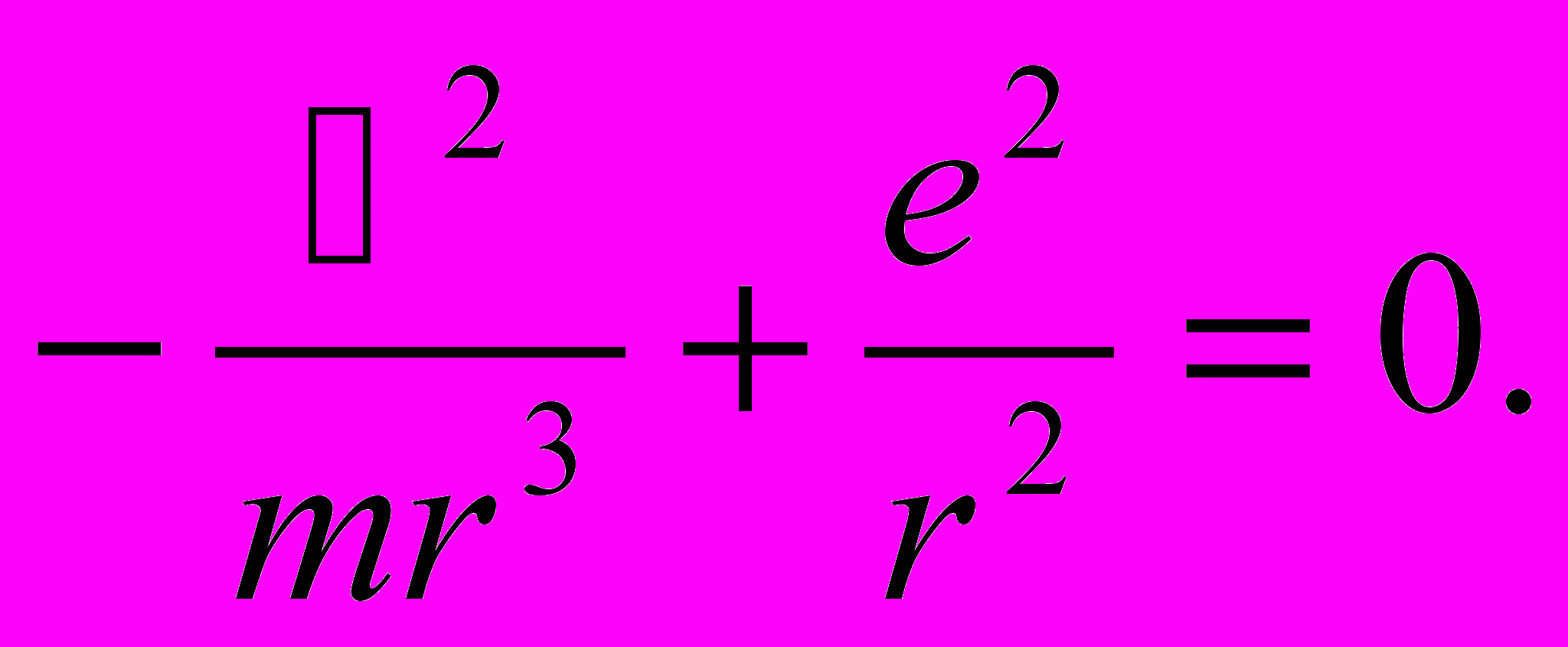
Отсюда следует, что
| r = ћ2/me2. | (12.4) |
Полученный результат полностью совпадает с воровским радиусом.
Подставив (12.4) в (12.3), найдем энергию Eмин:
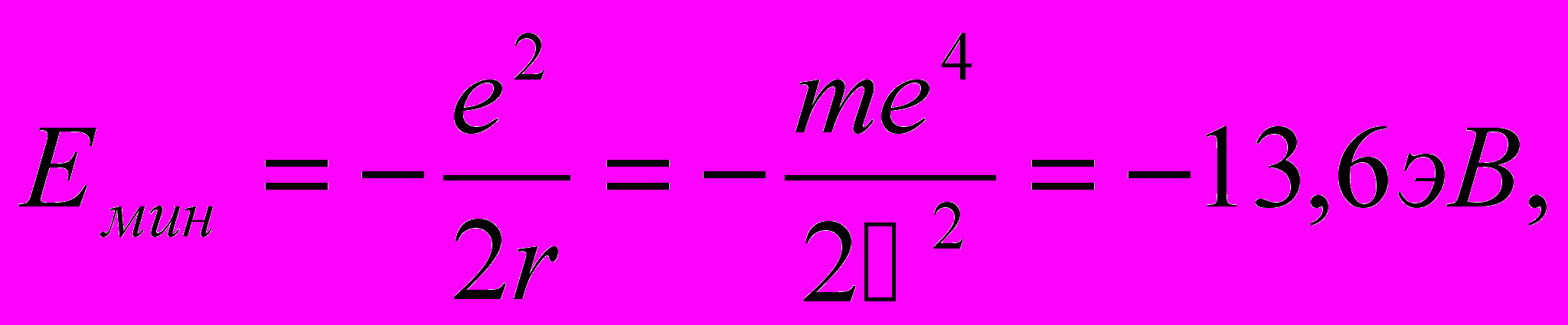 | (12.5) |
что также совпадает с энергией основного состояния атома водорода.
Совпадение этих грубых оценок с точными значениями r и E следует считать случайным. Важно лишь то, что получен верный порядок этих величин и что, основываясь на волновых представлениях, или принципе неопределенности, можно понять, почему атомный электрон не падает на ядро. Размер атома является результатом компромисса двух слагаемых энергии (12.3), имеющих противоположные знаки. Если увеличить отрицательное слагаемое (потенциальную энергию), уменьшив r, то увеличится кинетическая энергия, и наоборот.
Таким образом, соотношение неопределенностей позволяет сделать ряд важных выводов:
- Невозможно состояние, в котором частица находилась бы в состоянии покоя.
- При рассмотрении движения квантового объекта необходимо во многих случаях отказаться от самого понятия классической траектории.
- Часто теряет смысл деление полной энергии Е частицы (как квантового объекта) на потенциальную U и кинетическую К. В самом деле, первая, т. е. U, зависит от координат, а вторая — от импульса. Эти же динамические переменные не могут иметь одновременно определенного значения.
- Соотношение неопределенностей проявляет себя в атоме подобно силам отталкивания на малых расстояниях. В результате электрон находится в среднем на таком расстоянии от ядра, на котором действие этих сил отталкивания компенсируется силой кулоновского притяжения.
12.2. Волновая функция и ее интерпретация
Для микрочастиц из-за соотношения неопределенностей классическое определение состояния частицы (координаты и импульс), вообще говоря, утрачивает смысл. Это относится и к понятию силы, которая по определению является функцией классического состояния.
В соответствии с корпускулярно-волновым дуализмом в квантовой теории состояние частицы задается пси-функцией Ψ(r, t), которая является комплексной величиной и формально обладает волновыми свойствами.
Для понимания физического смысла пси-функции рассмотрим результаты опытов при прохождении пучка моноэнергетических электронов через двойную щель шириной порядка 1 мкм (рис.12.1).
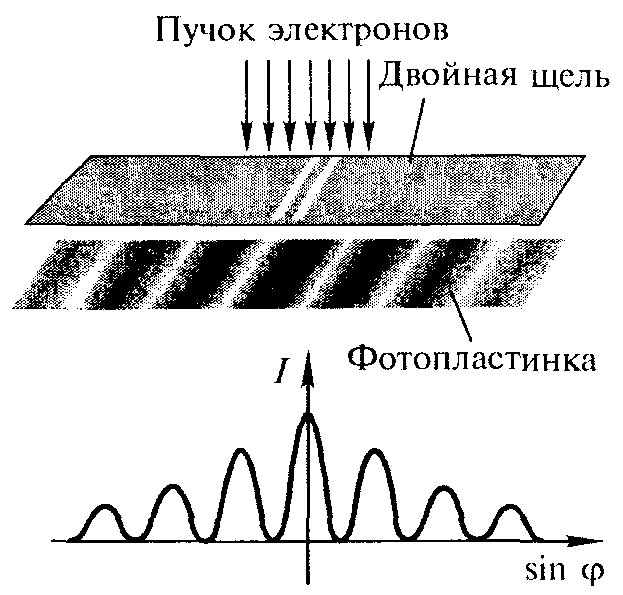
Рис. 12.1.
Места попадания электронов регистрируются на фотопластинке в виде точек. На фотопластинке проявляется четкое распределение интенсивности, подобное дифракционной картине волн , что доказывает наличие у электронов волновых свойств. Отметим, что при уменьшении потока электронов, падающих на щель, но при увеличении времени экспозиции характер дифракционной картины не меняется.
Согласно волновым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой полны. По представлениям фотонной теории, интенсивность определяется числом фотонов, попадающих в данную точку дифракционной картины. Следовательно, число фотонов в данной точке дифракционной картины задается квадратом амплитуды световой волны, в то время как для одного фотона квадрат амплитуды определяет вероятность попадания фотона в ту или иную точку.
Наличие максимумов в дифракционной картине с точки зрения волновой теории означает, что эти направления соответствуют наибольшей интенсивности волн де Бройли. С другой стороны, интенсивность волн де Бройля оказывается больше там, где имеется большее число частиц, т. е. интенсивность волн де Бройли и данной точке пространства определяет число частиц, попавших в эту точку. Таким образом, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая. Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории.
Как уже указывалось, с движением частицы, обладающей определенной энергией и импульсом, связывается плоская волна де Бройля. Однако в общем случае (произвольное движение частицы в произвольных силовых полях) состояние частицы в квантовой механике задается более сложной, вообще говоря комплексной, функцией Ψ(r, t), зависящей от координат и времени. Эту функцию называют волновой функцией (или пси-функцией). В частном случае свободного движения частицы волновая функция переходит в плоскую волну де Бройля.
Движение любой микрочастицы по отдельности подчиняется вероятностным законам (М. Борн, 1926 г.). В квантовой теории постановка вопроса состоит не в точном предсказании событий, а в определении вероятностей этих событий. Пси-функция Ψ(r, t) и является той величиной, которая позволяет находить все вероятности. Например, вероятность нахождения частицы в интересующем нас объеме dV в момент t определяется как
| dP = |Ψ|2dV = ΨΨ*dV, | (12.6) |
где Ψ* — комплексно-сопряженная функция. Поскольку в общем случае Ψ — комплексная функция, а вероятность должна быть всегда действительной и положительной величиной, то за меру интенсивности принимается квадрат модуля волновой функции. Отсюда плотность вероятности, т. е. вероятность нахождения частицы в единице объема,
| Р =|Ψ|2 = ΨΨ* . | (12.7) |
Эта величина является экспериментально наблюдаемой, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению. Таким образом, физический смысл имеет не сама Ψ-функция, а квадрат ее модуля |Ψ|2, которым задается интенсивность волн де Бройля.
Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна
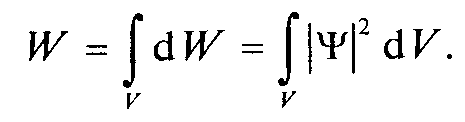 | (12.8) |
Проинтегрировав выражение (12.4) в бесконечных пределах или по той области, где Ψ отлично от нуля, получим вероятность того, что частица в момент времени t находится где-то в пространстве. Это есть вероятность достоверного события, а ее в теории вероятностей считают равной 1. Поэтому принимают, что
| ∫ |Ψ|2dV = ∫ ΨΨ*dV = 1, | (12.9) |
где интеграл берется по всему пространству или по той области, в которой Ψ отлична от нуля. Условие нормировки (12.5) означает, что во всей области, где Ψ ≠ 0, частица находится с достоверностью. Пси-функцию, удовлетворяющую условию (12.9), называют нормированной.
Условие (12.9) может оказаться невозможным, например, в случае, если Ψ -функция представляет собой плоскую волну де-Бройля, когда вероятность обнаружения частицы одинакова во всех точках пространства. Такие случаи следует рассматривать как идеализацию реальной ситуации, где частица находится в большой, но ограниченной области пространства, и тогда трудность устраняется.
В квантовой теории принимается как один из основных постулатов принцип суперпозиции пси-функций. Если у некоторой системы возможными являются состояния Ψ1 и Ψ2, то для нее существует также состояние
| Ψ = c1Ψ1 + c2Ψ2 | (12.10) |
где с1 и с2 — некоторые постоянные коэффициенты. Найдя таким образом Ψ, можно далее определить и плотность вероятности ΨΨ* пребывания системы в этом состоянии.
12.3. Уравнение Шрёдингера
Развивая идеи де-Бройля о волновых свойствах вещества, Э.Шрёдингер постулировал в 1926 г. уравнение — основное уравнение нерелятивистской квантовой теории: уравнение Шредингера. Данное уравнение было именно найдено, оно является новым фундаментальным законом, который невозможно вывести из прежних представлений и теорий. Справедливость этого уравнения установлена тем, что все вытекающие из него следствия подтверждены экспериментом. Уравнение Шредингера играет в квантовой теории такую же роль, как основное уравнение динамики (2-й закон Ньютона) в нерелятивистской механике.
Сформулировав это уравнение, Шредингер сразу же применил его к атому водорода и получил для уровней энергии спектр, точно совпадающий со спектром по первоначальной теории Бора и соответственно — с результатами наблюдений.
Уравнение Шредингера имеет следующий вид:
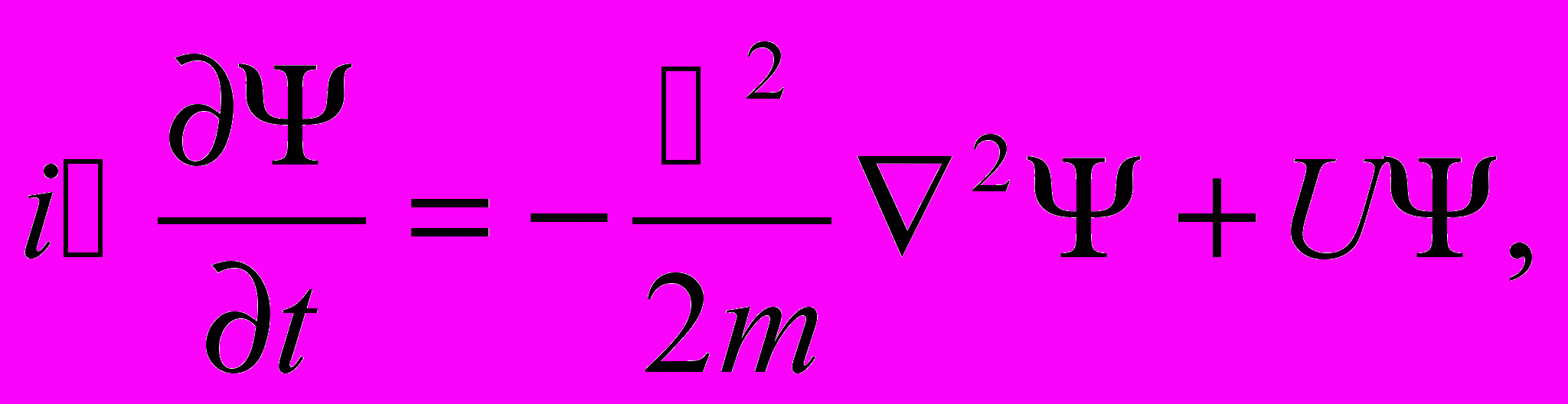 | (12.11) |
где i — мнимая единица (√ -1), т — масса частицы, U(x, y, z, t) — потенциальная функция частицы в силовом поле, в котором она движется; Ψ(х, у, z, t) — искомая волновая функция частицы;
 ≡ ∆ — оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам:
≡ ∆ — оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам: 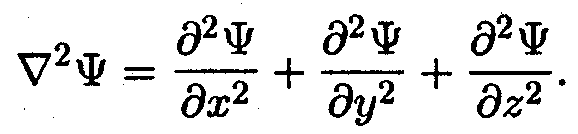 | (12.12) |
Уравнение (12.11) называют общим уравнением Шредингера или временным уравнение Шредингера. Уравнение Шредингера справедливо для любой частицы, движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью υ << с. Оно дополняется условиями, накладываемыми на волновую функцию:
1) Так как волновая функция — объективная характеристика состояния микрочастиц, то она должна удовлетворять ряду ограничений. Она должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).
2) Производные ∂Ψ/∂x, ∂Ψ/∂y, ∂Ψ/∂z, ∂Ψ/∂t должны быть непрерывны;
3) Функция |Ψ|2 должна быть интегрируема; это условие в простейших условиях сводится к условию нормировки вероятностей (12.9).
Особую роль в квантовой теории играют стационарные состояния — состояния, в которых все наблюдаемые физические величины не меняются с течением времени. Сама Ψ -функция, как уже говорилось, принципиально ненаблюдаемая. В стационарных состояниях она имеет вид
| Ψ(r, t) = Ψ(r) e-iωt, ω = E/ћ, | (12.13) |
где функция Ψ(r) не зависит от времени.
При таком виде Ψ -функции плотность вероятности Р остается постоянной. В самом деле,
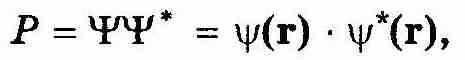 | (12.14) |
т. е. действительно, плотность вероятности Р от времени не зависит.
Для нахождения функции Ψ(r) в стационарных состояниях подставим выражение (12.13) в уравнение (12.11), получим
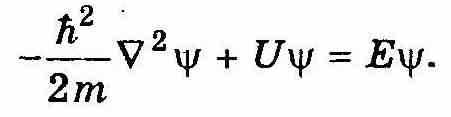 | (12.15) |
Это уравнение называют уравнением Шредингера для стационарных состояний. Обратим внимание на следующую особенность уравнения (12.15). В то время как, согласно интерпретации пси-функции, частица, как говорят, «размазана» в пространстве, потенциальная энергия U рассматривается в (12.15) как функция локализованной точечной частицы в силовом поле. То есть потенциальная энергия — функция U(r) —здесь определяется классически, как если бы никакими волновыми свойствами частица не обладала.
Перепишем уравнение (12.15) в виде
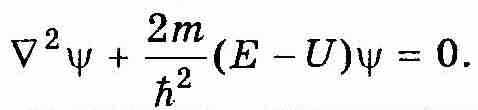 | (12.16) |
Квантование. Физический смысл имеют лишь те решения уравнения (12.16), которые удовлетворяют естественным или стандартным условиям. Эти условия состоят в том, что пси-функция Ψ(r) должна быть конечной, однозначной, непрерывной и гладкой (т. е. без изломов) во всем пространстве, даже в тех точках (линиях, поверхностях), где потенциальная энергия U(r) терпит разрыв.
Решения, удовлетворяющие этим условиям, оказываются возможными лишь при некоторых значениях энергии Е. Их называют собственными значениями, а функции Ψ(r), являющиеся решениями уравнения (12.16) при этих значениях энергии, — собственными функциями, принадлежащими собственным значениям Е. В этом и состоит естественный и общий принцип квантования.
Собственные значения энергии Е и принимаются за возможные значения энергии в соответствующих стационарных состояниях. Эти значения энергии Е могут быть дискретными (квантованными) или непрерывными, образуя дискретный или непрерывный энергетический спектр.
