Физические основы механики

Вид материала

Документы

Содержание Кинематика материальной точки Динамика частицы Динамика системы частиц Работа и энергия Динамика релятивистской частицы Релятивистская кинематика Механические колебания Момент импульса. Вращение твёрдого тела. Элементарная теория гироскопа Элементы теории упругости Элементы гидродинамики Понятие о фазовой ячейке и фазовом объёме. Темы лекций Задание по физике Темы семинарских II – задачи, которые студент должен решить обязательно для сдачи задания. Они должны быть оформлены студентами в своих тетрадях. Задачи нулевой группы M распадается на две одинаковые частицы с массами m Q = 10 и частотой собственных колебаний  ... Полное содержание

Подобный материал:

• Программа вступительного экзамена в аспирантуру по курсу физика (Специальность 01., 82.16kb.
• Программа вступительных экзаменов по специальности 01. 04. 07 Физика конденсированного, 70.65kb.
• Методические рекомендации при изучении курса общей физики Физика. Часть I. Физические, 202.17kb.
• Сэр Исаа́к Нью́тон, 191.11kb.
• Б. Е. Победря 1 год Задача годового курса 40 лекций + 40 семинар, 27.75kb.
• 1 Основные физические свойства жидкостей Определение жидкости, 379.06kb.
• Лекций: 34 Практических: 18 Лабораторных: 0 sm. 5 Сопротивление материалов и основы, 22.99kb.
• Основы квантовой механики, 33.02kb.
• Рабочая программа учебной дисциплины "основы теоретической физики", 190.56kb.
• Аннотация рабочей программы дисциплины основы механики сплошной среды уровень основной, 22.79kb.

Физические основы механики


Предмет физики. Физика как наиболее фундаментальная наука о природе. Физика как часть общечеловеческой культуры. Роль физики в становлении специалиста. Методы физических исследований. Физика как культура моделирования. Место физики среди других дисциплин. Физика и математика. Физика и естествознание. Философия и физика. Важнейшие этапы истории физики. Компьютеры в современной физике. Роль измерений в физике. Единицы измерений и системы единиц. Международная система единиц СИ. Предмет механики. Кинематика и динамика. Описание состояния в классической механике, релятивистской механике, квантовой механике.

Кинематика материальной точки. Материальная точка (частица). Кинематическое описание движения. Система отсчёта и система координат. Радиус-вектор. Элементы векторной алгебры. Производная от функции, сложной функции, вектор-функции. Смысл производной в физике. Степени свободы и обобщённые координаты. Движение точки по окружности. Угловая скорость и угловое ускорение. Поступательное и вращательное движения абсолютно твёрдого тела. Вектор угловой скорости. Нормальное, тангенциальное и полное ускорение. Движение точки вдоль плоской кривой. Радиус кривизны траектории.

Динамика частицы. Понятие состояния в классической механике. Основная задача динамики. Первый закон Ньютона. Инерциальные и неинерциальные системы отсчёта. Импульс частицы. Закон сохранения импульса как фундаментальный закон природы. Уравнение движения. Масса частицы. Сила как производная от импульса по времени. Второй закон Ньютона как уравнение движения.

Динамика системы частиц. Закон сохранения импульса и третий закон Ньютона. Центр масс системы частиц. Закон движения центра масс. Система центра масс. Реактивное движение.

Работа и энергия. Работа силы. Мощность. Кинетическая энергия. Связь между кинетическими энергиями в различных системах отсчёта. Консервативные и неконсервативные силы. Потенциальная энергия. Закон сохранения энергии в механике. Общефизический закон сохранения энергии. Законы сохранения и симметрия пространства и времени. Столкновения частиц. Порог реакции.

Динамика релятивистской частицы. Импульс релятивистской частицы. Уравнение движения релятивистской частицы. Кинетическая энергия релятивистской частицы. Инвариантность уравнения движения относительно преобразования Лоренца. Физический смысл преобразований Лоренца. Принципы относительности Галилея и Эйнштейна.

Релятивистская кинематика. Псевдоевклидовость пространства-времени. Инварианты преобразований Лоренца. Относительность понятия одновременности. Сокращение длины и замедление времени.

Механические колебания. Гармонический осциллятор: свободные и затухающие колебания. Декремент затухания, добротность. Фазовая плоскость. Возбуждение осциллятора периодическими толчками и синусоидальной силой. Амплитуда и фаза при вынужденных колебаниях. Резонансные кривые. Осциллятор как спектральный прибор. Физический смысл спектрального разложения. Параметрические колебания. Автоколебания.

Момент импульса. Момент импульса материальной точки относительно центра и оси. Момент силы. Закон сохранения момента импульса для системы частиц.

Закон всемирного тяготения. Теорема Гаусса. Финитные и инфинитные движения. Движение планет. Законы Кеплера. Космические скорости.

Вращение твёрдого тела. Вращение твёрдого тела вокруг неподвижной оси. Момент инерции. Кинетическая энергия вращающегося тела. Уравнения движения твёрдого тела. Качение. Физический маятник.

Элементарная теория гироскопа. Главные оси инерции. Свободное вращение симметричного волчка. Гироскоп.

Неинерциальные системы отсчёта. Второй закон Ньютона в неинерциальных системах отсчёта. Силы инерции. Относительное, переносное и кориолисово ускорения. Центробежная и кориолисова силы. Маятник Фуко. Инертная и гравитационная массы. Обобщённый принцип относительности Галилея.

Элементы теории упругости. Растяжение, сдвиг. Упругие и пластические деформации. Закон Гука. Модули упругости. Коэффициент Пуассона. Упругая энергия деформации. Скорость распространения упругих возмущений. Волновые процессы: бегущие и стоячие волны.

Элементы гидродинамики. Линии тока, стационарное и нестационарное течение жидкости и газа. Уравнение Бернулли. Формула Торричелли. Силы вязкости и формула Пуазейля. Ламинарное и турбулентное течения. Число Рейнольдса. Образование подъёмной силы при обтекании крыла. Эффект Магнуса.

Понятие о фазовой ячейке и фазовом объёме.

Границы применимости представлений классической механики. Волновая гипотеза де-Бройля.


Литература


Основная литература


1. Сивухин Д.В. Общий курс физики. Т. 1. Механика. – М.: Наука, 1989.

2. Кингсеп А.С., Локшин Г.Р., Ольхов О.А. Основы физики. Курс общей физики. Т. 1. Механика, электричество и магненизм, колебания и волны, волновая оптика. – М.: Физматлит, 2001.

3. Гладун А.Д. Элементы релятивистской механики. М.: МФТИ, 2003.

4. Белонучкин В.Е. Относительно относительности. – М.:МФТИ, 1996.

5. Кириченко Н.А. Теория относительности. Учебное пособие. М.: МФТИ, 2001.

Дополнительная литература:


1. Хайкин С.Э. Физические основы механики. – М.: Наука, 1971.

2. Киттель Ч., Найт У., Рудерман М. Механика. – М.: Наука, 1983.

3. Фейнман Р. Фейнмановские лекции по физике. Вып. 1, 2. – М.: Мир, 1977.

4. Ландау Л.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики. Механика и молекулярная физика. – М.: Наука, 1965.

5. Ландау Л.Д., Лифшиц Е.М. Краткий курс теоретической физики. Механика. Электродинамика. – М.: Наука, 1969.

План лекций

для студентов 1-го курса на осенний семестр

2009/2010 учебного года

Дата	Темы лекций
1, 7 сентября	Введение. Предмет и роль физики. Механика. Элементы кинематики.
8, 14 сентября	Динамика частицы и системы частиц. Законы Ньютона.
15, 21 сентября	Работа и энергия.
22, 28 сентября	Релятивистское уравнение движения и его инвариантность. Общая формулировка принципа относительности.
29 сент., 5 октября	Закон сохранения момента импульса. Тяготение. Теорема Гаусса.
6, 12 октября	Вращение твёрдого тела вокруг оси. Момент инерции.
13, 19 октября	Плоское движение твёрдого тела.
20, 26 октября	Главные оси инерции. Гироскопы.
27 окт., 2 ноября	Незатухающие и затухающие колебания.
3, 9 ноября	Вынужденные колебания. Параметрические колебания. Волны.
10, 16 ноября	Неинерциальные системы отсчёта.
17, 23 ноября	Элементы теории упругости.
24, 30 ноября	Элементы гидродинамики.
1, 7 декабря	Фазовая ячейка. Границы применимости представлений классической механики.

ЗАДАНИЕ ПО ФИЗИКЕ

для студентов 1-го курса на осенний семестр

Дата	№ сем.	Темы семинарских занятий	Задачи
			0 группа	I группа	II груп.	III груп.
1 5 сент.	1	Уравнения движения и их интегрирование.	1, 2, 3, 4	1.4; 2.35; 2.56; (2.43)	1.13; 2.6; 2.41	2.45
7–12 сент.	2	Законы сохранения импульса и энергии. Работа, мощность.	5, 6, 7, 8	4.20; 4.25; 4.47; (4.67)	4.35; 4,37; 4.41	4.49
14–19 сент.	3	Движение тел с переменной массой.	9, 10, 11, 12	3.11; 3.25; 3.43; (3.31)	3.3; 3.41; 3.42	3.48
21–26 сент.	4	Упругие и неупругие столкновения.	13, 14, 15, 16	4.73; 4.98; 4.110; (4.80)	4.90; 4.96; 4.108	4.103
28 сен.– 3 окт.	5	Уравнение движения релятивистской частицы. Преобразования Лореца.	17, 18, 19, 20	8.48; 8.59; 8.3; (8.77)	8.68; 8.43; 8.76	8.73
5–10 окт.	6	Закон сохранения момента импульса. Тяготение. Теорема Гаусса.	21, 22, 23, 24	6.15; 7.61; 7.85; (7.132)	6.2; 7.11; 7.136	7.92
12 17 окт.	7	Вращение твёрдого тела.	25, 26, 27, 28	9.1; 9.71; 9.97; (9.76)	9.108; 9.125; 9.24	9.182
19 24 окт.	8	Плоское движение твёрдого тела.	29, 30, 31, 32	9.84; 9.115; 9.162; (9.79)	9.82; 9.75 9.164	9.66
25 октября (воскр.)		Общекурсовая контрольная работа (по первым 7-ми семинарам)
26–31 окт.	9	Разбор контрольной работы. Сдача 1-го задания.
2–6 нояб.	10	Гироскопы. Колебания материальной точки.	33, 34, 35, 36	11.1; 11.14; 5.22; (5.44)	11.2; 5.49; 5.71	11.16
9–14 нояб.	11	Колебания твёрдого тела. Волны.	37, 38, 39, 40	10.4; 10.55; 10.43; (10.59)	10.40; 10.48; 10.57	10.72
16–21 нояб.	12	Неинерциальные системы отсчета.	41, 42, 43, 44	12.7; 12.19; 12.45; (12.35)	12.26; 12.34; 12.71	12.49
23–28 нояб.	13	Элементы теории упругости.	45, 46, 47, 48	13.7; 13.33; 13.39; (13.34)	13.5; 13.18; 13.37	13.31
30 нояб. –5 дек.	14	Элементы гидродинамики. Понятие о фазовой ячейке. Волновая гипотеза.	49, 50, 51, 52	14.6; 14.17; 14.24; (14.29)	14.25; 14.30; 14.36	14.2
7–11 дек.	15	Контрольная работа по 2-му заданию (по группам)
14–19 Дек.	16	Сдача 2-го задания. Зачёт. Закрытие зачётных ведомостей.

Примечание

1. Номера задач указаны по “Сборнику задач по общему курсу физики. Ч. 1. Механика и молекулярная физика”. Под ред. В.А. Овчинкина. М., МФТИ, 2002.

2. При выполнении заданий предусмотрена следующая вариативность - в каждой теме семинара задачи разбиты на 4 группы:

0 – задачи, которые студент должен решать в течение недели к следующему семинару и которые затем студенты должны разбирать в начале семинара;

I – задачи, которые рекомендуется разбирать на семинаре.
В скобках приведены номера дополнительных задач, которые могут быть разобраны на семинаре;

II – задачи, которые студент должен решить обязательно для сдачи задания. Они должны быть оформлены студентами в своих тетрадях.

III – задачи, которые не являются обязательными для решения при сдаче заданий студентами 1, 3, 7 и 9 факультетов.

Преподаватель на семинарах может разбирать и другие задачи по своему выбору.

Задачи нулевой группы

(в скобках – номер по задачнику под ред. В.А. Овчинкина)


1. (1.12) В открытом море на экваторе стоит высокая вертикальная скала. Как будет двигаться по этой скале тень, отбрасываемая сферической поверхностью Земли при заходе Солнца? Найти ускорение такого движения. Радиус Земли R = 6400 км. За какое время тень переместится от основания до вершины скалы, если высота последней h = 1 км?

Ответ: a = 4²R/T²_сут = 3,4 см/c²; t = (2h/a)^1/2 = 4 мин.

2. Тело начинает вращаться с угловым ускорением, равным 0,04 с^2. Через какое время t после начала вращения полное ускорение произвольной точки тела будет направлено под углом 76° к вектору скорости этой точки?

Ответ: t = 10 с.

3. Мяч посылается с начальной скоростью v₀ = 19,5 м/с под углом  = 45° к горизонту. В тот же момент времени навстречу мячу стартует игрок, находившийся на расстоянии l = 55 м. С какой скоростью u он должен бежать, чтобы успеть схватить мяч до удара о землю?

Ответ: u = 5,8 м/с.

4. Тело брошено со скоростью v₀ = 10 м/с под углом  = 45° к горизонту. Найти радиус кривизны R траектории тела через время t = 1 с после начала движения.

Ответ: R = 6,4 м.


5. На концах и в середине невесомого стержня длины l = 1,5 м расположены одинаковые шарики. Стержень ставят вертикально и отпускают. Считая, что трение между плоскостью и нижним шариком отсутствует, определить скорость верхнего шарика в момент удара о горизонтальную плоскость.

Ответ: 6 м/с.


6. Угол наклона ленты подъёмника к горизонту  = 5,7°. При каком максимальном ускорении ленты поднимаемый ящик не будет скользить по ленте подъёмника? Коэффициент трения между ящиком и лентой  = 0,2. Лента подъёмника не прогибается, ускорение свободного падения g принять равным 10 м/с².

Ответ: 1 м/с².


7. Груз, висящий на лёгкой пружине жёсткостью k = 400 Н/м, растягивает её на величину x = 3 см. Какую работу надо затратить, чтобы утроить удлинение пружины, прикладывая к грузу вертикальную силу?

Ответ: 0,72 Дж.

8. (4.16) Лодка длиной L наезжает, двигаясь по инерции, на отмель и останавливается из-за трения, когда половина её длины оказывается на суше. Какова была начальная скорость лодки V? Коэффициент трения равен k.

Ответ:

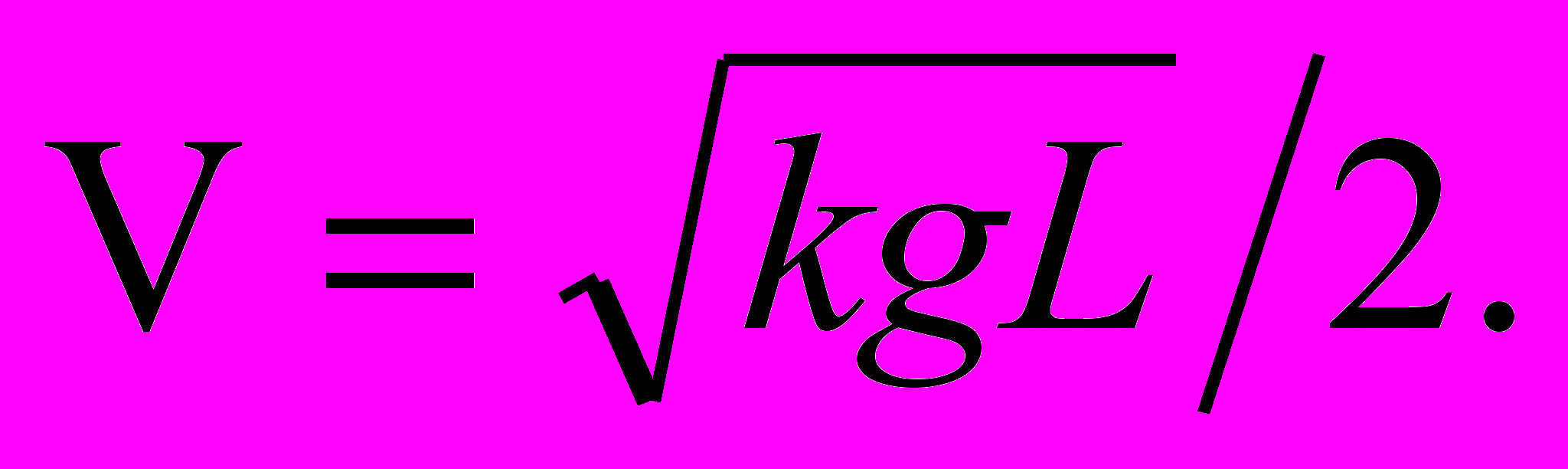
9. (3.6) В одном изобретении предлагается на ходу наполнять платформы поезда углём, падающим вертикально из неподвижного бункера на платформу. Какова должна быть приложенная к платформе сила тяги, если на неё погружают m = 10 т угля за t = 2 с, и за это время она проходит равномерно L = 10 м? Трением при движении платформы пренебречь.

Ответ: F  25 кН.


10. (3.1) Найти выражение ускорения и скорости платформы, движущейся под действием постоянной горизонтальной силы f, если на платформе лежит песок, который высыпается через отверстие в платформе. За 1 с высыпается масса m песка, в момент времени t = 0 скорость платформы V равна нулю, а масса песка и платформы вместе равна М.

Ответ: dV/dt = f /(M – mt);V = (f /m)ln(M /(M – mt)).

11. Две ракеты, начиная движение в отсутствие внешних сил, могут достичь одинаковой максимальной скорости. У первой ракеты топливо составляет 50% массы, у второй – 75%. Во сколько раз отличаются скорости истечения газов?

Ответ: .

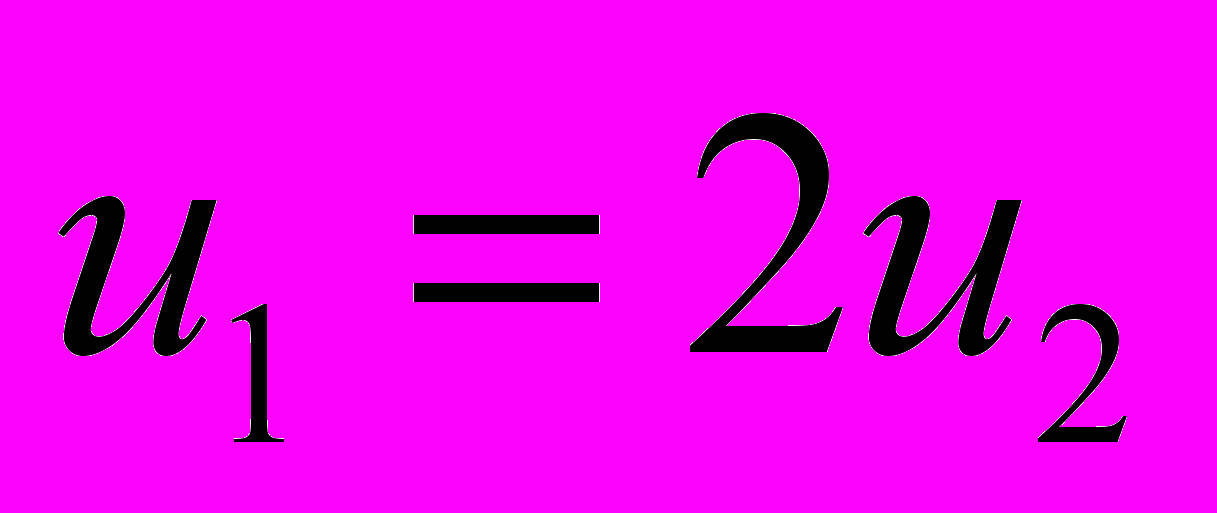12. (3.29). Двигатель метеорологической ракеты дважды запускается на короткое время: при взлете и при возвращении на Землю для обеспечения мягкой посадки. Масса ракеты перед стартом М, после посадки – m. Какова масса ракеты М₁ после старта? Сопротивлением воздуха во все время полета пренебречь.

Ответ: M₁ = (Mm)^1/2.

13. Частица массы m испытывает упругое столкновение с неподвижной частицей массы М. Определить потерю энергии частицей при столкновении, считая удар центральным.

Ответ: 4mM/(m + M)².

14. Частица массы М упруго сталкивается с неподвижной частицей массы m = М/2. Определить максимальный угол отклонения первой частицы после столкновения.

Ответ: 30.

15. (4.109).Найти минимальную относительную скорость 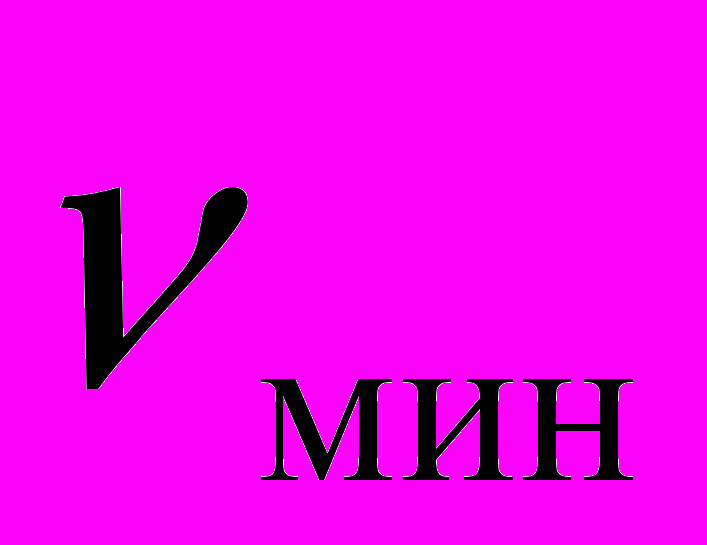двух одинаковых метеоритов, необходимую для их нагрева и полного испарения в результате столкновения. Теплота нагревания и испарения 1 г вещества метеоритов составляет Q = 10¹⁰эрг/г.

Ответ: 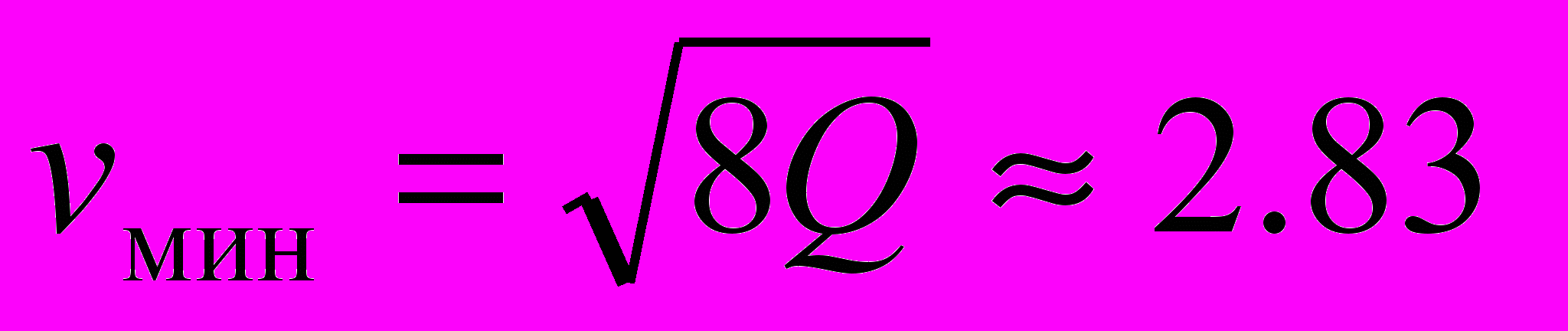км/с.

16. Найти давление, производимое потоком частиц массой m с концентрацией n, падающих со скоростью V на неподвижную стенку под углом  к нормали. Соударения считать упругими.

Ответ: .

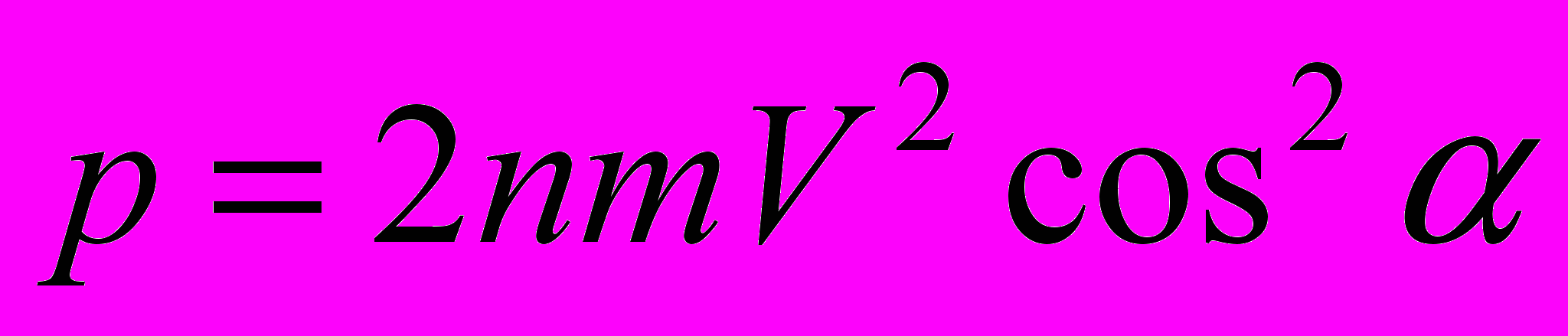17. Какую работу необходимо совершить, чтобы увеличить скорость частицы с массой m₀ от 0,6c до 0,8с? Сравнить полученный результат со значением, вычисленным по классической формуле.

Ответ: , .

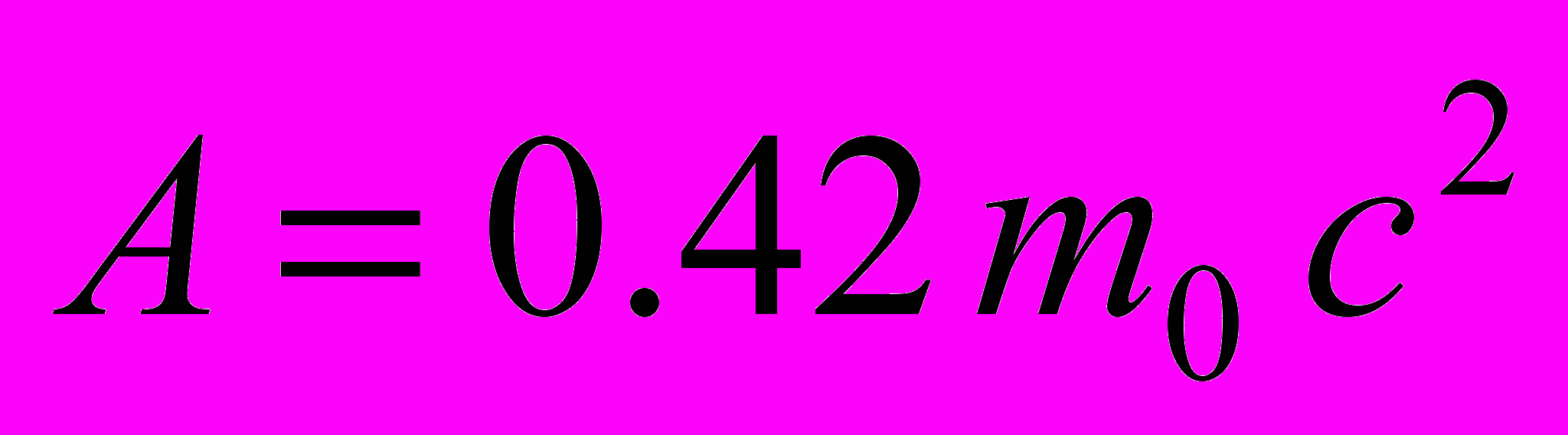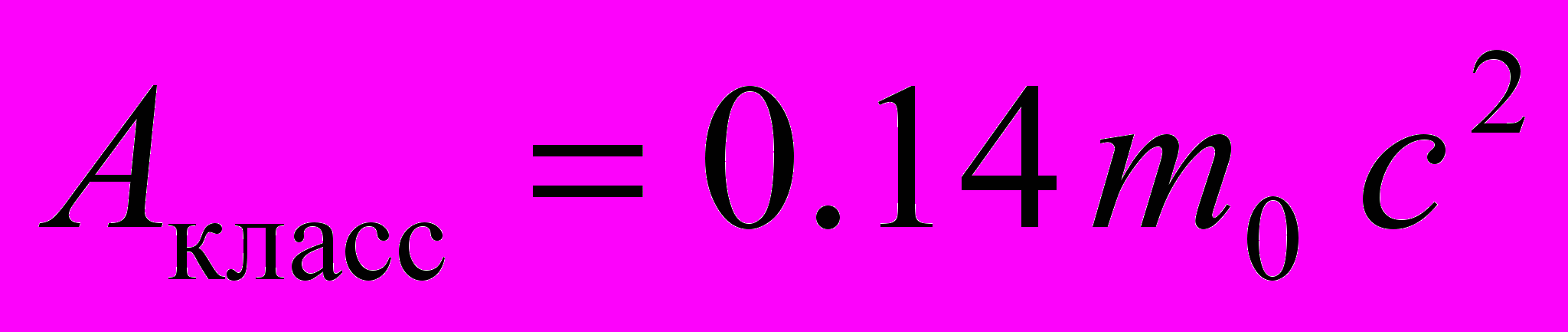18. Неподвижная частица массы M распадается на две одинаковые частицы с массами m = 0,4M каждая. Найти скорость v, с которой движутся эти частицы.

Ответ: v = 0,6c.

19. Собственное время жизни некоторой частицы равно  = 10^–6 с. Чему равен интервал s между рождением и распадом этой частицы?

Ответ: s = 300 м.

20. Две частицы летят по одной прямой с одинаковыми скоростями v = 0,75с в направлении мишени, причём вторая частица попадает в мишень через промежуток времени  = 10^–8 с после первой. Найти расстояние l₀ между частицами в полёте в системе отсчёта, связанной с ними.

Ответ: l₀ = 3,4 м.

21. Земля и Венера обращаются вокруг Солнца по орбитам, принимаемым приближённо за круговые с радиусами R₁ = 1,510⁸ км и R₂ = 1,0810⁸ км соответственно. Найти отношение их линейных скоростей.

Ответ: v₁/v₂ = 0,85.


22. Спутник движется по круговой орбите. Во сколько раз надо увеличить кинетическую энергию спутника, чтобы он покинул Землю?

Ответ: в 2 раза.


23. Определить радиус круговой орбиты искусственного спутника Земли, если всё время он находится над одной и той же точкой земной поверхности на экваторе.

Ответ: R = 4,210⁴ км.

24. Найти изменение ускорения свободного падения на глубине h. На какой глубине 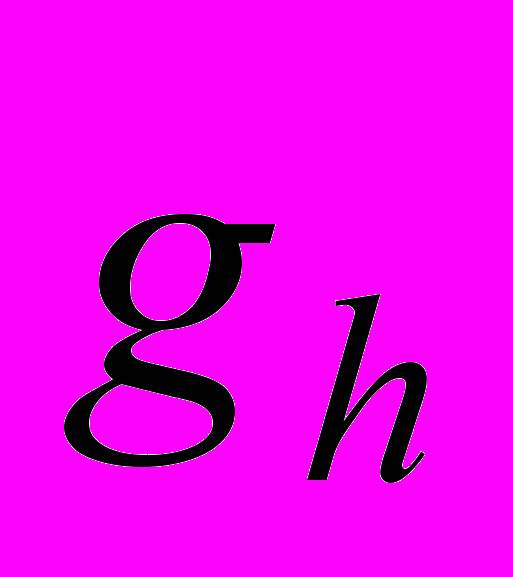составляет 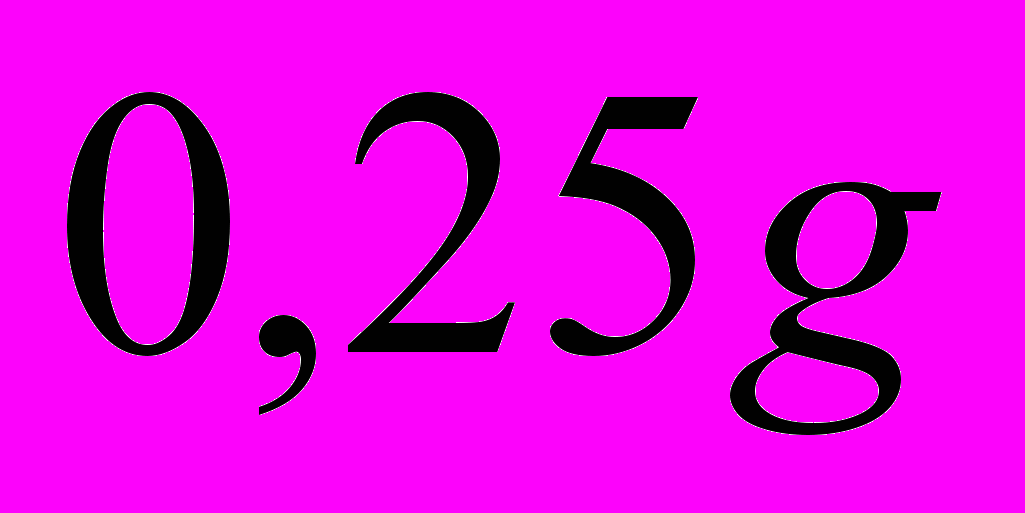ускорения свободного падения у поверхности Земли? Плотность Земли считать постоянной.

Ответ: .

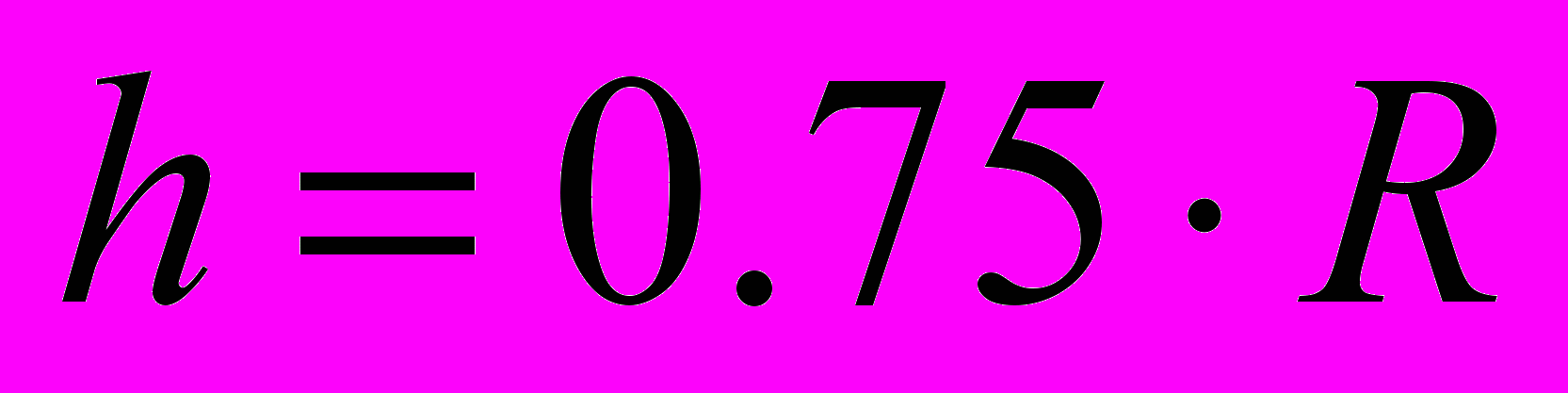25. Вычислить момент инерции I однородного цилиндра массы m, длины l и радиуса R относительно оси, проходящей через центр масс перпендикулярно оси симметрии цилиндра.

Ответ: .

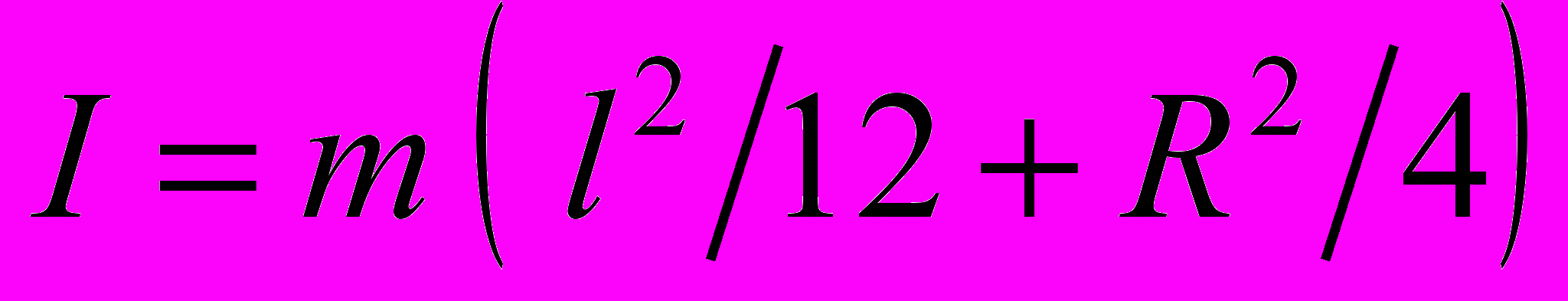26. (9.11) На тяжёлый барабан, вращающийся вокруг горизонтальной оси, намотан лёгкий гибкий шнур. По шнуру лезет вверх обезьяна массой М. Определить её ускорение относительно шнура, если её скорость относительно земли постоянна. Момент инерции барабана равен I, его радиус R.

Ответ: a = mgR²/I.

27. Сплошной маховик массой 20 кг и радиусом 120 мм вращается, совершая 600 об/мин. С какой силой надо прижать к нему тормозную колодку, чтобы он остановился за 3 с, если коэффициент трения равен 0,1?

Ответ: N = 250 Н.

28.  Две гири с массами m₁ = 2 кг и m₂ = 1 кг соединены нитью, перекинутой через блок массой m = 1 кг. Найти ускорение a, с которым движутся гири, и силы натяжения T₁ и T₂ нитей, к которым подвешены гири. Блок считать однородным диском, трением в оси блока пренебречь.

Ответ: а = 2,8 м/с², T₁ = 14,0 Н; T₂ = 12,6 Н.

29. Тонкое кольцо радиуса R и массы m раскручено до угловой скорости  и поставлено вертикально на горизонтальную плоскость с коэффициентом трения k. С какой скоростью v будет двигаться кольцо после прекращения проскальзывания?

Ответ: v = R/2.

30. Найти скорости движения центров масс шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости 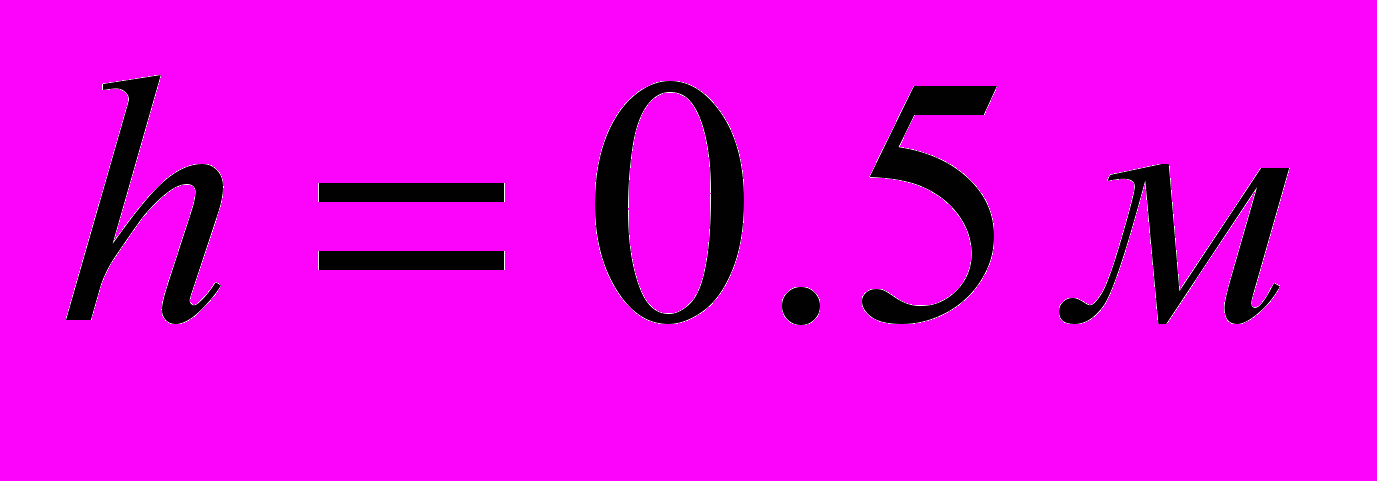, начальная скорость всех тел 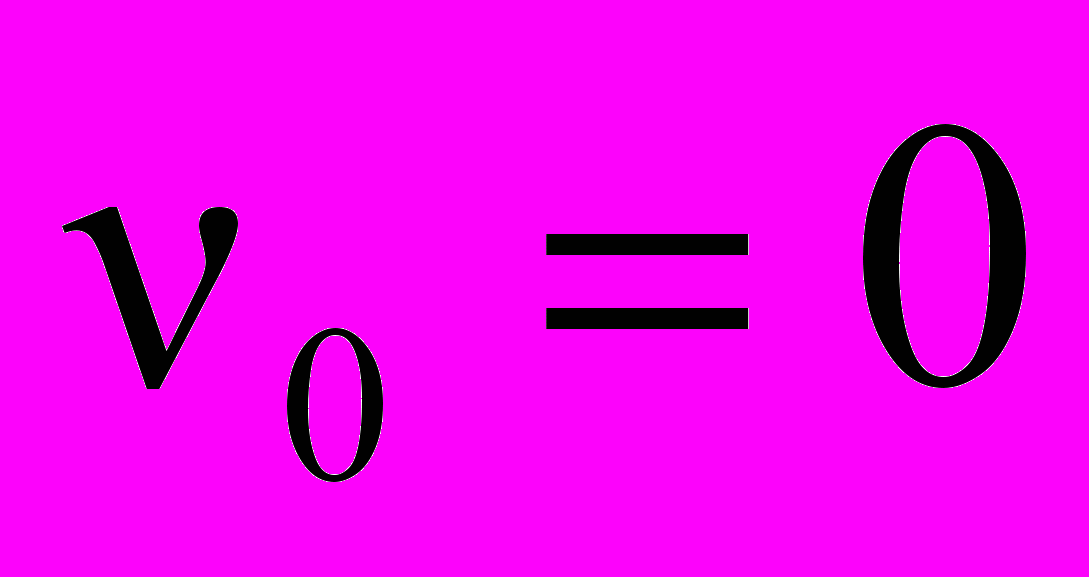. Сравнить найденные скорости со скоростью тела, скользящего с такой наклонной плоскости без трения.

Ответ: v = 2,65 м/с; 2,56 м/с; 2,21 м/с; 3,13 м/с.


31. Шар вкатывается без проскальзывания вверх по наклонной плоскости. В нижней точке плоскости центр масс шара обладал скоростью v₀ = 4,9 м/с. Определить максимальную высоту h подъёма шара.

Ответ: h = 1,7 м.


32. Высокая стальная фабричная труба треснула у основания и обвалилась. Найти нормальное ускорение верхней точки трубы как функцию угла между трубой и вертикалью. Может ли это ускорение превысить величину g ?

Ответ:


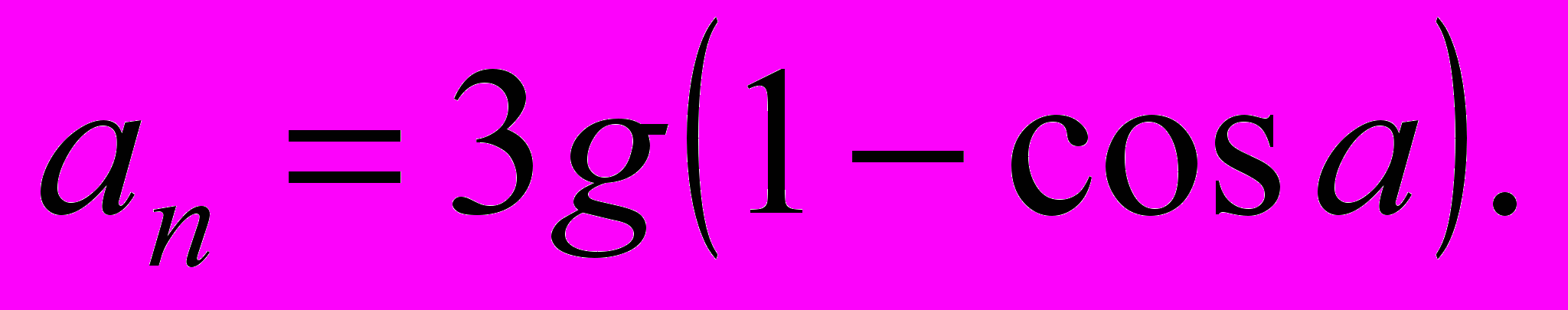
33. (11.7) В районе северного полюса на Землю падает метеорит под углом 45° к вертикали. Масса метеорита 1000 т, его скорость 20 км/с. Определить, на сколько повернётся земная ось в результате соударения с метеоритом. Масса Земли 610²⁴ кг, её радиус 6400 км.

Ответ:  = 1,2710^-17 рад.


34. Артиллерийский снаряд летит в воздухе, вращаясь вокруг оси симметрии со скоростью . Результирующая сила сопротивления воздуха, равная F, приложена на расстоянии l от центра масс снаряда и направлена параллельно касательной к траектории полёта. Момент инерции снаряда относительно оси симметрии I. Найти время T полного оборота оси симметрии снаряда вокруг касательной к траектории его центра масс.

Ответ:


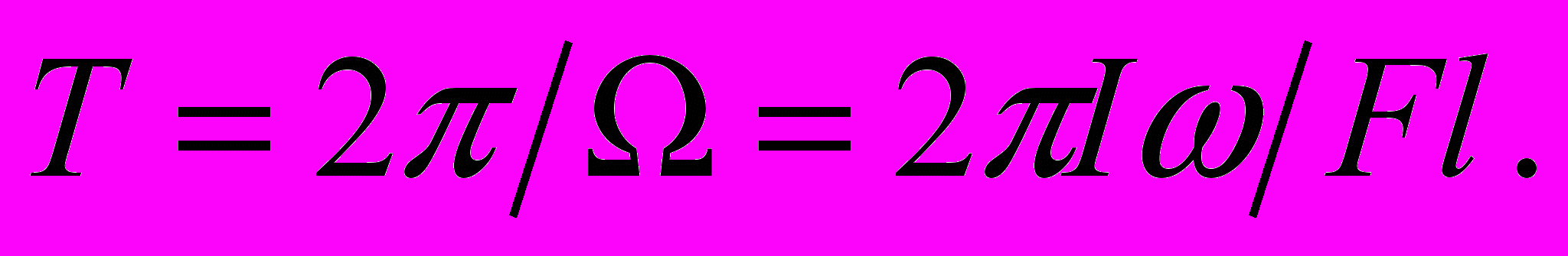
35.  Чашка пружинных весов массы m₁ совершает вертикальные гармонические колебания с амплитудой А. Когда чашка находилась в крайнем нижнем положении, на неё без удара положили груз массы m₂, в результате чего колебания прекратились. Определить первоначальный период колебаний чашки.

Ответ: .

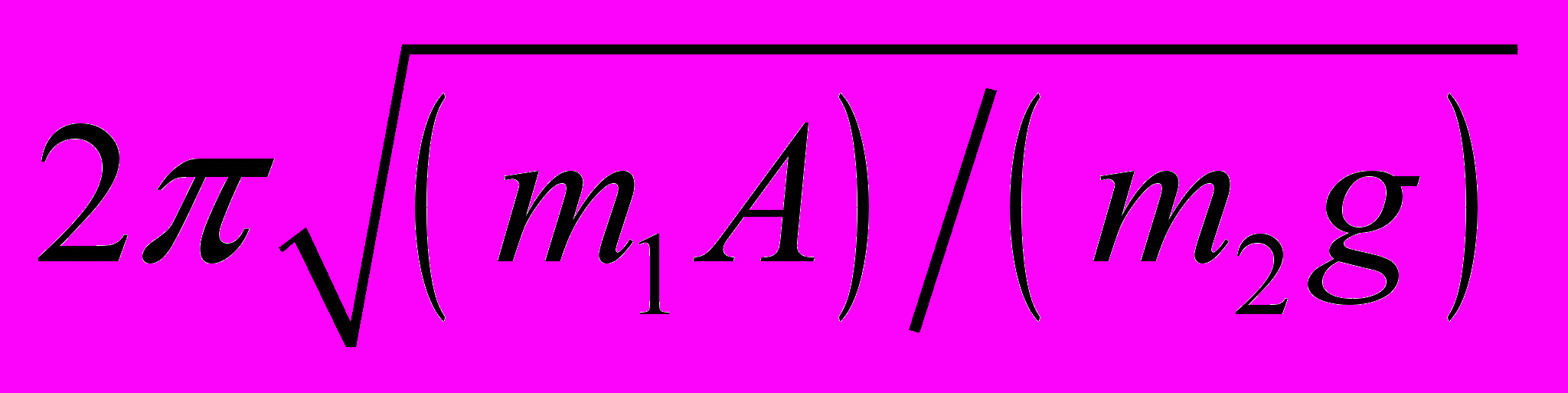36.  Для резонансного обнаружения малых вынуждающих сил используют монокристалл сапфира с добротностью Q = 10⁹ и частотой собственных колебаний  = 10⁴ с^–1. Какое время  нужно ждать, чтобы колебания монокристалла установились?

Ответ:   210⁵ c.

37. Однородный шарик подвешен на нити, длина которой равна радиусу шарика 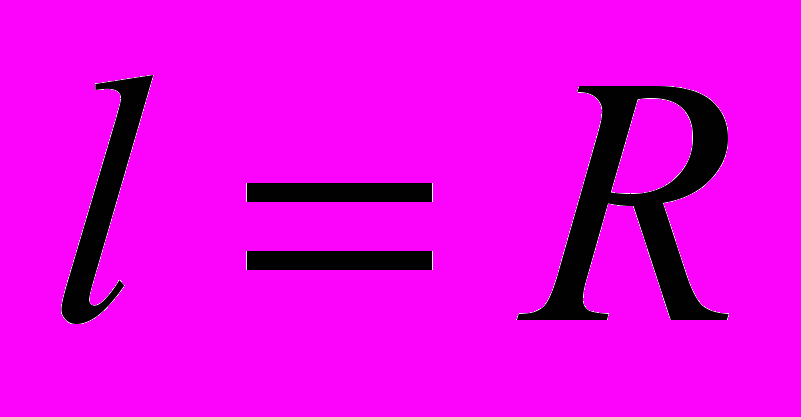. Во сколько раз период малых колебаний 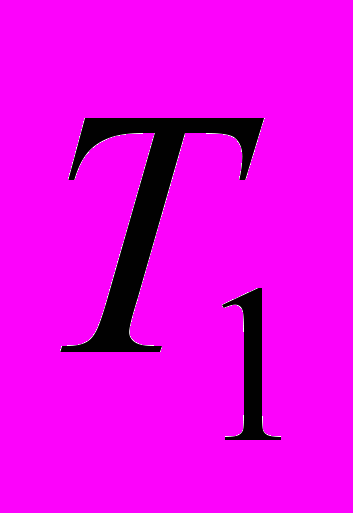этого маятника больше периода малых колебаний 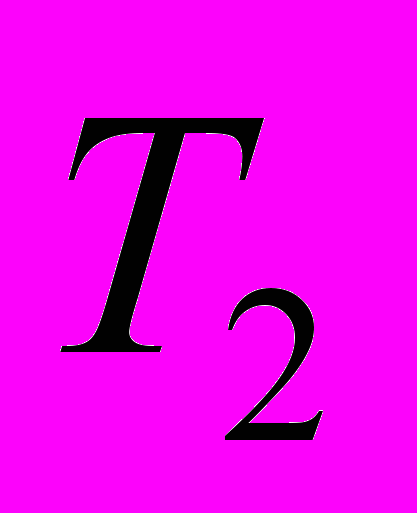математического маятника с таким же расстоянием от центра масс до точки подвеса?

Ответ: Т₁/Т₂=1,05.

38. (10.6) Сплошной однородный диск радиусом 10 см колеблется около горизонтальной оси, перпендикулярной к плоскости диска и проходящей через край диска. Какой длины должен быть математический маятник, имеющий тот же период колебаний, что и диск?

Ответ: 15 см.

39. (10.8) На каком расстоянии S от середины стержня следует подвесить однородный стержень длиной l, чтобы частота его колебаний была максимальна? Чему равна эта частота?

Ответ: S_max = 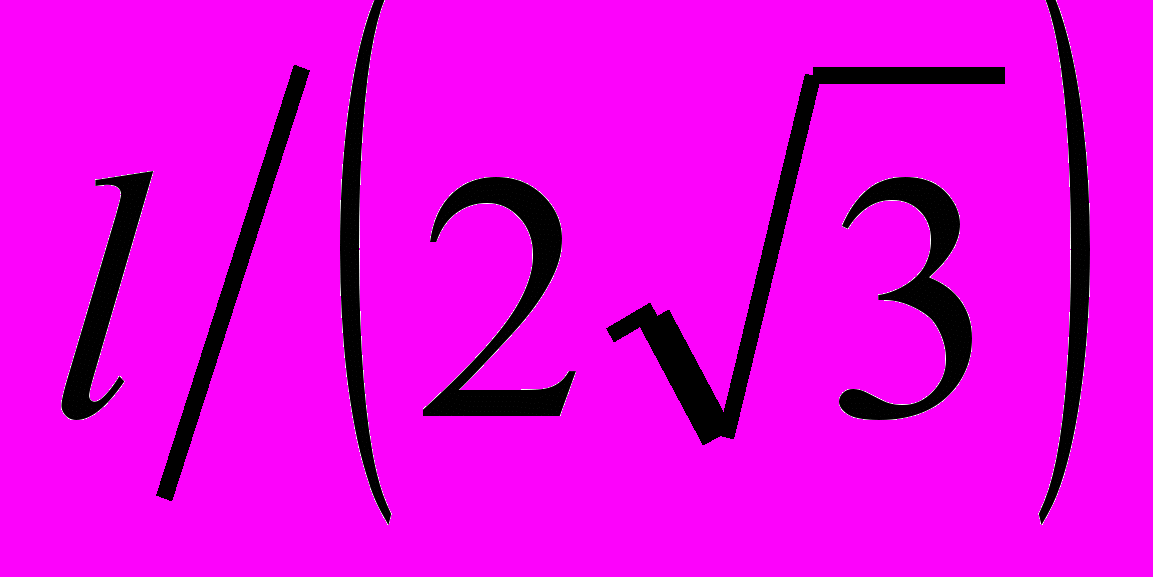; ²_max .

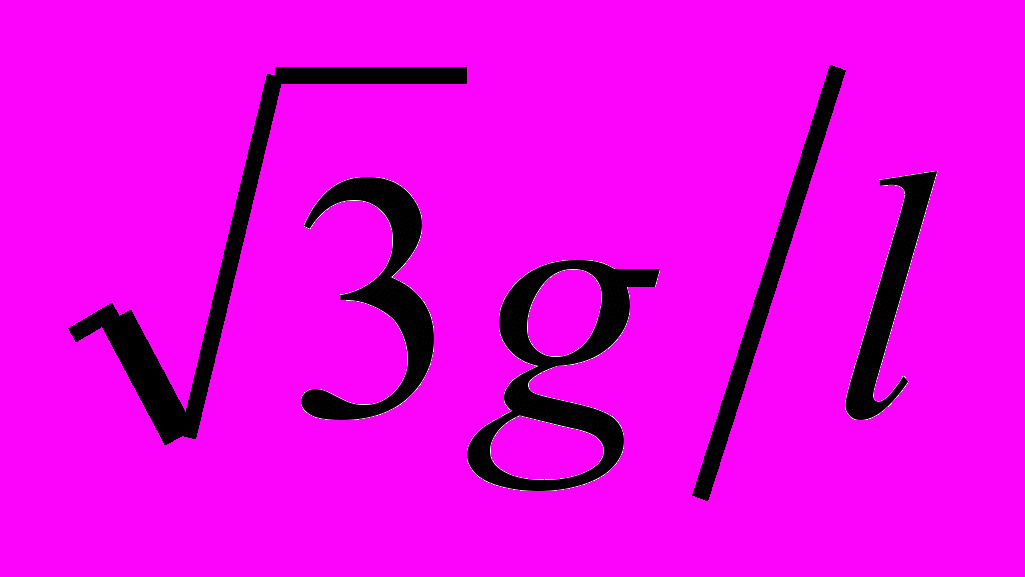40. (10.65) Как следует изменить натяжение струны, чтобы она давала тон в три раза более низкий?

Ответ: уменьшить в 9 раз.

41. Тело, падающее с высоты h, отклоняется из-за вращения Земли на некоторое расстояние х. На какое расстояние оно сместится при падении с высоты 2h?

Ответ: .

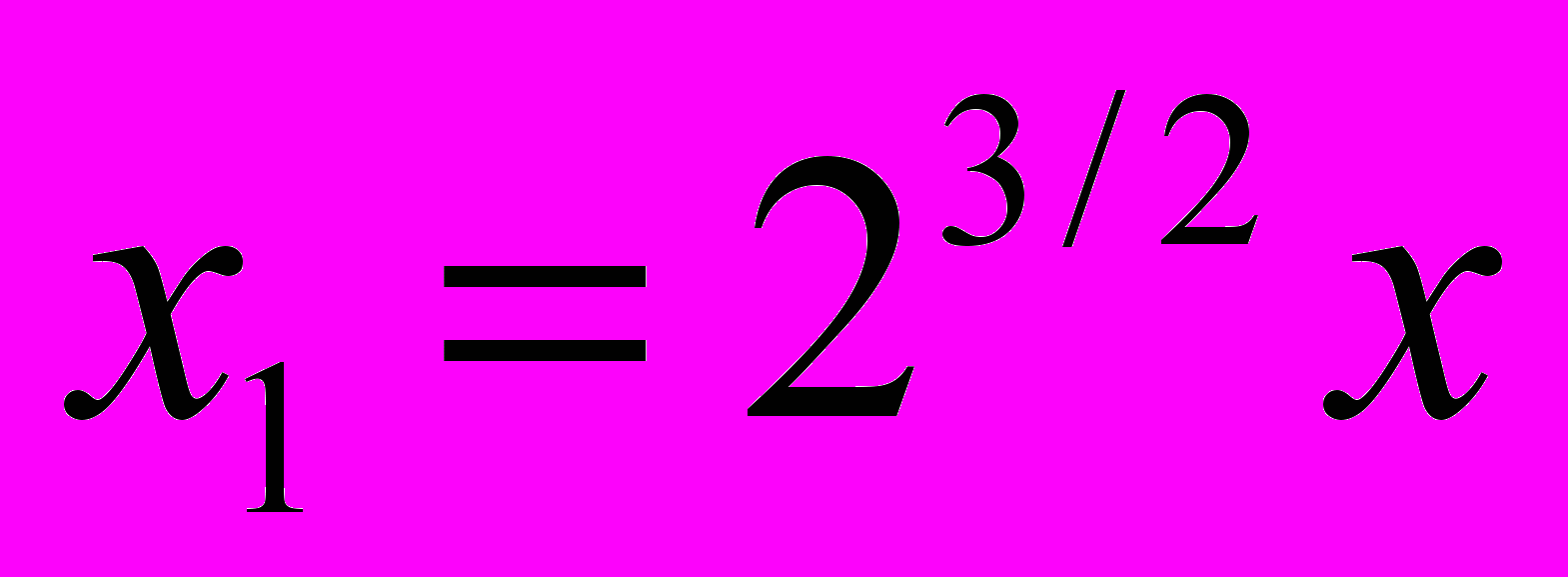42. Диск совершает n = 70 об/мин. Где можно положить на диск тело, чтобы оно не соскользнуло? Коэффициент трения тела о диск k = 0,44. Решить задачу в инерциальной и неинерциальной системах отсчёта.

Ответ: на расстоянии меньше 8 см от центра диска.

43. На какую часть 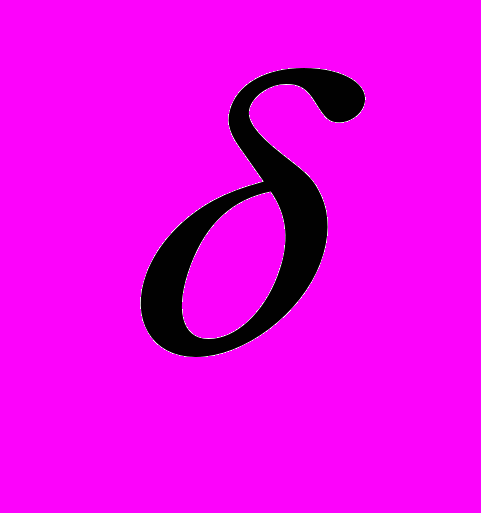уменьшается вес тела в Долгопрудном (широта 56^о) вследствие вращения Земли?

Ответ: .

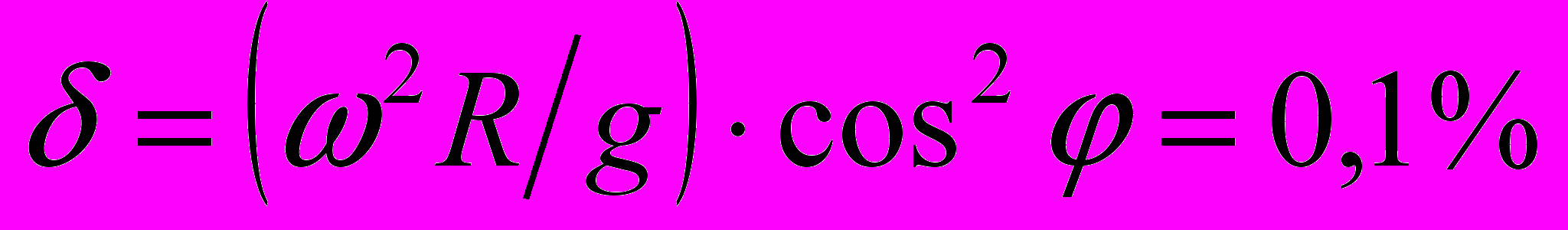44. (12.38) Какую работу должен совершить человек, чтобы пройти от периферии к центру карусели, равномерно вращающейся с угловой скоростью  = 1 рад/с, если радиус карусели R = 5 м, а масса человека M = 60 кг?

Ответ: А  750 Дж.

45. (13.1.) Стальной канат, который выдерживает вес неподвижной кабины лифта, имеет диаметр d = 9 мм. Какой диаметр D должен иметь канат, если кабина лифта может иметь ускорение до 8g?

Ответ: D = 27 мм.

46.(13.12) Найти упругую энергию, запасённую в шаре радиусом R, имеющим модуль всестороннего сжатия K и подвергнутом всестороннему давлению Р.

Ответ: U = 2R³P²/3K.

47. (13.17.) На вертикально расположенный резиновый жгут диаметром d₀ насажено лёгкое стальное кольцо слегка меньшего диаметра d  d₀ . Считая известным модуль Юнга E и коэффициент Пуассона  для резины, определить, с каким усилием F нужно растягивать жгут, чтобы кольцо с него соскочило. В расчётах весом резинового жгута пренебречь.

Ответ: .

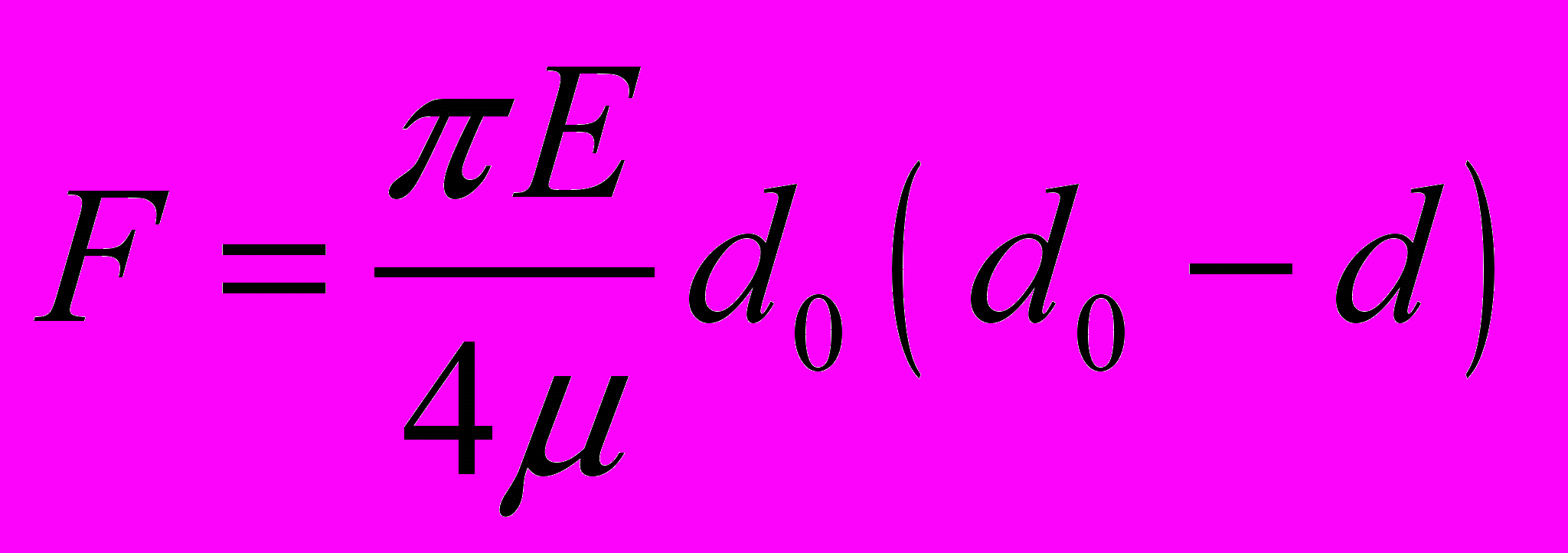48. Два стержня одинаковой длины – один сечения S из вещества с модулем Юнга Е, другой сечения 2S с модулем Юнга 2Е – растягиваются одинаковыми силами. Во сколько раз отличаются энергии их упругой деформации?

Ответ: .

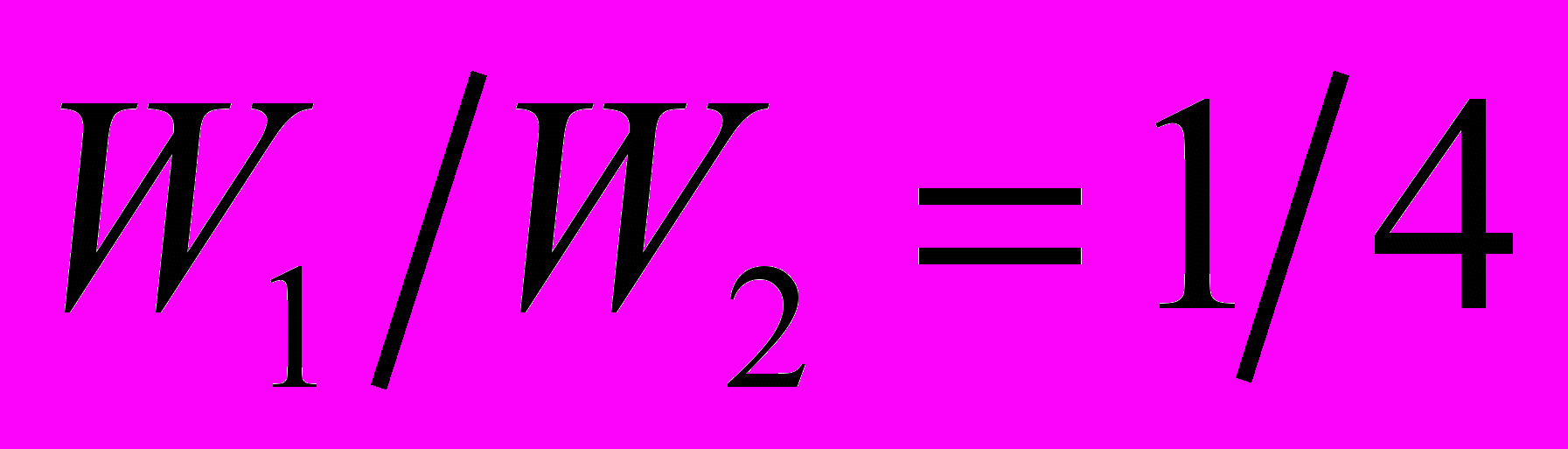49. (14.7) На горизонтальной поверхности стола стоит цилиндрический сосуд, в который налита вода до уровня H (относительно поверхности стола). На какой высоте h (относительно поверхности стола) надо сделать отверстие в боковой стенке сосуда, чтобы струя воды встречала поверхность стола на максимальном расстоянии от сосуда? Вычислите это расстояние.

Ответ: h = H/2; S_max = H.

50. (14.8) Определить скорость V стационарного истечения через малое отверстие струи идеальной несжимаемой жидкости, находящейся под давлением P в закрытом сосуде. Атмосферное давление P₀. Высота столба жидкости над отверстием h.

Ответ:

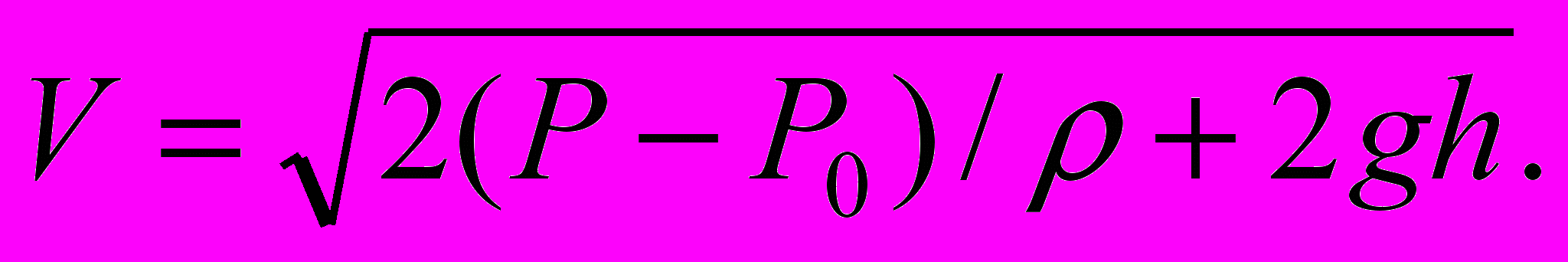
51. (14.11). В сосуд налита вода до высоты H. В дне сосуда проделано круглое отверстие радиусом 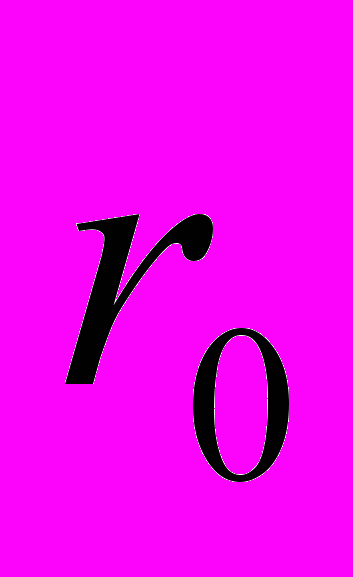. Найти радиус r(y) струи воды, вытекающей из отверстия, в зависимости от расстояния у от дна сосуда.

Ответ: .

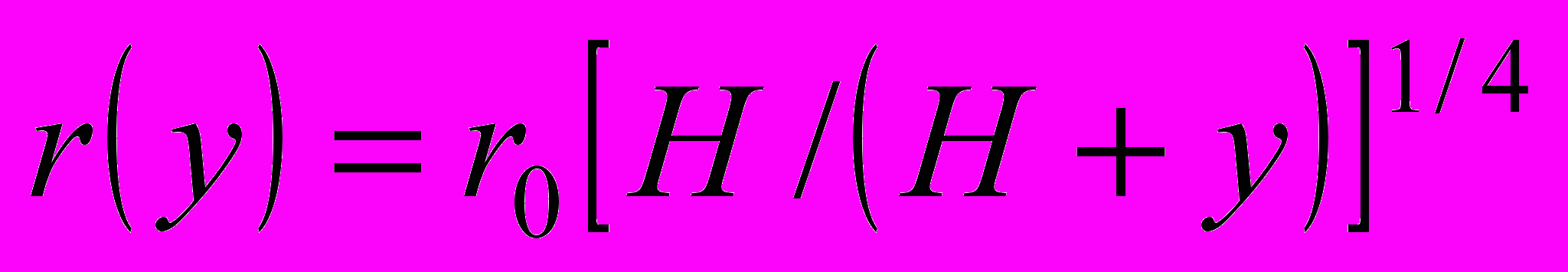52. В цилиндрический сосуд радиуса R и высоты H налита вода до высоты 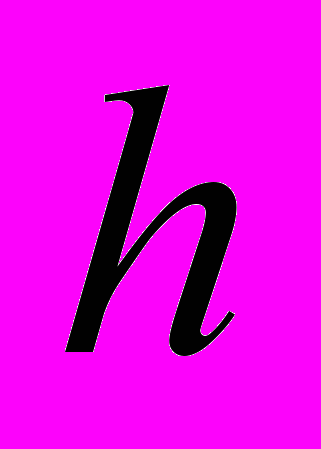. При какой скорости вращения сосуда вокруг вертикальной оси вода начнёт выплёскиваться через край?

Ответ: .
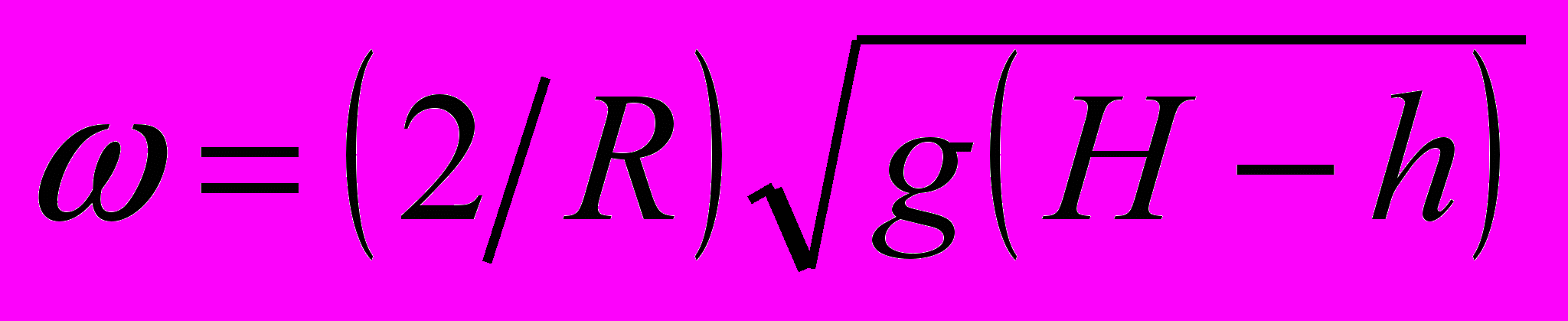