Лекция 12. Элементы квантовой механики

Вид материала

Лекция

Содержание 12.8. Квантование момента импульса М в пространстве является неопределенным. Наглядно подобную ситуацию можно попытаться представить так: вектор М

Подобный материал:

• 14. Элементы квантовой статистики и зонной теории твердого тела, 460.81kb.
• Основы квантовой механики, 33.02kb.
• Спецкурс для студентов 6-го курса Объем учебной нагрузки: 24 час лекции, 34.24kb.
• Развитие теоретической физики в ХХ веке шло под флагом зарождения, развития и становления, 110.96kb.
• Будем пытаться строить модель сознания в духе математики квантовой механики, 181.49kb.
• Спецкурс для студентов 5-го и 6-го курсов Объем учебной нагрузки: 48 час лекции, 80.81kb.
•  Элементы квантовой механики и физики атомов, молекул, твердых тел, 156.85kb.
• Элементы квантовой механики Атом Резерфорда – Бора и гипотеза де Бройля Ядерная модель, 38.71kb.
• Программа учебной дисциплины вариационные методы в физике (спецкурс, дисциплины, 147.31kb.
• Физические основы механики, 237.04kb.

12.7. Операторы физических величин. Собственные состояния

Операторы. Оператором называют символическое обозначение математической операции, которую необходимо совершить с интересующей нас функцией. Операторы принято обозначать буквами со «шляпкой», например , и его действие на некоторую функцию f(x) записывают как f(x).

Общее утверждение квантовой теории заключается в том, что среднее значение любой физической величины Q находится по формуле

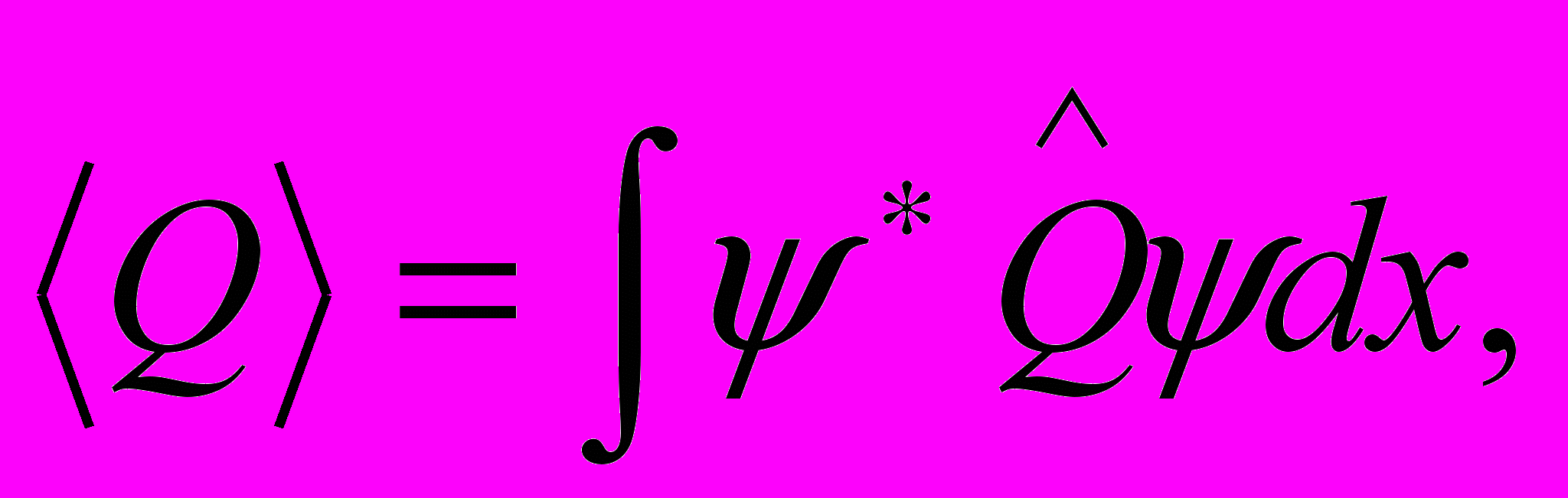(12.45)

где -оператор физической величины Q. Операторами величин x и p_x являются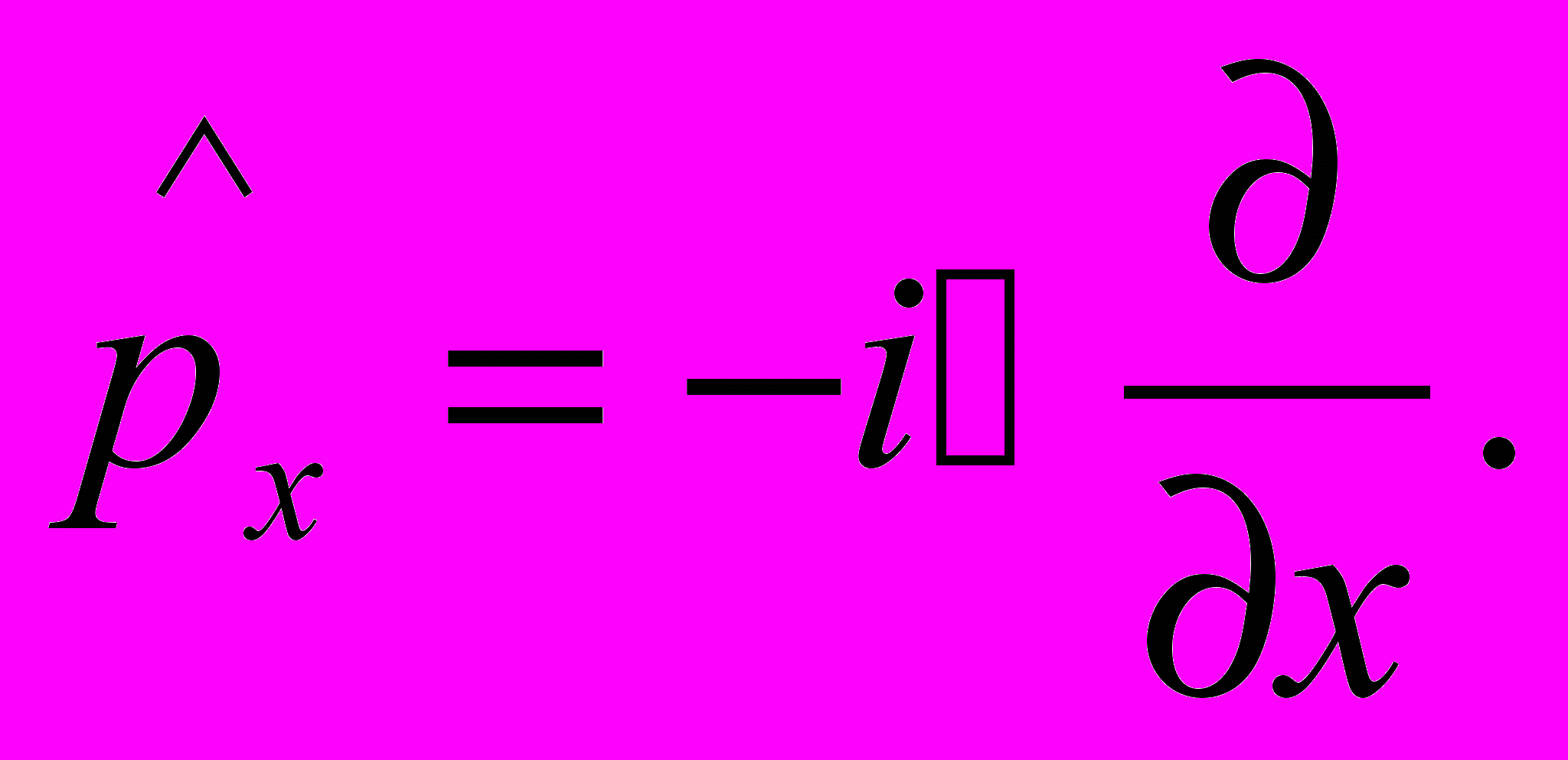

(12.46)

Аналогично для операторов

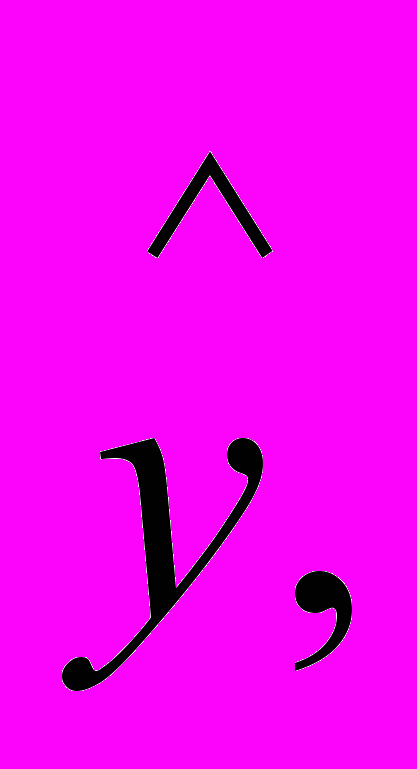
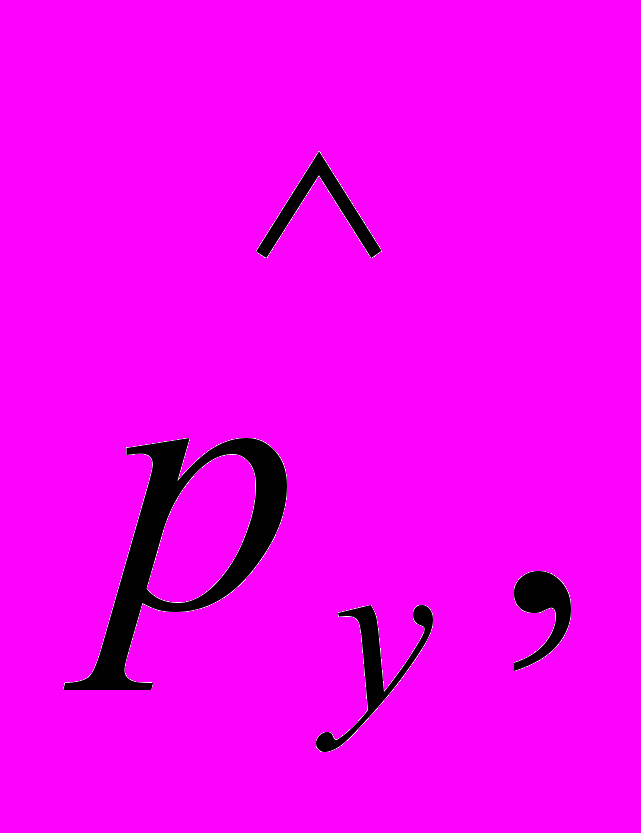
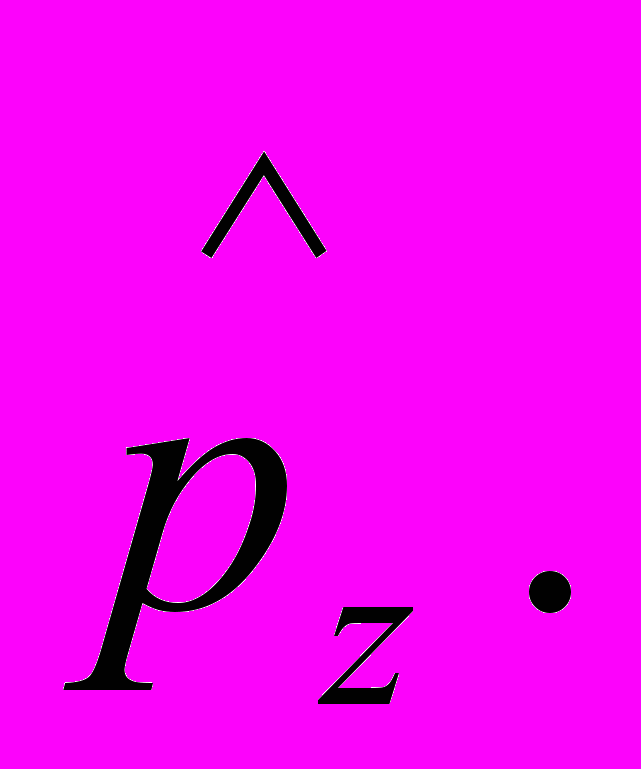
Общее правило, позволяющее находить операторы других физических величин, таково:

формулы классической физики для связи между величинами в квантовой теории следует рассматривать как формулы, связывающие операторы этих величин.

Оператор полной энергии частицы — гамильтониан имеет вид: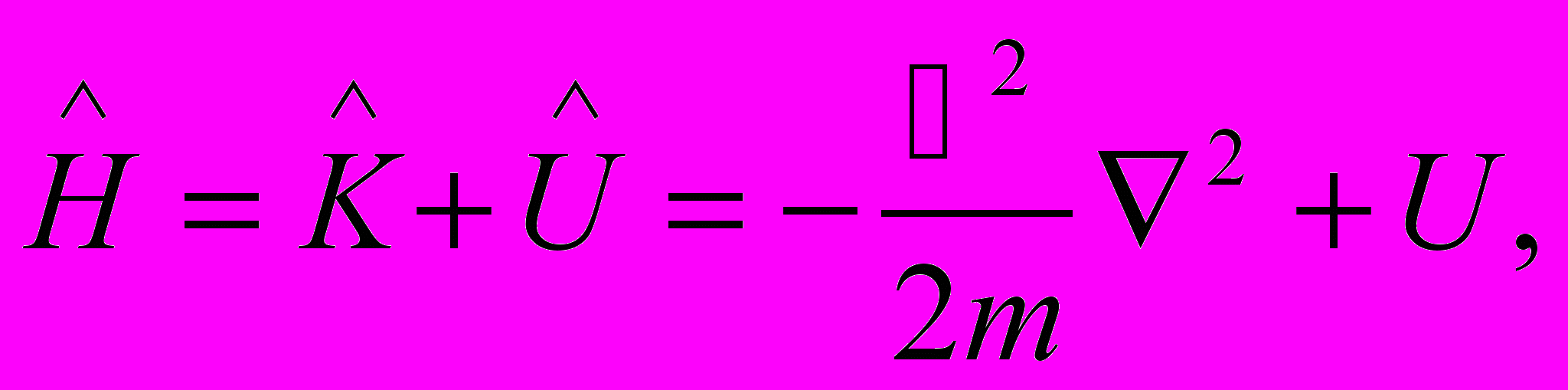

(12.47)

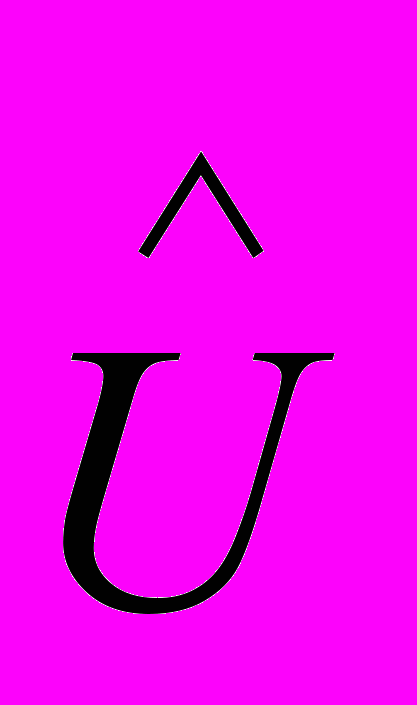где и - операторы кинетической потенциальной энергии, - это лапласиан.

Найдем с помощью оператора полной энергии (12.47) связь между средними значениями полной <E>, кинетической <K> и потенциальной <U> энергий:

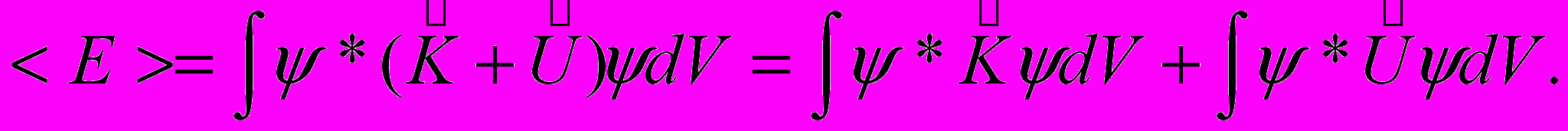(12.48)

Отсюда, используя определение среднего значения (12.45) получаем

<E> = <K> + <U>.

(12.49)

Полученное равенство не эквивалентно Е = К + U классической механики. Действительно, в силу соотношения неопределенностей величины К и U не могут одновременно иметь определенные значения, поскольку К зависит от импульса р, a U — от координаты х. Формула (12.49) показывает, однако, что в квантовой механике классическая связь сохраняется между средними значениями Е, К и U.

Собственные состояния. Одним из основных постулатов квантовой теории является утверждение, что состояние, в котором физическая величина Q имеет определенное значение, описывается _Ψ-функцией, являющейся решением уравнения

Ψ = QΨ,

(12.50)

где— оператор физической величины Q.

Физический смысл могут иметь лишь такие решения (12.50), которые всюду конечные, однозначные, непрерывные и гладкие. Эти условия, как уже говорилось, называют естественными или стандартными.

Функции, являющиеся решением уравнения (12.50) и удовлетворяющие естественным условиям, называют собственными функциями оператора. Те значения Q, при которых такие решения существуют, называют собственными значениями физической величины Q. Такие состояния и называют собственными.


12.8. Квантование момента импульса

Момент импульса. Момент импульса М является одной из важнейших характеристик движения. Однако в квантовой теории мо­мент импульса существенно отличается от классического. А именно, модуль момента импульса может быть задан сколь угодно точно только с одной из проекций, например, М_г. Другие две проекции оказываются полностью неопределенными.

Это означает, что направление момента М в пространстве является неопределенным. Наглядно подобную ситуацию можно попытаться представить так: вектор М как-то «размазан» по образующим конуса, ось которого совпадает с направлением координатной оси Z (рис. 12.12). В этом случае вполне определенное значение имеет лишь проекция М_г. Другие две проекции, М_х и М_у, оказываются полностью неопределенными.


Рис. 12.12.


Модуль момента импульса. Для определения квадрата момента необходимо решить уравнение

(12.51)

Оператор 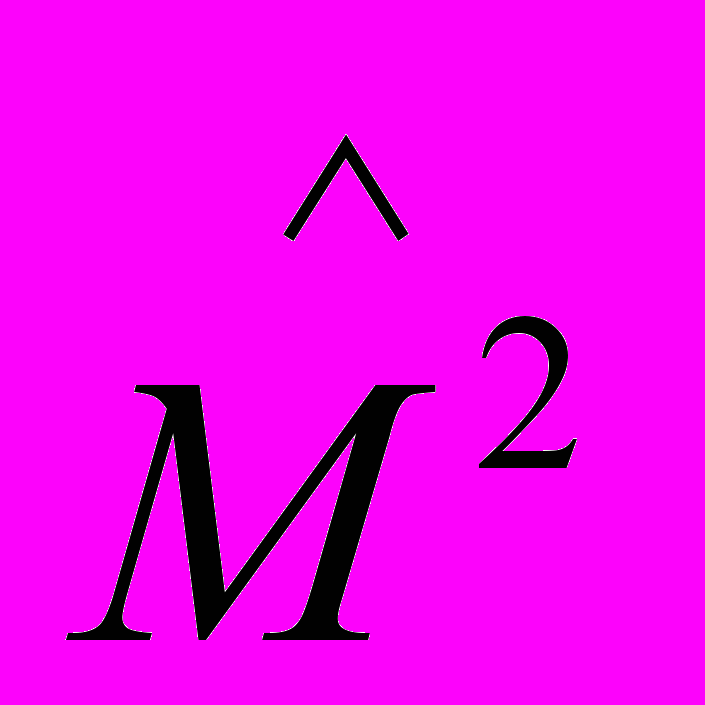достаточно сложный, и решение этого уравнения является очень громоздким. Поэтому ограничимся приведением окончательных результатов, причем только для собственных значений данного оператора:

М2 = l( l + 1)ћ2, l = 0, 1, 2, …,

(12.52)

где l — орбитальное (или азимутальное) квантовое число. Отсюда модуль момента

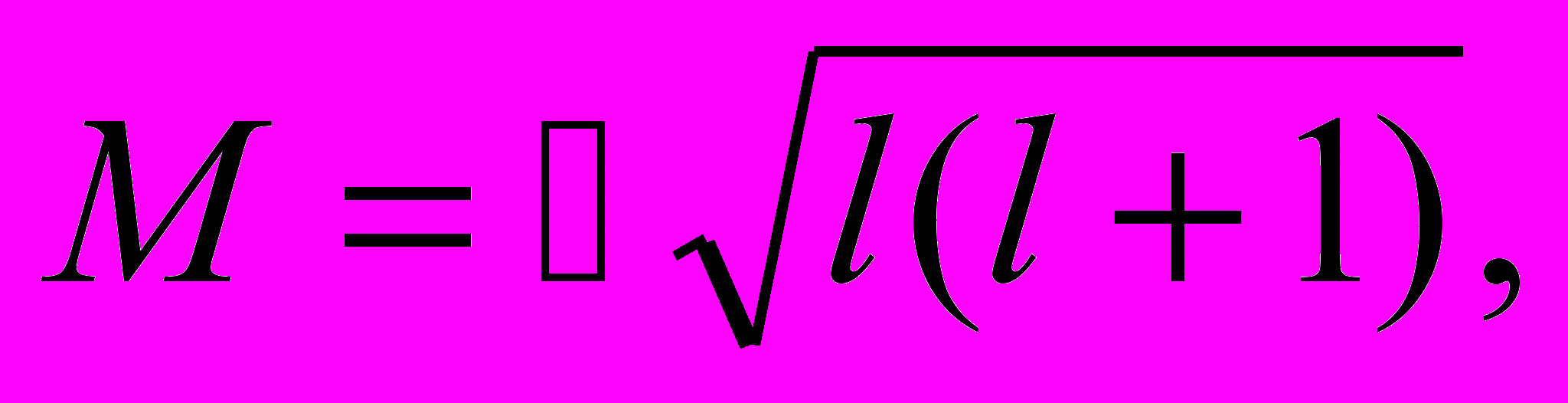l = 0, 1, 2, …,(n-1).

(12.53)

Видно, что эта величина является дискретной (квантованной).

Следует отметить, что между классическим моментом импульса и соответствующим ему оператором имеется существенное различие. Классический момент [r р] зависит от выбора точки О, относительно которой берется радиус-вектор r. Оператор же момента импульса не зависит от выбора точки О (в этом можно убедиться, записав проекции момента в сферических координатах). Оператор момента импульса зависит только от направления координатных осей. Поэтому его называют оператором углового момента. Собственные значения операторов квадрата и проекции углового момента, 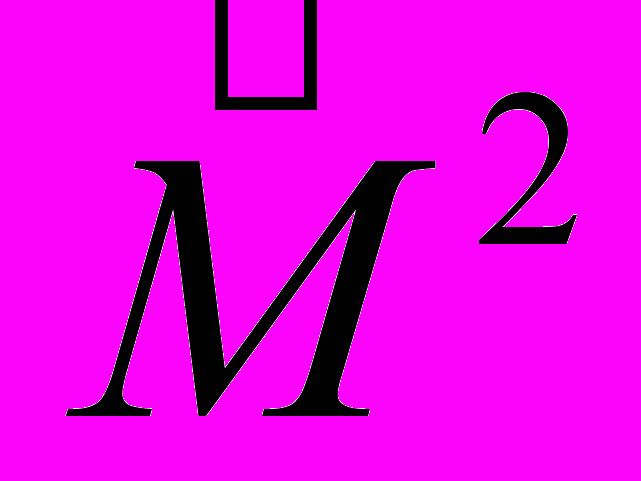и 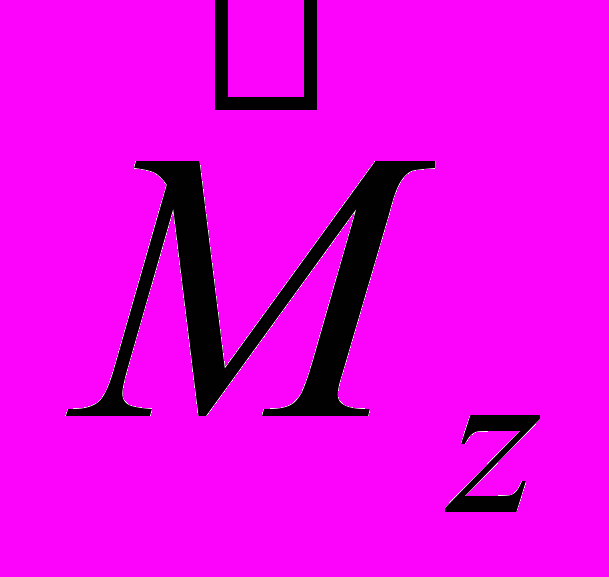также не зависят от выбора точки О.

Проекция момента М _z. Рассмотрим решение уравнения

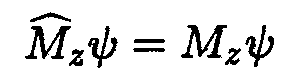(12.54)

В сферических координатах (r, θ, φ) оператор проекции момента импульса на полярную ось z (от которой отсчитывается полярный угол θ) имеет вид

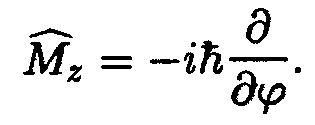(12.54)

Для определения собственных значений и собственных функций этого оператора надо, согласно (12.50) и (12.54), решить уравнение

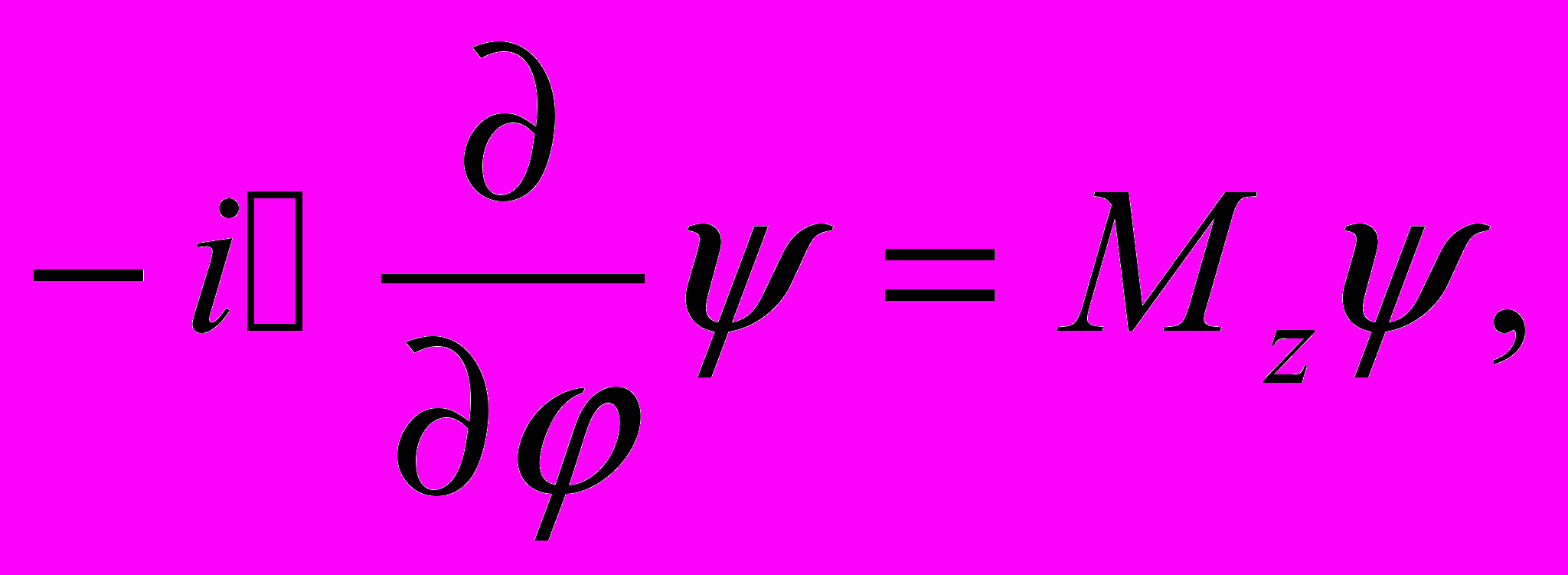(12.55)

где φ – азимутальный угол в полярной системе координат.

Подстановка ψ = C exp (αφ) приводит после сокращения на общий множитель ехр (αφ) к алгебраическому уравнению,



из которого α = iМ _z /ћ. Значит, решение уравнения (12.55) таково:

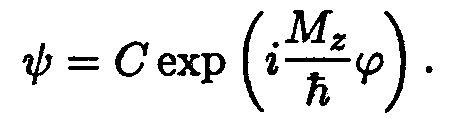(12.56)

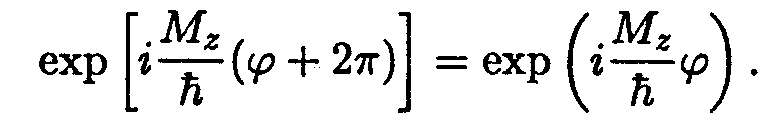
Эта функция конечна, непрерывна и гладкая. Она должна быть и однозначной, для чего должно быть выполнено условие ψ (φ + 2π) = ψ (φ) или

Это условие будет выполнено, если положить M _z = mћ, где т —целое положительное или отрицательное число либо нуль. Следовательно, оператор 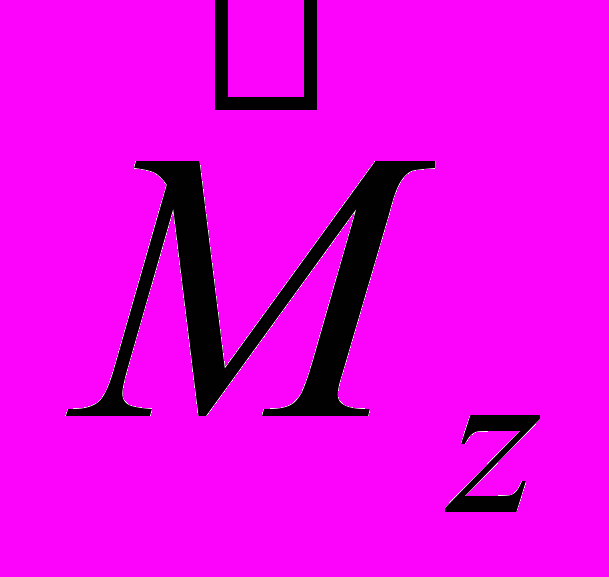обладает дискретным спектром:

Mz = m ħ, m = 0, ± 1, ± 2, …

(12.57)

Поскольку ось Z выбирают произвольно, равенство (12.57) означает, что проекция углового момента на любое направление квантуется. Схематически это показано на рис. 12.13.

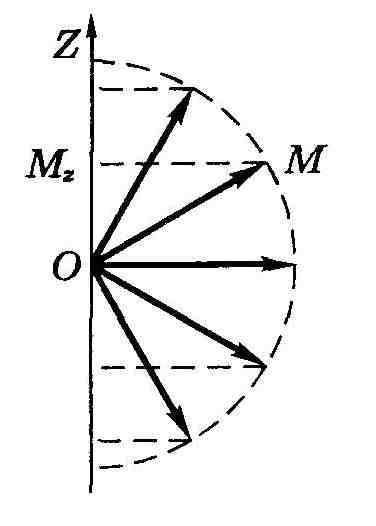Число т называют магнитным квантовым числом. С точки зрения квантовой теории волновая функция ψ_l, соответствующая определенному квантовому числу l, представляет собой суперпозицию состояний (ψ_lm -функций), отличающихся друг от друга квантовым числом т. Иначе говоря, состояние с заданным l является вырожденным по т, причем кратность вырождения, т. е. число различных значений т, как следует из (12.57), равно 2l + 1. Как будет показано в дальнейшем, вырождение снимается при помещении атома в магнитное поле.

Рис. 12.13.






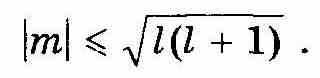
Проекция вектора не может быть больше модуля этого вектора, т. е. |M_z| ≤ М, поэтому в соответствии с (12.53) и (12.57) должно выполняться условие

Отсюда следует, что максимальное значение |т| равно l.

Видно, что при заданном l число т принимает 2l + 1 значений:




образующих спектр величины М_z. В квантовой теории при указании орбитального момента принято называть только l, поскольку оно задает как модуль углового момента, так и все возможные значения его проекций на ось Z. Так например, когда говорят, что орбитальный момент l= 2, то имеется в виду модуль М момента и спектр М_z:







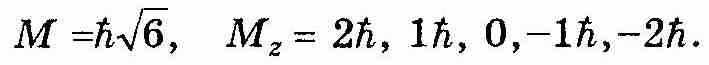
Напишем вместе полученные результаты:

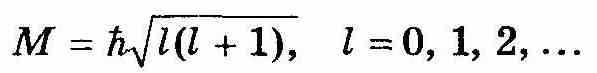	(12.58)
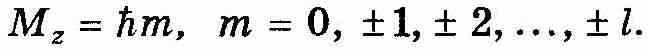	(12.59)

Полученные результаты, определяющие возможные значения М и М_z, называют пространственным квантованием. Для наглядности пространственное квантование обычно представляют графически (см. рис. 12.13).