К. Е. Карасёв Введение в теорию конечных автоматов

Вид материала

Учебное пособие

Содержание 1.Определение конечного автомата. Упражнение 1.1. Приведите пример детерминированной, но не ограниченно-детерминированной функции. Функция, вычисляемая автоматом, является о.-д. функцией. Для любой о.-д. функции существует автомат, её вычисляющий. Приведённые ниже соотношения связывают последовательность входных символов автомата x(t)=( x 1.8. Смоделируйте конечным автоматом работу лифта. 2.Отношения эквивалентности автоматов и их состояний Неотличимость состояний Эквивалентное определение. Упражнение 2.3. Приведите пример такой пары автоматов. 3.Стохастические функции конечных автоматов 3.2. Посчитайте стохастическую функцию автомата с диаграммой Мура следующего вида 3.3.Найдите стохастические функции автоматов из упражнений 1.2-1.6. 4. Эксперименты над автоматами Кратным безусловным Простой условный Кратный условный Длина эксперимента – максимальная длина слова, которое может быть введено в автомат при применении эксперимента. Объём 4.1. Переформулируйте теорему Мура о различении состояний, используя понятия теории экспериментов. 4.3. Пусть n – фиксированное натуральное число, {А} – класс автоматов Мура A=({1..n}, {0,1} 5. Синтез схем из функциональных элементов ... Полное содержание

Подобный материал:

• Виртуальная лаборатория обучения генетическому программированию для генерации управляющих, 64.24kb.
• Рабочая программа Дисциплины «Теория автоматов» Для студентов специальности 23010065, 57.28kb.
• Прикладная теория цифровых автоматов, 27.51kb.
• Джон Р. Хикс. "Стоимость и капитал", 4314.44kb.
• Царев Федор Николаевич Разработка метода совместного применения генетического программирования, 417.18kb.
• А. В. Корицкий введение в теорию человеческого капитала учебное пособие, 1340.03kb.
• Полная программа на прологе 6 Схема ответов на вопросы по результатам практических, 73.73kb.
• Курсовая работа "Синтез дискретных устройств управления", 306.46kb.
• Лекция №11 «Антивирусные программы», 55.93kb.
• Г. В. Мелихов миф. Идентичность. Знание: введение в теорию социально-антропологических, 741.74kb.

Министерство образования Российской Федерации Московский государственный технический университет «СТАНКИН»

К.Е.Карасёв

Введение в теорию конечных автоматов Учебное пособие

Москва, 2007

Предисловие

Данное пособие составлено на основе полугодового курса, прочитанного автором для студентов МГТУ «СТАНКИН» в 2005 и 2006 годах. В пособии представлены краткие теоретические сведения и задачи по таким основным разделам теории конечных автоматов, как: основы теории автоматов, теория экспериментов над автоматами, стохастические функции автоматов, реализация автоматов схемами, теория регулярных языков. С учётом особенностей учебной программы, в пособие также включены темы из смежных областей дискретной математики – синтез схем из функциональных элементов, теория алгоритмов (машина Тьюринга), теория рекурсивных функций. Также в пособие включены сведения, имеющие практическое применение в области программирования: регулярные выражения в современных языках программирования, понятие формальной грамматики.

Для изучения этого курса теории автоматов желательно наличие следующих предварительных знаний:

• основы теории графов;
  
• теория функций алгебры логики;
  
• теория вероятностей, понятие цепи Маркова (для изучения стохастических функций автоматов).
  

Для рассмотрения некоторых задач и примеров также полезно знание начал абстрактной алгебры (линейная алгебра, конечные группы и кольца).

Задачи и упражнения в пособии расставлены по возможности в порядке возрастания сложности. Как правило, если в данном пособии приводится доказательство некоторого утверждения, это доказательство является конструктивным алгоритмом для решения задач.

Задачи и упражнения выделены полужирным шрифтом.

1.Определение конечного автомата.

Определение. Конечным инициальным автоматом (или просто автоматом) называется шестёрка (A, Q, B, , , q₀), где:

A – конечное множество произвольной природы, называемое входным алфавитом автомата (в дальнейшем под алфавитом будет пониматься конечное множество произвольной природы, его элементы будем называть символами);

Q – конечное множество, называемое алфавитом состояний автомата;

B – конечное множество, называемое выходным алфавитом автомата;

 – отображение :AXQ→Q, называемое функцией переходов автомата;

 – отображение :AXQ→B, называемое функцией выходов автомата;

q₀ - элемент алфавита Q, называемый начальным состоянием автомата.

Это определение соответствует следующей математической модели. Некоторое устройство – конечный автомат – принимает сигналы, являющиеся символами алфавита A и выдаёт сигналы – символы алфавита B, при этом устройство принимает конечное число состояний, и сигнал на выходе определяется только сигналом на входе и состоянием автомата. Состояние автомата в сущности есть содержимое его памяти. Время в этой модели предполагается дискретным, переменная t принимает значения из множества натуральных чисел. Обозначим x(t) символ, принимаемый автоматом в момент времени t, y(t) – символ, выводимый автоматом, q(t) – состояние автомата в момент времени t. Эти функции от t связываются следующими соотношениями:



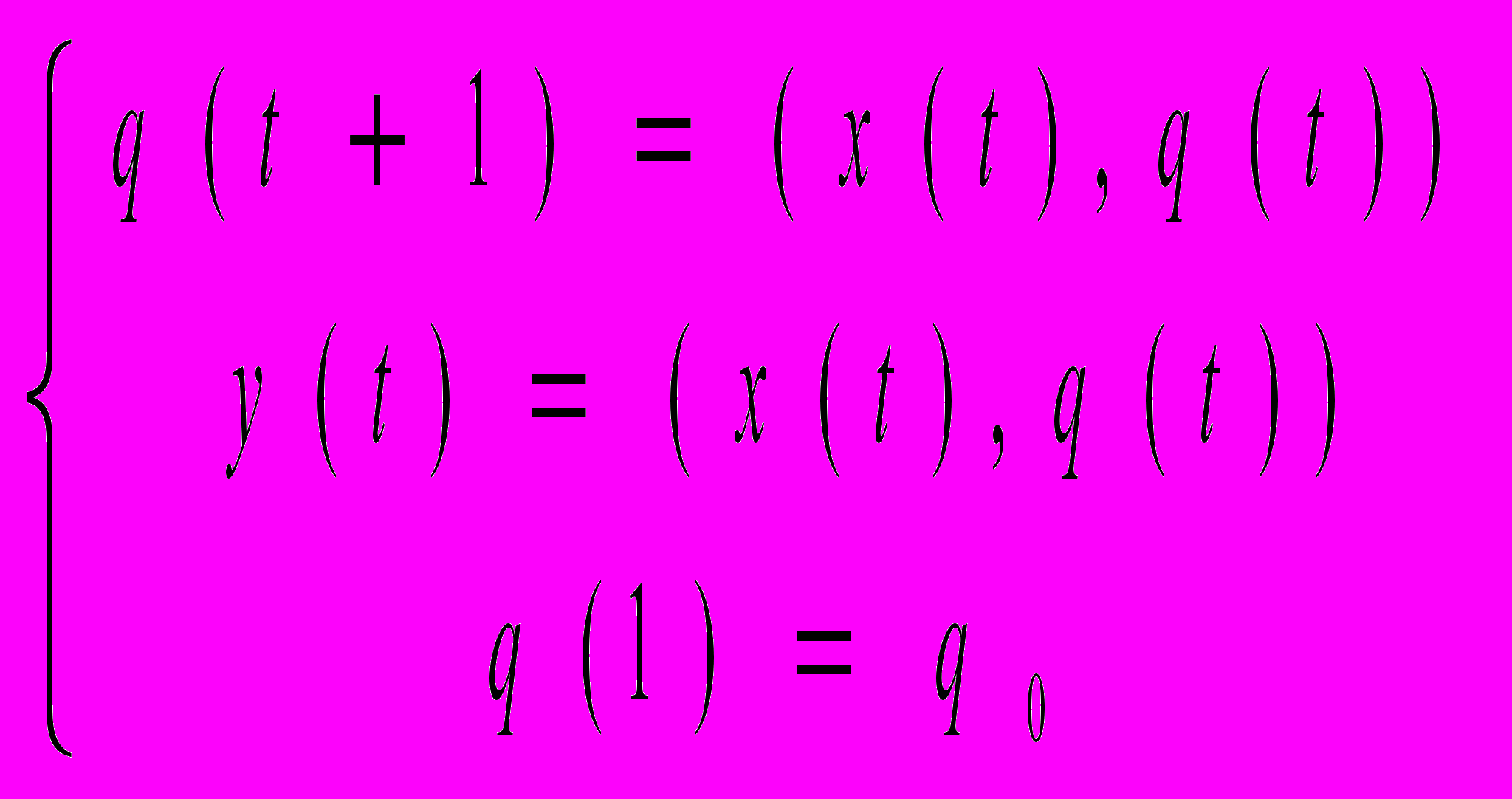
Эти соотношения называются уравнениями переходов и выходов автомата (первое – уравнение переходов, второе – уравнение выходов). Поскольку множества, на которых эти функции определены, конечны, эти функции (а следовательно, и весь автомат) можно описать таблицей. Назовём таблицу для функции таблицей переходов. Мы говорим, что символ x переводит автомат из состояния q в состояние q,x).

Другой подход к определению автомата – понятие ограниченно-детерминированной функции. Назовём словом в алфавите A произвольную конечную упорядоченную последовательность символов из этого алфавита. Множество всех слов в алфавите A обозначается A*. Пусть функция f:A*→B* отображает слова в алфавите A в слова в алфавите B. Функция называется детерминированной, если она, во-первых, сохраняет длину слова, и, во-вторых, если в двух словах в алфавите A совпадают первые n символов, то и в словах – образах этих слов при применении функции f – первые n символов совпадают. Условие детерминированности можно записать следующим образом: если ax₁ и ax₂ – два слова из A* с общим началом a , то f(ax_i)=by_i , где b – общее начало длины, равной длине a, двух слов by₁ и by₂. Таким образом, для любого слова a существует функция f_a:A*→B*, такая, что f(ax)=bf_a(x). Функция f_a также будет детерминированной: в самом деле, f_a сохраняет длину слова, и, если f_a(cx)=dy, то f(acx)=bdy, и если f(acx’)=bdy’, следовательно, f_a(cx’)=dy’. Мы видим, что любая детерминированная функция f для каждого слова a из A* определяет детерминированную функцию f_a, которая называется остаточной функцией функции f.

Определение. Если для всех слов a число различных остаточных функций f_a конечно, то функция f называется ограниченно-детерминированной (сокращённо о.-д.) функцией.

Упражнение 1.1. Приведите пример детерминированной, но не ограниченно-детерминированной функции.

Каждому автомату с входным алфавитом A и выходным алфавитом B можно поставить в соответствие функцию f, переводящую слово =a(1)a(2)…a(t) в слово =b(1)b(2)…b(t), где t – переменная времени. В этом случае говорят, что автомат вычисляет функцию f. Справедливо следующее утверждение:

Функция, вычисляемая автоматом, является о.-д. функцией. Для любой о.-д. функции существует автомат, её вычисляющий.

Функцию, которую автомат вычисляет, обычно называют поведением автомата.

Если остаточные функции о.д. функции известны, то автомат можно построить, взяв в качестве множества состояний множество (множество классов эквивалентности) остаточных функций, взять функцию переходов, удовлетворяющую соотношению f_, x)= f_x и функцию выходов f_, x)= f_x).

Кроме таблиц наглядным способом изображения конечного автомата являются диаграммы переходов, или диаграммы Мура. Диаграмма Мура представляет собой ориентированный граф, каждая вершина которого соответствует состоянию автомата, а каждое ребро, идущее из вершины q_i в вершину q_j, соответствует значению функции переходов (x,q_i)=q_j . и помечено парой (x,(x,q_i)), и, наоборот, для каждого значения аргументов функции переходов в диаграмме существует такое ребро. Обычно в вершины графа изображаются кругами, начальное состояние помечается звёздочкой. Пара (x,y) у ребра графа изображается без скобок через дробь: x/y.

Функция переходов автомата доопределяется до расширенной функции переходов автомата: пусть x=(x₁,...,x_k)∈A*, q₁∈Q и (x_i,q_i)=q_i+1. Тогда положим (x,q₁)=q_k+1 и будем говорить, что слово x переводит автомат из состояния q₁ в состояние q_i+1.

Упражнения. Приведённые ниже соотношения связывают последовательность входных символов автомата x(t)∈{0,1} и выходных у(t)∈{0,1}. Построить таблицу для функций переходов и выходов автомата, диаграмму Мура.

2. y(t)=x(t-1) & x(t-2), y(1)=y(2)=0.
   

Решение. Выход автомата целиком определяется парой значений входного символа в два предыдущих момента времени - «последний» и «предпоследний символ». Именно эти значения имеет смысл хранить в качестве состояния автомата. При этом функция переходов должна быть устроена таким образом, что при вводе символа он становится «последним» символом, «последний» символ становится «предпоследним», а «предпоследний» символ «забывается».

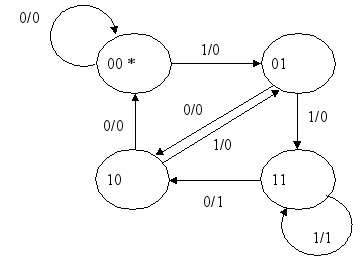
Итак, состоянием автомата будет двоичный вектор q₁q₂=(q₁,q₂), связанный с входными символами соотношениями q₁(t)=x(t-1), q₂(t)=x(t-2). Соотношения можно переписать в виде q₁(t+1)=x(t), q₂(t+1)=q₁(t). Для соответствия функции условиям y(1)=y(2)=0 дополним уравнения переходов значениями q₁(0)=q₂(0)=0. Функция выходов примет вид (x,q₁,q₂)=q₁&q₂.

Таблица функции переходов автомата примет следующий вид:

x	(00,x)	(01,x)	(10,x)	(11,x)
0	00	10	00	10
1	01	11	01	11

Диаграмма Мура автомата примет вид:

3. 
   y(t)=x(1)→x(t)
   
4. y(t)=x(2)⋁x(t)
   
5. y(t)=x(t)&(x(t-1)⋁x(1)),x(0)=1
   
6. В автомат последовательно вводятся цифры натурального числа (рассмотреть два варианта – с начала и с конца). Автомат в каждый момент выводит остаток от деления уже введённого на этот момент числа на n, n<10. Покажите, что такой автомат существует. Постройте диаграмму Мура для n=2,3,4,5.
   

Приведённые ниже соотношения связывают последовательность входных символов автомата x(t)=( x₁(t), x₂(t))∈{0,1} и выходных у(t)∈{0,1}. Построить таблицу для функций переходов и выходов автомата, диаграмму Мура.

3. y(t)=x₁(t-1)→x₂ (t)
   
4. y(t)=x₁(t)+ x₂(t) x₁(1)
   
5. y(t)=x₁(1)&( x₂(t) ⋁ x₂(1))
   

Следующие задачи заключаются в моделировании конечными автоматами реально используемых технических устройств. (Конечно, наиболее яркие примеры – микроэлектронные устройства, от электронных часов до компьютера). Для решения задач следует перейти от модели с непрерывным временем к модели с дискретным. Можно считать n-ными (имеющими номер) те моменты времени, когда системе подаётся очередной сигнал. Также полезно понятие так называемого асинхронного автомата, функция переходов которого удовлетворяет соотношению (xx,q)=(x,q) – автомата, меняющего своё состояние только при изменении входного сигнала.

3. Смоделируйте конечным автоматом работу 4-значной железнодорожной автоблокировки. Путь двухпутной линии, предназначенный для движения в одном направлении, разделён светофорами на блок-участки – участки, на каждом из которых по требованиям безопасности не должно находиться более одного поезда. Светофор сочетанием огней показывает, сколько за ним свободных блок-участков (красный огонь – участок за светофором занят, красный и жёлтый – один, жёлтый – два, зелёный – три или более). Светофор принимает показания следующего по ходу светофора, а также определяет, занят ли блок-участок непосредственно за ним.
   

1.8. Смоделируйте конечным автоматом работу лифта.