К. Е. Карасёв Введение в теорию конечных автоматов

Вид материала

Учебное пособие

Содержание 5. Синтез схем из функциональных элементов Упражнение 4.1. Реализуйте схемой из функциональных элементов функцию f(x,y,z,t)= 6.Операции над автоматами Параллельное соединение Упражнение 6.3. Покажите, что в схеме автомата, полученного путём суперпозиции, нет ориентированных циклов. 6.7. Докажите, что существует полная относительно композиции система из одного автомата. 6.9.Постройте схемы, реализующие автоматы из задач 1.2 – 1.5.

Подобный материал:

• Виртуальная лаборатория обучения генетическому программированию для генерации управляющих, 64.24kb.
• Рабочая программа Дисциплины «Теория автоматов» Для студентов специальности 23010065, 57.28kb.
• Прикладная теория цифровых автоматов, 27.51kb.
• Джон Р. Хикс. "Стоимость и капитал", 4314.44kb.
• Царев Федор Николаевич Разработка метода совместного применения генетического программирования, 417.18kb.
• А. В. Корицкий введение в теорию человеческого капитала учебное пособие, 1340.03kb.
• Полная программа на прологе 6 Схема ответов на вопросы по результатам практических, 73.73kb.
• Курсовая работа "Синтез дискретных устройств управления", 306.46kb.
• Лекция №11 «Антивирусные программы», 55.93kb.
• Г. В. Мелихов миф. Идентичность. Знание: введение в теорию социально-антропологических, 741.74kb.

5. Синтез схем из функциональных элементов

Эта глава посвящена реализации схемами из функциональных элементов функций алгебры логики и не использует результаты теории автоматов, однако необходима для следующей главы. Определение. Схемой из функциональных элементов, реализующей набор двоичных функций, называется ориентированный граф, имеющий следующие типы вершин:

вершины-входы, из которых исходит ровно одно ребро и ни одно не входит. Они соответствуют двоичным входам автомата;

вершины-выходы, в которые входит ровно одно ребро и ни одно не исходит. Они соответствуют функциям, реализованным схемой;

узловые вершины, в которые входит одно ребро и выходит некоторое количество рёбер (но не наоборот, т.е. более одного ребра входить не может!);

вершины-функциональные элементы, каждой из которых сопоставлена некоторая функция, причём каждое входящее ребро соответствует двоичной переменной этой функции. Предполагается, что все функциональные элементы, входящие в схемы, взяты из некоторого конечного множества, называемого базисом (при этом, в отличие от обычного понятия базиса, не требуется его неизбыточность). Мы будем рассматривать в основном базис, состоящий из дизъюнктора, конъюнктора и инвертера – функциональных элементов, соответствующих дизъюнкции, конъюнкции и отрицанию. Ввиду симметричности дизъюнкции и конъюнкции, мы не будем помечать рёбра, входящие в функциональные элементы, именами переменных функций.

Если функцию можно записать формулой в некотором базисе, то её можно реализовать схемой в базисе из соответствующих функциональных элементов; однако вполне возможно, что в схеме будет меньше элементов, чем функциональных символов в наиболее простой формуле.


Упражнение 4.1. Реализуйте схемой из функциональных элементов функцию f(x,y,z,t)=.


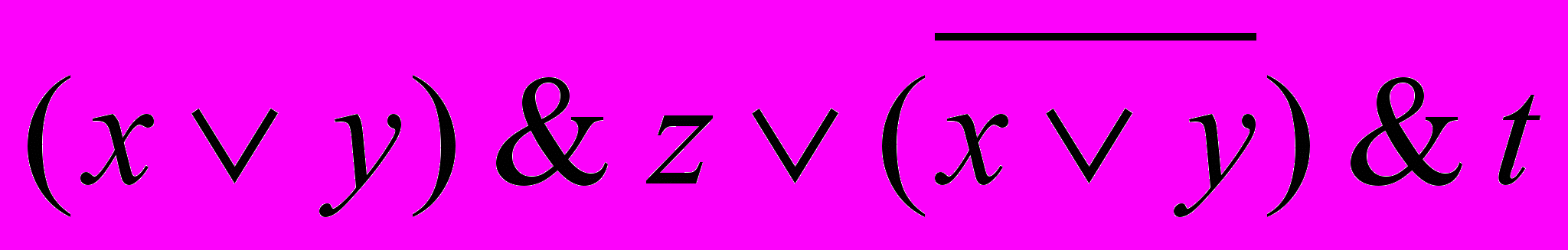В схеме будет 5 элементов – против 6 функциональных символов в формуле.

Обозначим L(f) минимальную сложность схемы, реализующей функцию f, в стандартном базисе, и L(n) – максимальное значение функции L(f) для всех функций f от n переменных. Функция L(n) называется функцией Шеннона.

Теорема. Функция L(n) имеет асимптотический порядок роста 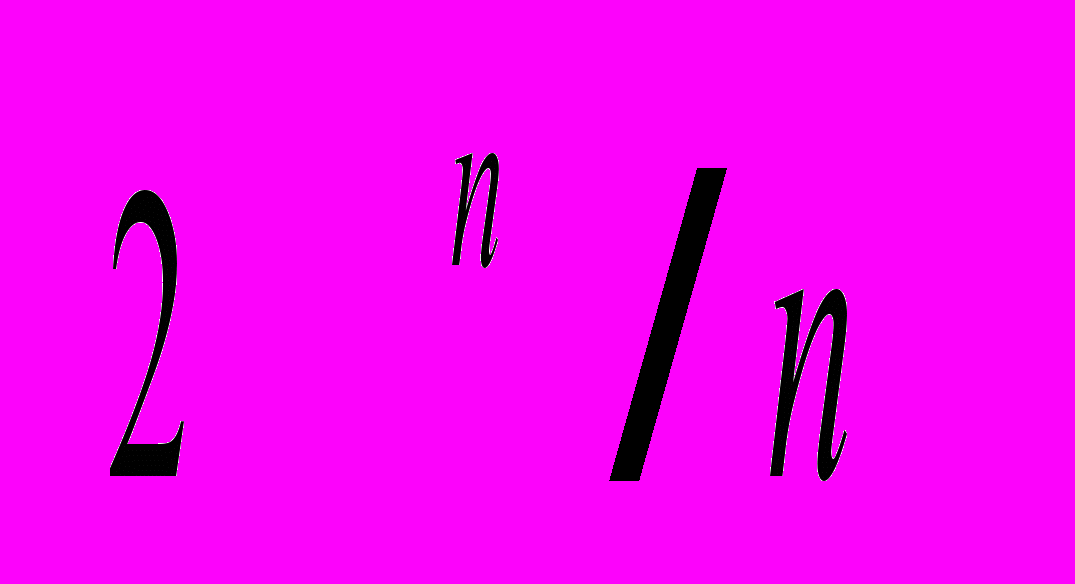. Это означает, что любую функцию можно реализовать схемой сложности не более С*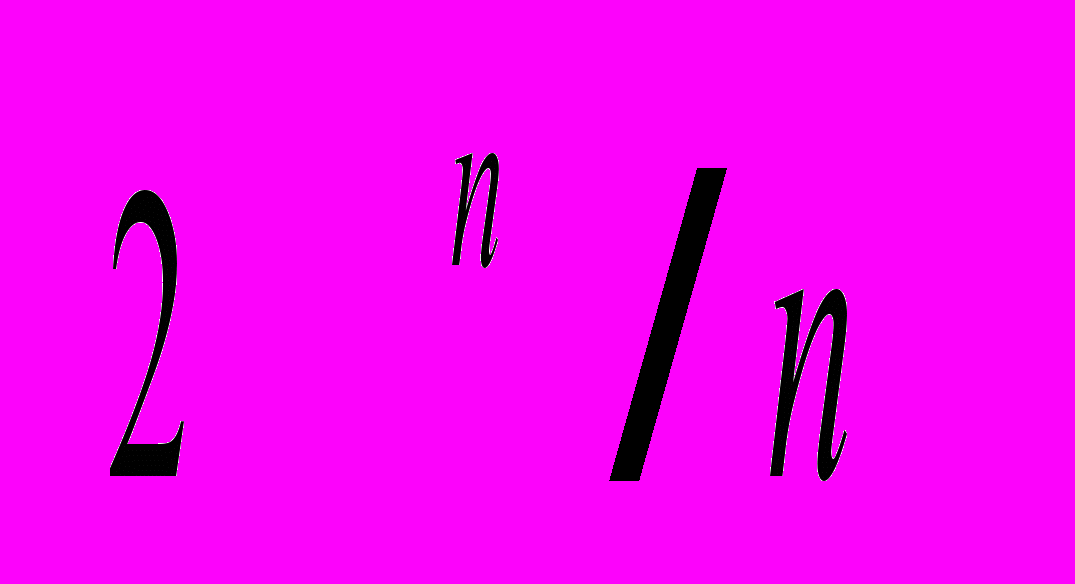, где можно взять C=8 для всех функций и всё меньшее C для функций от достаточно большого числа переменных.


Упражнение 5.1. Реализуйте одной схемой все функции от 2 (3, 4, n…) переменных. Оцените сложность схемы.


Удобный способ реализации функций алгебры логики СФЭ основан на следующей идее. Набор переменных функции разделяется на две части, функция f (x₁,x₂,…x_k,y₁,y₂,…y_n) представляется в виде

f=

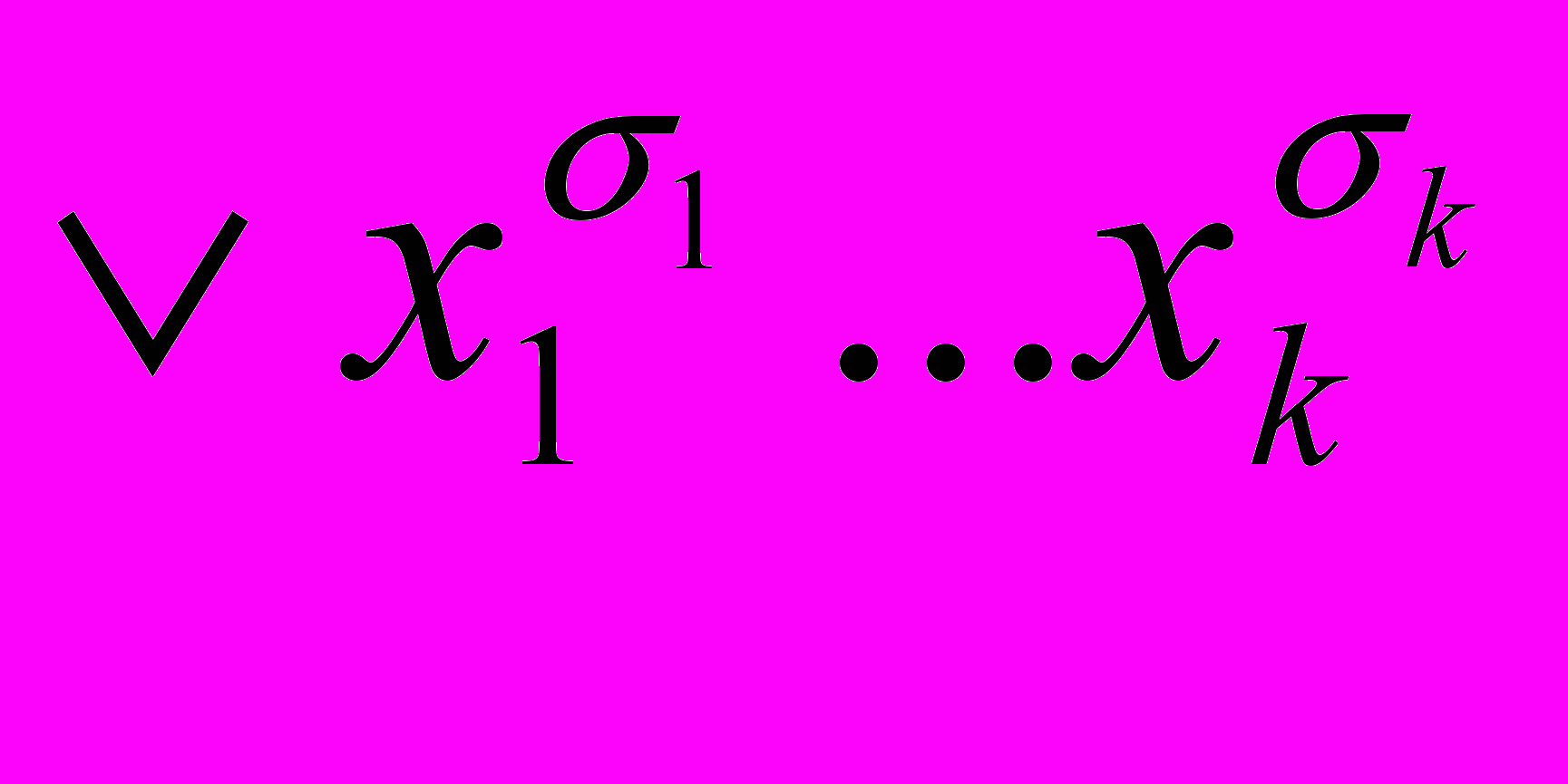
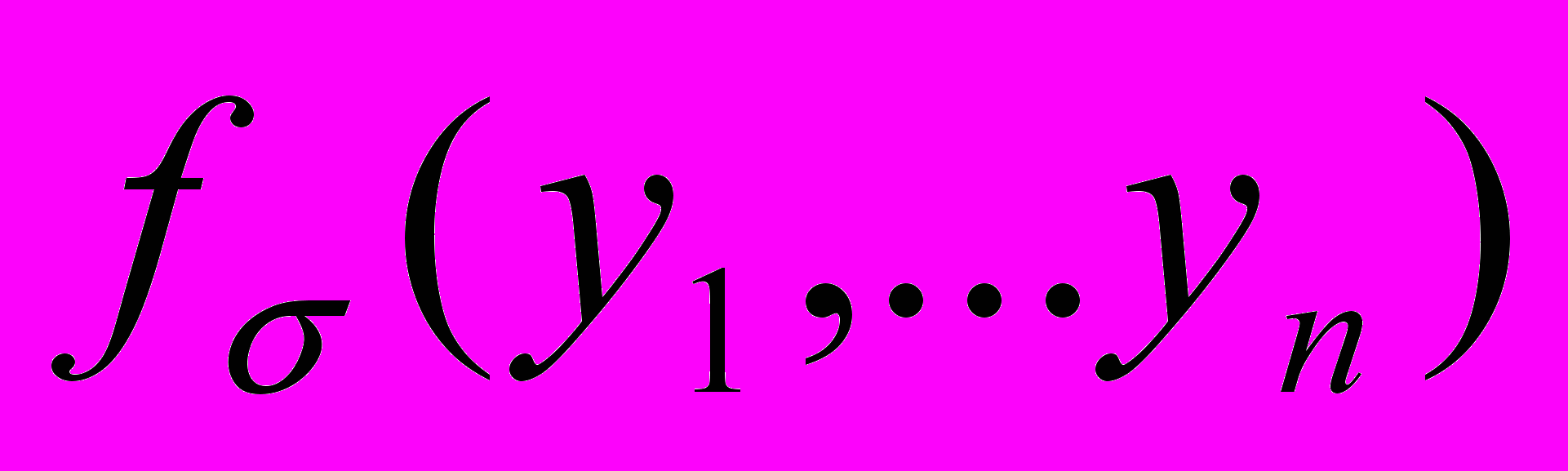
причём число различных функций 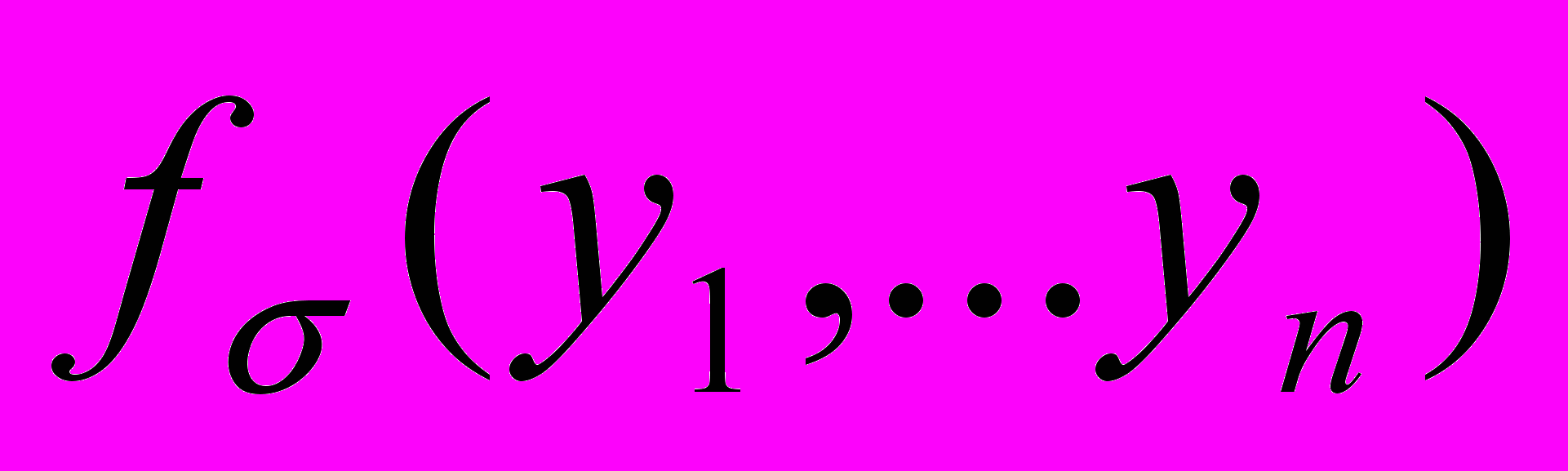относительно мало, и схема, реализующая функцию f cостоит из схемы, реализующей все функции 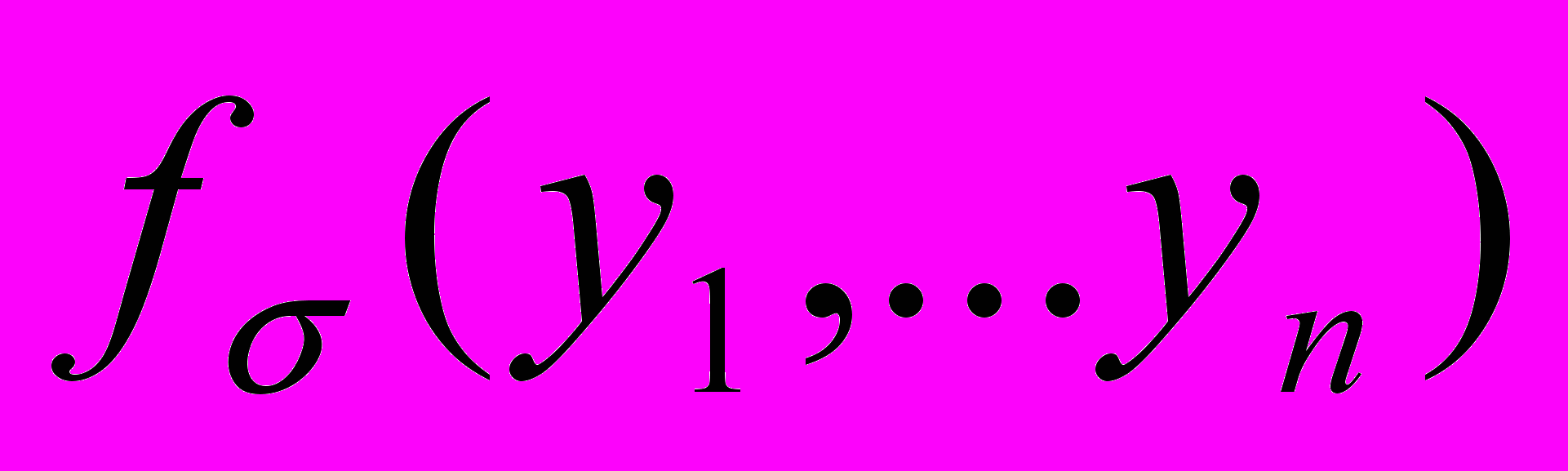, k инвертеров и соответствующего числа дизъюнкторов и конъюнкторов.


Упражнение 5.2. Возьмите произвольный двоичный вектор из 16 компонент и реализуйте соответствующую ему функцию от 4 переменных схемой.

6.Операции над автоматами

В этой главе мы рассмотрим, как автоматы соединяются между собой, рассмотрим задачу о синтезе автомата – построении его из некоторого набора автоматов путём определённых операций.

Чтобы автоматы можно было соединять между собой, следует ограничить множество автоматов так, чтобы рассматриваемые автоматы были «совместимы».

Определение. Назовём автомат двоичным, если его входной и выходной алфавит есть декартова степень (декартово произведение нескольких экземпляров) множества E={0,1}, то есть множество двоичных векторов.

На самом деле класс двоичных автоматов достаточно универсален. Утверждение. Любой автомат изоморфен некоторому двоичному автомату.

Доказательство. Пусть дан автомат (A, Q, B, , , q₀). Возьмём числа k и l, такие, что 2^k≥|A| и 2^l≥|B|. Существуют инъективные отображения f:A→E^k и g:B→E^l, называемые кодированиями входного и выходного алфавита соответственно. Отображение, обратное к f, будет биекцией, определённой на f(A) - части E^k; доопределим его как-нибудь на остальной части E^k, получив таким образом отображение f^-1 из E^k на A. Рассмотрим двоичный автомат (E^k, Q, E^l, ', ', q₀) c функциями переходов и выходов:

'(x,q)=(f^-1(x ),q),

'(x,q)=g((f^-1(x ),q)).

Здесь x=(x₁,...x_k ) - входной символ двоичного автомата, из алфавита E^k.. Мы видим, что при вводе в автомат этот символ «декодируется» отображением f^-1, а выходной символ «кодируется» отображением g. Легко видеть, что этот автомат будет изоморфен исходному.

Если у двоичного автомата входной алфавит и выходной алфавит, будем говорить, что автомат имеет k двоичных входов и l двоичных выходов. Соответствующие входы и выходы на схемах обозначаются стрелками, входящими/выходящими в прямоугольник (или другую фигуру), обозначающую автомат.

Для того, чтобы строго определить, что есть соединение автоматов, введём следующие операции над двоичными автоматами:

1. Операция добавления фиктивного входа. Автомат (E^k, Q, E^l, , , q₀) при добавлении (k+1)-го фиктивного входа преобразуется в автомат (E^k+1, Q, E^l-1, ', , q₀), где
   '((x₁,...x_k+1),q)=((x₁,...x_k ),q). Аналогично вводится операция добавления фиктивного входа под любым другим номером.
   
2. Операция удаления фиктивного входа. Пусть i-тый вход автомата фиктивен, то есть функции переходов и выходов не зависят существенно от компоненты x_i входного вектора x. Тогда можно преобразовать данный автомат в автомат(E^k-1, Q, E^l, ', ', q₀) с функцией переходов '((x₁,...x_i-1,x_i+1, ,.._.x_k, ),q)=((x₁,...x_k ),q) и аналогично изменённой функцией выходов.
   
3. Операция удаления выхода. Автомат (E^k, Q, E^l, , , q₀) при удалении i-го выхода преобразуется в автомат (E^k, Q, E^l-1, , ', q₀), где '(q,x)=(y₁,...y_i-1,y_i+1, ,..._.y_k, ), если '(q,x)=(y₁,...y_i-1,y_i,y_i+1, ,..._.y_k, ).
   
4. Операция склеивания (отождествления) входов. Автомат (E^k, Q, E^l, , , q₀) при склеивании i-го и j-го выхода преобразуется в автомат (E^k-1, Q, E^l, ', ', q₀), с функцией переходов
   '((x₁,...x_i-1,x_i+1,,..,x_j,..._.x_k, ),q)=(x₁,...x_i-1,x_j,x_i+1,,..,x_i-1,x_i,x_i+1,..._.x_k, ),q)
   (на место i-го входа подставляется j-й) и аналогично изменённой функцией выходов.
   
5. Параллельное соединение автоматов. Рассмотрим автоматы A₁=(E^k, Q₂, E^l, ₁, ₁, q₁) и A₂=(E^m, Q₂, Eⁿ, ₂, ₂, q₂). Параллельное соединение автоматов – автомат A₃=(E^k+m, Q₁×Q₂, E^l+n, , , q) с функциями переходов и выходов:
   ((x₁,x₂),(q₁,q₂))=(₁(x₁,q₁),₂(x₂,q₂)),
   ((x₁,x₂),(q₁,q₂))=(₁(x₁,q₁),₂(x₂,q₂))
   и начальным состоянием q=(q₁,q₂). (Здесь под x₁ и x₂ понимаются не компоненты одного двоичного вектора, а два вектора – один размерности k, второй размерности m. Аналогично (x₁,x₂) – это двоичный вектор размерности k+m.
   
6. Последовательное соединение автоматов. Рассмотрим автоматы A₁=(E^k, Q₂, E^l, ₁, ₁, q₁) и A₂=(E^k, Q₂, E^l, ₂, ₂, q₂). Соединим i-тый выход первого автомата с j-тым входом второго. Получится автомат A₄=(E^k+m-1, Q₁×Q₂, E^l+n, , , q) со следующими функциями переходов и выходов:
   ((x₁,z₂),(q₁,q₂))=(₁(x₁,q₁),₂(u₂,q₂)),
   ((x₁,z₂),(q₁,q₂))=(₁(x₁,q₁),₂(u₂,q₂)).
   Здесь z₂ – вектор размерности m-1 , представляющий собой x₂ с изъятой j-той компонентой, u₂ - вектор x₂, в котором j-тая компонента заменена на i-тую компоненту вектора ₁(x₁,q₁). Аналогично можно соединить большее число выходов с таким же количеством входов, это также будет операцией 6; в частности, при соединении 0 выходов и входов операция аналогична операции 7.
   
7. Операция обратной связи. Скажем, что j-тый вход автомата A₁=(E^k, Q₂, E^l, , , q₁) зависит с задержкой от i-го входа, если j-тая компонента функции (x,q) не зависит существенно от i-той компоненты вектора x. Тогда можно построить автомат A₅=(E^k-1, Q₂, E^l, ', ', q₁) с функциями переходов и выходов '(z,q)=(u,q), '(z,q)=(u,q), где z – вектор размерности m-1 , представляющий собой x с изъятой j-той компонентой, u - вектор x, в котором j-тая компонента заменена на i-тую компоненту вектора '(z,q). Таким образом, эта операция – своеобразное последовательное соединение автомата с самим собой.
   
8. 
   

Упражнение 6.1. Покажите, что операция 6 сводится к операциям 5 и 7.

Упражнение* 6.2. Покажите, что операция последовательного соединения с автоматом, имеющим одно состояние, приводит к автомату, гомоморфному данному.


Определение. Операции 1-6 в совокупности называются операциями суперпозиции автоматов, операции 1-7 – операциями композиции. Множество функций, получаемых из функций данного множества M операциями суперпозиции (в том числе и конечным числом последовательно применяемых операций) будем называть замыканием множества M относительно оператора суперпозиции  и обозначать (M). Множество функций, получаемых из функций данного множества M операциями композиции (также в любом числе) будем называть замыканием множества M относительно оператора композиции  и обозначать (M).

Подобно булевым функциям, процесс построения автоматов путём композиции или суперпозиции можно изображать схемами.

Определение. Схемой автомата называется ориентированный граф со следующими видами вершин:

вершины-входы, из которых исходит ровно одно ребро и ни одно не входит. Они соответствую двоичным входам автомата;

вершины-выходы, в которые входит ровно одно ребро и ни одно не исходит. Они соответствую двоичным выходам автомата ;

узловые вершины, в которые входит одно ребро и выходит некоторое количество рёбер (но не наоборот, т.е. более одного ребра входить не может!);

вершины-автоматы, каждой из которых сопоставлен некоторый двоичный автомат, причём каждое входящее ребро соответствует двоичной компоненте входного вектора, а каждое исходящее – выходного.

Операциям над автоматами очевидным образом ставятся в соответствие операции над схемами: удаление выхода – удаление вершины-выхода и ведущего к ней ребра, склеивание входов – добавление узловой вершины и перенаправление входившего ребра в узловую вершину, из которой два ребра ведут к склеиваемым входам и так далее.


Упражнение 6.3. Покажите, что в схеме автомата, полученного путём суперпозиции, нет ориентированных циклов.

Очевидно, для любого множества M справедливо M⊆(M)⊆(M). Однако существуют множества M, для которых включение (M)⊆(M) нестрогое, поэтому добавление операции обратной связи существенно. Назовём множество автоматов полным относительно данного оператора замыкания (K или ), если для любого автомата существует автомат в замыкании данного множества относительно данного оператора, изоморфный этому автомату.

Теорема. 1.Никакая конечная система автоматов не может быть полной относительно оператора  . 2. Существует конечная система автоматов, полная относительно оператора K.

Доказательство(2). Начнём строить автоматы путём операций композиции из некоторого множества автоматов с рассмотрения автоматов с одним состоянием (без памяти). Выход такого автомата зависит только от входа в данный момент времени; таким образом, значение на каждом двоичном выходе автомата – булева функция от значений на входах автомата; двоичные автоматы без памяти и булевы операторы – в сущности одно и то же. Операция подстановки для булевых функций эквивалентна операции последовательного соединения для соответствующих автоматов; следовательно, если данную функцию или оператор можно реализовать схемой в данной системе функций, то соответствующий автомат является суперпозицией автоматов, соответствующих функциям данной системы.

Построим конечную систему автоматов, полную относительно операций композиции. Назовём задержкой (с нулевым начальным состоянием) следующий автомат:





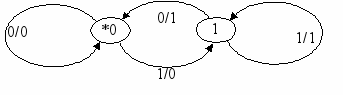
Поведение задержки описывается соотношениями y(t+1)=x(t), y(0)=0.


Упражнение 6.4. Выпишите уравнение поведения а) двух последовательно соединённых задержек; б) n последовательно соединённых задержек. Постройте диаграмму Мура для двух последовательно соединённых задержек.


Системой автоматов, полной относительно композиции будет множество, состоящее из задержки и системы автоматов с одним состоянием, соответствующим функциям какой-либо полной системы булевых функций (например, конъюнкции, дизъюнкции и отрицания).

Пусть дан некоторый двоичный автомат. Ниже приводится примерное описание процесса построения эквивалентного ему автомат из задержек и элементов базиса путём наших операций.

1. Закодируем множество состояний автомата двоичными векторами (аналогично кодированию входного и выходного алфавитов в первой теореме главы). Будем считать, что состояние автомата есть двоичный вектор; наложим также ограничение, что начальное состояние автомата кодируется нулевым вектором. Если число состояний не является степенью 2, то двоичные вектора, не входящие в образ кодирующего отображения, являются недостижимыми состояниями;
   
2. Поскольку состояния автомата, входные и выходные векторы есть двоичные вектора, функции переходов и выходов – булевы операторы. Реализуем их схемой в данной нами полной системе булевых функций.
   
3. Возьмём батарею задержек - параллельно соединённые задержки в количестве, равном числу компонент состояния автомата. Очевидно, батарея также описывается уравнениями y(t+1)=x(t), y(0)=0, где x и y теперь обозначают двоичные вектора.
   
4. Соединим оператор, реализующий функцию переходов, последовательно с батареей задержек (по всем выходам в соответствующем порядке). Применим операцию обратной связи к полученному автомату по выходам батареи и входам, соответствующим вектору состояния.
   
5. Соединим полученный автомат последовательно с автоматом, реализующим функцию выходов (по выходам батареи и входам, соответствующим вектору состояния). Применим операцию обратной связи аналогичным путём. Склеим входы автомата, соответствующие одним и тем же компонентам. Удалим выходы, идущие непосредственно из задержек.
   

П
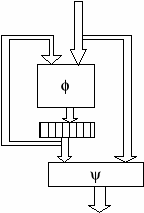
олученная схема автомата выглядит следующим образом:


Широкими стрелками здесь обозначены группы стрелок в числе, равном числу соответствующих входов и выходов, прямоугольниками с символами f и y – схемы, реализующие функции переходов и выходов соответственно, прямоугольником с вертикальной штриховкой – батарея задержек.

Поскольку автоматы, реализующие двоичные операторы – автоматы с одним состоянием, в сущности состоянием автомата на схеме будет состояние батареи задержек. Соответствие уравнений переходов уравнениям данного автомата проверяется достаточно очевидно. Следовательно данный автомат – автомат с требуемым поведением, эквивалентный исходному.


6.5. Покажите, что в этом автомате любой ориентированный цикл проходит через задержку.

6.6. Пользуясь результатами предыдущей главы, постройте верхнюю оценку для числа элементов схемы автомата (где в качестве полной системы берётся система из конъюнкции, дизъюнкции и отрицания) в зависимости от числа состояний, размерности входного и выходного алфавитов

6.7. Докажите, что существует полная относительно композиции система из одного автомата.

6.8.Докажите, что в полной относительно композиции системе автоматов существует полная относительно композиции конечная подсистема.

6.9.Постройте схемы, реализующие автоматы из задач 1.2 – 1.5.

6.10.Постройте схему, реализующую автомат A₀ из задачи 3.4 при i=0.

Постройте схему при n=2^p, p-целое, имеющую не более O(p) элементов.