Geum.ru

К. Е. Карасёв Введение в теорию конечных автоматов

Вид материалаУчебное пособие

Содержание


7. Алгебра разбиений множества состояний. Декомпозиция автомата.
Упражнение* 7.2. Покажите, что произведение разбиений - наибольшее разбиение, не меньшее каждого из них.
Следствия из теоремы.
Подобный материал:
1   2   3   4   5   6   7

7. Алгебра разбиений множества состояний. Декомпозиция автомата.


Важным этапом в реализации автомата схемой является выбор кодирования состояний – соотношения между состояниями автомата и двоичными векторами – наборами значений двоичных переменных состояния. Описанный ниже аппарат алгебры разбиений множества состояний автомата помогает найти более оптимальное кодирование состояний – то, при котором можно построить схему автомата с меньшим числом элементов. Это упрощение достигается уменьшением числа существенных переменных функций, стоящих в правых частях уравнений переходов.

Рассмотрим разбиение множества состояний автомата Q, то есть набор блоков Б1, Б2 … Бk – подмножеств множества Q, непустых, попарно непересекающихся и в объединении дающих всё множество Q. В данной главе состояний автоматов обычно будут обозначаться цифрами, а разбиения будут обозначаться перечислением блоков: например, {1,2}{3,4}{5} – разбиение множества из 5 состояний автомата.

Определение. Говорят, что разбиения 1 и 2 образуют пару разбиений, если из того, что состояния q1 и q2 принадлежат одному блоку разбиения 1, следует, что для любого входного символа a состояния (a,q1) и (a,q2) принадлежат одному блоку разбиения 2. Иными словами, образ любого блока первого разбиения при действии функции переходов лежит целиком в одном из блоков второго разбиения. Обозначать это также будем: (1,2) – пара разбиений. (Следует обратить внимание, что не всякие два разбиения образуют пару).

Определение. Говорят, что разбиение множества состояний есть разбиение со свойством подстановки (сокращённо с.п.), если оно образует пару само с собой.

Пример. Обозначим 1 разбиение, имеющее один блок – всё множество состояний автомата; обозначим 0 разбиение, в каждом блоке которого содержится только одно состояние. Тогда для любого разбиения (0,) и (,1) – пары разбиений; в частности, 0 и 1 – с.-п. разбиения. Пары разбиений и с.-п. разбиения, не упомянутые в этом примере, мы будем называть нетривиальными.

В дальнейшем нам понадобятся некоторые алгебраические действия над разбиениями.

Определение. Говорят, что разбиение 1 не больше разбиения , если каждый блок разбиения 1 является подмножеством блока . Обозначение: 1≤Так на множестве разбиений вводится отношение частичного порядка.

Для любого разбиения справедливо 0≤≤1.

Определение. Произведением двух разбиений называется разбиение, состоящее из всех попарных пересечений блоков первого и второго разбиения. Обозначение: 1∙ .Аналогично определяется произведение трёх и более разбиений.

Определение. Суммой двух (или более) разбиений называется наименьшее разбиение, не меньшее каждого из них. Обозначение суммы двух разбиений: 1+.


Упражнение 7.1. Пусть – разбиение. Чему равны +, ∙, +, ∙0, +, ∙1? Монотонны ли функции суммы и произведения (относительно введённого порядка)? *Справедлив ли дистрибутивный закон?

Упражнение* 7.2. Покажите, что произведение разбиений - наибольшее разбиение, не меньшее каждого из них.


Пусть состояния автомата кодируются набором переменных q1 q2 … qk. Скажем, что группа переменных (в частности, это может быть одна переменная) соответствует данному разбиению множества состояний, если значение этой группы переменных для данного состояния есть номер блока разбиения, в котором это состояние лежит. При синтезе автомата происходит обратный процесс – разбиениям автомата ставятся в соответствии переменные, которые впоследствие образуют полный набор для кодирования состояний. (Если попытаться строго определить, что такое переменная состояния, независимо от всего способа кодирования, получится, что переменная есть разбиение (из двух блоков, если переменная двоичная), и наоборот).

Утверждение. Объединению двух групп переменных соответствует произведение соответствующих разбиений. Пересечению двух групп переменных соответствует сумма соответствующих разбиений.

Утверждение. Произведения состояний, которым соответствуют переменные, кодирующие состояния автомата (группы из одной переменной), образуют в произведении разбиение 0. Обратно, пусть существует набор разбиений автомата, образующих в произведении разбиение 0. Тогда все группы переменных, соответствующие данным разбиениям, образуют полный набор переменных, кодирующих состояния.

Теорема. («Неравенство потока информации») Если два разбиения множества состояний автомата образуют пару, то группа переменных, соответствующая второму разбиению в следующий момент времени, зависит только от входа автомата и от группы переменных, соответствующих второму разбиению.

Пример. Рассмотрим автомат со следующей таблицей переходов:

q(t)
,q(t))
1,q(t))

1
1
2

2
3
4

3
2
1

4
4
3

Для этого автомата справедливо:
  • разбиение {1,4}{2,3} – с.п.-разбиение;
  • разбиения 1 ={1,2}{3,4} и ={1,3}{2,4} образуют пару;
  • разбиения и 1 (в другом порядке) также образуют пару.

Для реализации автомата схемой удобно воспользоваться двумя последними утверждениями. Введём кодирование состояний таким образом, чтобы разбиению i соответствовала переменная qi:

q
1
2
3
4

q1
0
0
1
1

q
0
1
0
1

С учётом кодирования, можно представить уравнения переходов автомата в двоичном виде:


Мы видим, что благодаря найденным парам разбиений система уравнений получилась довольно простой.


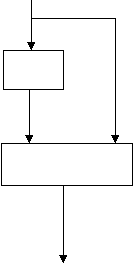
Следствия из теоремы. 1. Если существует нетривиальное с.п.-разбиение множества состояний автомата, то автомат можно представить как суперпозицию двух автоматов в следующем виде:

Здесь верхний автомат, хранит группу переменных, соответствующую с.п.-разбиению, а нижний автомат – остальные переменные. Из теоремы следует, что состояния верхнего автомата не зависят от состояний (и вывода) нижнего, поэтому такое представление возможно. Оно называется последовательной декомпозицией автомата. В силу нетривиальности разбиения оба автомата имеют более 1 состояния, т.е сами нетривиальны.

2.Если существуют два нетривиальных с.-п. разбиения, произведения которых равны 0, автомат можно представить в следующем виде:





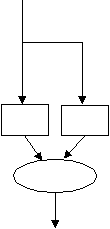
Здесь эллипсом внизу обозначен автомат с одним состоянием. Это представление называется параллельной декомпозицией автомата.

Упражнение. Найдите пары разбиений и основанные на них, по возможности более оптимальные схемы для следующих автоматов, заданных таблицами переходов:

7.3.

q(t)
,q(t))
1,q(t))
2,q(t))

1
6
1
3

2
5
1
4

3
4
1
5

4
3
2
6

5
2
3
5

6
1
4
6



7.4.


q(t)
,q(t))
1,q(t))
2,q(t))
2,q(t))

1
3
1
4
2

2
1
5
4
2

3
3
4
4
5

4
5
1
4
2

5
5
4
3
5