К. Е. Карасёв Введение в теорию конечных автоматов

Вид материала

Учебное пособие

Содержание 2.Отношения эквивалентности автоматов и их состояний Неотличимость состояний Эквивалентное определение. Упражнение 2.3. Приведите пример такой пары автоматов. 3.Стохастические функции конечных автоматов 3.2. Посчитайте стохастическую функцию автомата с диаграммой Мура следующего вида 3.3.Найдите стохастические функции автоматов из упражнений 1.2-1.6.

Подобный материал:

• Виртуальная лаборатория обучения генетическому программированию для генерации управляющих, 64.24kb.
• Рабочая программа Дисциплины «Теория автоматов» Для студентов специальности 23010065, 57.28kb.
• Прикладная теория цифровых автоматов, 27.51kb.
• Джон Р. Хикс. "Стоимость и капитал", 4314.44kb.
• Царев Федор Николаевич Разработка метода совместного применения генетического программирования, 417.18kb.
• А. В. Корицкий введение в теорию человеческого капитала учебное пособие, 1340.03kb.
• Полная программа на прологе 6 Схема ответов на вопросы по результатам практических, 73.73kb.
• Курсовая работа "Синтез дискретных устройств управления", 306.46kb.
• Лекция №11 «Антивирусные программы», 55.93kb.
• Г. В. Мелихов миф. Идентичность. Знание: введение в теорию социально-антропологических, 741.74kb.

2.Отношения эквивалентности автоматов и их состояний

Уравнения переходов, диаграммы Мура или таблицы функций переходов и выходов однозначно задают поведение автомата; обратное может быть неверно. В связи с этим для автоматов и их состояний вводятся различные отношения эквивалентности.

Рассмотрим вначале несколько полезных определений.

Состояние автомата называется достижимым (из начального состояния), если существует слово, переводящее автомат из начального состояния в данное. Очевидно, поведение автомата не изменится, если из множества его состояний убрать все недостижимые состояния и соответственно сократить область определения функций переходов и выходов.

Автомат называется связным, если все его состояния достижимы, и сильно связным, если при этом любое состояние достижимо из другого.

Неотличимость состояний. Два состояния автомата называются неотличимыми, если не существует слова, различающего эти состояния, то есть слова, которое при вводе в данный автомат, находящийся в одном или другом состоянии вызывает вывод автоматом разных слов. Неотличимым состояниям соответствует одна и та же остаточная функция о.-д. функции, вычисляемой автоматом.

Справедлива следующая теорема Мура: если два состояния автомата отличимы, то существует слово длины не более |Q|-1, различающее эти состояния, где |Q| - число состояний автомата.


Упражнение 2.1. Приведите пример автомата с числом состояний не менее 4, для которого любые два состояния а) различаются словом длины 1; б) различаются словом длины не менее 2, причём какие-то два не различаются словом длины 1.

Упражнение 2.2. Приведите пример автомата, для которого эта оценка достигается, то есть существуют два отличимых состояния, не различаемые словом длины меньшей, чем |Q|-1.

Обобщением неотличимых состояний одного автомата являются неотличимые состояния двух автоматов. Два состояния двух автоматов называются неотличимыми, если не существует слова, различающего эти состояния, то есть слова, которое при вводе в первый автомат, находящийся в первом состоянии и второй автомат, находящийся во втором состоянии вызывает вывод автоматом разных слов.

Определение. Назовём два автомата эквивалентными, если они имеют одинаковое поведение, то есть вычисляют одну и ту же о.-д. функцию.

Эквивалентное определение. Два автомата эквивалентны, если их начальные состояния неотличимы друг от друга.

Определение Скажем, что автомат является автоматом приведённого вида, если все его состояния достижимы и попарно отличимы.

Для любого автомата существует эквивалентный ему автомат приведённого вида. Однако приведённый вид не ещё задаёт автомат однозначно: существуют эквивалентные автоматы приведённого вида с разным числом состояний.


Упражнение 2.3. Приведите пример такой пары автоматов.

(Решение можно получить из нижеприведённых соображений).


У автоматов существует приведённый вид с более однозначно определённым набором состояний. В этом виде функция переходов имеет вид (x,q)=((x,q)), где  – некоторая функция, то есть вывод автомата в данный момент времени зависит от состояния, в которое он переходит. В самом деле, рассмотрим произвольный автомат, состояния которого - пары вида (q,y), где q – достижимое состояние исходного автомата, а y – одно из значений функции (x,q') для тех пар (x,q') при, которых (x,q')=q. В качестве начального состояния можно взять какую-либо пару (x,q₀), где q₀ – начальное состояние исходного автомата. Преобразованная функция переходов будут иметь вид '(x,(q,y))=('(x,q),'(x,q)), функция  имеет вид (q,y)=y.

В диаграмме Мура таких автоматов в круге, изображающем состояние, обычно пишут символ, выводимый автоматом, когда он в это состояние переходит.


Упражнение 2.4. Приведите автоматы, построенные в упражнениях 1.2 -1.5 к вышеуказанному виду.

3.Стохастические функции конечных автоматов

Понятие конечного автомата связано с понятием цепи Маркова, также моделирующим объект с несколькими состояниями в дискретном времени (Существует также понятие вероятностного автомата, для которого входной символ задаёт набор вероятностей перехода автомата в другие состояния – обобщение как конечного автомата, так и цепи Маркова).

Пусть задан сильно связный (см. определение в следующей главе) автомат с входным и выходным алфавитом {0,1}, и на его вход подаётся случайная последовательность символов. Подобная система из генератора случайных чисел и конечного автомата меняет свои состояния по законам цепи Маркова. Функция f(p), выражающая зависимость частоты появления единицы в выходной последовательности символов от входной (при длине входного слова, стремящейся к бесконечности) называется стохастической функцией автомата. Она определяется по стационарному распределению соответствующей цепи Маркова.

Теорема. 1)Стохастическая функция любого конечного автомата равна частному двух многочленов с целыми коэффициентами.

2) Пусть функция f(x) определена на интервале (0,1), на этом интервале принимает значения из отрезка [0,1] (причём если эта функция где-либо принимает значения 0 или 1, то она – константа) и представима в виде частного двух многочленов с целыми коэффициентами, второй из которых – знаменатель – больше 0 на всём интервале (0,1). Тогда существует конечный автомат, для которого f(x) – стохастическая функция.


3.1. Постройте автомат со стохастической функцией, равной а) ½ б) x/2.


Для расчёта стохастической функции автомата следует сделать следующее:

1.Обозначить состояния числами от 1 до n.

1. Построить матрицу А(x) размерности nXn, На пересечении i-го столбца и j-той строки должно быть:

• 1, если автомат переходит из состояния i в состояние j безусловно;
  
• x, если автомат переходит из состояния i в состояние j при вводе 1;
  
• 1-x, если автомат переходит из состояния i в состояние j при вводе 0;
  
• 0 в остальных случаях.
  

2. Решить линейную систему уравнений Ay=y (другими словами, найти собственный вектор, соответствующий собственному значению 1) при условии, что сумма координат вектора y будет равна 1. Этот вектор будет задавать стационарное распределение вероятности в соответствующей цепи Маркова.
   
3. Стохастическая функция будет иметь вид
   

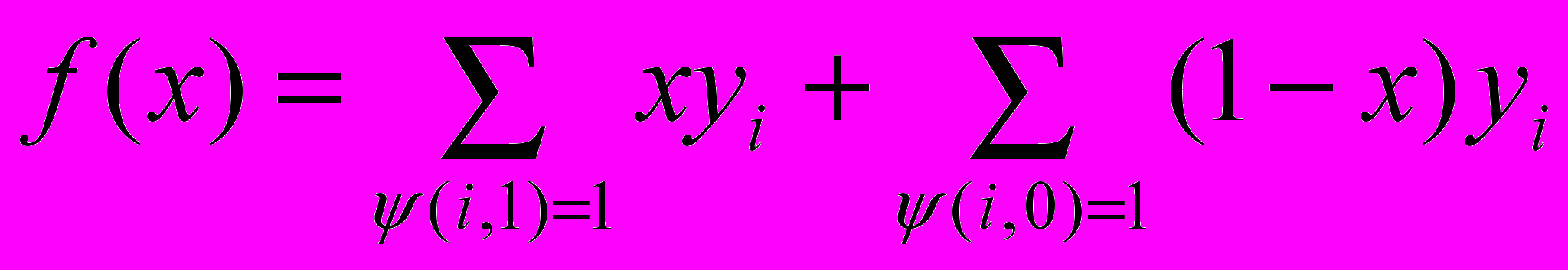
Здесь суммирование ведётся по тем состояниям, в которых автомат выводит 1 при вводе 1 (первая сумма) или при вводе 2 (вторая сумма).


3.2. Посчитайте стохастическую функцию автомата с диаграммой Мура следующего вида:






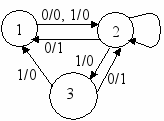
Решение. Матрица переходов в соответствующей цепи Маркова примет вид:



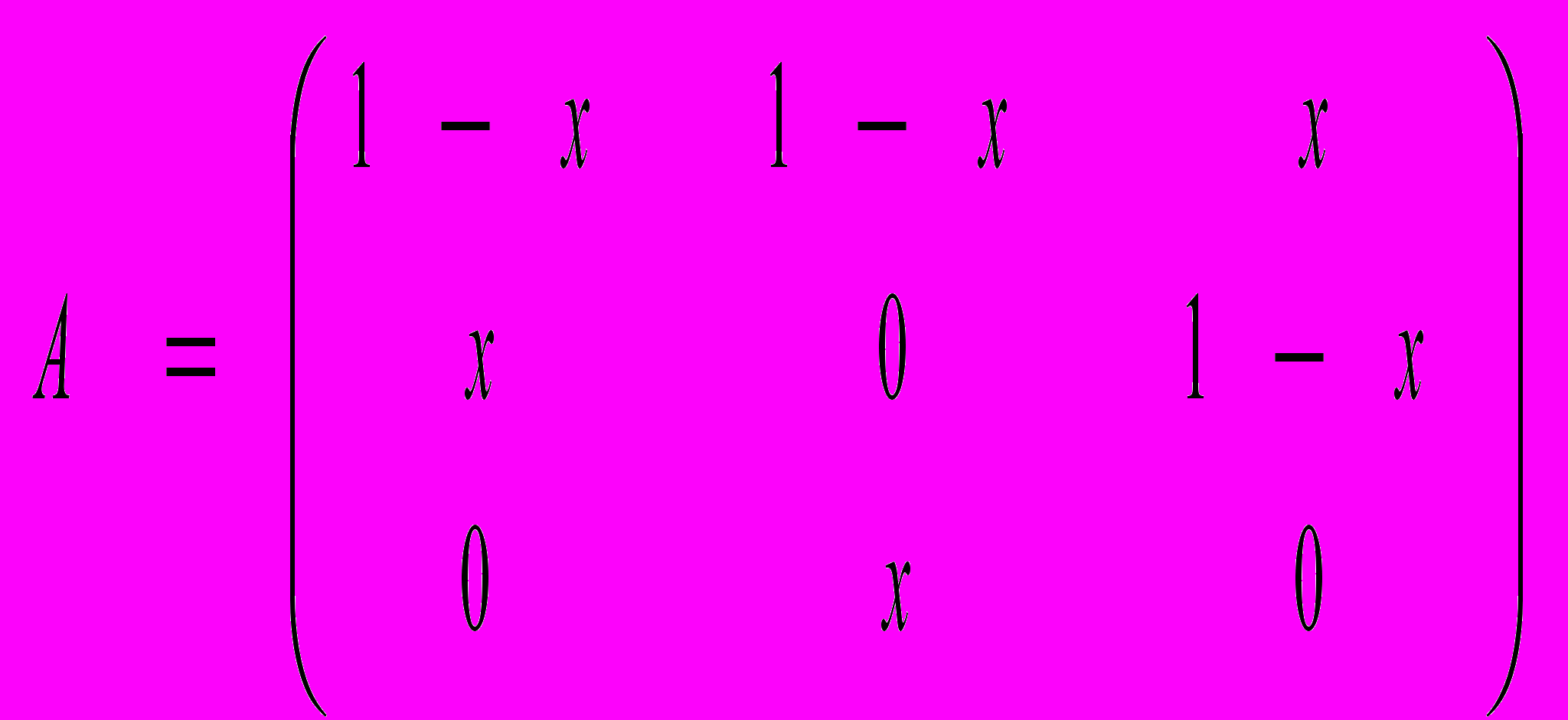
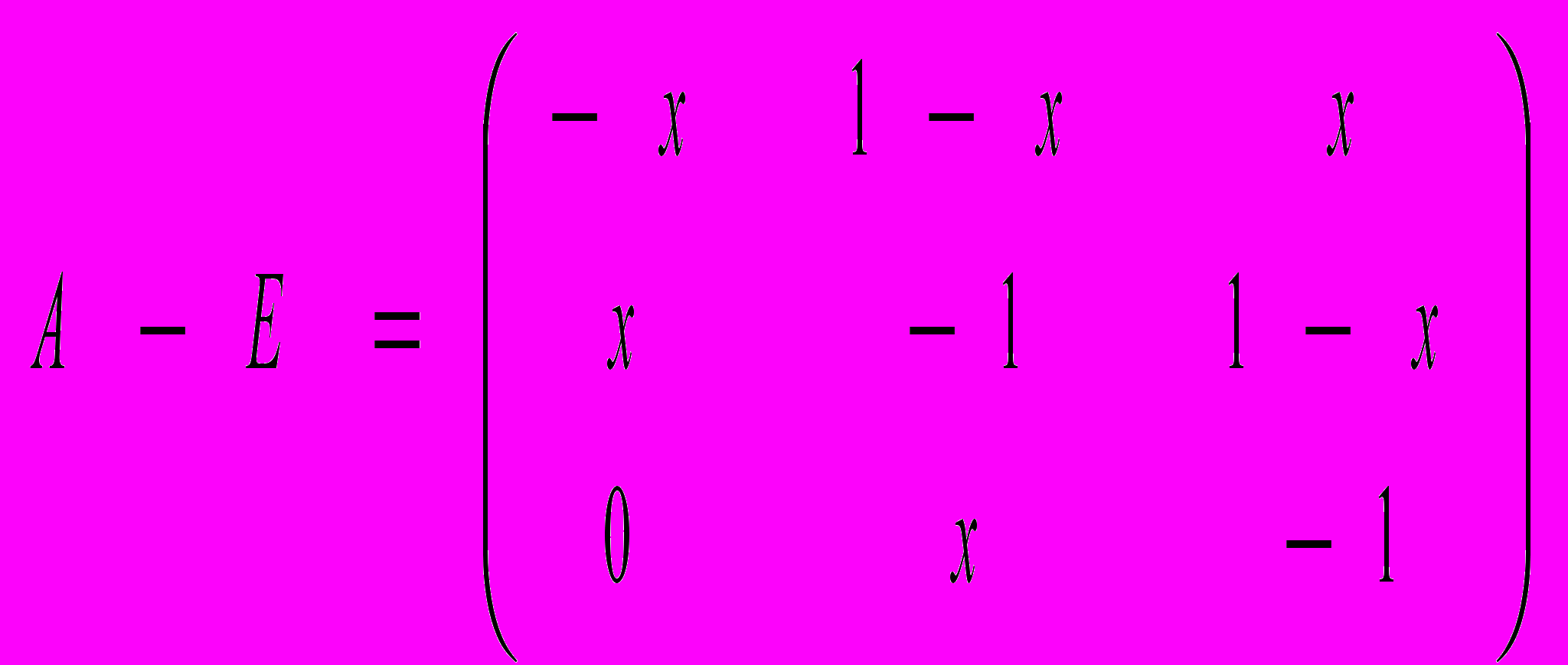
Решим систему уравнений:



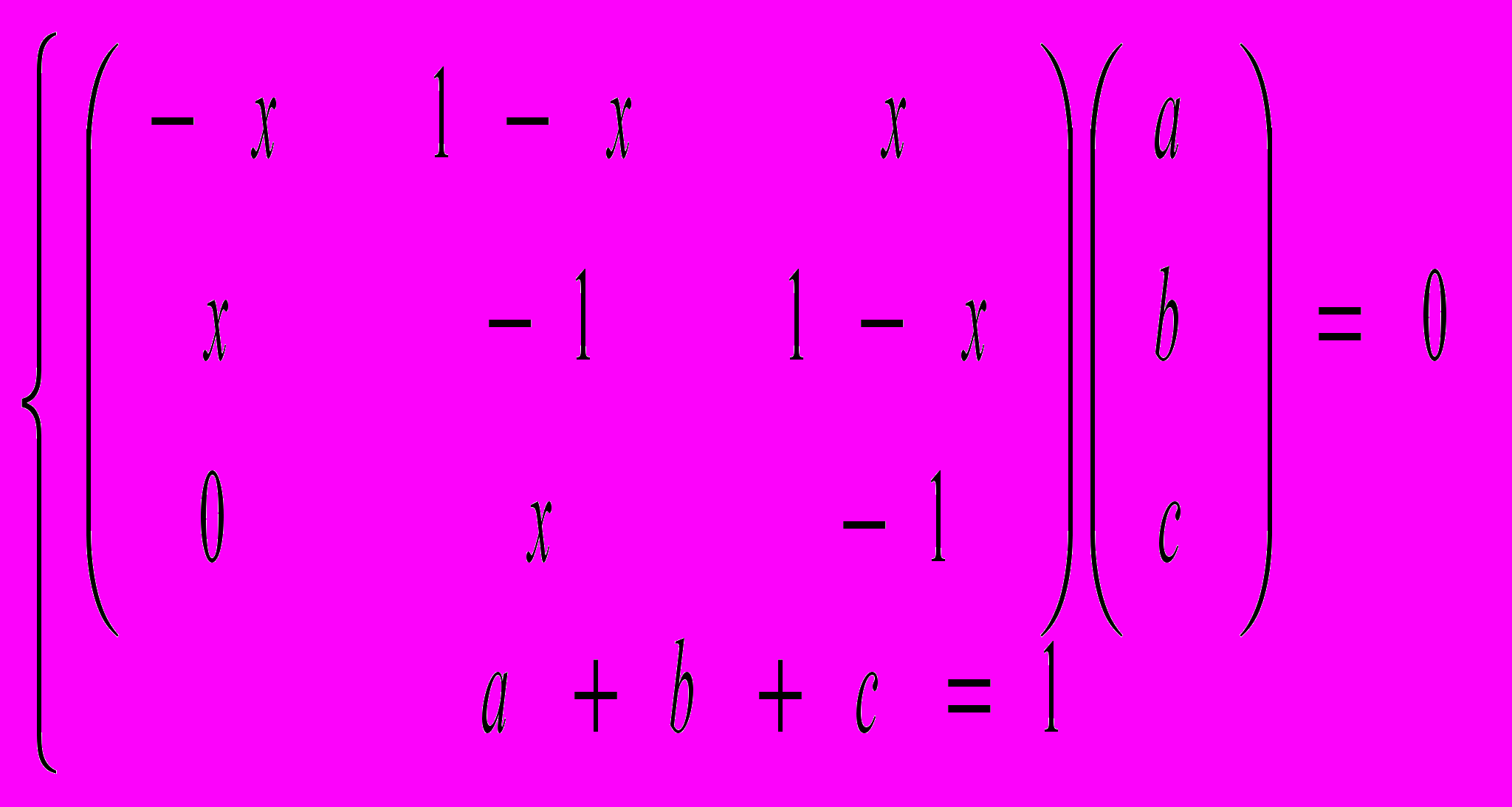
Где, естественно, х – параметр, а a, b и c – переменные – стационарное распределение вероятностей.

Тогда из первого уравнения bx=c;

из второго ax – b +(1 - x)bx=0

откуда a=b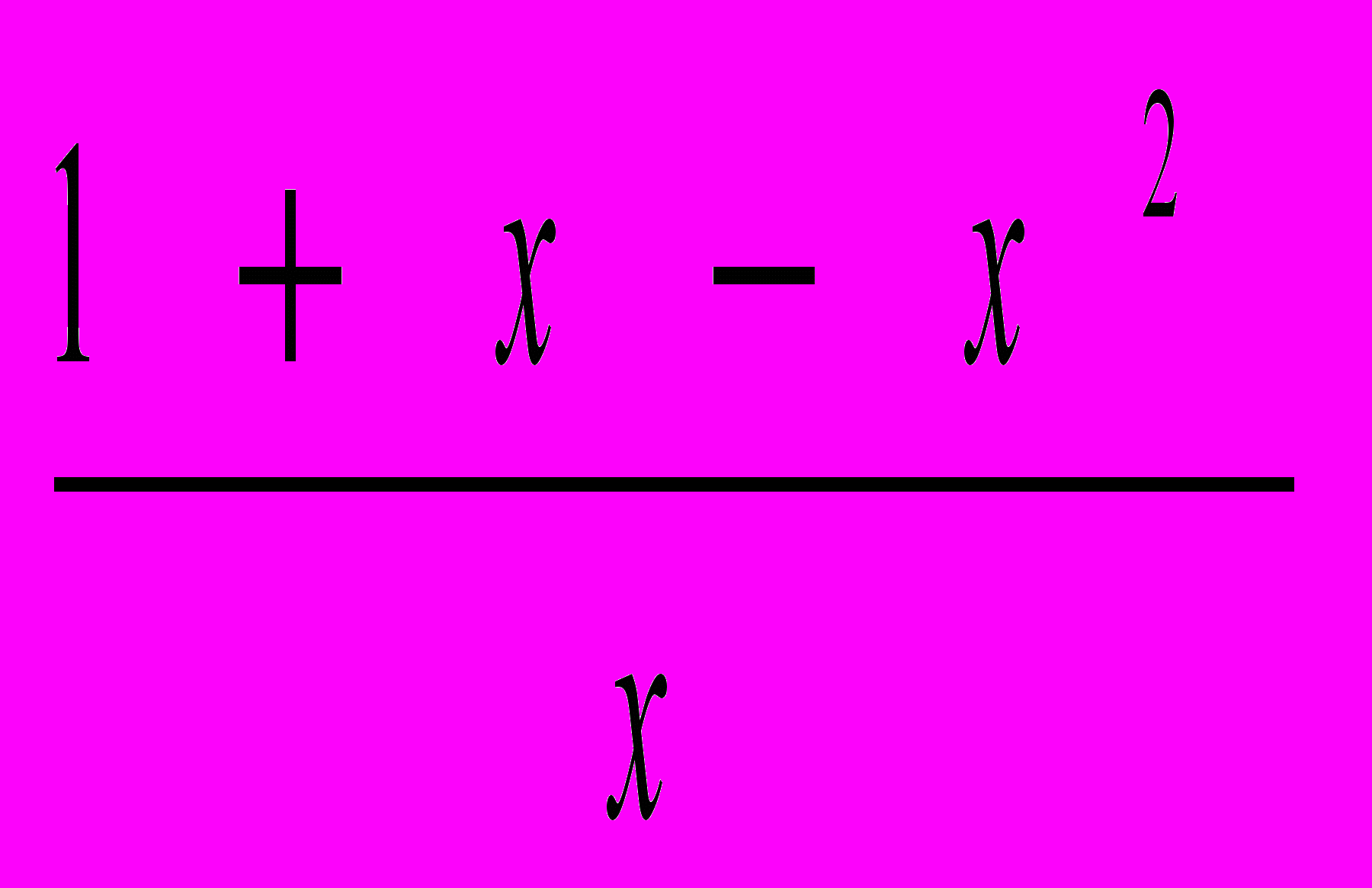при x>0

и b(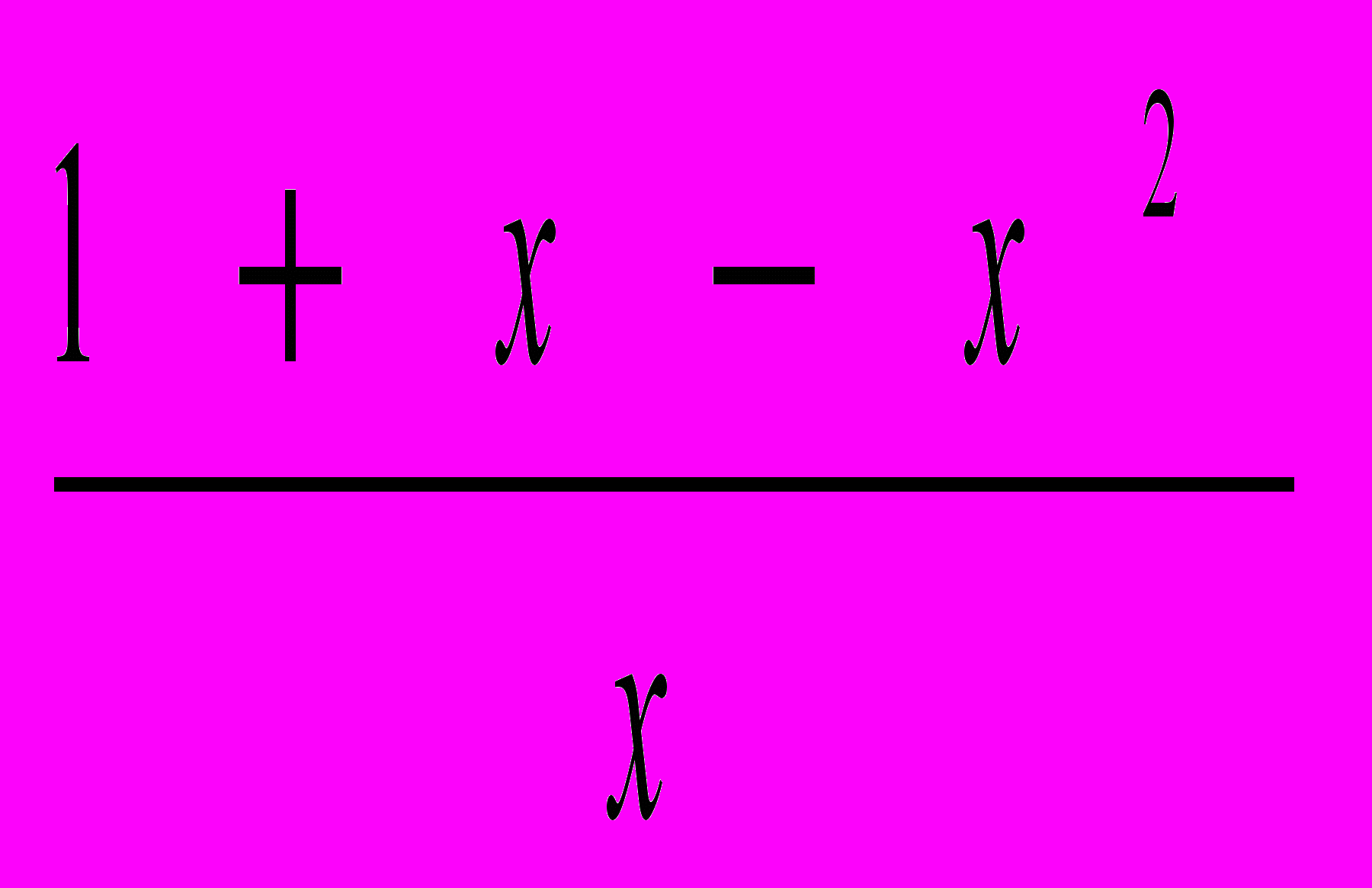+1+x)=1,

откуда b=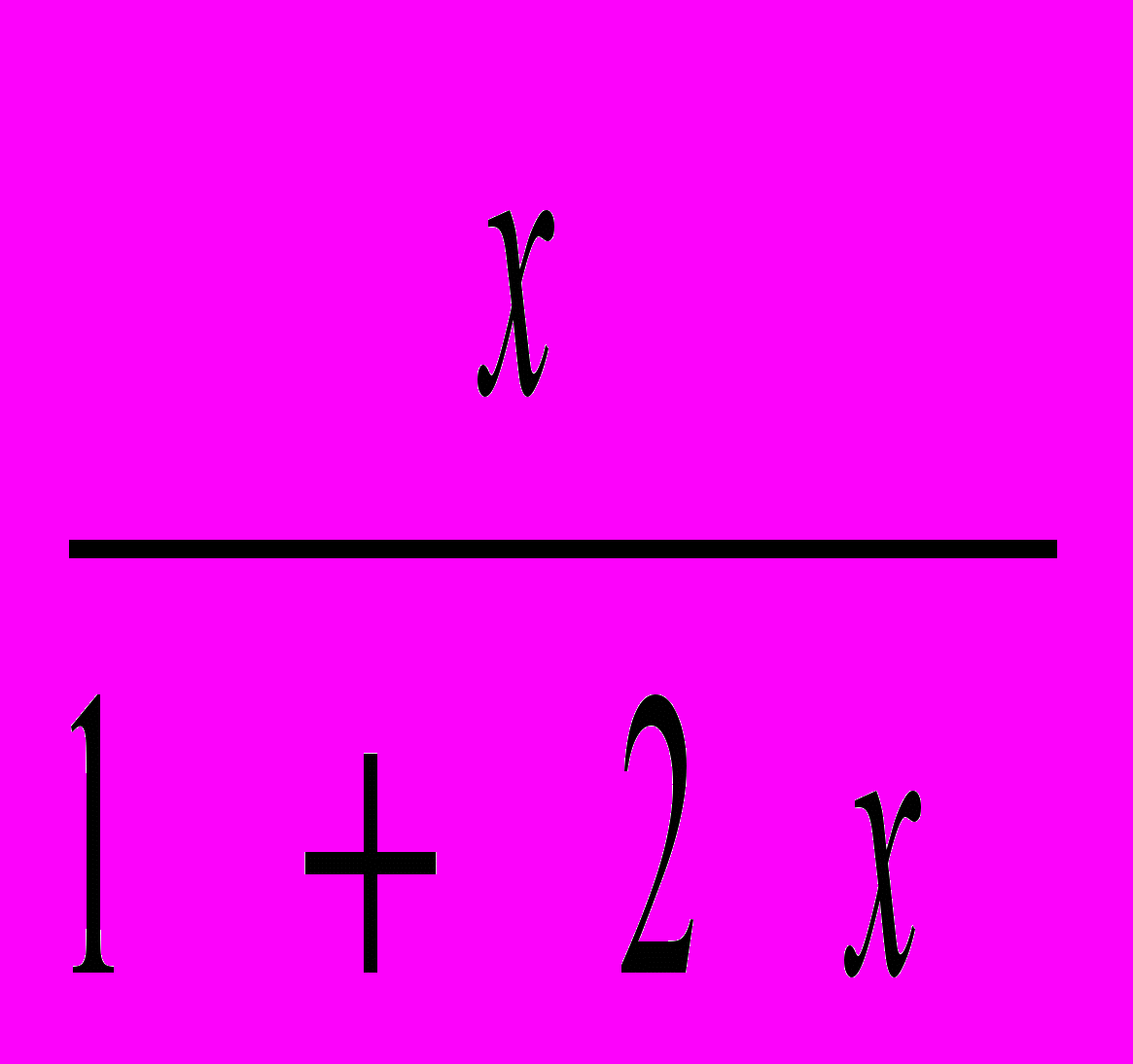. Поскольку автомат выводит 1 только при одном переходе, стохастическая функция равна b(1-x)=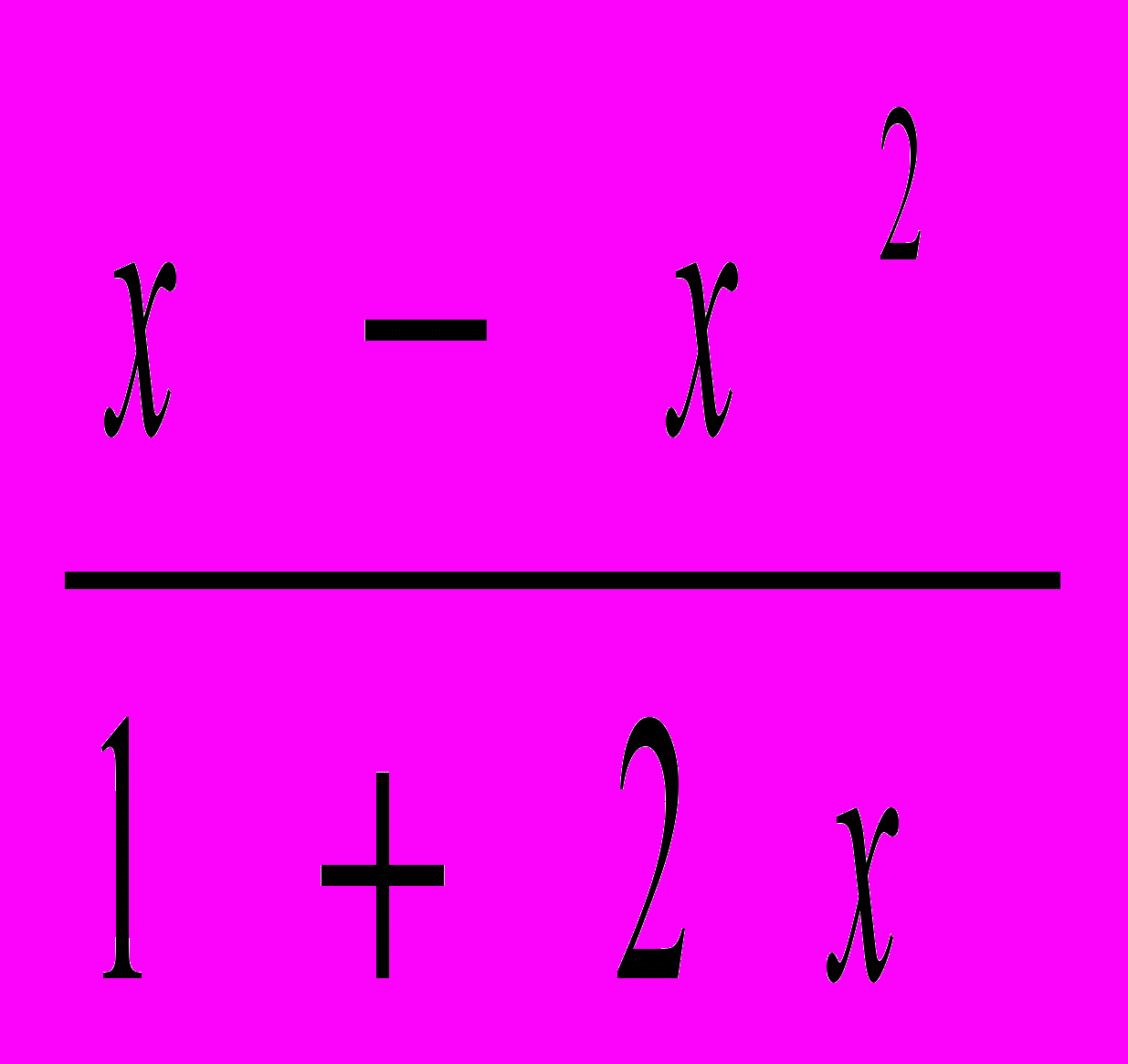

3.3.Найдите стохастические функции автоматов из упражнений 1.2-1.6.