К. Е. Карасёв Введение в теорию конечных автоматов

Вид материала

Содержание

8. Регулярные языки и теорема Клини
A , то его итерация обозначается A
Теорема Клини.
Лемма. Любой регулярный язык представим источником. Доказательство
Следствия из теоремы Клини.
В последующих задачах приведено регулярное выражение. Для языка, задаваемого этим выражением, проведите следующие действия

Подобный материал:

1 2 3 4 5 6 7

8. Регулярные языки и теорема Клини

Словом в алфавите A, как и ранее, называется конечную упорядоченную последовательность символов из этого алфавита. В теории регулярных языков, однако, к словам обычно добавляется так называемое пустое слово, обозначаемое . Конкатенацией двух данных слов называется слово, образованное из первого приписыванием второго в конце (например, конкатенация слов 12 и 34 есть слово 1234).  – нейтральный элемент относительно конкатенации: для любого слова a справедливо a=a=a. Языком в алфавите A называется произвольное множество слов в этом алфавите.

Рассмотрим следующие операции над языками.

Конкатенация языков – язык, состоящий из всех конкатенаций слов двух данных языков; то есть, язык C является конкатенацией языков A и B (обозначение: C=AB), ели он состоит из всех слов вида ab, где a и b – слова языков A и B соответственно.
Итерация языка – множество слов, являющихся конкатенацией произвольного (включая 0) числа слов данного языка, то есть слов вида x₁ x₂ … x_k , где x₁,x₂,…x_k – слова данного языка. Например, если язык A состоит из слов a и b, то в язык B, являющийся его итерацией, входят слова , a, b, ab, bba, aaba и так далее. Обозначение: B=A*.
Объединение языков – объединение их как множеств. Обычно оно обозначается, как и в теории множеств, знаком U; однако, возможно обозначение в виде вертикальной черты: C=A|B.

Определение. Язык в алфавите A называется регулярным, если его можно получить путём применения конечного числа операций конкатенации, итерации объединения из следующих языков, называемых элементарными:

Пустой язык;
Язык, состоящий из одного пустого слова {}.
Язык, состоящий из одного однобуквенного слова: {a}, a∊A.

В частности, язык, состоящий из одного слова регулярен, так как получается итерацией из языков, состоящих из однобуквенных слов, соответствующих каждой букве; язык, состоящий из конечного числа слов также регулярен, поскольку получается операцией объединения из языков предыдущего вида.

Пусть алфавит A не содержит следующих шести символов: ø ,*, U,  , ( и ). Будем называть слово в алфавите A, расширенном с помощью этих шести символов, обозначающее процесс получения данного регулярного языка из элементарных языков, регулярным выражением. Можно также использовать дополнительные символы, каждый из которых один заменяет некоторое регулярное выражение (и обозначает язык). Обозначения таковы:

Элементарный язык {a} обозначается a; язык {обозначается , пустой язык обозначается ø.
Если язык A обозначен одним символом A , то его итерация обозначается A*, иначе, если язык обозначен выражением B, итерация обозначается (B)*. (С этой точки зрения обозначение множества всех слов A* согласуется с тем, что это множество есть итерация языка A, состоящего из всех однобуквенных слов и обозначаемого тем же символом, что и алфавит).
Объединение двух языков обозначается A U B, где A и B – регулярные выражения для них.
Конкатенация языков, обозначенных A и B, обозначается AB, если ни один из них не получен путём объединения; в противном случае она обозначается A(B), (A)B, (A)(B), где скобки ставятся вокруг выражения, соответствующего объединённому языку.

Данные правила устанавливают «приоритет операций» при чтении регулярного выражения: сначала выполняется итерация, затем конкатенация и только затем объединение. Например, язык 10* состоит из слов 1, 10, 100, 1000…, а язык (10)* - из слов , 10, 1010, 101010… Язык является регулярным тогда и только тогда, когда он представим регулярным выражением.

Пусть у некоторого автомата выходной алфавит есть {0,1}, и начальное состояние q₀. Скажем, что автомат принимает слово х, если (x,q₀)=1. Определение. Автомат представляет данный язык тогда и только тогда, когда язык состоит из всех слов, которые автомат принимает.

Мы видим, что язык, представимый автоматом зависит только от поведения автомата, но не от его внутренней структуры. В связи с этим удобно представить автомат в виде эквивалентного ему автомата вида, описанного в конце главы 2; при этом состояния автомата разобьются на принимающие - те, приходя в которые автомат выводит 1 – и непринимающие. Автомат принимает слово тогда и только тогда, когда оно приводит его из начального состояния в одно из принимающих.

Теорема Клини. Язык является регулярным тогда и только тогда, когда он представим некоторым конечным автоматом.

Доказательство. Пусть дан некоторый автомат, выходной алфавит которого {0, 1}. Построим регулярное выражение для языка, представляемого данным автоматом. Перенумеруем некоторым образом состояния автомата от 1 до n и в дальнейшем будем считать, что множество состояний автомата – начальный отрезок натурального ряда. Введём вспомогательные языки : L^k_ij - множество слов, переводящих автомат из состояния i в состояние j, так, что промежуточные состояния (в которые автомат попадает в процессе введения этого слова) имеют номер не более k.

Язык L⁰_ijне содержит слов длины более 1 – слова, в него входящие, переводят автомат из состояния i в состояние j вообще без промежуточных состояний. Следовательно, L⁰_ij={a ∊ A: (a,i)=j}. - регулярный язык, регулярное выражение для него строится очевидным образом.

Пусть построены регулярные выражения для всех языков L^k_ij, km_ij=L^m-1_ijU( L^m^-1_im(L^m^-1_mm)*L^m-1_mj). Следовательно, если L^k_ij, km_ij тоже. По индукции доказывается, что и все языки Lⁿ_ij регулярны. Пусть начальное состояние автомата имеет номер a. Язык, представляемый автоматом – объединение языков Lⁿ_ai, для которых i – принимающее состояние, следовательно – он регулярен. В конкретных задачах зачастую не обязательно строить все языки , достаточно обойтись более простыми рассуждениями о конкретном автомате.

Докажем теорему Клини в обратную сторону. Для этого введём понятие источника (другие названия – обобщённый источник, недетерминированный автомат). Источником в алфавите A называется ориентированный граф со следующими пометками:

одна из вершин помечена как начало источника, другая – конец источника. (При этом в начало могу приходить рёбра, а из конца – исходить).
Каждому ребру приписан либо символ из алфавита A, либо символ пустой строки .

Каждому ориентированному пути из начала источника в конец можно сопоставить слово в алфавите A следующим образом: символы, приписанные последовательным рёбрам пути, образуют слово в алфавите AU{; удалением всех символов  из этого слова получаем слово, требуемое нами. Говорят, что источник представляет данный язык, если язык состоит из слов, соответствующих всем путям из начала в конец источника.

Пример: Данный источник представляет регулярный язык 0(11)*0:

З

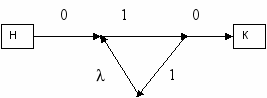
десь прямоугольниками с буквами Н и К обозначены начало и конец источника. Лемма. Любой регулярный язык представим источником.

Д

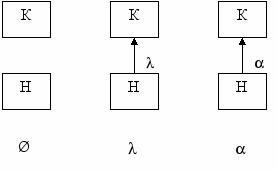
оказательство. Источники, представляющий пустой язык, имеет начало и конец, но не имеет ни одного ребра. Источники, представляющие языки, состоящие из одного пустого или однобуквенного слова, имеют одно ребро с соответствующей пометкой. Это можно изобразить так:

Если в источник, представляющий данный язык, добавить рёбра, идущее от конца к началу и обратно и помеченные , получим источник, представляющий итерацию данного языка. Пусть имеются источники, представляющие языки A и B. Построим источники, представляющий AB следующим образом: Изменим метку начала для источника B на Н2, метку конца для источника A на K1, объединим источники в один орграф и соединим вершины К1 и Р2 ребром, помеченным l. Любой путь, соединяющий в полученном источнике начало и конец, состоит из пути от начала Н в К1, нового ребра и из пути от H2 в конец К. Следовательно, любое слова в языке, представляемом новым источником, есть слово из конкатенации AB и наоборот.

Аналогично строится источник, представляющий AB. Изменим метки начал и концов двух источников на Н1, Н2, К1 и К2 соответственно, объединим источники, добавим две вершины – начало Н и конец К, проведём новые рёбра из Н в Н1 и Н2, из К1 и К2 в К, помеченные символом пустого слова. Любой путь из Н в К проходит либо через Н1 и К1, либо через Н2 и К2, и после прихода в R путь продолжаться не может.

М

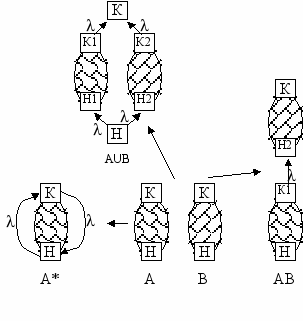
ы получили процесс построения источников для элементарных регулярных языков и операции над источниками, соответствующие операциям над языками, сохраняющим регулярность. Поскольку любой регулярный язык строится из элементарных путём этих операций, для любого языка можно построить источник, его реализующий. Схематично этот процесс можно представить так:

В конкретных задачах зачастую можно упростить источник с сохранением представляемого источником языка. Скажем, что вершина b следует непосредственно за вершиной a, если существует путь из a в b, содержащий только рёбра, помеченные . Часто можно удалить ребро, помеченное  и «склеить» вершину с одной или несколькими непосредственно следующими за ней. Однако совсем избавиться от пометок  невозможно: например, построив стандартным способом источники для (0U1)* и 0*1*, удалив все рёбра, помеченные  и объединив вершины с непосредственно следующими за ними, мы получим два одинаковых источника (упражнение 8.1. - проверьте).

Итак, для регулярного языка построен источник, его представляющий. Осталось построить автомат, реализующий тот же язык, что источник. Это процесс называется детерминизацией автомата. Автомат по источнику строится следующим образом:

его выходной алфавит – тот же, что и для источника; выходной алфавит {0,1};

состояния автомата – множества вершин источника (рассматриваются только состояния, достижимые из начального); На этом множестве можно ввести отношение. Скажем, что вершина b следует непосредственно за вершиной a, если существует путь из a в b, содержащий только рёбра, помеченные . Это отношение не является отношением эквивалентности; однако, если в некотором состоянии содержится данная вершина, то в нём содержатся и все вершины, непосредственно следующие за ней;
начальное состояние автомата – множество, состоящее из начала источника и всех вершин, непосредственно следующих за ним;
значение функции перехода от символа x и состояния - множества вершин S – все вершины, к которым от вершин множества S ведут рёбра, помеченные символом x, а также непосредственно следующие за последними;
принимающие состояния – множества вершин, содержащие вершину-конец.

Следствия из теоремы Клини.

Дополнение к регулярному языку – регулярный язык. В самом деле, возьмём автомат, представляющий данный язык и заменим метки состояний: объявим принимающие состояния непринимающими и наоборот. Полученный автомат будет принимать ровно те же слова, что не принимал первый, следовательно, представлять дополнение к исходному языку.
Пересечение, симметрическая разность и пр. регулярных языков – регулярный язык.

8.2. Даны два автомата, представляющие языки. Как построить схему автомата, представляющего их пересечение?

Решение. Конечно, можно было бы обойтись применением доказательства теоремы Клини, но есть более короткий путь к решению. Построим схемы двух автоматов, возьмём их прямое произведение () и присоединим к автомату последовательно конъюнктор.

В последующих задачах приведено регулярное выражение. Для языка, задаваемого этим выражением, проведите следующие действия:

Постройте обобщённый источник, представляющий данный язык.
Постройте конечный автомат, представляющий данный язык.
Найдите нетривиальную пару разбиений или с.п.-разбиение состояний данного автомата.
Постройте схему, реализующую данный автомат (используя построенную пару разбиений/с.п.-разбиение).
Выпишите регулярное выражение, представляющее язык – дополнение к L.

1(11)*U01*

Решение. 1.Вышеуказанным способом построим источник, представляющий данный язык:

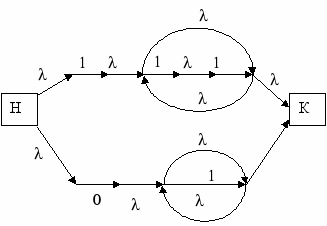
Однако легко видеть, что язык представляется и более простым источником. Построим его и обозначим вершины буквами:

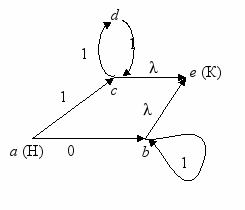
2. В требуемом автомате достижимыми будут следующие состояния:

S₁ ={a} – начальное состояние;

S₂={b,e}=(0,S₁) – принимающее состояние;

S₃={c,e}=(1,S₁) – принимающее состояние;

S₄={d}=(1,S₃);

S₅= ø =(0,S₃)=(0,S₄)=(0,S₂);

Остальные значения функции переходов: (1,S₂)= S₂;(1,S₄)= S₃;(0,S₅)=(1,S₅)= S₅. Таблица переходов имеет следующий вид (опустим символ S, и будем далее обозначать состояния цифрами):

q	1	2	3	4	5
(0,q)	2	5	5	5	5
(1,q)	3	2	4	3	5

3.Мы видим, что разбиение {1,3,4}{2,5} является с.п.-разбиением для этого автомата.

4.Закодируем состояния значениями переменных q₁ , q₂ и q₃так, чтобы было номером блока разбиения, в которое входит данное состояние:

q	1	2	3	4	5
q₁	0	1	0	0	1
q₂	0	0	1	0	1
q₃	0	0	0	1	0

Мы выбрали q₃=1 только для состояния 4 из соображений, что у q(t+1) как у функции от q(t) только одно значение 4. Двоичная реализация функции переходов, таким образом, примет вид:

q₁(t+1)=

;

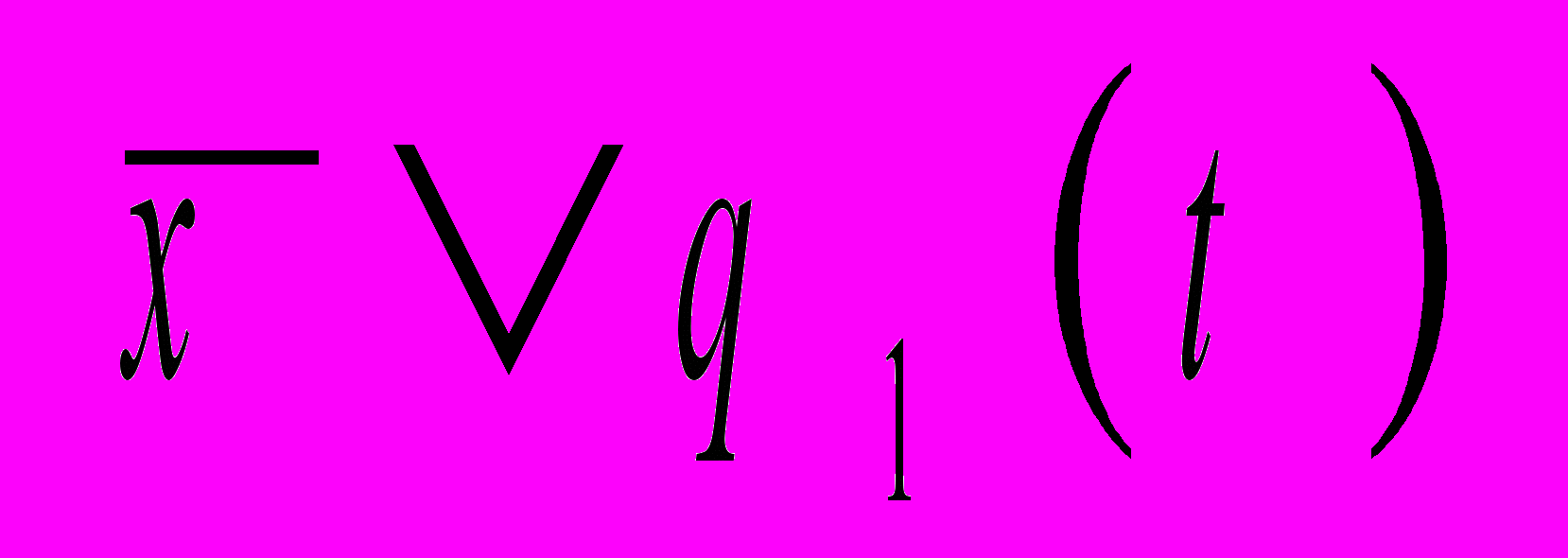q₂(t+1)=

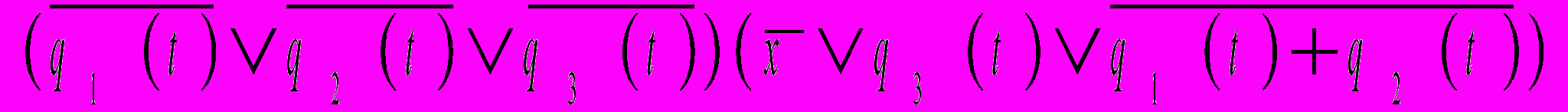
q₃(t+1)=

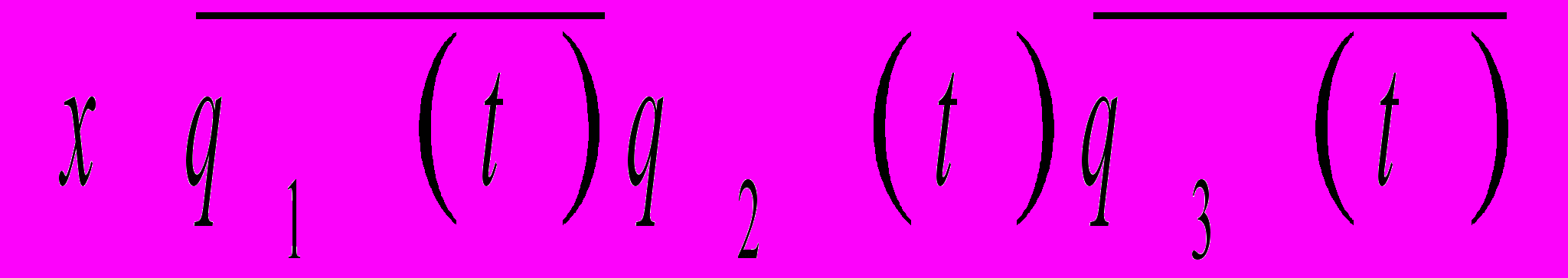
Функция выходов, в зависимости от нового состояния автомата:

(q(t+1))=(q₁+q₂).

5. Построим диаграмму переходов автомата, реализующего дополнение к исходному языку. Для этого заменим принимающие состояния на непринимающие и обратно. Диаграмма будет такой:

З
1

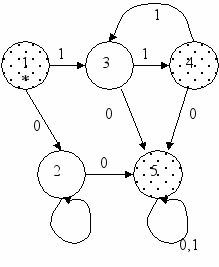
десь принимающие состояния показаны узором из точек. Мы видим, что пути из начального состояния в принимающие следующие:

нулевой путь, соответствующий слову ;

пути в S₄ через S₃ с возможными возвратами в S₃; этим путям соответствуют слова языка 11(11*)

пути в S₅ через S₂ и далее по любому символу из S₅ в S₅ – слова 01*0(0U1)*;
пути в S₅ через S₃ или S₄ – слова 11*0(0U1)*.

Объединяя полученные языки, соответствующие всем классам путей, получаем, что дополнение к исходному языку – язык U11(11)*U01*0(0U1)* U11*0(0U1)*. Полученное выражение можно упростить – легко видно, что (11)* U(0U1)1*0(0U1)* - тот же язык.

То же для следующих языков:

8.4. 1*U(0*1)*

8.5. 1*U(10)*1

8.6. 1*0U0*1*

8.7. 1*0 U 10*0

8.8. (1(00)*)U((00*)1)

8.9. (01)*U0*1*

8.10. (0U 01)*(10)*1

Blog

К. Е. Карасёв Введение в теорию конечных автоматов

Содержание

8. Регулярные языки и теорема Клини