Geum.ru

К. Е. Карасёв Введение в теорию конечных автоматов

Вид материалаУчебное пособие

Содержание


9.Машина Тьюринга
10.Однородные структуры.
10.1. Покажите, что однородная структура может моделировать машину Тьюринга.
Подобный материал:
1   2   3   4   5   6   7

9.Машина Тьюринга


Машина Тьюринга – одно из первых строгих математических определений алгоритма. Машина Тьюринга – одно из возможных обобщений автомата на бесконечное множество состояний. Машина Тьюринга, как и автомат преобразовывает слова... Эвристическое понятие алгоритма как последовательности действий, «шагов» для решения класса задач предполагает следующие свойства:
  • Все возможные условия задачи образуют счётное множество;
  • Существует конечное число возможных «действий» с условиями, которые можно сделать в течение одного «шага».
  • Любая частная задача решается в течение конечного числа шагов.

Определение. Машина Тьюринга представляет собой следующую модель вычислительного устройства в дискретном времени. Пусть задан алфавит A, содержащий «пустой» символ . Машина состоит из ленты и головки. Лента состоит из счётного числа ячеек, на которой записаны элементы языка A, то есть в каждый момент времени задано отображение множества целых числе в алфавит A , называемое состоянием ленты - существует отображение s(n,t):ℤXℕ→A . Ленту геометрически изображают бесконечной в обе стороны, направленной налево и направо. Предполагается, что в начальный момент времени на ленте левее некоторой ячейки и правее некоторой ячейки записаны только символы . Головка машины Тьюринга – конечный автомат с входным алфавитом A и выходным алфавитом – декартовым произведеним AX{L,R,S}. В каждый момент времени задано целое число – положение головки на ленте p(t). В каждый момент времени головка машины читает элемент ленты s(p(t)), находящийся по её положению, переходит в новое состояние и выводит пару (a,d), a∈A, d∈{L,R,S}. Символ a записывается на место, соответствующее положению головки: s(p(t),t+1)=a. В зависимости от символа d головка перемещается влево (L) или вправо (R) или останавливается и подаёт сигнал о завершении решения задачи (S) – головка меняет своё положение, например, если d=L, то p(t+1)=p(t)-1.

Машина Тьюринга является простейшим примером автомата с красками в лабиринте. Машина обобщается на случай многомерной ленты, двумерной ленты с возможностью двигаться только в трёх направлениях и так далее. При этом любая задача, решаемая на машине с многомерной лентой, есть алгоритмически разрешимая задача и разрешима на обычной машине Тьюринга, определённой выше.

Уравнения переходов головки называют программой машины Тьюринга.

Пусть на множестве A* задана частичная функция (или, что то же самое, задана функция на подмножестве этого множества). Говорят, что функция вычислима, если существует такая машина Тьюринга, которая из написанного на ленте слова, для которого функция определена, строит слово-значение функции на этом слове и останавливается; если же функция не определена на этом слове, то не останавливается ни при каком t. Говорят также, что машина Тьюринга решает задачу, заключающуюся в вычислении значения данной функции; если для данной функции машины Тьюринга не существует, говорят, что функция невычислима, и соответствующая задача алгоритмически неразремшима.

Теорема. Алгоритмически неразрешимые задачи существуют. В самом деле, множество машин Тьюринга с заданным алфавитом и попарно неизоморфными головками счётно, а множество функций f:A*→A* имеет мощность континуум.

Упражнение 9.1. Постройте программу машины Тьюринга в алфавите {,0,1}, приписывающей к строке из единиц справа 1, если число единиц нечётно, и 0, если чётно.

10.Однородные структуры.


Однородная структура является более современным обобщением автомата на бесконечное число состояний, нежели машина Тьюринга. Однородная структура – соединение счётного числа экземпляров одного автомата, расположенных в целочисленной решётке. Автоматы называются ячейками структуры. Далее рассмотрим двумерные структуры. Поведение структуры задаётся функцией s(x,y,t): ℤXℤXℕ→Q, где Q – множество состояний ячейки. Для структуры задаётся шаблон соседства T – конечный набор двумерных целочисленных векторов, показывающий, с какими ячейками каждая связана (Чаще всего используется шаблон {(0,1), (0,-1), (1,0), (-1,0)} – ячейка связана с четырьмя соседними в общепринятом смысле). Вместо традиционных функций переходов и выходов рассматривается локальная функция переходов , определённая на множестве Qk+1, где k - число элементов в шаблоне соседства. Поведение структуры описывается уравнением s(x,y,t+1)=(s(x,y,t),s(x+u1,y+v1,t),...,s(x+uk,y+vk,t)), где (u1,v1),...,(uk,vk) – векторы шаблона соседства. На структуру накладываются дополнительные условия: во-первых, q0,q0,...,q0)=q0, где q0 – начальное состояние ячейки; во-вторых, в начальный момент времени только конечное число ячеек находятся не в начальном состоянии.

10.1. Покажите, что однородная структура может моделировать машину Тьюринга.

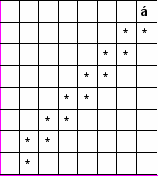
Однородные структуры могут применяться для моделирования биологического процесса роста живого организма. При этом ячейка в начальном состоянии обозначает пространство, не занятое клеткой (условие означает тогда, что клетки не зарождаются «из ничего», но только путём размножения соседних клеток), ячейки в других состояниях – различные клетки в разных стадиях развития, а локальная функция переходов – генетическую программу клетки.

В следующих задачах предлагается «вырастить» изображённую структуру (пустыми клетками изображены ячейки в начальном состоянии, пометками – в каких-либо других) из «зародыша», то есть построить локальную функцию переходов, при которой однородная структура из состояния, в котором только одна клетка находится не в начальном состоянии, с течением времени приближается к указанной бесконечной конфигурации.



10.2.
10.3








10.4
10.5