Geum.ru

Н. Г. Чернышевского Экономический факультет утверждаю " " 20 г. Рабочая программа

Вид материалаРабочая программа

Содержание


Находим значения Т+Е как Y-S – в аддитивной модели. Находим значения Т*Е как Y/S – в мультипликативной модели.
Итого за i квартал
Скорректированная сезонная компонента Si
Задания для самостоятельной работы
Подобный материал:
1   2   3   4   5   6
Находим значения Т+Е как Y-S – в аддитивной модели.
  • Находим значения Т*Е как Y/S – в мультипликативной модели.

    Шаг 4. Определение трендовой компоненты ряда.
    1. Трендовая компонента ряда определяется с помощью построения регрессионной модели, параметры которой находятся методом наименьших квадратов.
    2. С помощью уравнения регрессии находим теоретические уровни трендовой компоненты Т для каждого момента времени t.

    Шаг 5. Находим значения Т+S в аддитивной модели или Т*S в мультипликативной модели.

    Шаг 6. Находим случайную компоненту Е= Y-(T+S) в аддитивной модели и Е= Y/(T*S) в мультипликативной модели

    Шаг 7. Оценка качества модели.
    1. Находим сумму квадратов случайной компоненты.
    2. Находим отношение суммы квадратов случайной компоненты к общей сумме квадратов отклонений уровней ряда от его среднего значения:


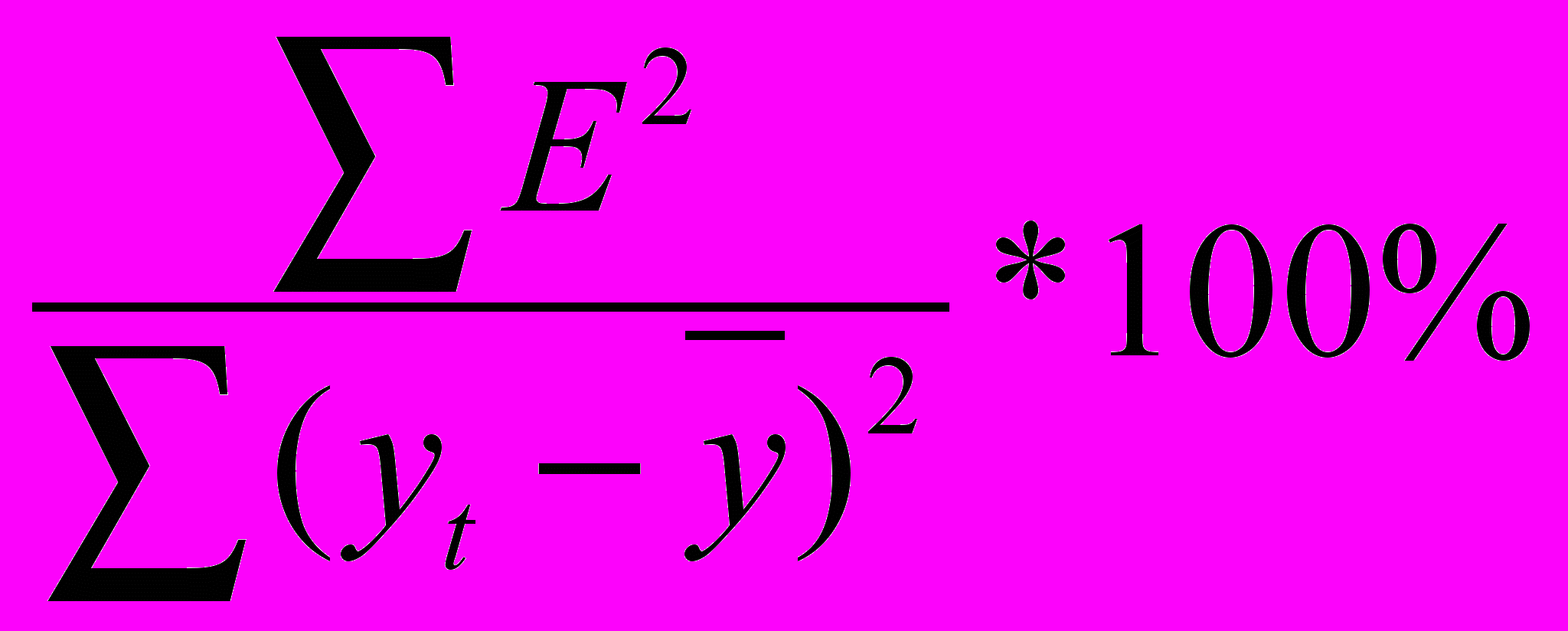
    Алгоритм применение фиктивных переменных в оценке сезонных компонент:

    Строится модель множественной регрессии вида:

    ;

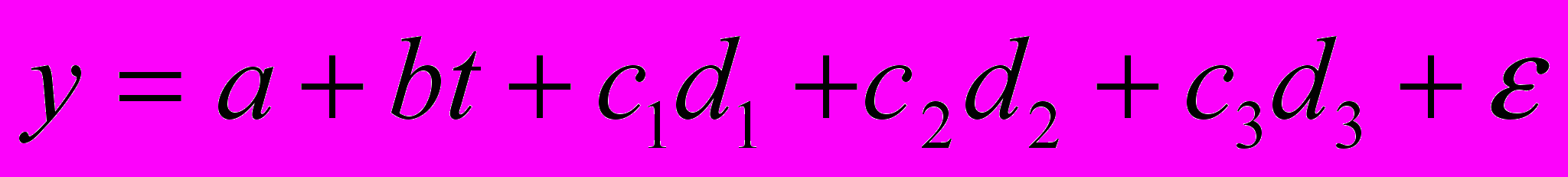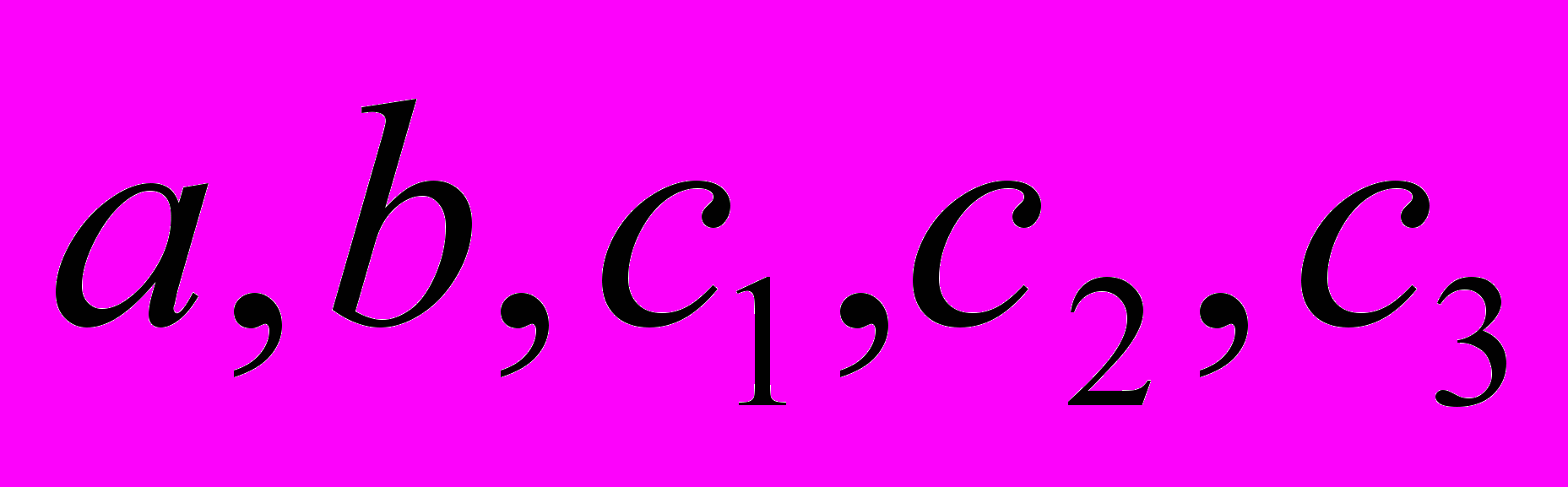    - параметры модели;

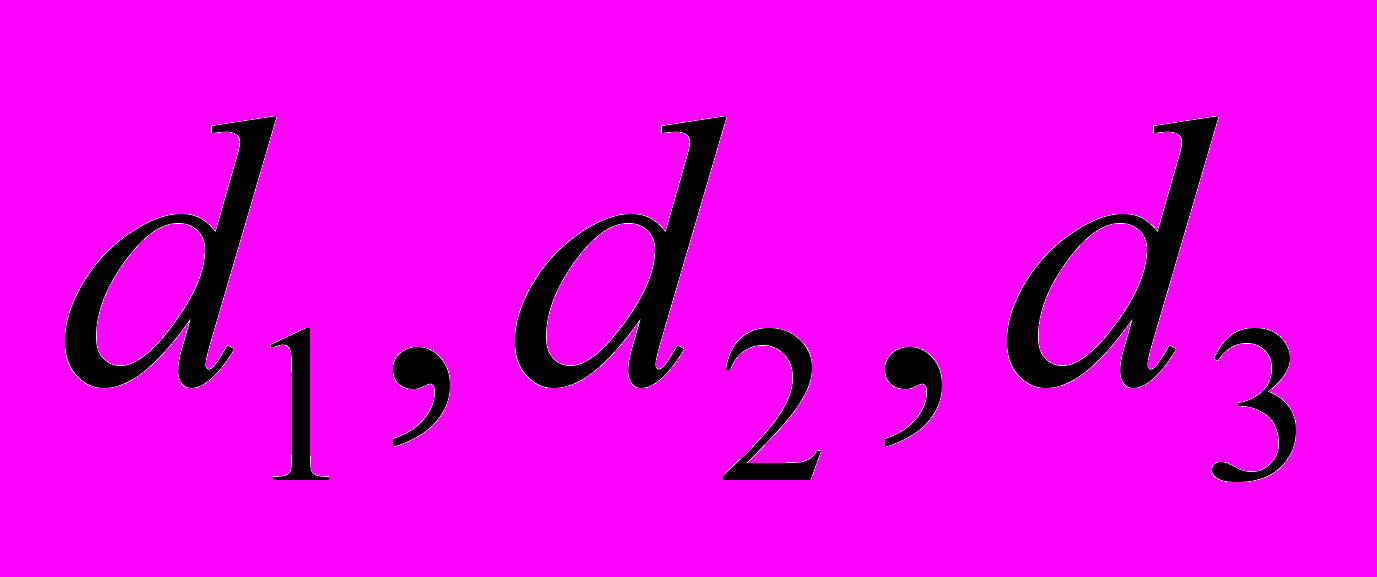    - фиктивные переменные;

    ;



    .


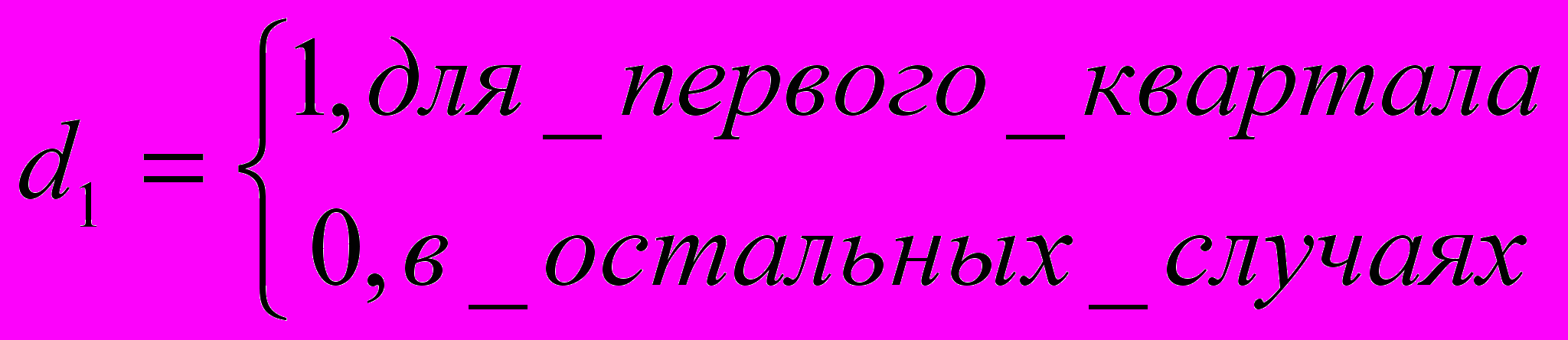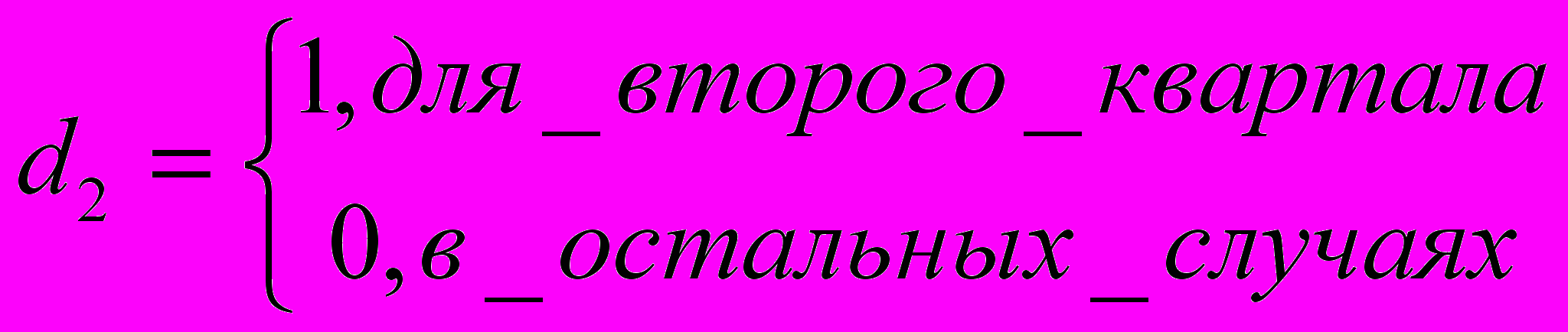
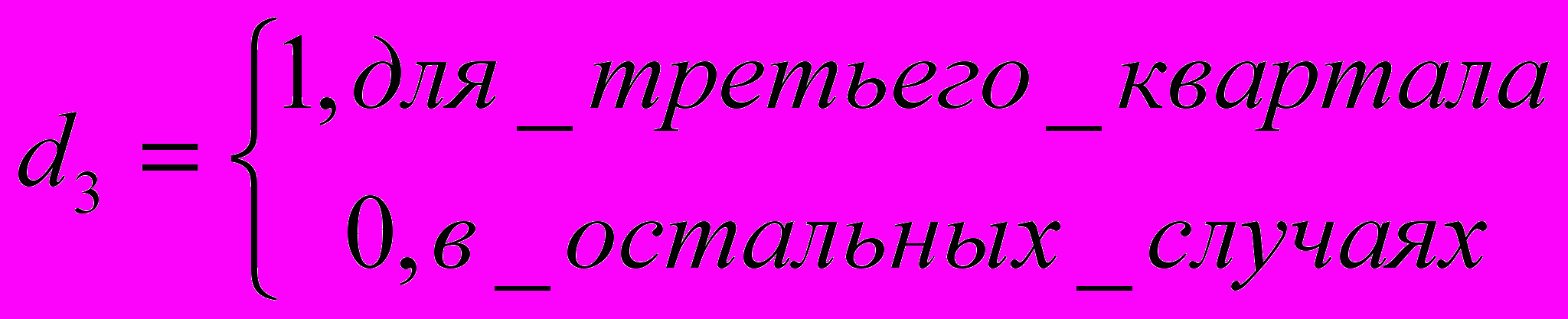    Пример построения аддитивной модели временного ряда с помощью пакета Excel и оценка ее значимости.

    Задание.

    Собраны статистические данные потребления электроэнергии за 4 года.
    1. Построить коррелограмму временного ряда.
    2. Методом скользящей средней вычислить сезонную, трендовую и случайную компоненту аддитивной модели.
    3. С помощью фиктивных переменных вычислить сезонную, трендовую и случайную компоненту аддитивной модели. (Приложение В3)




    № квартала t
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16

    Yt
    6
    4,4
    5
    9
    7,2
    4,8
    6
    10
    8
    5,6
    6,4
    11
    9
    6,6
    7
    10,8


    1. Коррелограмма временного ряда потребления электроэнергии:

    Лаг
    Коэффициент автокорреляции уровней

    1
    0,165

    2
    0,5666

    3
    0,113

    4
    0,983

    5
    0,1187

    6
    0,722

    7
    0,003

    8
    0,97


    2. Метод скользящей средней

    Шаг 1. Выравнивание исходных уровней ряда методом скользящей средней

    Таблица 1.

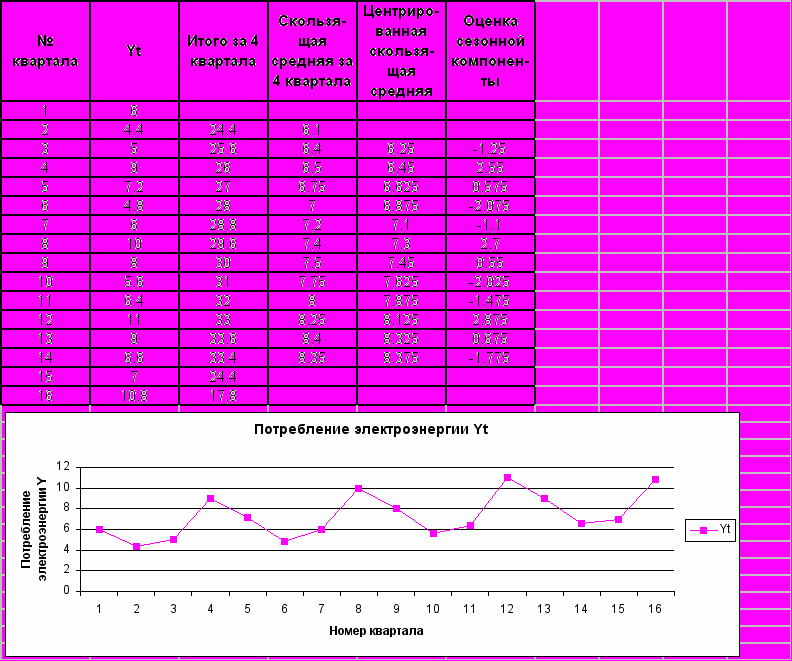    Шаг 2. Оценка сезонной компоненты:

    Таблица 2.

    Показатели
    Год
    № квартала i







    1
    2
    3
    4




    1
    -
    -
    -1,25
    2,55




    2
    0,575
    -2,075
    -1,1
    2,7




    3
    0,55
    -2,025
    -1,475
    2,875




    4
    0,675
    -1,775
    -
    -

    Итого за i квартал



    1,8
    -5,875
    -3,825
    8,125

    Средняя оценка сезонной компоненты для i – го квартала



    0,6
    -1,958
    -1,275
    2,708

    Скорректированная сезонная компонента Si



    0,58125
    -1,978
    -1,294
    2,69


    Корректирующий коэффициент

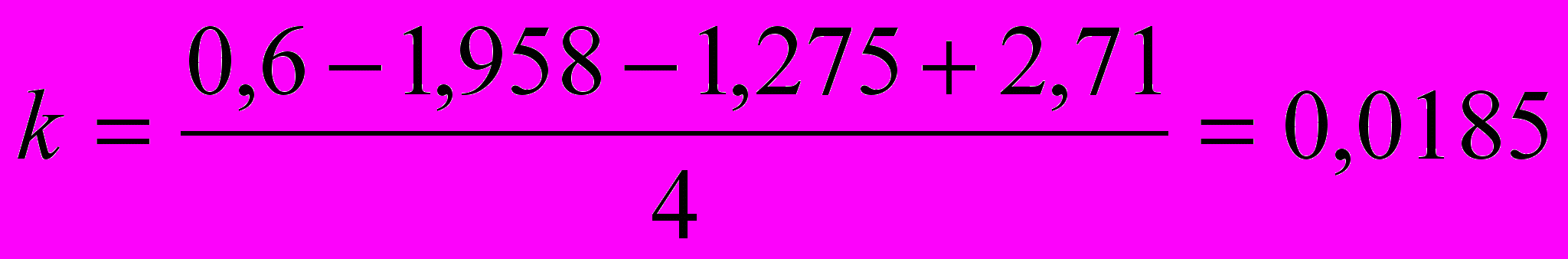
    Шаг 3. Элиминирование влияния сезонной компоненты: (Y-S) (гр.4.)

    Шаг 4. Определение трендовой компоненты ряда. (гр. 5.)

    Шаг 6. Находим значения Т+S (гр.6.)

    Шаг 7. Находим случайную компоненту Е= Y-(T+S) (гр. 7.)

    Таблица 3.




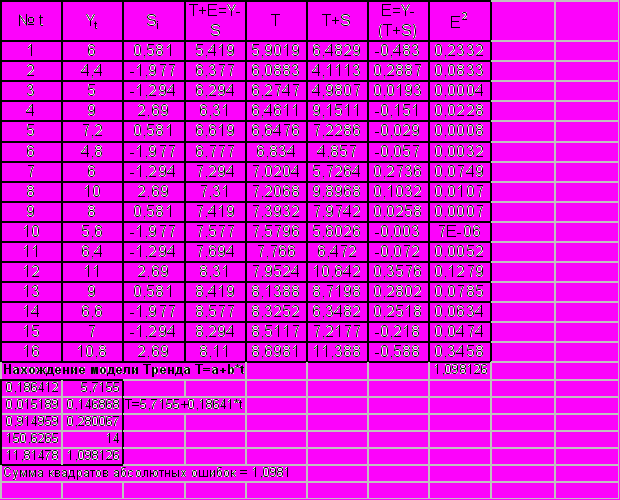
    Шаг 8. Оценка качества модели.

    Сумма квадратов абсолютных ошибок:  Е2 = 1,0981

    Отношение суммы квадратов случайной компоненты к общей сумме квадратов отклонений уровней ряда от его среднего значения:




    Вывод: Построенная аддитивная модель объясняет 98,5% общей вариации уровней временного ряда потребления электроэнергии за 16 кварталов исследуемых 4 – х лет и ее можно использовать в прогнозах будущего потребления электроэнергии.


    3. Вычисление сезонной и трендовой компонент с помощью фиктивных переменных. (Приложение)


    Задания для самостоятельной работы:

    № 1 .

    По статистическим данными постройте модель временного ряда. С помощью коэффициентов автокорреляции определите ее структуру и тип модели. Спрогнозируйте с помощью модели валовой доход в 5-м году работы компании. С помощью фиктивных переменных вычислить сезонную, трендовую и случайную компоненту аддитивной модели




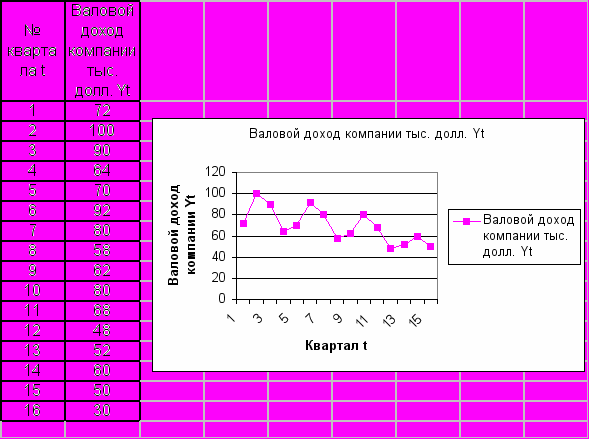
    №2

    По статистическим данным, описывающим поквартальное производство масла и объем его продаж на внутреннем рынке за 2 гола постройте модели временных рядов и спрогнозируйте по ним величины производства и объем продаж в следующие 3 года. С помощью фиктивных переменных вычислить сезонную, трендовую и случайную компоненту аддитивной модели




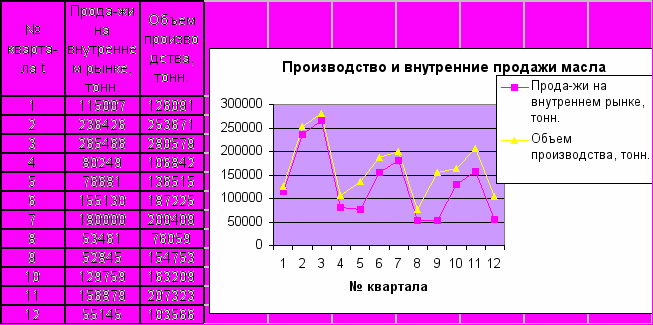
    №3.

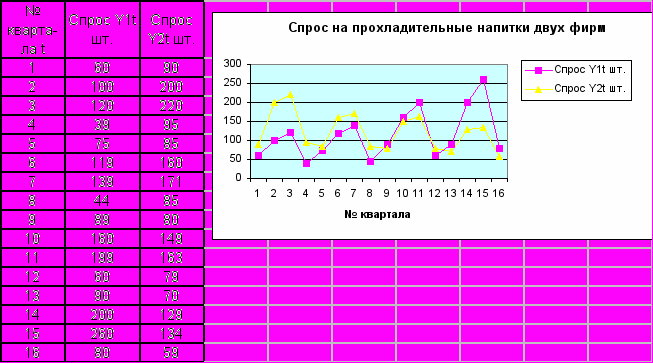
    По статистическим данным, описывающим объем спроса на прохладительные напитки двух фирм в течение 4-х лет, постройте модели временных рядов, описывающих динамику спроса обеих фирм. С помощью фиктивных переменных вычислить сезонную, трендовую и случайную компоненту аддитивной модели. Спрогнозируйте квартал, когда одна из фирм покинет рынок. Каков будет объем спроса в этот момент у фирмы- конкурента?




    №4.

    По данными постройте модель временного ряда продаж компании, млн. долл. Определите ее структуру. Спрогнозируйте с помощью модели продажи в 2007 - м году.

    Год
    Квартал
    Продажи
    Год

    Квартал
    Продажи

    1999
    1
    2292
    2003
    1
    2643

    2
    2450
    2
    2811

    3
    2363
    3
    2679

    4
    2477
    4
    2736

    2000
    1
    2063
    2004
    1
    2692

    2
    2358
    2
    2871

    3
    2316
    3
    2900

    4
    2366
    4
    2811

    2001
    1
    2268
    2005
    1
    2497

    2
    2533
    2
    2792

    3
    2479
    3
    2838

    4
    2625
    4
    2780

    2002
    1
    2616
    2006
    1
    2778

    2
    2793
    2
    3066

    3
    2656
    3
    3213

    4
    2746
    4
    2928


    №5

    Даны поквартальные данные о прибыли компании за последние четыре года, тыс. долл. Постройте мультипликативную модель временного ряда. Спрогнозируйте прибыль компании во втором квартале шестого года работы компании.
    Год 1
    Год 2
    Год 3
    Год 4

    Год
    1
    2
    3
    4
    1
    2
    3
    4
    1
    2
    3
    4
    1
    2
    3
    4

    Прибыль
    72
    70
    62
    52
    100
    92
    80
    60
    90
    80
    68
    50
    64
    58
    48
    30


    №6.

    Даны данные о квартальных продажах фирмы, тыс. долл. Постройте мультипликативную модель временного ряда. Спрогнозируйте объем продаж в 1996 г.

    Год
    Квартал
    Продажи
    Год

    Квартал
    Продажи

    1990
    1
    232,7
    1993
    1
    178,3

    2
    309,2
    2
    274,5

    3
    310,7
    3
    295,4

    4
    293,0
    4
    286,4

    1991
    1
    205
    1994
    1
    190,8

    2
    234,4
    2
    263,5

    3
    285,4
    3
    318,8

    4
    258,7
    4
    305,3

    1992
    1
    193,2
    1995
    1
    242,6

    2
    263,7
    2
    318,8

    3
    292,5
    3
    329,6

    4
    315,2
    4
    338,2



    Тема 6. Системы эконометрических уравнений.

    Вопросы для обсуждения:
    1. Объясните, почему построение систем эконометрических уравнений важно в экономических исследованиях?
    2. В чем сходство и различие моделей эконометрических уравнений с простыми моделями множественной регрессий?
    3. Приведите примеры экономических процессов и явлений, которые могут быть описаны системами независимых, рекурсивных и взаимозависимых уравнений.
    4. Почему необходимо преобразовывать структурную форму модели в приведенную?
    5. В каком случае вся модель является идентифицируемой и сверхидентифицируемой?


    Задания для самостоятельной работы:

    № 1.

    Проверьте, идентифицируема ли эконометрическая модель:

    Y1= b12y2 + b13 y3 + a11x1 + a12x2 ;