Geum.ru

Курс лекций для студентов специальности 140104 «Промышленная теплоэнергетика»

Вид материалаКурс лекций

Содержание


Функция распределения ошибок
X. Смысл функции (X)
X располагаются вблизи X
Ошибки прямых измерений
Пример расчета погрешности прямого измерения
Подобный материал:
1   ...   6   7   8   9   10   11   12   13   14

Функция распределения ошибок


В дальнейшем будем исходить из предположения, что вое промахи исключены, а систематические ошибка или исключены, идя учтены, а погрешность измерений определяется только случайными ошибками. В математической статистике доказывается, что, если при измерениях действует очень большое количество случайных факторов и влияние каждого из этих факторов на результат измерения довольно мало, то ошибки измерений распределены по нормальному закону, описываемому уравнением:

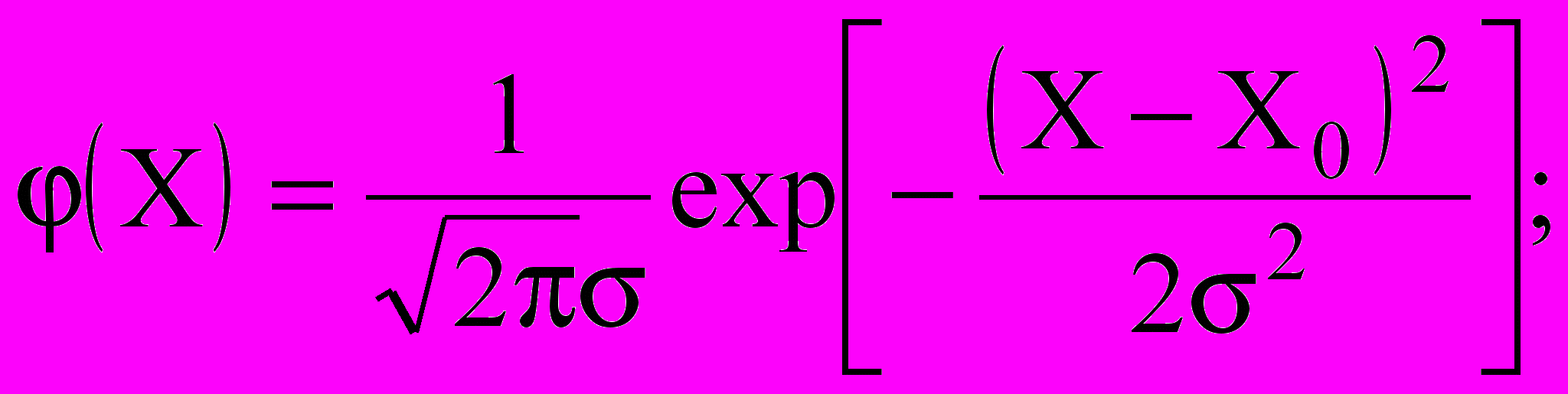(2а)

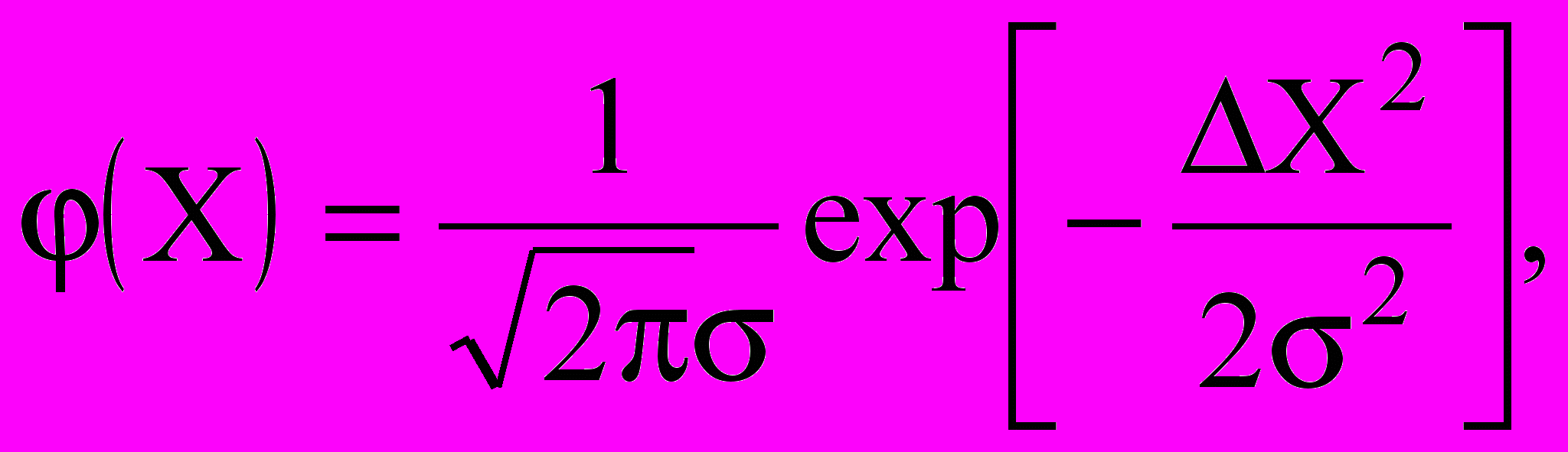(2б)

где: (X) - плотность вероятности распределения;

2 - некоторая постоянная величина, называемая дисперсией и имеющая размерность квадрата измеряемой величины X.

Смысл функции (X) можно пояснить на следующем примере. Пусть при измерении некоторой физической величины X подучена выборка объема n: X1, X2…Xn. Выберем некоторый достаточно узкий интервал измерения X, например, от X' до X". Допустим, что из полученных n измерений в интервал от X'' до Х'' попало m значений X. Тогда будет справедливо приближенное равенство

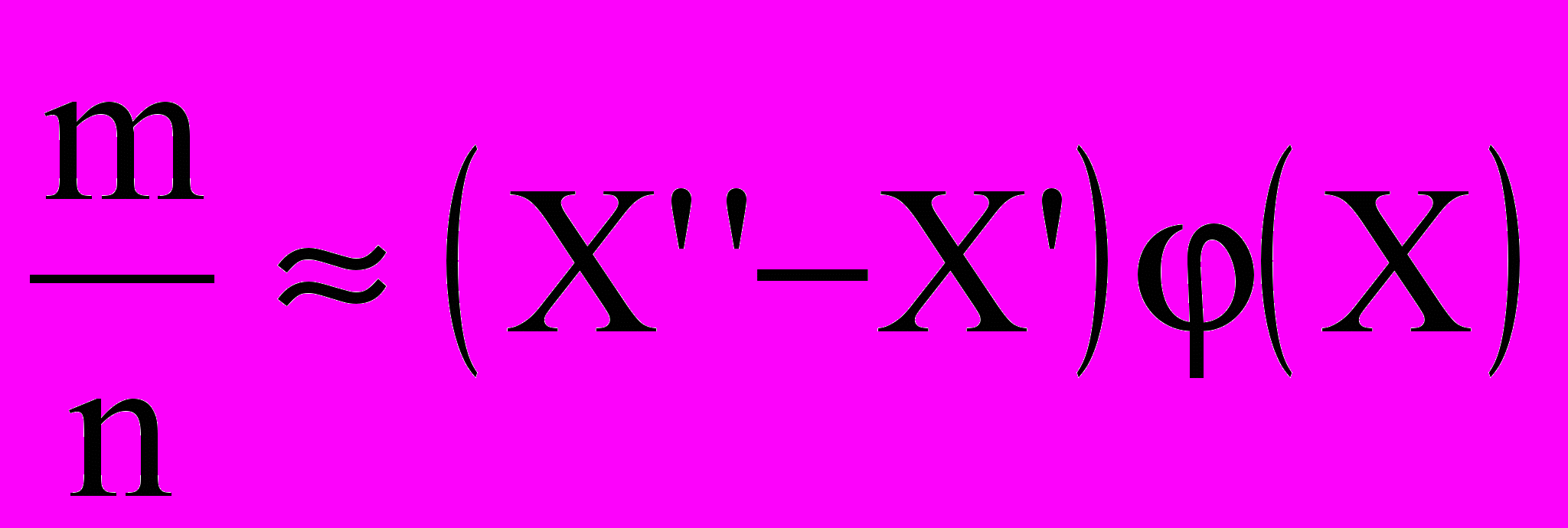. (3)

Соотношение (3) даст строгое равенство в пределе при n и (X’’-X’)0. Отношение 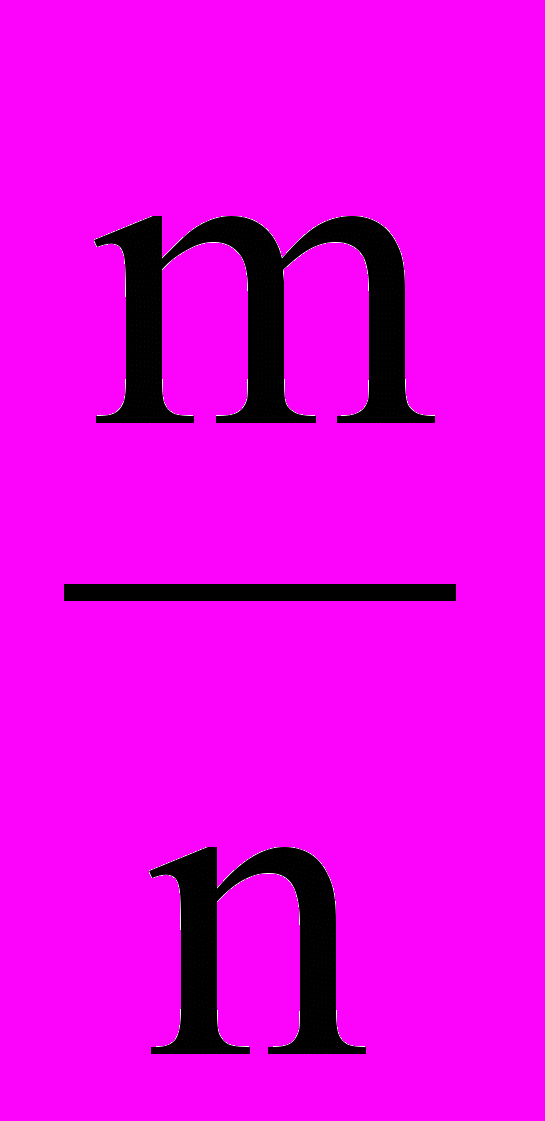, а следовательно, и (X’’-X’)(X) равно доле общего числа замеров, для которых значение X лежит в пределах от X’’ до X’. Другими словами, 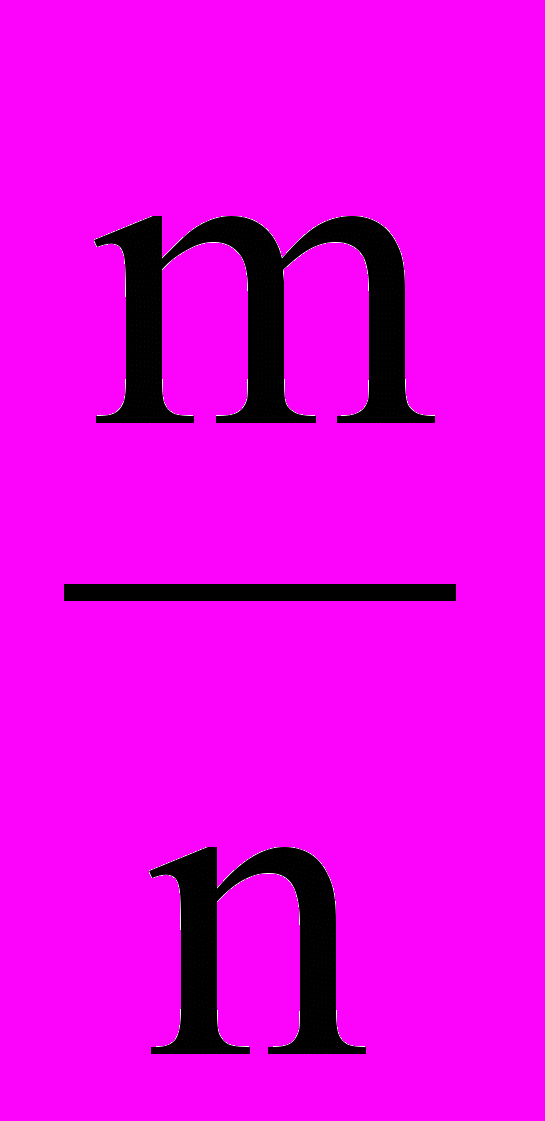и (X’’-X’)(X) представляют вероятность того, что измеренное значение X будет лежать в пределах от Х’ до X”.

Опыт показывает, что в подавляющем большинстве случаев ошибки подчиняются нормальному закону распределения. Нормальное распределение обладает следующими свойствами:

1) ошибки X, равные по величине и противоположные по знаку, встречаются одинаково часто, т.е. значения X<Х0 и X>X0 равновероятны;

2) наиболее вероятны малые по величине ошибки, а большие ошибки - маловероятны, так что большинство измеренных значений X располагаются вблизи X0, где (X) максимальна.

Дисперсия 2 характеризует разброс, рассеяние данного ряда измерений; чек больше 2 тем больше разброс. Характеризуя точность измерения, нужно указать не только величину ошибки, но и ее вероятность. Дисперсия не является случайной величиной – она зависит от свойств приборов, от подготовленности экспериментатора и т.д.

Ранее отмечалось, что истинное значение X0 измеряемой величины не известно, не сможем его найти и при измерениях. Однако, если распределение ошибок подчиняется нормальному распределению, то наилучшей оценкой Х0, наилучшим приближением Х0 является среднее арифметическое для выборки (выборочное среднее )

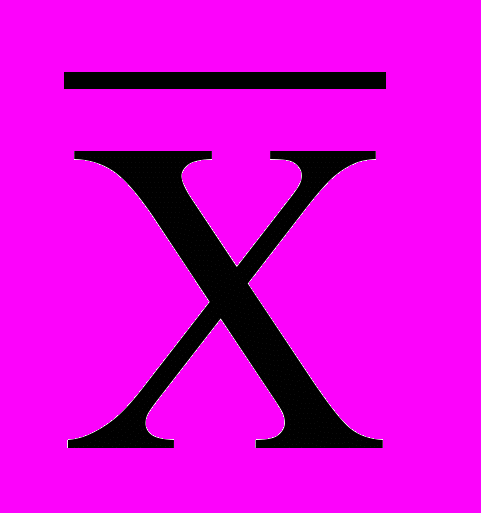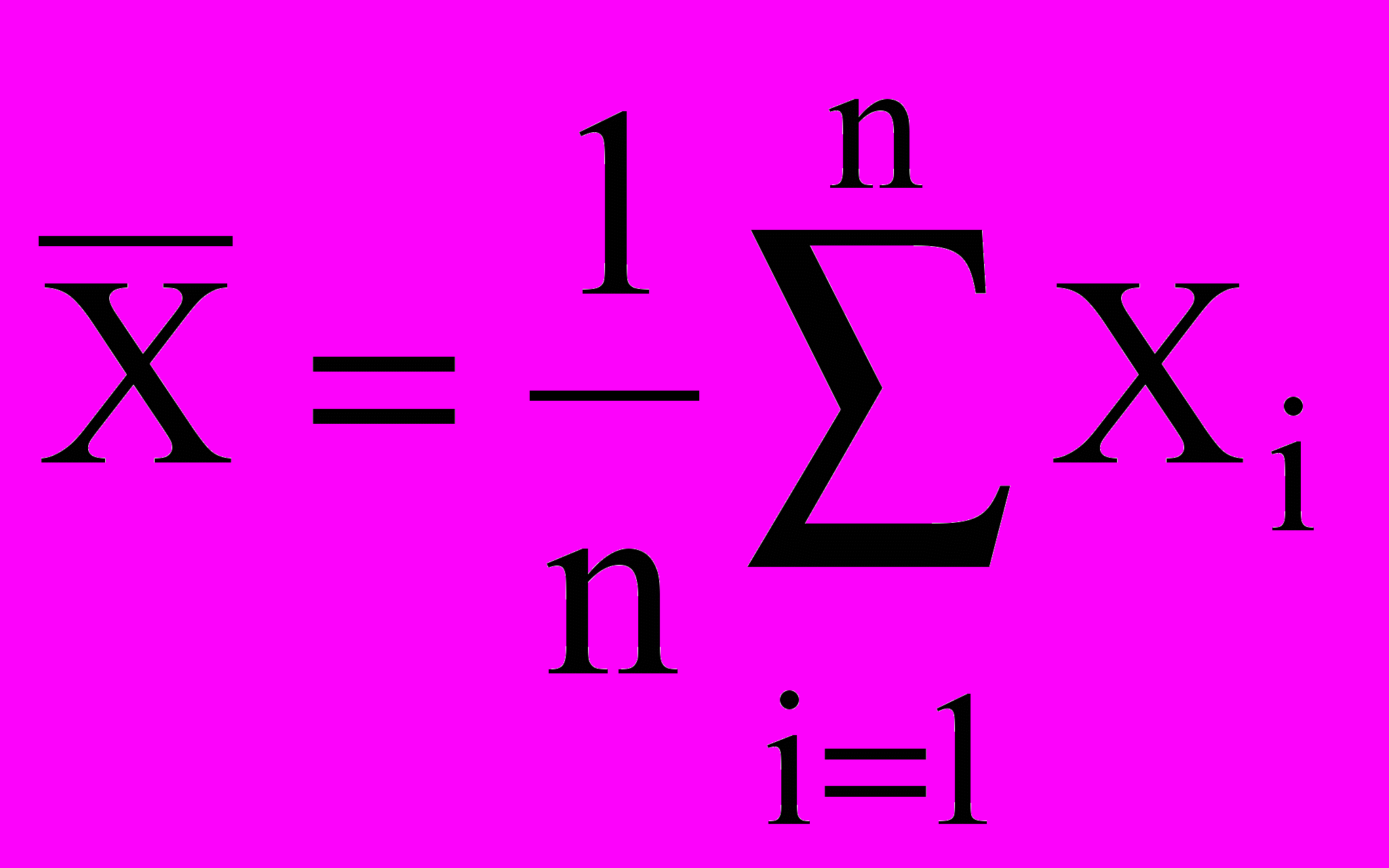. (4)

В дальнейшем во всех практических расчетах вместо Х0 используется 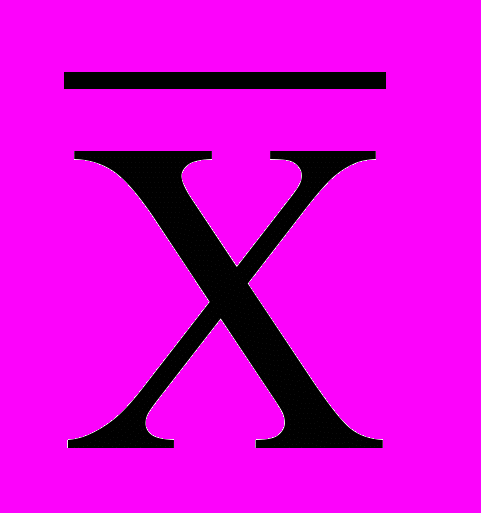, а величина погрешности рассчитывается как

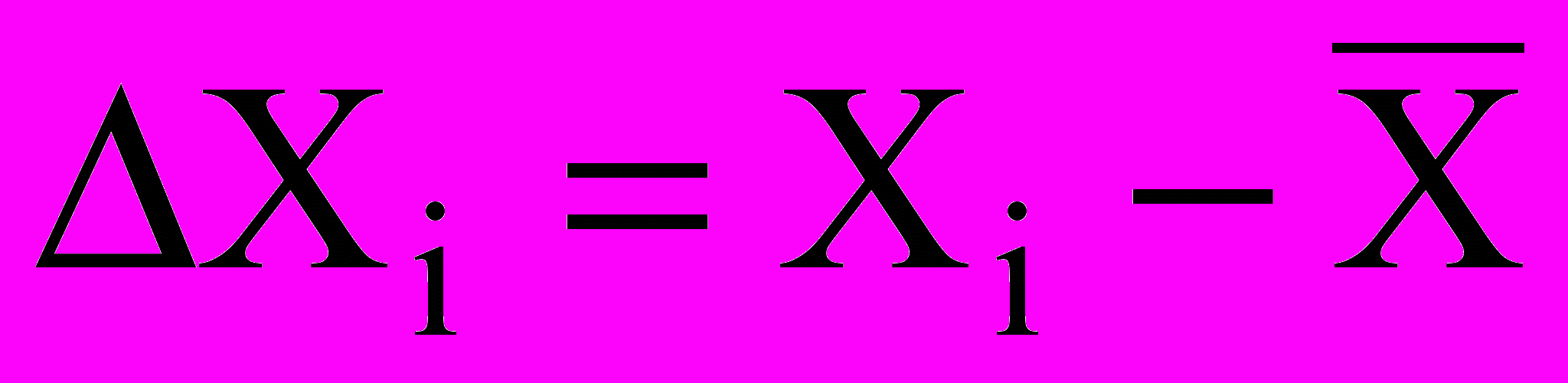(5)

Ошибки прямых измерений

В раздела "Функция распределения" отмечалось, что для того, чтобы охарактеризовать точность, измерения, необходимо указать интервал значений случайной величины X и указать вероятность Р, с которой истинное значение Х0 попадает в этот интервал. Этот интервал, называемый доверительным, включает значение X от до 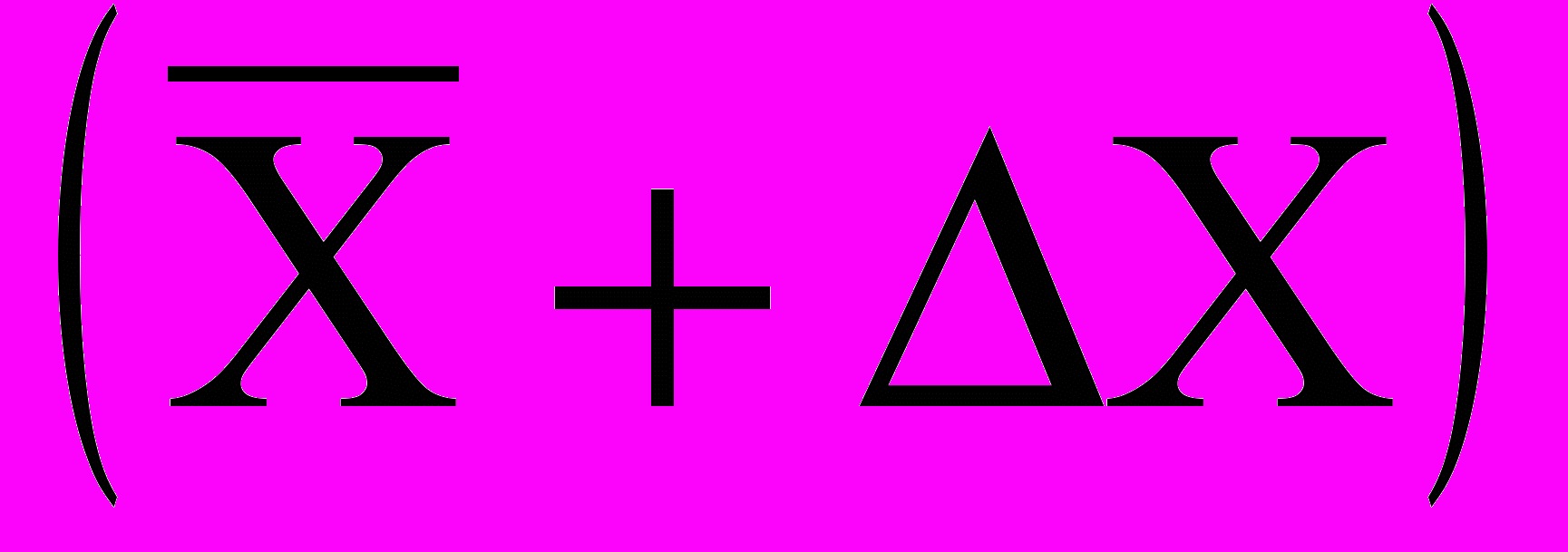Вероятность Р попадания Х0 в доверительный интервал носит название доверительной вероятности.

Для нахождения X при заданном Р находят среднюю квадратическую погрешность среднего арифметического значения X для ряда измерений по формуле

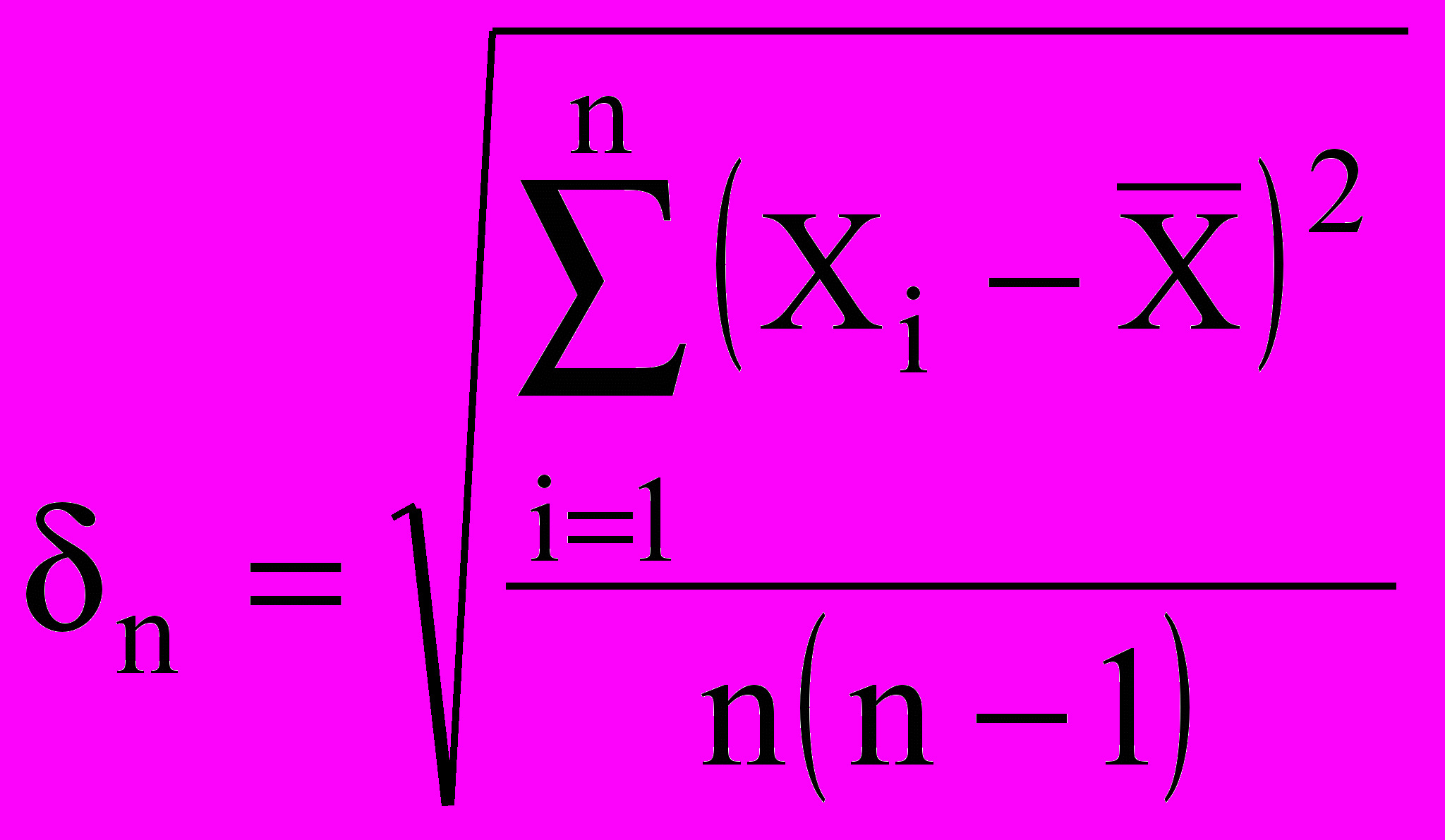, (6)

тогда погрешность Х имеет вид

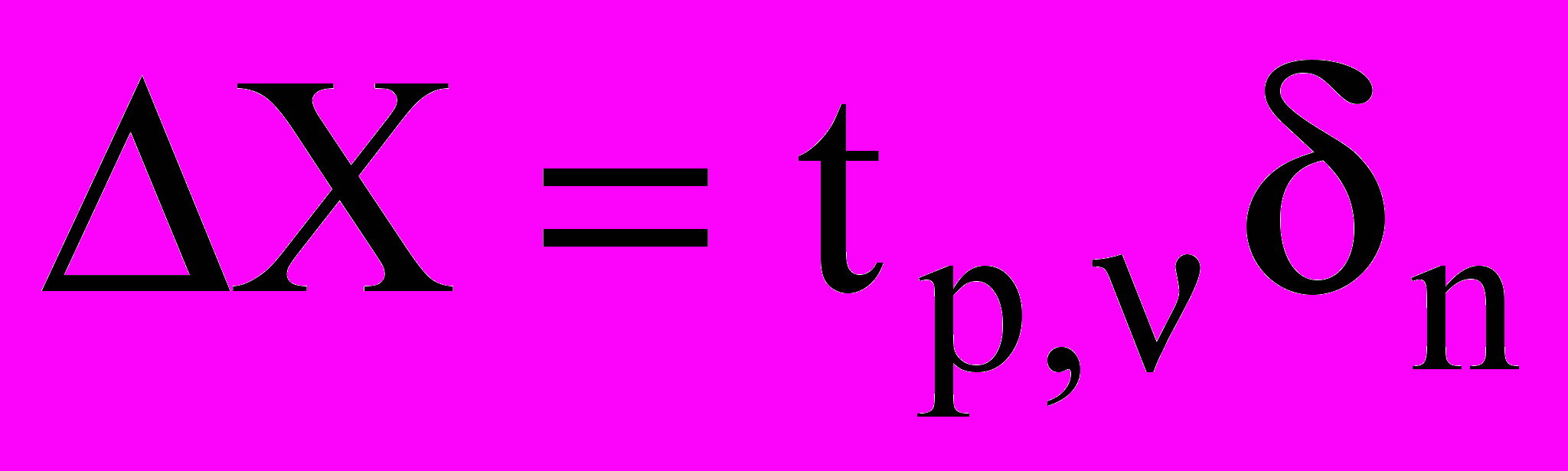, (7)

где tp, - коэффициент, зависящий от величины доверительной вероятности Р и числа измерений n (так называемый коэффициент Стьюдента); tp, рассчитывается по числу степеней свободы  на основании распределения Стьюдента. Значения tp, приведены в табл.1. Число степеней свободы  в распределении Стьюдента равно полному числу измерений n за вычетом числа уравнений связи, накладываемых на Хi в выборке. В нашем случае уравнений связи два (уравнения (4) и (6)), так что

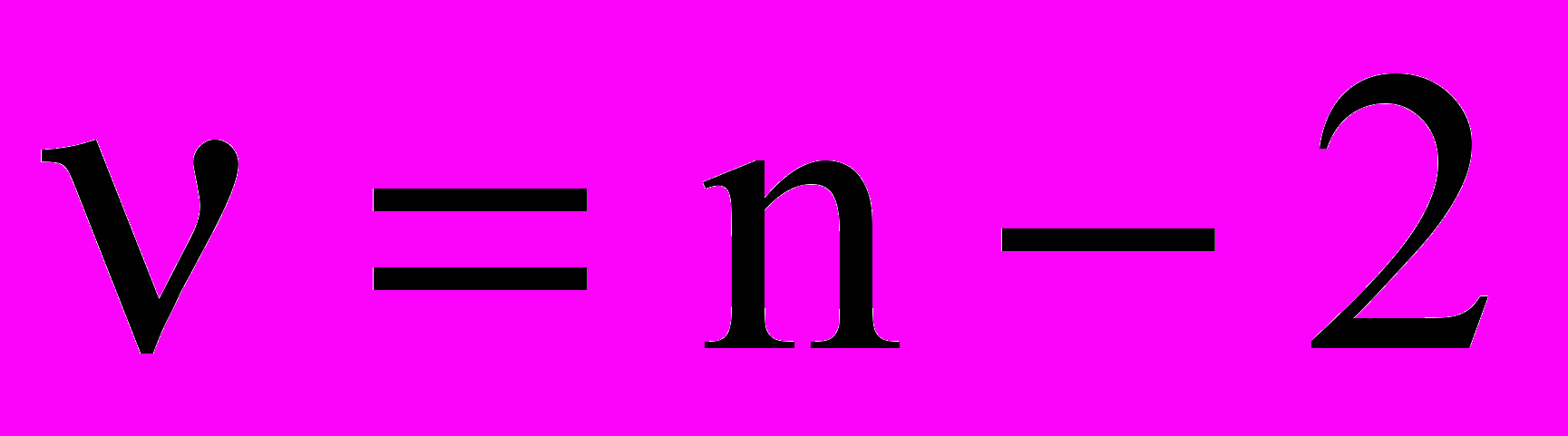. (8)

Таблица 1

№ п/п
P
0,60
0,70
0,80
0,90
0,95
0,98
0,99

1


1,376
1,963
3,078
6,314
12,706
31,821
63,657

2
1,061
1,386
1,386
2,920
4,303
6,965
9,925

3
0,978
1,250
1,635
2,353
3,182
4,540
5,841

4
0,941
1,90
1,533
2,132
2,776
3,757
4,604

5
0,920
1,156
1,476
2,015
2,571
3,365
4,032

6
0,906
1,134
1,440
1,943
2,447
3,143
3,703

7
0,896
1,119
1,415
1,895
2,365
2,998
3,499

8
0,889
1,108
1,397
1,860
2,306
2,896
3,355

9
0,883
1,100
1,383
1,833
2,262
2,821
3,250

10
0,879
1,093
1,372
1,812
2,228
2,764
3,169

11
0,876
1,088
1,363
1,796
2,201
2,718
3,106

12
0,873
1,083
1,356
1,782
2,179
2,681
3,055

13
0,870
1,079
1,350
1,771
2,160
2,650
3,020

14
0,868
1,076
1,345
1,761
2,145
2,624
2,977

15
0,866
1,074
1,341
1,753
2,131
2,602
2,947



Пример расчета погрешности прямого измерения


В результате 8 измерений давления ртутным манометром получили следующие результаты в мм.рт.ст.764,8; 764,3; 772,0; 764,5; 762,5; 764,8 и 766,0. Находим:

1. Среднее арифметическое из результатов измерений по формуле (4)



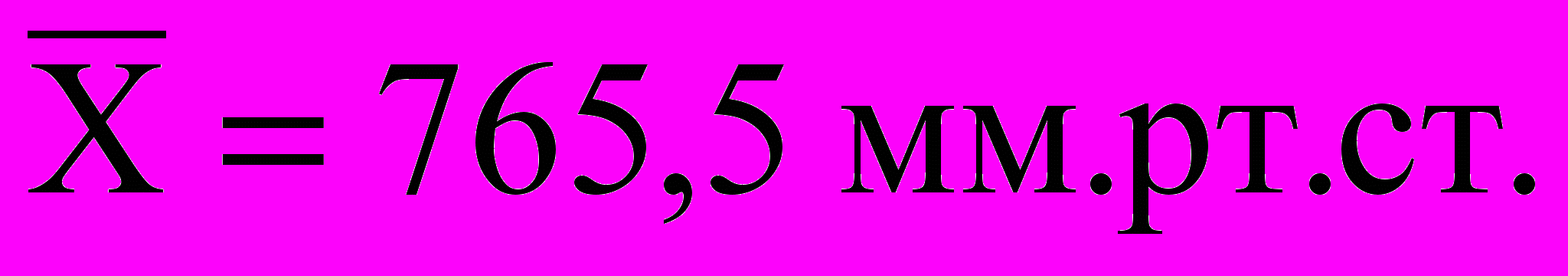
2. Среднюю квадратическую погрешность среднего арифметического 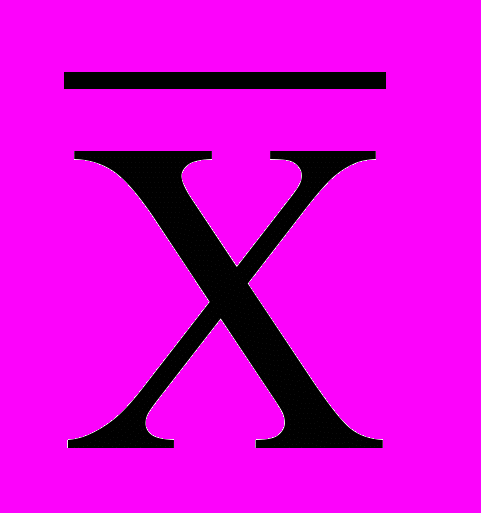из ряда n=8 измерений по формуле (6)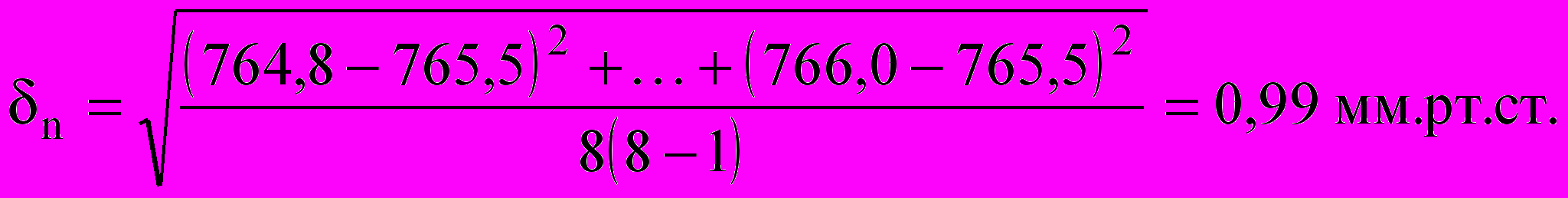



3. Для 95% доверительной вероятности, т.е. Р=0,95, n=8, =6 в табл. 1.



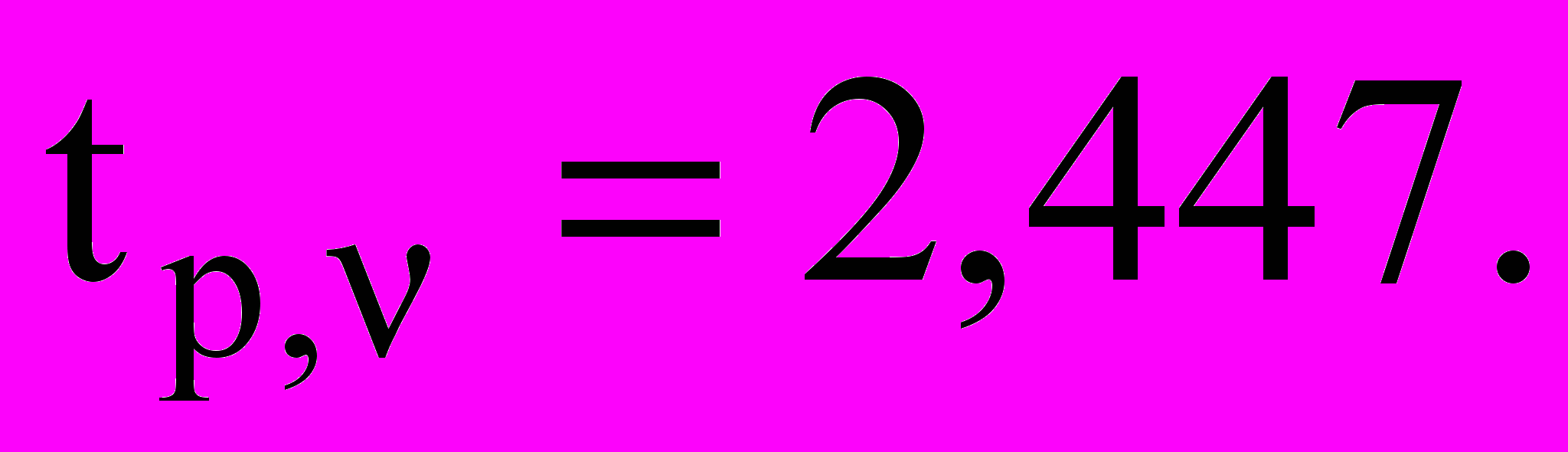
4. По формуле (7)



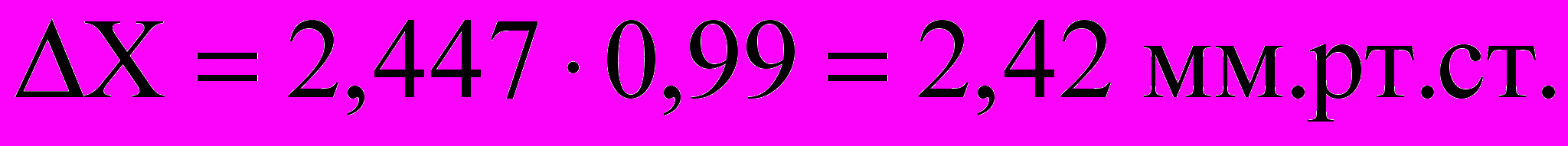
Для окончательной записи результата измерений полученные данные следует округлить. Правила округления: 1. Если округляемая цифра меньше 5, результат округляется в меньшую сторону (цифра, предшествующая округляемой, не изменится, округляемая отбрасывается); 2. Бели округляемая цифра больше 5, результат округляется в большую сторону (цифра, предшествующая округляемой, увеличивается на единицу); 3. Если округляемая цифра равна 5, то если ей предшествует четная цифра, результат округляется в меньшую сторону, если нечетная - в большую сторону. Например, 2,34 округляется до 2,3

2,36 до 2,4

2,35 до 2,4

Если необходимо округлить несколько значений цифр, то округление производится последовательно. Например, 1,255 нужно, округлить до десятых долей. Последовательно проводя округление, получим 1,26 и окончательно 1,3.

Среднее значение 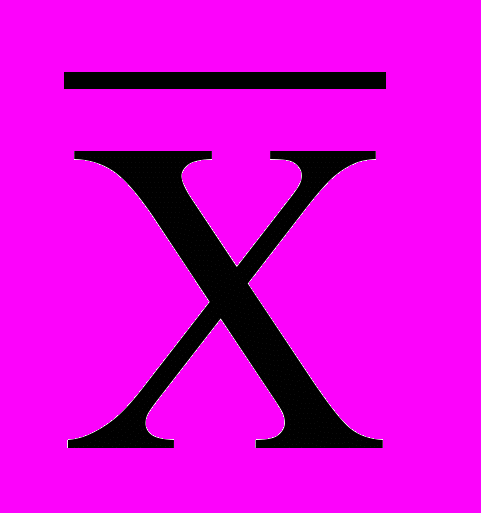и погрешность Х округляются до одинакового разряда.

Формулы теории погрешностей тем точнее, чем больше число измерений, поэтому при 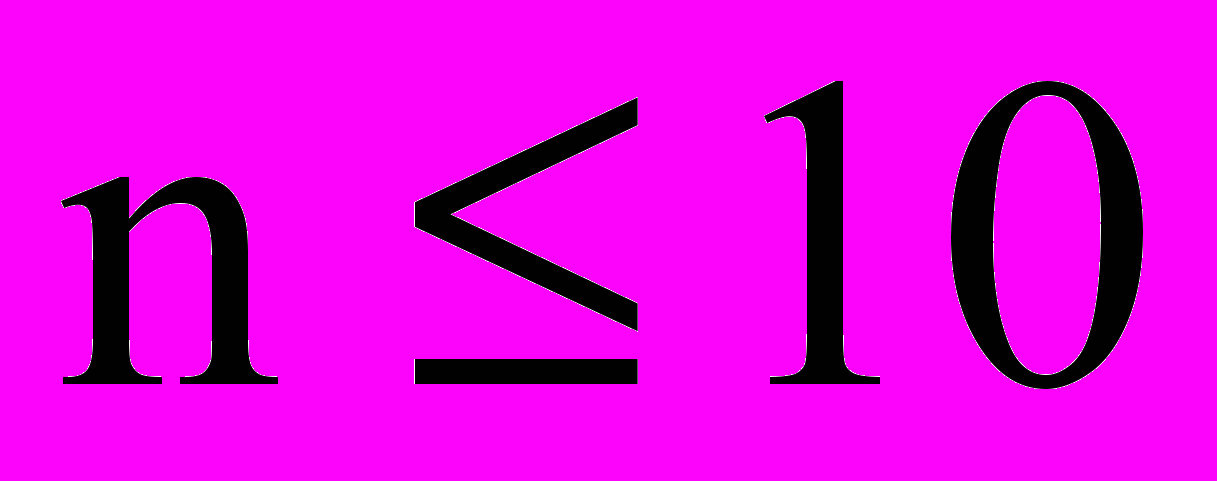погрешность Х следует округлить до одной значащей цифры.

В предыдущем примере X округляется до Х=2мм.рт.ст. Поскольку изменилось Х, изменится и доверительная вероятность.

Оценим новую доверительную вероятность. Для этого найдем новое значение коэффициента Стьюдента по формуле (7)



По табл.1 замечаем, что при =6 значение tp,=2,02 лежит между значениями 1,948 (в столбце с Р=0,90) и 2,447 (в столбце с Р=0,95). Линейной интерполяцией находим значение Р, соответствующее tp,=2,02.



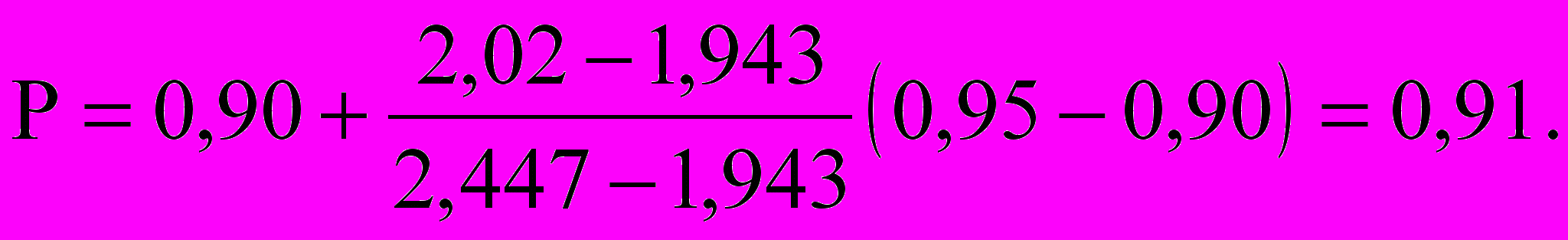
Рассчитываем далее относительную погрешность



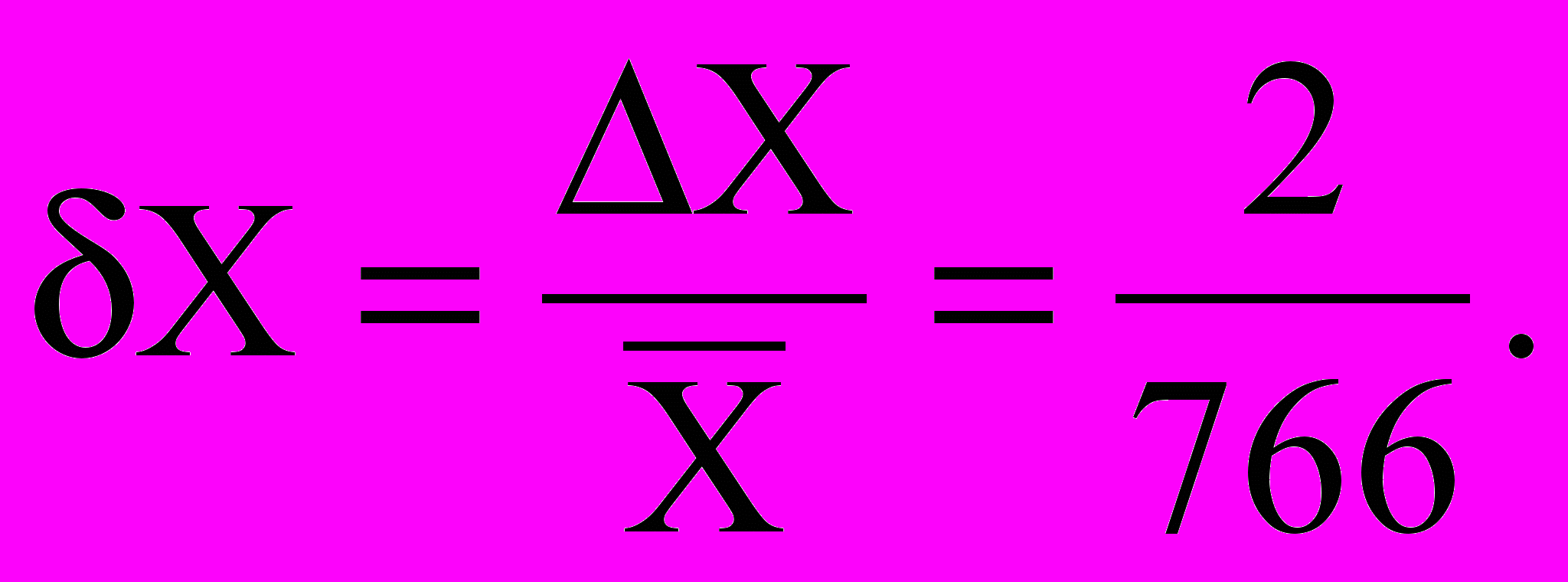
Теперь можно записать окончательный результат измерения в виде: При Р=0,91X=(076,6+2)мм.рт.ст.



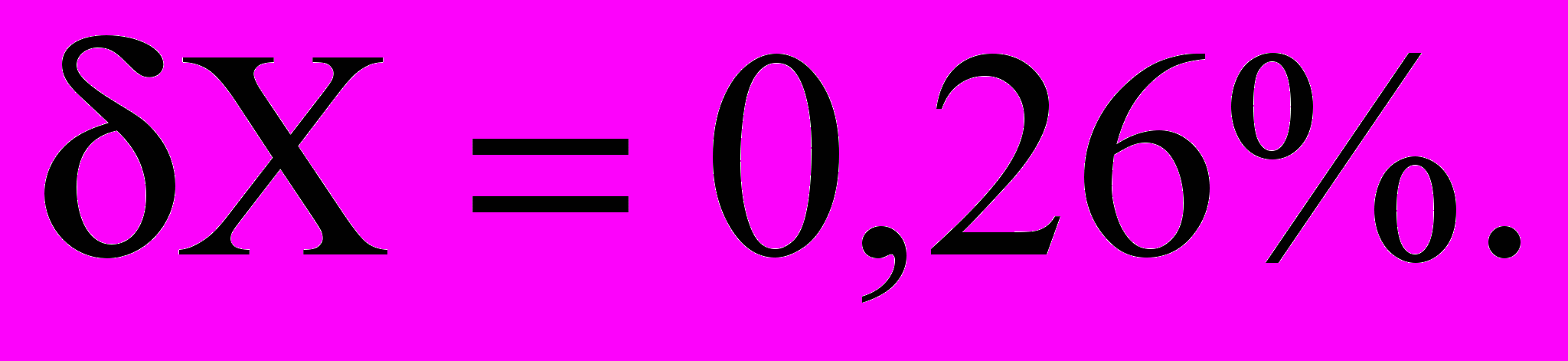
Примечание. Если полученное значение Х оказалось меньше цены деления измерительного прибора, его следует округлить до цены деления прибора и определить доверительную вероятность, соответствующую округленному значению X.


.