Лекция №6 «Ряды динамики»
| Вид материала | Лекция |
СодержаниеОпределение средних уровней ряда. Индексом сезонности |
- Кыргызско-турецкий университет «манас» силлабус, 108.52kb.
- Ряды динамики, 73.43kb.
- Конспект лекций по дисциплине Статистика Модуль, 213.5kb.
- Тема Ряды динамики Все явления изменяются во времени, вместе с этим изменяются, 622.77kb.
- Курсовая работа по дисциплине «Статистика» на тему "Аналитические показатели рядов, 396.09kb.
- Лекция 26. Степенные ряды, 46.31kb.
- Лекция Случайные процессы и временные ряды. Типы стационарности случайных процессов., 91.21kb.
- Высшая математика с-6,12 (ЭнМИ), 112.41kb.
- Моделирование динамики конфигураций организационных систем на сетях петри, когнитивных, 33.91kb.
- Экскурс в историю Простое и сложное поведение. Порядок в хаосе Прообразы динамического, 24.79kb.
Лекция №6
«Ряды динамики».
План:
1. Ряды динамики и их виды.
2. Показатели динамичности ряда и методы их вычисления.
3. Средние показатели динамичности ряда.
4. Выявление основной тенденции динамики.
5. Приёмы изучения сезонных колебаний.
1) Ряды динамики и их виды.
Рядами динамики в статистике называются ряды, последовательно расположенные в хронологическом порядке показателей, которые характеризуют развитие явлений во времени.
Цель статистического изучения рядов динамики заключается в следующем: выявления направленности развития явления, изучений скорости развития явлений.
Все ряды динамики состоят из 2-х элементов:
- показателя времени (t);
- уровня ряда (у).
Ряды динамики в зависимости от вида приводимых в них показателей могут быть рядами динамики абсолютных, относительных и средних величин.
Исходными или первоначальными являются ряды динамики абсолютных величин. Ряды динамики относительных и средних величин являются производными от абсолютных. Ряды динамики абсолютных величин делятся на моментные и интервальные.
Моментными рядами динамики называются ряды, которые характеризуют уровень развития явления на определенный момент времени.
Интервальными рядами называются ряды, которые характеризуют уровень развития общественных явлений за определенный период времени.
Особенности рядов динамики:
1. В интервальном ряду показатели наблюдают не в порядке единовременного учета, а путем постоянного их учета во времени. В результате такого постоянного во времени наблюдения образуются ежедневные, еженедельные, ежемесячные,
Ежеквартальные, ежегодные итоги не только по отдельным предприятиям и отраслям, но и по всему народному хозяйству в целом.
2. Существует разница в понятии интервал в моментном интервальном рядах знания. В моментном ряду интервал – это промежуток времени между датами, на которые приведены сведения. В интервальном ряду интервал – это промежуток времени, за который обобщены приводимые сведения ( характеризующие только промежуток между определенными датами).
3. Из этих 2-х особенностей вытекает следующее свойство: показатели интервальных рядов динамики обладает свойством суммарности, а моментные ряды этим свойством не обладают.
Анализируя ряды динамики , особое внимание нужно обращать на сопоставимость уровней или данных в рядах динамики. Проблема сопоставимости данных особенно остро стоит в рядах динамики, потому что они могут охватывать значительные периоды времени, за которые могли произойти перемены или изменения, приводящие к несопоставимости статистических данных.
Причинами несопоставимости данных могут быть:
- территориальные изменения;
- изменение единиц счета;
- изменение курса валют;
- различная степень охвата единиц явления статистическим наблюдением;
- несовершенные методологии статистического наблюдения.
2) Показатели динамичности ряда и методы их вычисления.
При изучении рядов динамики можно решить несколько задач:
- охарактеризовать интенсивность отдельных изменений в уровнях ряда от периода к периоду или от даты к дате;
- определяются средние показатели временного ряда за тот или иной период;
- выявить основные закономерности динамики исследуемого явления на отдельных этапах и в целом за рассмотренный период;
- выявить факторы, обуславливающие изменения изучаемого явления и объектов во времени;
- дать прогноз развития явления на будущее.
Динамический ряд представляет собой ряд последовательных уровней, в результате сравнения которых получается система абсолютных и относительных показателей к числу которых относятся:
- абсолютный прирост;
- коэффициент роста;
- темп роста;
- темп прироста;
- абсолютное значение 1% прироста.
Если сравнению подлежат несколько последовательных уровней, то возможны 2 варианта сопоставления:
- Если каждый уровень динамики ряда сравнивать с одним и тем же предшествующем уровнем принятым за базу сравнения ( в качестве базисного выбирается как правило самый 1-й уровень динамического ряда) называется сравнением с постоянной базой или базисной.
- Если каждый уровень динамического ряда сравнивается с непосредственным ему предшествующем, то такое сравнение называется сравнение с переменной базой или цепным.
Для характеристики закономерности явлений по времени используются следующие показатели:
1. абсолютный прирост
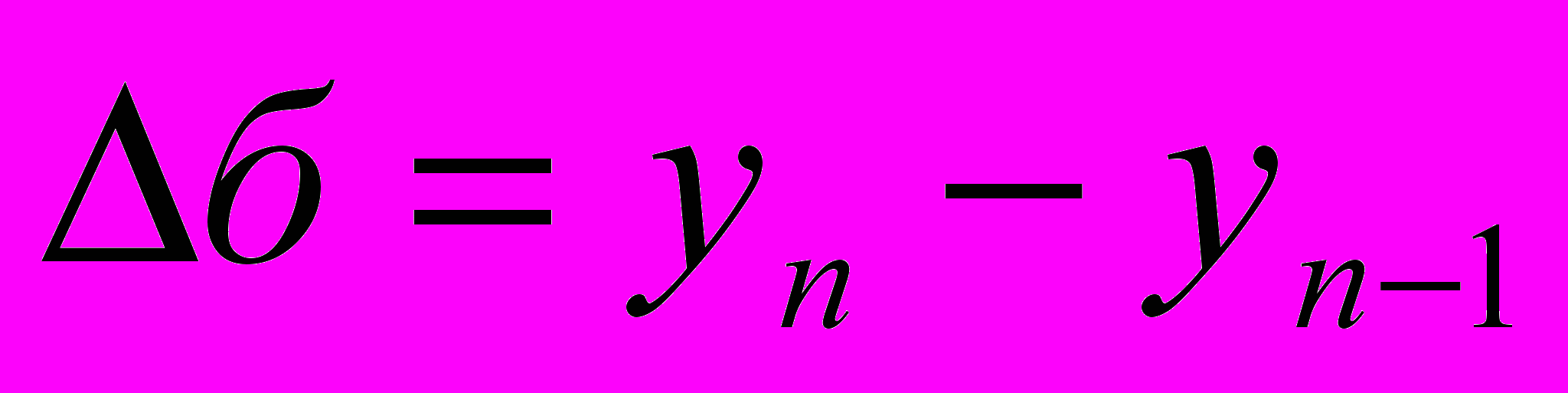 - базисный
- базисный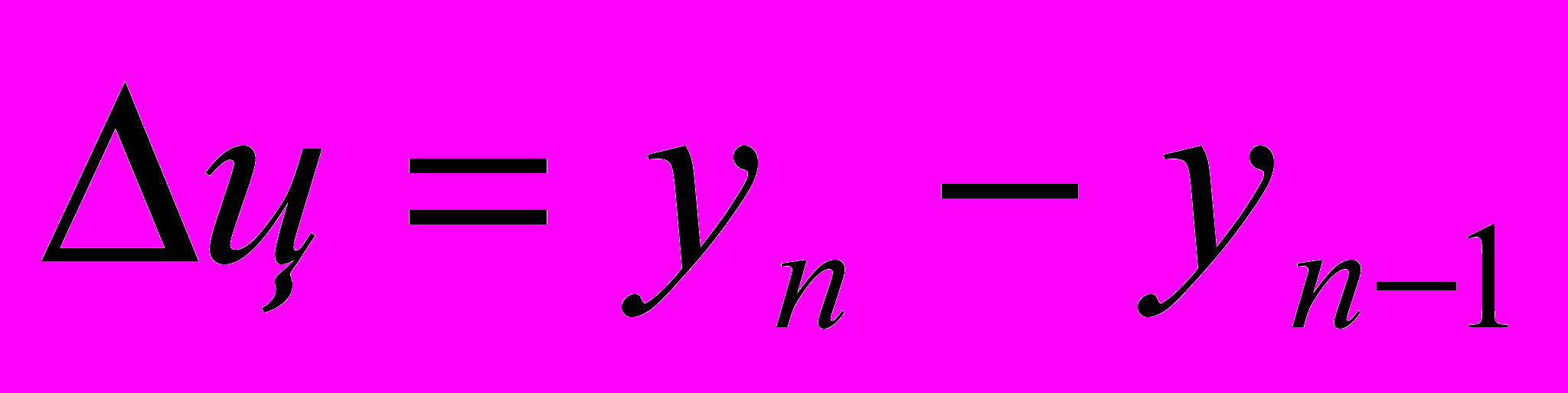 - цепной
- цепной2. коэффициент роста
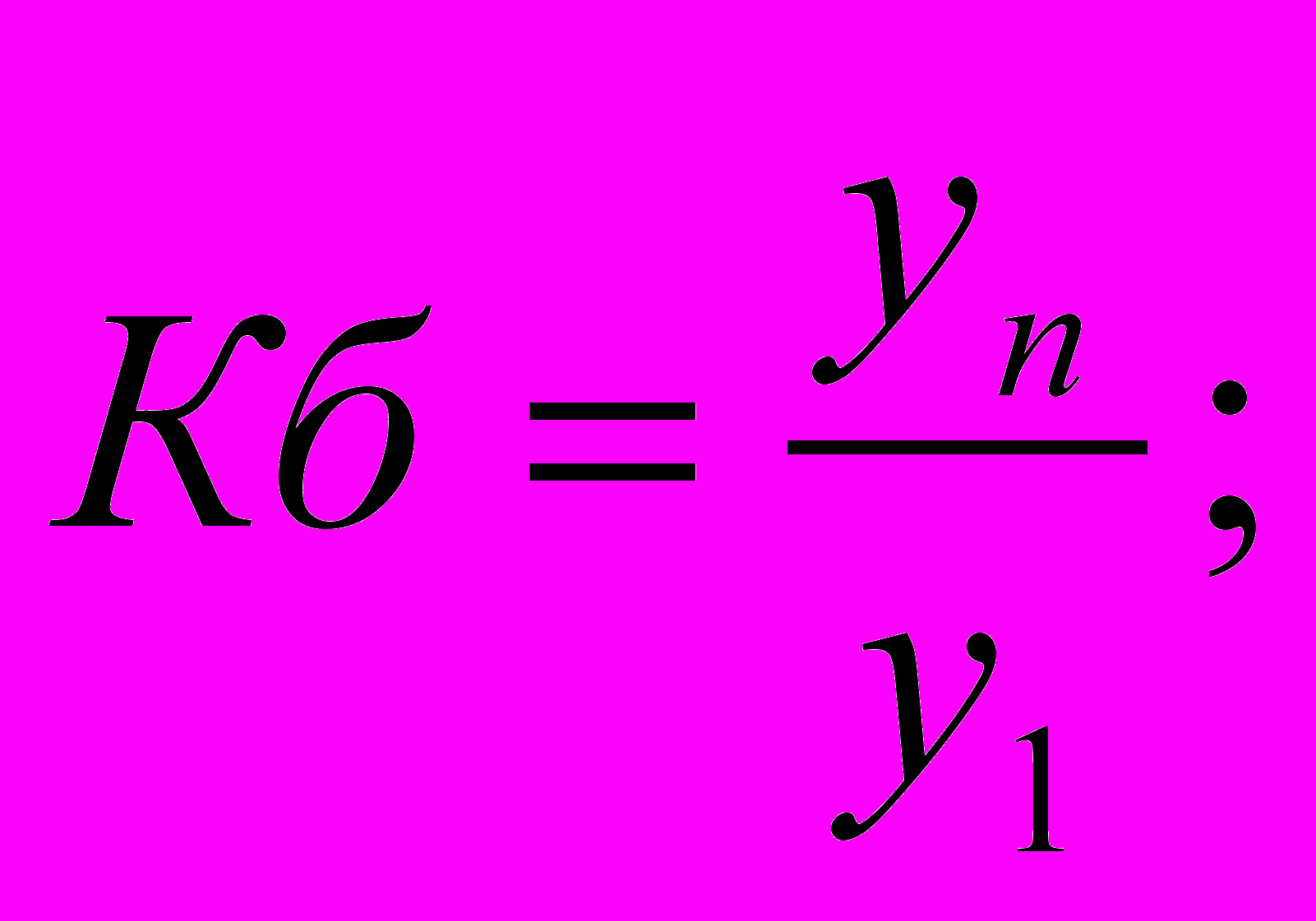
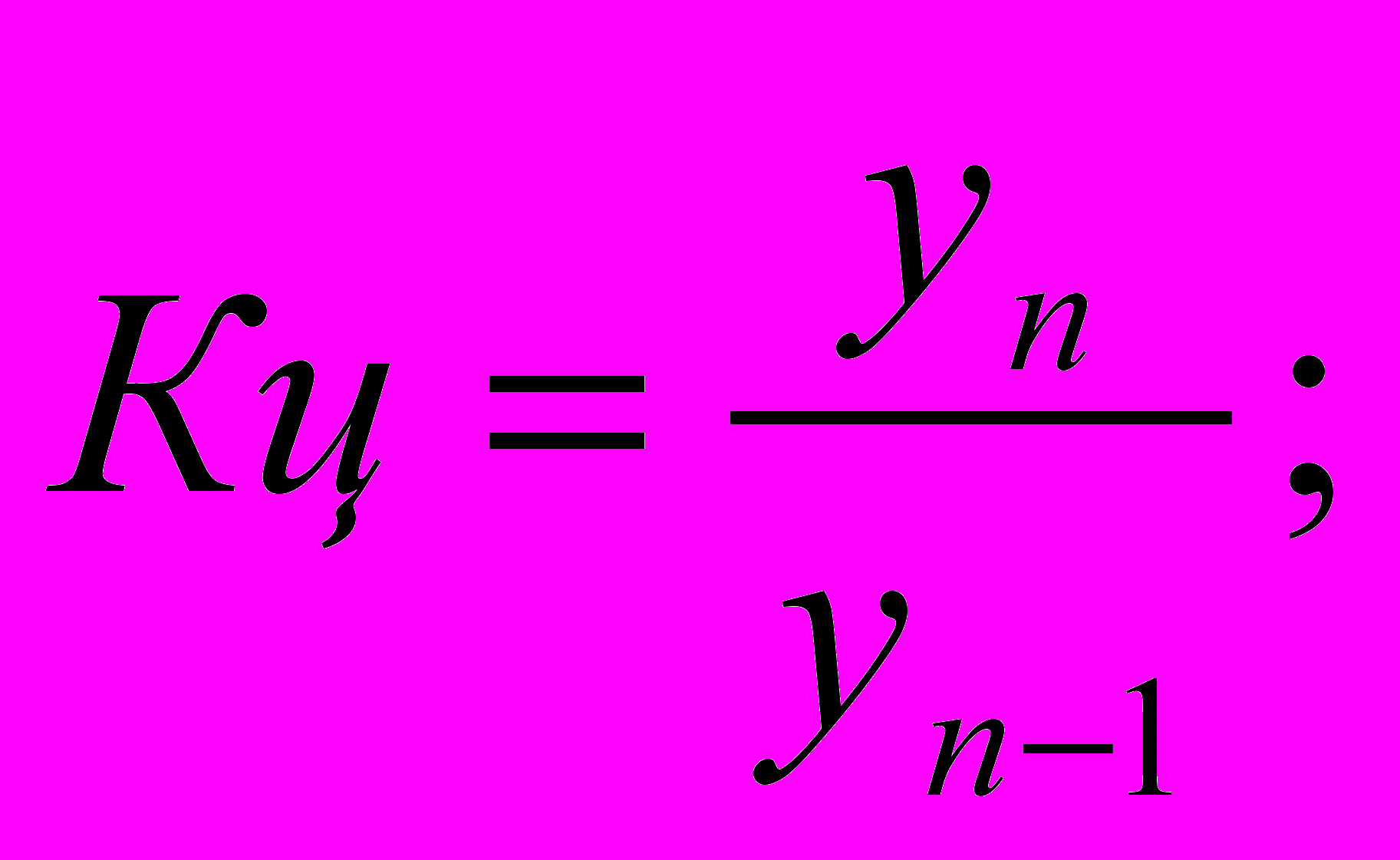
3. темп роста
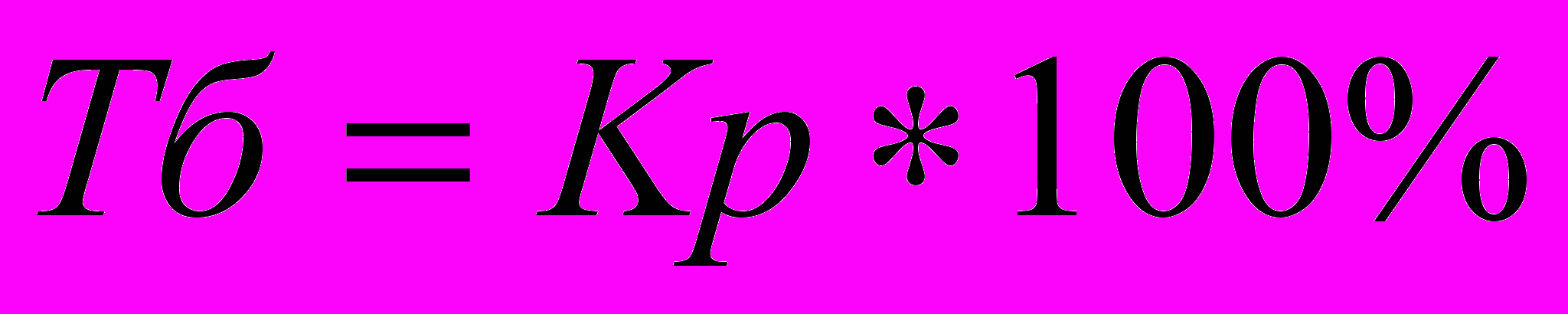
4. темп прироста
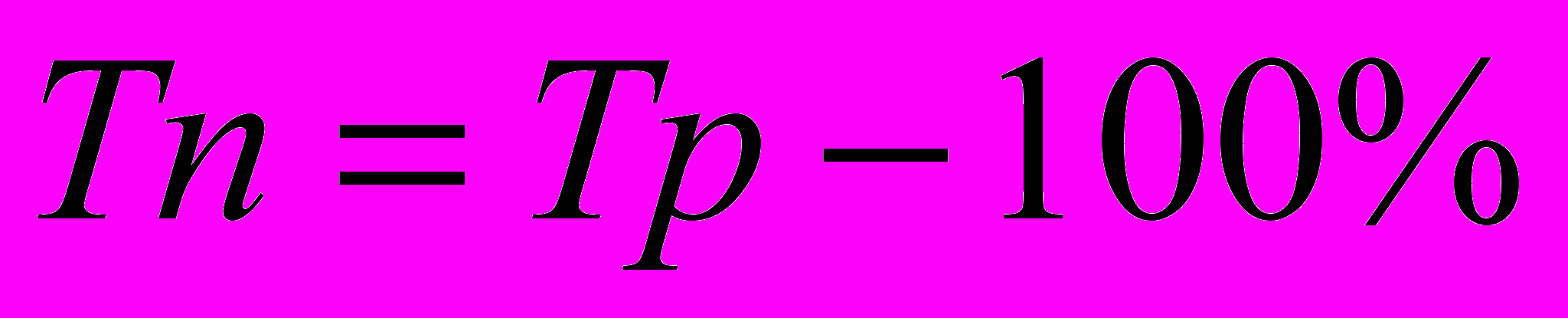
5. абсолютное значение 1% прироста
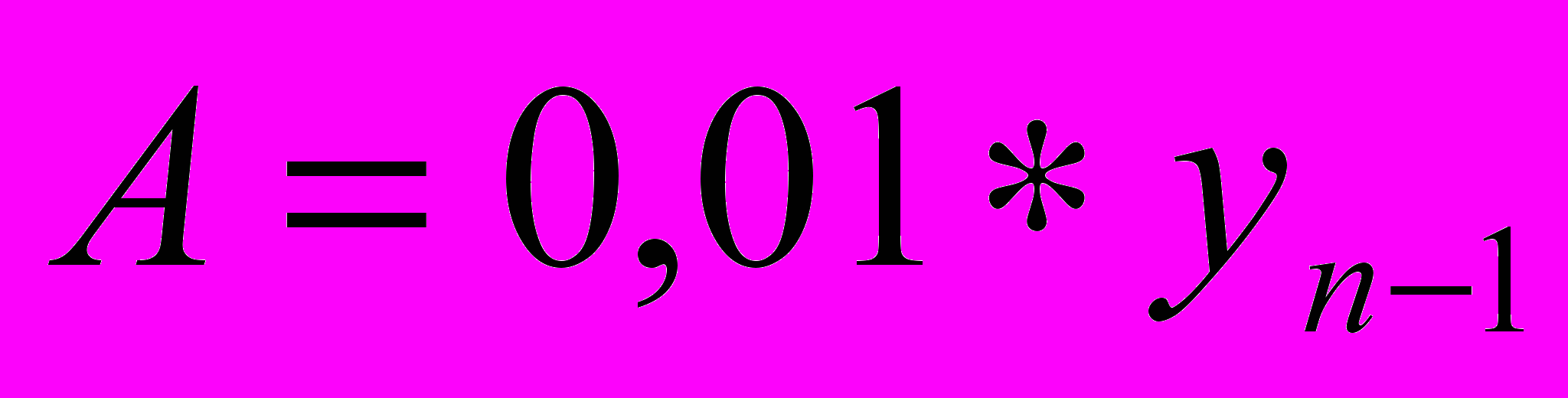
3) Средние показатели динамичности ряда.
Для обобщения характеристик динамики исследуемого явления за ряд периодов определения различного рода средние показатели, основными из которых являются:
- средние показатели уровней ряда;
- средние показатели изменений уровней ряда.
Определение средних уровней ряда.
а) Для интервального временного ряда абсолютных показателей средний уровень ряда за период, определенный по формуле средней арифметической простой:
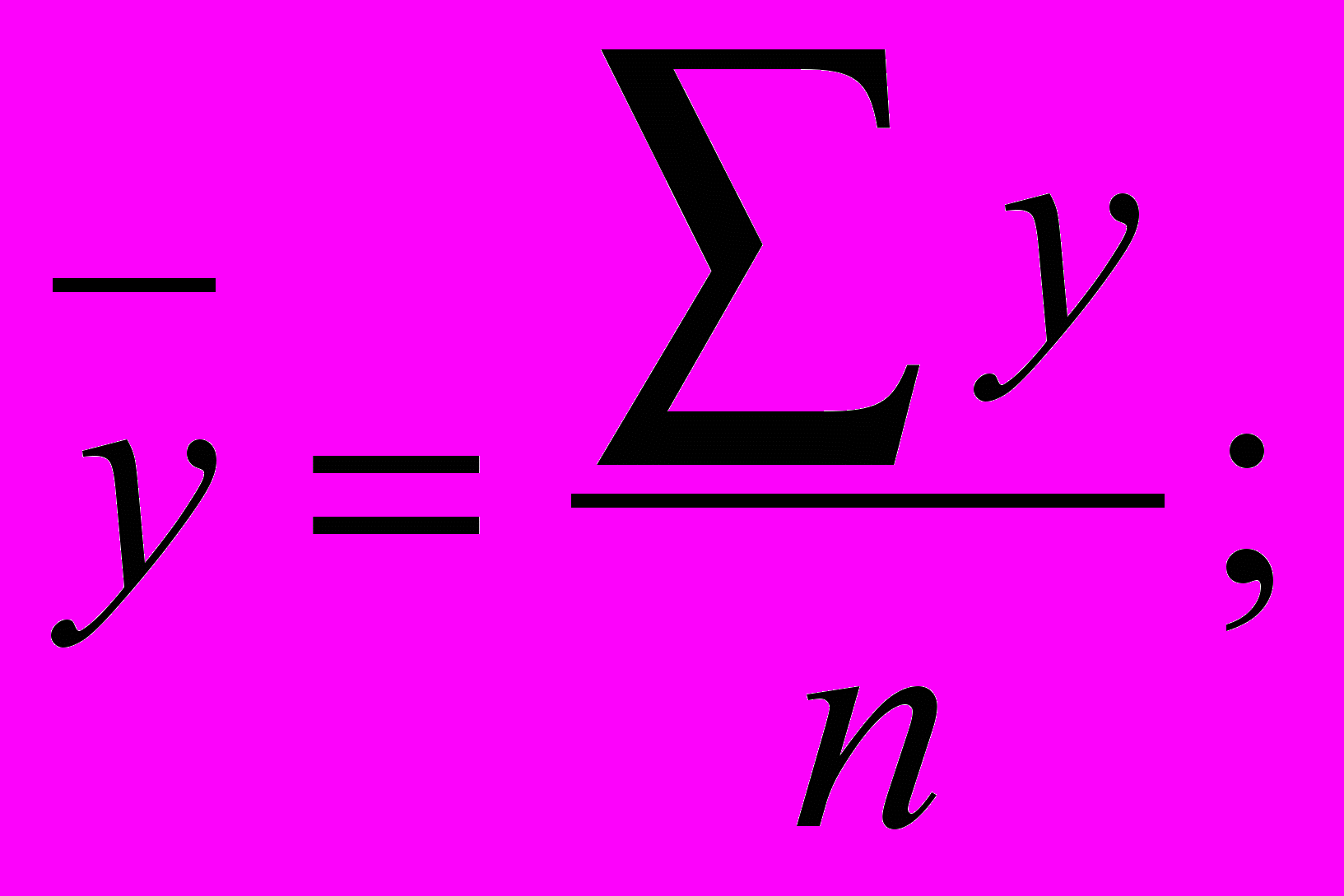
б) для моментного временного ряда с равным промежутком между датами равна удаленным датам друг от друга средних уровней ряда может быть рассчитана по формуле средней хронологической:
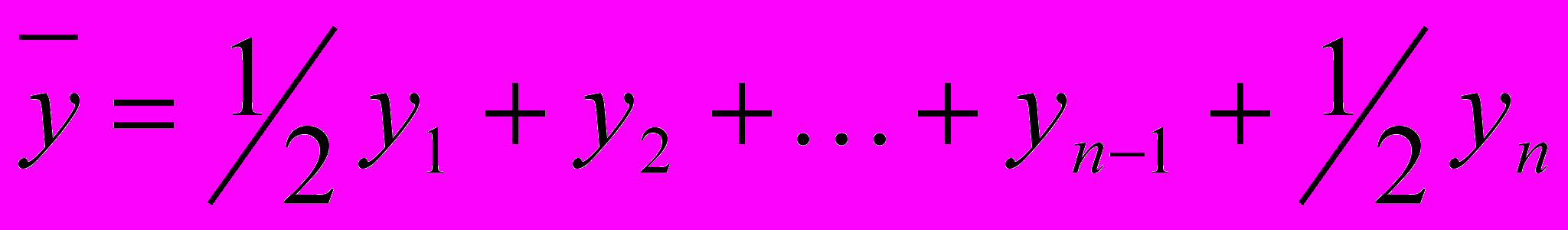
в) для определения средней уровня моментного ряда с неравным промежутком средней уровня определяется по средней арифметической взвешенной:
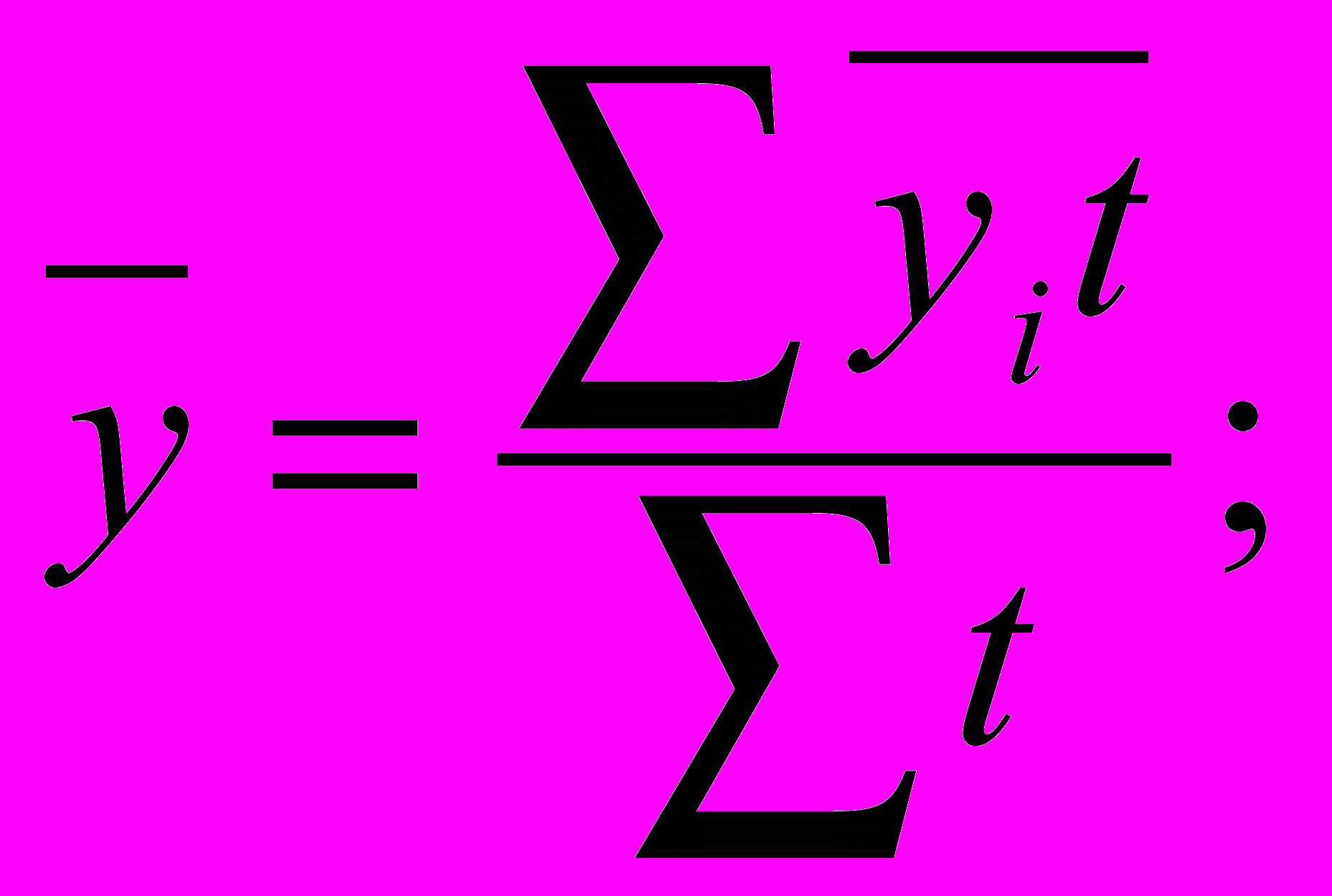
где t – количество дней, месяцев между смешенными датами.
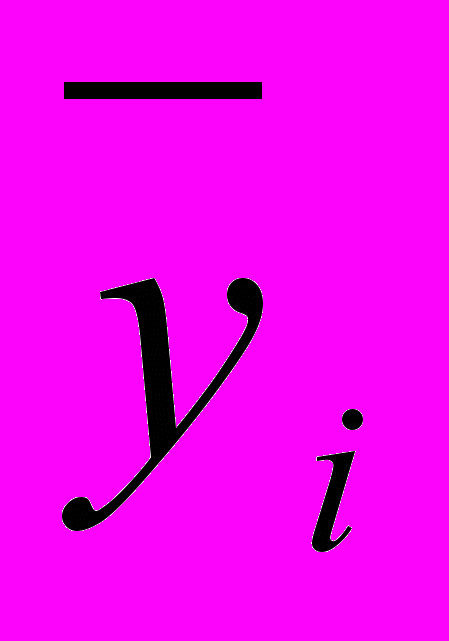 - средняя арифметическая простая 2-х смежных уровней
- средняя арифметическая простая 2-х смежных уровнейСредний показатель изменения уровня ряда:
а) средний абсолютный прирост
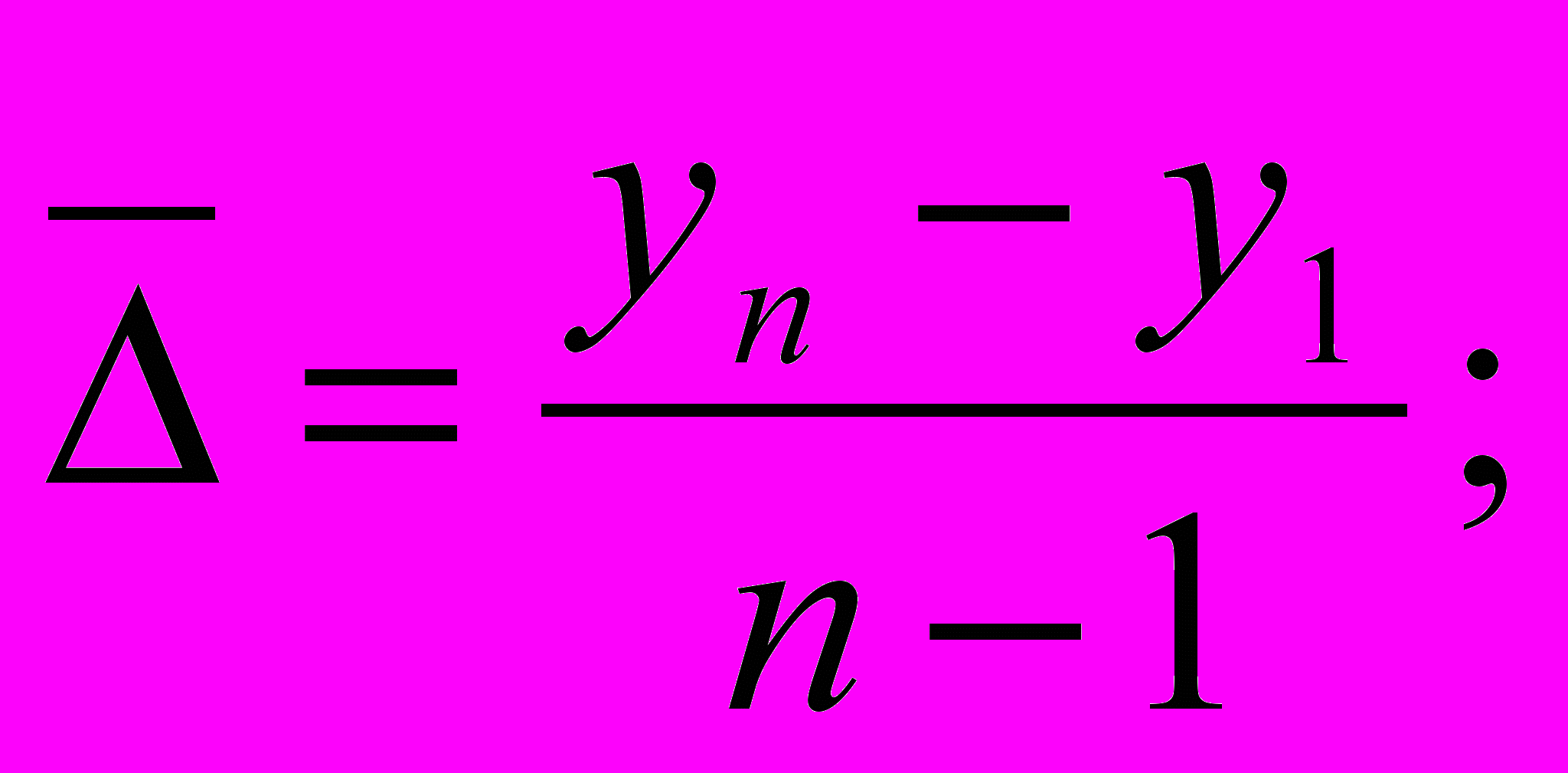
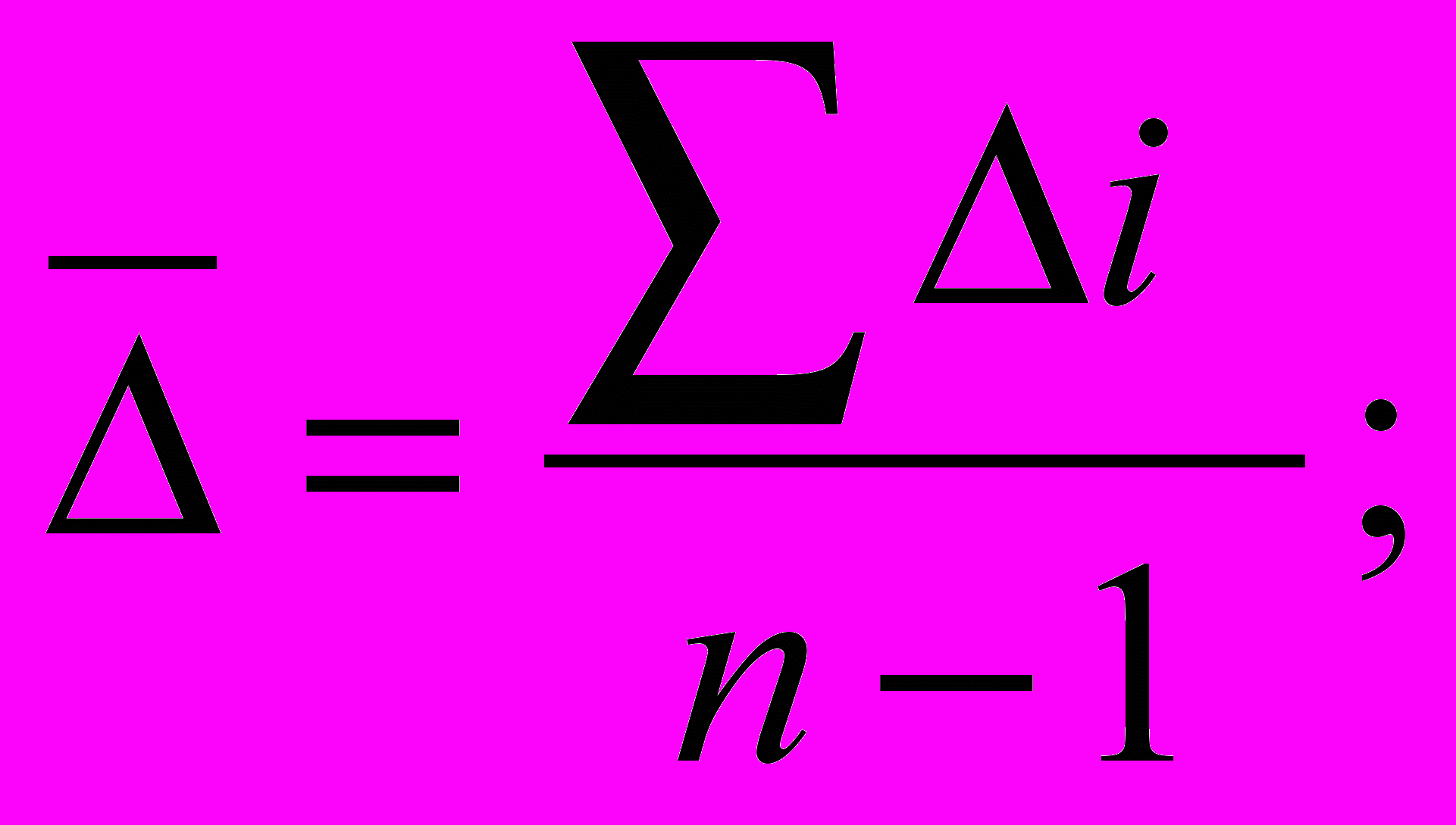
б) коэффициент роста
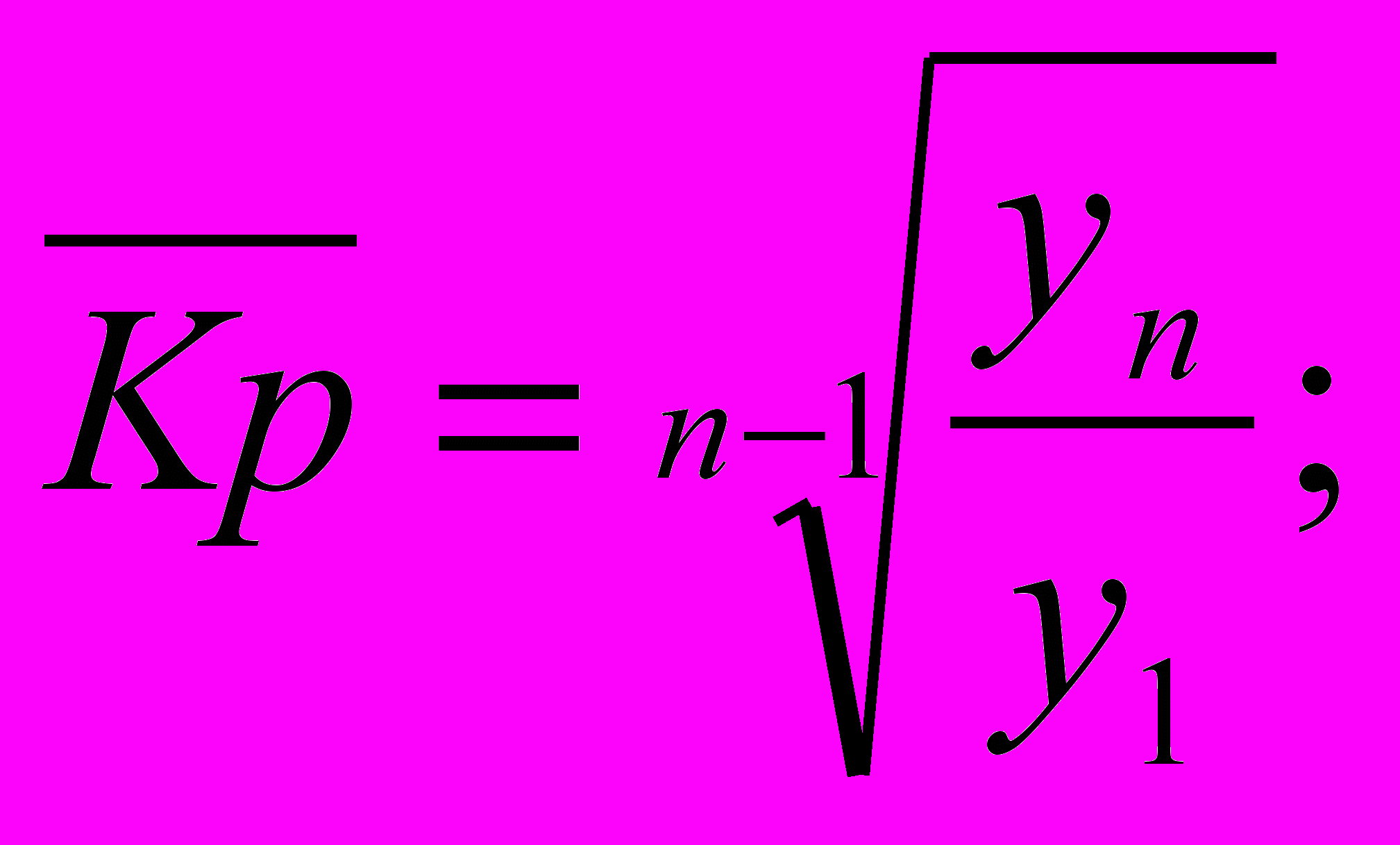
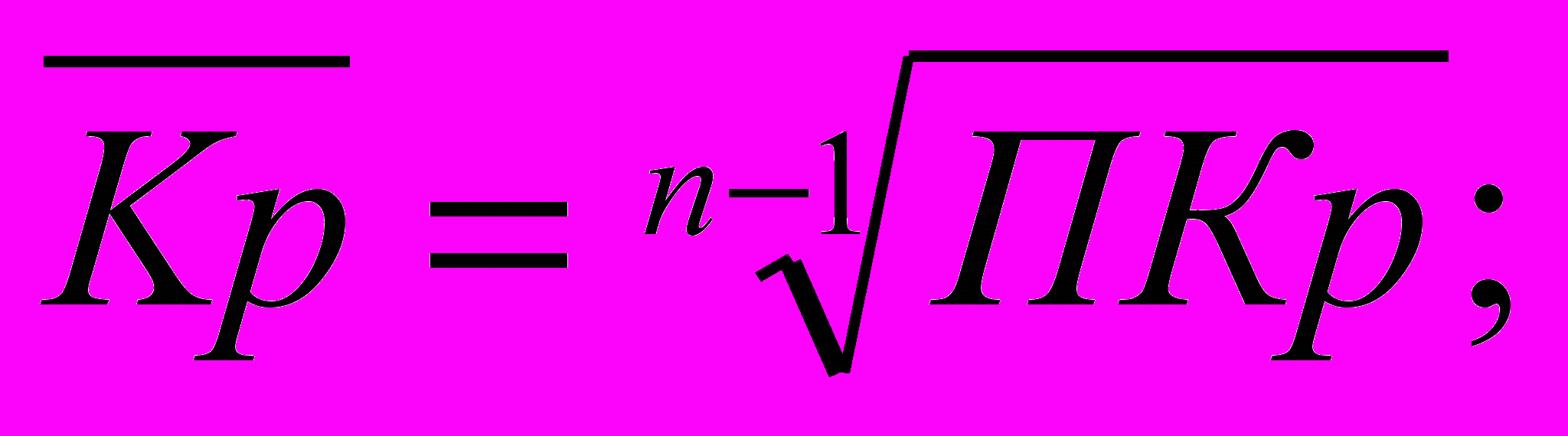
в) средний темп роста
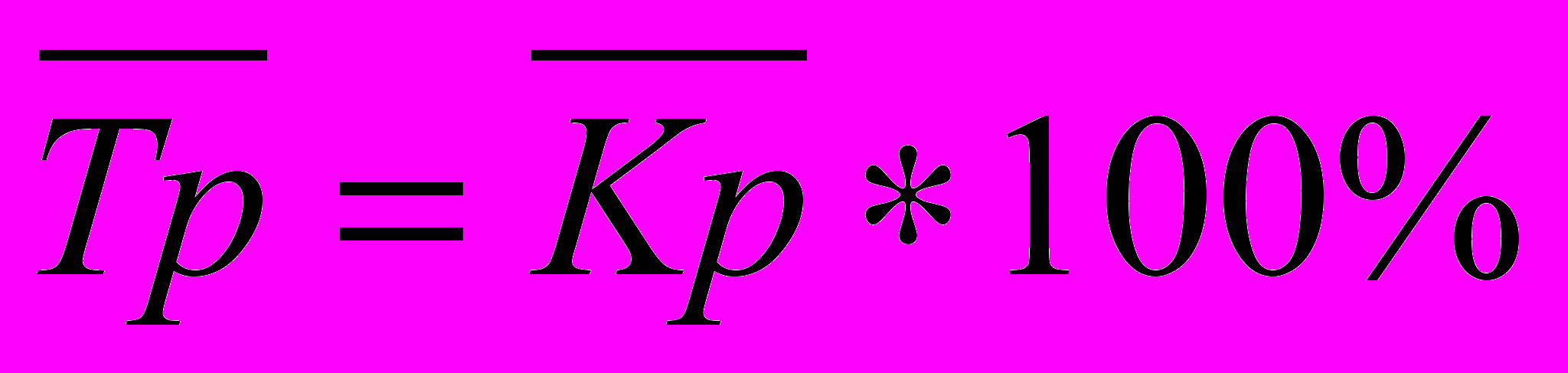
г) темп прироста
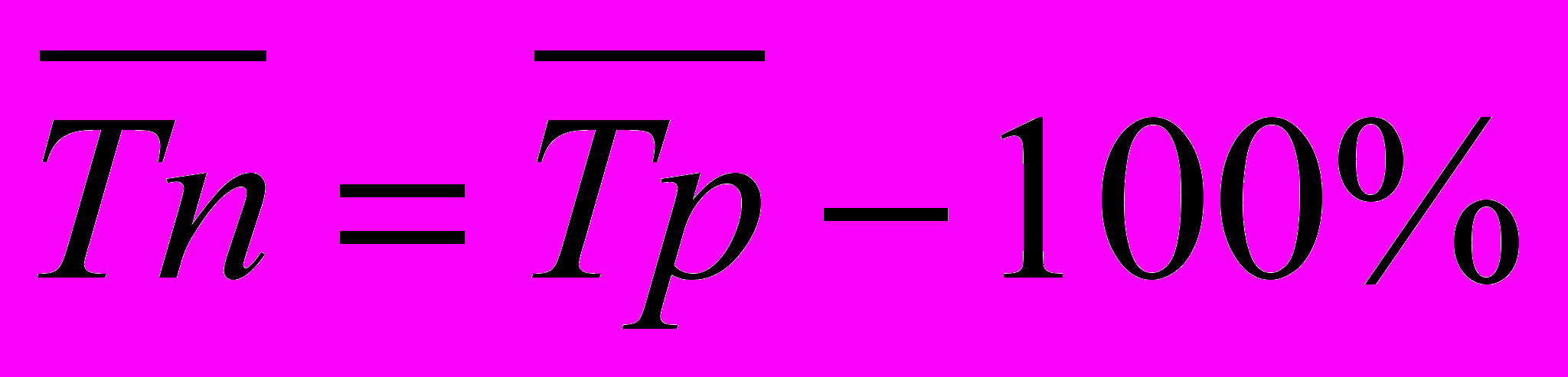
4) Выявление основной тенденции динамики.
При анализе ряда динамики, возникает задача выявления основной тенденции развития исследуемого явления. Такая задача возникает при изучении сезонных колебаний, при прогнозировании данного явления на будущее и других случаях. Существует несколько методов выявления, основными из которых являются:
- Сглаживание рядов динамики с помощью скользящей средней;
- Аналитическое выравнивание уровня ряда по прямой.
1) Для определения скользящей средней формируются укрупненные интервалы, состоящие из одинакового числа уровней, каждый последующий интервал получается, постепенно сдвигаясь от начального уровня динамического ряда на 1 уровне, тогда 1 интервал будет в себя включать следующие уровни:
I
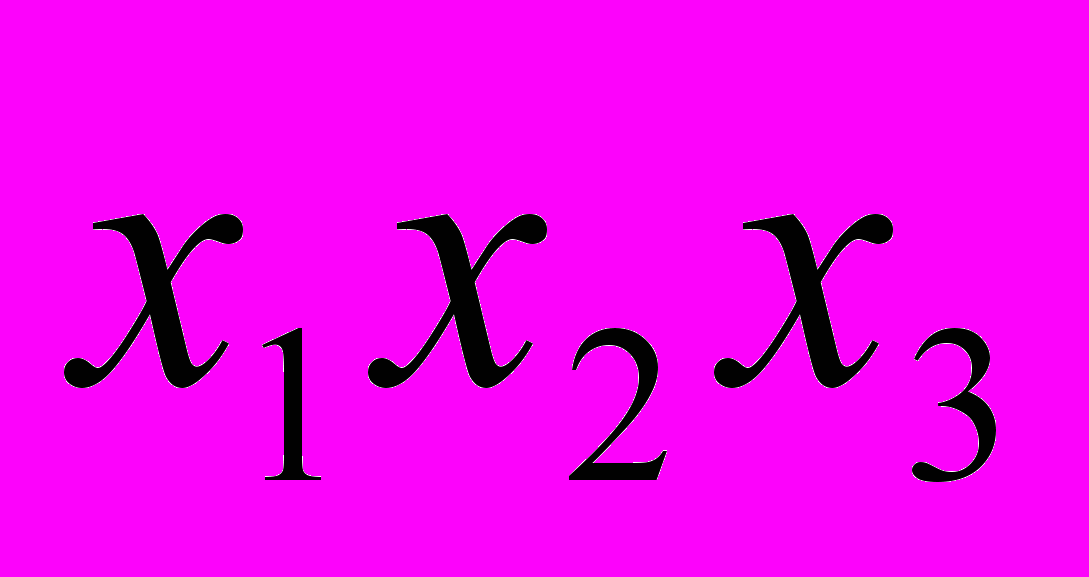
II
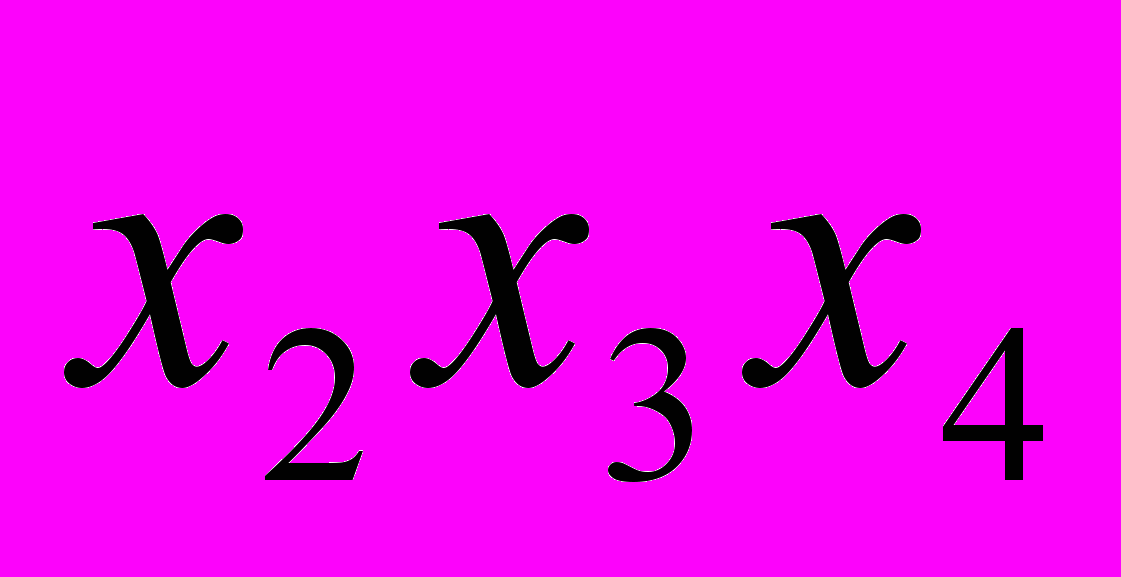
III
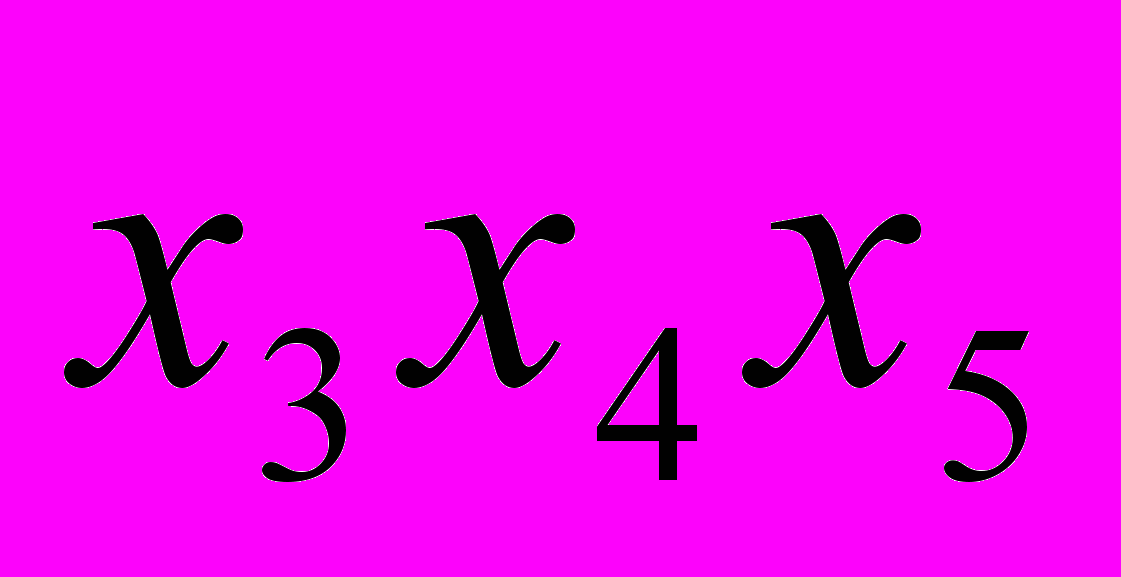
Так интервал сглаживается и как бы скользит по динамическому ряду с шагом равным 1. По сформулированным укрупненным интервалам определяют сумму значений уровней, на основе которой рассчитываются скользящие средние.
Полученные средние относятся к середине укрупненного интервала.
2) Аналитическое выравнивание ряда динамики по прямой имеет перед собой задачу найти плавную линию развития изучаемого явления (тренд), который будет характеризовать основную тенденцию динамики. Для того чтобы представить количественную тенденцию используют различные математические функции, прежде всего на график наносят фактические уровни ряда динамики, которые будут представлены в виде ломаной линии. Полученный график будет отражать, как основную тенденцию динамики, так и различные отклонения от нее, вызванные различными факторами.
Чтобы выявить основную тенденцию нужно выразить эту ломаную линию, т.е. нужно построить тренд:

Тренд
В основе подбора или построения тренда берутся функции выражающие функцию зависимость уровней ряда от времени.
В основе подбора наиболее подходящей функции должен лежать теоретический анализ сущности данного явления. Если теоретический анализ показывает, что данное явление развивается в арифметической прогрессии, т.е. с равными абсолютными приростами, то в таком случае для построения тренда применяется уравнение прямой. Если теоретический анализ показывает, что данное явление развивается в геометрической прогрессии, т.е. с равными относительными приростами, то необходимо применять функции кривых. Например: линейно-логарифмических.
Выравнивание уровней ряда по прямой.
Может быть выражено следующей формулой: yt=a+Bt или yx=a0+a1x,
где yt – выровненное значение уровней динамики ряда (представляет собой ординаты точек прямой)
t – показатель времени (моментные, интенсивные).
Задача аналитического выравнивания сводится к тому, чтобы фактические уровни ряда заменить теоретическими (выровненными, расчетными), т.е. вычисленными с помощью уравнения приведенного выше.
Данная задача решается с помощью метода наименьших квадратов, суть которых в том, что сумма квадратов отклонений (т.е. разность между фактическим и теоретическим уровнем была минимальной)
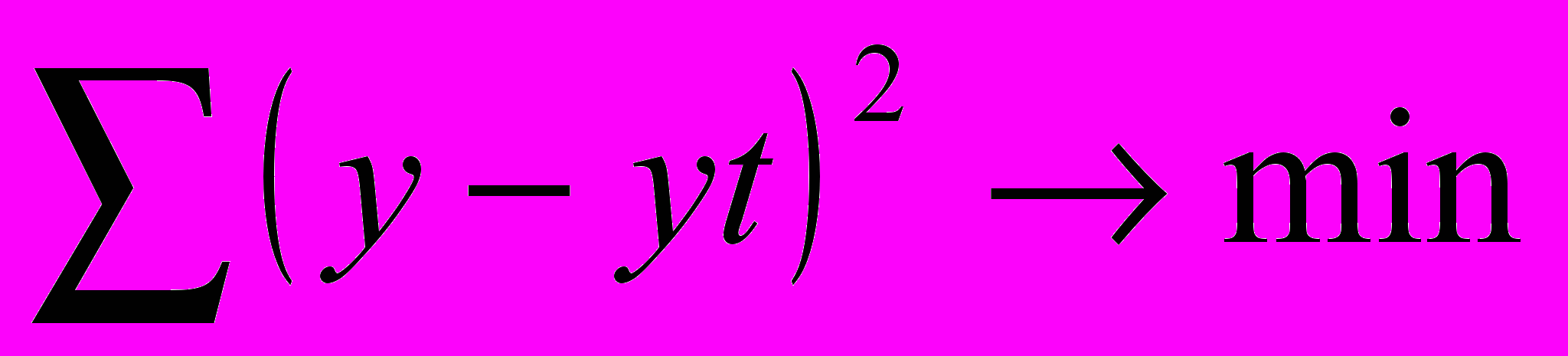
Используя метод наименьших квадратов уравнения прямой, может нам дать систему 2-х нормальных уравнений:
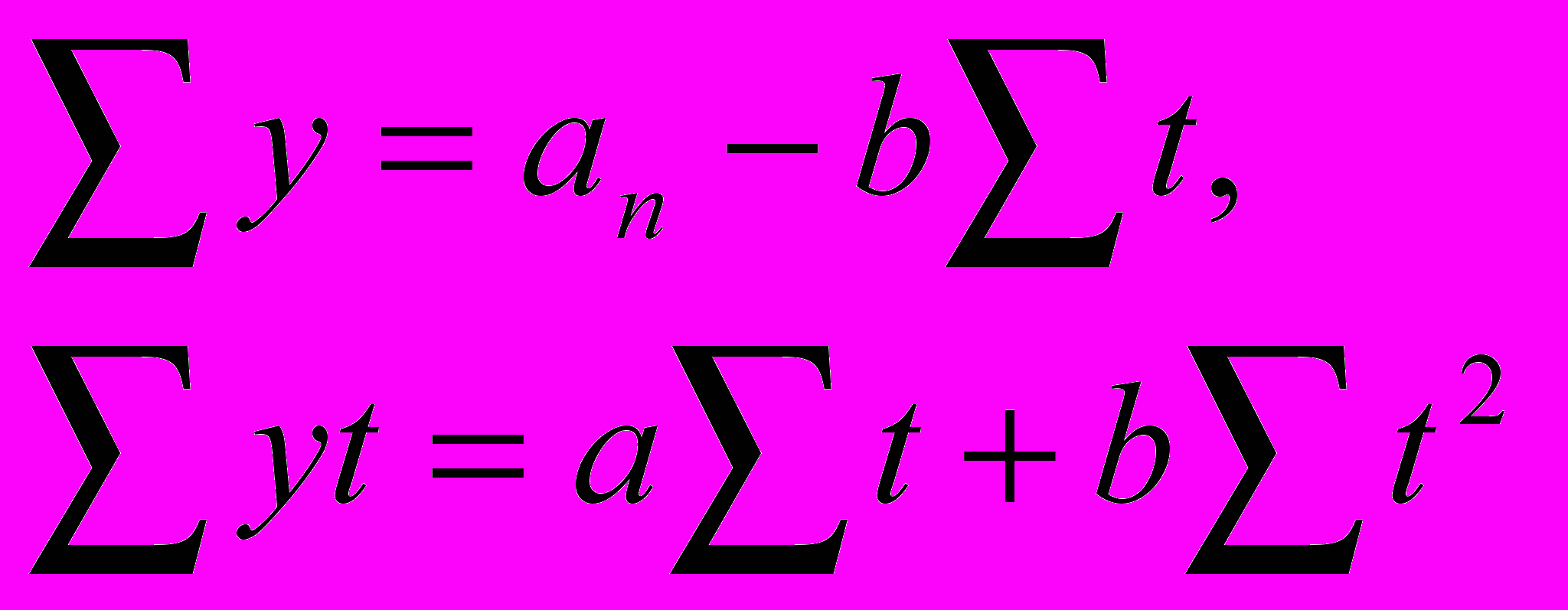
Т.к. в рядах динамики значение t является показателем времени, то всегда им можно придать такое значение, чтобы их сумма была равна нулю.
Если сумма t=0, то система принимает следующий вид:
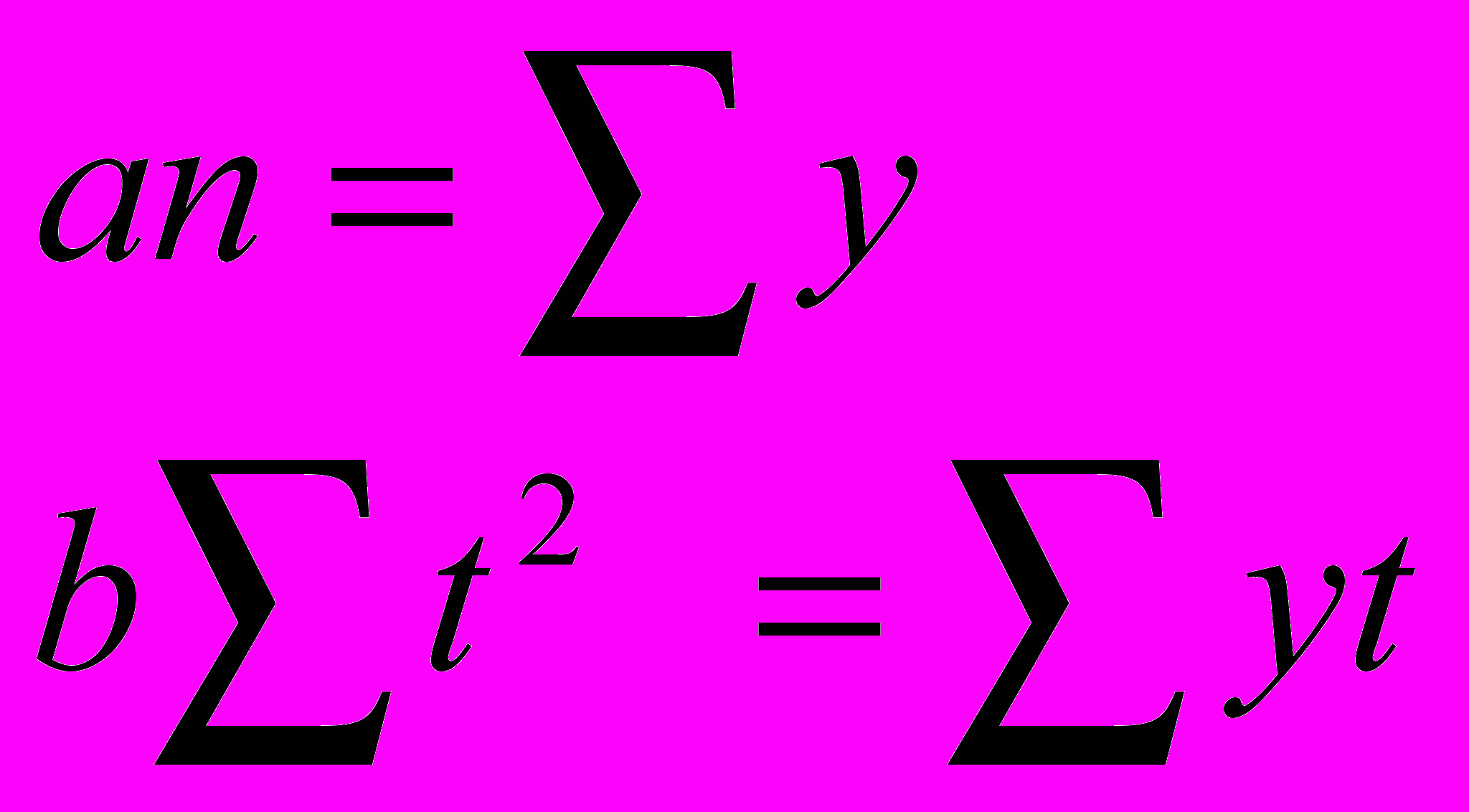
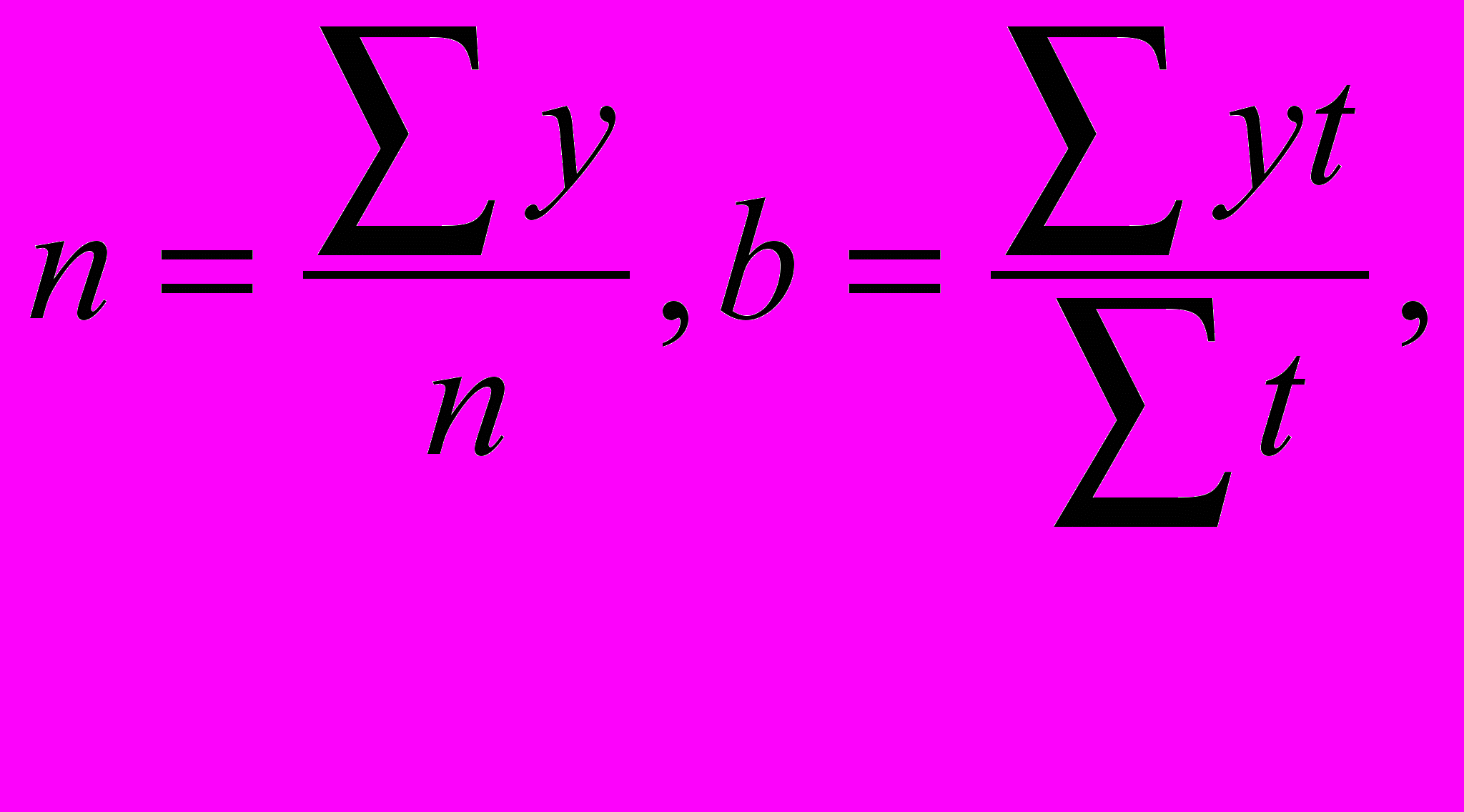 где n – количество временных дат или уровней ряда.
где n – количество временных дат или уровней ряда.Аналитическое выравнивание может быть проведено и по функциям более высокого порядка таким же образом с использованием метода наименьших квадратов.
5) Приемы изучений сезонных колебаний.
Сезонными колебаниями называют более или менее устойчивые внутригодовые колебания в рядах динамики, обусловленными специфическими условиями производства и потребления данного товара.
Сезонные колебания характеризуются специфическими показателями, которые называются индексами сезонности, совокупность которых образует сезонную волну.
Индексом сезонности называется средняя, вычисленная из процентных отношений по одноименным месяцам фактических уровней к выровненным уровням.
Для выявления сезонных колебаний обычно берут данные за несколько лет, распространенно чаще всего по месяцам. Несколько лет (обычно не менее 3-х) берутся для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы сезонные условия 1 года.
Если динамический ряд не содержит определенных тенденций развития, то прежде, чем вычислить сезонную волну фактические данные должны быть обработаны таким образом, чтобы была выявлена общая тенденция развития явления.
Для этого используют аналитическое выравнивание ряда.
Формула для расчета индекса сезонности имеет следующий вид:

Если исходный временной ряд содержит ярко выраженную тенденцию в развитии, то индекс сезонности непосредственно исчисляется по фактическим данным, без предварительного выравнивания, тогда формула расчета индекса сезонности принимает следующий вид:

-
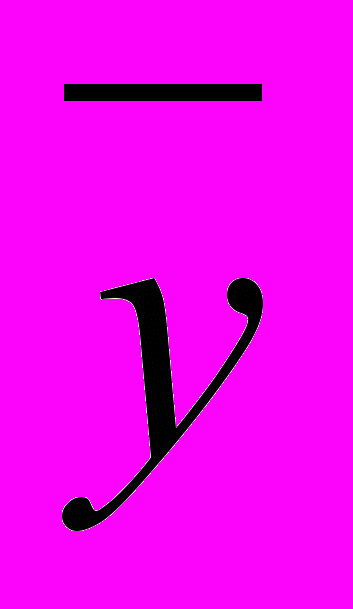 постоянная общая средняя
постоянная общая средняя-
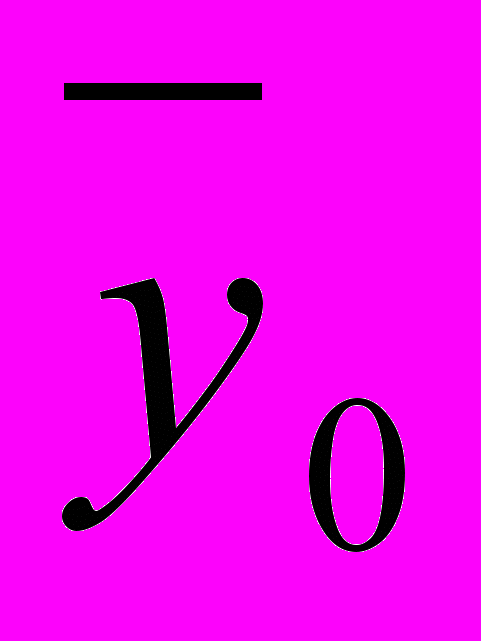 средняя за исследованные годы
средняя за исследованные годы
