Тема Ряды динамики Все явления изменяются во времени, вместе с этим изменяются и их количественные (в частности, статистические) показатели

Вид материала

Документы

Содержание 7.2. Характеристики рядов динамики Средний уровень ряда динамики Абсолютный прирост –это величина, равная разности между уровнями показателя. Средний абсолютный прирост Средний темп роста Коэффициент опережения Абсолютное ускорение роста Коэффициент ускорения Абсолютное значение одного процента прироста – 7.3. Определение тенденций развития Контрольные вопросы Тема 8. Индексы 8.1. Индивидуальные и общие индексы 8.2. Агрегатные индексы 8.3. Расчет агрегатных индексов путем усреднения индивидуальных 8.4. Факторный анализ 8.5. Общий индекс средних величин Себестоимость, грн./шт. Индекс объема Затраты труда на 1 изд,час ... Полное содержание

Подобный материал:

• Ряды динамики, 73.43kb.
• Лекция №6 «Ряды динамики», 196.16kb.
• Внешняя трудовая миграция, 178.75kb.
• Задачи и виды группировок Статистические ряды распределения Абсолютные показатели, 18.57kb.
• Содержание Обобщенная модель управления запасами, 372.31kb.
• 1 измерение температуры. Шкалы температур. Классификация методов и приборов температурой, 948.25kb.
• Конспект лекций по дисциплине Статистика Модуль, 213.5kb.
• Кыргызско-турецкий университет «манас» силлабус, 108.52kb.
• Анализ работы районного методического кабинета управления образования администрации, 1331.86kb.
• Методика лечебного голодания по Бухингеру, 67.58kb.

Тема 7. Ряды динамики

Все явления изменяются во времени, вместе с этим изменяются и их количественные (в частности, статистические) показатели. Ряд динамики (временной, хронологический ряд) – это последовательность статистических показателей, изменяющихся в зависимости от времени. Эти показатели описываются функциями времени y(t_i).

7.1. Виды рядов динамики

Различают моментные и интервальные ряды динамики (РД). Моментные РД описывают последовательности показателей в дискретные моменты времени t_i.


Пример 7.1. Деньги на счету клиента банка на 1-е число каждого месяца представлены моментным РД (тыс. грн.) рис.7.1.




Рис.7.1


Интервальные РД характеризуют последовательности показателей в смежные интервалы времени t_i.


Пример 7.2. Поквартальные инвестиции во внедрение сотовой связи (в млн. грн.) представлены интервальным РД рис.7.2.



Рис.7.2

Кроме того, РД классифицируют на одномерные (для одного показателя) и многомерные (для двух и более показателей). Наглядное представление одномерных рядов дают графики (диаграммы). Для многомерных рядов динамики обычно используют табличное представление показателей.
^

7.2. Характеристики рядов динамики

Наиболее распространенными характеристиками РД являются:

• средний уровень y ;
  
• абсолютный прирост ;
  
• средний абсолютный прирост ;
  
• темп роста Т;
  
• темп прироста ;
  
• коэффициент опережения К_оп;
  
• абсолютное значение одного процента прироста А%.
  

^

Средний уровень ряда динамики

Д
ля интервальных РД с n равными интервалами средний уровень ряда определяется обычным средним арифметическим

г
де y_i=y(t_i) – показатели на i-м интервале. Для неравных интервалов t_i используется формула среднего взвешенного


П
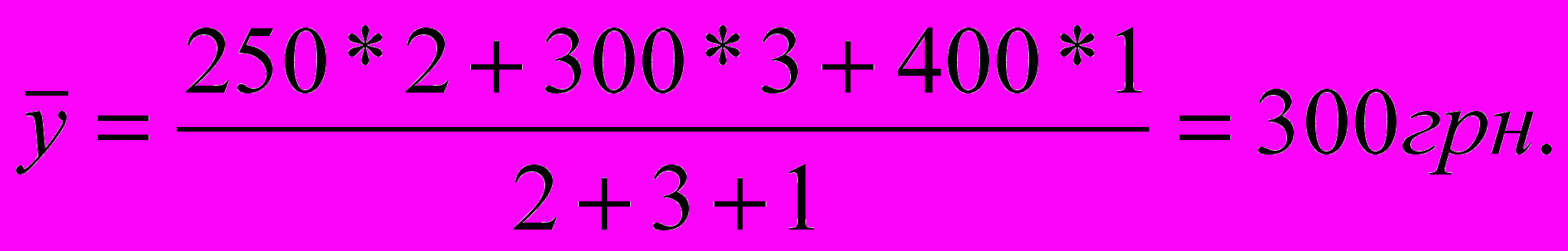
ример 7.3. Месячные заработки работников предприятия составляли в январе – феврале 250 грн., в марте – мае 300 грн., в июне – 400 грн. Согласно (7.2) среднемесячный заработок за полгода составляет

Д
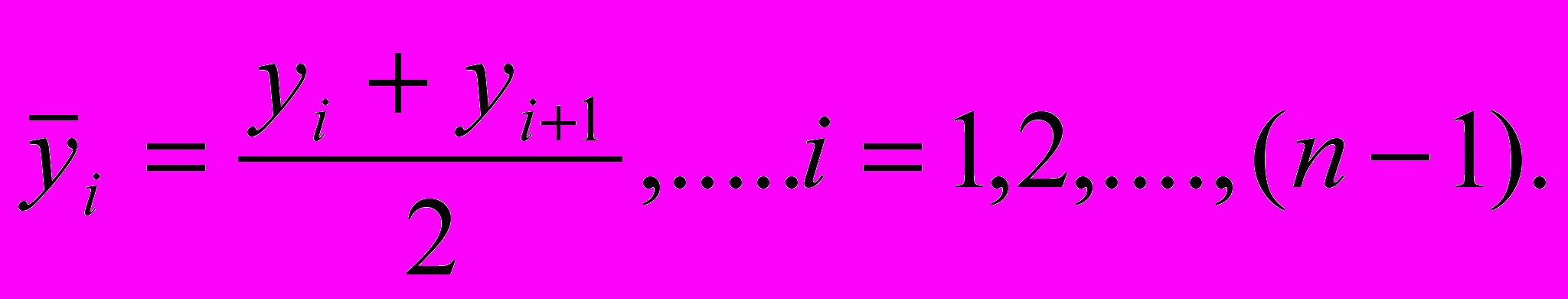
ля моментных РД среднее значение можно получить, если привести моментные показатели к интервальным. Для n смежных моментов среднее интервальное значение показателя равно

П
рименяя к среднему интервальному формулу (7.1), получим

Для неравных интервалов, соответственно

г
де t_i – длительности интервалов.


Пример 7.4. Состояние кассы на 1 число каждого месяца приведено в таблице (тыс. грн.)

ti	1.01	1.02	1.03	1.04	1.05	1.06
yi	200	300	100	300	300	200

П
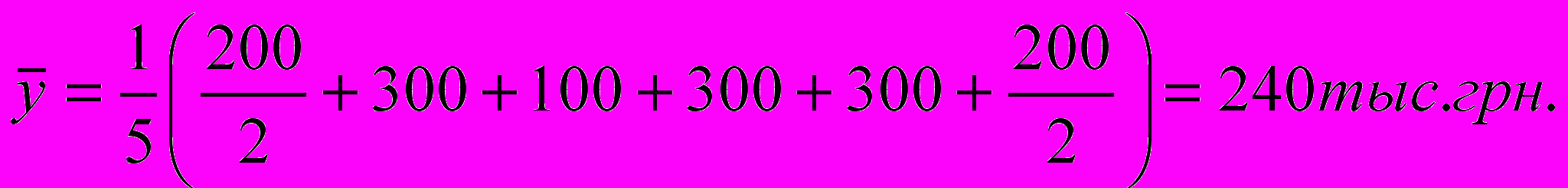
о формуле (7.4) имеем
^

Абсолютный прирост –это величина, равная разности между уровнями показателя.

Различают цепной абсолютный прирост

_i=y_i-y_i-1, i=2,3,…,n, (7.5)

и базисный абсолютный прирост

_ib=y_i-y_1, i=2,3,…,n. (7.6)

Они определяют соответственно приросты между смежными уровнями и между i-м уровнем и начальным. Очевидно, что базисный равен сумме цепных приростов




^

Средний абсолютный прирост

О
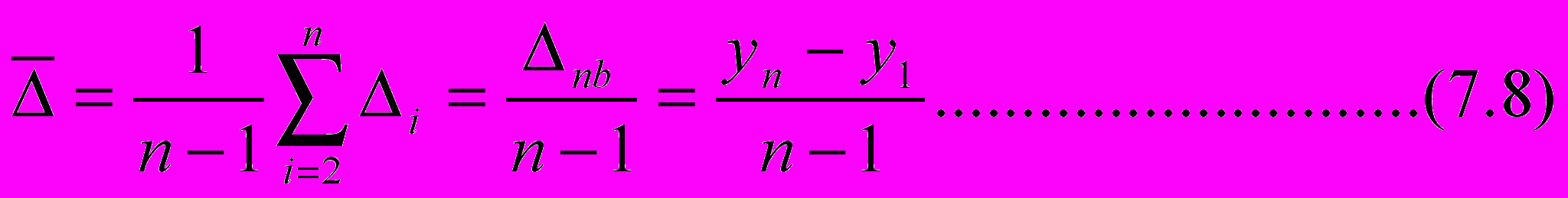
н определяется как среднее арифметическое цепных абсолютных приростов

Как видим, для его определения достаточно знать начальный и конечный уровни показателя.

Пример 7.5. Инфляция в январе 1993г. составляла 15% в месяц, а в январе 1994г. – 27%. Определить средний прирост инфляции в месяц за 1993г.

В
соответствии с (7.8)

Таким образом, инфляция возрастала в среднем на 1% в месяц.


Темп роста

В отличие от предыдущей характеристики темп роста является относительным показателем (безразмерным). По аналогии с приростами определим:

• ц
  епной темп роста
  

• б
  азисный темп роста
  

О
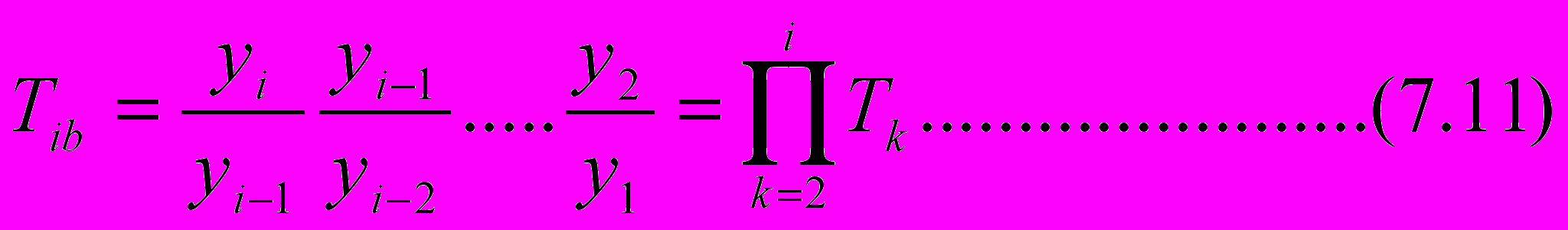
чевидно, что последний можно выразить через произведение цепных

^

Средний темп роста

П
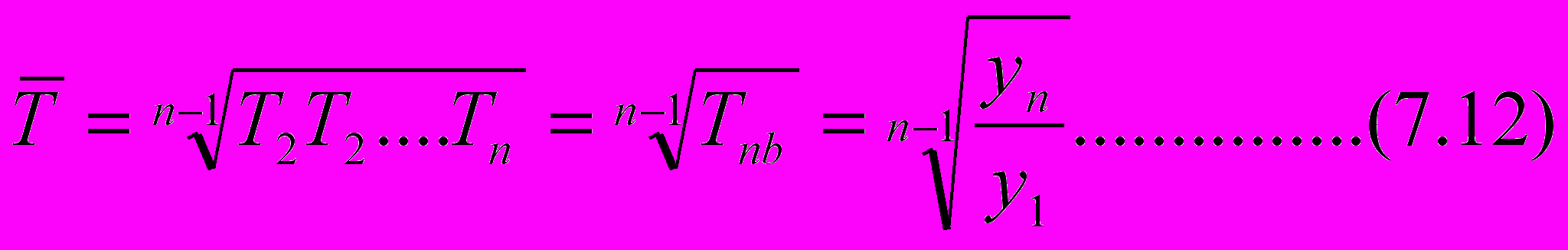
оскольку темп роста на общей длительности РД определяется произведением цепных, средний темп роста определяется как среднее геометрическое из (n-1) значений цепных темпов роста

Если интервалы РД неодинаковы, то они разбиваются на меньшие одинаковые интервалы и используется эта же формула, но постоянные темпы роста будут возводиться в соответствующие степени.

Пример 7.6. Средние цены на бензин А-95 в первом полугодии составляли (грн./литр)

январь	февраль	март	апрель	май	июнь
1,16	1,1	1,03	1,02	1,04	1,32

Определить цепные темпы роста и средний темп роста цен.

По формулам (7.10), (7.12) получим

T₂=1,1/1,16=0,948; T₃=1,03/1,1=0,936; T₄=1,02/1,03=0,99;

T
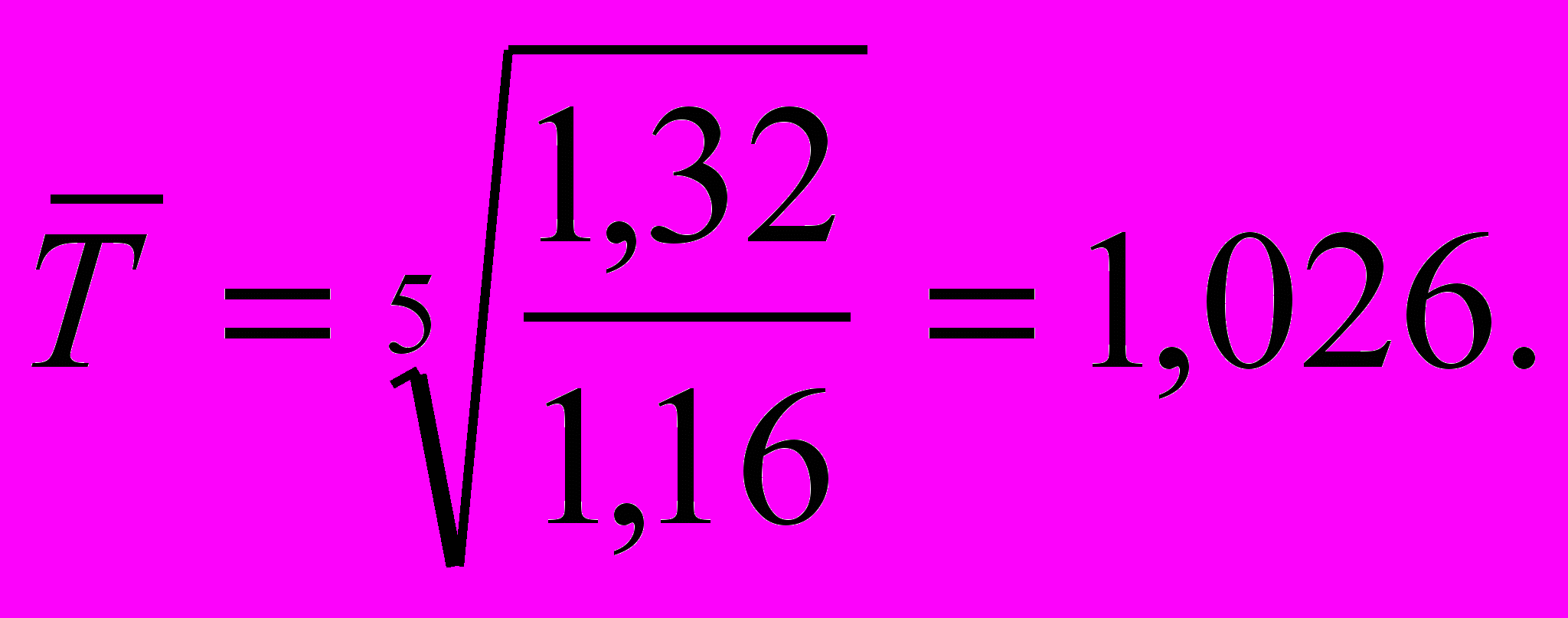
₅ =1,04/1,02=1,02; T₆=1,32/1,04=1,26;

Пример 7.7. Темпы роста курса ценных бумаг в январе – феврале составляли 1,05, а в марте – мае – 1,1. Определить средний темп роста за 6 месяцев (по отношению к декабрю предыдущего года).

С
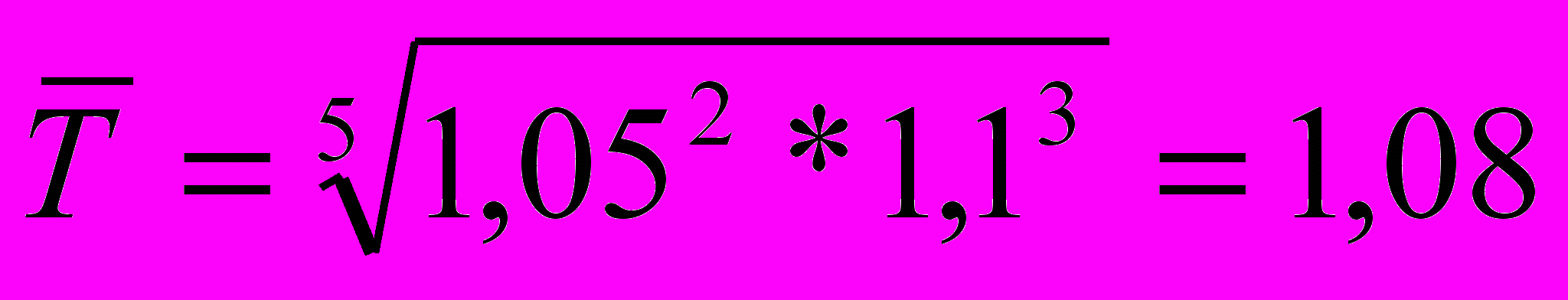
огласно (7.12)


Темп прироста

Он связан с темпом роста как

=Т-1. (7.13)

Здесь, как и ранее, определяются цепные и базисные темпы прироста. Средний темп прироста не определяется.

Часто темп прироста выражают в процентах, тогда величину  умножают на 100.


Пример 7.8. Определить цепные темпы прироста цен на бензин в примере 7.6 (в процентах).

₂%=94,8-100= -5,2%; ₃%=93,6-100= -6,4%; ₄%=99-100= - 1%;

₅%=102-100=2%; ₆%=126-100=26%.

Отрицательные приросты означают падение цен, а положительные – повышение. Скачки цен чаще всего порождаются искусственным дефицитом товара.


^ Коэффициент опережения

О
н определяется при сравнении двух РД как отношение базисных темпов роста этих рядов за одинаковый период времени

где в числителе и знаменателе записаны базисные темпы роста 1-го и 2-го ряда динамики соответственно.


Пример 7.9. За последние 20 лет валовой национальный продукт США вырос на 96%, а Сингапура – на 260%. Определить коэффициент опережения Сингапура.

Так как T_nb⁽¹⁾=3,6, a T_nb⁽²⁾=1,96, то К₀=3,6/1,96=1,84. Следовательно, по темпам роста ВНП Сингапур почти вдвое опережает США.


^ Абсолютное ускорение роста

Оно определяется как разность

_i= _i - _i-1=(y_i-y_i-1)-(y_i-1-y_i-2)= y_i+y_i-2-2y_i-1.

Для нарастающего ряда при _i>0 говорят об ускорении, а при _i<0 – о замедлении роста. Для убывающего ряда, наоборот, положительное _i свидетельствует о замедлении, а отрицательное – об ускорении роста.


^ К
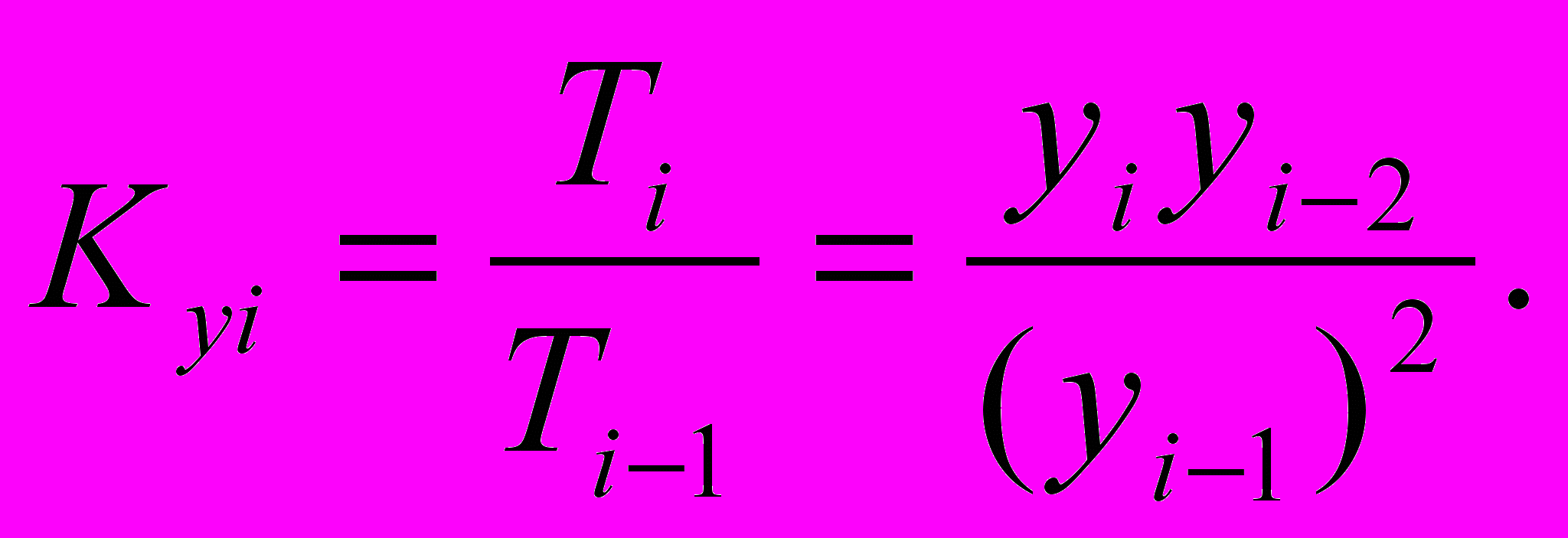
оэффициент ускорения

Это относительный показатель, равный

Очевидно, если К_у>1, имеет место ускорение, а при К_у <1 – замедление роста.


Пример 7.10. В течение 3-х лет уровень инфляции составлял 160%, 110% и 70%. Определить абсолютное ускорение и коэффициент ускорения.

Согласно приведенных определений


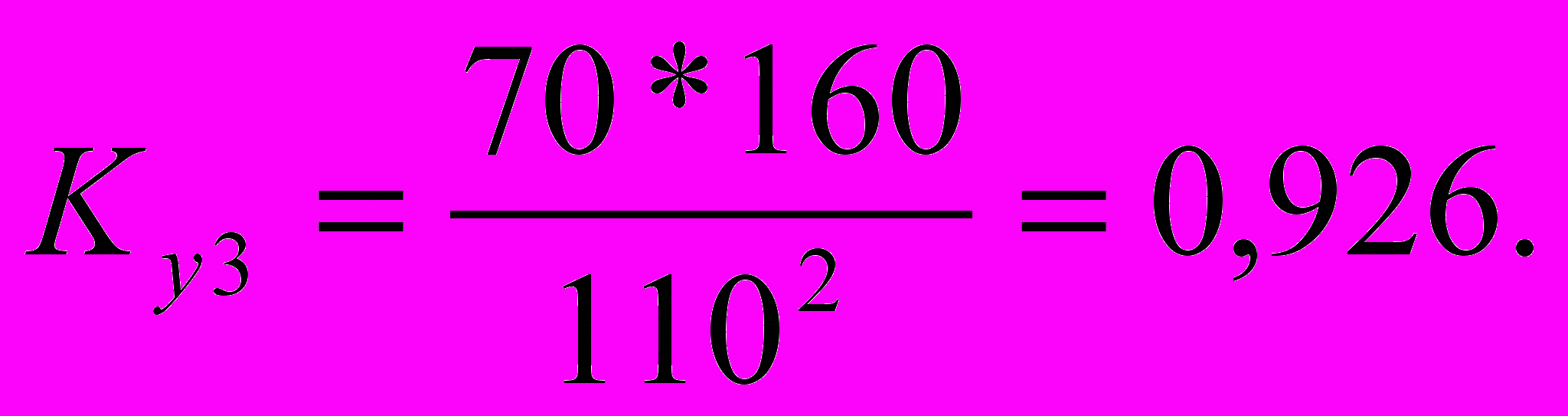
₃=70+160-2*110=10%,

Таким образом, для убывающего ряда динамики мы получили >0 и

К_у <1, т.е. имеет место замедление роста инфляции. Коэффициент ускорения более удобен как параметр ускорения (замедления), так как вывод не оговаривается условиями нарастающего или убывающего ряда.

^ А
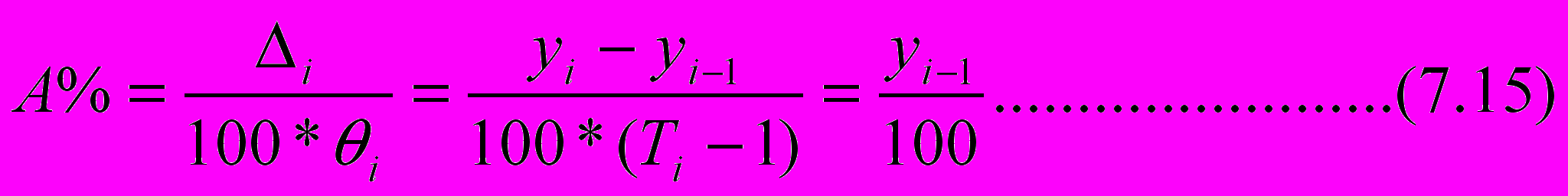
бсолютное значение одного процента прироста – это отношение абсолютного прироста к темпу прироста, выраженному в процентах

Как видим, этот показатель не зависит от прироста, а определяется как сотая доля предшествующего уровня РД. Например, если в прошлом году курс доллара составлял 3,6 грн., то значение А%=3,6 коп.
^

7.3. Определение тенденций развития

Ряды динамики в определенные периоды имеют тенденции (тренды) к росту, падению, ускорению, замедлению. Эти временные зависимости (функции) наиболее наглядно представляются графиками (диаграммами). В непрерывном времени характерные тренды изображены на рис.7.1 (а – равномерные тренды роста и падения, б – ускоренные тренды, в – замедленные тренды).




Рис.7.1


Часто реальные зависимости средних показателей y(t_i) аппроксимируются теоретическими функциями. Наиболее распространенными являются:

• линейная функция y(t)=a₀+a₁t;
  
• парабола y^(t)= a₀+a₁t+a₂t²;
  
• экспонента y^=a₀e^t.
  

При линейном тренде, как и в модели линейной регрессии, аппроксимирующая прямая строится с использованием метода наименьших квадратов (МНК), обеспечивающего наименьшую ошибку приближения. Для i-го значения ряда ошибка аппроксимации равна

e_i=y_i^*-y_i=a₀+a₁t_i-y_i.

В
ведем функцию суммы квадратов ошибок Е=е_i², тогда средний квадрат ошибки минимален при

Д
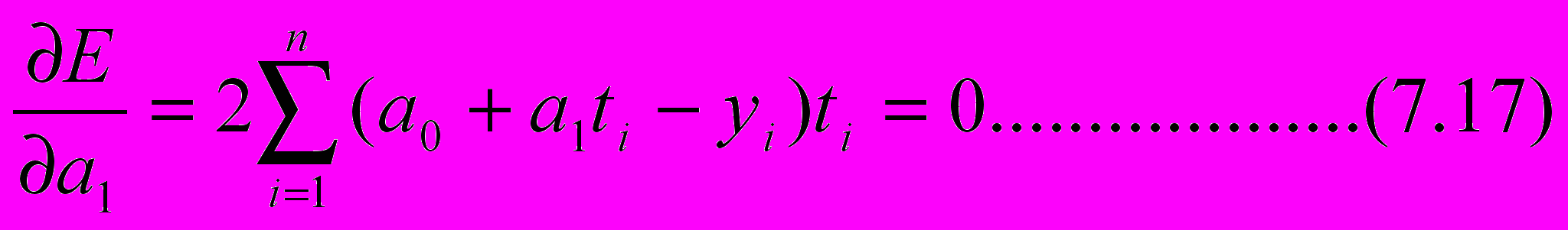
ля упрощения формул отсчет времени удобно выбрать относительно середины РД, так чтобы


Тогда коэффициенты тренда из (7.16), (7.17) равны

П

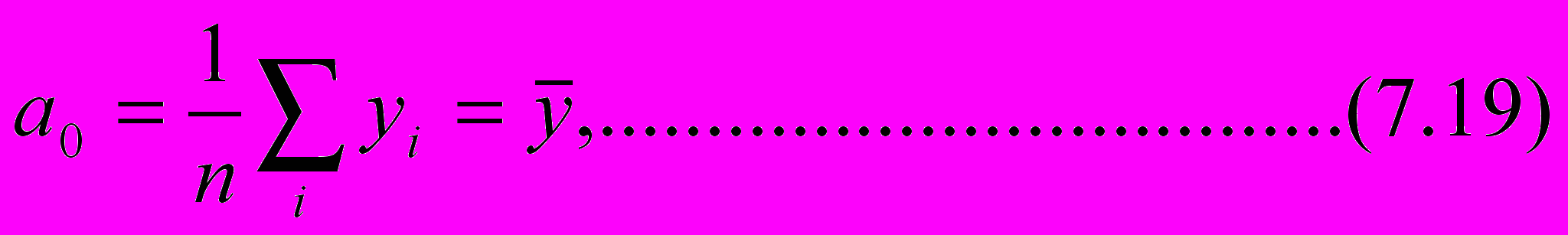
ример 7.11. За три первых месяца года цены на сахар в среднем составляли 1,05 грн., 1,08 грн., 1, 14 грн. за килограмм. Построить линейный тренд динамики цен.

П
ринимая согласно (7.18) {t_i}={-1,0,1} из (7.19), (7.20) получаем

Таким образом, уравнение тренда y^*=1,09+0,045t, а ошибки аппроксимации в трех точках равны:

t₁= -1, e₁=y^*(-1) – y₁=1,09-0,045-1,05= - 0,005;

t₂= 0, e₂= y^*(0) – y₂ =1,09 – 1,08 =0,01;

t₃= 1, e₃= y^*(1) – y₁=1,135 – 1,14= - 0,005,

при этом суммарная ошибка е_i=0. Коэффициент а₁=0,045 является производной тренда и характеризует сглаженный трендом рост цен на сахар в месяц (4,5 коп). Коэффициент а₀=1,09 имеет смысл среднего арифметического ряда динамики (средняя цена сахара за 3 месяца).

Уравнение тренда можно использовать для прогноза на ближайшее будущее, при условии устойчивости состояния рынка. Например, прогнозируемая цена на сахар в 4-й месяц будет оцениваться как y₄^*=1,09+0,045t₄=1,18 грн./кг.


Задачи

1. Число введенных в эксплуатацию аппаратов сотовой связи фирмы в 1995-1999гг составляло

Годы	1995	1996	1997	1998	1999
Число апп.	5600	8200	10400	11900	11200

Определить цепные и базисные абсолютные приросты и темпы прироста, а также средний абсолютный прирост.

2. Используя взаимосвязь между характеристиками динамики, заполните пустые клетки таблицы

Годы	Производ- ство ТВ, тыс.шт.	Цепные характеристики динамики
		Абс. при- рост, тыс. шт.	Темпы роста	Темпы прироста, %	Абс. зн.1% прироста, тыс. шт.
1993	400	-	-	-	-
1994		30
1995				5
1996			1,7
1997
1998				6	4,50

3. Темпы прироста курса ценных бумаг (в %) двух эмитентов за 4 года представлены в таблице

Эмитент	1994	1995	1996	1997
А	3,3	2,7	4,6	4,9
В	1,6	1,8	2,5	1,7

Определить темпы роста и темпы прироста за 1994 – 1997 гг., а также среднегодовой темп роста за данный период.


4. Продажа населению города стройматериалов за три года составляла

Товары	1996	1997	1998
Вагонка, м2	50	65	88
Цемент, тыс. т.	44	98	126
Плитка керам., м2	20	45	70

По каждому товару вычислить цепные и базисные темпы роста и прироста, абсолютные приросты, абсолютные ускорения роста и коэффициенты ускорения.

5. В течение 4-х лет годовые выпуски автомобилей концерна равнялись 2067, 2280, 2725, 2970 тыс. автомобилей в год. Построить линейный тренд ряда динамики и определить прогноз на 5-й год.
^

Контрольные вопросы

1. Как определяются моментные и интервальные ряды динамики?
   
2. Перечислите основные характеристики рядов динамики.
   
3. Как определяется среднее значение уровней для интервального и моментного ряда?
   
4. Что такое цепной и базисный:
   

• абсолютный прирост;
  
• темп роста;
  
• темп прироста?
  

5. Как определить средний абсолютный рост и средний темп роста?
   
6. Какими характеристиками определяются процессы ускорения и замедления динамики показателей?
   
7. Для каких целей используется коэффициент опережения?
   
8. Дайте определение абсолютного значения одного процента прироста. Что он характеризует?
   
9. Какие типы трендов Вам известны? Приведите примеры равномерных, ускоренных, замедленных трендов.
   
10. Как построить модель линейного тренда? Какие ее свойства? Как использовать эту модель для прогнозирования экономической тенденции?